Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil
Abstract
1. Introduction
2. Materials and Methods
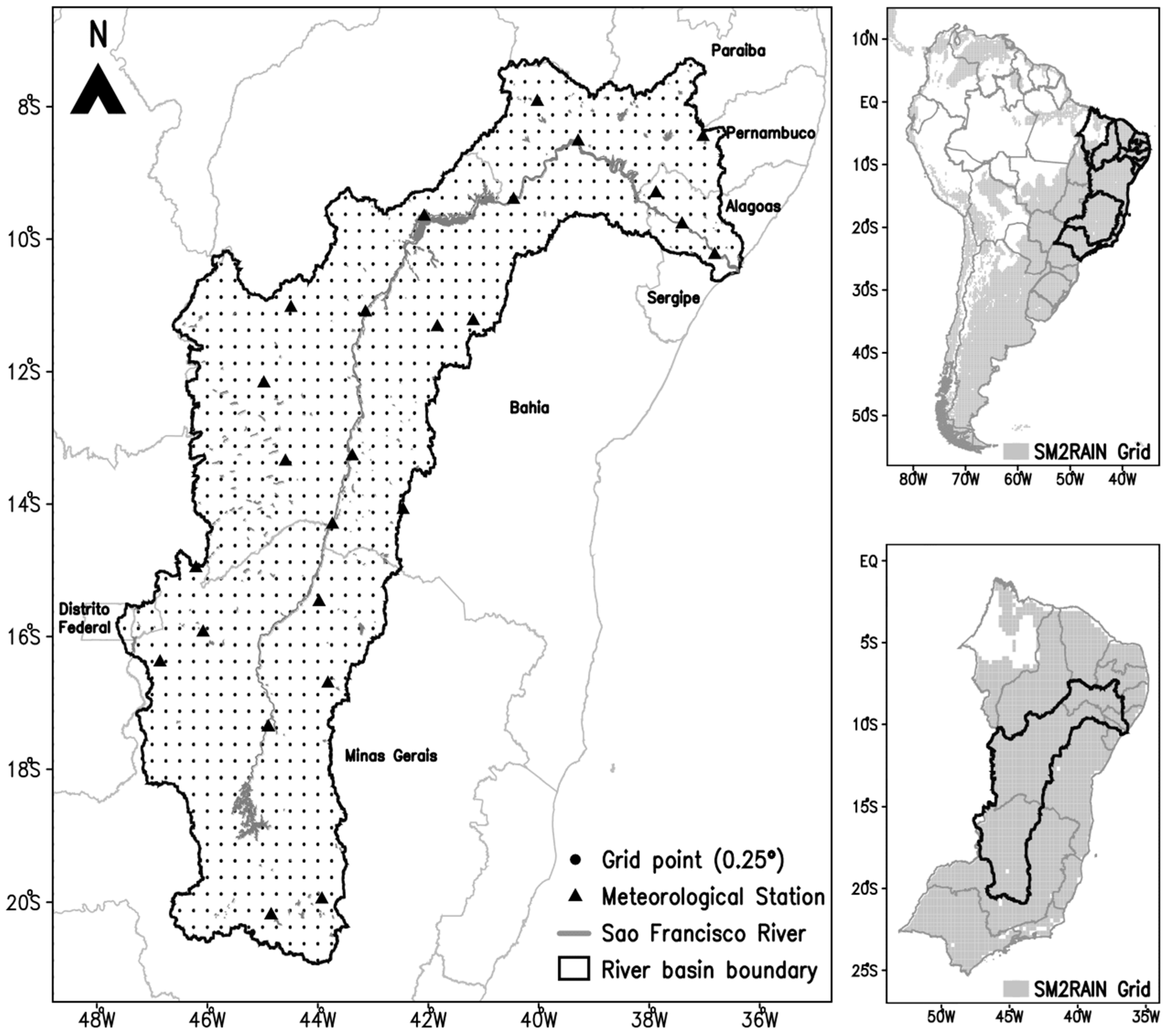
2.1. Study Area
2.2. Rainfall Dataset
2.3. Rainfall Metrics
2.4. Statistical Measures
3. Results
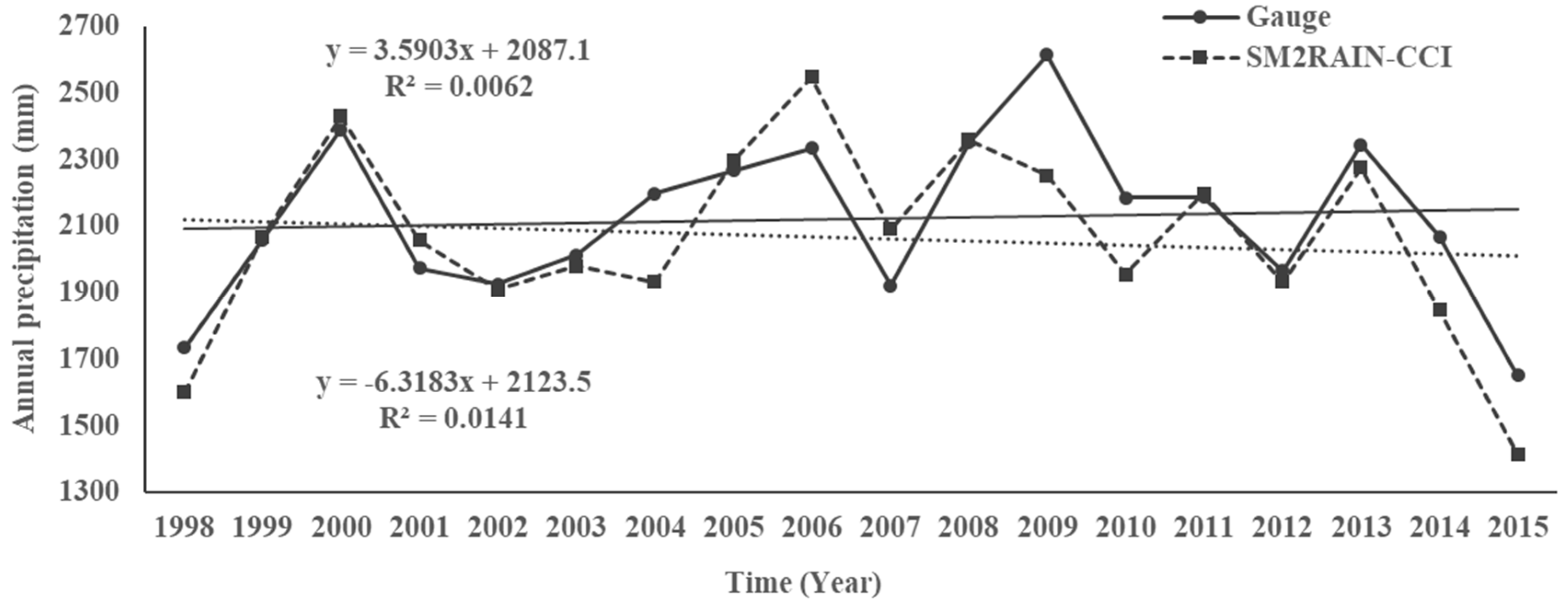
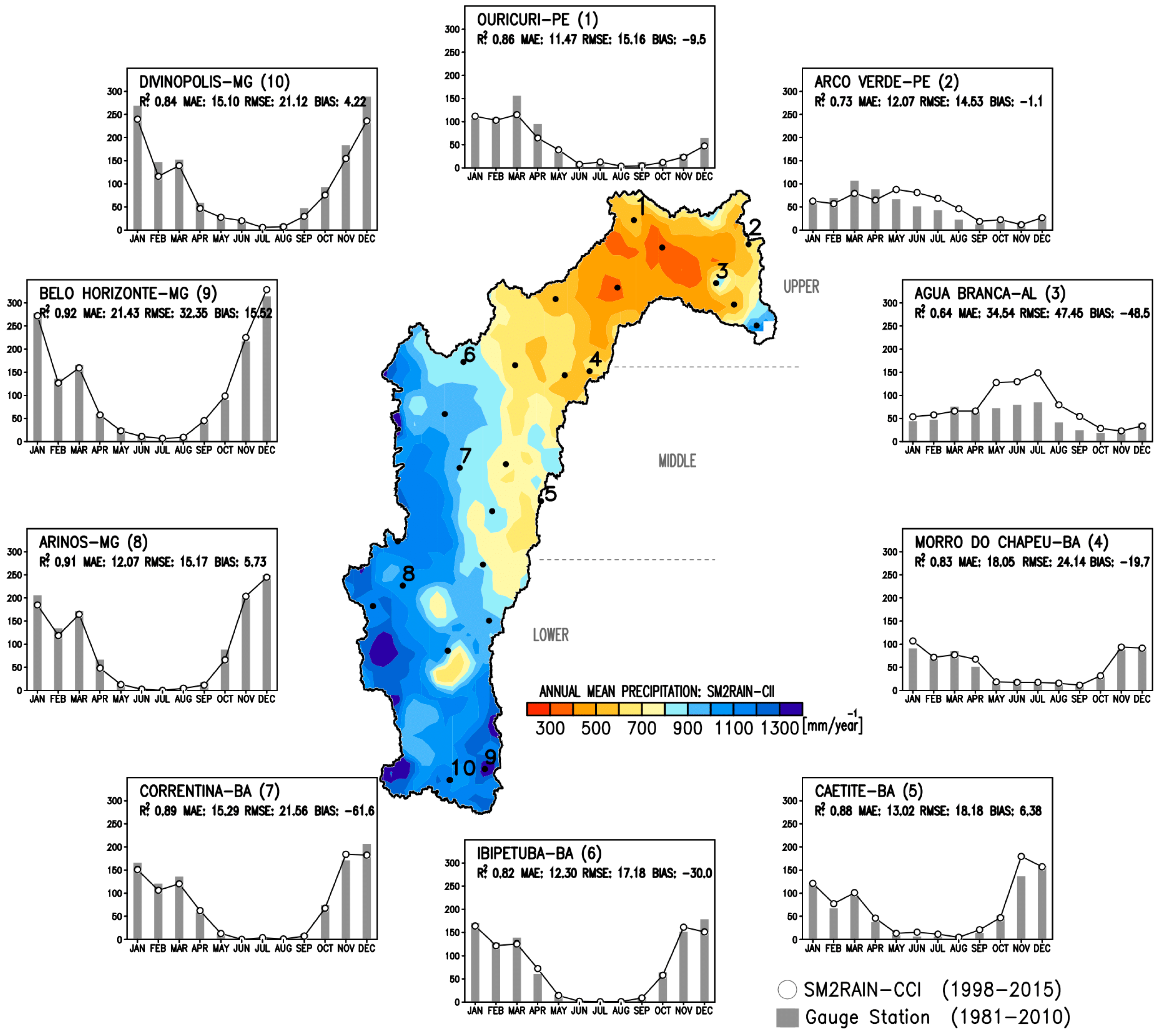
3.1. Validation of SM2RAIN-CCI with Ground Stations Rainfall Data
3.2. Comparison between Satellite Products SM2RAIN-CCI, CHIRPS, and CMORPH
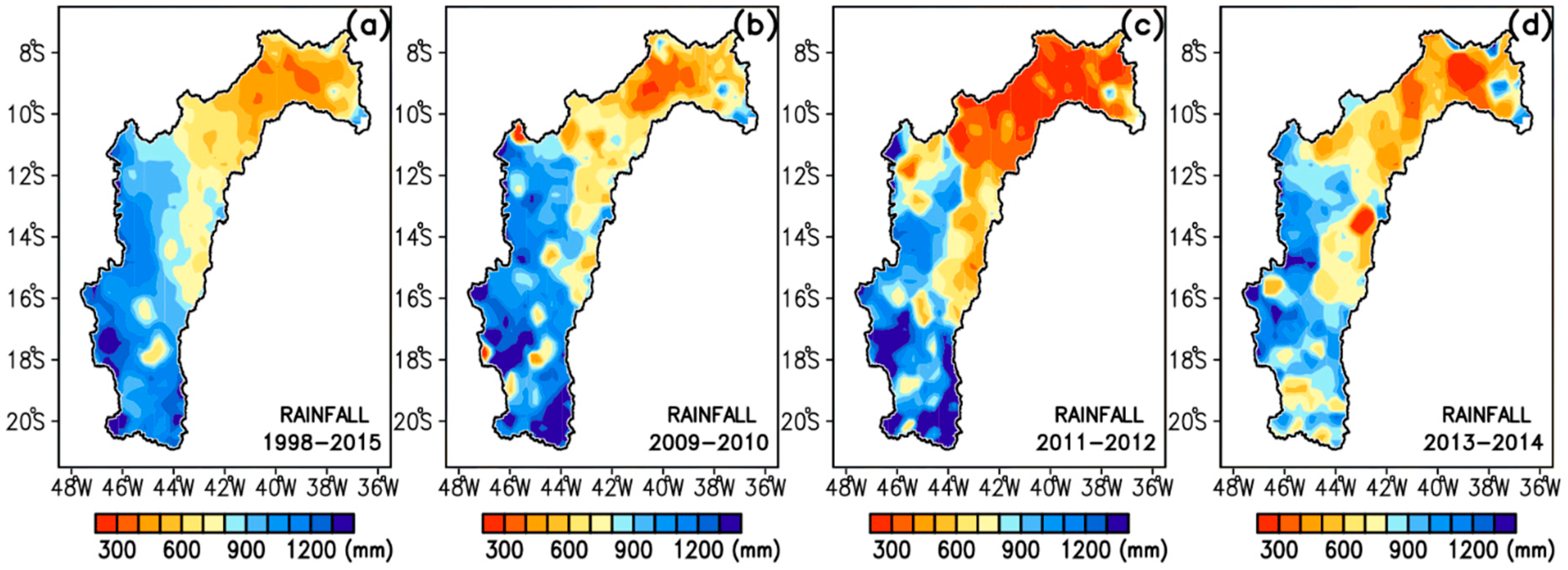
3.3. Analysis of Rainfall Metrics for 1998–2015, 2009–2010, 2011–2012, 2013–2014 Periods
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Garreaud, R.D.; Vuille, M.; Compagnucci, R.; Marengo, J. Present-day South American climate. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 180–195. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U.; Schroder, M.; Stender, P. Global gridded precipitation over land: A description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data 2014, 6, 49–60. [Google Scholar] [CrossRef]
- Levy, M.C.; Cohn, A.; Lopes, A.V.; Thompson, S.E. Addressing rainfall data selection uncertainty using connections between rainfall and streamflow. Sci. Rep. 2017, 7, 219. [Google Scholar] [CrossRef]
- Ferguson, D.B.; Masayesva, A.; Meadow, A.M.; Crimmins, M.A. Rain Gauges to Range Conditions: Collaborative Development of a Drought Information System to Support Local Decision-Making. Weather Clim. Soc. 2016, 8, 345–359. [Google Scholar] [CrossRef]
- Borga, M.; Stoffel, M.; Marchi, L.; Marra, F.; Jakob, M. Hydrogeomorphic response to extreme rainfall in headwater systems: Flash floods and debris flows. J. Hydrol. 2014, 518, 194–205. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Nogueira, S.C.; Moreira, M.; Lordelo Volpato, M. Evaluating Precipitation Estimates from Eta, TRMM and CHRIPS Data in the South-Southeast Region of Minas Gerais State—Brazil. Remote Sens. 2018, 10, 313. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Puca, S.; Rinollo, A.; Wagner, W. Integration of Satellite Soil Moisture and Rainfall Observations over the Italian Territory. J. Hydrometeorol. 2015, 16, 1341–1355. [Google Scholar] [CrossRef]
- Crow, W.T.; Huffman, G.J.; Bindlish, R.; Jackson, T.J. Improving Satellite-Based Rainfall Accumulation Estimates Using Spaceborne Surface Soil Moisture Retrievals. J. Hydrometeorol. 2009, 10, 199–212. [Google Scholar] [CrossRef]
- Pellarin, T.; Louvet, S.; Gruhier, C.; Quantin, G.; Legout, C. A simple and effective method for correcting soil moisture and precipitation estimates using AMSR-E measurements. Remote Sens. Environ. 2013, 136, 28–36. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Gabellani, S.; Puca, S.; Wagner, W. Rainfall-runoff modelling by using SM2RAIN-derived and state-of-the-art satellite rainfall products over Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 163–173. [Google Scholar] [CrossRef]
- Satgé, F.; Ruelland, D.; Bonnet, M.-P.; Molina, J.; Pillco, R. Consistency of satellite-based precipitation products in space and over time compared with gauge observations and snow-hydrological modelling in the Lake Titicaca region. Hydrol. Earth Syst. Sci. 2019, 23, 595–619. [Google Scholar] [CrossRef]
- Bezerra, B.G.; Silva, L.L.; Santos e Silva, C.M.; de Carvalho, G.G. Changes of precipitation extremes indices in São Francisco River Basin, Brazil from 1947 to 2012. Theor. Appl. Climatol. 2019, 135, 565–576. [Google Scholar] [CrossRef]
- Sun, T.; Ferreira, V.; He, X.; Andam-Akorful, S. Water Availability of São Francisco River Basin Based on a Space-Borne Geodetic Sensor. Water 2016, 8, 213. [Google Scholar] [CrossRef]
- Creech, C.T.; Siqueira, R.B.; Selegean, J.P.; Miller, C. Anthropogenic impacts to the sediment budget of São Francisco River navigation channel using SWAT. Int. J. Agric. Biol. Eng. 2015, 8, 140–157. [Google Scholar]
- Ummenhofer, C.C.; Meehl, G.A. Extreme weather and climate events with ecological relevance: A review. Philos. Trans. R. Soc. B Biol. Sci. 2017, 372, 20160135. [Google Scholar] [CrossRef]
- De Jong, P.; Tanajura, C.A.S.; Sánchez, A.S.; Dargaville, R.; Kiperstok, A.; Torres, E.A. Hydroelectric production from Brazil’s São Francisco River could cease due to climate change and inter-annual variability. Sci. Total Environ. 2018, 634, 1540–1553. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Morais, B.S. Identification of precipitation zones within São Francisco River basin (Brazil) by global wavelet power spectra. Hydrol. Sci. J. 2013, 58, 789–796. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; da Silva, R.M.; de Araújo Passos, J.S. Integrated spatiotemporal trends using TRMM 3B42 data for the Upper São Francisco River basin, Brazil. Environ. Monit. Assess. 2018, 190, 175. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Ciabatta, L.; Moramarco, T.; Penna, D.; Zuecco, G.; Martínez-Fernández, J. Rainfall estimation from in situ soil moisture observations at several sites in Europe: An evaluation of the SM2RAIN algorithm. J. Hydrol. Hydromech. 2015, 63, 201–209. [Google Scholar] [CrossRef]
- Ciabatta, L.; Massari, C.; Brocca, L.; Gruber, A.; Reimer, C.; Hahn, S.; Paulik, C.; Dorigo, W.; Kidd, R.; Wagner, W. SM2RAIN-CCI: A new global long-term rainfall data set derived from ESA CCI soil moisture. Earth Syst. Sci. Data 2018, 10, 267–280. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfield, M.; Pedreros, D.; Verdin, J.; Rowland, J.; Romero, B.; Husak, G.; Michaelsen, J.; Verdin, A. A Quase-Global Precipitation Time Series for Drought Monitoring; US Geological Survey: Reston, VA, USA, 2014.
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Michaelsen, J. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Xie, P.; Joyce, R.; Wu, S.; Yoo, S.-H.; Yarosh, Y.; Sun, F.; Lin, R. Reprocessed, Bias-Corrected CMORPH Global High-Resolution Precipitation Estimates from 1998. J. Hydrometeorol. 2017, 18, 1617–1641. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado, W. Impacts of satellite-based precipitation datasets on rainfall–runoff modeling of the Western Amazon basin of Peru and Ecuador. J. Hydrol. 2015, 528, 599–612. [Google Scholar] [CrossRef]
- Cattani, E.; Merino, A.; Guijarro, J.; Levizzani, V. East Africa Rainfall Trends and Variability 1983–2015 Using Three Long-Term Satellite Products. Remote Sens. 2018, 10, 931. [Google Scholar] [CrossRef]
- Zeleňáková, M.; Purcz, P.; Blišťan, P.; Vranayová, Z.; Hlavatá, H.; Diaconu, D.; Portela, M. Trends in Precipitation and Temperatures in Eastern Slovakia (1962–2014). Water 2018, 10, 727. [Google Scholar] [CrossRef]
- Larbi, I.; Hountondji, F.; Annor, T.; Agyare, W.; Mwangi Gathenya, J.; Amuzu, J. Spatio-Temporal Trend Analysis of Rainfall and Temperature Extremes in the Vea Catchment, Ghana. Climate 2018, 6, 87. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.; Barbosa, H.; Rossato Spatafora, L. Assessment of SM2RAIN-Derived and State-of-the-Art Satellite Rainfall Products over Northeastern Brazil. Remote Sens. 2018, 10, 1093. [Google Scholar] [CrossRef]
- Polzin, D.; Hastenrath, S. Climate of Brazil’s nordeste and tropical atlantic sector: Preferred time scales of variability. Rev. Bras. Meteorol. 2014, 29, 153–160. [Google Scholar] [CrossRef]
- Paredes Trejo, F.; Brito-Castillo, L.; Barbosa Alves, H.; Guevara, E. Main features of large-scale oceanic-atmospheric circulation related to strongest droughts during rainy season in Brazilian São Francisco River Basin. Int. J. Climatol. 2016, 36, 4102–4117. [Google Scholar] [CrossRef]
- Gomes, H.B.; Ambrizzi, T.; Herdies, D.L.; Hodges, K.; Pontes da Silva, B.F. Easterly Wave Disturbances over Northeast Brazil: An Observational Analysis. Adv. Meteorol. 2015, 2015, 176238. [Google Scholar] [CrossRef]
- Valverde, M.C.; Marengo, J.A. Extreme rainfall índices in the hydrographic basins of Brazil. Open J. Mod. Hydrol. 2014, 4, 10–26. [Google Scholar] [CrossRef]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—Past, present, and future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
- Getirana, A. Extreme water deficit in Brazil detected from space. J. Hydrometeorol. 2016, 17, 591–599. [Google Scholar] [CrossRef]
- Pereira, M.P.S.; Justino, F.; Malhado, A.C.M.; Barbosa, H.; Marengo, J. The influence of oceanic basins on drought and ecosystem dynamics in Northeast Brazil. Environ. Res. Lett. 2014, 9, 124013. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.J.; Barbosa, H.A.; Lakshmi Kumar, T.V. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A.; Camargo, H.; Riveros, M.P.; Pabló, A.D. Two Contrasting Severe Seasonal Extremes in Tropical South America in 2012: Flood in Amazonia and Drought in Northeast Brazil. J. Clim. 2013, 26, 9137–9154. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Lakshmi Kumar, T.V. Influence of rainfall variability on the vegetation dynamics over Northeastern Brazil. J. Arid Environ. 2016, 124, 377–387. [Google Scholar] [CrossRef]

| Full Name | Acronym | Data Source | Temporal Coverage | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|---|
| Soil Moisture to Rain from ESA Climate Change Initiative | SM2RAIN-CCI | S | 1998–2015 | Daily | 0.25° × 0.25° |
| Climate Hazard Group InfraRed Precipitation with Station | CHIRPS | S, R, G | 1981–present | Daily | 0.05° × 0.05° |
| CPC MORPHing technique bias corrected | CMORPH-CRT | S, G | 1998–present | 30 min | 0.08° × 0.08° |
| Indices (Units) | Definition |
|---|---|
| PRCPTOT (mm) | Total daily precipitation with RR ≥1 mm |
| CDD (days) | Maximum number of consecutive dry days (RR <1 mm) |
| CWD (days) | Maximum number of consecutive wet days (RR ≥1 mm) |
| Season | Validation Station | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper | Middle | Lower | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| R2 | December–January–February | 0.74 | 0.89 | 0.59 | 0.59 | 0.61 | 0.72 | 0.80 | 0.76 | 0.32 | 0.83 |
| March–April–May | 0.82 | 0.82 | 0.64 | 0.74 | 0.81 | 0.64 | 0.73 | 0.85 | 0.86 | 0.66 | |
| June–July–August | 0.34 | 0.85 | 0.04 | 0.03 | 0.79 | 0.02 | 0.03 | 0.82 | 0.64 | 0.77 | |
| September–October–November | 0.86 | 0.60 | 0.77 | 0.73 | 0.76 | 0.86 | 0.79 | 0.87 | 0.35 | 0.78 | |
| MAE (mm) | December–January–February | 22.75 | 12.98 | 14.24 | 27.98 | 25.68 | 22.46 | 18.32 | 20.36 | 34.97 | 26.81 |
| March–April–May | 16.34 | 16.91 | 37.94 | 18.5 | 14.16 | 12.17 | 15.87 | 13.52 | 13.91 | 13.06 | |
| June–July–August | 2.98 | 10.81 | 64.67 | 10.58 | 0.881 | 1.955 | 7.1 | 1.24 | 4.01 | 1.95 | |
| September–October–November | 3.84 | 7.37 | 21.32 | 15.16 | 11.37 | 12.64 | 19.9 | 13.18 | 32.83 | 18.61 | |
| RMSE (mm) | December–January–February | 30.91 | 18.38 | 20.25 | 39.23 | 37.09 | 27.23 | 25.35 | 26.76 | 60.31 | 36.64 |
| March–April–May | 20.52 | 22.14 | 52.42 | 25.53 | 18.03 | 18.13 | 20.91 | 15.81 | 18.89 | 19.83 | |
| June–July–August | 4.61 | 7.43 | 84.18 | 12.15 | 1.646 | 5.85 | 11.47 | 1.95 | 5.86 | 3.23 | |
| September–October–November | 4.63 | 10.17 | 32.97 | 19.67 | 15.97 | 17.53 | 28.53 | 16.16 | 44.36 | 24.81 | |
| BIAS (%) | December–January–February | −11.9 | 2.07 | −12.6 | −38.3 | 11.99 | 2.90 | −10.2 | 3.02 | 12.28 | 3.64 |
| March–April–May | 4.03 | 7.36 | −43.0 | −22.7 | −1.42 | 2.51 | −14.1 | 9.02 | 15.62 | 8.09 | |
| June–July–August | −27.9 | −6.58 | −70.2 | 15.61 | 13.66 | −128 | −200 | 4.60 | 10.58 | 2.13 | |
| September–October–November | −2.32 | −7.42 | −68.4 | −33.5 | 1.32 | 2.33 | −22.3 | 6.28 | 23.62 | 3.02 | |
| PRCPTOT (1998–2015) | Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upper | Middle | Lower | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Trend nature | − | − | + | − | − | − | − | − | + | − |
| Trend significant | No | Yes | Yes | No | No | No | No | No | Yes | No |
| Sen’s slope | 17.3 | −30.3 | −25.4 | 22.2 | −21.4 | −40.3 | −23.4 | −9.86 | −84.2 | 25.3 |
| Available years | 10 | 15 | 13 | 12 | 12 | 16 | 15 | 16 | 8 | 11 |
| Average (mm) | 574 | 703 | 602 | 664 | 836 | 877 | 959 | 1100 | 1458 | 1106 |
| SD (mm) | 154 | 215 | 149 | 164 | 209 | 207 | 229 | 206 | 319 | 336 |
| CWD (1998–2015) | Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upper | Middle | Lower | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Trend nature | − | NA | − | − | + | − | + | + | + | + |
| Trend significant | No | No | No | No | No | No | No | No | No | No |
| Sen’s slope | −0.12 | −0.23 | −0.27 | −0.25 | 0.00 | −0.63 | −0.08 | 0.00 | 0.15 | 0.07 |
| Available years | 13 | 7 | 15 | 16 | 15 | 16 | 15 | 16 | 13 | 13 |
| Average (days) | 3 | 5 | 4 | 5 | 6 | 6 | 8 | 12 | 15 | 12 |
| SD (days) | 1 | 3 | 2 | 2 | 3 | 3 | 4 | 4 | 6 | 4 |
| CDD (1998–2015) | Station | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Upper | Middle | Lower | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Trend nature | + | NA | − | + | − | + | − | + | + | + |
| Trend significant | Yes | No | No | No | No | No | No | No | Yes | No |
| Sen’s slope | 2.23 | −2.80 | −3.81 | 0.50 | −2.08 | 0.81 | 0.16 | 1.50 | 8.00 | 3.40 |
| Available years | 14 | 8 | 15 | 16 | 15 | 16 | 15 | 16 | 14 | 12 |
| Average (days) | 151 | 117 | 126 | 121 | 112 | 115 | 88 | 92 | 134 | 89 |
| SD (days) | 54 | 61 | 49 | 48 | 41 | 50 | 44 | 47 | 67 | 44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souto, J.; Beltrão, N.; Teodoro, A. Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil. Geosciences 2019, 9, 144. https://doi.org/10.3390/geosciences9030144
Souto J, Beltrão N, Teodoro A. Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil. Geosciences. 2019; 9(3):144. https://doi.org/10.3390/geosciences9030144
Chicago/Turabian StyleSouto, Jefferson, Norma Beltrão, and Ana Teodoro. 2019. "Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil" Geosciences 9, no. 3: 144. https://doi.org/10.3390/geosciences9030144
APA StyleSouto, J., Beltrão, N., & Teodoro, A. (2019). Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil. Geosciences, 9(3), 144. https://doi.org/10.3390/geosciences9030144






