Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data
Abstract
1. Introduction
2. Study Area, Materials, and Methods
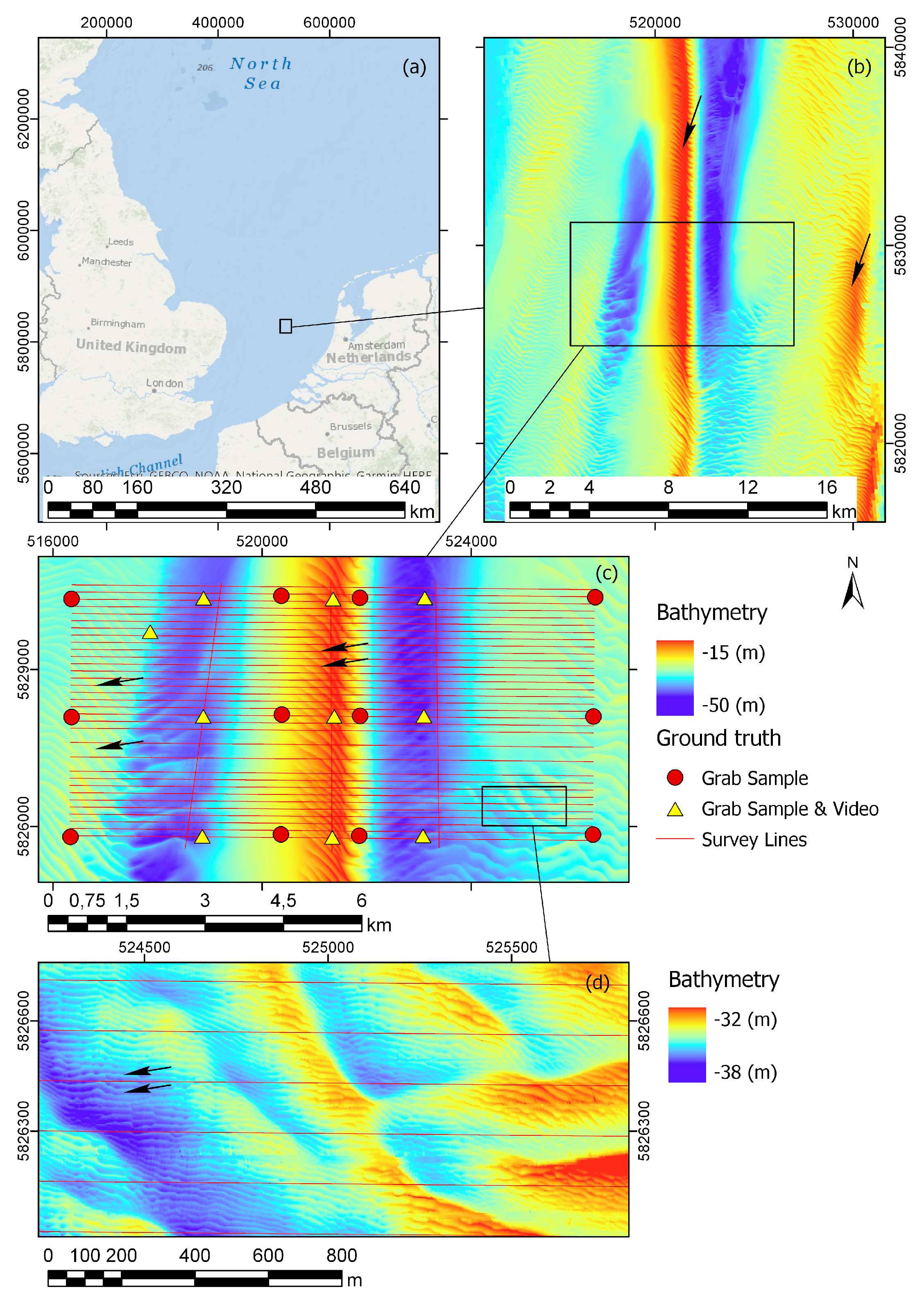
2.1. Study Area
2.2. Multibeam Echosounder Data
2.2.1. Multibeam Echosounder Settings
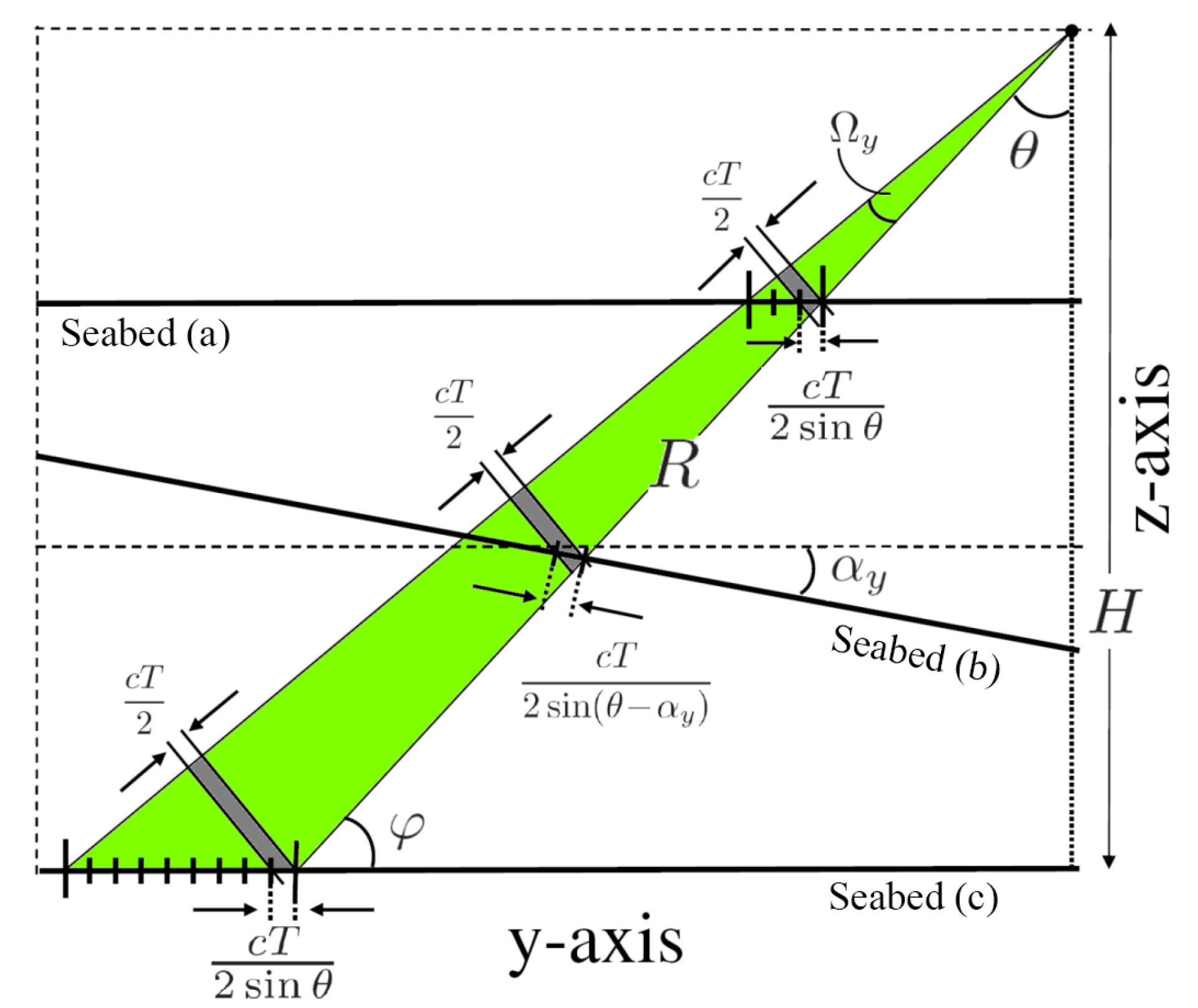
2.2.2. Backscatter Corrections for Seafloor Slopes
2.2.3. Bayesian Classification Method
2.2.4. Two Levels of Data Averaging
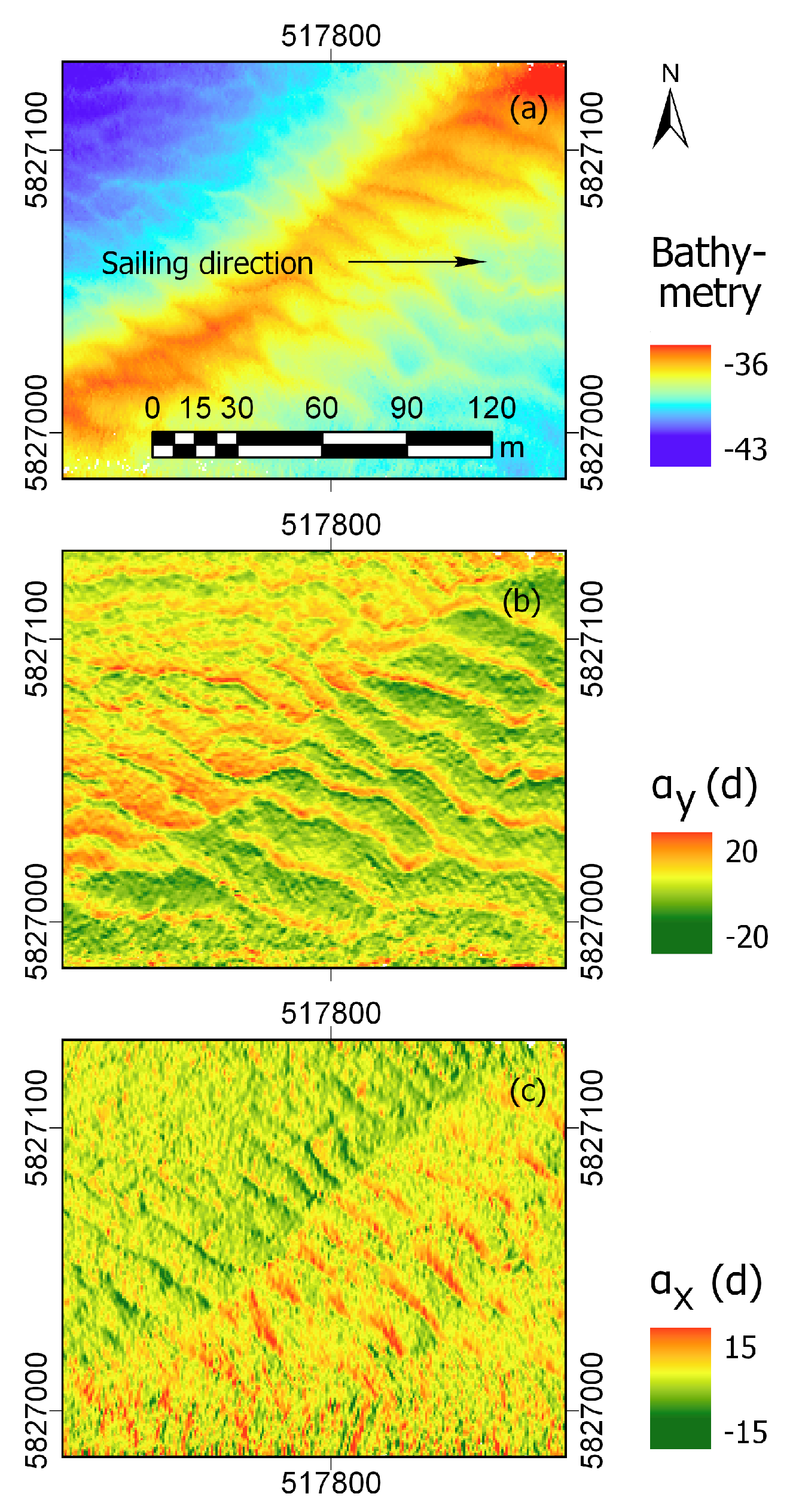
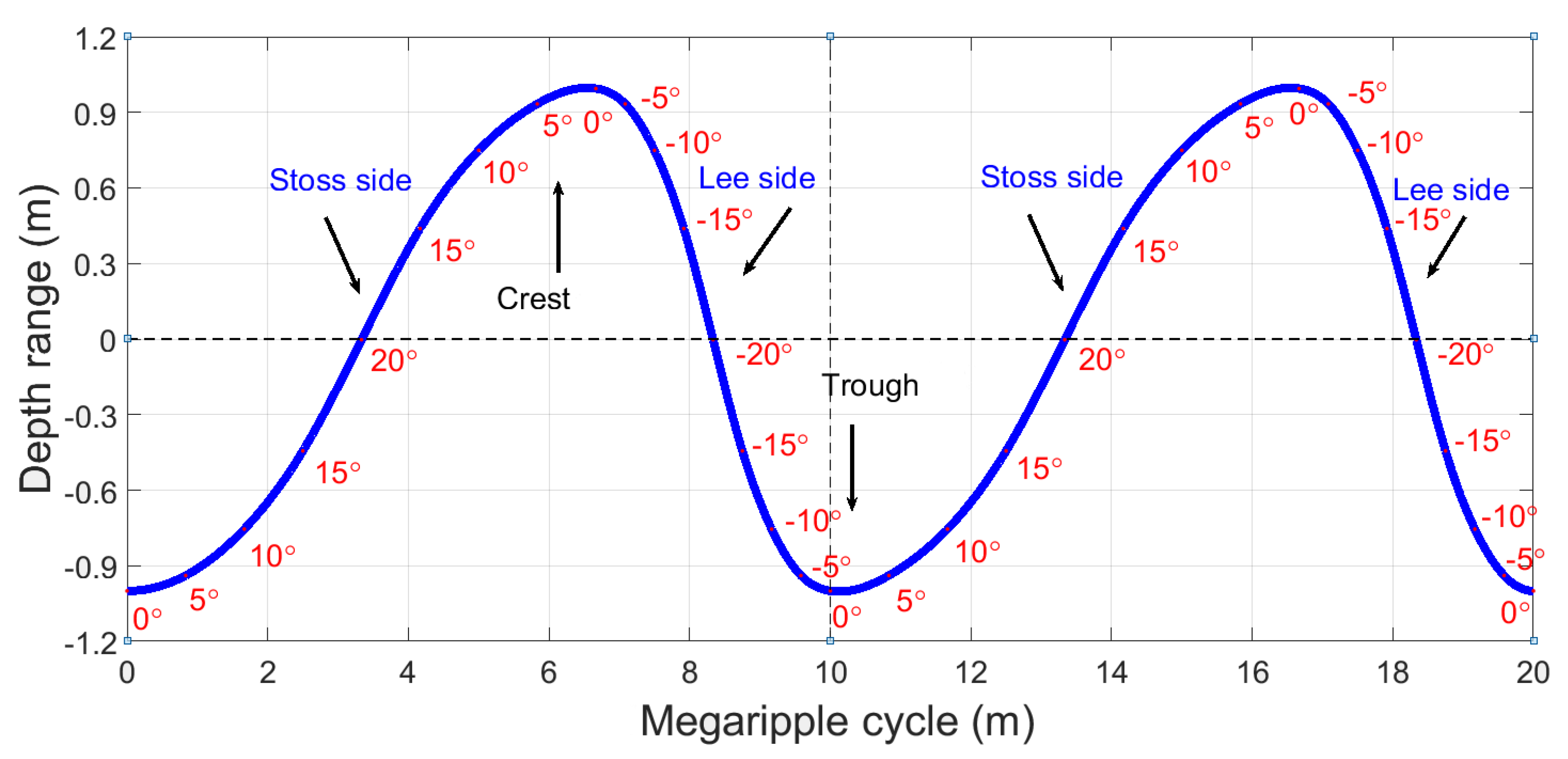
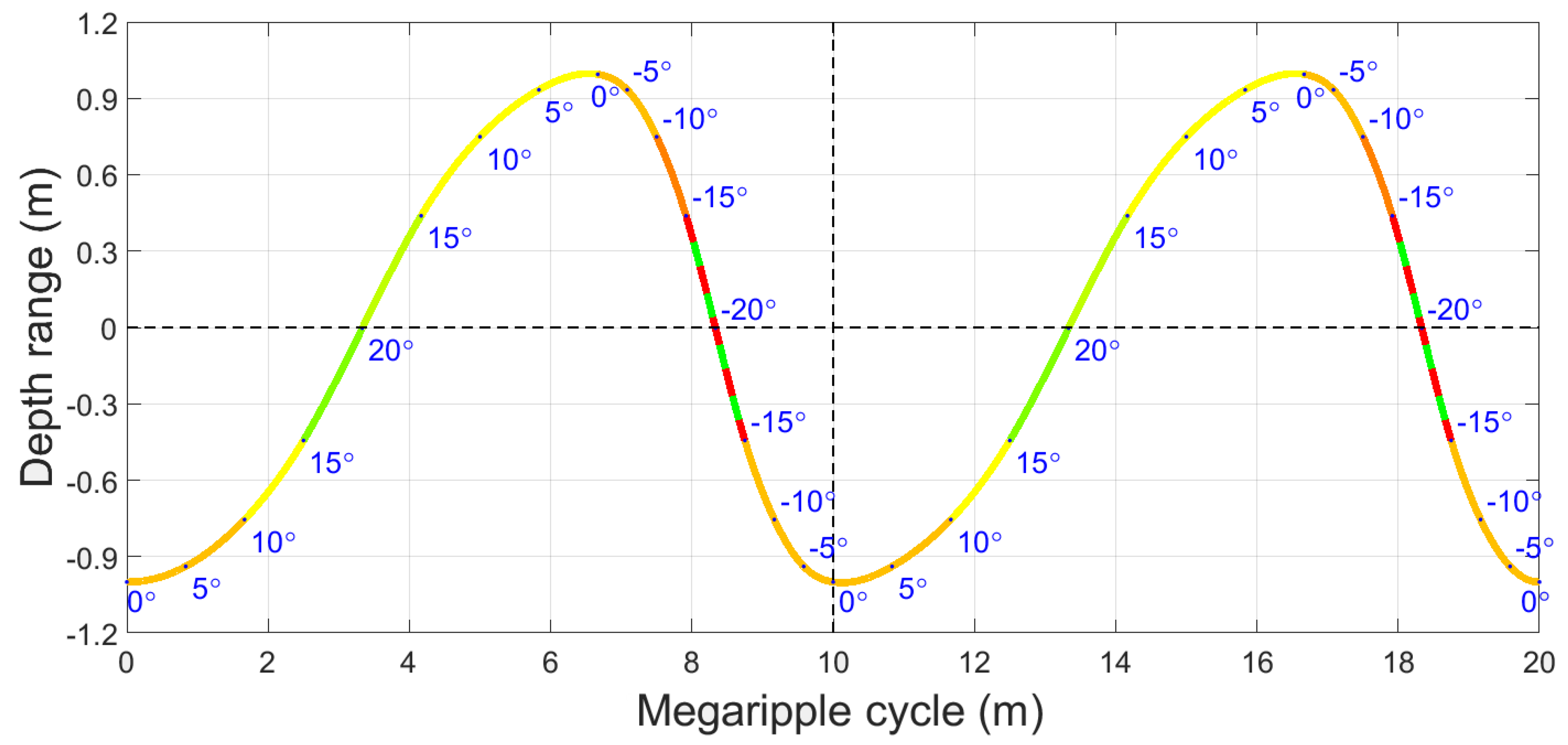
2.2.5. Megaripple Partitioning
2.3. Video Data
2.4. Grab Sample Data
3. Results and Discussion
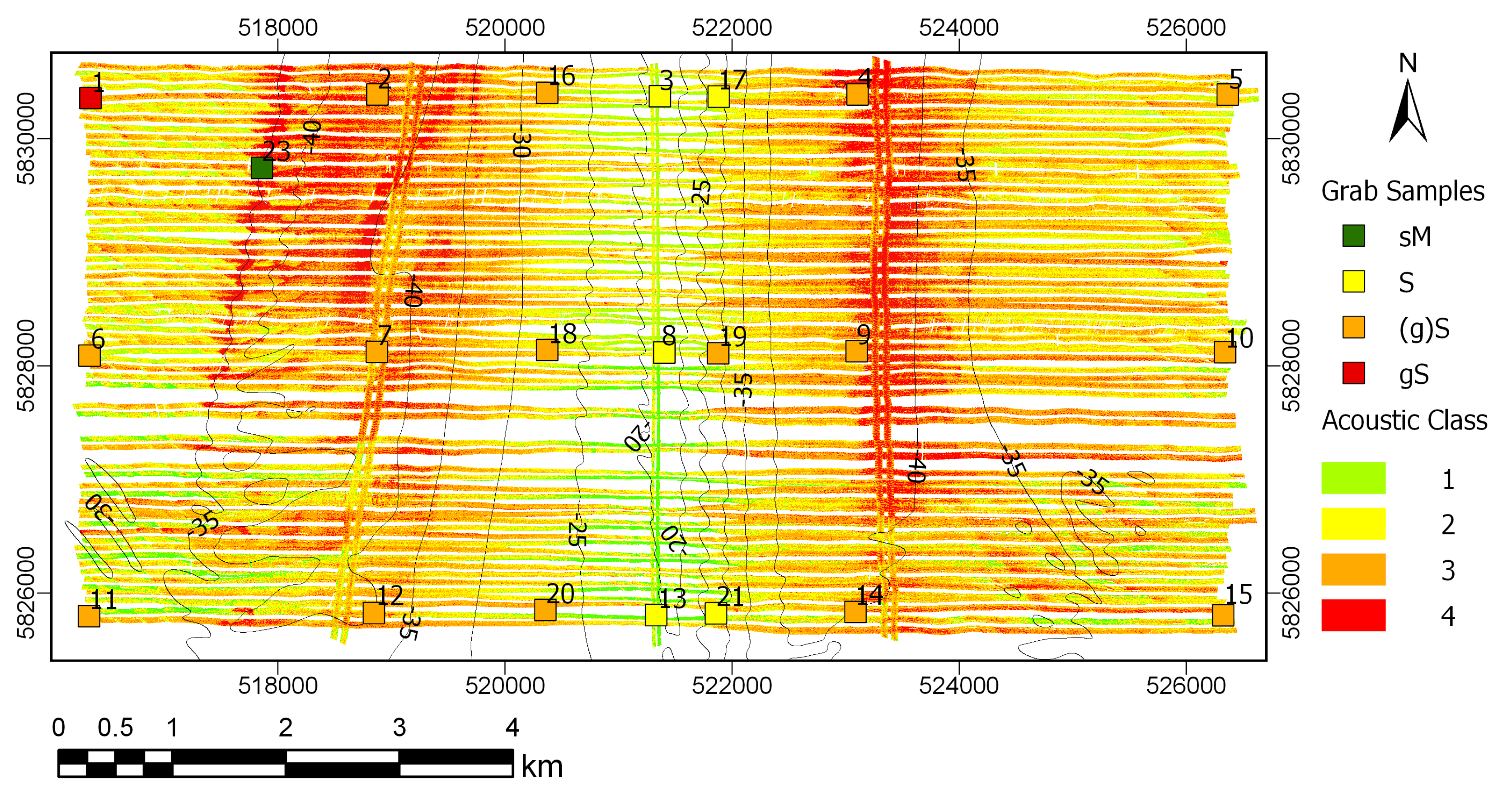
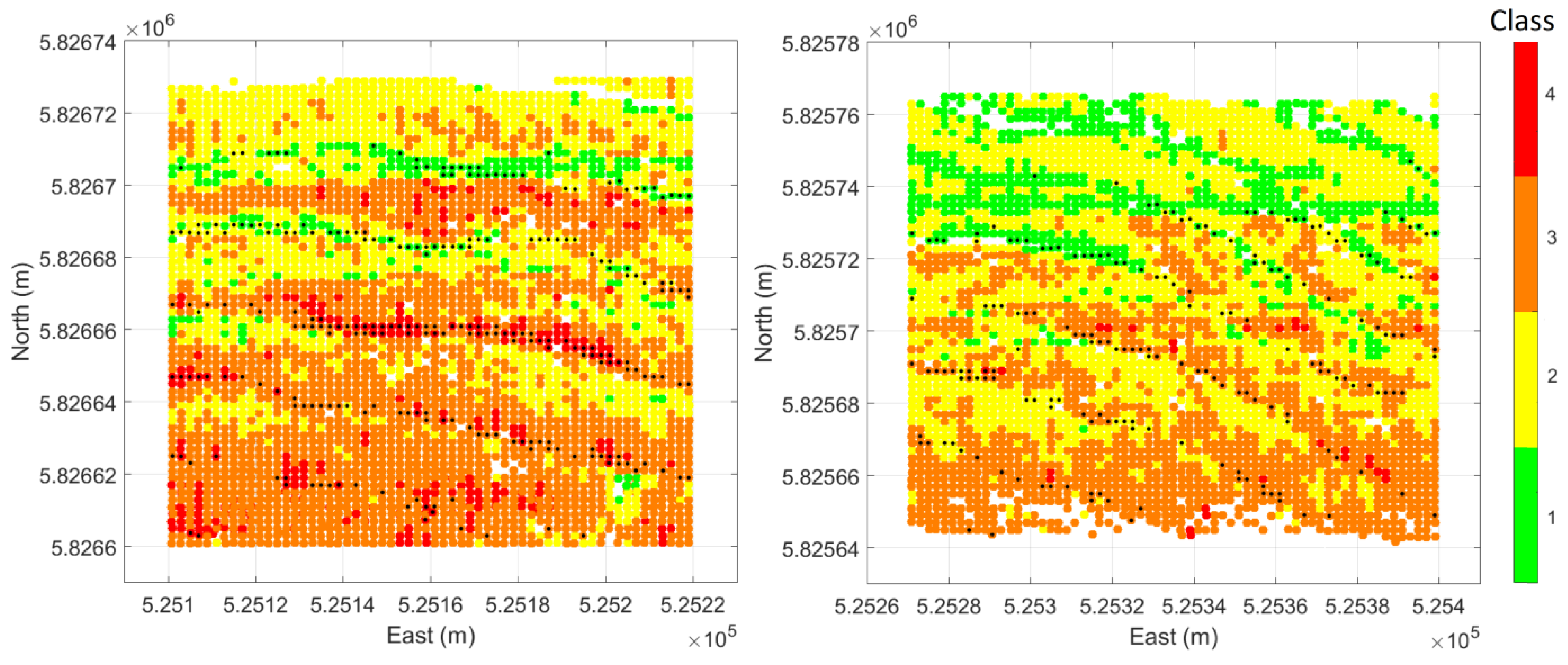
3.1. Acoustic Classification Results
3.2. Ground Truth Data
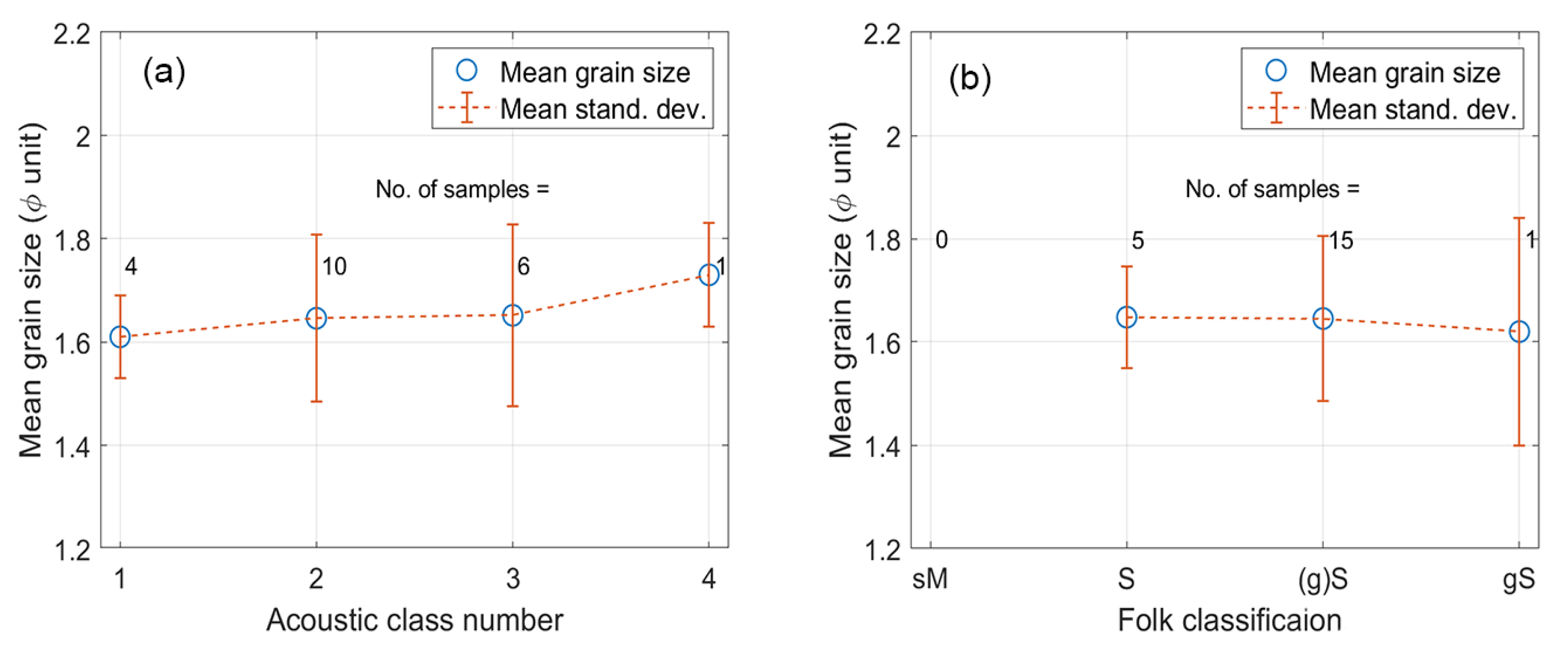
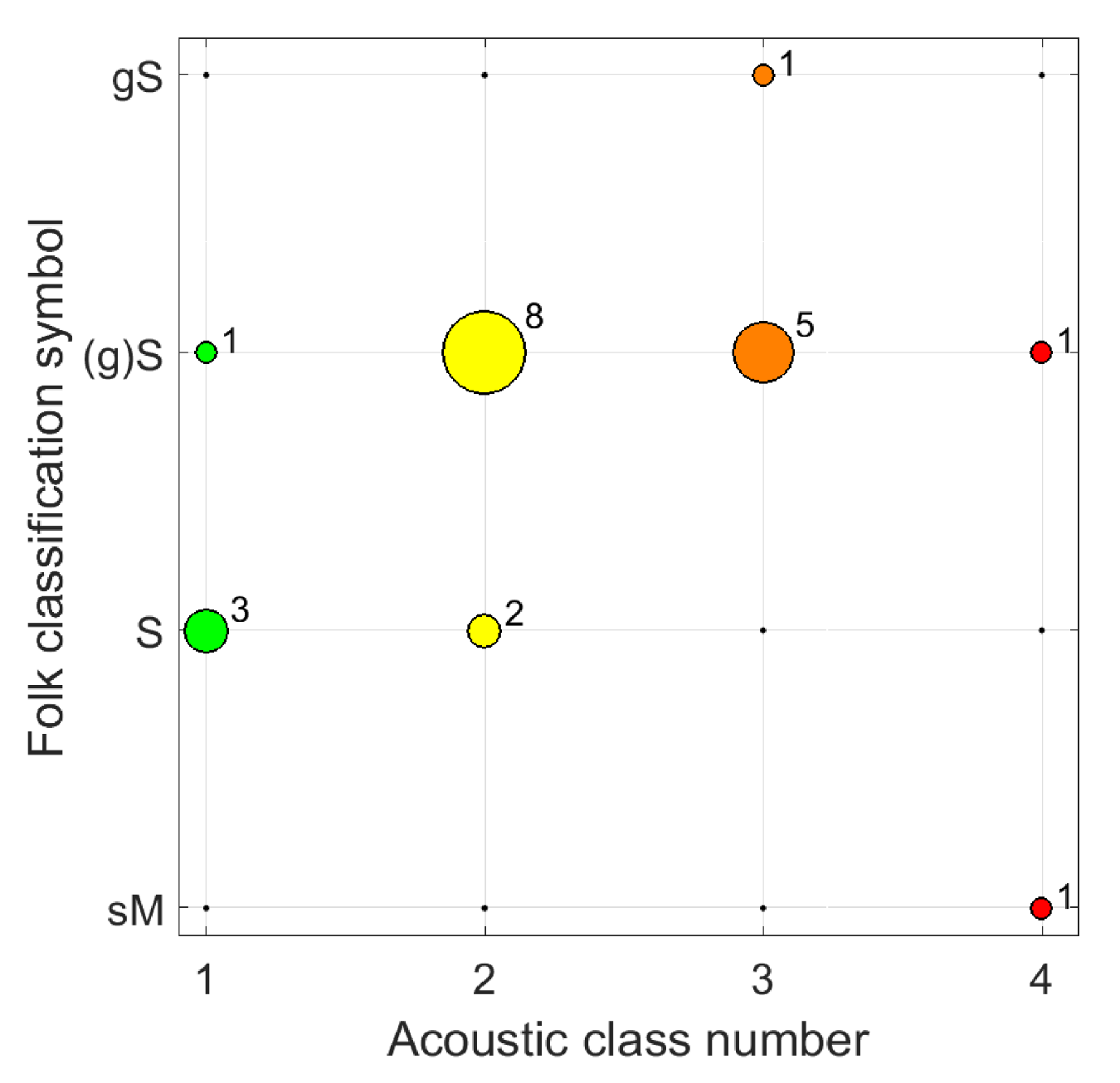
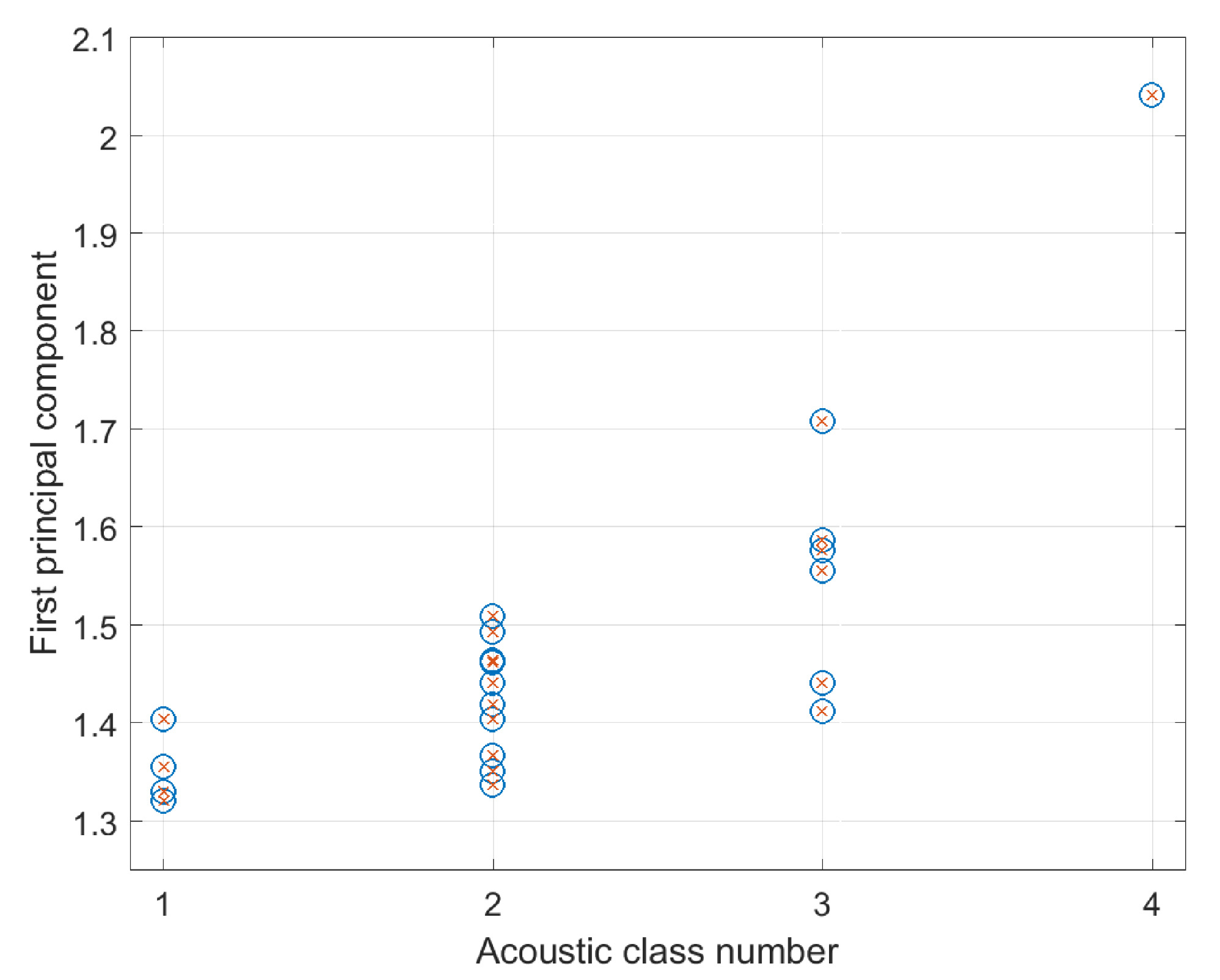
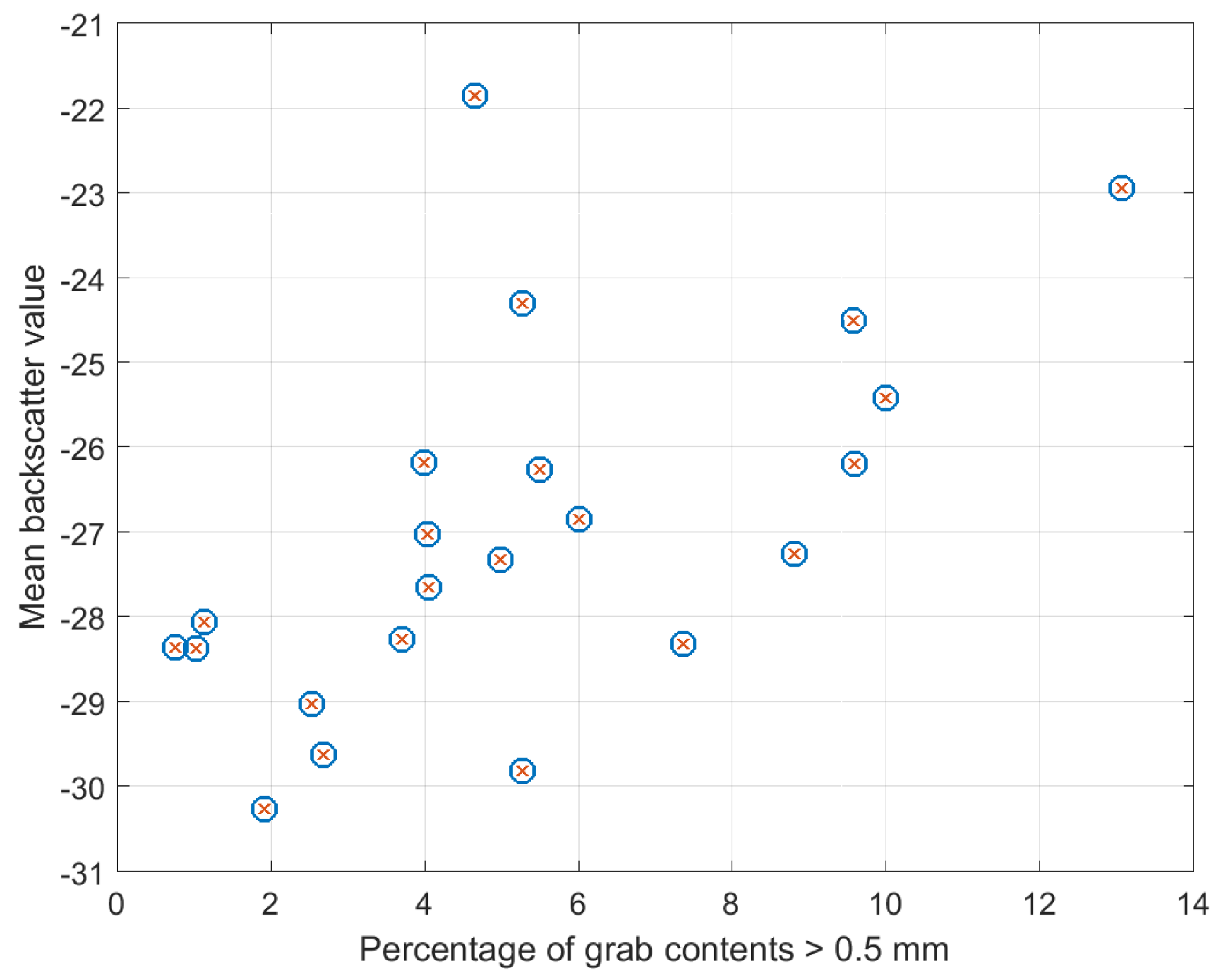
3.3. Full Spectrum of Grain Size Distribution for Classification
3.4. Geo-Acoustic Versus Spatial Resolution
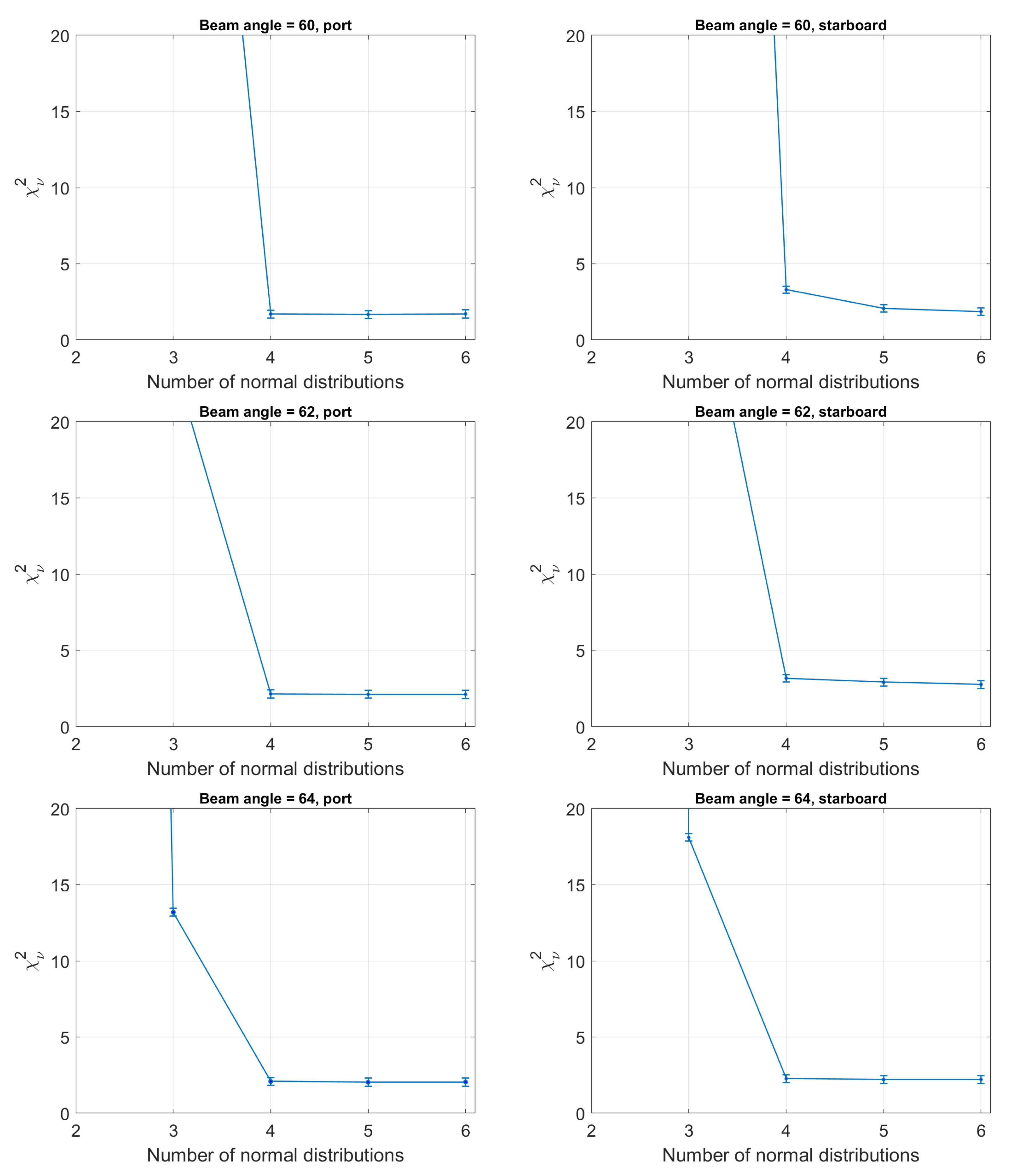
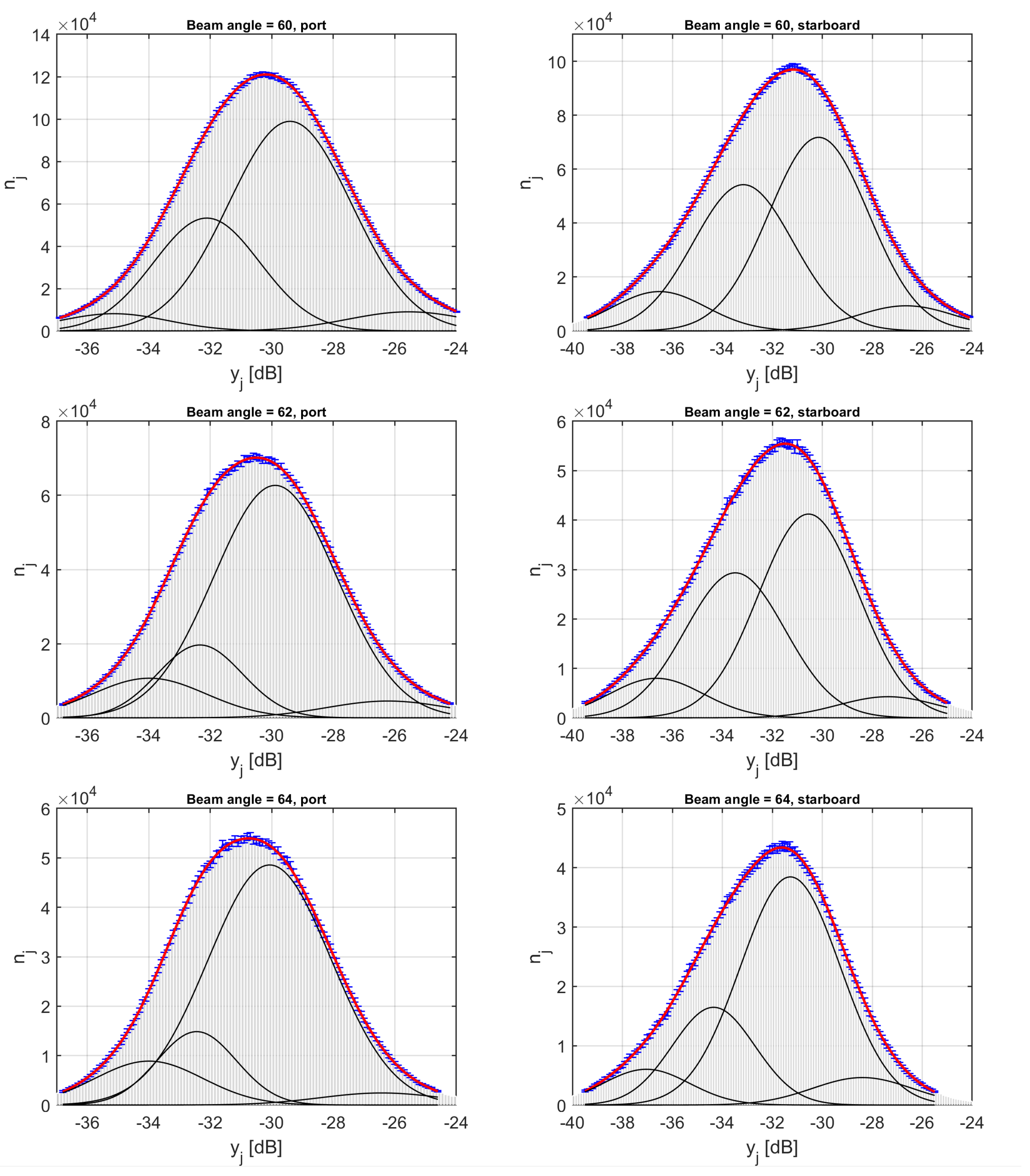
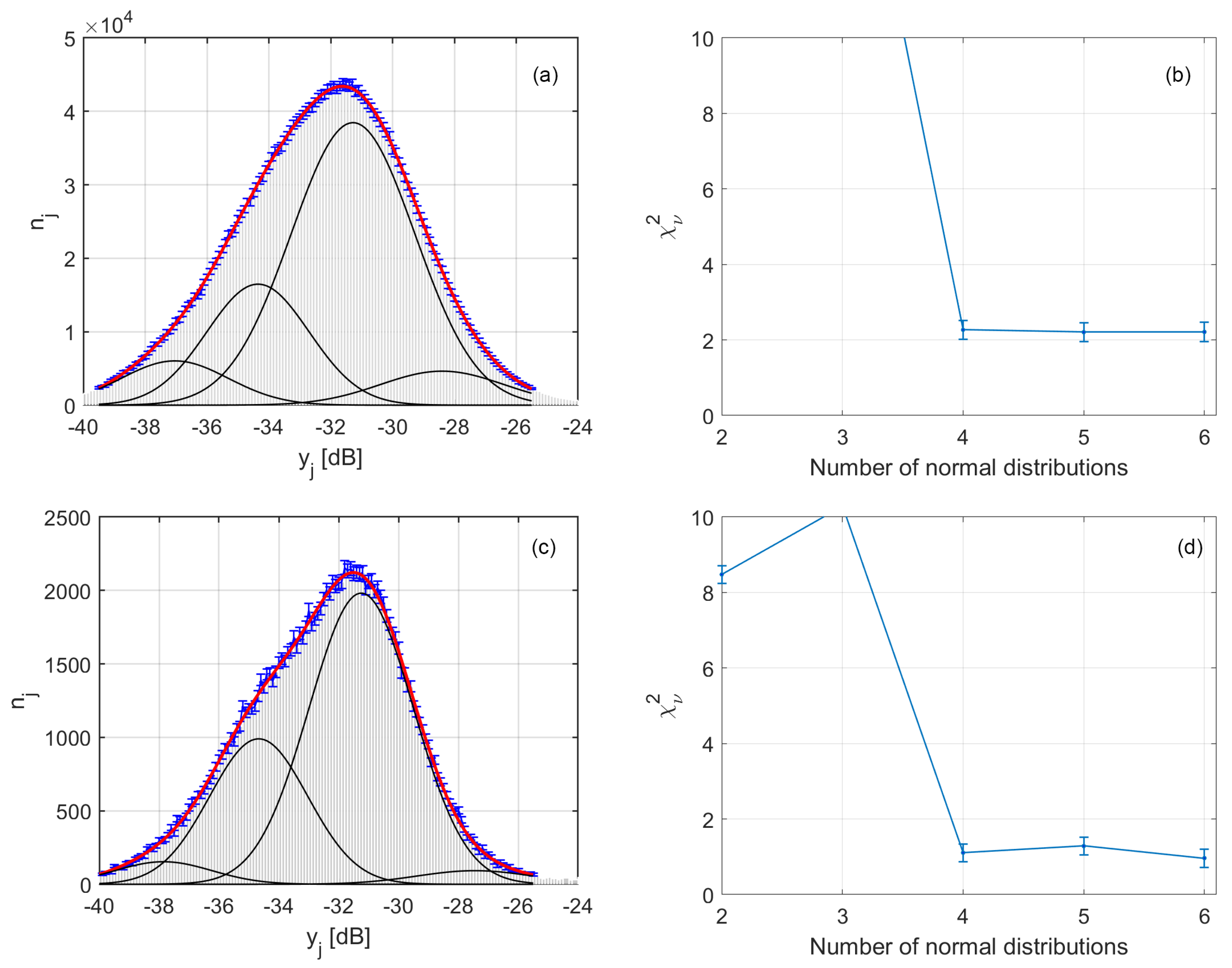
- The above averaging procedure can in principle reduce the noise of the backscatter data. This may, however, not decrease the standard deviation proportionally to the square root of the number of scatter pixels represented. This is because this rule is valid only for independent and identically distributed data. This cannot be the case for the backscatter data averaged over a small surface patch, because the variation and uncertainty in the BS data has independent and dependent components. The independent component is known as noise, which can be averaged out. This however does not hold for the dependent component, which is intrinsic to acoustic sediment properties and its heterogeneity. The fact that the two histograms in Figure 15 look similar also verifies the above reasoning; otherwise the second data set would have a significantly narrower histogram due to the averaging procedure.
- There is a trade-off between the spatial and geo-acoustic resolutions. While heavier averaging increases the geo-acoustic resolution of the classification, it directly decreases its spatial resolution. Narrower and relatively more separated Gaussians as well as chi-squared values closer to 1, obtained for the averaged data set (Figure 15 bottom subplots), indicate a better geo-acoustic resolution.
- The results obtained in Figure 15 show that the means and standard deviations of the Gaussians are characteristic of the acoustic properties of the sediment types. Given that the mean grain sizes of the grab samples suggested a homogeneous seabed in this survey area, it might be thought that if the parameters of the Gaussian were given a significant range within which they could vary, only one (or a few) Gaussians would be fitted to the entire histogram. The results show that this is not the case. For both datasets, the bounds for the standard deviation were set to a range of 0.5–2 dB but for neither dataset were the lower or upper bounds used after the curve fitting was implemented. This indicates that the Bayesian classification results are not significantly affected by the averaging procedure.
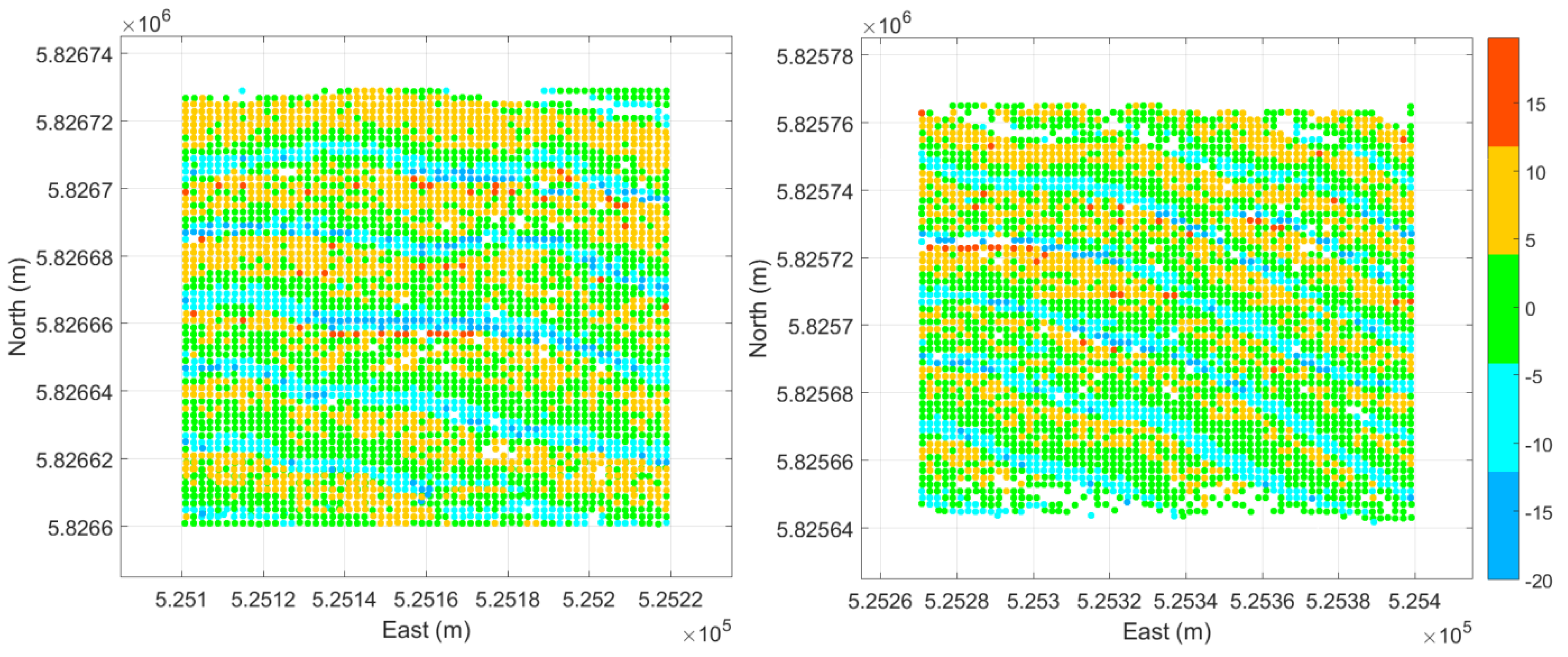
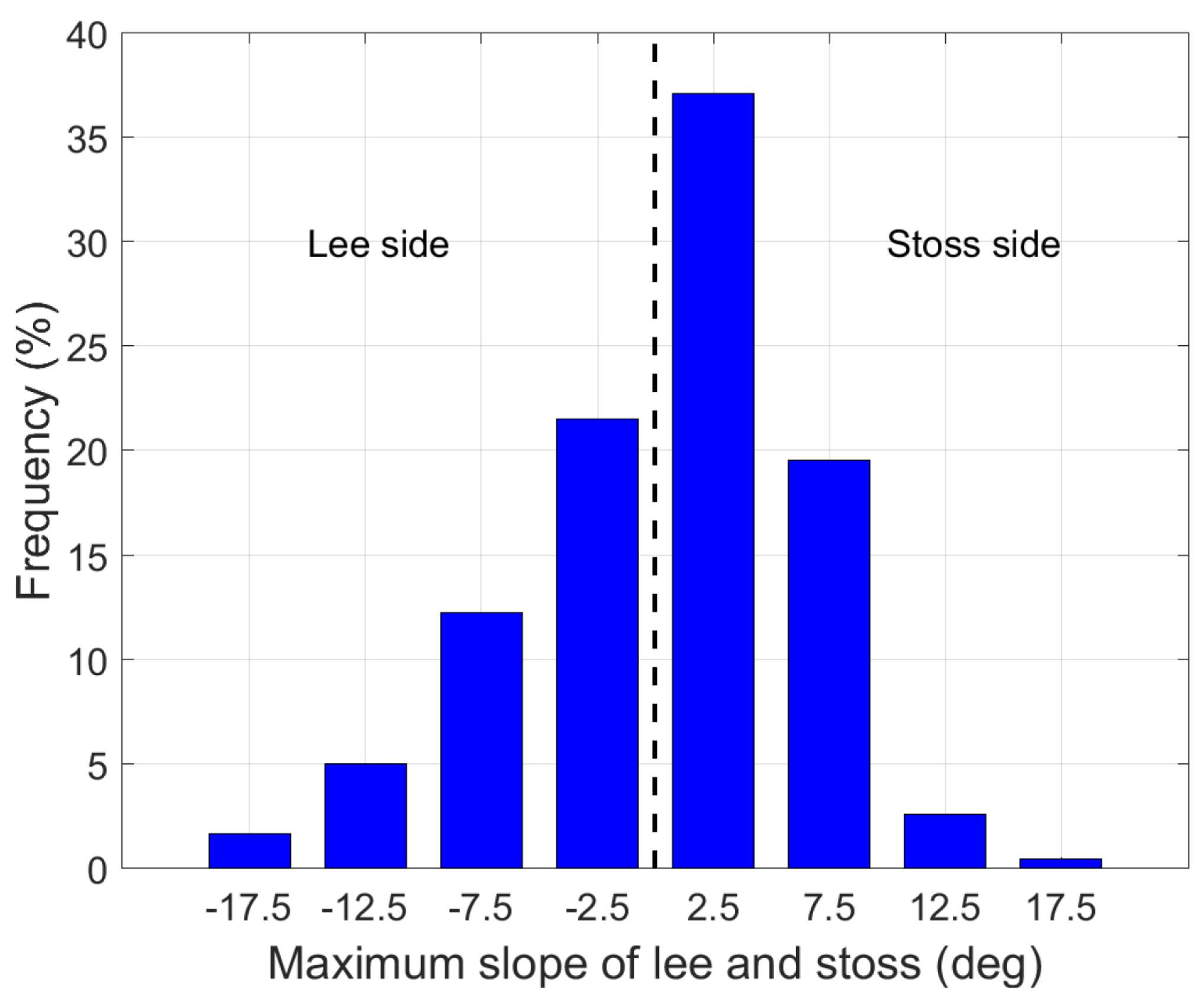
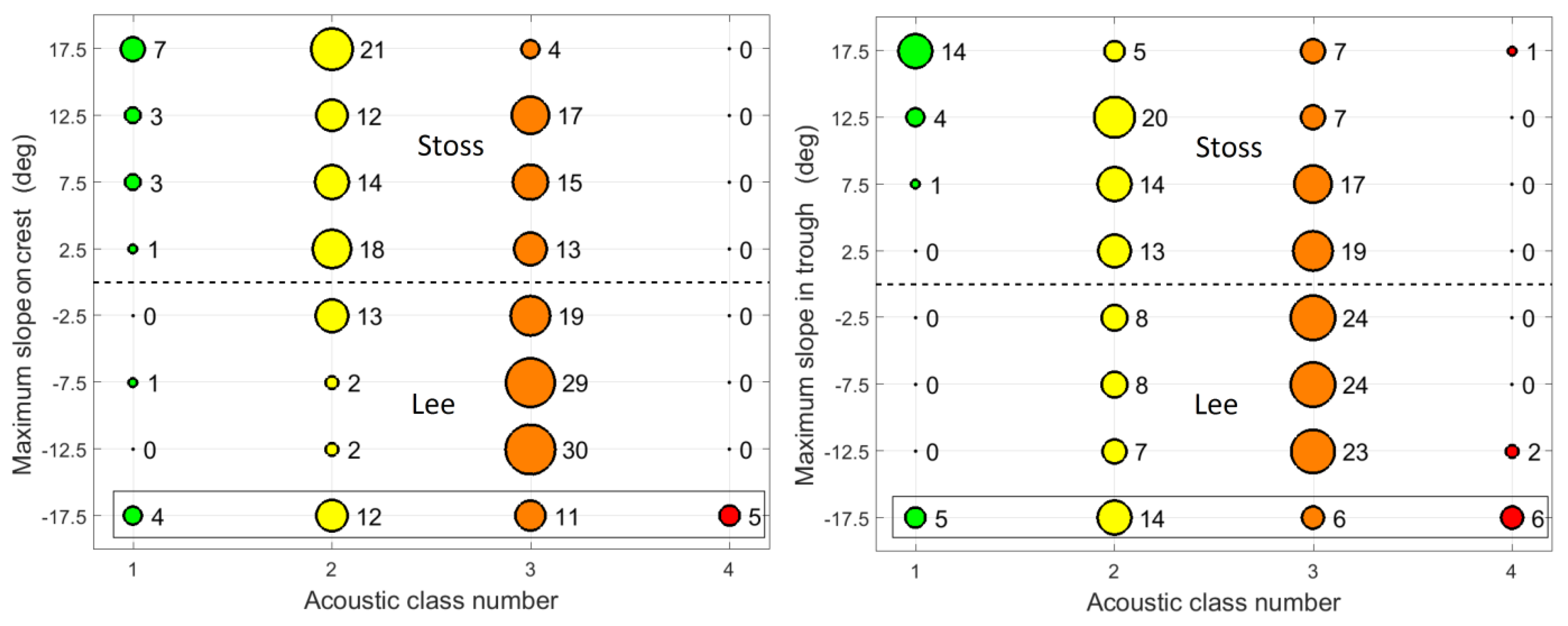
3.5. Classifying Sediments Over Megaripples
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MBES | Multibeam echosounder |
| SBES | Singlebeam echosounder |
| BS | Backscatter |
| NIOZ | Royal Netherlands Institute for Sea Research |
| SIS | Seafloor information system |
| GPS | Global positioning system |
| MRU | Motion reference unit |
| UTM | Universal Transverse Mercator |
| PDFs | Probability density functions |
| AC | Acoustic class |
| PSA | Particle size analysis |
| sM | Sandy mud |
| S | Sand |
| (g)S | Slightly gravely sand |
| gS | Gravely sand |
| PCA | Principal component analysis |
| PC | Principal component |
| BC | Bin center |
| DISCLOSE | DIstribution, StruCture and functioning of LOwresilience benthic communities |
| and habitats of the Dutch North SEa | |
| dB | Decibel |
| m | Meter |
| mm | Millimeter |
| m | Micrometer |
| s | Microsecond |
References
- Roos, P.C.; Wemmenhove, R.; Hulscher, S.J.; Hoeijmakers, H.W.; Kruyt, N. Modeling the effect of nonuniform sediment on the dynamics of offshore tidal sandbanks. J. Geophys. Res. Earth Surf. 2007, 112, 2005JF000376. [Google Scholar] [CrossRef]
- Stolk, A. Variation of sedimentary structures and grainsize over sandwaves. Mar. Sandwave Dyn. 2000, 1, 23–24. [Google Scholar]
- Svenson, C.; Ernstsen, V.B.; Winter, C.; Bartholomä, A.; Hebbeln, D. Tide-driven sediment variations on a large compound dune in the Jade tidal inlet channel, Southeastern North Sea. J. Coast. Res. 2009, 1, 361–365. [Google Scholar]
- Van Lancker, V.; Jacobs, P. The dynamical behaviour of shallow-marine dunes. In Proceedings of the International Workshop on Marine Sandwave, Lille, France, 23–24 March 2000; pp. 213–220. [Google Scholar]
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Marsh, I.; Brown, C. Neural network classification of multibeam backscatter and bathymetry data from Stanton Bank (Area IV). Appl. Acoust. 2009, 70, 1269–1276. [Google Scholar] [CrossRef]
- Ojeda, G.Y.; Gayes, P.T.; Van Dolah, R.F.; Schwab, W.C. Spatially quantitative seafloor habitat mapping: Example from the northern South Carolina inner continental shelf. Estuar. Coast. Shelf Sci. 2004, 59, 399–416. [Google Scholar] [CrossRef]
- Clarke, J.H.; Danforth, B.; Valentine, P. Areal seabed classification using backscatter angular response at 95 kHz. In Proceedings of the SACLANTCEN Conference on High Frequency Acoustics in Shallow Water, Lerici, Italy, 30 June–4 July 1997; pp. 243–250. [Google Scholar]
- Lamarche, G.; Lurton, X.; Verdier, A.L.; Augustin, J.M. Quantitative characterisation of seafloor substrate and bedforms using advanced processing of multibeam backscatter—Application to Cook Strait, New Zealand. Cont. Shelf Res. 2011, 31, S93–S109. [Google Scholar] [CrossRef]
- Brown, C.J.; Todd, B.J.; Kostylev, V.E.; Pickrill, R.A. Image-based classification of multibeam sonar backscatter data for objective surficial sediment mapping of Georges Bank, Canada. Cont. Shelf Res. 2011, 31, S110–S119. [Google Scholar] [CrossRef]
- Eleftherakis, D.; Amiri-Simkooei, A.; Snellen, M.; Simons, D.G. Improving riverbed sediment classification using backscatter and depth residual features of multi-beam echo-sounder systems. J. Acoust. Soc. Am. 2012, 131, 3710–3725. [Google Scholar] [CrossRef] [PubMed]
- Snellen, M.; Gaida, T.C.; Koop, L.; Alevizos, E.; Simons, D.G. Performance of Multibeam Echosounder Backscatter-Based Classification for Monitoring Sediment Distributions Using Multitemporal Large-Scale Ocean Data Sets. IEEE J. Ocean. Eng. 2019, 44, 142–155. [Google Scholar] [CrossRef]
- Simons, D.G.; Snellen, M. A Bayesian approach to seafloor classification using multi-beam echo-sounder backscatter data. Appl. Acoust. 2009, 70, 1258–1268. [Google Scholar] [CrossRef]
- Alevizos, E.; Snellen, M.; Simons, D.G.; Siemes, K.; Greinert, J. Acoustic discrimination of relatively homogeneous fine sediments using Bayesian classification on MBES data. Mar. Geol. 2015, 370, 31–42. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.; Snellen, M.; Simons, D.G. Riverbed sediment classification using multi-beam echo-sounder backscatter data. J. Acoust. Soc. Am. 2009, 126, 1724–1738. [Google Scholar] [CrossRef] [PubMed]
- Esri. World Topographic Map. Online Baselayer Database. 2012. Available online: http://www.arcgis.com/home/item.html?id=30e5fe3149c34df1ba922e6f5bbf808f (accessed on 20 February 2019).
- Van Dijk, T.A.; van Dalfsen, J.A.; Van Lancker, V.; van Overmeeren, R.A.; van Heteren, S.; Doornenbal, P.J. Benthic habitat variations over tidal ridges, North Sea, The Netherlands. In Seafloor Geomorphology as Benthic Habitat; Elsevier: Amsterdam, The Netherlands, 2012; pp. 241–249. [Google Scholar]
- Herman, P.; Beauchard, O.; van Duren, L. De staat van de Noordzee. Noordzeedagen. 2014. Available online: https://www.noordzeeloket.nl/publish/pages/123326/digitaal_overzicht_-_de_staat_van_de_noordzee_2015_4778.pdf (accessed on 21 February 2019).
- MSL SWAN Annual Mean Significant Wave Height. MetOcean Online Database. Available online: https://app.metoceanview.com/hindcast/ (accessed on 21 February 2019).
- Knaapen, M.A. Sandbank occurrence on the Dutch continental shelf in the North Sea. Geo-Mar. Lett. 2009, 29, 17–24. [Google Scholar] [CrossRef]
- Lindenbergh, R.C.; van Dijk, T.A.; Egberts, P.J. Separating bedforms of different scales in echo sounding data. In Coastal Dynamics 2005: State of the Practice; ASCE Library: Reston, VA, USA, 2006; pp. 1–14. [Google Scholar]
- Knaapen, M. Sandwave migration predictor based on shape information. J. Geophys. Res. Earth Surf. 2005, 110. [Google Scholar] [CrossRef]
- Nemeth, A. Modelling Offshore Sand Waves. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2003. [Google Scholar]
- Idier, D.; Ehrhold, A.; Garlan, T. Morphodynamique d’une dune sous-marine du détroît du pas de Calais. Comptes Rendus Geosci. 2002, 334, 1079–1085. [Google Scholar] [CrossRef]
- Teunissen, P. Testing Theory: An Introduction; Delft University of Technology: Delft, The Netherlands, 2000. [Google Scholar]
- Teunissen, P.; Simons, D.; Tiberius, C. Probability and Observation Theory; Delft University Press: Delft, The Netherlands, 2004. [Google Scholar]
- Sheehan, E.V.; Stevens, T.F.; Attrill, M.J. A quantitative, non-destructive methodology for habitat characterisation and benthic monitoring at offshore renewable energy developments. PLoS ONE 2010, 5, e14461. [Google Scholar] [CrossRef] [PubMed]
- Folk, R.L.; Ward, W.C. Brazos River bar [Texas]; a study in the significance of grain size parameters. J. Sediment. Res. 1957, 27, 3–26. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Collier, J.; Brown, C. Correlation of sidescan backscatter with grain size distribution of surficial seabed sediments. Mar. Geol. 2005, 214, 431–449. [Google Scholar] [CrossRef]
- Eleftherakis, D.; Snellen, M.; Amiri-Simkooei, A.; Simons, D.G.; Siemes, K. Observations regarding coarse sediment classification based on multi-beam echo-sounder’s backscatter strength and depth residuals in Dutch rivers. J. Acoust. Soc. Am. 2014, 135, 3305–3315. [Google Scholar] [CrossRef] [PubMed]
- Simons, D.G.; Snellen, M.; Ainslie, M.A. A multivariate correlation analysis of high-frequency bottom backscattering strength measurements with geotechnical parameters. IEEE J. Ocean. Eng. 2007, 32, 640–650. [Google Scholar] [CrossRef]
- Jackson, D.R.; Baird, A.M.; Crisp, J.J.; Thomson, P.A. High-frequency bottom backscatter measurements in shallow water. J. Acoust. Soc. Am. 1986, 80, 1188–1199. [Google Scholar] [CrossRef]
- Van Der Reijden, K.J.; Koop, L.; O’flynn, S.; Garcia, S.; Bos, O.; Van Sluis, C.; Maaholm, D.J.; Herman, P.M.; Simons, D.G.; Olff, H. Discovery of Sabellaria spinulosa reefs in an intensively fished area of the Dutch Continental Shelf, North Sea. J. Sea Res. 2019, 144, 85–94. [Google Scholar] [CrossRef]

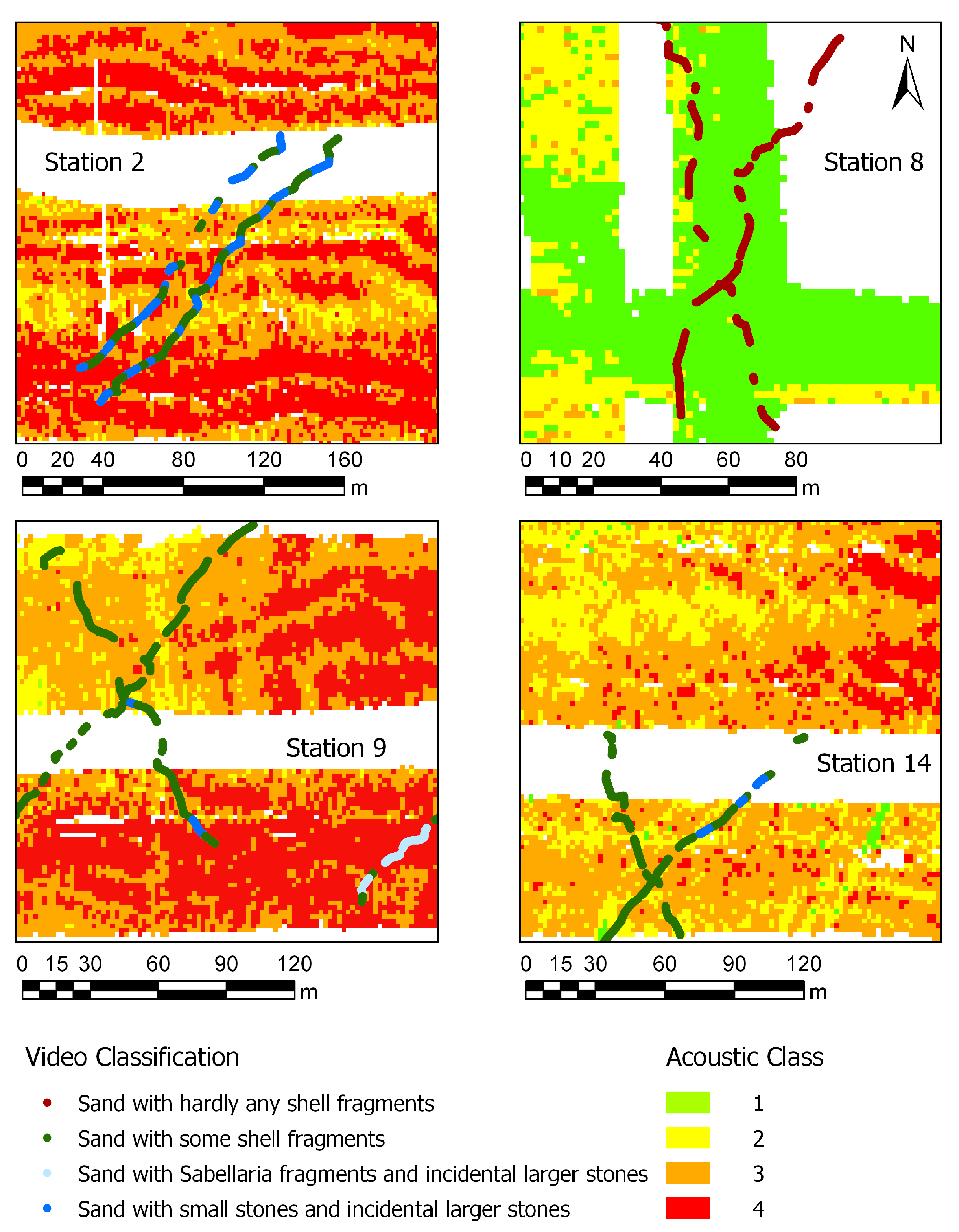
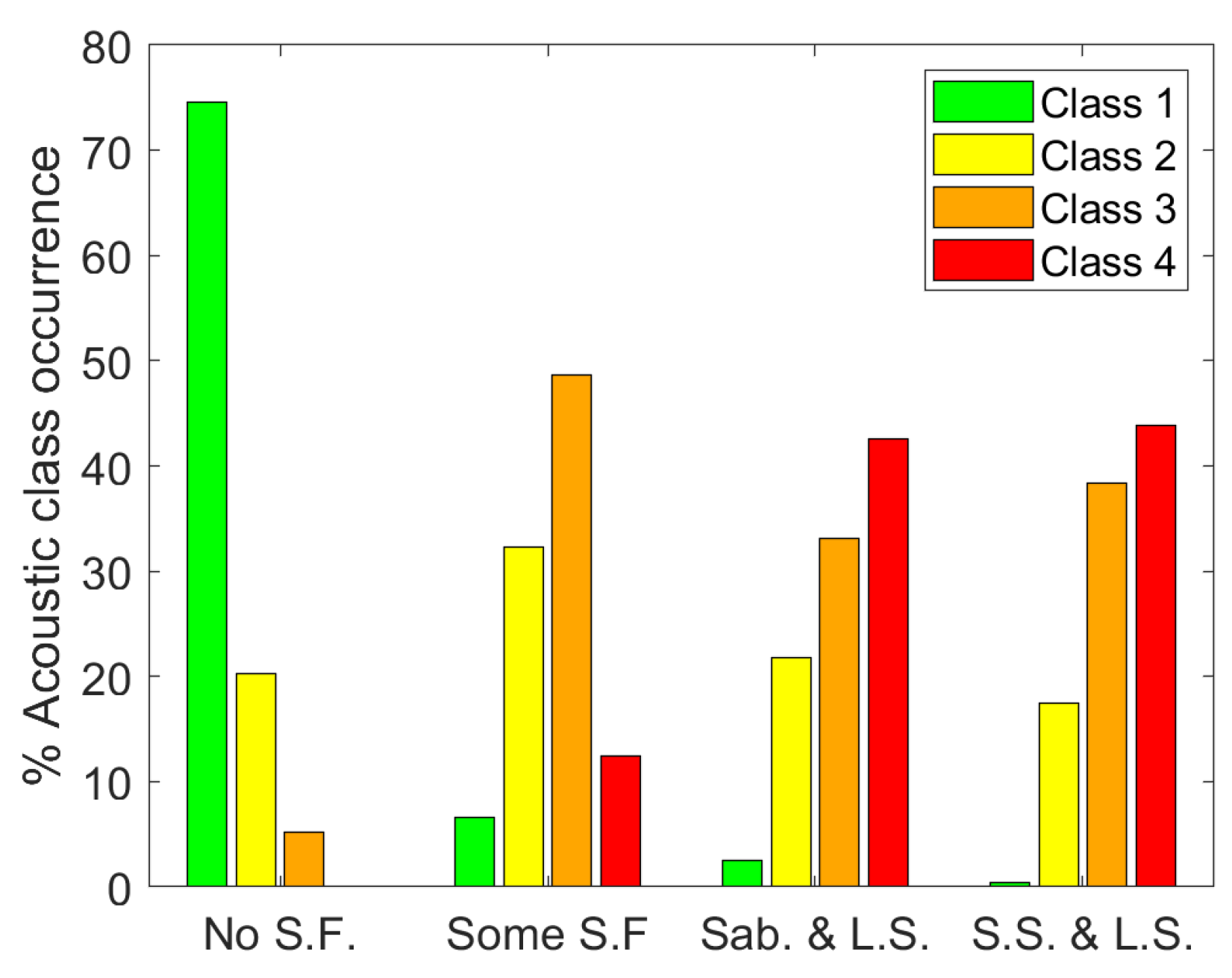
| Classification | Number of Frames | % of Total Frames |
|---|---|---|
| Sand with hardly any shell fragments | 4495 | 27.1% |
| Sand with some shell fragments | 8651 | 52.1% |
| Sand with Sabellaria fragments and incidental larger stones | 1257 | 7.6% |
| Sand with small stones and incidental larger stones | 2191 | 13.2% |
| Total | 16,594 | 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koop, L.; Amiri-Simkooei, A.; J. van der Reijden, K.; O’Flynn, S.; Snellen, M.; G. Simons, D. Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data. Geosciences 2019, 9, 142. https://doi.org/10.3390/geosciences9030142
Koop L, Amiri-Simkooei A, J. van der Reijden K, O’Flynn S, Snellen M, G. Simons D. Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data. Geosciences. 2019; 9(3):142. https://doi.org/10.3390/geosciences9030142
Chicago/Turabian StyleKoop, Leo, Alireza Amiri-Simkooei, Karin J. van der Reijden, Sarah O’Flynn, Mirjam Snellen, and Dick G. Simons. 2019. "Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data" Geosciences 9, no. 3: 142. https://doi.org/10.3390/geosciences9030142
APA StyleKoop, L., Amiri-Simkooei, A., J. van der Reijden, K., O’Flynn, S., Snellen, M., & G. Simons, D. (2019). Seafloor Classification in a Sand Wave Environment on the Dutch Continental Shelf Using Multibeam Echosounder Backscatter Data. Geosciences, 9(3), 142. https://doi.org/10.3390/geosciences9030142





