Northern Hemisphere Snow-Cover Trends (1967–2018): A Comparison between Climate Models and Observations
Abstract
1. Introduction
2. Materials and Methods
3. Results
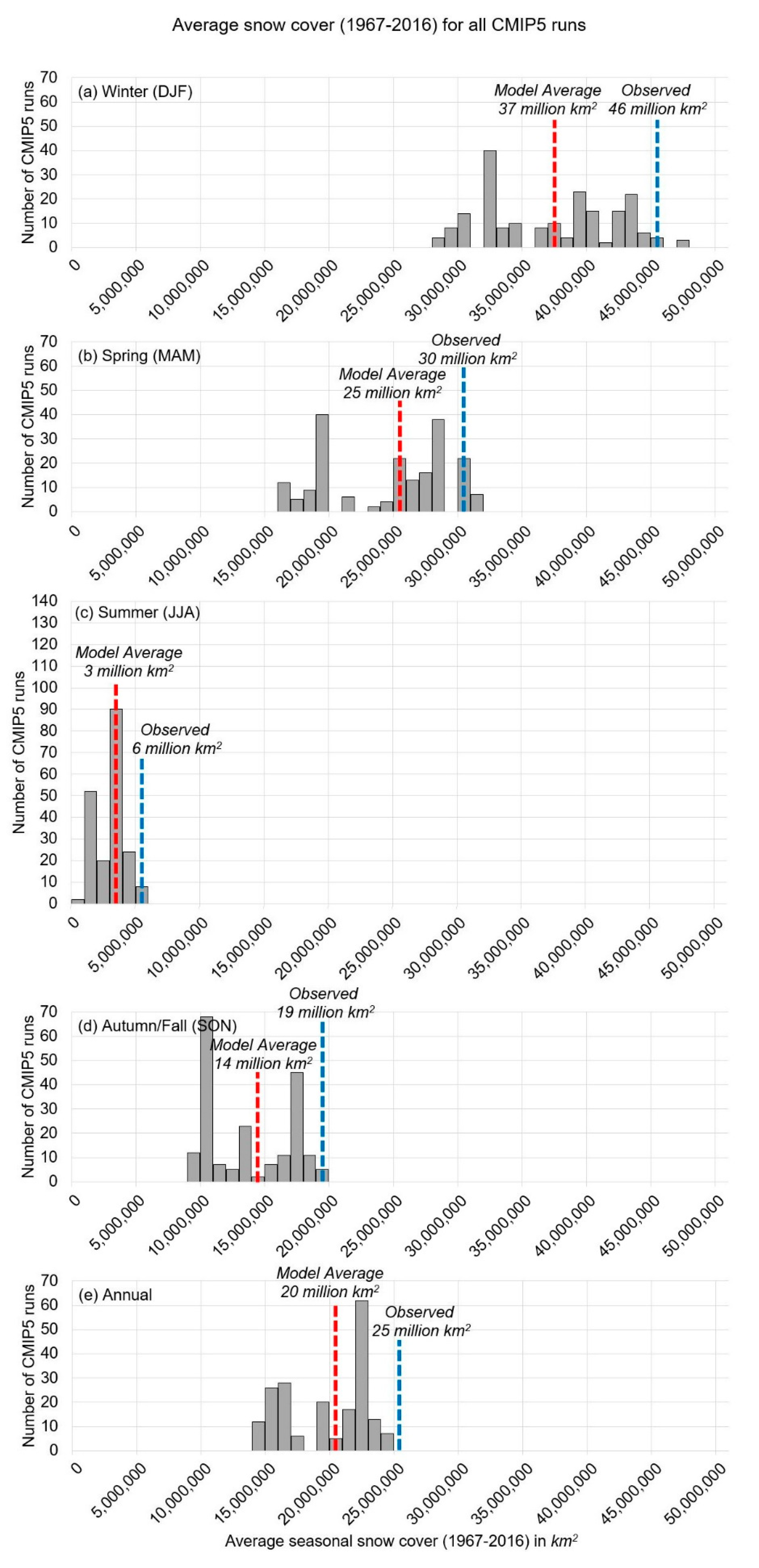
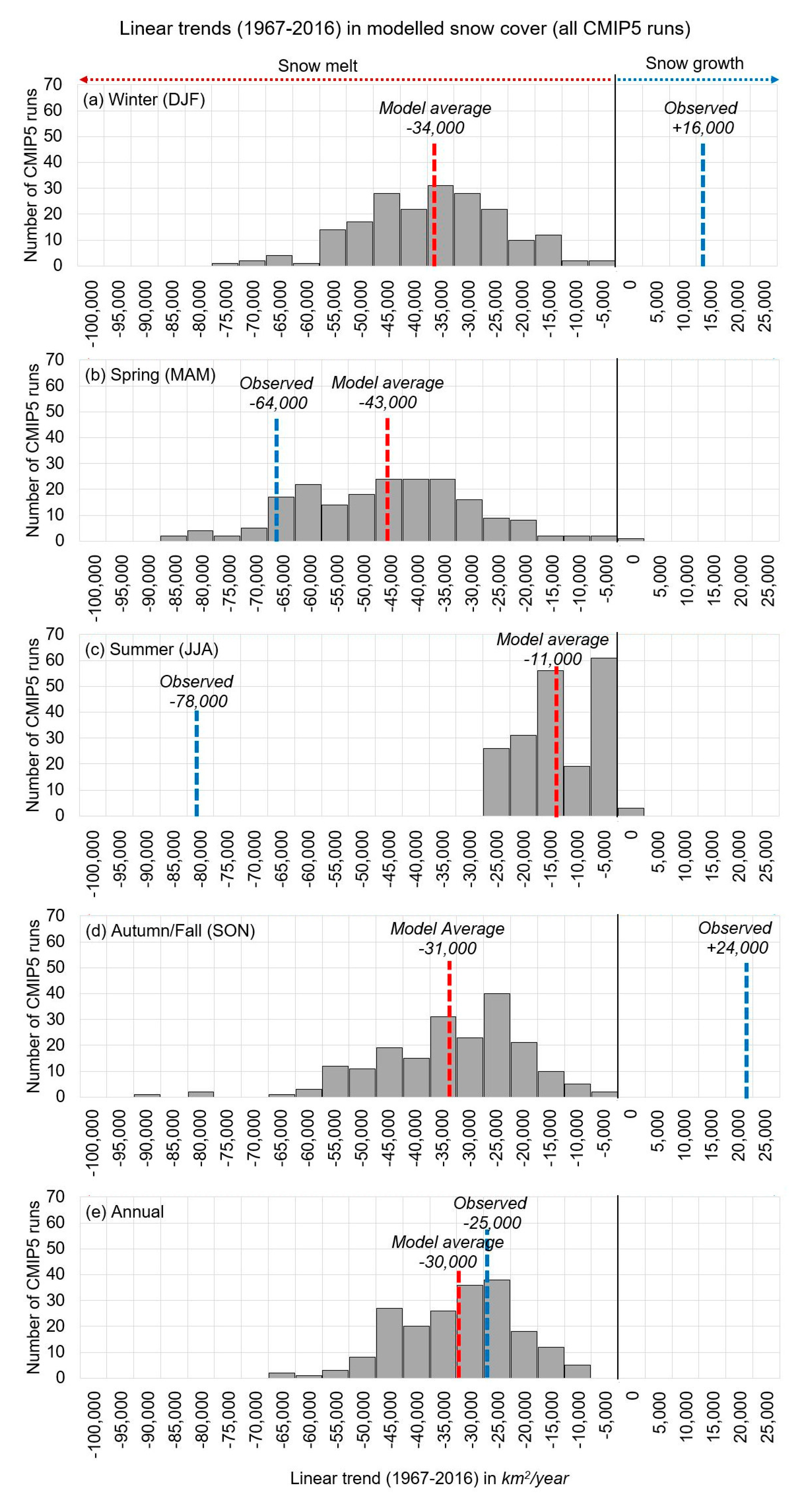
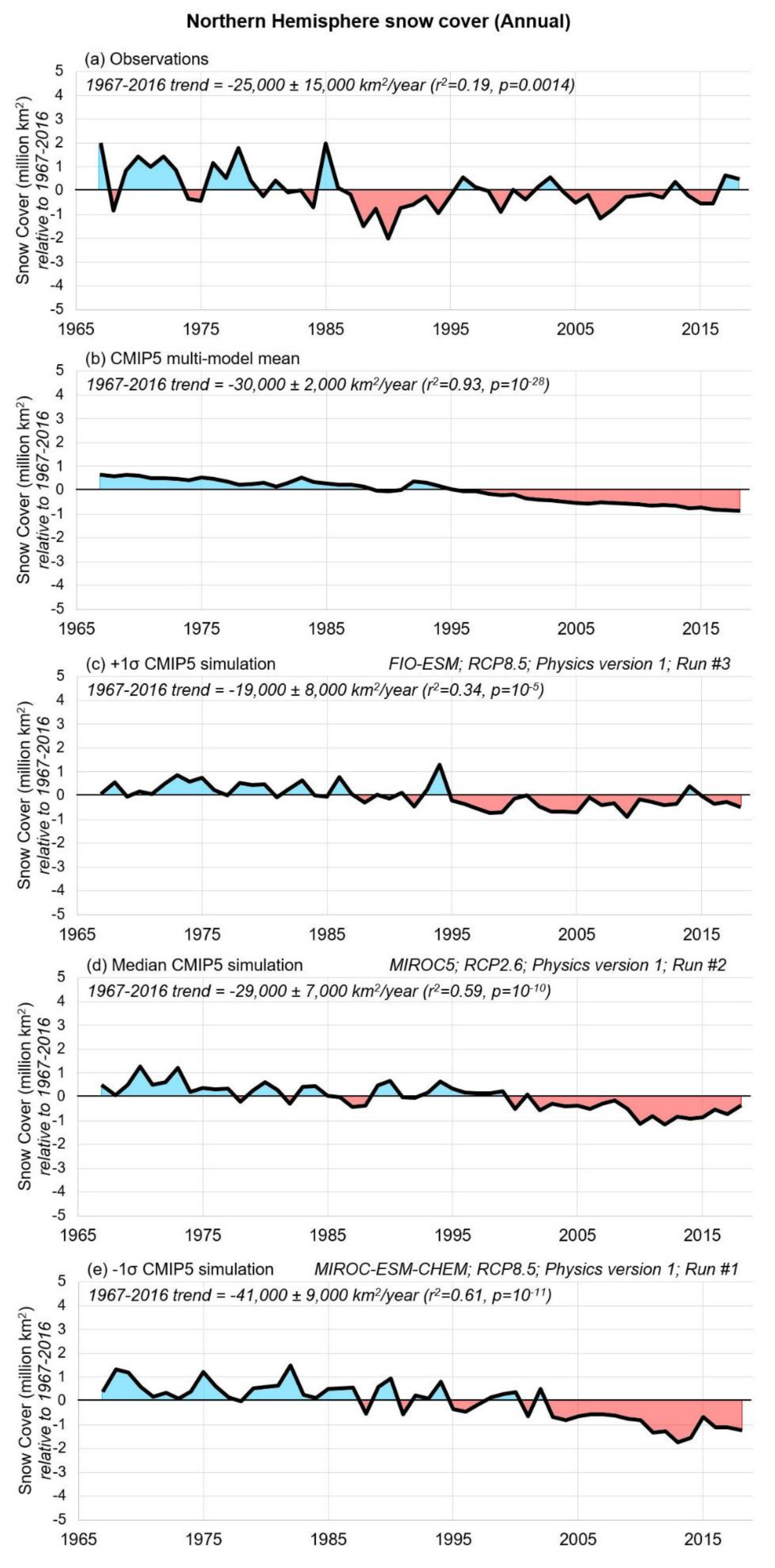
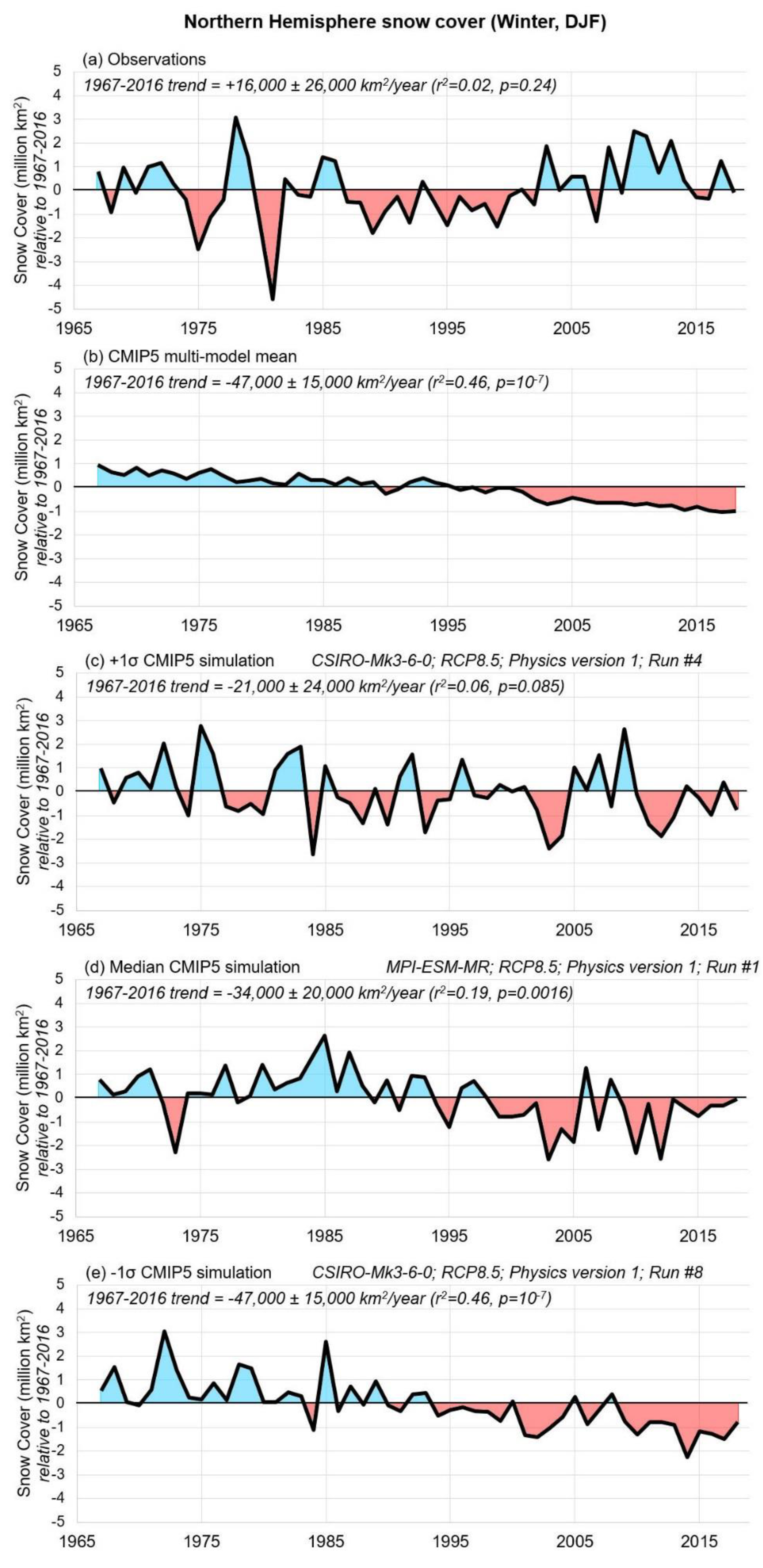
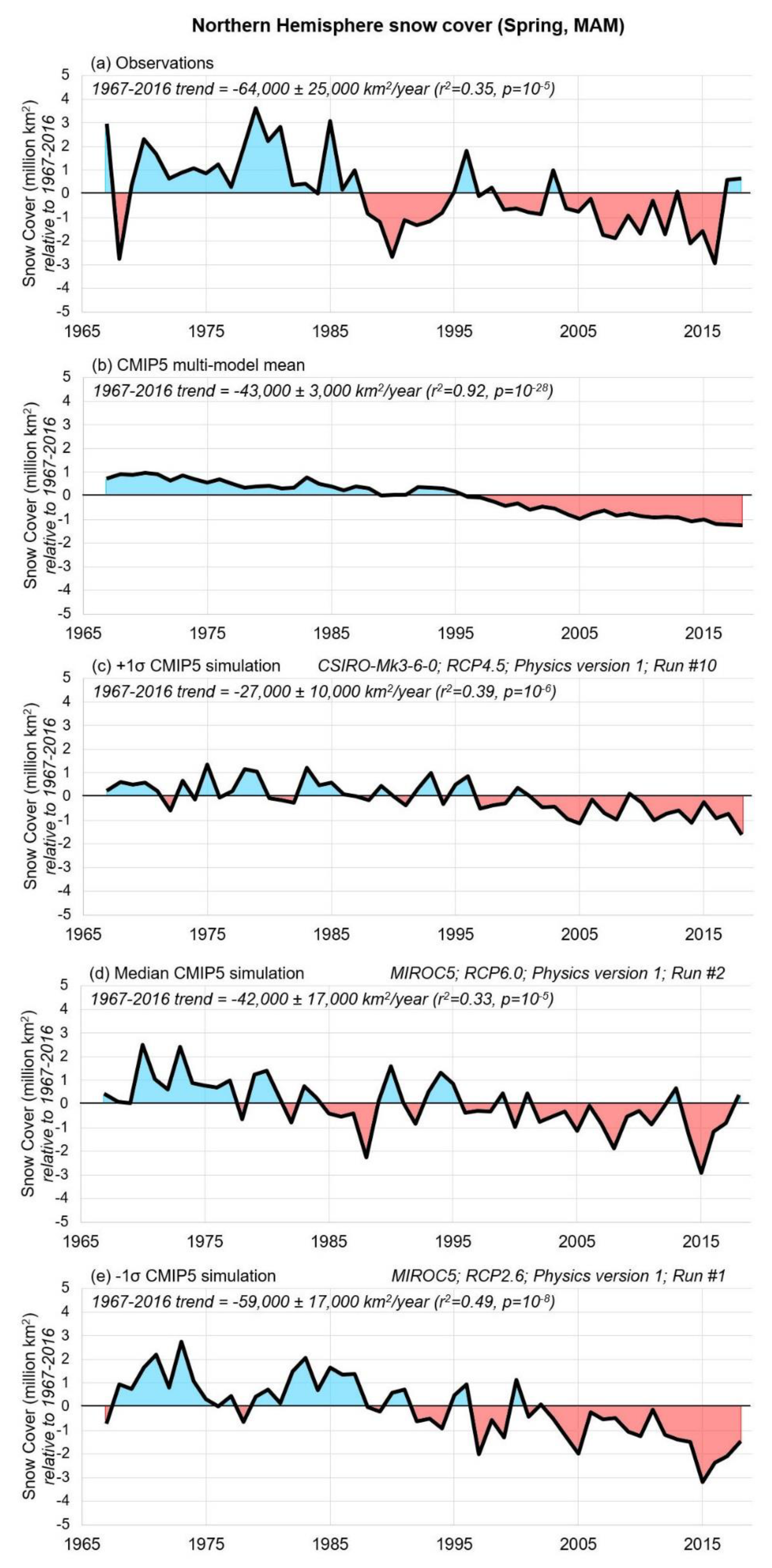
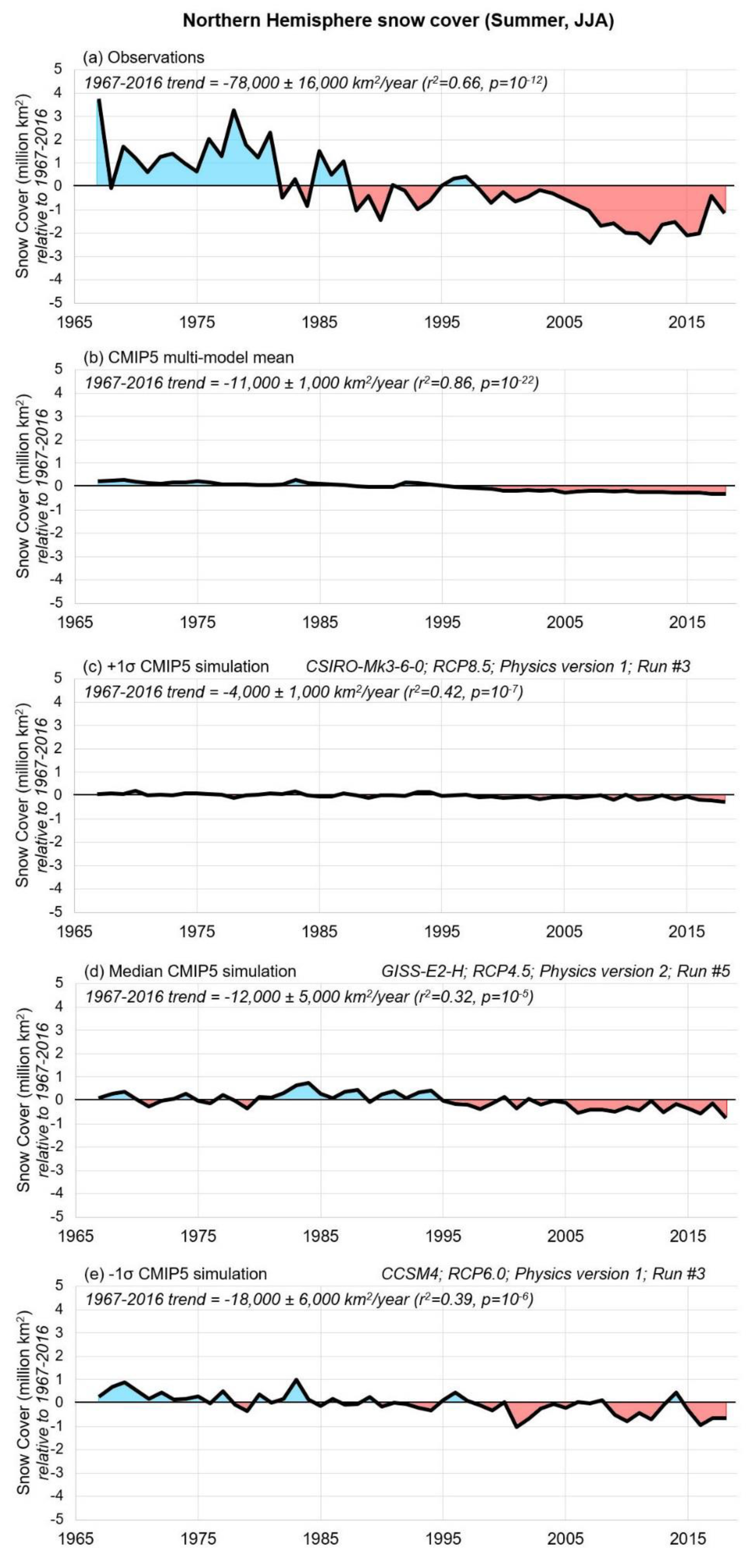
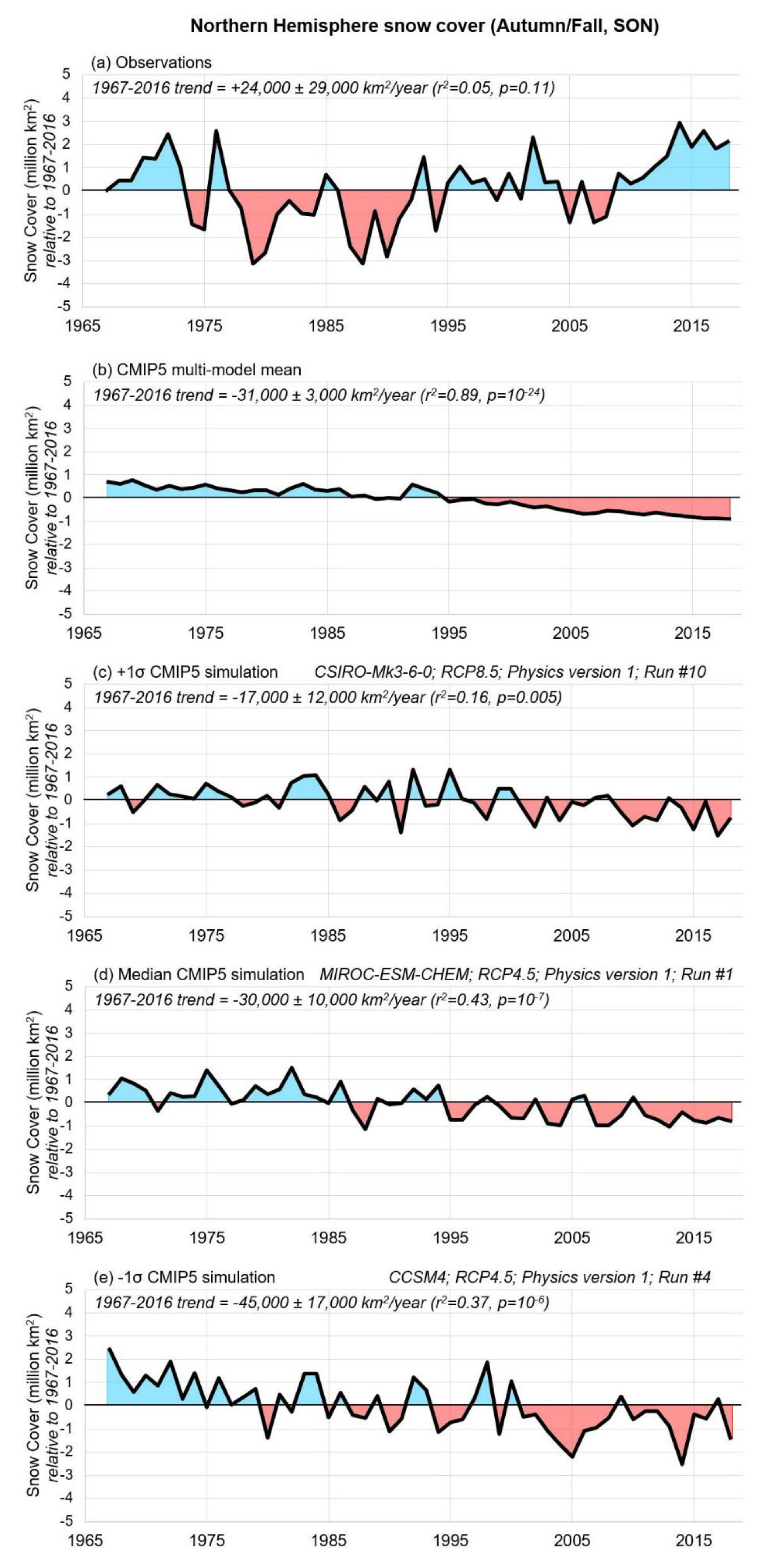
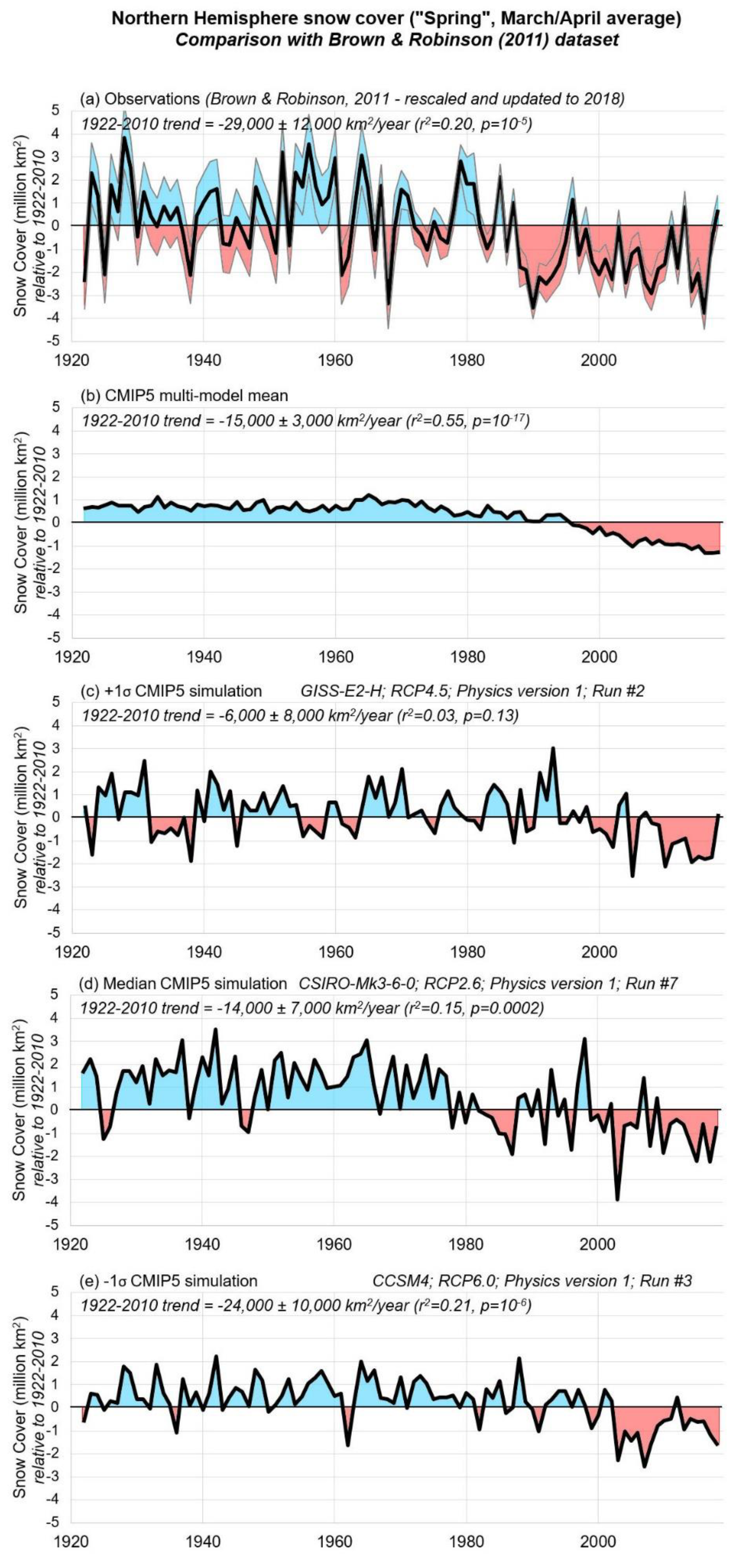
3.1. Comparison of CMIP5 Climate Modelled Snow-Cover Trends to the Satellite-Derived Rutgers Dataset
- External radiative forcing from “anthropogenic factors”. This includes many factors, but atmospheric greenhouse gas and stratospheric aerosol concentrations are the main components.
- External radiative forcing from “natural factors”. Currently, models consider only two: changes in total solar irradiance (“solar”) and stratospheric aerosols from volcanic eruptions (“volcanic”).
- Internal variability. This is the year-to-year random fluctuations in a given model run. As we will discuss below, some argue that this can be treated as an analogue for natural climatic inter-annual variability.
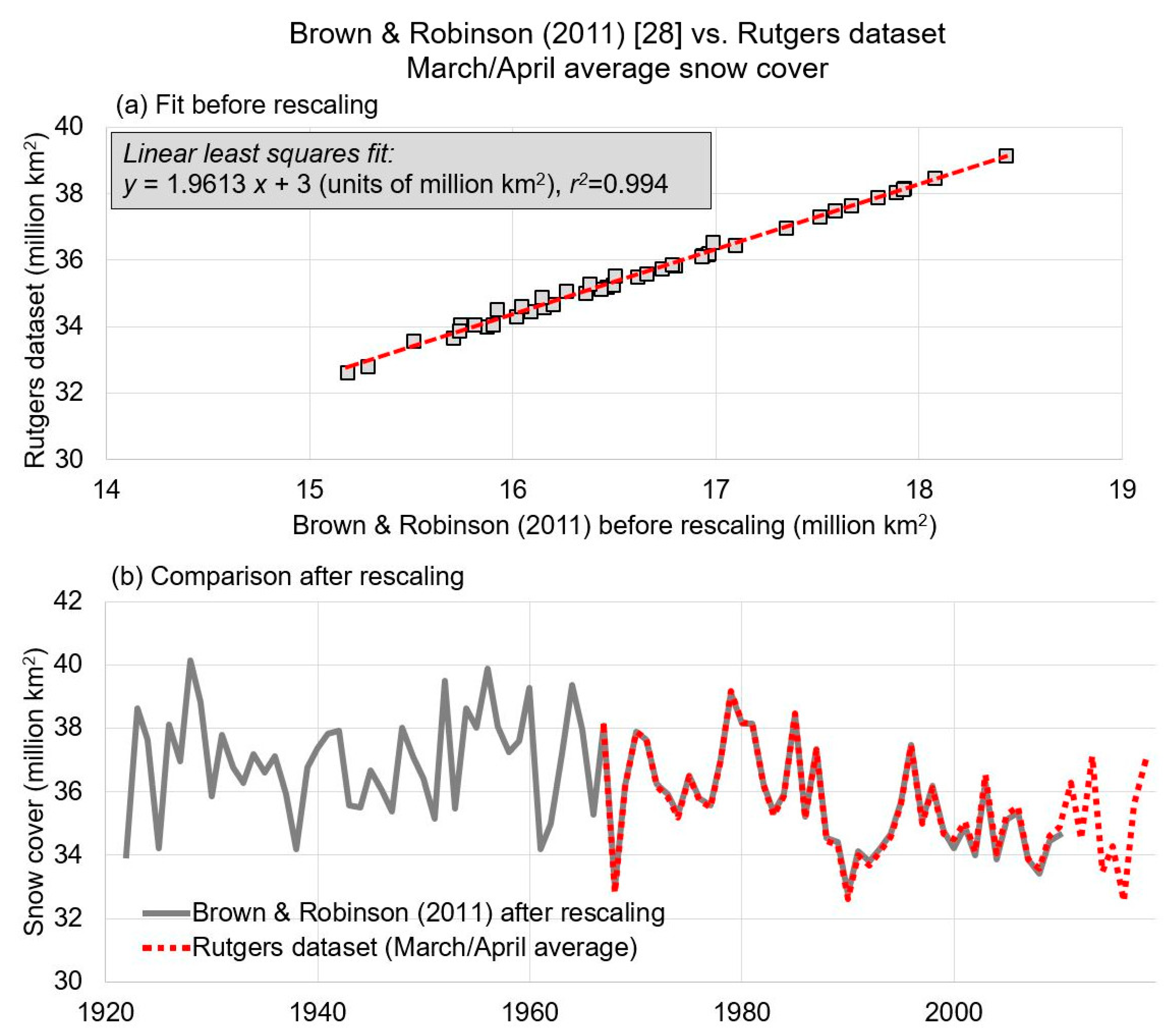
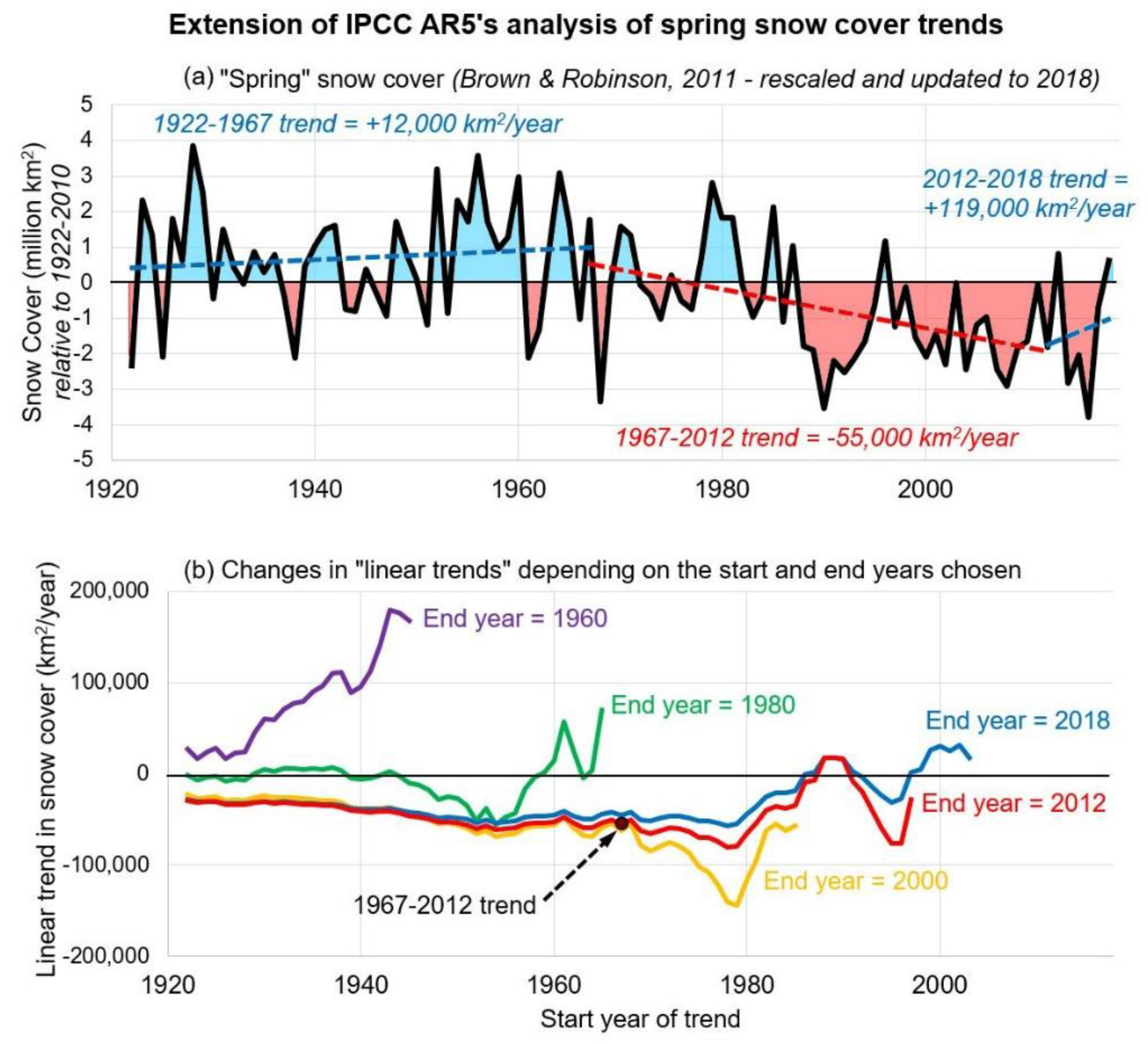
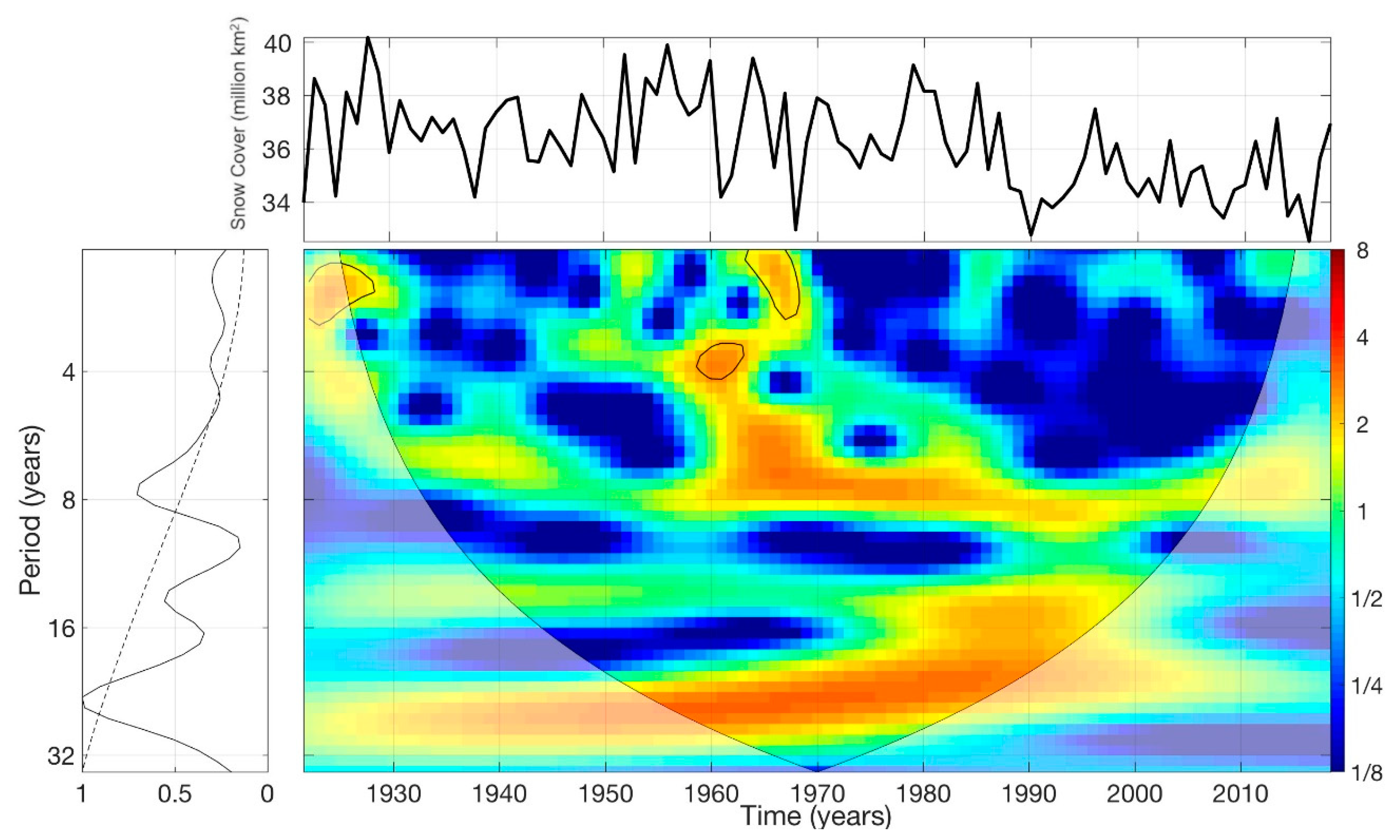
3.2. Comparison of CMIP5 Climate-Modelled March/April Trends to the Updated Brown and Robinson Time-Series (1922–2018)
“There is very high confidence that the extent of Northern Hemisphere snow cover has decreased since the mid-20th century (see Figure SPM.3). Northern Hemisphere snow cover extent decreased 1.6% [0.8 to 2.4%] per decade for March and April, and 11.7% [8.8 to 14.6%] per decade for June, over the 1967 to 2012 period. During this period, snow cover extent in the Northern Hemisphere did not show a statistically significant increase in any month.”.([29], pp. 7–8)
4. Discussion and Conclusions
- (1)
- Northern Hemisphere snow cover trends are largely determined by their modelled global air temperature trends.
- (2)
- They contend that global temperature trends since the mid-20th century are dominated by a human-caused global warming from increasing atmospheric greenhouse gas concentrations [29].
- (a)
- (b)
- The models might be overestimating the magnitude of human-caused global warming, and thereby overestimating the “human-caused” contribution to snow-cover trends. This would be consistent with several recent studies which concluded that the “climate sensitivity” to greenhouse gases of the climate models is too high [56,57,58].
- (c)
- The models might be underestimating the role of natural climatic changes. For instance, the CMIP5 models significantly underestimate the naturally occurring multidecadal trends in Arctic sea ice extent [1]. Others have noted that the climate models are poor at explaining observed precipitation trends [47,48,59], and mid-to-upper atmosphere temperature trends [44,45,46].
- (d)
- The models might be misattributing natural climate changes to human-caused factors. Indeed, Soon et al. [32] showed that the CMIP5 models neglected to consider any high-solar variability estimates for their “natural forcings”. If they had, much or all of the observed temperature trends could be explained in terms of changes in the solar output.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Connolly, R.; Connolly, M.; Soon, W. Re-calibration of Arctic sea ice extent datasets using Arctic surface air temperature records. Hydrol. Sci. J. 2017, 62, 1317–1340. [Google Scholar] [CrossRef]
- Hachem, S.; Duguay, C.R.; Allard, M. Comparison of MODIS-derived land surface temperatures with ground surface and air temperature measurements in continuous permafrost terrain. Cryosphere 2012, 6, 51–69. [Google Scholar] [CrossRef]
- Veettil, B.K.; Kamp, U. Remote sensing of glaciers in the tropical Andes: A review. Int. J. Remote Sens. 2017, 38, 7101–7137. [Google Scholar] [CrossRef]
- Zemp, M.; Hoelzle, M.; Haeberli, W. Six decades of glacier mass-balance observations: A review of the worldwide monitoring network. Ann. Glaciol. 2009, 50, 101–111. [Google Scholar] [CrossRef]
- Chahine, M.T. The hydrological cycle and its influence on climate. Nature 1992, 359, 373–380. [Google Scholar] [CrossRef]
- Sturm, M.; Goldstein, M.A.; Parr, C. Water and life from snow: A trillion dollar science question. Water Resour. Res. 2017, 53, 3534–3544. [Google Scholar] [CrossRef]
- Boelman, N.T.; Liston, G.E.; Gurarie, E.; Meddens, A.J.H.; Mahoney, P.J.; Kirchner, P.B.; Bohrer, G.; Brinkman, T.J.; Cosgrove, C.L.; Eitel, J.H.; et al. Integrating snow science and wildlife ecology in Arctic-boreal North America. Environ. Res. Lett. 2019, 14, 010401. [Google Scholar] [CrossRef]
- Manabe, S.; Wetherald, R.T. The effects of doubling the CO2 concentration on the climate of a General Circulation Model. J. Atmos. Sci. 1975, 32, 3–15. [Google Scholar] [CrossRef]
- Kukla, G. Climatic role of snow covers. In Sea Level, Ice and Climatic Change, Proceedings of the Symposium, XVII General Assembly IUGS, Canberra, Australia, 2–15 December 1979; Pub. No. 131; International Association of Hydrological Sciences: London, UK, 1981; pp. 79–107. [Google Scholar]
- Robinson, D.A.; Dewey, K.F. Recent secular variations in the extent of Northern Hemisphere snow cover. Geophys. Res. Lett. 1990, 17, 1557–1560. [Google Scholar] [CrossRef]
- Roesch, A. Evaluation of surface albedo and snow cover in AR4 coupled climate models. J. Geophys. Res. 2006, 111, D15111. [Google Scholar] [CrossRef]
- Räisänen, J. Warmer climate: Less or more snow? Clim. Dyn. 2008, 30, 307–319. [Google Scholar] [CrossRef]
- Brown, R.D.; Mote, P.W. The response of Northern Hemisphere snow cover to a changing climate. J. Clim. 2009, 22, 2124–2145. [Google Scholar] [CrossRef]
- Brutel-Vuilmet, C.; Ménégoz, M.; Krinner, G. An analysis of present and future seasonal Northern Hemisphere land snow cover simulated by CMIP5 coupled climate models. Cryosphere 2012, 7, 67–80. [Google Scholar] [CrossRef]
- Rupp, D.E.; Mote, P.W.; Bindoff, N.L.; Stott, P.A.; Robinson, D.A. Detection and attribution of observed changes in Northern Hemisphere spring snow cover. J. Clim. 2013, 26, 6904–6914. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Kushner, P.J.; Derksen, C. Interpreting observed northern hemisphere snow trends with large ensembles of climate simulations. Clim. Dyn. 2014, 43, 345–359. [Google Scholar] [CrossRef]
- Najafi, M.R.; Zwiers, F.W.; Gillett, N.P. Attribution of the spring snow cover extent decline in the Northern Hemisphere, Eurasia and North America to anthropogenic influence. Clim. Chang. 2016, 136, 571–586. [Google Scholar] [CrossRef]
- Thackeray, C.W.; Fletcher, C.G.; Mudryk, L.R.; Derksen, C. Quantifying the uncertainty in historical and future simulations of Northern Hemisphere spring snow cover. J. Clim. 2016, 29, 8647–8663. [Google Scholar] [CrossRef]
- Kukla, G.J.; Kukla, H.J. Increased surface albedo in the Northern Hemisphere. Science 1974, 183, 709–714. [Google Scholar] [CrossRef] [PubMed]
- Groisman, P.Ya.; Karl, T.R.; Knight, R.W. Observed impact of snow cover on the heat balance and the rise of continental spring temperatures. Science 1994, 263, 198–200. [Google Scholar] [CrossRef] [PubMed]
- Groisman, P.Ya.; Karl, T.R.; Knight, R.W.; Stenchikov, G.L. Changes of snow cover, temperature, and radiative heat balance over the Northern Hemisphere. J. Clim. 1994, 7, 1633–1656. [Google Scholar] [CrossRef]
- Robinson, D.A.; Dewey, K.F.; Heim, R., Jr. Global snow cover monitoring: An update. Bull. Am. Meteorol. Soc. 1993, 74, 1689–1696. [Google Scholar] [CrossRef]
- Robinson, D.A.; Estilow, T.W.; NOAA CDR Program. NOAA Climate Data Record (CDR) of Northern Hemisphere (NH) Snow Cover Extent (SCE); Version 1; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2012. [CrossRef]
- Estilow, T.W.; Young, A.H.; Robinson, D.A. A long-term Northern Hemisphere snow cover extent data record for climate studies and monitoring. Earth Syst. Sci. Data 2015, 7, 137–142. [Google Scholar] [CrossRef]
- Robinson, D.A.; Frei, A. Seasonal variability of northern hemisphere snow extent using visible satellite data. Prof. Geogr. 2000, 51, 307–314. [Google Scholar] [CrossRef]
- Foster, J.L.; Robinson, D.A.; Hall, D.K.; Estilow, T.W. Spring snow melt timing and changes over Arctic lands. Polar Geogr. 2008, 31, 145–157. [Google Scholar] [CrossRef]
- Frei, A.; Tedesco, M.; Lee, S.; Foster, J.; Hall, D.K.; Kelly, R.; Robinson, D.A. A review of global satellite-derived snow products. Adv. Space Res. 2012, 50, 1007–1029. [Google Scholar] [CrossRef]
- Brown, R.D.; Robinson, D.A. Northern Hemisphere spring snow cover variability and change over 1922-2010 including an assessment of uncertainty. Cryosphere 2011, 5, 219–229. [Google Scholar] [CrossRef]
- IPCC. Summary for policymakers. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group 1 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Derksen, C.; Brown, R. Spring snow cover extent reductions in the 2008-2012 period exceeding climate model projections. Geophys. Res. Lett. 2012, 39, L19504. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Soon, W.; Connolly, R.; Connolly, M. Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th century. Earth-Sci. Rev. 2015, 150, 409–452. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, W. Assessment of simulations of snow depth in the Qinghai-Tibetan Plateau using CMIP5 multi-models. Arct. Antarct. Alp. Res. 2015, 47, 611–625. [Google Scholar] [CrossRef]
- Wang, S.; Wu, C.; Wang, H.; Gonsamo, A.; Liu, Z. No evidence of widespread decline of snow cover on the Tibetan Plateau over 2000-2015. Sci. Rep. 2017, 7, 14645. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liang, S.; Cao, Y.; He, T. Distribution, attribution, and radiative forcing of snow cover changes over China from 1982 to 2013. Clim. Chang. 2016, 137, 363–377. [Google Scholar] [CrossRef]
- Cohen, J.L.; Furtado, J.C.; Barlow, M.A.; Alexeev, V.A.; Cherry, J.E. Arctic warming, increasing snow cover and widespread boreal winter cooling. Environ. Res. Lett. 2012, 7, 014007. [Google Scholar] [CrossRef]
- Liu, J.; Curry, J.A.; Wang, H.; Song, M.; Horton, R.M. Impact of declining Arctic sea ice on winter snowfall. Proc. Natl. Acad. Sci. USA 2012, 109, 4074–4079. [Google Scholar] [CrossRef]
- Chen, X.; Liang, S.; Cao, Y. Satellite observed changes in the Northern Hemisphere snow cover phenology and the associated radiative forcing and feedback between 1982 and 2013. Environ. Res. Lett. 2016, 11, 084002. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Liang, H.; Sun, Y.; Feng, Q.; Liang, T. Tracking snow variations in the Northern Hemisphere using multi-source remote sensing data (2000–2015). Remote Sens. 2018, 10, 136. [Google Scholar] [CrossRef]
- Brown, R.D.; Derksen, C. Is Eurasian October snow cover extent increasing? Environ. Res. Lett. 2013, 8, 024006. [Google Scholar] [CrossRef]
- Furtado, J.C.; Cohen, J.L.; Butler, A.H.; Riddle, E.E.; Kumar, A. Eurasian snow cover variability and links to winter climate in the CMIP5 models. Clim. Dyn. 2015, 45, 2591–2605. [Google Scholar] [CrossRef]
- Hanna, E.; Fettweis, X.; Hall, R.J. Recent changes in summer Greenland blocking captured by none of the CMIP5 models. Cryosphere 2018, 12, 3287–3292. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Douglass, D.H.; Christy, J.R.; Pearson, B.D.; Singer, S.F. A comparison of tropical temperature trends with model predictions. Int. J. Climatol. 2008, 28, 1693–1701. [Google Scholar] [CrossRef]
- Christy, J.R.; Herman, B.; Pielke, R., Sr.; Klotzbach, P.; McNider, R.T.; Hnilo, J.J.; Spencer, R.W.; Chase, T.; Douglass, D. What do observational datasets say about modeled tropospheric temperature trends since 1979? Remote Sens. 2010, 2, 2148–2169. [Google Scholar] [CrossRef]
- Christy, J.R.; Spencer, R.W.; Braswell, W.D.; Junod, R. Examination of space-based bulk atmospheric temperatures used in climate research. Int. J. Remote Sens. 2018, 39, 3580–3607. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.G.; Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Mamassis, N. A comparison of local and aggregated climate model outputs with observed data. Hydrol. Sci. J. 2010, 55, 1094–1110. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Anagnostopoulos, G.G.; Mamassis, N. Scientific dialogue on climate change: Is it giving black eyes or opening closed eyes? Hydrol. Sci. J. 2011, 56, 1334–1339. [Google Scholar] [CrossRef]
- Santer, B.D.; Thorne, P.W.; Haimberger, L.; Taylor, K.E.; Wigley, T.M.L.; Lanzante, J.R.; Solomon, S.; Free, M.; Gleckler, P.J.; Jones, P.D.; et al. Consistency of modelled and observed temperature trends in the tropical troposphere. Int. J. Climatol. 2008, 28, 1703–1722. [Google Scholar] [CrossRef]
- Santer, B.D.; Solomon, S.; Pallotta, G.; Mears, C.; Po-Chedley, S.; Fu, Q.; Wentz, F.; Zou, C.; Painter, J.; Cvijanovic, I.; et al. Comparing tropospheric warming in climate models and satellite data. J. Clim. 2017, 30, 373–392. [Google Scholar] [CrossRef]
- Huard, D. Discussion of “A comparison of local and aggregated climate model outputs with observed data”. Hydrol. Sci. J. 2011, 56, 1330–1333. [Google Scholar] [CrossRef][Green Version]
- Velasco Herrera, V.M.; Pérez-Peraza, J.; Soon, W.; Márquez-Adame, J.C. The quasi-biennial oscillation of 1.7 years in ground level enhancement events. New Astron. 2018, 60, 7–13. [Google Scholar] [CrossRef]
- Soon, W.; Velasco Herrera, V.M.; Cionco, R.G.; Qiu, S.; Baliunas, S.; Egeland, R.; Henry, G.W.; Charvátová, I. Covariations of chromospheric and photometric variability of the young Sun analogue HD 30495: Evidence for and interpretation of mid-term periodicities. Mon. Not. R. Astron. Soc. 2019, 483, 2748–2757. [Google Scholar] [CrossRef]
- Cionco, R.G.; Soon, W.W.-H. Short-term orbital forcing: A quasi-review and a reappraisal of realistic boundary conditions for climate modeling. Earth Sci. Rev. 2017, 166, 206–222. [Google Scholar] [CrossRef]
- Cionco, R.G.; Valentini, J.E.; Quaranta, N.E.; Soon, W.W.-H. Lunar fingerprints in the modulated incoming solar radiation: In situ insolation and latitudinal insolation gradients as two important interpretative metrics for paleoclimatic data records and theoretical climate modeling. New Astron. 2018, 58, 96–106. [Google Scholar] [CrossRef]
- Monckton, C.; Soon, W.W.-H.; Legates, D.R.; Briggs, W.M. Keeping it simple: The value of an irreducibly simple climate model. Sci. Bull. 2015, 60, 1378–1390. [Google Scholar] [CrossRef][Green Version]
- Bates, J.R. Estimating climate sensitivity using two-zone energy balance models. Earth Space Sci. 2016, 3, 207–225. [Google Scholar] [CrossRef]
- Lewis, N.; Curry, J. The impact of recent forcing and ocean heat uptake data on estimates of climate sensitivity. J. Clim. 2018, 31, 6051–6071. [Google Scholar] [CrossRef]
- Legates, D.R. Climate models and their simulation of precipitation. Energy Environ. 2014, 25, 1163–1175. [Google Scholar] [CrossRef]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. Should we apply bias correction to global and regional climate model data? Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
| Modelling Group | Country | Model Name | RCP2.6 | RCP4.5 | RCP6.0 | RCP8.5 | Total |
|---|---|---|---|---|---|---|---|
| Beijing Climate Center | China | bcc-csm1-1 | 1 | 1 | 0 | 1 | 3 |
| bcc-csm1-1-m | 1 | 1 | 1 | 0 | 3 | ||
| Beijing Normal University | China | BNU-ESM | 1 | 1 | 0 | 1 | 3 |
| Canadian Centre for Climate Modelling and Analysis | Canada | CanESM2 | 5 | 5 | 0 | 5 | 15 |
| National Center for Atmospheric Research | USA | CCSM4 | 6 | 6 | 6 | 6 | 24 |
| Community Earth System Model Contributors | USA | CESM1-BGC | 0 | 1 | 0 | 1 | 2 |
| CESM1-CAM5 | 2 | 2 | 2 | 3 | 9 | ||
| Centre National de Recherches Météorologiques | France | CNRM-CM5 | 1 | 1 | 0 | 5 | 7 |
| Commonwealth Scientific and Industrial Research Organisation | Australia | CSIRO-Mk3-6-0 | 10 | 10 | 10 | 10 | 40 |
| Laboratory of Numerical Modelling for Atmospheric Sciences and Geophysical Fluid Dynamics (LASG) | China | FGOALS-g2 | 1 | 1 | 0 | 1 | 3 |
| First Institute of Oceanography | China | FIO-ESM | 3 | 3 | 3 | 3 | 12 |
| NASA Goddard Institute for Space Studies | USA | GISS-E2-H | 3 | 15 | 3 | 3 | 24 |
| GISS-E2-H-CC | 0 | 1 | 0 | 0 | 1 | ||
| GISS-E2-R | 0 | 1 | 0 | 0 | 1 | ||
| GISS-E2-R-CC | 0 | 1 | 0 | 0 | 1 | ||
| Institute for Numerical Mathematics | Russia | inmcm4 | 0 | 1 | 0 | 1 | 2 |
| Japan Agency for Marine–Earth Science and Technology | Japan | MIROC5 | 3 | 3 | 3 | 3 | 12 |
| MIROC-ESM | 1 | 1 | 1 | 1 | 4 | ||
| MIROC-ESM-CHEM | 1 | 1 | 1 | 1 | 4 | ||
| Max Planck Institute | Germany | MPI-ESM-LR | 3 | 3 | 0 | 3 | 9 |
| MPI-ESM-MR | 1 | 3 | 0 | 1 | 5 | ||
| Meteorological Research Institute | Japan | MRI-CGCM3 | 1 | 1 | 1 | 1 | 4 |
| Norwegian Climate Centre | Norway | NorESM1-M | 1 | 1 | 1 | 1 | 4 |
| NorESM1-ME | 1 | 1 | 1 | 1 | 4 | ||
| 15 modelling groups | 9 countries | 24 models | 46 | 65 | 33 | 52 | 196 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Connolly, R., 1; Connolly, M.; Soon, W.; Legates, D.R.; Cionco, R.G.; Velasco Herrera, V.M. Northern Hemisphere Snow-Cover Trends (1967–2018): A Comparison between Climate Models and Observations. Geosciences 2019, 9, 135. https://doi.org/10.3390/geosciences9030135
Connolly R 1, Connolly M, Soon W, Legates DR, Cionco RG, Velasco Herrera VM. Northern Hemisphere Snow-Cover Trends (1967–2018): A Comparison between Climate Models and Observations. Geosciences. 2019; 9(3):135. https://doi.org/10.3390/geosciences9030135
Chicago/Turabian StyleConnolly, Ronan 1, Michael Connolly, Willie Soon, David R. Legates, Rodolfo Gustavo Cionco, and Víctor. M. Velasco Herrera. 2019. "Northern Hemisphere Snow-Cover Trends (1967–2018): A Comparison between Climate Models and Observations" Geosciences 9, no. 3: 135. https://doi.org/10.3390/geosciences9030135
APA StyleConnolly, R., 1, Connolly, M., Soon, W., Legates, D. R., Cionco, R. G., & Velasco Herrera, V. M. (2019). Northern Hemisphere Snow-Cover Trends (1967–2018): A Comparison between Climate Models and Observations. Geosciences, 9(3), 135. https://doi.org/10.3390/geosciences9030135





