High Resolution Satellite Images for Instantaneous Shoreline Extraction Using New Enhancement Algorithms
Abstract
1. Introduction
State-of-the-Art of Shoreline Detection
- Video systems [8,9]: The technique is used mainly with a network of fixed terrestrial cameras (e.g., ARGUS [11]) and Siren) from a few units up to tens, installed at prominent points in the landscape or on specially-positioned supports. They acquire at intervals of up to 10 hz, encompassing 180° views and allowing total coverage of about 4–6 km of beach. The acquired images are oblique and require orthorectification operations, as well as georeferencing with algorithms derived from classical photogrammetry;
- Aerophotogrammetric/UAV survey [12,13,14,15,16,17,18,19,20]: This does not provide a detailed relief, but represents the entire study area at the time of acquisition. Achievable precisions are at the centimeter-subcentimeter level, but the costs are high. “Ad hoc” flights must be planned, and above all, it is significantly influenced by weather conditions (sunny and minimal wind conditions are needed); this leads to limitations on flight seasons;
- Satellite remote sensing [21,22]: This refers to the latest-generation remote sensing satellites, which are becoming more effective as compared to those available previously. Traditionally, medium resolution satellites (e.g., Landsat and Sentinel-2) have been used advantageously for coastline studies that did not require very high accuracy. Satellites with high and very high resolution are required because they are particularly advantageous compared to traditional photogrammetric aerial acquisitions. High spatial resolution remote sensing satellites allow data to be acquired and processed more quickly, with comparable precision, while offering a very high level of detail. Furthermore, the fundamental ability to capture the scene in several spectral bands allows more information to be extracted than is extractable from images covering only the visible part of the electromagnetic spectrum and thus allows thematic maps of the territory to be created through multispectral classification. Another advantage, which makes this technique more attractive than the others, is that satellite revisit times are very short (a few days), which allows the area to be studied on images taken at different times.
2. Case Study
2.1. WorldView-2
2.2. Data Pre-Processing
- orthorectification;
- georeferencing;
- resampling;
- pansharpening.
2.3. Data Processing with Common Filters
2.3.1. Decorrelation Stretch
2.3.2. Normalized Difference Vegetation Index
2.3.3. WorldView Water Index
2.3.4. Unsupervised and Supervised Classification
2.4. Data Processing with the ACM System
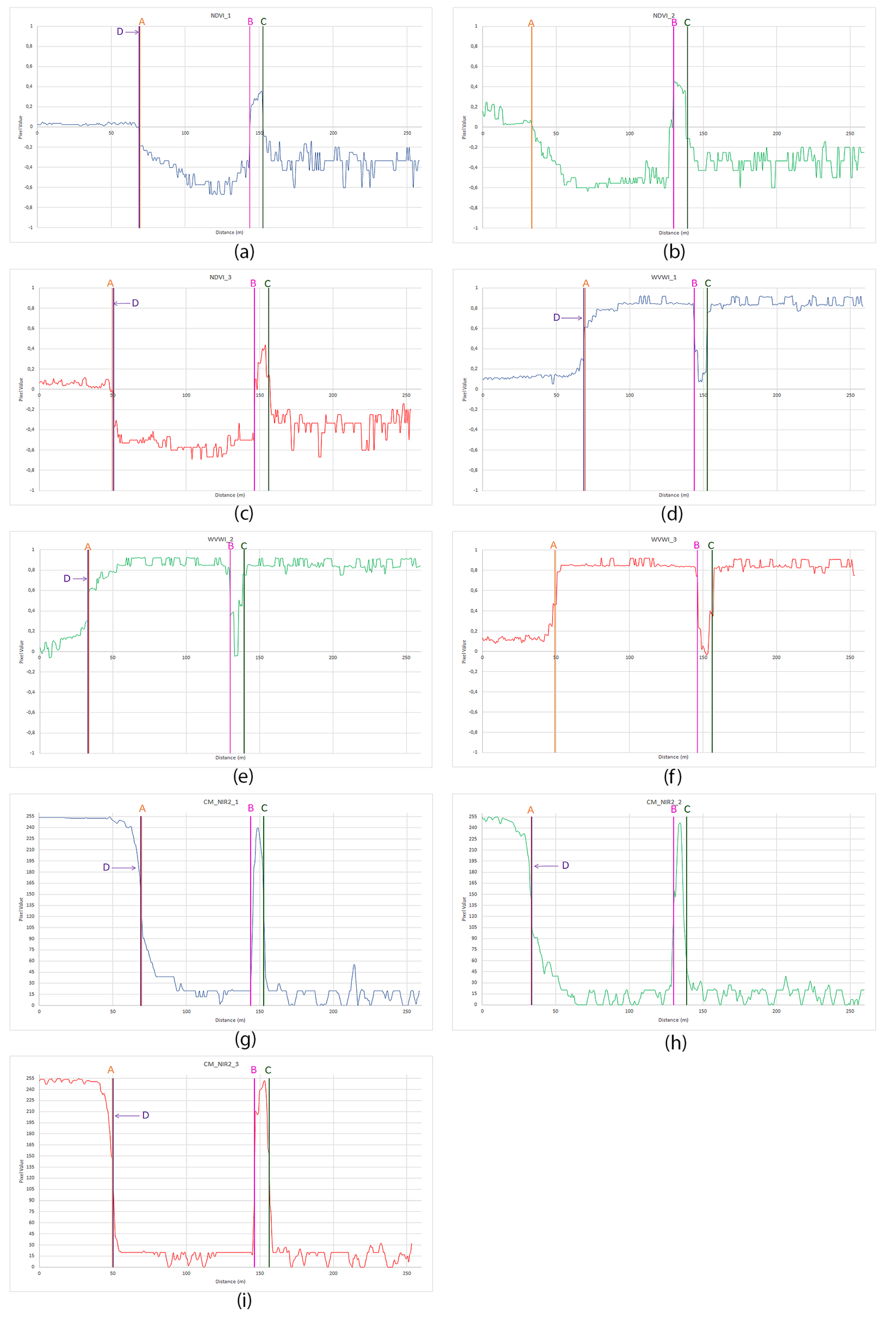
2.5. Analysis of Results
- a four-band image (coastal, red, green, and blue);
- an image containing only the coastal blue band (which is specific for coastal studies);
- an image with the coastal blue band plus NIR2;
- an image with only the NIR2 band.
3. Discussion of Results and Conclusions
- their ability to define the contours of real images was excellent;
- their adaptation to satellite imagery made them a powerful tool for digital image processing, and they can be used for automatic territory analysis;
- they were capable of distinguishing noise and salient forms within the image.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACM | Active Connections Matrix |
| GPS | Global Positioning System |
| WGS84 | World Geodetic System 1984 |
| GCP | Ground Control Point |
| CP | Check Point |
| DN | Digital Number |
| HCS | Hyperspherical Color Space |
| PCA | Principal Component Analysis |
| NDVI | Normalized Difference Vegetation Index |
| WVWI | WorldView Water Index |
| AR | Automata Rule |
| New IAC | New Interactive Activation and Competition |
| New CS | New Constraints Satisfaction Network |
| CM | Contractive Maps |
| Anti-CM | Anti-Contractive Maps |
Appendix A.
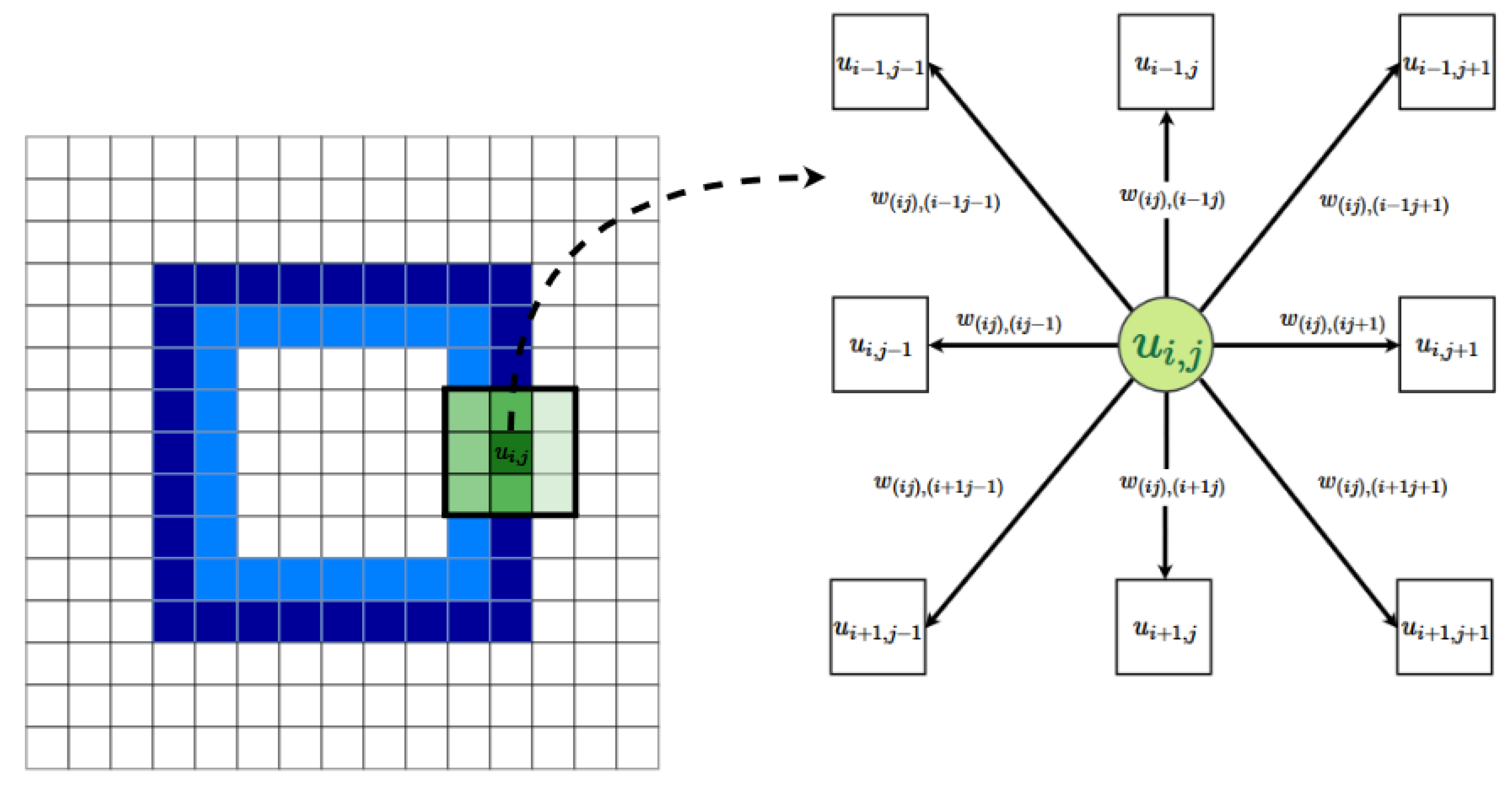
Appendix A.1. Automata Rule
Appendix A.2. New IAC
Appendix A.3. New CS
Appendix A.4. Contractive Maps
| Name | Equation |
|---|---|
| Mean | |
| Variance | |
| Maximum | |
| Minimum |
Appendix B.
Appendix ACM Elaboration




References
- Istituto Superiore per la Protezione e Ricerca Ambientale (ISPRA). Mare e Ambiente Costiero. 2011. Available online: http://www.isprambiente.gov.it/it/pubblicazioni/stato-dellambiente/ tematiche-in-primo-piano-annuario-dei-dati-ambientali-2011 (accessed on 17 October 2016).
- Istituto Superiore per la Protezione e Ricerca Ambientale (ISPRA). Mare e Ambiente Costiero. 2014–2015. Available online: http://www.isprambiente.gov.it/it/pubblicazioni/stato-dellambiente/ tematiche-in-primo-piano-annuario-dei-dati-ambientali-2014-2015 (accessed on 17 October 2016).
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Lasalandra, M.G. Metodologia per la Mappatura Delle Spiagge e Della Dinamica Litoranea Mediante la Classificazione di Immagini Digitali, ISPRA, 2009. Available online: http://www.isprambiente.gov.it/contentfiles/00004400/4488-lasalandra.zip/atdownload/file (accessed on 23 January 2017).
- Aguilar, F.J.; Fernández, I.; Pérez, J.L.; López, A.; Aguilar, M.A.; Mozas, A.; Cardenal, J. Preliminary results on high accuracy estimation of shoreline change rate based on coastal elevation models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 33, 986–991. [Google Scholar]
- Baiocchi, V.; Dominici, D.; Ialongo, R.; Milone, M.V.; Mormile, M. DSMs Extraction Methodologies from EROS-B “Pseudo-Stereopairs”, PRISM Stereopairs in Coastal and Post-seismic Areas. In Computational Science and Its Applications—ICCSA 2013. ILecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Palazzo, F.; Latini, D.; Baiocchi, V.; Del Frate, F.; Giannone, F.; Dominici, D.; Remondiere, S. An application of COSMO-SkyMed to coastal erosion studies. Eur. J. Remote Sens. 2012, 45, 361–370. [Google Scholar] [CrossRef]
- Carli, S.; Cipriani, L.E.; Bresci, D.; Danese, C.; Iannotta, P.; Pranzini, E.; Wetzel, L. 6. Tecniche di Monitoraggio Dell’evoluzione Delle Spiagge. In REGIONE TOSCANA. Il Piano Regionale di Gestione Integrata Della Costa ai fini del Riassetto Idrogeologico. Erosione Costiera; EDIFIR: Firenze, Italy, 2004; pp. 125–192. [Google Scholar]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. Assessment and integration of conventional, RTK-GPS and image-derived beach survey methods for daily to decadal coastal monitoring. Coast. Eng. 2011, 58, 194–205. [Google Scholar] [CrossRef]
- Morton, R.A.; Leach, M.P.; Paine, J.G.; Cardoza, M.A. Monitoring beach changes using GPS surveying techniques. J. Coast. Res. 1993, 702–720. [Google Scholar]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Mills, J.P.; Buckley, S.J.; Mitchell, H.L.; Clarke, P.J.; Edwards, S.J. A geomatics data integration technique for coastal change monitoring. Earth Surf. Processes Landf. 2005, 30, 651–664. [Google Scholar] [CrossRef]
- Gonçalves, J.A.; Henriques, R. UAV photogrammetry for topographic monitoring of coastal areas. ISPRS J. Photogramm. Remote Sens. 2015, 104, 101–111. [Google Scholar] [CrossRef]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 111–124. [Google Scholar]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for coastal surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Papakonstantinou, A.; Topouzelis, K.; Pavlogeorgatos, G. Coastline zones identification and 3D coastal mapping using UAV spatial data. ISPRS Int. J. Geo-Inf. 2016, 5, 75. [Google Scholar] [CrossRef]
- Stockdonf, H.F.; Sallenger, A.H.; List, J.H.; Holman, R.A. Estimation of shoreline position and change using airborne topographic lidar data. J. Coast. Res. 2002, 502–513. [Google Scholar]
- Paravolidakis, V.; Moirogiorgou, K.; Ragia, L.; Zervakis, M.; Synolakis, C. Coastline extraction from aerial images based on edge detection. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 2016 3, 153–158. [Google Scholar] [CrossRef]
- Lee, I.C.; Wu, B.; Li, R. Shoreline extraction from the integration of lidar point cloud data and aerial orthophotos using mean-shift segmentation. In Proceedings of the ASPRS Annual Conference, Baltimore, MD, USA, 9–13 March 2009; Volume 2, pp. 3033–3040. [Google Scholar]
- Paravolidakis, V.; Ragia, L.; Moirogiorgou, K.; Zervakis, M. Automatic Coastline Extraction Using Edge Detection and Optimization Procedures. Geosciences 2018, 8, 407. [Google Scholar] [CrossRef]
- Dominici, D.; Beltrami, G.M.; De Girolamo, P. Ortorettifica di Immagini satellitari ad alta risoluzione finalizzata al monitoraggio costiero a scala regionale. Stud. Cost. 2006, 11, 145–146. [Google Scholar]
- Di, K.; Wang, J.; Ma, R.; Li, R. Automatic shoreline extraction from high-resolution IKONOS satellite imagery. In Proceedings of the ASPRS 2003 Annual Conference, Anchorage, AK, USA, 5–9 May 2003; Volume 3. [Google Scholar]
- Digital Globe. Available online: https://www.digitalglobe.com (accessed on 17 October 2016).
- ERDAS IMAGINE|Hexagon Geospatial. Planetek, ERDAS IMAGINE TourGuide, PRODUCER Suite of Power Portfolio by Hexagon Geospatial; ERDAS IMAGINE|Hexagon Geospatial: Madison, AL, USA, 2015. [Google Scholar]
- Padwick, C.; Deskevich, M.; Pacifici, F.; Smallwood, S. WorldView-2 Pansharpening. In Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010. [Google Scholar]
- ERDAS IMAGINE|Hexagon Geospatial. Planetek, ERDAS IMAGINE, Software, PRODUCER Suite of Power Portfolio by Hexagon Geospatial; ERDAS IMAGINE|Hexagon Geospatial: Madison, AL, USA, 2015. [Google Scholar]
- Wolf, A.F. Using WorldView-2 Vis-NIR multispectral imagery to support land mapping and feature extraction using normalized difference index ratios. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII; International Society for Optics and Photonics: Washington, DC, USA, 2012; Volume 8390. [Google Scholar]
- Gandhi, G.M.; Parthiban, S.; Thummalu, N.; Christy, A. NDVI: Vegetation change detection using remote sensing and GIS—A case study of Vellore District. Procedia Comput. Sci. 2015, 57, 1199–1210. [Google Scholar] [CrossRef]
- NDVI. MODIS U.S. 16-Day Vegetation Index Product. University of Maryland. 2013. Available online: http://glcf.umd.edu/data/ndvi/description.shtml (accessed on 24 September 2018).
- Bao, G.; Qin, Z.; Bao, Y.; Zhou, Y.; Li, W.; Sanjjav, A. NDVI-based long-term vegetation dynamics and its response to climatic change in the Mongolian Plateau. Remote Sens. 2014, 6, 8337–8358. [Google Scholar] [CrossRef]
- Land Info. Available online: http://www.landinfo.com/WorldView2.htm (accessed on 4 June 2018).
- Buscema, P.M. Sistemi ACM e Imaging Diagnostico: Le Immagini Mediche Come Matrici Attive di Connessioni; Springer Science & Business Media: Milano, Italy, 2006. [Google Scholar]
- Buscema, M.; Grossi, E. J-Net System: A New Paradigm for Artificial Neural Networks Applied to Diagnostic Imaging. In Applications of Mathematics in Models, Artificial Neural Networks and Arts; Springer Publishing House: Dordrecht, The Netherlands, 2010; pp. 431–455. [Google Scholar]
- Buscema, P.M. ACM Batch, Semeion Software #33, Semeion, Rome, Italy. Available online: www.semeion.it (accessed on 4 June 2018).
- Maglione, P.; Parente, C.; Vallario, A. Coastline extraction using high resolution WorldView-2 satellite imagery. Eur. J. Remote Sens. 2014, 47, 685–699. [Google Scholar] [CrossRef]







| 1950/1999 Variations >±25 m | 2000/2007 Variations >±5 m | |||
|---|---|---|---|---|
| Low-lying coastal | km | % | km | % |
| Total | 4862 | 100.0 | 4715 | 100.0 |
| Stable | 2387 | 49.1 | 2737 | 58.0 |
| Modified | 2227 | 45.8 | 1744 | 37.0 |
| Undefined | 248 | 5.1 | 234 | 5.0 |
| Modified | 2227 | 45.8 | 1744 | 37.0 |
| Backwardness | 1170 | 24.1 | 895 | 19.0 |
| Progress | 1058 | 21.8 | 849 | 18.0 |
| NDVI | WVWI | CM_NIR2 | |
|---|---|---|---|
| Profile 1 | |||
| Profile 2 | Not well defined | ||
| Profile 3 | 1.00 | Not well defined |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dominici, D.; Zollini, S.; Alicandro, M.; Della Torre, F.; Buscema, P.M.; Baiocchi, V. High Resolution Satellite Images for Instantaneous Shoreline Extraction Using New Enhancement Algorithms. Geosciences 2019, 9, 123. https://doi.org/10.3390/geosciences9030123
Dominici D, Zollini S, Alicandro M, Della Torre F, Buscema PM, Baiocchi V. High Resolution Satellite Images for Instantaneous Shoreline Extraction Using New Enhancement Algorithms. Geosciences. 2019; 9(3):123. https://doi.org/10.3390/geosciences9030123
Chicago/Turabian StyleDominici, Donatella, Sara Zollini, Maria Alicandro, Francesca Della Torre, Paolo Massimo Buscema, and Valerio Baiocchi. 2019. "High Resolution Satellite Images for Instantaneous Shoreline Extraction Using New Enhancement Algorithms" Geosciences 9, no. 3: 123. https://doi.org/10.3390/geosciences9030123
APA StyleDominici, D., Zollini, S., Alicandro, M., Della Torre, F., Buscema, P. M., & Baiocchi, V. (2019). High Resolution Satellite Images for Instantaneous Shoreline Extraction Using New Enhancement Algorithms. Geosciences, 9(3), 123. https://doi.org/10.3390/geosciences9030123









