Rock Mass Behavior under Tunnel Widening in Asymmetric and Symmetric Modes Considering Different Shapes and Parametric Conditions
Abstract
1. Introduction
2. Engineering Overview and Numerical Methods
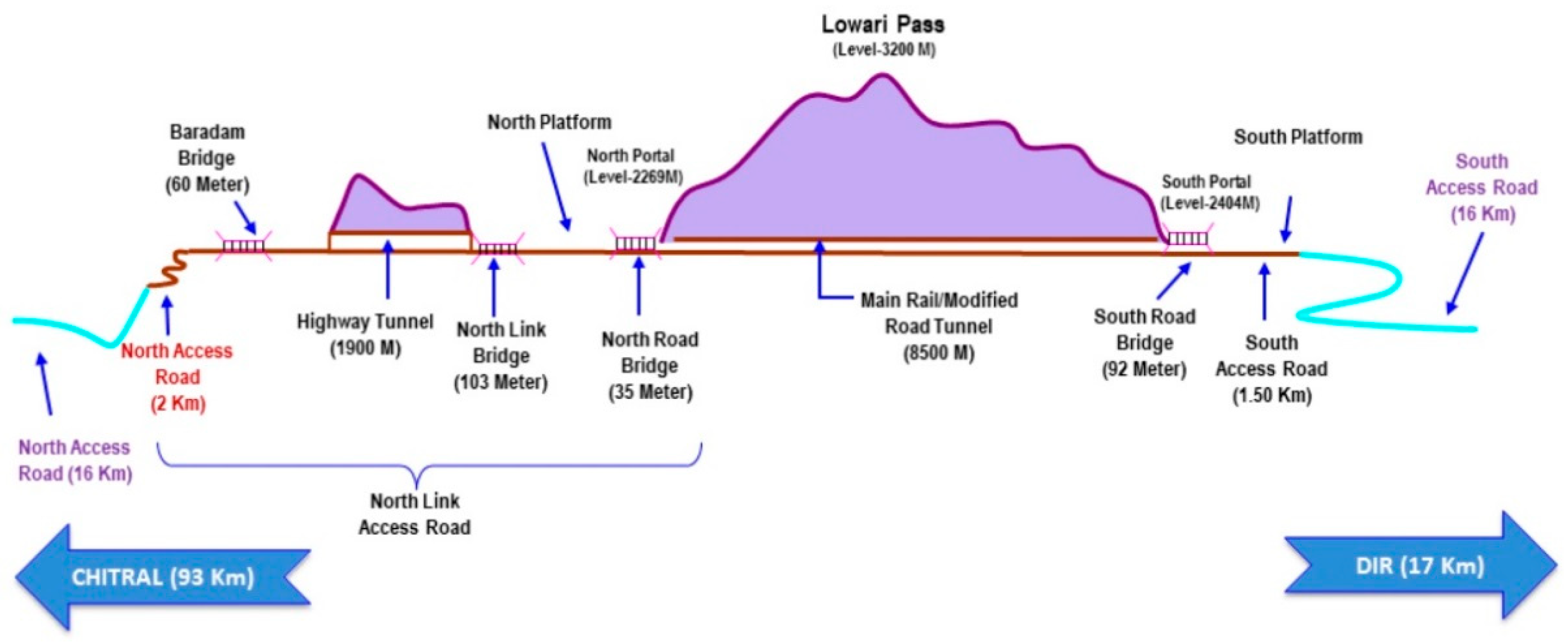
2.1. Lowari Tunnel Project
2.1.1. Geology of the Site
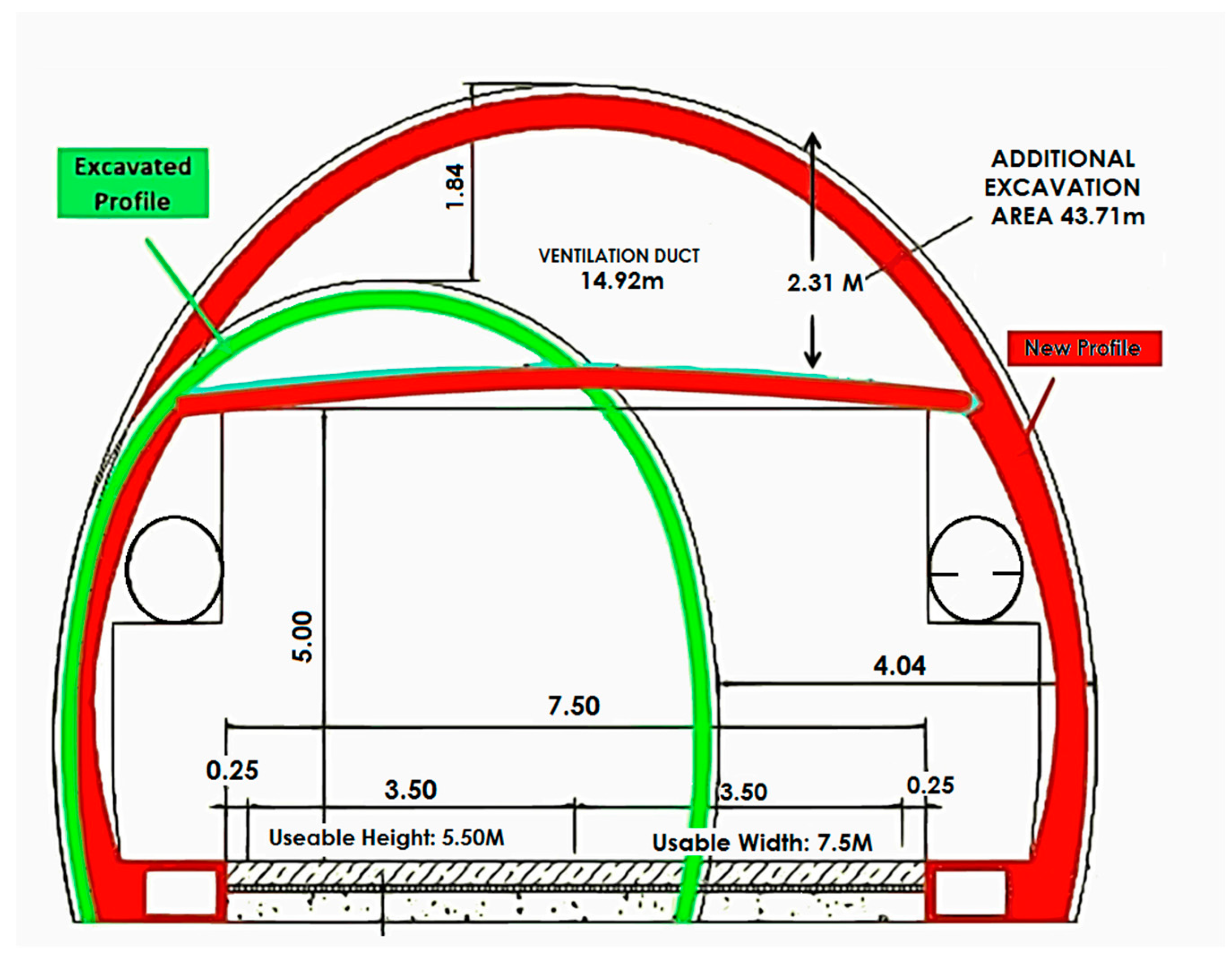
2.1.2. Conversion of Rail to Road Tunnel
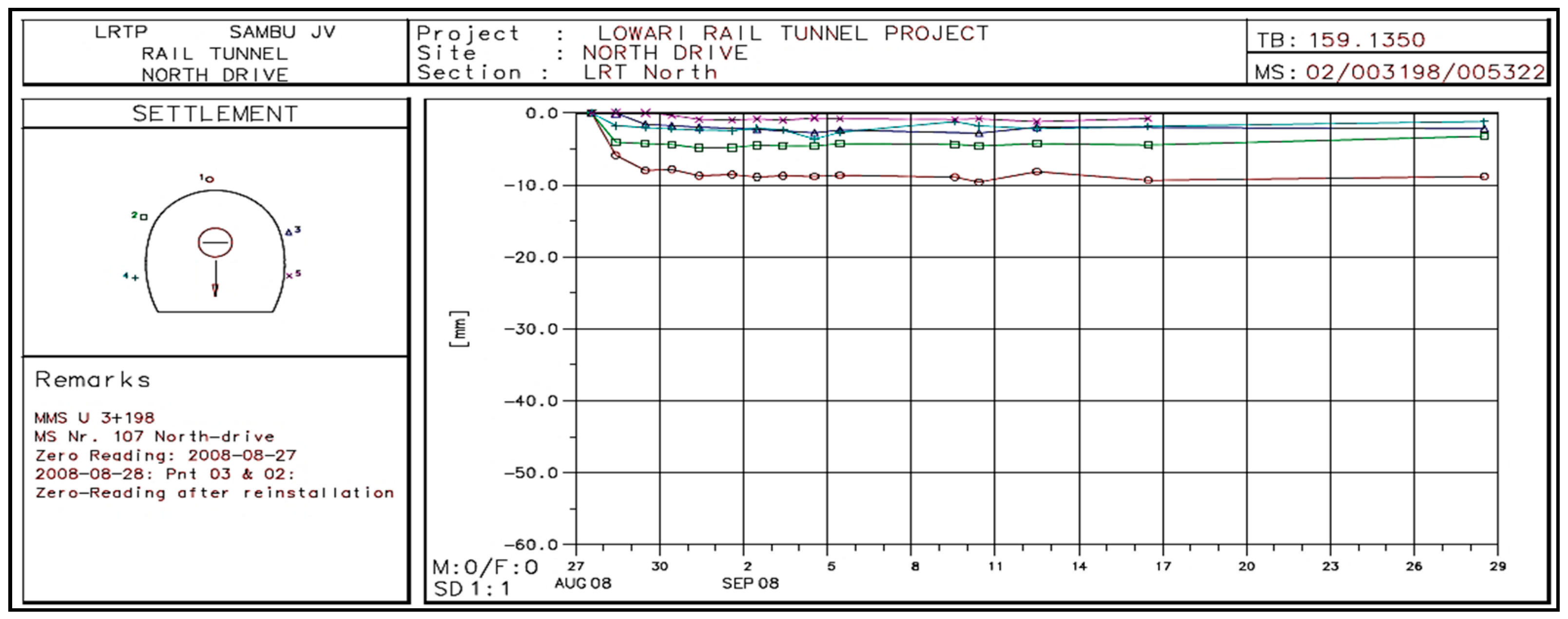
2.2. Correlation of Tunnel Deformation Obtained through In Situ Monitoring and Numerical Simulation
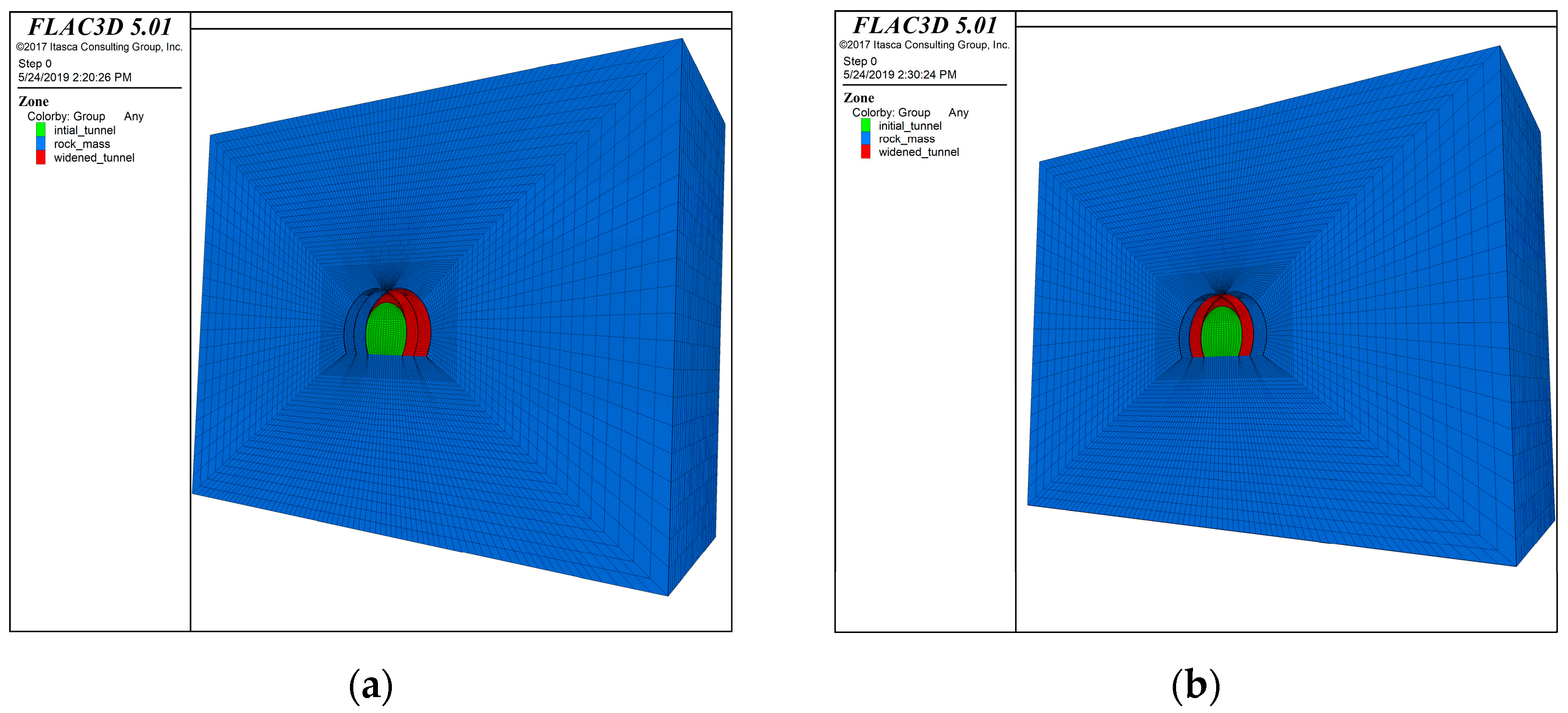
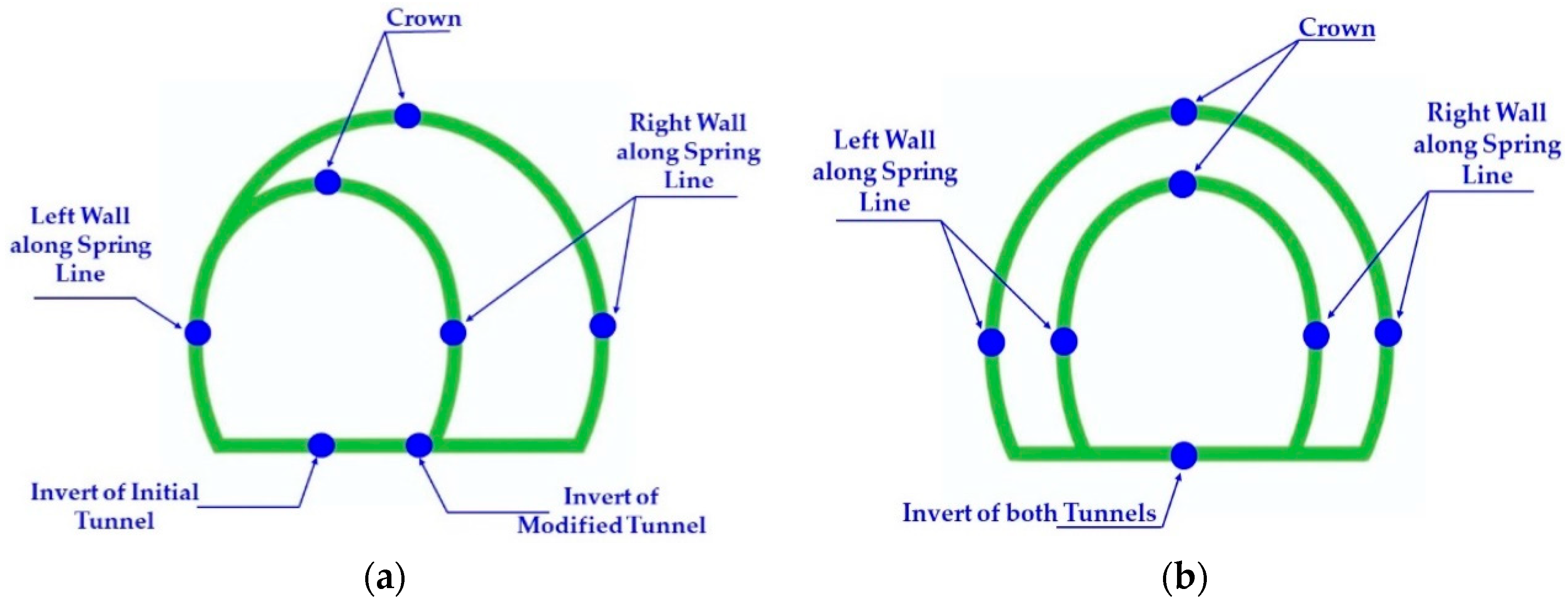
2.3. Initial Model Preparation for Asymmetric and Symmetric Widening
3. Simulation of Asymmetric and Symmetric Widening Models
3.1. Different Tunnel Modes for Evaluation
3.2. Different Tunnel Shapes for Evaluation
3.3. Models Geometry and Tunnel Support Characteristics
4. Results
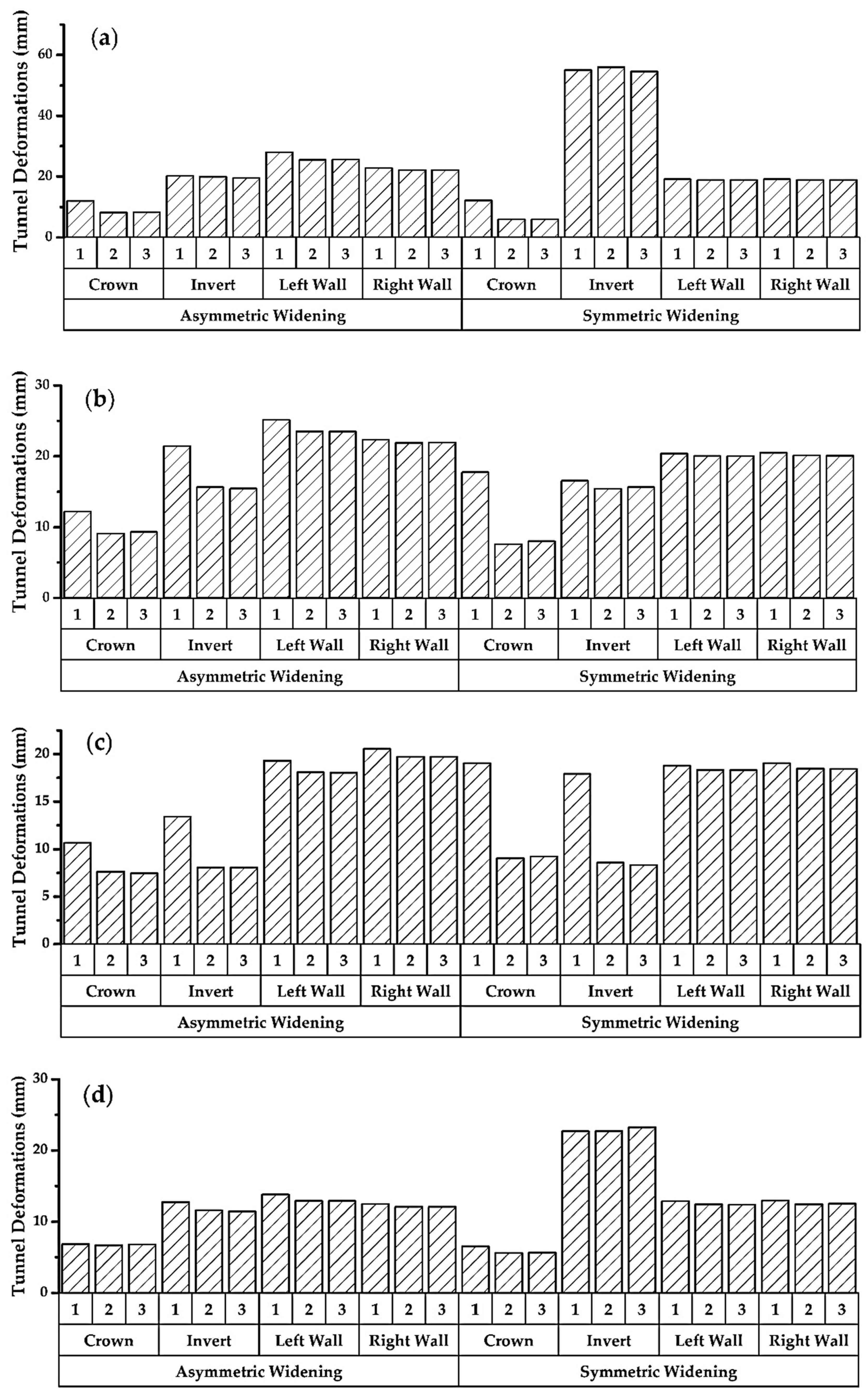
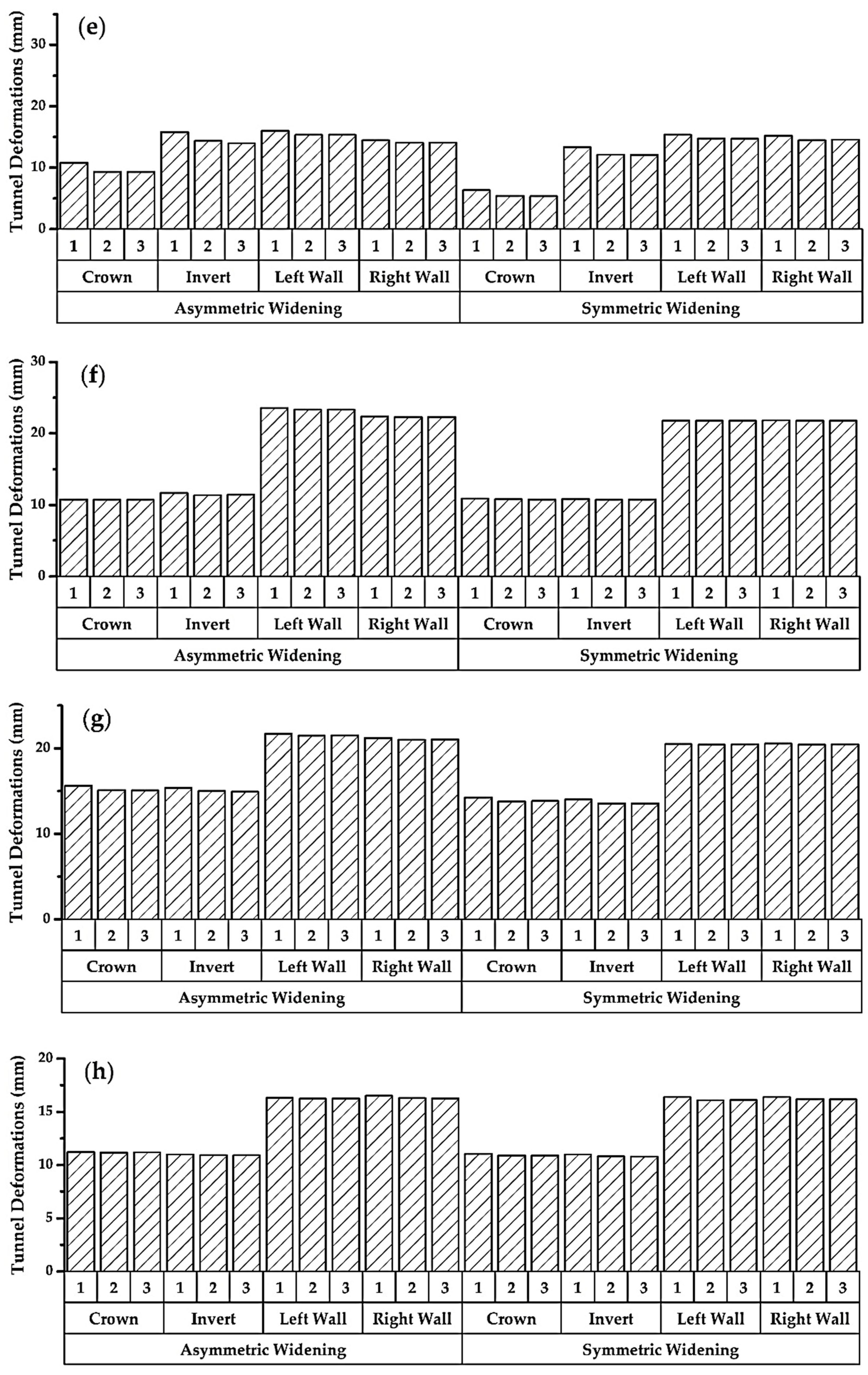
4.1. Simulated Deformation of Different Tunnel Shapes
4.2. Full Factorial Design
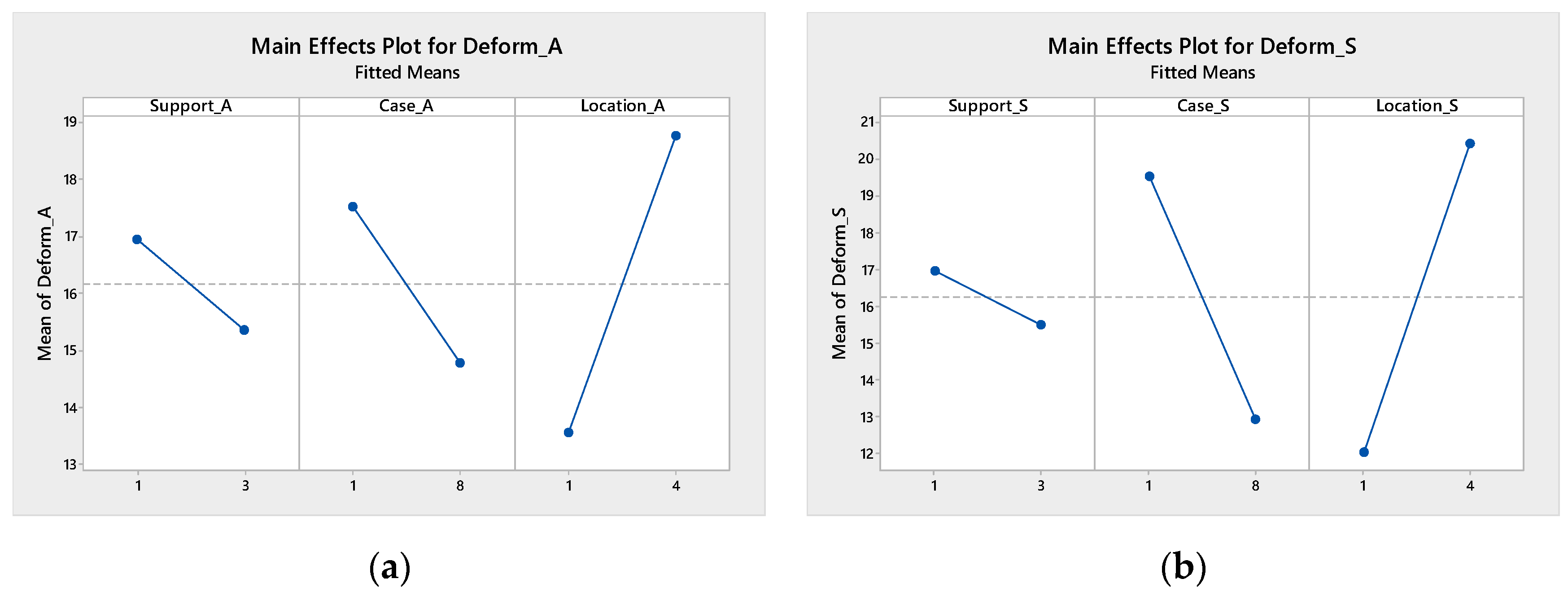
4.2.1. Main Effect Plot
4.2.2. Interaction Effect Plot
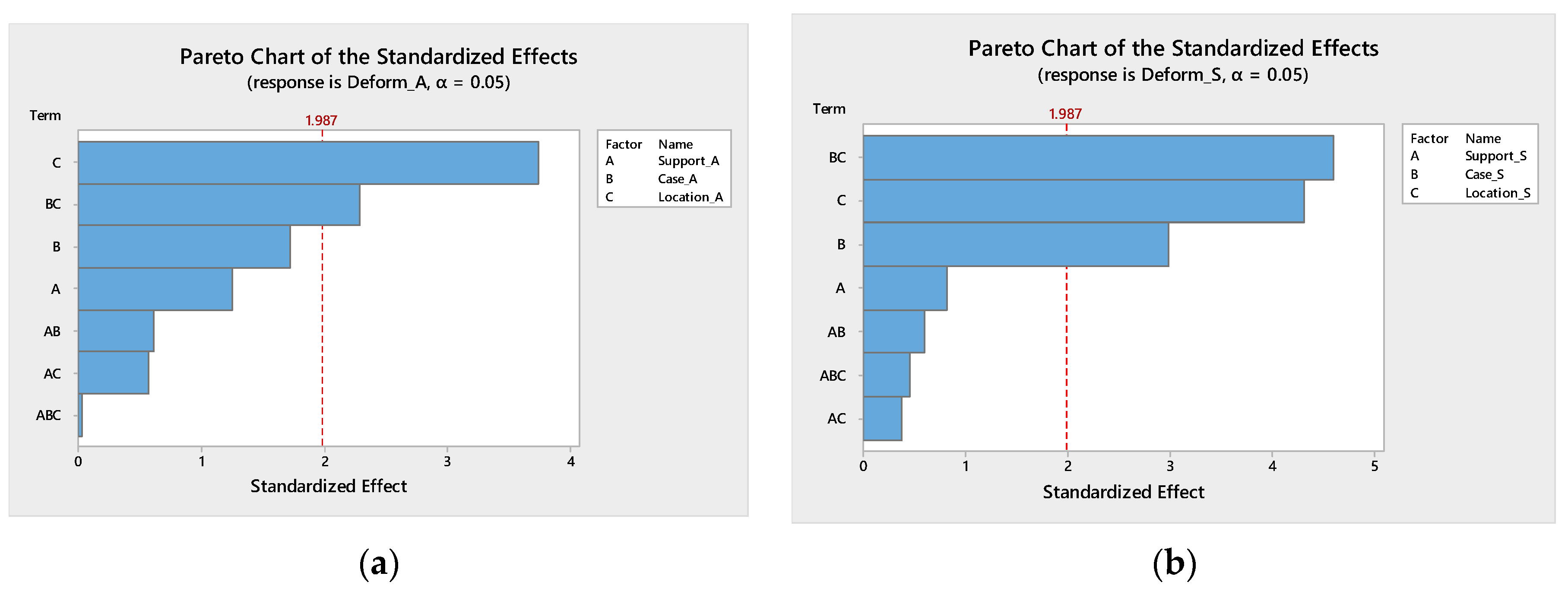
4.2.3. Pareto Chart
4.3. Parametric Study
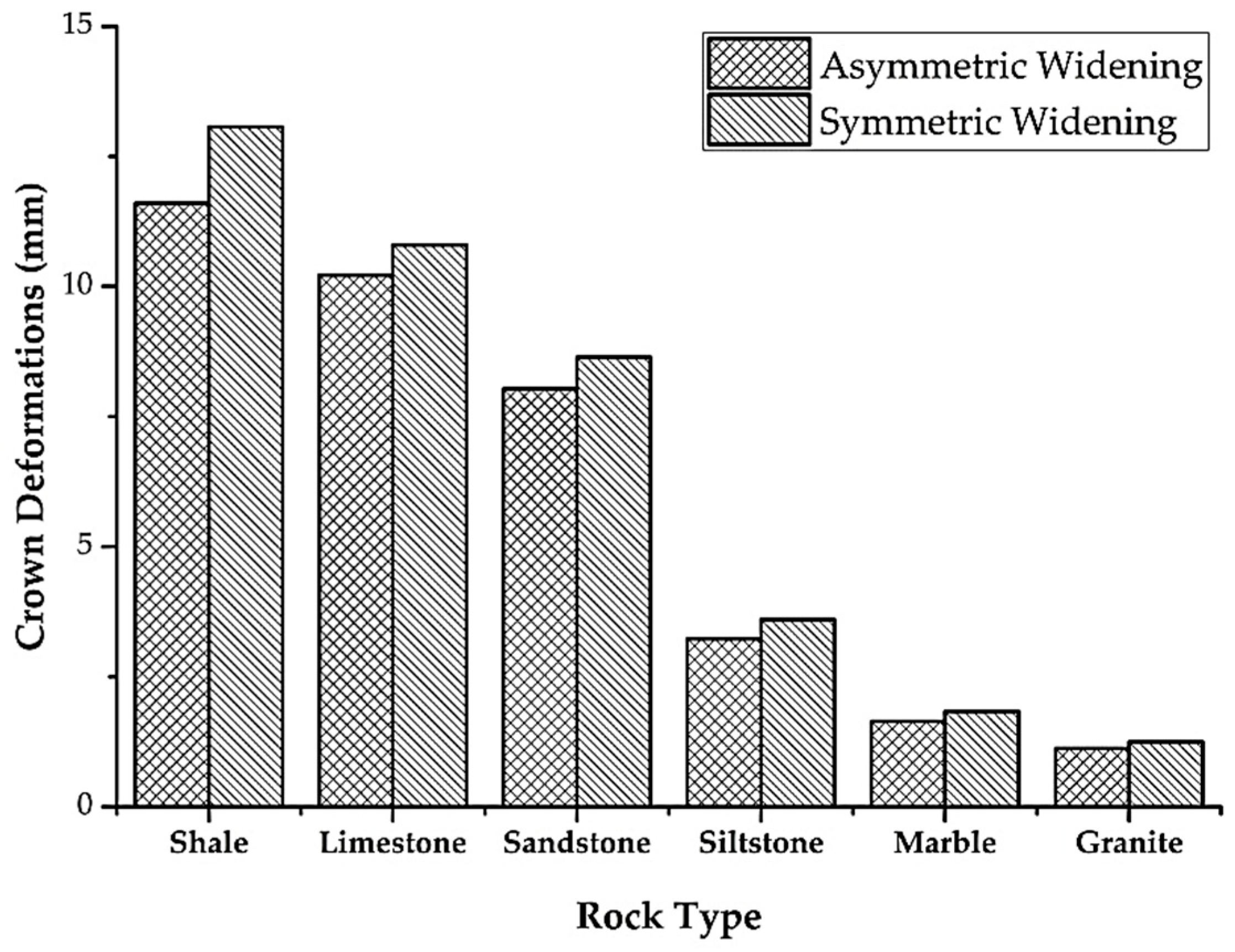
4.3.1. The Effects of Different Rock Types on Rock Mass Behavior
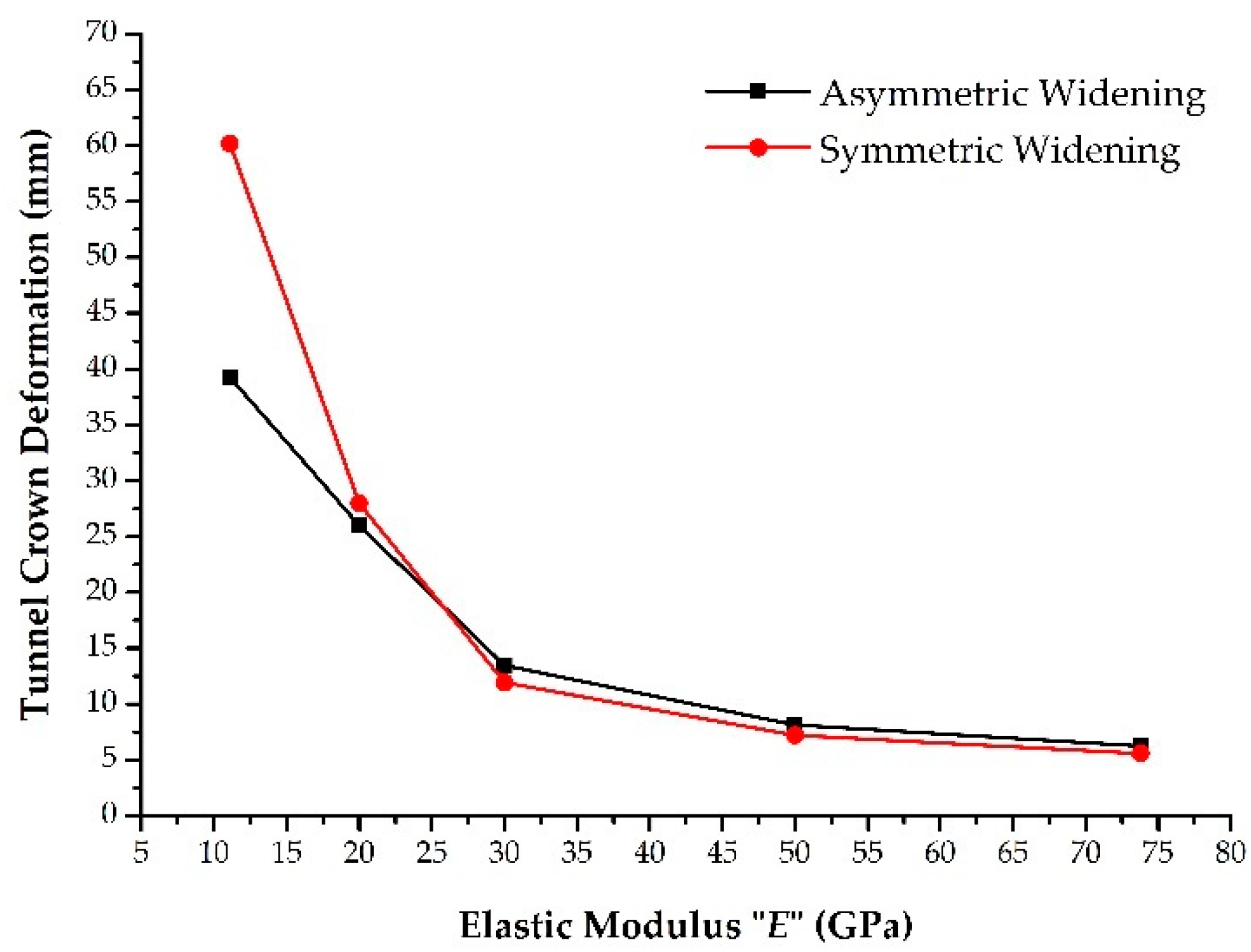
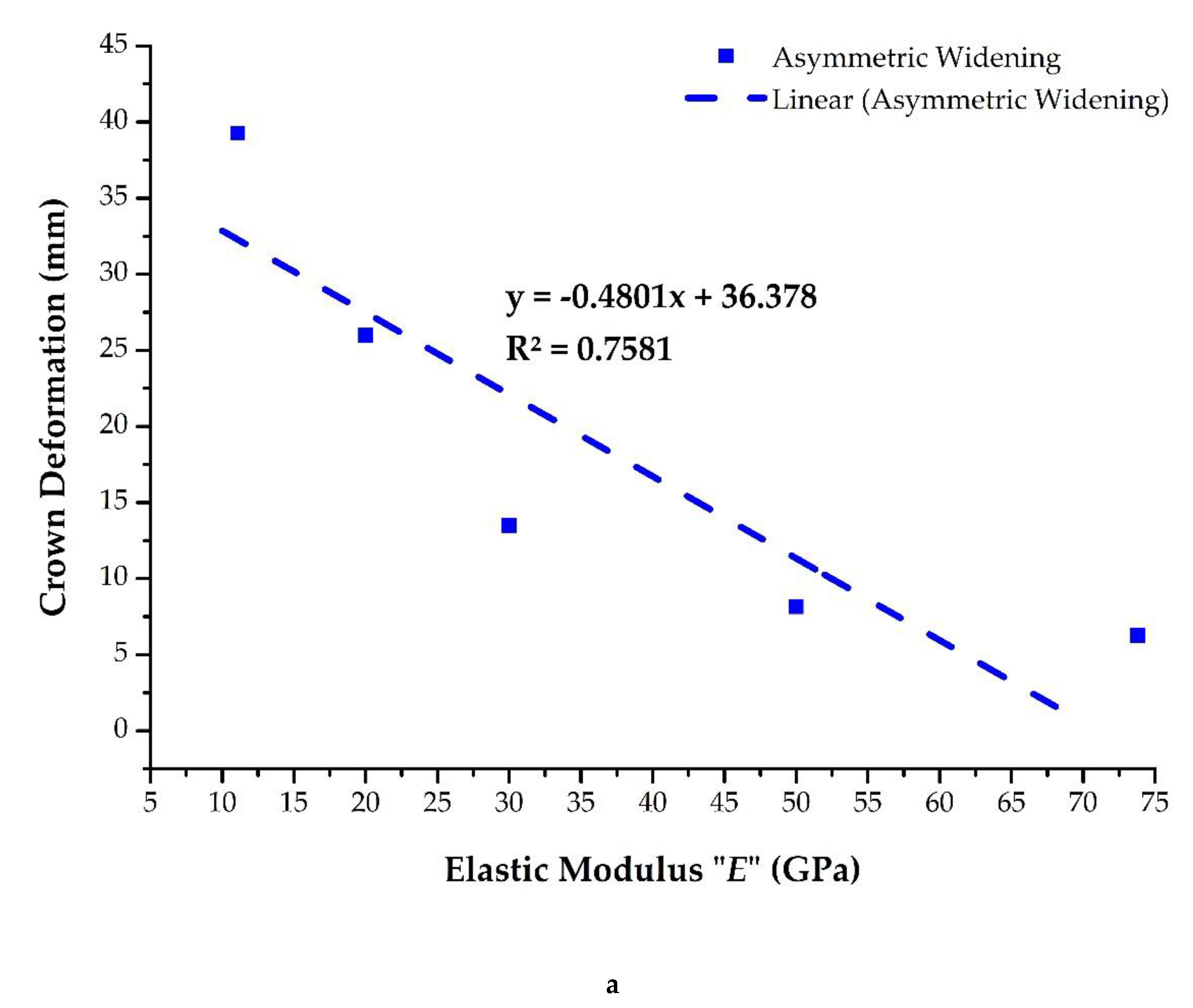
4.3.2. The Effect of the Elastic Modulus (E) on Rock Mass Behavior
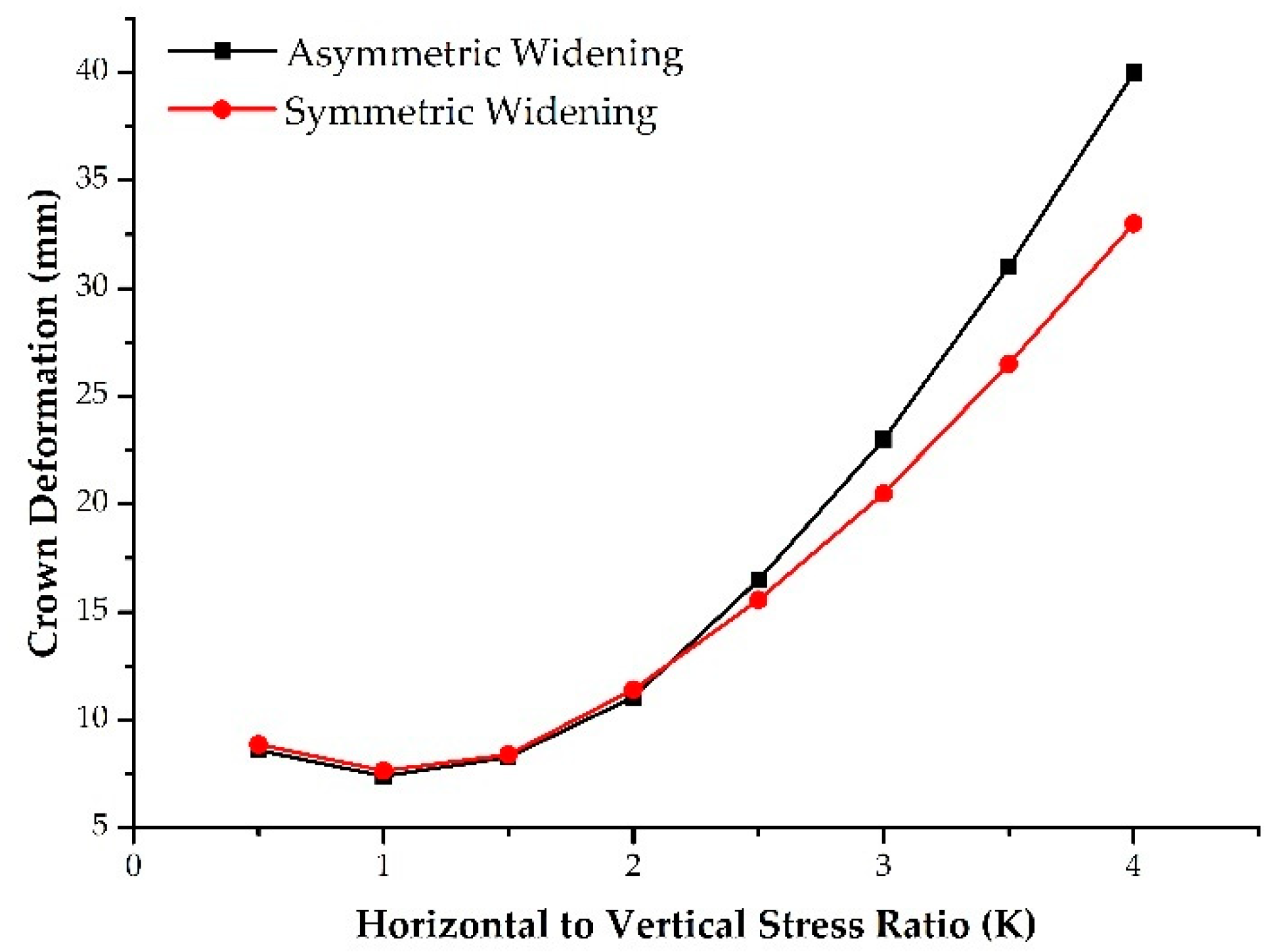
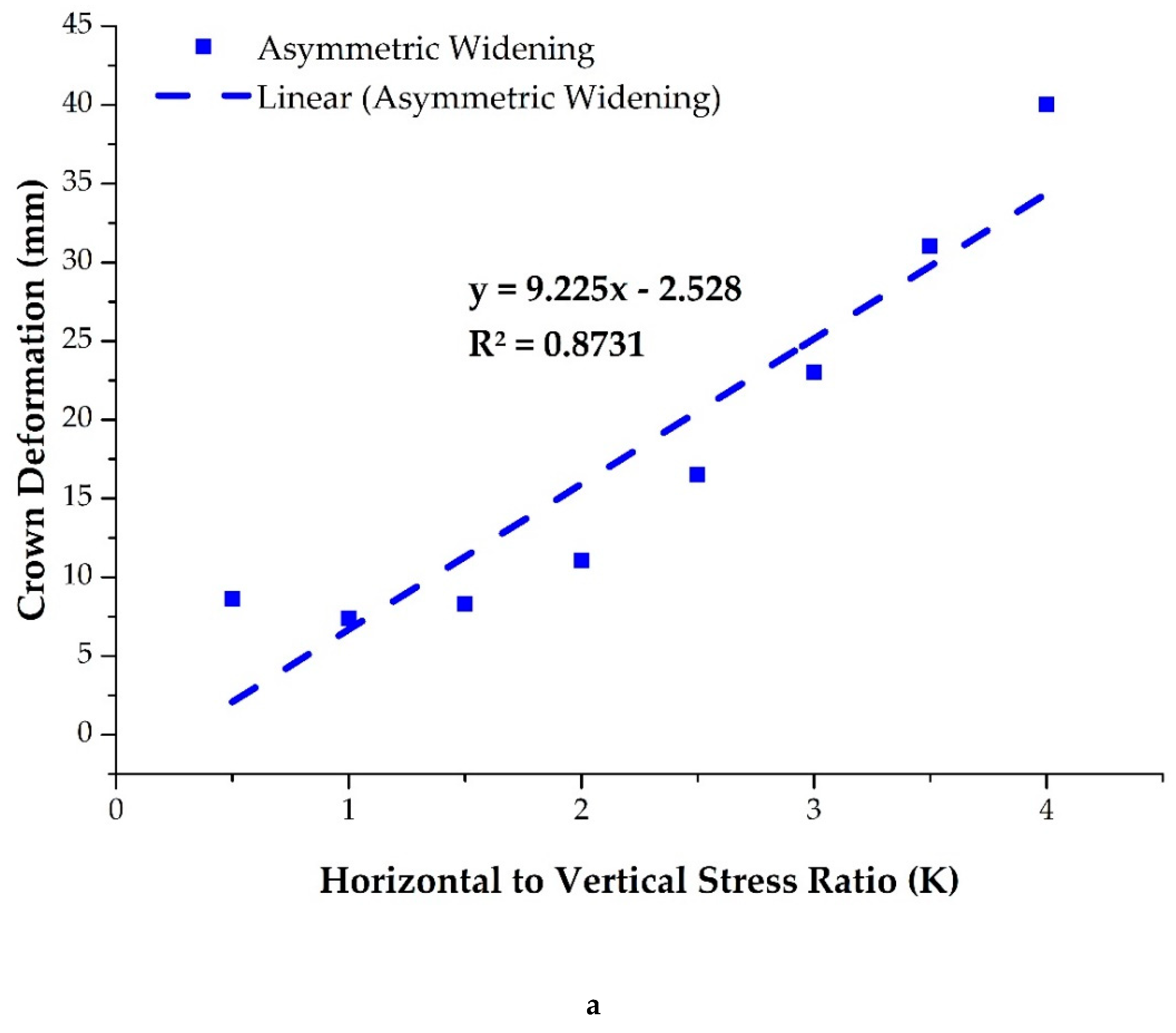
4.3.3. The Effect of the Horizontal to Vertical Stress Ratio (K) on Rock Mass Behavior
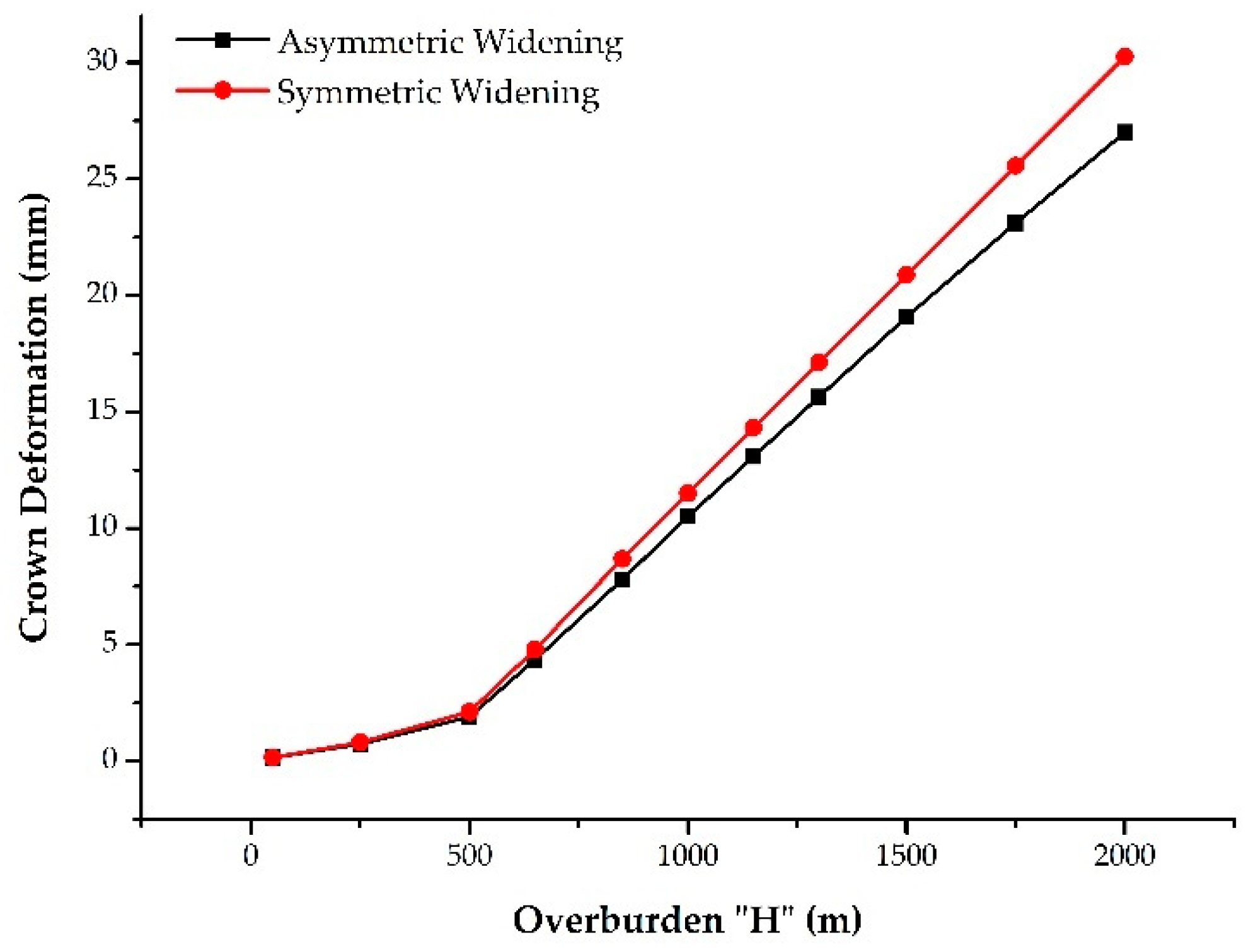
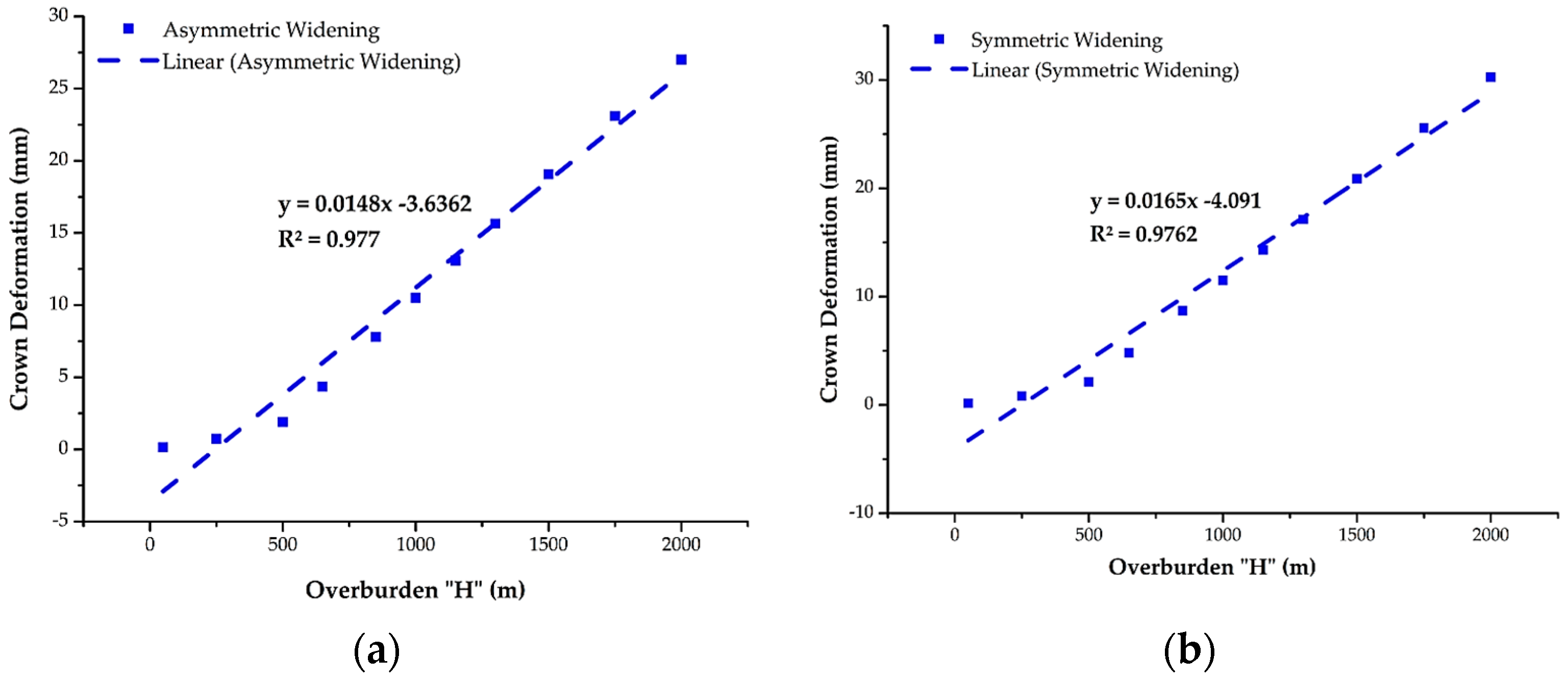
4.3.4. Effect of the Overburden Height (H) on Rock Mass Behavior
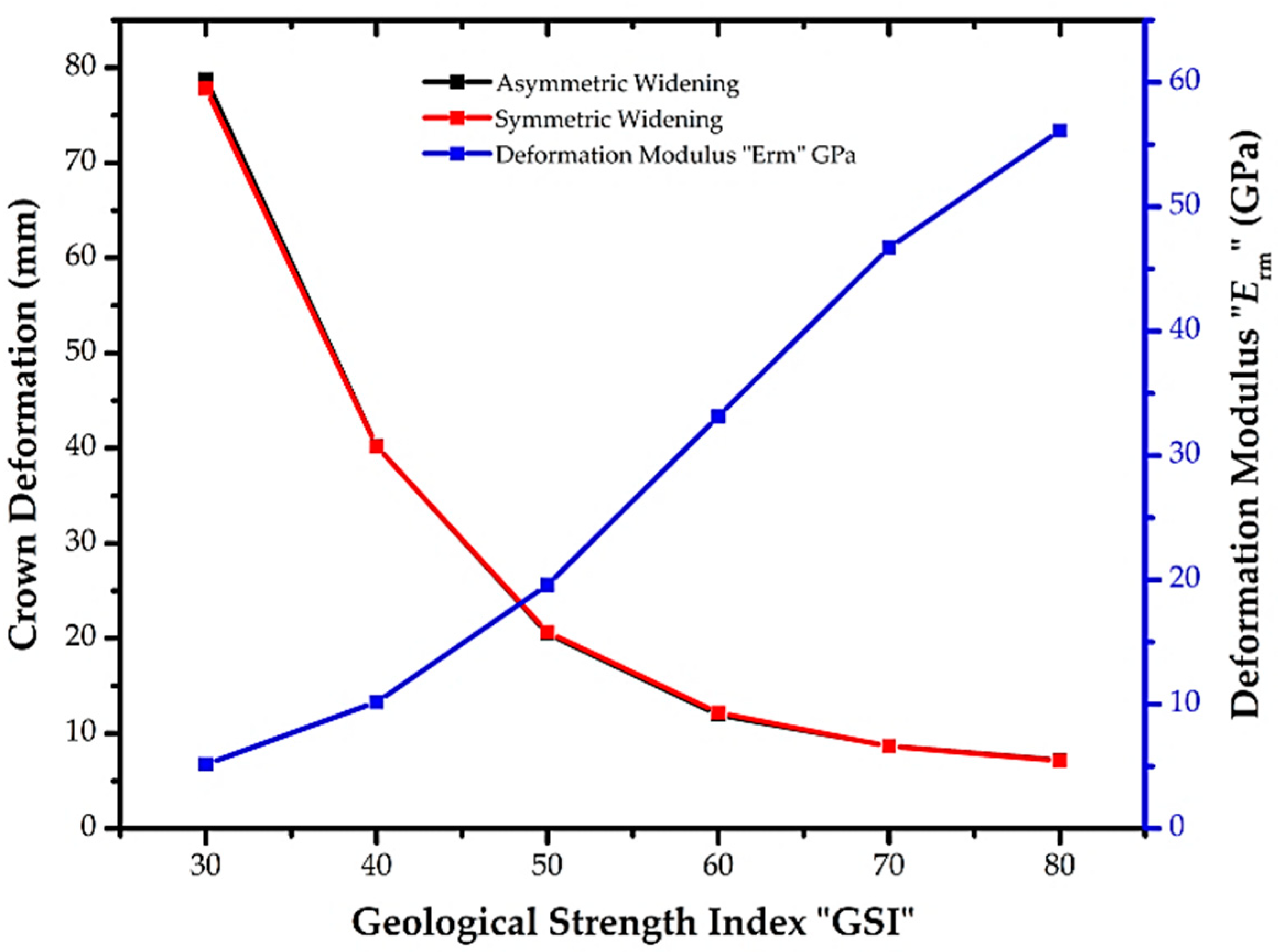
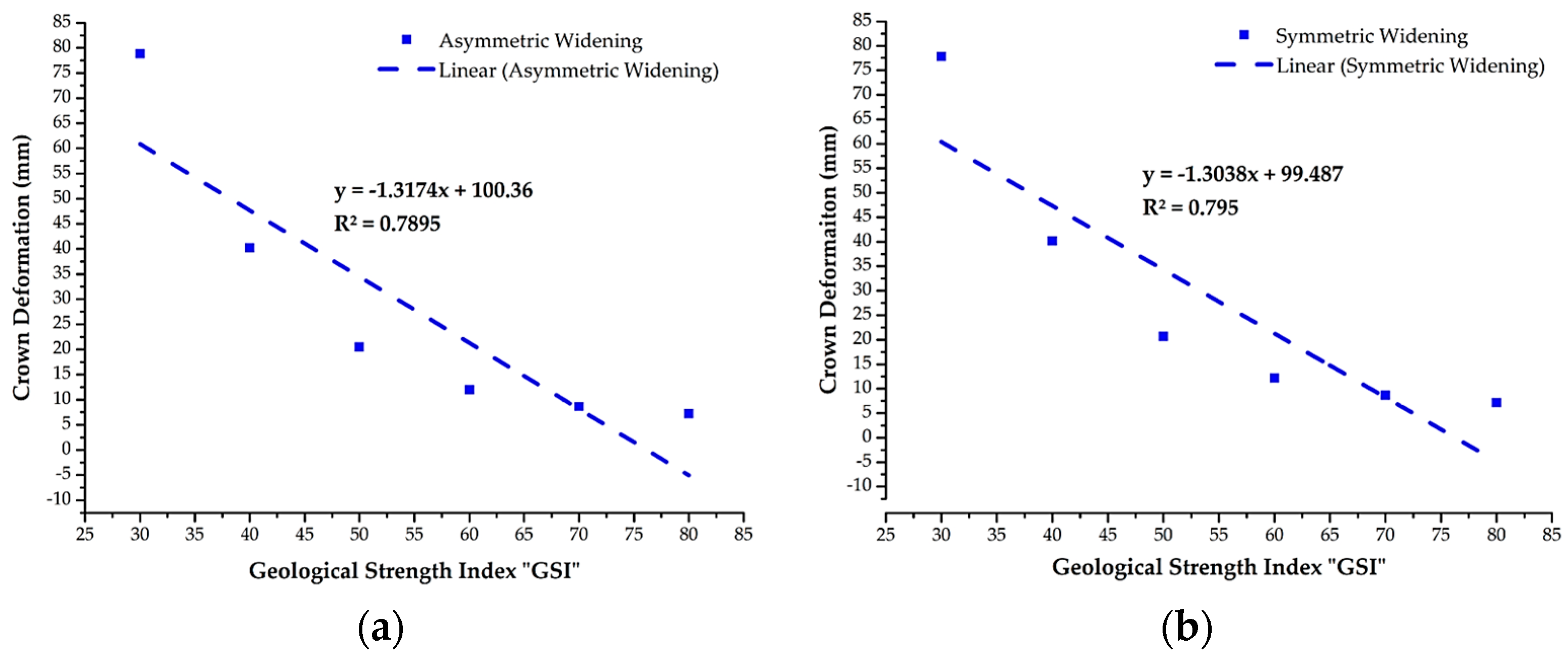
4.3.5. Effect of the Geological Strength Index (GSI) on Rock Mass Behavior
5. Conclusions
- During symmetrical widening, tunnels with a round shape, like horseshoe and semicircular with flatbed, have accumulated stress and deformations at the invert, whereas such deformations can be controlled through asymmetric widening of the tunnel.
- By introducing the round invert to round shape tunnels, the deformations at invert can be minimized. Moreover, in contrast to the flatbed case, symmetric widening can provide more controlled tunnel deformations than asymmetric widening.
- Symmetric widening is recommended for circular tunnels under unsupported conditions; however, there is the same behavior for both types of widening in the case of tunnel support.
- There is an insignificant effect of the difference between asymmetric and symmetric widening in regular shaped tunnels, i.e., box, rectangular, and semi-elliptical shapes.
- In the asymmetric condition, the tunnel’s left side wall remains unaltered during tunnel widening, which provides support to the open cavity around the excavation periphery.
- In the statistical analysis, it was found that the tunnel support system in different tunnel shapes decreases tunnel deformation by an average of 13.33% in asymmetric tunnel widening and around 8.82% in symmetric tunnel widening.
- The shotcrete provides more stability in the widening process, especially in asymmetric widening. However, the rock bolts reduce the deformation but impart less effect on the difference in deformation between the two widening modes.
- The differences in tunnel monitoring locations, i.e., crown, right wall, left wall, and invert have significant relationships with each other and with the interaction of different tunnel support modes.
- The tunnel deformation is inversely proportional to the rock strength, wherein the ratio of the difference in deformation at the crown of the horseshoe tunnel between asymmetric and symmetric widening is the same from high to low strength rock.
- In a parametric study, the results revealed that the lower elastic modulus value, higher horizontal to vertical stress ratio, and higher overburden height values have a greater difference in deformation for both widening options.
- Geological Strength Index variation is inversely proportional to tunnel deformation, whereas it imparts an insignificant deformation difference between asymmetric and symmetric widening.
- The study provides a better understanding and guidelines for the planning stage of tunnel and cavern widening scenarios for different shapes under different in situ stress conditions and with different underground support conditions under a variety of parametric conditions, which ultimately increases the tunnel and cavern stability as well as the safety and provides a viable economical solution.
- For future research, it is advisable to work out the rock mass behavior with different widths and the size of asymmetric and symmetric widening of different shapes of the tunnel. Furthermore, the effect of asymmetric widening tunnel on the Longitudinal Displacement Profile (LDP) should also be studied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| σv | Vertical stress, MPa |
| σci | Uniaxial compressive strength, MPa |
| D | Disturbance factor |
| Ei | Elastic modulus, GPa |
| Eh | Average deformation modulus, GPa |
| MR | Modulus ratio |
| Z | Vertical height of rock over the tunnel, m |
References
- Simon, J.L. The Economics of Population Growth; Princeton University Press: Princeton, NJ, USA, 2019; Volume 5403. [Google Scholar]
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Space Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Babar Khan, T.H.J.; Jamil, S.M. Effect of Symmetric and Asymmetric Widening of Tunnel on Rock Mass Behaviour in Various Rock Types and In Situ Stress State. In 7th Annual International Conference on Architecture and Civil Engineering—ACE-2019; GSTF, Ed.; GSTF: Singapore, 2019; p. 10. [Google Scholar]
- Li, C.C. Principles of rockbolting design. J. Rock Mech. Geotech. Eng. 2017, 9, 396–414. [Google Scholar] [CrossRef]
- Shang, J.; Yokota, Y.; Zhao, Z.; Dang, W. DEM simulation of mortar-bolt interface behaviour subjected to shearing. Constr. Build. Mater. 2018, 185, 120–137. [Google Scholar] [CrossRef]
- Bertuzzi, R. Back-analysing rock mass modulus from monitoring data of two tunnels in Sydney, Australia. J. Rock Mech. Geotech. Eng. 2017, 9, 877–891. [Google Scholar] [CrossRef]
- Choi, H.-J.; Kim, D.-K. A study on the enlargement of 2-Lane road tunnel under construction. J. Korean Tunn. Undergr. Space Assoc. 2011, 13, 33–50. [Google Scholar]
- Andrea, O. Design and excavation for the widening of a railway tunnel: The case of the Castellano tunnel in Italy. In Proceedings of the SEE Tunnel: Promoting Tunneling in SEE Region“ITA WTC 2015 Congress and 41st General Assembly, Dubrovnik, Croatia, 22–28 May 2015. [Google Scholar]
- Lunardi, P. Method for Widening Road, Superhighway or Railway Tunnels, Without Interrupting the Traffic. U.S. Patent 6,375,390, 23 April 2002. [Google Scholar]
- Lunardi, P.; Calcerano, G. A new construction method for widening highway and railway tunnels. In Atti del Congresso Internazionale su Progress in Tunnelling After; Pàtron Editore: Bologna, Italy, 2000. [Google Scholar]
- Lee, M.-H.; Koh, S.-Y.; Kim, B.-J.; Jang, Y.-S.; Yun, J.-N. Stability evaluation on widening of parallel tunnels. In Geotechnical Aspects of Underground Construction in Soft Ground; CRC Press: Boca Raton, FL, USA, 2014; p. 269. [Google Scholar]
- Hu, J.; Huang, L. Research on Wallrock Deformation and Mechanical Properties of In-Situ Expansion Tunnel. Technol. Highw. Transp. 2011, 6, 21. [Google Scholar]
- Hu, J.; Chen, L.; Huang, L. Research on Expansion Modes of Two-lane to Four-lane Tunnels. Technol. Highw. Transp. 2010, 5, 93–97. [Google Scholar]
- Jafri, T.; Yoo, H. REV Application in DEM Analysis of Non-Vibrational Rock Splitting Method to Propose Feasible Borehole Spacing. Appl. Sci. 2018, 8, 335. [Google Scholar] [CrossRef]
- Jing, L.; Hudson, J. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Debecker, B. Influence of Planar Heterogeneities on the Fracture Behaviour of Rock. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2009. [Google Scholar]
- Cai, M.; Horii, H. A constitutive model and FEM analysis of jointed rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 351–359. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Shang, J.; Zhao, Z.; Ma, S. On the shear failure of incipient rock discontinuities under CNL and CNS boundary conditions: Insights from DEM modelling. Eng. Geol. 2018, 234, 153–166. [Google Scholar] [CrossRef]
- Prazeres, P.G.; Thoeni, K.; Beer, G. Nonlinear analysis of NATM tunnel construction with the boundary element method. Comput. Geotech. 2012, 40, 160–173. [Google Scholar] [CrossRef]
- FLAC 3D: Fast Lagrangian Analysis of Continua in 3 Dimensions; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2015.
- Chakeri, H.; Unver, B.; Ozcelik, Y. A novel relationship for predicting the point of inflexion value in the surface settlement curve. Tunn. Undergr. Space Technol. 2014, 43, 266–275. [Google Scholar] [CrossRef]
- Petterson, M.G. The Structure, Petrology and Geochemistry of the Kohistan Batholith, Gilgit, Kashmir, N. Pakistan. Ph.D. Thesis, University of Leicester, Leicester, UK, 1984. [Google Scholar]
- Petterson, M. The plutonic crust of Kohistan and volcanic crust of Kohistan-Ladakh, north Pakistan/India: Lessons learned for deep and shallow arc processes. Geol. Soc. Lond. Spec. Publ. 2018, 483, 123–164. [Google Scholar] [CrossRef]
- Geoconsult, M.S. Geotechnical Interpretative Report; Wiley: Salzburg, Austria, 2004. [Google Scholar]
- Kirsch, C. Die theorie der elastizitat und die bedurfnisse der festigkeitslehre. Z. Des Ver. Dtsch. Ing. 1898, 42, 797–807. [Google Scholar]
- Brown, E.; Hoek, E. Trends in relationships between measured rock in-situ stresses and depth, lnt. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 211–215. [Google Scholar] [CrossRef]
- Sheorey, P. A theory for in situ stresses in isotropic and transverseley isotropic rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 23–34. [Google Scholar] [CrossRef]
- Hoek, E.; Marinos, P. Tunnelling in overstressed rock. In Proceeding of the EUROCK2009, Dubrovnik, Croatia, 29–31 October 2009. [Google Scholar]
- Jaeger, J.C.; Cook, N.G.; Zimmerman, R. Fundamentals of Rock Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 1997, 34, 1165–1186. [Google Scholar] [CrossRef]
- Deere, D.U. Geological Considerations, Rock Mechanics in Engineering Practice, Stagg and Zienkiewicz; John Wiley: New York, NY, USA, 1968. [Google Scholar]
- Goodman, R.E. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1989; Volume 8. [Google Scholar]
- Inc., I. C. G. FLAC 3D User’s Guide; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2013. [Google Scholar]
- Hoek, E.; Marinos, P. Predicting tunnel squeezing problems in weak heterogeneous rock masses. Tunn. Tunn. Int. 2000, 32, 45–51. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion-2002 edition. Proc. NARMS-Tac 2002, 1, 267–273. [Google Scholar]
- SWECO. Final Feasibility Study and Design Review; SWECO: Islamabad, Pakistan, 1995. [Google Scholar]
- Goodman, R. Effect of Joints on the Strength of Tunnels. In Clearinghouse Fed Sci & Tech Info; National Association of Housing & Redeve: Washington, DC, USA, 1968. [Google Scholar]
- Marinos, P.; Marinos, V.; Hoek, E. Geological Strength Index (GSI). A characterization tool for assessing engineering properties for rock masses. In Underground Works under Special Conditions; Taylor and Francis: Lisbon, Portugal, 2007; pp. 13–21. [Google Scholar]
- Ali, Y.; Irfan, M.; Ahmed, S.; Khanzada, S.; Mahmood, T. Investigation of factors affecting dynamic modulus and phase angle of various asphalt concrete mixtures. Mater. Struct. 2016, 49, 857–868. [Google Scholar] [CrossRef]








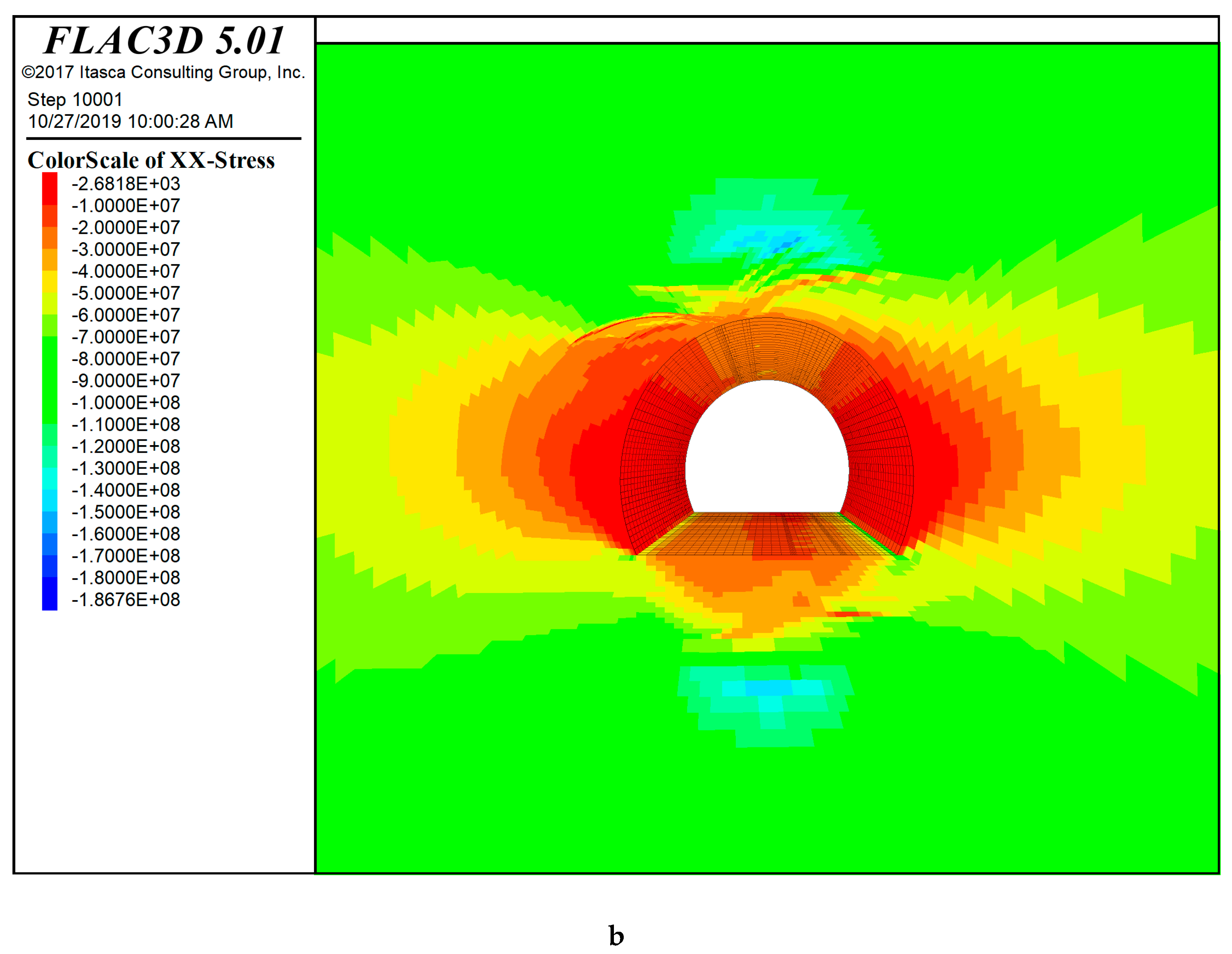
| Description | Detail |
|---|---|
| Rock Type | Granite Gniess with intercalation of Amphibolite |
| Uniaxial Compressive Strength (σci) | 150 MPa |
| Geological Strength Index (GSI) | 60 |
| Poisson’s Ratio (ʋ) | 0.25 |
| Modulus Ratio (MR) | 425 |
| Elastic Modulus of Intact Rock (Ei) | 63.75 GPa |
| Deformation Modulus (Erm) | 33.15 GPa |
| Bulk Modulus (K) | 22.10 GPa |
| Shear Modulus (G) | 13.26 GPa |
| Disturbance Factor (D) | 0 |
| Hoek–Brown parameter (mi) | 30 |
| Hoek–Brown parameter (mb) | 7.19 |
| Hoek–Brown parameter (s) | 0.01174 |
| Hoek–Brown parameter (a) | 0.5028 |
| Tunnel Radius (m) | Horizontal to Vertical Stress Ratio (K) | Vertical Stress σz (MPa) | Horizontal Stress σx (MPa) | Longitudinal Stress σy (MPa) | Displacement at Crown of Small Tunnel (mm) | |
|---|---|---|---|---|---|---|
| Field Monitored Value | Numerical Calculated Value | |||||
| 2.5 | 2 | 34 | 68 | 34 | 8.25 | 8.10 |
| Widening Pattern | Mode-A (Tunnel without Any Support System) | Mode-B (Tunnel with 200 mm Thick Shotcrete Only) | Mode-C (Tunnel with 200 mm Thick Shotcrete + Rock Bolts) |
|---|---|---|---|
| Asymmetric Widening |  | 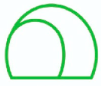 |  |
| Symmetric Widening |  | 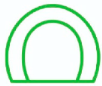 | 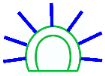 |
| Case | Different Types of Tunnel Shapes | Asymmetric Widening | Symmetric Widening |
|---|---|---|---|
| a. | Horseshoe Shape without Invert |  |  |
| b. | Horseshoe Shape with Invert |  |  |
| c. | Circular Shape |  |  |
| d. | Semicircular Shape without Invert | 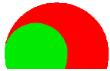 |  |
| e. | Semicircular Shape with Invert |  |  |
| f. | Box/Square Shape |  |  |
| g. | Rectangular Shape |  |  |
| h. | Semi-Elliptical Shape |  |  |
| Rock Bolts Parameters | |
| Rock Bolt | SN Type Rock Bolt |
| Bolt Length | 4 m |
| Elastic Modulus | 45,000 MPa |
| Cross-Sectional Area | 1.57 × 10−3 m2 |
| Bolt Ultimate Tensile Capacity | 250 KN |
| Grout Bond Stiffness | 1.75 × 107 N/m/m |
| Grout Cohesive Strength | 2.0 × 105 N/m |
| Shotcrete Parameters | |
| Shotcrete Thickness | 200 mm |
| Elastic Modulus (E) | 10.5 GPa |
| Poisson’s ratio (v) | 0.25 |
| Variable | Abbreviation | Levels |
|---|---|---|
| Support/Mode | Support-A or Support-S (where A and S, respectively, indicate asymmetric and symmetric) | 1 = Tunnel without Support 2 = Tunnel with 200 mm Shotcrete 3 = Tunnel with 200 mm Shotcrete + Rock Bolts |
| Case | Case-A or Case-S | 1 = Horseshoe Shape without Invert 2 = Horseshoe Shape with Invert 3 = Circular Shape 4 = Semicircular Shape without Invert 5 = Semicircular Shape with Invert 6 = Box Shape 7 = Rectangular Shape 8 = Semi-elliptical Shape |
| Location | Location-A or Location-S | 1 = Crown (Z-Axis Displacement) 2 = Right Spring Line (X-Axis Displacement) 3 = Left Spring Line (X-Axis Displacement) 4 = Invert (Z-Axis Displacement) |
| Rock Type | Modulus of Elasticity “E” (GPa) | Poisson’s Ratio “v” | Bulk Modulus “K” (GPa) | Shear Modulus “G” (GPa) | Tensile Strength (MPa) | Friction Angle (Degrees) | Cohesion (MPa) |
|---|---|---|---|---|---|---|---|
| Shale | 11.1 | 0.29 | 8.8 | 4.3 | - | 14.4 | 38.4 |
| Sandstone | 19.3 | 0.38 | 26.8 | 7.0 | 1.17 | 27.8 | 27.2 |
| Siltstone | 26.3 | 0.22 | 15.6 | 10.8 | - | 32.1 | 34.7 |
| Limestone | 28.5 | 0.29 | 22.6 | 11.1 | 1.58 | 42.0 | 6.72 |
| Marble | 55.8 | 0.25 | 37.2 | 22.3 | - | 31.0 | 66.2 |
| Granite | 73.8 | 0.22 | 43.9 | 30.2 | - | 51.0 | 55.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, B.; Jamil, S.M.; Kim, J.J.; Jafri, T.H.; Kim, J. Rock Mass Behavior under Tunnel Widening in Asymmetric and Symmetric Modes Considering Different Shapes and Parametric Conditions. Geosciences 2019, 9, 518. https://doi.org/10.3390/geosciences9120518
Khan B, Jamil SM, Kim JJ, Jafri TH, Kim J. Rock Mass Behavior under Tunnel Widening in Asymmetric and Symmetric Modes Considering Different Shapes and Parametric Conditions. Geosciences. 2019; 9(12):518. https://doi.org/10.3390/geosciences9120518
Chicago/Turabian StyleKhan, Babar, Syed Muhammad Jamil, Jung Joo Kim, Turab H. Jafri, and Jonguk Kim. 2019. "Rock Mass Behavior under Tunnel Widening in Asymmetric and Symmetric Modes Considering Different Shapes and Parametric Conditions" Geosciences 9, no. 12: 518. https://doi.org/10.3390/geosciences9120518
APA StyleKhan, B., Jamil, S. M., Kim, J. J., Jafri, T. H., & Kim, J. (2019). Rock Mass Behavior under Tunnel Widening in Asymmetric and Symmetric Modes Considering Different Shapes and Parametric Conditions. Geosciences, 9(12), 518. https://doi.org/10.3390/geosciences9120518





