Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test
Abstract
1. Introduction
2. Materials and Methods
2.1. Data and Field of Study
2.2. Standardized Precipitation-Evapotranspiration Index (SPEI)
2.3. Quantile Regression (QR)
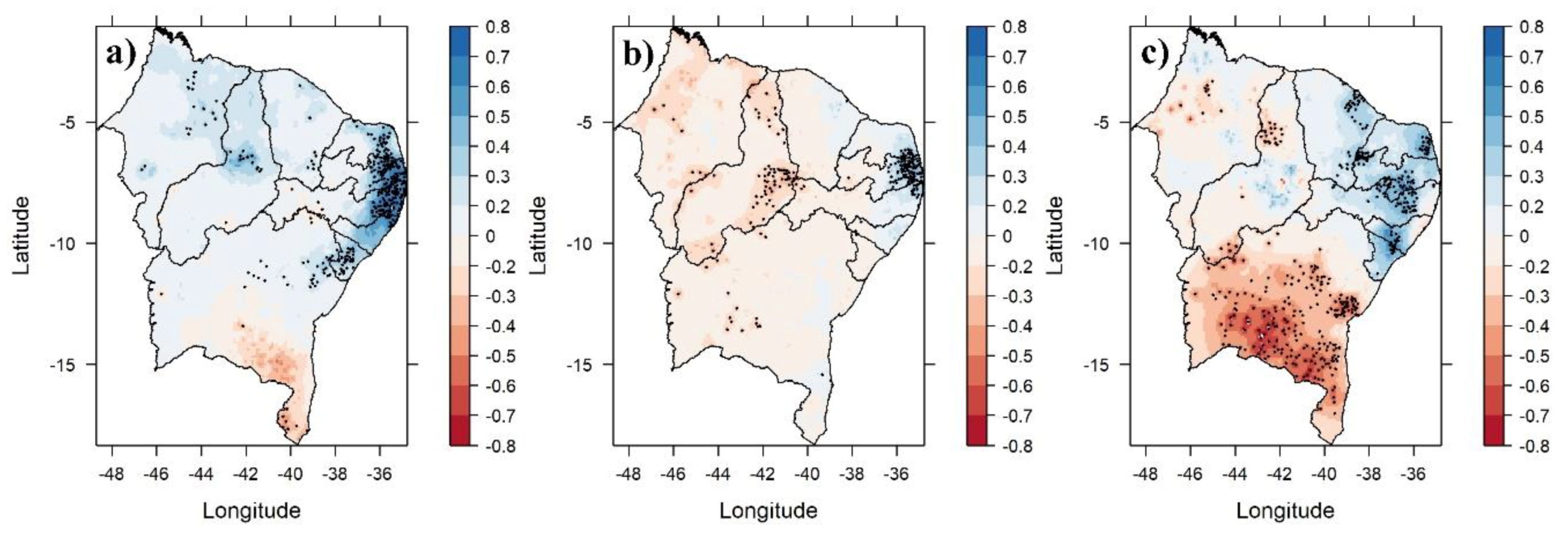
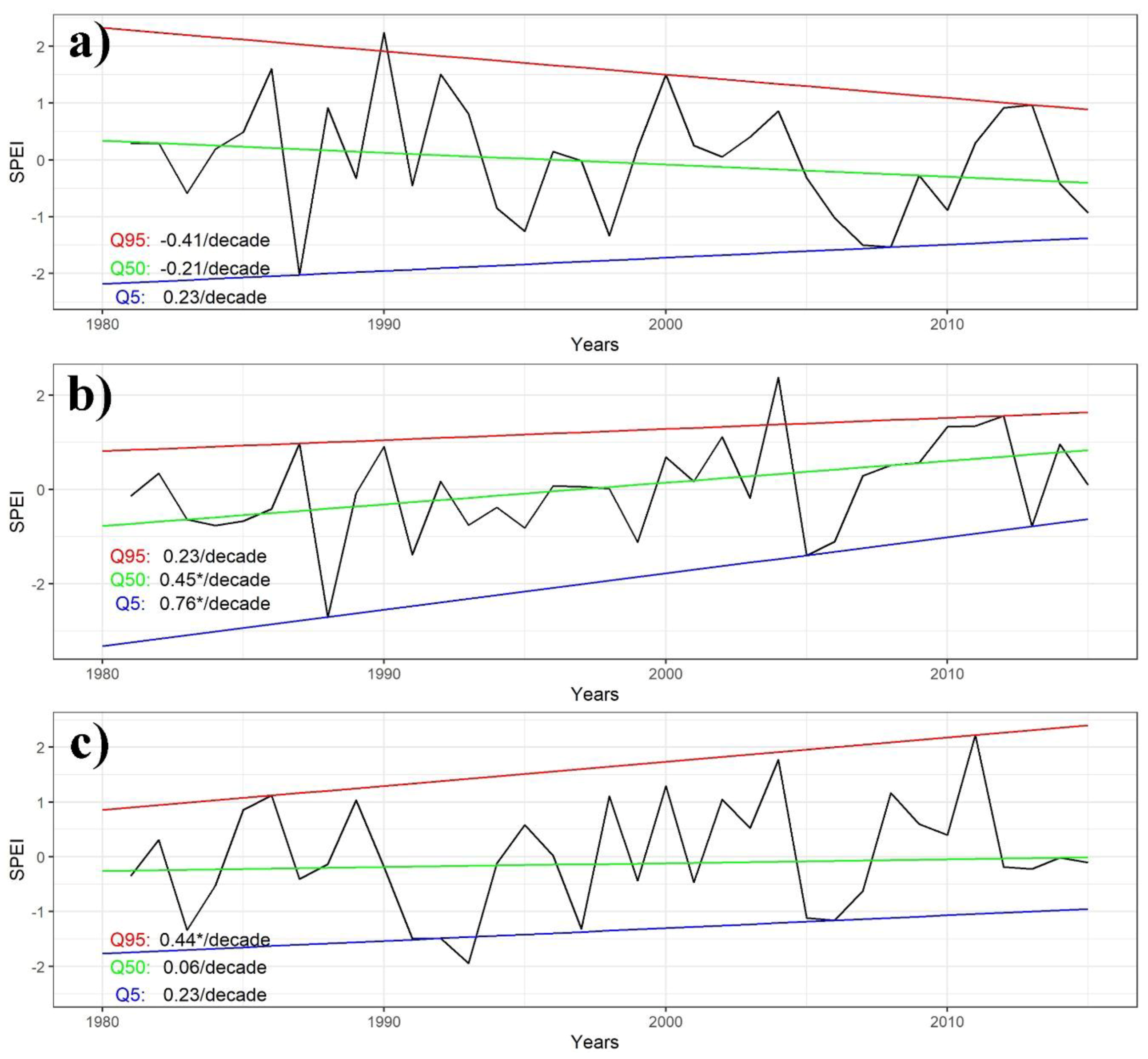
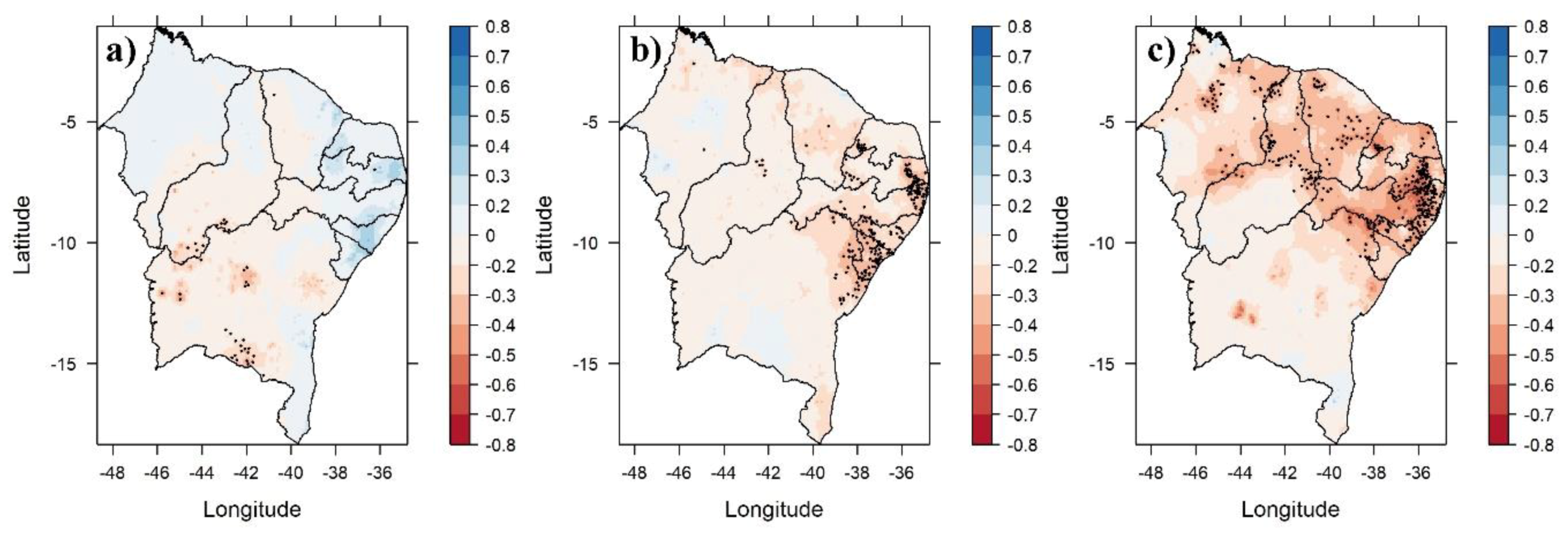
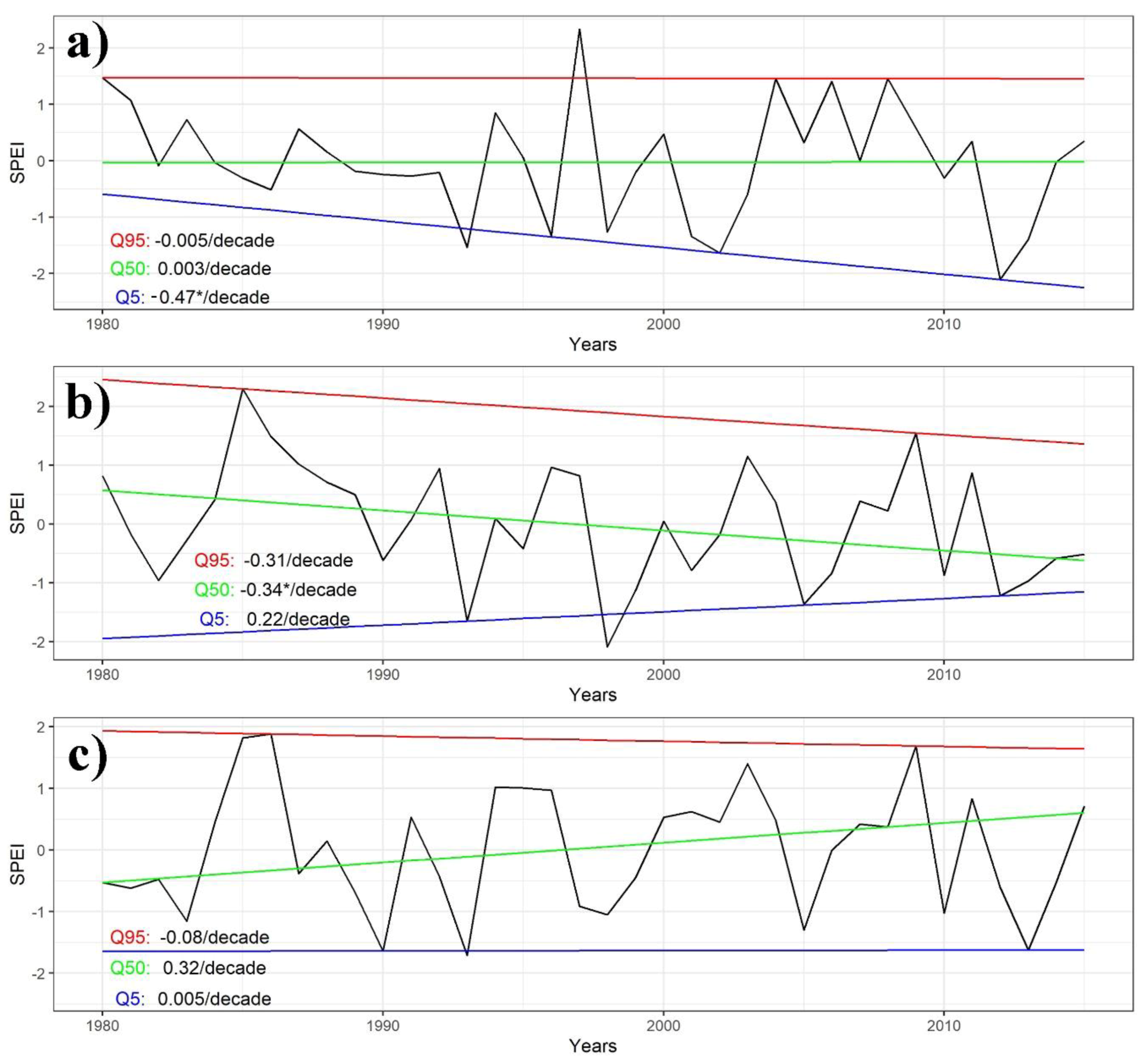
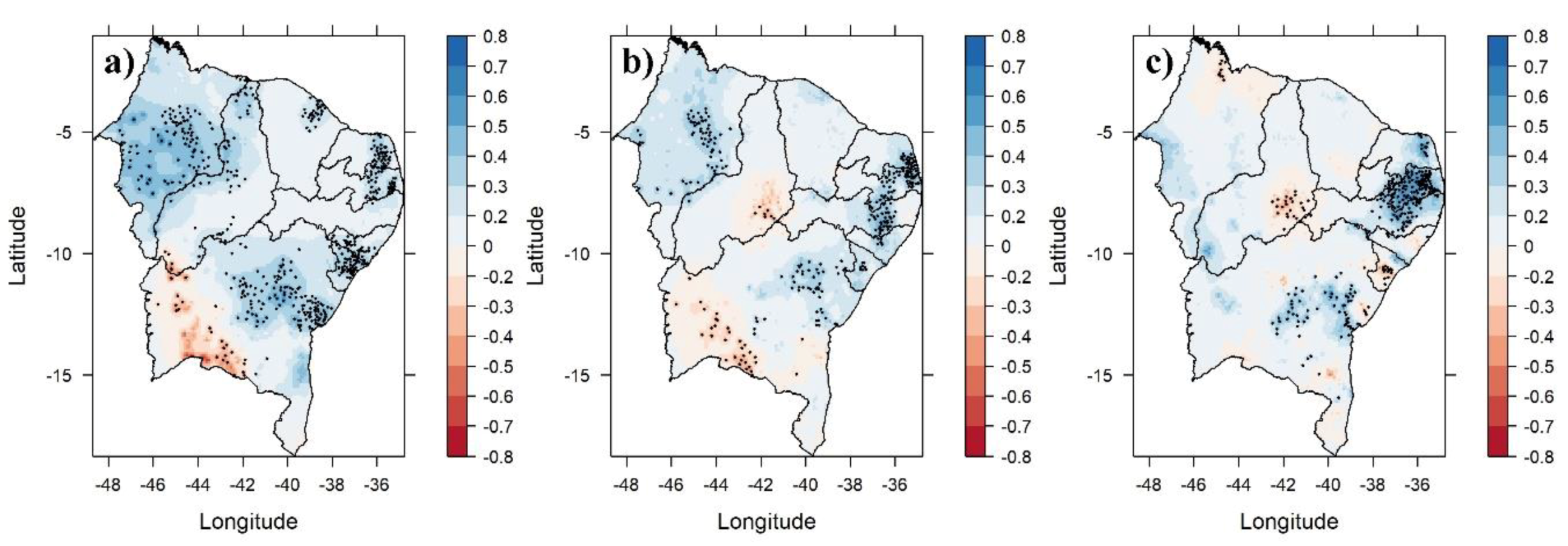
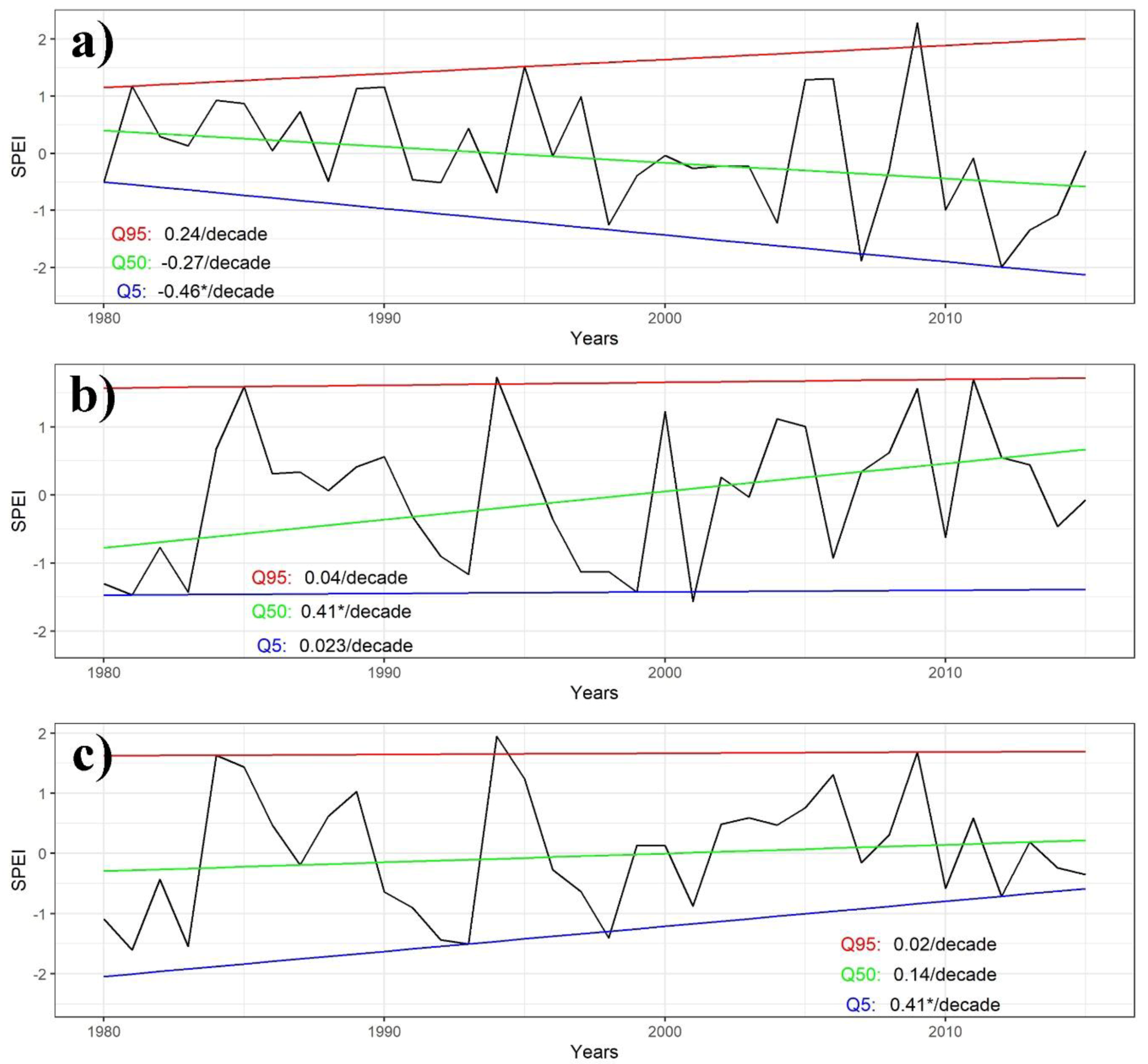
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alvala, R.C.S.; Cunha, A.P.M.A.; Brito, S.S.B.; Seluchi, M.E.; Marengo, J.A.; Moraes, O.L.L.; Carvalho, M.A. Drought monitoring in the Brazilian Semiarid region. An. Acad. Bras. Ciências 2017, 91, 1–15. (In Portugal) [Google Scholar] [CrossRef] [PubMed]
- Cunha, A.P.M.A.; Alvalá, R.C.S.; Nobre, C.A.; Carvalho, M.A. Monitoring vegetative drought dynamics in the Brazilian semiarid Region. Agric. For. Meteorol. 2015, 214, 494–505. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Tomasella, J.; Ribeiro-Neto, G.G.; Brown, M.; Garcia, S.R.; Brito, S.B.; Carvalho, M.A. Changes in the spatial-temporal patterns of droughts in the Brazilian Northeast. Atmos. Sci. Lett. 2018, 19, 1–8. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Alvalá, R.C.S.; Cunha, A.P.M.A.; Brito, S.S.B.; Moraes, O.L.L. Climatic characteristics of the 2010–2016 drought in the semiarid Northeast Brazil region. An. Acad. Bras. Ciências 2018, 90, 1973–1985. (In Portugal) [Google Scholar] [CrossRef]
- Martins, E.S.P.R.; Coelho, C.A.S.; Haarsma, R.; Otto, F.E.L.; King, A.D.; Van Oldenborgh, G.J.; Kew, S.; Philip, S.; Júnior, F.C.V.; Cullen, H. A multimethod attribution analysis of the prolonged northeast brazil hydrometeorological drought (2012–16). Bull. Am. Meteorol. Soc. 2018, 99, 65–69. [Google Scholar] [CrossRef]
- Martins, M.A.; Tomasella, J.; Rodriguez, D.A.; Alvalá, R.C.; Giarolla, A.; Garofolo, L.L.; Júnior, J.L.S.; Paolicchi, L.T.; Pinto, G.L. Improving drought management in the Brazilian semiarid through crop forecasting. Agric. Syst. 2018, 160, 21–30. [Google Scholar] [CrossRef]
- Blunden, J.; Arndt, D.S. Supplement: State of the Climate in 2013. Bull. Am. Met. Soc. 2014, 95, ES1–ES22. [Google Scholar] [CrossRef]
- Alves, J.M.; Repelli, C.A. A variabilidade pluviométrica no setor norte do nordeste e os eventos El Nino-Oscilação Sul (ENOS). Rev. Bras. Meteorol. 1992, 7, 583–592. (In Portugal) [Google Scholar]
- Hastenrath, S.; Greischar, L. Circulation mechanisms related to northeast Brazil rainfall anomalies. J. Geophys. Res. Space Phys. 1993, 98, 5093–5102. [Google Scholar] [CrossRef]
- Rao, V.B.; De Lima, M.C.; Franchito, S.H. Seasonal and Interannual Variations of Rainfall over Eastern Northeast Brazil. J. Clim. 1993, 6, 1754–1763. [Google Scholar]
- Kousky, V.E. Frontal Influences on Northeast Brazil. Mon. Weather Rev. 1979, 107, 1140–1153. [Google Scholar] [CrossRef]
- Kousky, V.E.; Gan, M.A. Upper tropospheric cyclonic vortices in the tropical South Atlantic. Tellus 1981, 33, 538–551. [Google Scholar] [CrossRef]
- Costa, R.L.; De Souza, E.P.; Silva, F.D.D.S. Aplicação de uma teoria termodinâmica no estudo de um Vórtice Ciclônico de Altos Níveis sobre o nordeste do Brasil. Rev. Bras. Meteorol. 2014, 29, 96–104. [Google Scholar] [CrossRef]
- Cordeiro, E.S.; Fedorova, N.; Levit, V. Synoptic and thermodynamic analysis of events with thunderstorms for alagoas state in a period of 15 years (1998–2012). Rev. Bras. Meteorol. 2018, 33, 685–694. [Google Scholar] [CrossRef]
- Moura, A.D.; Shukla, J. On the dynamics of droughts in northeast Brazil: Observations, theory and numerical experiments with a general circulation model. J. Atmos. Sci. 1981, 38, 2653–2675. [Google Scholar] [CrossRef]
- Hastenrath, S. Interannual Variability and Annual Cycle: Mechanisms of Circulation and Climate in the Tropical Atlantic Sector. Mon. Weather Rev. 1984, 112, 1097–1107. [Google Scholar] [CrossRef]
- De Carvalho, M.; Ângelo, V.; Oyama, M.D. Variabilidade da largura e intensidade da Zona de Convergência Intertropical atlântica: Aspectos observacionais. Rev. Bras. Meteorol. 2013, 28, 305–316. [Google Scholar] [CrossRef]
- Silva, V.B.S.; Kousky, V.E.; Silva, F.D.S.; Salvador, M.A.; Aravequia, J.A. The 2012 severe drought over Northeast Brazil. Bull. Am. Met. Soc. 2013, 94, S240. [Google Scholar]
- Kayano, M.T.; Andreoli, R.V. Relationships between rainfall anomalies over northeastern Brazil and the El Niño–Southern Oscillation. J. Geophys. Res. Space Phys. 2006, 111, 13102. [Google Scholar] [CrossRef]
- Gomes, H.B.; Ambrizzi, T.; Herdies, D.L.; Hodges, K.; Da Silva, B.F.P. Rcio Easterly Wave Disturbances over Northeast Brazil: An Observational Analysis. Adv. Meteorol. 2015, 2015, 1–20. [Google Scholar] [CrossRef]
- Gomes, H.B.; Ambrizzi, T.; Da Silva, B.F.P.; Hodges, K.; Dias, P.L.S.; Herdies, D.L.; Silva, M.C.L.; Gomes, H.B. Climatology of easterly wave disturbances over the tropical South Atlantic. Clim. Dyn. 2019, 53, 1393–1411. [Google Scholar] [CrossRef]
- Kousky, V.E.; Kayano, M.T. Principal Modes of Outgoing Longwave Radiation and 250-mb Circulation for the South American Sector. J. Clim. 1994, 7, 1131–1143. [Google Scholar] [CrossRef]
- Kayano, M.T.; Andreoli, R.V. Decadal variability of northern northeast Brazil rainfall and its relation to tropical sea surface temperature and global sea level pressure anomalies. J. Geophys. Res. 2004, 109, C11. [Google Scholar] [CrossRef]
- Kayano, M.T.; Capistrano, V.P. How the Atlantic Multidecadal Oscillation (AMO) modifies the ENSO influence on the South American rainfall. Int. J. Climatol. 2014, 34, 162–178. [Google Scholar] [CrossRef]
- Barreto, N.J.C.; Mesquita, M.S.; Mendes, D.; Spyrides, M.H.C.; Pedra, G.U.; Lucio, P.S. Maximum covariance analysis to identify intraseasonal oscillations over tropical Brazil. Clim. Dyn. 2017, 49, 1583–1596. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A Self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Boston, MA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; Lόpez-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vincente-Serrano, S.M.; Beguería, S.; Lόpez-Moreno, J.I.; Angulo, M.; Kenawy, A.E. A new global 0.5 degrees gridded dataset (1901–2006) of a multiscalar drought index: Comparison with current drought index datasets based on the Palmer Drought Severity Index. J. Hydrometeorol. 2010, 11, 1033–1043. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Molina, C.A.; Lorenzo, A.S.; Revuelto, J.; Tejeda, E.M.; Lopez-Moreno, J.I.; Espejo, F.L. Sensitivity of reference evapotranspiration to changes in meteorological parameters in Spain (1961–2011). Water Resour. Res. 2014, 50, 8458–8480. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar]
- Liu, S.; Kang, W.; Wang, T. Drought variability in Inner Mongolia of northern China during 1960–2013 based on standardized precipitation evapotranspiration index. Environ. Earth Sci. 2016, 75, 145. [Google Scholar] [CrossRef]
- Manatsa, D.; Mushore, T.; Lenouo, A. Improved predictability of drought over Southern Africa using the standardized precipitation evapotranspiration index and ENSO. Theor. Appl. Climatol. 2017, 127, 259–274. [Google Scholar] [CrossRef]
- Hui-Mean, F.; Yusop, Z.; Yusof, F. Drought analysis and water resource availability using standardised precipitation evapotranspiration index. Atmos. Res. 2018, 201, 102–115. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, W.; Chen, Q.; Yao, Y.; Liu, K. Analysis of Changes in Precipitation and Drought in Aksu River Basin, Northwest China. Adv. Meteorol. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Turkes, M.; Tatli, H. Use of the standardized precipitation index (SPI) and a modified SPI for shaping the drought probabilities over Turkey. Int. J. Clim. 2009, 29, 2270–2282. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Talaee, P.H. Temporal trends and spatial characteristics of drought and rainfall in arid and semiarid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Silva, V.P.R. On climate variability in Northeast of Brazil. J. Arid Environ. 2004, 58, 575–596. [Google Scholar] [CrossRef]
- Ganguli, P.; Reddy, M.J. Evaluation of trends and multivariate frequency analysis of droughts in three meteorological subdivisions of western India. Int. J. Climatol. 2014, 34, 911–928. [Google Scholar] [CrossRef]
- Degefu, M.A.; Bewket, W. Variability and trends in rainfall amount and extreme event indices in the Omo-Ghibe River Basin, Ethiopia. Reg. Environ. Chang. 2014, 14, 799–810. [Google Scholar] [CrossRef]
- Dashtpagerdi, M.M.; Kousari, M.R.; Vagharfard, H.; Ghonchepour, D.; Hosseini, M.E.; Ahani, H. An investigation of drought magnitude trend during 1975–2005 in arid and semi-arid regions of Iran. Environ. Earth Sci. 2015, 73, 1231–1244. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994; Volume 57. [Google Scholar]
- Efron, B. Second thoughts on the bootstrap. Stat. Sci. 2003, 18, 135–140. [Google Scholar] [CrossRef]
- LePage, R.; Billard, L. Exploring the Limits of Bootstrap; Wiley: Nova Iorque, NY, USA, 1992. [Google Scholar]
- Filho, T.K.; Assad, E.D.; Lima, P.R.S.R. Regiões pluviometricamente homogêneas no Brasil. Pesqui. Agropecu. Bras. 2005, 40, 311–322. (In Portugal) [Google Scholar] [CrossRef]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in Brazil (1980–2013). Int. J. Climatol. 2016, 36, 2644–2659. [Google Scholar] [CrossRef]
- Liu, B.; Liu, F.; Wang, C.; Mei, S. Unit commitment considering flexibility and uncertainty of wind power generation. Power Syst. Technol. 2015, 39, 730–736. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements-FAO irrigation and Drainage Paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Raes, D. The ETo Calculator; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2012. [Google Scholar]
- Paredes-Trejo, F.; Barbosa, H.; Dos Santos, C.A.C. Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil. Remote Sens. 2019, 11, 1113. [Google Scholar] [CrossRef]
- Silva, P.E.; Silva, C.M.S.; Spyrides, M.H.C.; Andrade, L.M.B. Análise de Índices de Extremos Climáticos no Nordeste e Amazônia Brasileira para o Período entre 1980 a 2013. Anuário Inst. Geociências 2019, 42, 137–148. (In Portugal) [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-moments approach for regional flood frequency analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Franzke, C. A novel method to test for significant trends in extreme values in serially dependent time series. Geophys. Res. Lett. 2013, 40, 1391–1395. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 751. [Google Scholar]
- Barbosa, S.M. Quantile trends in Baltic sea level. Geophys. Res. Lett. 2008, 35, 22. [Google Scholar] [CrossRef]
- Lee, K.; Baek, H.-J.; Cho, C. Analysis of changes in extreme temperatures using quantile regression. Asia-Pac. J. Atmos. Sci. 2013, 49, 313–323. [Google Scholar] [CrossRef]
- Dhakal, N.; Tharu, B. Spatio-temporal trends in daily precipitation extremes and their connection with North Atlantic tropical cyclones for the southeastern United States. Int. J. Clim. 2018, 38, 3822–3831. [Google Scholar] [CrossRef]
- Farias, R.F.D.L.; Nóbrega, R.S.; Dos Santos, C.A.C. Variabilidade temporal e espacial da precipitação pluviométrica em Pernambuco através de índices de extremos climáticos. Rev. Bras. Meteorol. 2015, 30, 171–180. [Google Scholar]
- Santos, C.A.C.; Brito, J.I.B. Análise dos índices de extremos para o semi-árido do Brasil e suas relações com TSM e IVDN. Rev. Bras. Meteorol. 2007, 22, 303–312. [Google Scholar] [CrossRef]
- Medeiros, S.E.L.; Abrahão, R.; García-Garizábal, I.; Idmon Melo, B.M.P.; Pereira, L.S. Assessment of precipitation trends in the Sertão Paraibano Mesoregion. Rev. Bras. Meteorol. 2018, 33, 344–352. [Google Scholar] [CrossRef]
- Salviano, M.F.; Groppo, J.D.; Pellegrino, G.Q. Análise de Tendências em Dados de Precipitação e Temperatura no Brasil. Rev. Bras. Meteorol. 2016, 31, 64–73. [Google Scholar] [CrossRef]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil-past, present, and future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
- Jenkins, K.; Warren, R. Quantifying the impact of climate change on drought regimes using the Standardised Precipitation Index. Theor. Appl. Climatol. 2015, 120, 41–54. [Google Scholar] [CrossRef]
- Oliveira, P.T.; Silva, C.M.S.; Lima, K.C. Climatology and trend analysis of extreme precipitation in subregions of Northeast Brazil. Theor. Appl. Climatol. 2017, 130, 77–90. [Google Scholar] [CrossRef]
- Silva, V.P.R.; Oliveira, S.D.; Hoekstra, A.Y.; Dantas-Neto, J.; Campos, J.H.B.C.; Braga, C.C.; Araujo, L.E.; Aleixo, D.O.; Brito, J.I.B.; Souza, M.D.; et al. Water footprint and virtual water trade of Brazil. Water 2016, 8, 517. [Google Scholar] [CrossRef]
- Lemos, M.C.; Finan, T.J.; Fox, R.W.; Nelson, D.R.; Tucker, J. The Use of Seasonal Climate Forecasting in Policymaking: Lessons from Northeast Brazil. Clim. Chang. 2002, 55, 479–507. [Google Scholar] [CrossRef]
- Marengo, J.A.; Soares, W.R.; Tomasella, J.; Alves, L.M.; Rodriguez, D.A. The drought of 2010 in the context of historical droughts in the Amazon region. Geophys. Res. Lett. 2011, 38, L12703. [Google Scholar] [CrossRef]
- Trejo, F.P.; Brito-Castillo, L.; Alves, H.B.; Guevara, E. Main features of large-scale oceanic-atmospheric circulation related to strongest droughts during rainy season in Brazilian São Francisco River Basin. Int. J. Climatol. 2016, 36, 4102–4117. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Kumar, T.L.; Paredes, F.; Elliott, S.; Ayuga, J.; Kumar, T.L. Assessment of Caatinga response to drought using Meteosat-SEVIRI Normalized Difference Vegetation Index (2008–2016). ISPRS J. Photogramm. Remote Sens. 2019, 148, 235–252. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Lisboa Costa, R.; Barros Gomes, H.; Herdies, D.L.; Rodrigues da Silva, V.d.P.; Candido Xavier, A. Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test. Geosciences 2019, 9, 457. https://doi.org/10.3390/geosciences9110457
da Rocha Júnior RL, dos Santos Silva FD, Lisboa Costa R, Barros Gomes H, Herdies DL, Rodrigues da Silva VdP, Candido Xavier A. Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test. Geosciences. 2019; 9(11):457. https://doi.org/10.3390/geosciences9110457
Chicago/Turabian Styleda Rocha Júnior, Rodrigo Lins, Fabrício Daniel dos Santos Silva, Rafaela Lisboa Costa, Heliofábio Barros Gomes, Dirceu Luis Herdies, Vicente de Paulo Rodrigues da Silva, and Alexandre Candido Xavier. 2019. "Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test" Geosciences 9, no. 11: 457. https://doi.org/10.3390/geosciences9110457
APA Styleda Rocha Júnior, R. L., dos Santos Silva, F. D., Lisboa Costa, R., Barros Gomes, H., Herdies, D. L., Rodrigues da Silva, V. d. P., & Candido Xavier, A. (2019). Analysis of the Space–Temporal Trends of Wet Conditions in the Different Rainy Seasons of Brazilian Northeast by Quantile Regression and Bootstrap Test. Geosciences, 9(11), 457. https://doi.org/10.3390/geosciences9110457







