Coupled Analysis of Desiccation Cracking in Unsaturated Soils through a Non-Local Mathematical Formulation
Abstract
1. Introduction
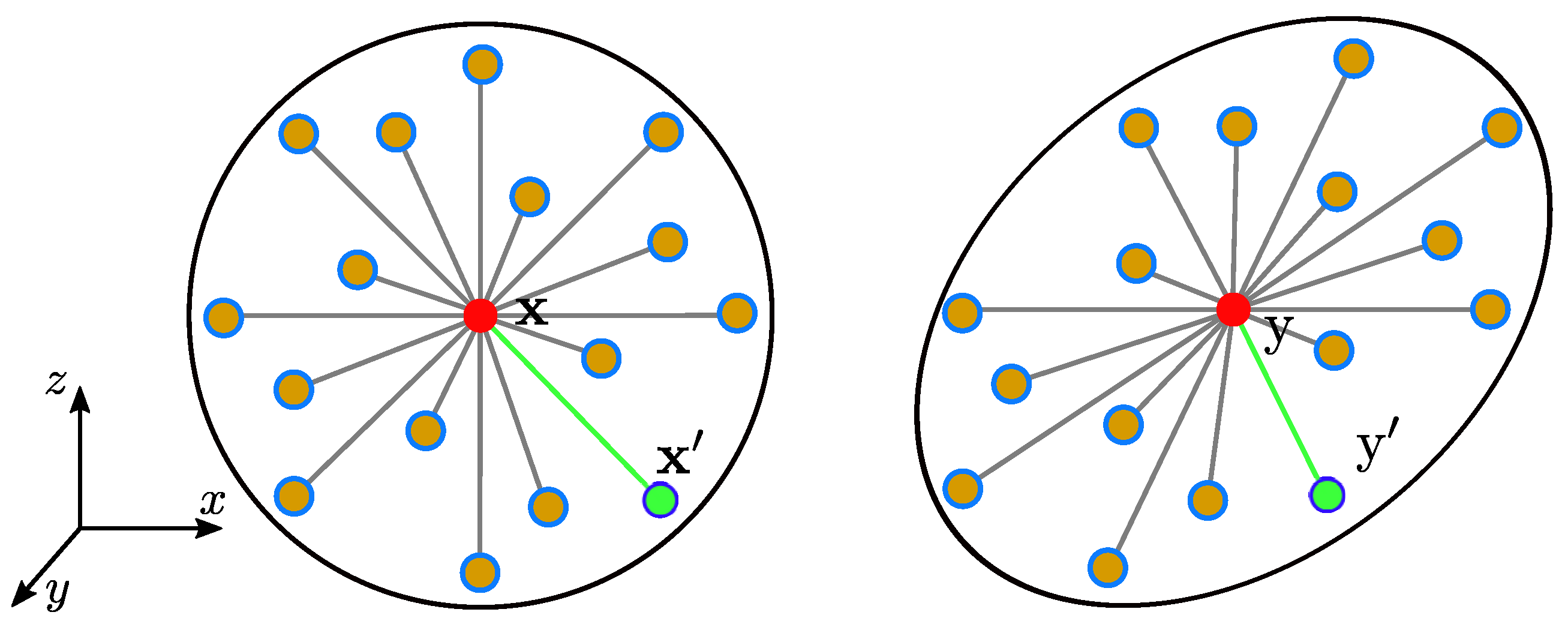
2. Mathematical Framework
2.1. State-Based Peridynamic Poroelasticity
2.2. Constitutive Models
2.3. Damage Model
3. Numerical Examples
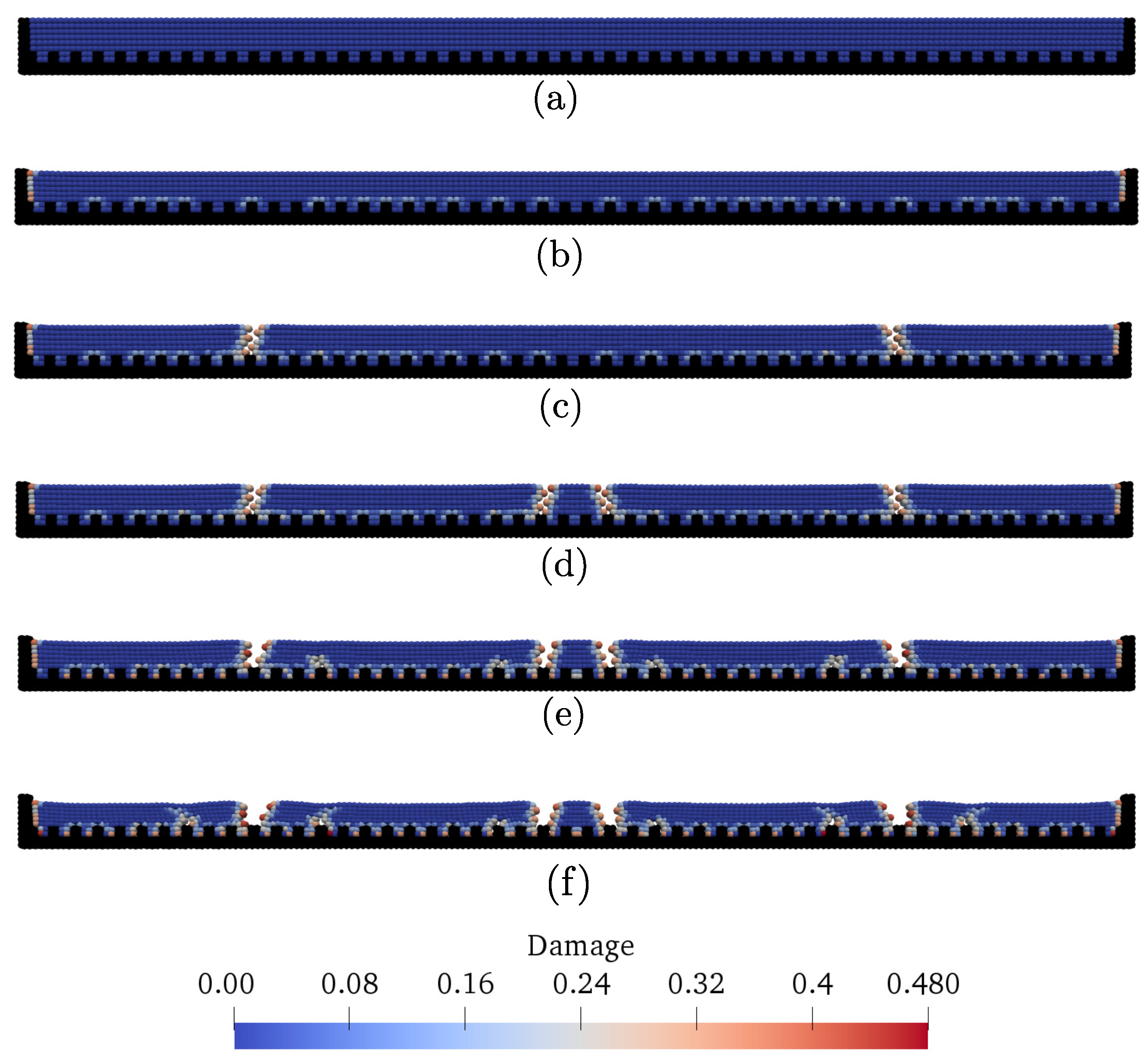
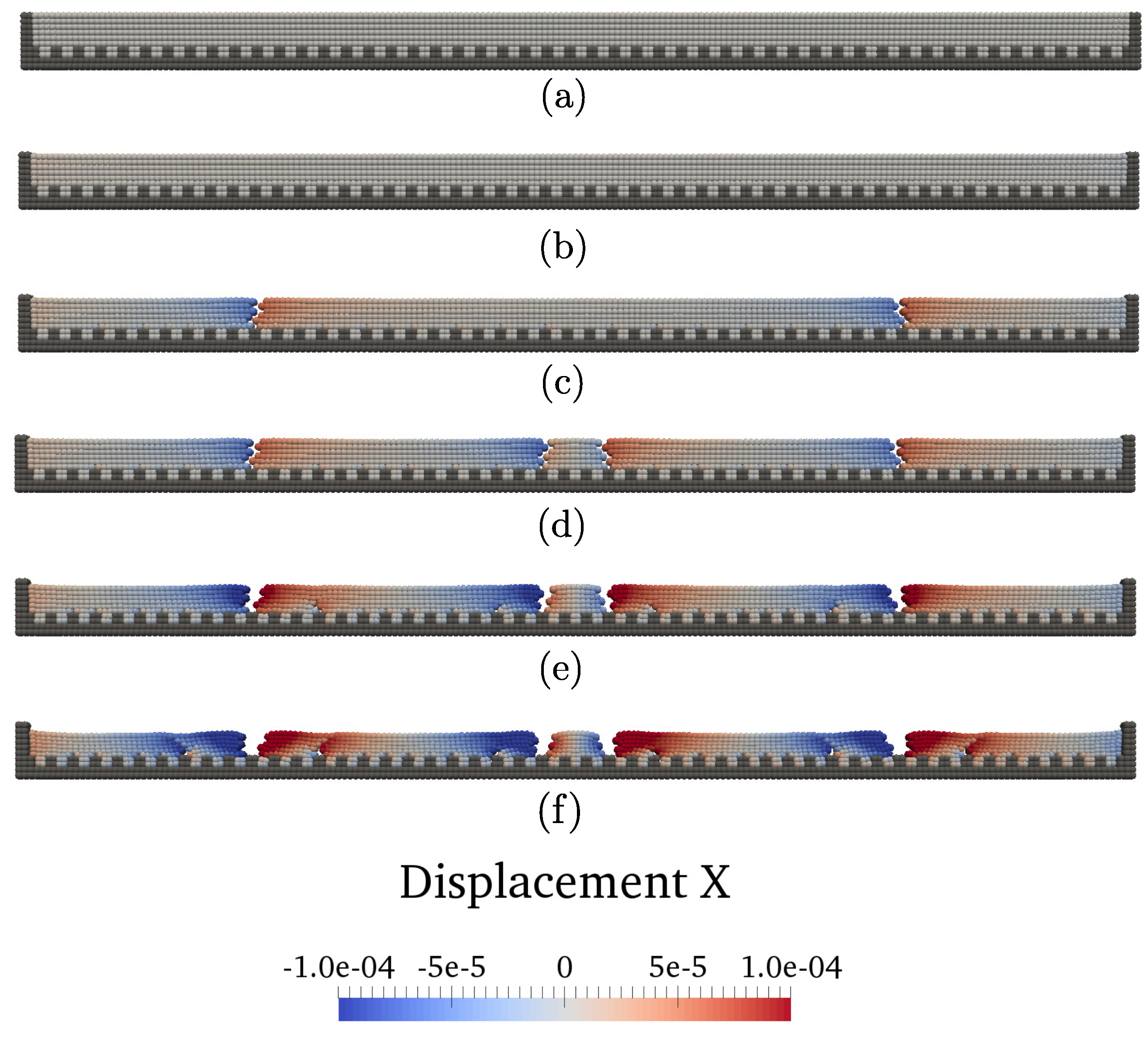
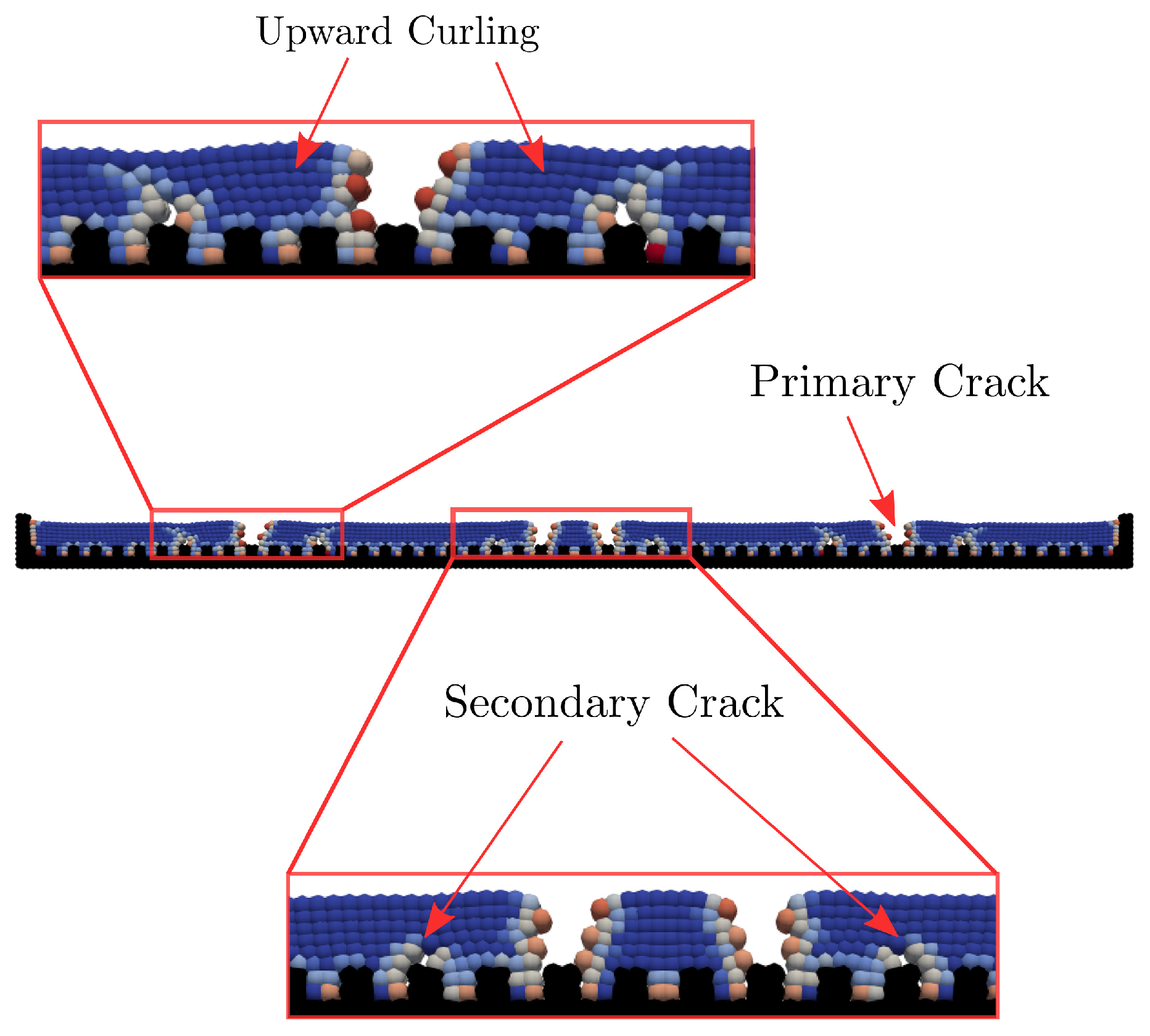
3.1. One-Dimensional Cracking in a Linearly Restrained Soil Bar
3.2. Two-Dimensional Cracking in a Thin Disc Soil Sample
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, N.; Asce, M.; Likos, W.J. Suction Stress Characteristic Curve for Unsaturated Soil; American Society of Civil Engineers: Reston, VA, USA, 2006. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Song, X.; Borja, R.I. Mathematical framework for unsaturated flow in the finite deformation range. Int. J. Numer. Methods Eng. 2014, 97, 658–682. [Google Scholar] [CrossRef]
- Song, X. Transient bifurcation condition of partially saturated porous media at finite strain. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 135–156. [Google Scholar] [CrossRef]
- Likos, W.J.; Song, X.; Xiao, M.; Cerato, A.; Lu, N. Fundamental Challenges in Unsaturated Soil Mechanics. In Geotechnical Fundamentals for Addressing New World Challenges; Springer: Berlin/Heidelberg, Germany, 2019; pp. 209–236. [Google Scholar]
- Miller, C.J.; Mi, H.; Yesiller, N. Experimental analysis of desiccation crack propagation in clay liners. J. Am. Water Resour. Assoc. 1998, 34, 677–686. [Google Scholar] [CrossRef]
- Li, J.H.; Zhang, L.M. Study of desiccation crack initiation and development at ground surface. Eng. Geol. 2011, 123, 347–358. [Google Scholar] [CrossRef]
- Puppala, A.J.; Katha, B.; Hoyos, L.R. Volumetric Shrinkage Strain Measurements in Expansive Soils Using Digital Imaging Technology; Technical Report 6; ASTM: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Puppala, A.J.; Pedarla, A.; Hoyos, L.R.; Zapata, C.; Bheemasetti, T.V. A semi-empirical swell prediction model formulated from ‘clay mineralogy and unsaturated soil’ properties. Eng. Geol. 2016, 200, 114–121. [Google Scholar] [CrossRef]
- Puppala, A.J.; Manosuthkij, T.; Nazarian, S.; Hoyos, L.R. Threshold moisture content and matric suction potentials in expansive clays prior to initiation of cracking in pavements. Can. Geotech. J. 2011, 48, 519–531. [Google Scholar] [CrossRef]
- Bagge, G. Tension cracks in saturated clay cuttings. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985; pp. 393–395. [Google Scholar]
- Silvestri, V.; Sarkis, G.; Bekkouche, N.; Soulié, M. Evapotranspiration, trees and damage to foundations in sensitive clays. Can. Geotech. Conf. 1992, 2, 533–538. [Google Scholar]
- Boynton, S.S.; Daniel, D.E. Hydraulic conductivity tests on compacted clay. J. Geotech. Eng. 1985, 111, 465–478. [Google Scholar] [CrossRef]
- Miller, C.J.; Mishra, M. Modeling of leakage through cracked clay liners - I: State of the art 1. J. Am. Water Resour. Assoc. 1989, 25, 551–556. [Google Scholar] [CrossRef]
- Albrecht, B.A.; Benson, C.H. Effect of desiccation on compacted natural clays. Geotech. Geoenviron. Eng. 2001, 127, 67–75. [Google Scholar] [CrossRef]
- Hoyos, L.R.; Arduino, P. Implicit Algorithm for Modeling Unsaturated Soil Response in Three-Invariant Stress Space. Int. J. Geomech. 2008, 8, 266–273. [Google Scholar] [CrossRef]
- Cao, J.; Jung, J.; Song, X.; Bate, B. On the soil water characteristic curves of poorly graded granular materials in aqueous polymer solutions. Acta Geotech. 2018, 13, 103–116. [Google Scholar] [CrossRef]
- Niu, W.J.; Ye, W.M.; Song, X. Unsaturated permeability of Gaomiaozi bentonite under partially free-swelling conditions. Acta Geotech. 2019, 1–30. [Google Scholar] [CrossRef]
- Borja, R.I.; Song, X.; Wu, W. Critical state plasticity. Part VII: Triggering a shear band in variably saturated porous media. Comput. Methods Appl. Mech. Eng. 2013, 261–262, 66–82. [Google Scholar] [CrossRef]
- Song, X.; Borja, R.I. Finite Deformation and Fluid Flow in Unsaturated Soils with Random Heterogeneity. Vadose Zone J. 2014, 13. [Google Scholar] [CrossRef]
- Song, X.; Wang, K.; Ye, M. Localized failure in unsaturated soils under non-isothermal conditions. Acta Geotech. 2018, 13, 73–85. [Google Scholar] [CrossRef]
- Song, X.; Wang, K.; Bate, B. A hierarchical thermo-hydro-plastic constitutive model for unsaturated soils and its numerical implementation. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 1785–1805. [Google Scholar] [CrossRef]
- Song, X.; Wang, M.C.; Zhang, K. Molecular dynamics modeling of unsaturated clay-water systems at elevated temperature. In Proceedings of the 7th International Conference on Unsaturated Soils 2018 (UNSAT2018), Hong Kong, China, 3–5 August 2018. [Google Scholar]
- Song, X.; Wang, M.C. Molecular dynamics modeling of a partially saturated clay-water system at finite temperature. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2129–2146. [Google Scholar] [CrossRef]
- Kleppe, J.H.; Olson, R.E. Desiccation cracking of soil barriers. In Hydraulic Barriers in Soil and Rock; ASTM International: West Conshohocken, PA, USA, 1985. [Google Scholar]
- Konrad, J.M.; Ayad, R. Desiccation of a sensitive clay: Field experimental observations. Can. Geotech. J. 1997, 34, 929–942. [Google Scholar] [CrossRef]
- Yesiller, N.; Miller, C.; Inci, G.; Yaldo, K. Desiccation and cracking behavior of three compacted landfill liner soils. Eng. Geol. 2000, 57, 105–121. [Google Scholar] [CrossRef]
- Peron, H.; Laloui, L.; Hueckel, T.; Hu, L.B. Desiccation cracking of soils. Eur. J. Environ. Civ. Eng. 2009, 13, 869–888. [Google Scholar] [CrossRef]
- Tang, C.S.; Shi, B.; Liu, C.; Suo, W.B.; Gao, L. Experimental characterization of shrinkage and desiccation cracking in thin clay layer. Appl. Clay Sci. 2011, 52, 69–77. [Google Scholar] [CrossRef]
- Lu, N.; Kaya, M. A Drying Cake Method for Measuring Suction-Stress Characteristic Curve, Soil-Water-Retention Curve, and Hydraulic Conductivity Function A Drying Cake Method for Measuring Suction-Stress Characteristic Curve, Soil-Water-Retention Curve, and Hydraulic Conductivity Function. Geotech. Test. J. 2013, 36, 1–19. [Google Scholar] [CrossRef]
- Konrad, J.M.; Ayad, R. An idealized framework for the analysis of cohesive soils undergoing desiccation. Can. Geotech. J. 1997, 34, 477–488. [Google Scholar] [CrossRef]
- Ayad, R.; Konrad, J.M.; Soulié, M. Desiccation of a sensitive clay: Application of the model CRACK. Can. Geotech. J. 1997, 34, 943–951. [Google Scholar] [CrossRef]
- Asahina, D.; Houseworth, J.; Birkholzer, J.; Rutqvist, J.; Bolander, J. Hydro-mechanical model for wetting/drying and fracture development in geomaterials. Comput. Geosci. 2014, 65, 13–23. [Google Scholar] [CrossRef]
- Rodríguez, R.; Sánchez, M.; Ledesma, A.; Lloret, A. Experimental and numerical analysis of desiccation of a mining waste. Can. Geotech. J. 2007, 44, 644–658. [Google Scholar] [CrossRef]
- Sánchez, M.; Manzoli, O.L.; Guimarães, L.J. Modeling 3-D desiccation soil crack networks using a mesh fragmentation technique. Comput. Geotech. 2014, 62, 27–39. [Google Scholar] [CrossRef]
- Vo, T.D.; Pouya, A.; Hemmati, S.; Tang, A.M. Numerical modelling of desiccation cracking of clayey soil using a cohesive fracture method. Comput. Geotech. 2017, 85, 15–27. [Google Scholar] [CrossRef]
- Gui, Y.; Zhao, Z.; Kodikara, J.; Bui, H.H.; Yang, S. Numerical modelling of laboratory soil desiccation cracking using UDEC with a mix-mode cohesive fracture model. Eng. Geol. 2016, 202, 14–23. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Peron, H.; Delenne, J.; Laloui, L.; El Youssoufi, M. Discrete element modelling of drying shrinkage and cracking of soils. Comput. Geotech. 2009, 36, 61–69. [Google Scholar] [CrossRef]
- Amarasiri, A.L.; Kodikara, J.K.; Costa, S. Numerical modelling of desiccation cracking. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 82–96. [Google Scholar] [CrossRef]
- Amarasiri, A.L.; Kodikara, J.K. Numerical Modeling of Desiccation Cracking Using the Cohesive Crack Method. Int. J. Geomech. 2013, 13, 213–221. [Google Scholar] [CrossRef]
- Sima, J.; Jiang, M.; Zhou, C. Numerical simulation of desiccation cracking in a thin clay layer using 3D discrete element modeling. Comput. Geotech. 2014, 56, 168–180. [Google Scholar] [CrossRef]
- Gui, Y.; Zhao, G.F. Modelling of laboratory soil desiccation cracking using DLSM with a two-phase bond model. Comput. Geotech. 2015, 69, 578–587. [Google Scholar] [CrossRef]
- Hirobe, S.; Oguni, K. Coupling analysis of pattern formation in desiccation cracks. Comput. Methods Appl. Mech. Eng. 2016, 307, 470–488. [Google Scholar] [CrossRef]
- Gui, Y.L.; Hu, W.; Zhao, Z.Y.; Zhu, X. Numerical modelling of a field soil desiccation test using a cohesive fracture model with Voronoi tessellations. Acta Geotech. 2018, 13, 87–102. [Google Scholar] [CrossRef]
- Schrefler, B.; Zhang, H.; Sanavia, L. Interaction between different internal length scales in strain localization analysis of fully and partially saturated porous media—The 1-D case. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 45–70. [Google Scholar] [CrossRef]
- Lazari, M.; Sanavia, L.; Schrefler, B. Local and non-local elasto-viscoplasticity in strain localization analysis of multiphase geomaterials. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 1570–1592. [Google Scholar] [CrossRef]
- Oka, F.; Shahbodagh, B.; Kimoto, S. A computational model for dynamic strain localization in unsaturated elasto-viscoplastic soils. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 138–165. [Google Scholar] [CrossRef]
- Hu, L.B.; Péron, H.; Hueckel, T.; Laloui, L. Desiccation shrinkage of non-clayey soils: Multiphysics mechanisms and a microstructural model. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1761–1781. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Silling, S.A.; Lehoucq, R. Peridynamic theory of solid mechanics. Adv. Appl. Mech. 2010, 44, 73–168. [Google Scholar]
- Silling, S. Dynamic fracture modeling with a meshfree peridynamic code. In Computational Fluid and Solid Mechanics 2003; Elsevier: Amsterdam, The Netherlands, 2003; pp. 641–644. [Google Scholar]
- Ouchi, H.; Katiyar, A.; York, J.; Foster, J.T.; Sharma, M.M. A fully coupled porous flow and geomechanics model for fluid driven cracks: A peridynamics approach. Comput. Mech. 2015, 55, 561–576. [Google Scholar] [CrossRef]
- Oterkus, S.; Madenci, E.; Oterkus, E. Fully coupled poroelastic peridynamic formulation for fluid-filled fractures. Eng. Geol. 2017, 225, 19–28. [Google Scholar] [CrossRef]
- Jabakhanji, R.; Mohtar, R.H. A peridynamic model of flow in porous media. Adv. Water Resour. 2015, 78, 22–35. [Google Scholar] [CrossRef]
- Jabakhanji, R. Peridynamic Modeling of Coupled Mechanical Deformations and Transient Flow in Unsaturated Soils. Ph.D. Thesis, Purdue University, West Lafayette, India, 2013. [Google Scholar]
- Song, X.; Khalili, N. A peridynamics model for strain localization analysis of geomaterials. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 77–96. [Google Scholar] [CrossRef]
- Song, X.; Menon, S. Modeling of chemo-hydromechanical behavior of unsaturated porous media: A nonlocal approach based on integral equations. Acta Geotech. 2018, 14, 1–21. [Google Scholar] [CrossRef]
- Song, X.; Menon, S. Modeling strain localization of unsaturated porous media with chemical effect through a novel non-local method. In Proceedings of the ISSMGE TC105 International Symposium IS-Atlanta 2018 on Geo-Mechanics from Micro to Macro in Research and Practice, Atlanta, GA, USA, 10–12 September 2018. [Google Scholar]
- Menon, S.; Song, X. A fully coupled state-based peri-hydromechanical model for geomaterials. In Proceedings of the First International Symposium on Computational & Geoenvironemental Geomechanics for Underground and Subsurface Structures, Nancy, France, 12–14 February 2019. [Google Scholar]
- Turner, D.Z. A non-local model for fluid-structure interaction with applications in hydraulic fracturing. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 391–400. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Foster, J.T.; Silling, S.A.; Chen, W. An energy based failure criterion for use with peridynamic states. Int. J. Multiscale Comput. Eng. 2011, 9, 675–688. [Google Scholar] [CrossRef]
- Silling, S.; Demmie, P.; Cole, R.; Taylor, P. EMU User’s Manual; Sandia National Laboratories: Albuquerque, NM, USA, 2006. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menon, S.; Song, X. Coupled Analysis of Desiccation Cracking in Unsaturated Soils through a Non-Local Mathematical Formulation. Geosciences 2019, 9, 428. https://doi.org/10.3390/geosciences9100428
Menon S, Song X. Coupled Analysis of Desiccation Cracking in Unsaturated Soils through a Non-Local Mathematical Formulation. Geosciences. 2019; 9(10):428. https://doi.org/10.3390/geosciences9100428
Chicago/Turabian StyleMenon, Shashank, and Xiaoyu Song. 2019. "Coupled Analysis of Desiccation Cracking in Unsaturated Soils through a Non-Local Mathematical Formulation" Geosciences 9, no. 10: 428. https://doi.org/10.3390/geosciences9100428
APA StyleMenon, S., & Song, X. (2019). Coupled Analysis of Desiccation Cracking in Unsaturated Soils through a Non-Local Mathematical Formulation. Geosciences, 9(10), 428. https://doi.org/10.3390/geosciences9100428



