Assessing Submarine Slope Stability through Deterministic and Probabilistic Approaches: A Case Study on the West-Central Scotia Slope
Abstract
1. Introduction
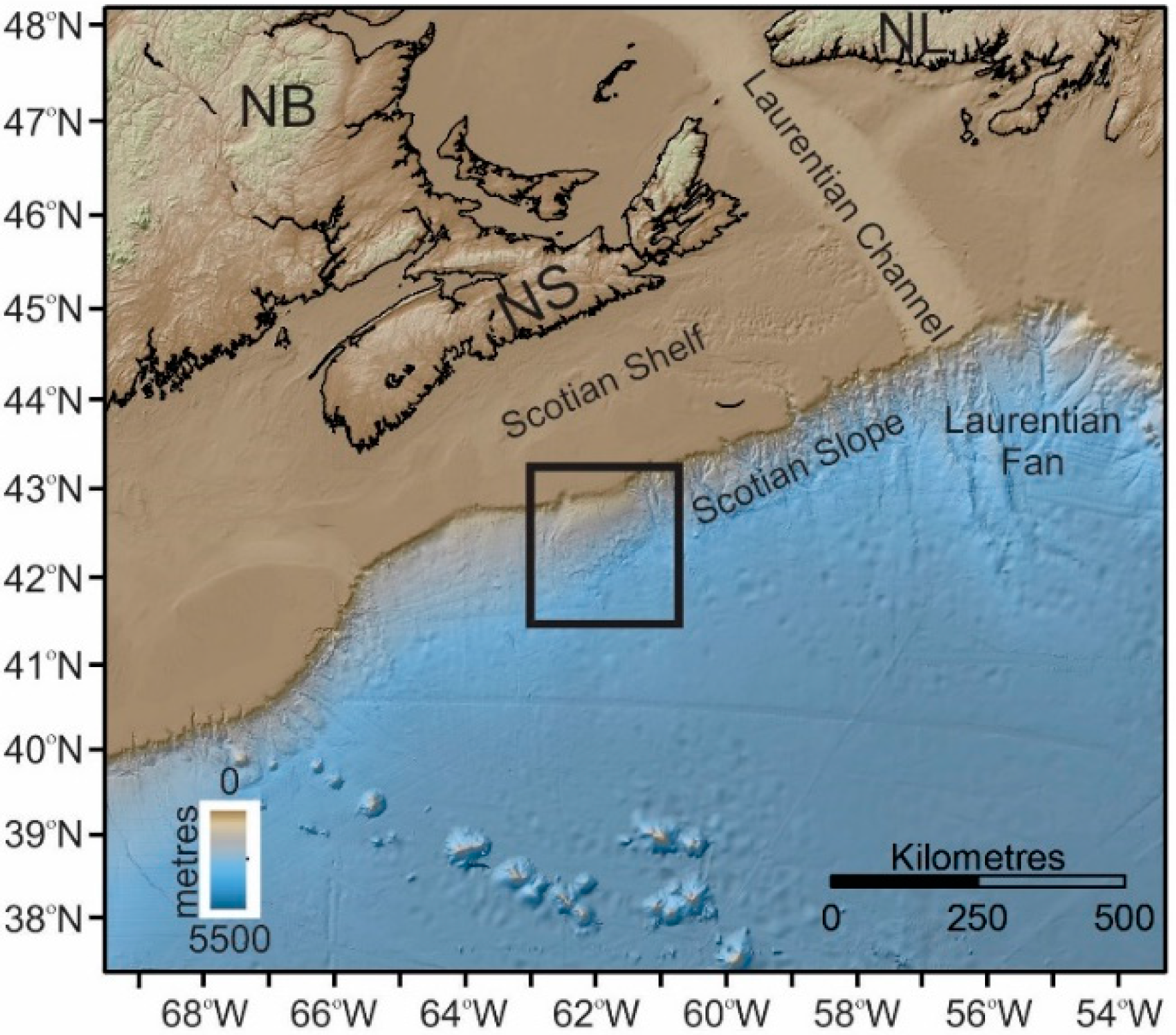
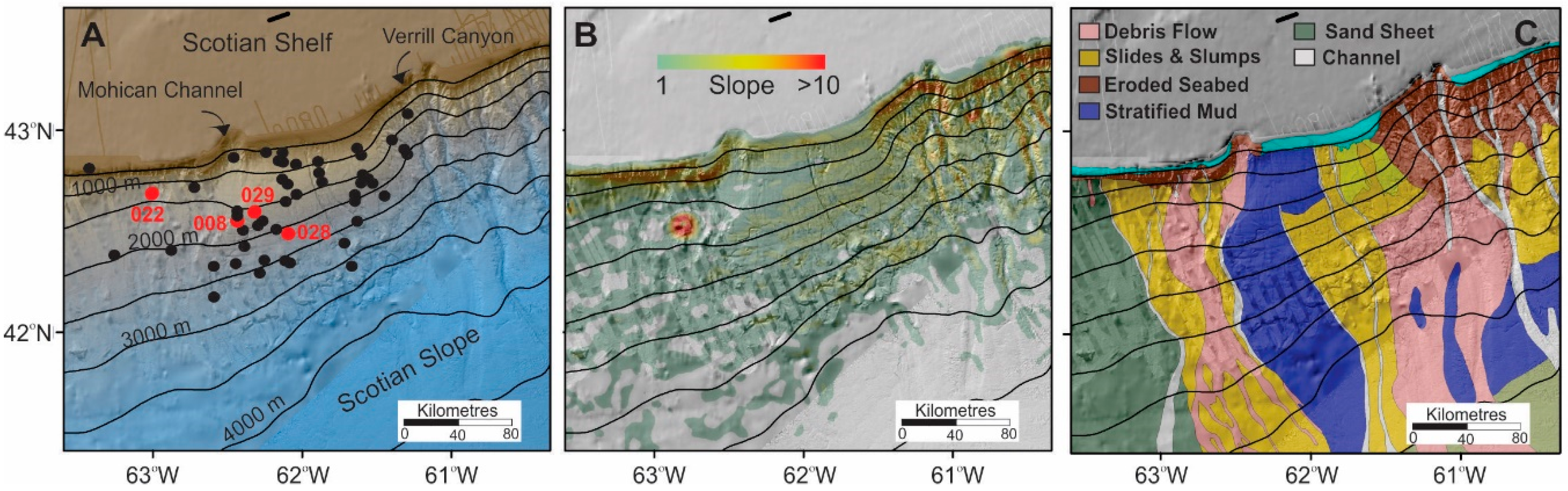
2. Geologic Setting
3. Methods
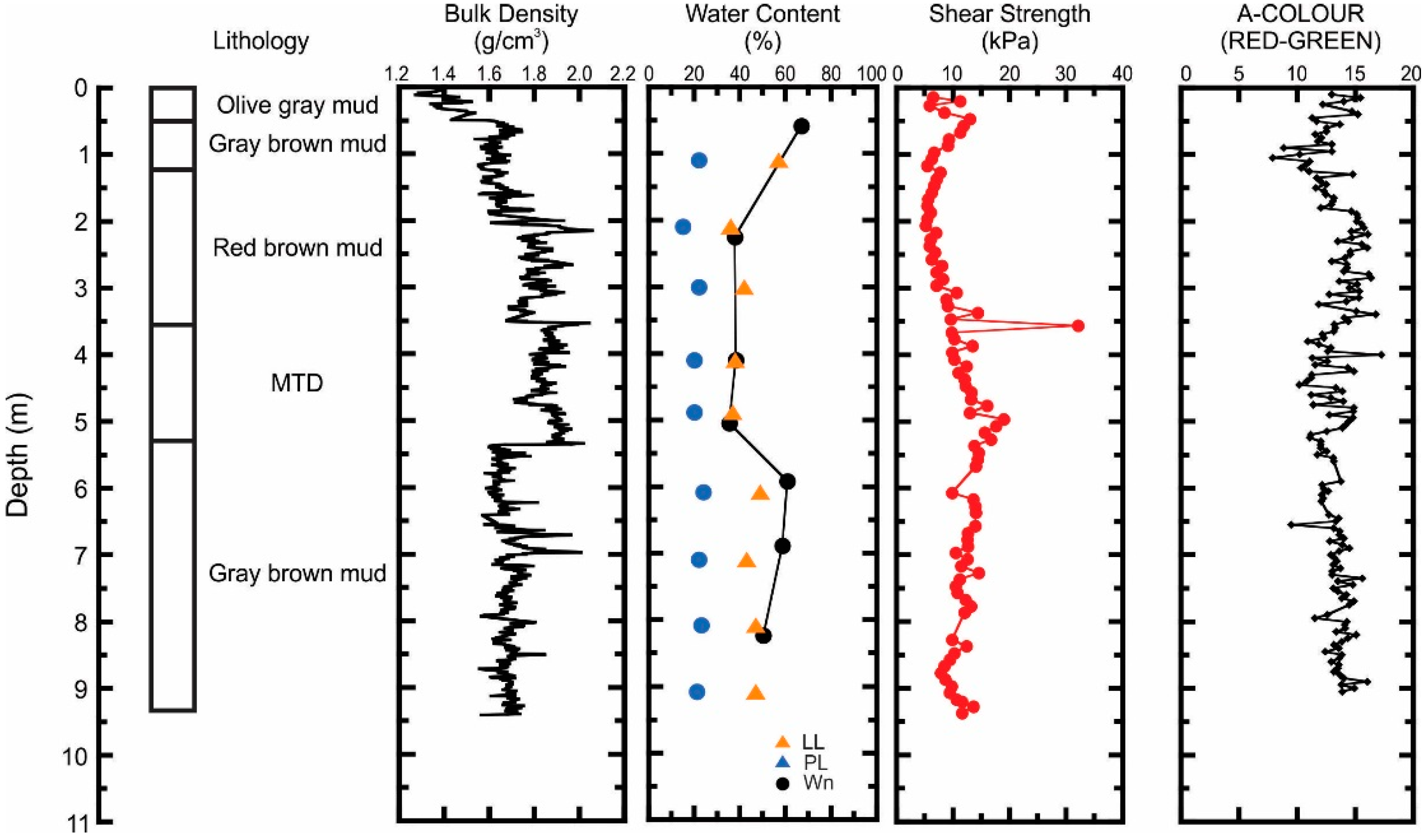
3.1. Sediment Coring and Physical Properties
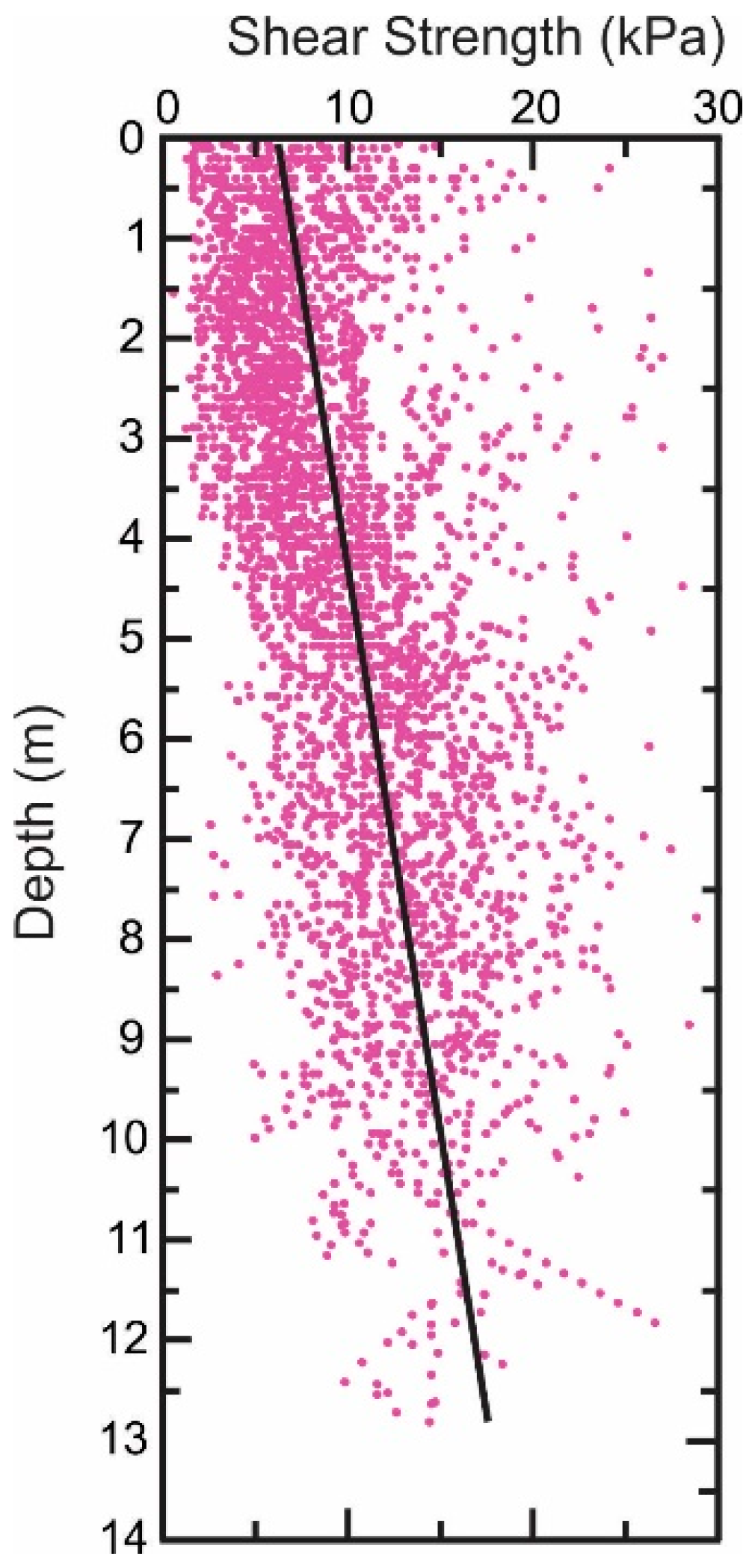
3.2. Data Processing
3.3. Probabilistic Soil Model
3.3.1. Estimation of φ Using Variance Function
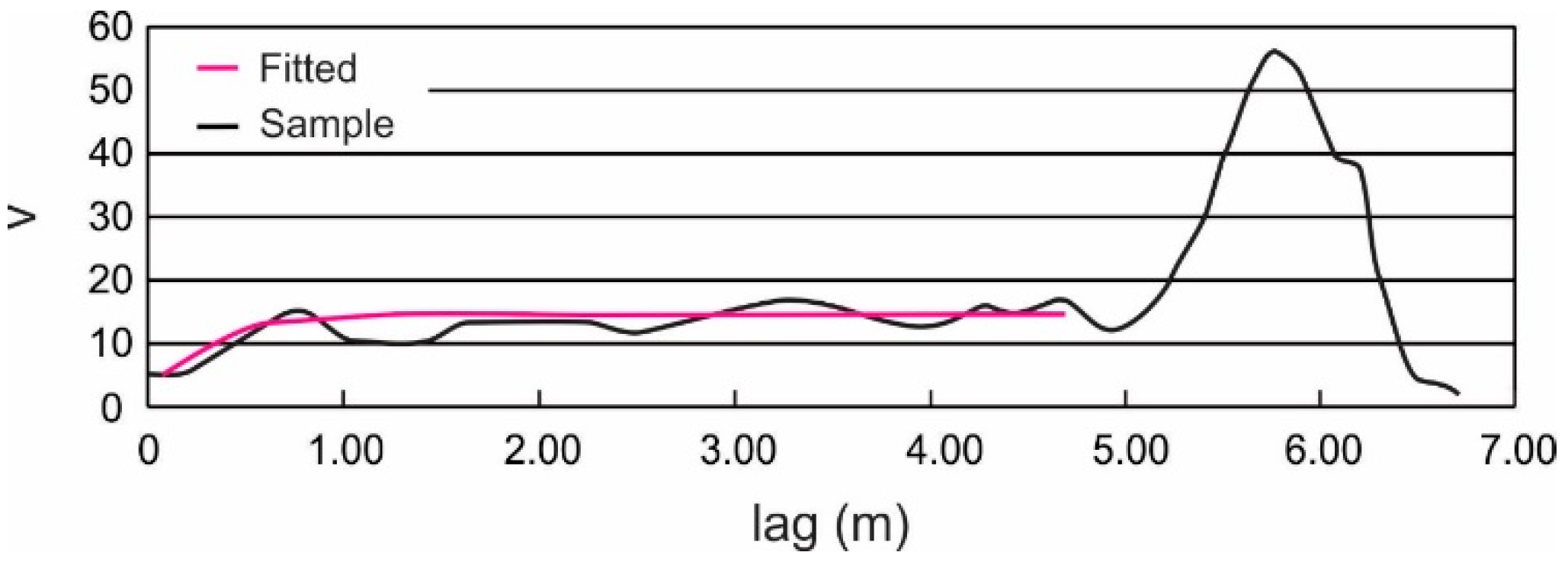
3.3.2. Estimation of θ Using the Semi-Variogram
3.3.3. Choice of Averaging Domain
4. Slope Stability Analysis
4.1. Deterministic Slope Stability Analysis
4.1.1. Deterministic Total Stress Stability Analysis (TSSA)
4.1.2. Deterministic Effective Stress Stability Analysis (ESSA)
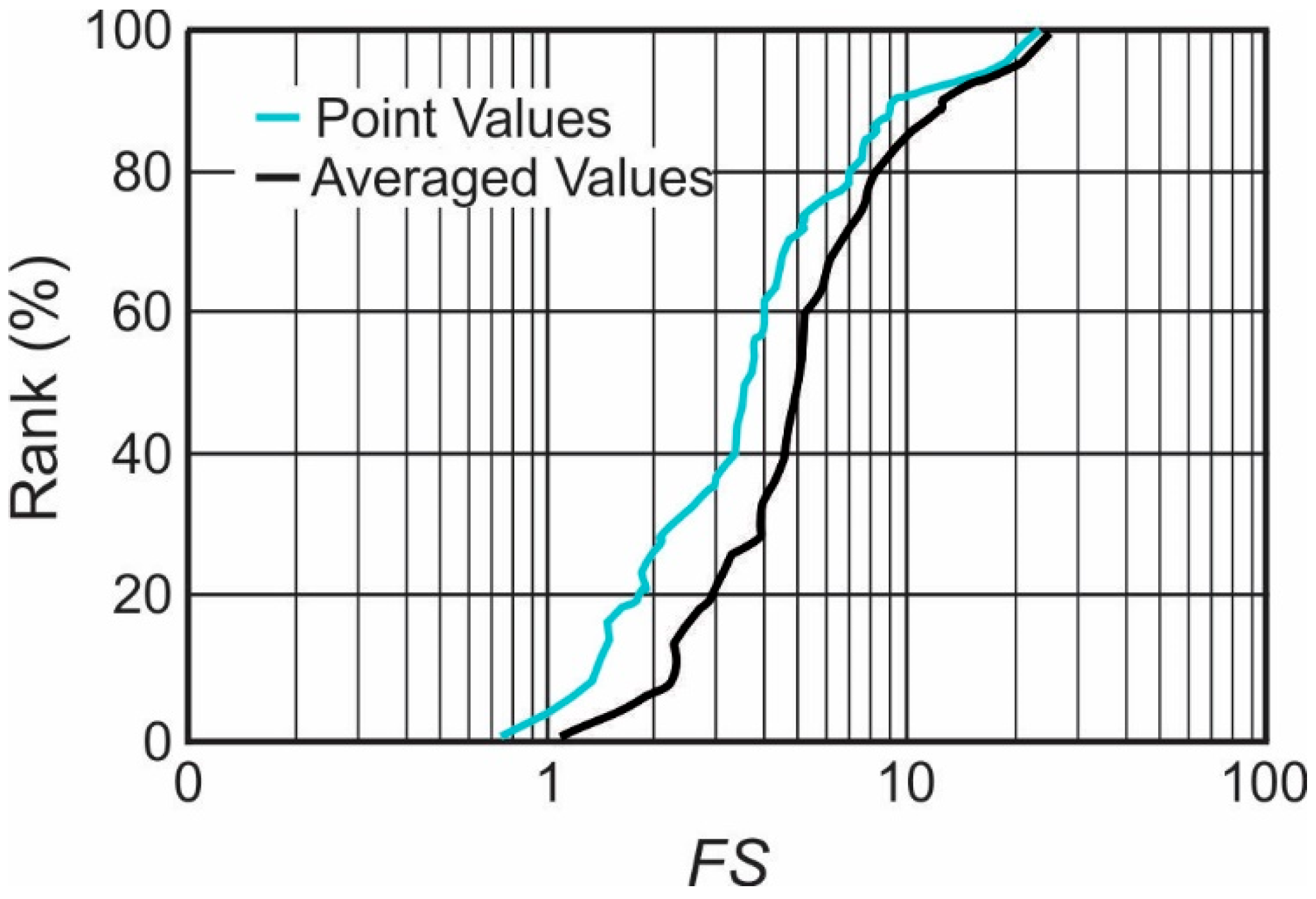
4.2. Probabilistic Slope Stability Analysis
4.2.1. Probabilistic Total Stress Stability Analysis (TSSA)
4.2.2. Probabilistic Effective Stress Analysis
5. Results and Discussion
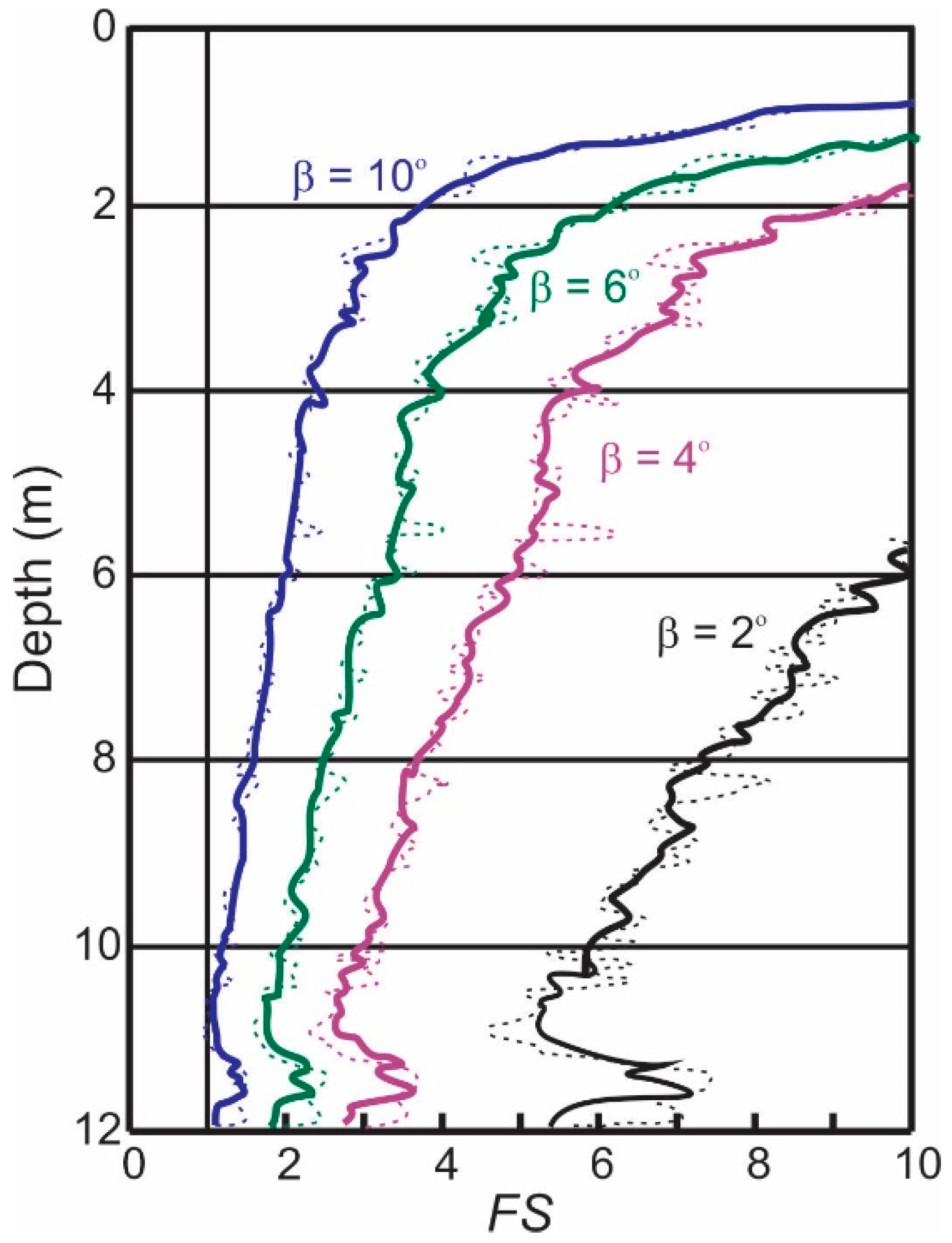
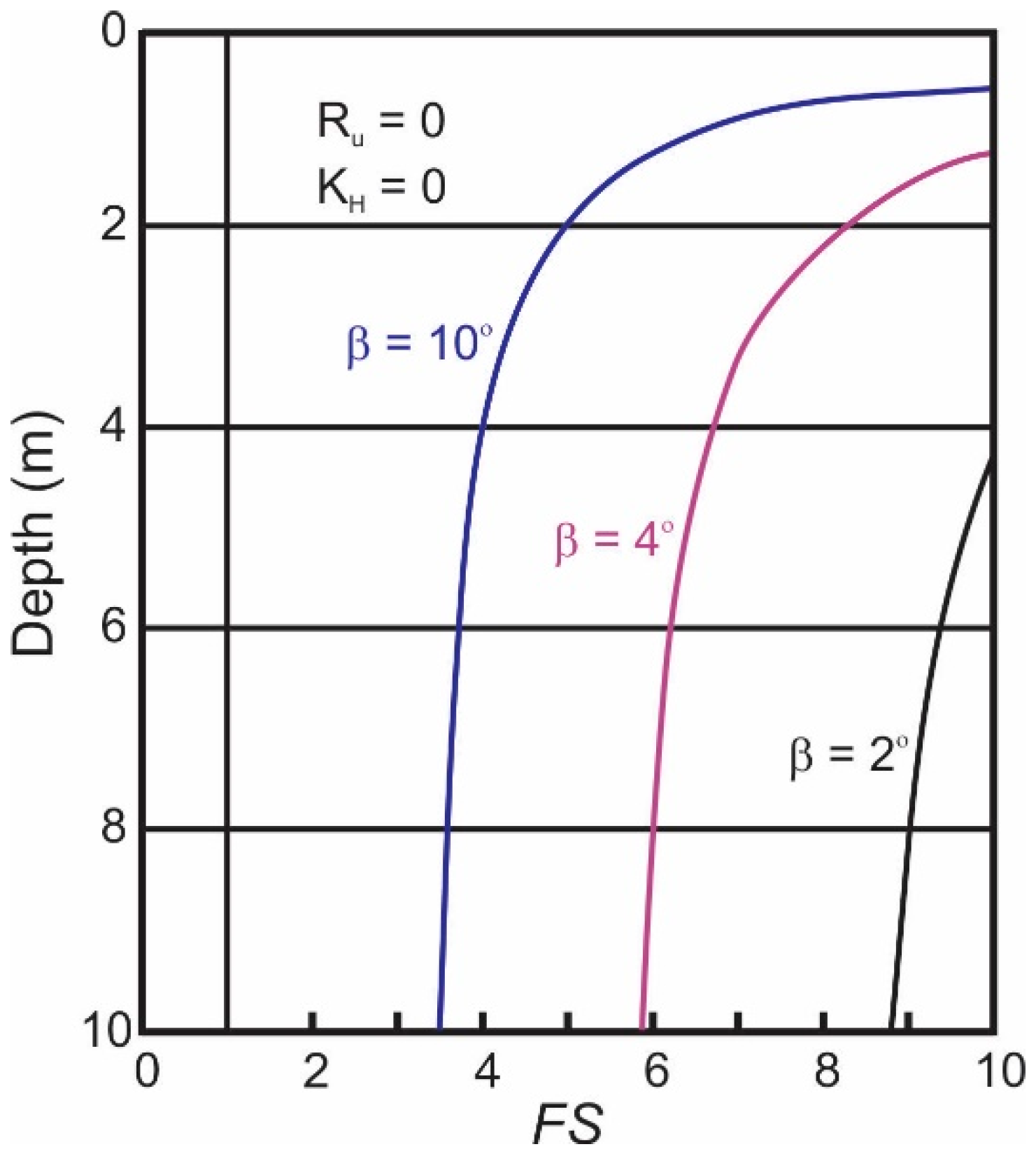
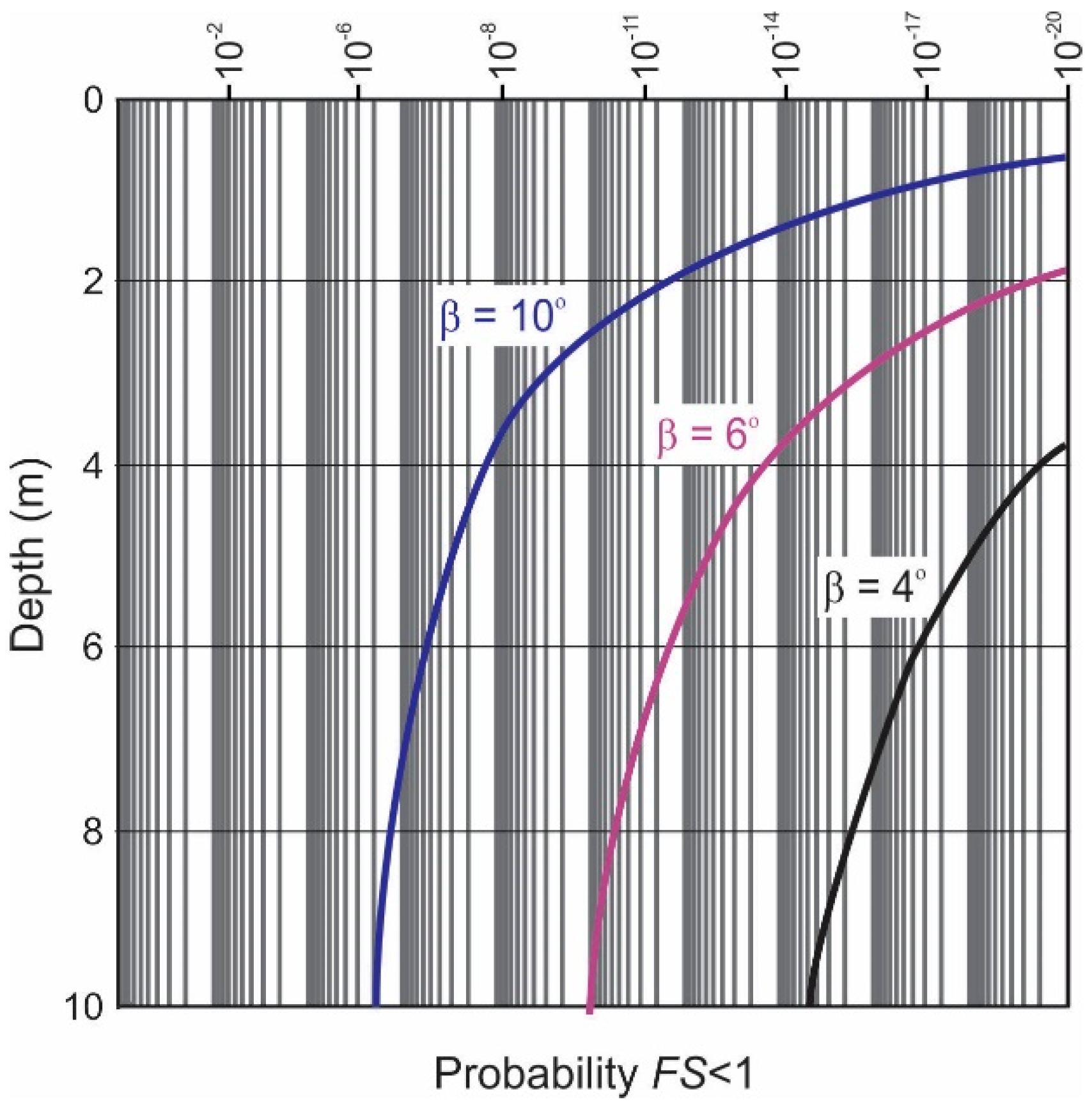
5.1. Total Stress Stability Analysis
5.2. Effective Stress Stability Analysis
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Locat, J.; Lee, H. Submarine landslides: Advances and challenges. Can. Geotech. J. 2002, 39, 193–212. [Google Scholar] [CrossRef]
- Hühnerbach, V.; Masson, D.G. Landslides in the North Atlantic and its adjacent seas: An analysis of their morphology, setting and behavior. Mar. Geol. 2004, 213, 343–362. [Google Scholar] [CrossRef]
- Heezen, B.C.; Ewing, M. Turbidity currents and submarine slumps, and the 1929 Grand Banks earthquake. Am. J. Sci. 1952, 250, 849–878. [Google Scholar] [CrossRef]
- Piper, D.J.W.; Cochonat, P.; Morrison, M.L. The sequence of events around the epicentre of the 1929 Grand Banks earthquake: Initiation of the debris flows and turbidity current inferred from side-scan sonar. Sedimentology 1999, 46, 79–97. [Google Scholar] [CrossRef]
- Schulten, I.; Mosher, D.C.; Krastel, S.; Piper, D.J.W.; Keinast, M. Surficial Sediment Failures due to the 1929 Grand Banks Earthquake, St. Pierre Slope. Subaqueous Mass Mov. Geol. Soc. Lond. Spec. Publ. 2018, 477, SP477.25. [Google Scholar] [CrossRef]
- Mosher, D.C.; Piper, D.J.W.; Campbell, C.D.; Jenner, K.A. Near-surface geology and sediment-failure geohazards of the central scotia slope. AAPG Bullet. 2004, 88, 703–723. [Google Scholar] [CrossRef]
- Deptuck, M.E.; Campbell, D.C. Widespread erosion and mass failure from the 51 Ma Montagnais marine bolide impact off southwestern Nova Scotia, Canada. Can. J. Earth Sci. 2012, 49, 1567–1594. [Google Scholar] [CrossRef]
- Mosher, D.C.; Xu, Z.; Shimeld, J. The Pliocene Shelburne mass-movement and consequent tsunami, western Scotian Slope. In Submarine Mass Movements and Their Consequences IV; Mosher, D.C., Shipp, C., Moscardelli, L., Chaytor, J., Baxter, C., Lee, H., Urgeles, R., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 28, pp. 765–776. [Google Scholar]
- Mosher, D.C.; Moscardelli, L.; Shipp, C.; Chaytor, J.; Baxter, C.; Lee, H.; Urgeles, R. Submarine Mass Movements and Their Consequences. In Submarine Mass Movements and Their Consequences; Mosher, D.C., Shipp, C., Moscardelli, L., Chaytor, J., Baxter, C., Lee, H., Urgeles, R., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 28, pp. 1–8. [Google Scholar]
- Bent, A.L. A complex double-couple source mechanism for the Ms 7.2 1929 Grand Banks earthquake. Bullet. Seismol. Soc. Am. 1995, 85, 1003–1020. [Google Scholar]
- Piper, D.J.W. The Geological Framework of Sediment Instability on the Scotian Slope: Studies to 1999; Open File 3920; Geological Survey of Canada: Ottawa, ON, Canada, 2001; p. 202. [Google Scholar]
- Piper, D.J.W.; Sparkes, R. Proglacial sediment instability features on the Scotian slope at 63 degrees W. Mar. Geol. 1987, 76, 15–31. [Google Scholar] [CrossRef]
- Mosher, D.C. A margin-wide BSR gas hydrate assessment: Canada’s Atlantic margin. J. Mar. Pet. Geol. 2011, 28, 1540–1553. [Google Scholar] [CrossRef]
- Nixon, M.F.; Grozic, J.L.H. A simple model for submarine slope stability analysis with gas hydrates. Nor. J. Geol. 2006, 89, 309–316. [Google Scholar]
- Lofi, J.; Inwood, J.; Proust, J.-N.; Monteverde, D.H.; Loggia, D.; Basile, C.; Otsuka, H.; Hayashi, T.; Stadler, S.; Mottl, M.J.; et al. Fresh-water and salt-water distribution in passive margin sediments; insights from Integrated Ocean Drilling Program Expedition 313 on the New Jersey margin. Geosphere 2013, 9, 1009–1024. [Google Scholar]
- Campbell, D.C.; Piper, D.J.W.; Mosher, D.C.; Jenner, K.A. Surficial Geology and Sun-Illuminated Seafloor Topography, Mohican Channel, Scotian Slope, Offshore Nova Scotia; “A” Series Map 2127A; Geological Survey of Canada: Ottawa, ON, Canada, 2008; 1 sheet. [Google Scholar] [CrossRef]
- Campbell, D.C.; Piper, D.J.W.; Mosher, D.C.; Jenner, K.A. Surficial Geology and Sun-Illuminated Seafloor Topography, Verrill Canyon, Scotian Slope, Offshore Nova Scotia; “A” Series Map 2128A; Geological Survey of Canada: Ottawa, ON, Canada, 2008; 1 sheet. [Google Scholar] [CrossRef]
- Piper, D.J.W. Late Cenozoic evolution of the continental margin of eastern Canada. Nor. J. Geol. 2005, 85, 231–244. [Google Scholar]
- Mosher, D.C.; Moran, K.M.; Zevenhuizen, J. Surficial Geology and Physical Properties 18: Scotian Slope: Verrill Canyon. In East Coast Basin Atlas Series: Scotian Shelf; Atlantic Geoscience Centre, Geological Survey of Canada: Dartmouth, NS, Canada, 1991; p. 145. [Google Scholar]
- Mosher, D.C.; Moran, K.M.; Hiscott, R.N. Late Quaternary sediment, sediment mass-flow processes and slope instability on the Scotian Slope. Sedimentology 1994, 41, 1039–1061. [Google Scholar] [CrossRef]
- Taylor, D.W. Stability of earth slopes. J. Boston Soc. Civ. Eng. 1937, 24, 197–246. [Google Scholar]
- Bishop, A.W. The use of the slip circle in the stability analysis of slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J.; de Wolfe, G.F. Numerical and analytical observations on long and infinite slopes. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 569–585. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J.; Fenton, G.A. On the reliability of earth slopes in three dimensions. Proc. R. Soc. A 2009, 465, 3145–3164. [Google Scholar] [CrossRef]
- Hicks, M.A.; Nuttal, J.D.; Chen, J. Influence of heterogeneity on 3D reliability and failure consequences. Comput. Geotech. 2014, 61, 198–208. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J.; Fenton, G.A. Probabilistic infinite slope analysis. Comput. Geotech. 2010, 38, 577–584. [Google Scholar] [CrossRef]
- Wade, J.A.; MacLean, B.C. Chapter 5: Aspects of the Geology of the Scotian Basin from Recent Seismic and Well Data. In The Geology of the Southeastern Margin of Canada; Keen, M.J., Williams, G.L., Eds.; Geological Survey of Canada: Ottawa, ON, Canada, 1990; Volume 2, pp. 190–238. [Google Scholar] [CrossRef]
- Swift, S.A. Late Pleistone sedimentation on the continental slope and rise off western Nova Scotia. Geol. Soc. Am. Bullet. 1985, 96, 832–841. [Google Scholar] [CrossRef]
- Piper, D.J.W.; Normark, W.R. Late Cenozoic sea level changes and the onset of glaciation: Impact on continental slope progradation off eastern Canada. Mar. Pet. Geol. 1989, 6, 336–348. [Google Scholar] [CrossRef]
- Mosher, D.C.; Piper, D.J.W.; Vilks, G.V.; Aksu, A.E.; Fader, G.B. Evidence for Wisconsinan glaciations in the Verrill Canyon Area, Scotian Slope. Quat. Res. 1989, 31, 27–40. [Google Scholar] [CrossRef]
- Stea, R.R.; Piper, D.J.W.; Fader, G.B.J.; Boyd, R. Wisconsinan glacial and sea level history of maritime Canada and adjacent continental shelf: A correlation of land and sea events. Geol. Soc. Am. Bullet. 1998, 110, 821–845. [Google Scholar] [CrossRef]
- Piper, D.J.W.; Mosher, D.C.; Newton, S. Ice-margin seismic stratigraphy of the central Scotian Slope eastern Canada. Geol. Surv. Can. Curr. Res. 2002, 2002-E16, 10. [Google Scholar]
- Mosher, D.C.; Campbell, D.C.; Gardner, J.V.; Piper, D.J.W.; Chaytor, J.D.; Rebesco, M. The role of deep-water sedimentary processes in shaping a continental margin: The Northwest Atlantic. Mar. Geol. 2017, 392, 245–259. [Google Scholar] [CrossRef]
- Skinner, L.C.; McCave, I.N. Analysis and modelling of gravity- and piston coring based on soil mechanics. Mar. Geol. 2003, 199, 181–204. [Google Scholar] [CrossRef]
- Weaver, P.P.E.; Schultheiss, P.J. Current methods for obtaining, logging and splitting marine sediment cores. Mar. Geophys. Res. 1990, 12, 85–100. [Google Scholar] [CrossRef]
- Head, K.H. Manual of Soil Laboratory Testing: Volume 3 Effective Stress Tests; Pentech Press: London, UK, 1992; p. 428. [Google Scholar]
- Vanmarcke, E.H. Probabilistic Modeling of Soil Profiles. J. Geol. Eng. Div. 1977, 103, 1227–1246. [Google Scholar]
- Vanmarcke, E.H. Reliability of Earth Slopes. J. Geol. Eng. Div. 1977, 103, 1247–1265. [Google Scholar]
- Fenton, G.A. Estimation for Stochastic Soil Models. ASCE J. Geotech. Geoenviron. Eng. 1999, 125, 470–485. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H.; Grigoriu, M.D. Reliability-Based Design of Foundations for Transmission Line Structures; Report TR-105000; Electric Power Research Institute: Palo Alto, CA, USA, 1995; p. 380. [Google Scholar]
| Station | Depth (m) | Bulk Density (g/cm3) | φ’ (°) | c’ (kPa) |
|---|---|---|---|---|
| 88010_022 | 8.80 | 1.89 | 27.4 | 6.4 |
| 2000_036_028 | 3.11 | 1.91 | 26.0 | 7.0 |
| 2000_036_029 | 8.00 | 1.79 | 27.8 | 6.7 |
| 2004_030_008 | 0.25 | 1.74 | 28.9 | 3.3 |
| 2004_030_008 | 0.50 | 1.78 | 31.1 | 1.6 |
| 2004_030_008 | 7.10 | 1.89 | 32.5 | 2.3 |
| Bulk Density (g/cm3) | Undrained Shear Strength (kPa) | |
|---|---|---|
| Minimum | 1.89 | 27.4 |
| Maximum | 1.91 | 26.0 |
| Mean | 1.79 | 27.8 |
| Standard Deviation | 1.74 | 28.9 |
| Coefficient of Varition (%) | 1.78 | 31.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacKillop, K.; Fenton, G.; Mosher, D.; Latour, V.; Mitchelmore, P. Assessing Submarine Slope Stability through Deterministic and Probabilistic Approaches: A Case Study on the West-Central Scotia Slope. Geosciences 2019, 9, 18. https://doi.org/10.3390/geosciences9010018
MacKillop K, Fenton G, Mosher D, Latour V, Mitchelmore P. Assessing Submarine Slope Stability through Deterministic and Probabilistic Approaches: A Case Study on the West-Central Scotia Slope. Geosciences. 2019; 9(1):18. https://doi.org/10.3390/geosciences9010018
Chicago/Turabian StyleMacKillop, Kevin, Gordon Fenton, David Mosher, Valerie Latour, and Perry Mitchelmore. 2019. "Assessing Submarine Slope Stability through Deterministic and Probabilistic Approaches: A Case Study on the West-Central Scotia Slope" Geosciences 9, no. 1: 18. https://doi.org/10.3390/geosciences9010018
APA StyleMacKillop, K., Fenton, G., Mosher, D., Latour, V., & Mitchelmore, P. (2019). Assessing Submarine Slope Stability through Deterministic and Probabilistic Approaches: A Case Study on the West-Central Scotia Slope. Geosciences, 9(1), 18. https://doi.org/10.3390/geosciences9010018





