Enhanced Characterization of the Krania–Elassona Structure and Functioning Allogenic Karst Aquifer in Central Greece
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Hydrogeological Research
2.3. SARIMA Models
3. Results and Discussion
3.1. Geological and Geomorphological Settings
- Lower horizon: The lower horizon occupies the eastern part of the tectonic window. It consists of medium- to thick-bedded, coarse to microcrystalline marbles, locally dolomitic, and is of light grey to white-grey color with a thickness of about 750 m.
- Mid horizon: The marbles of the intermediate horizon appear to be thin-bedded, locally foliated and rarely medium-bedded. The dark grey marbles of this horizon occupy the central part of the tectonic window. Their thickness reaches 700 m.
- Upper horizon: This horizon occupies the western part of the carbonate series and has a total thickness of about 400 m. It consists of medium-bedded and rarely thick-bedded marbles, locally dolomitic. They are mainly white in the lower parts of this horizon and grey at lesser depths. Very small percentages of lens-shaped mica schists occur in this section, which interfere with the crystalline marble of the top layer. The upper horizon is also characterized by sporadic mica schists. In many locations, such as NE of Loutro village, it is especially difficult to distinguish them from the expanded mica schists of the crystalline Pelagonian base.
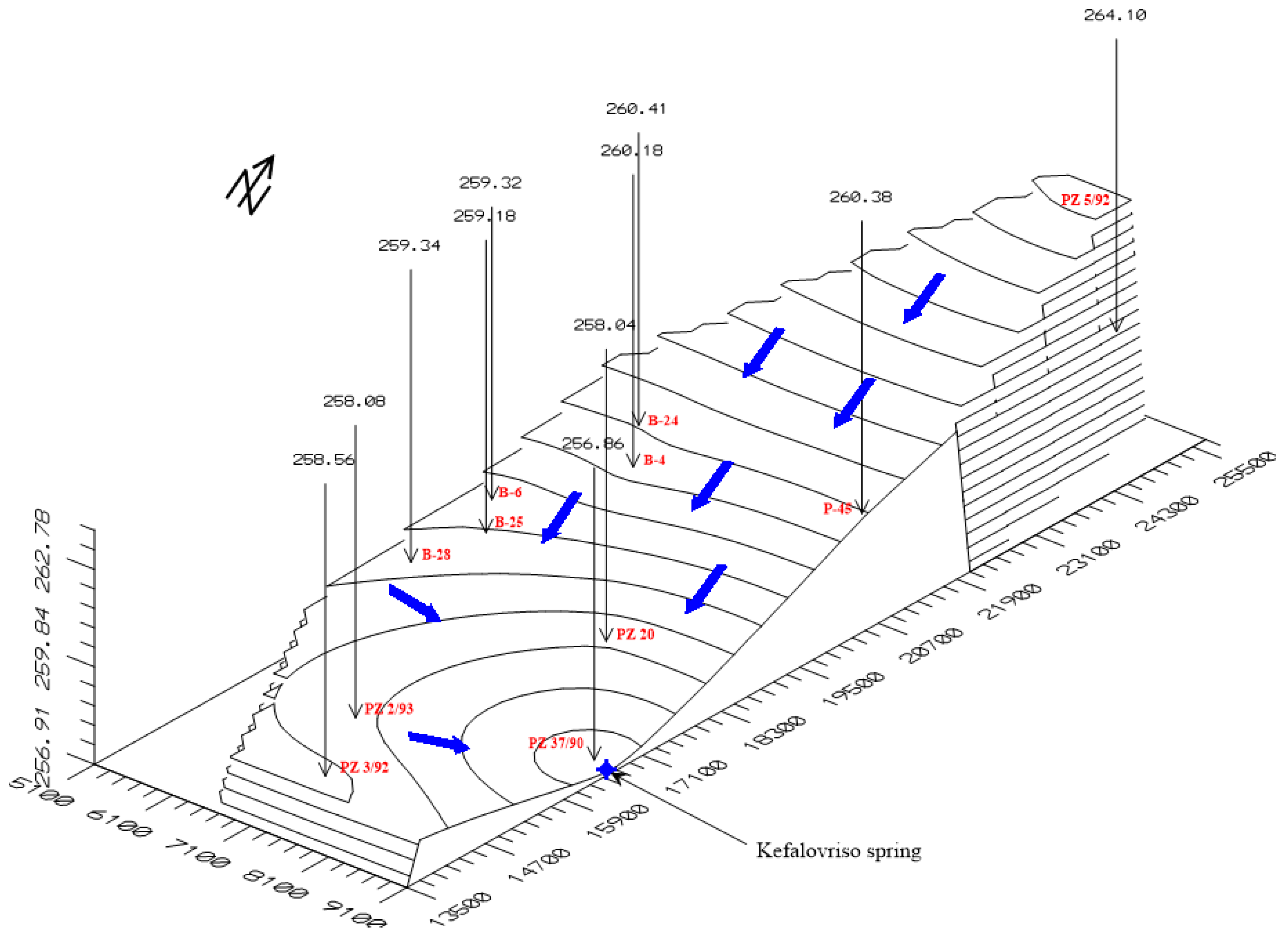
3.2. Hydrogeological Setting
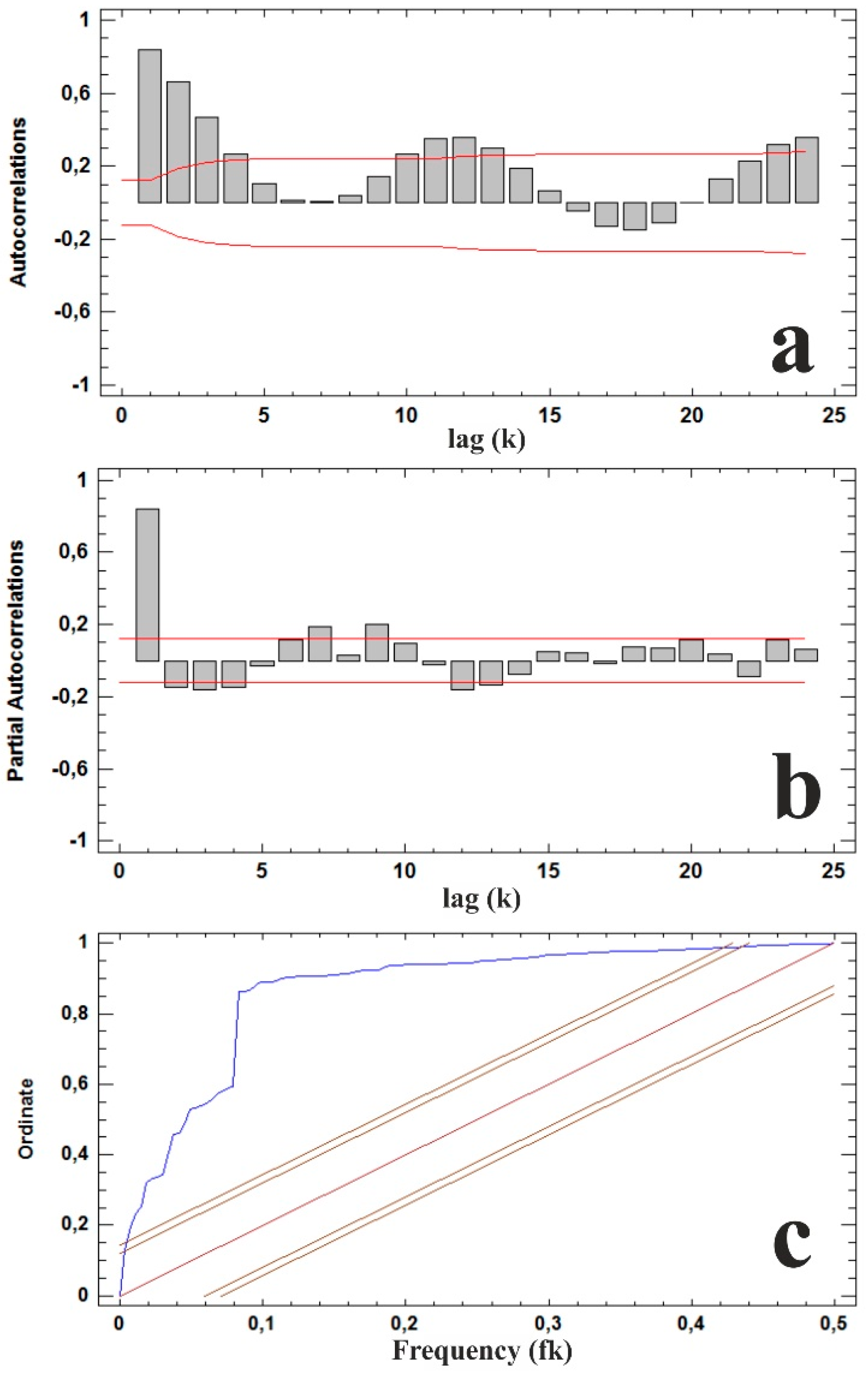
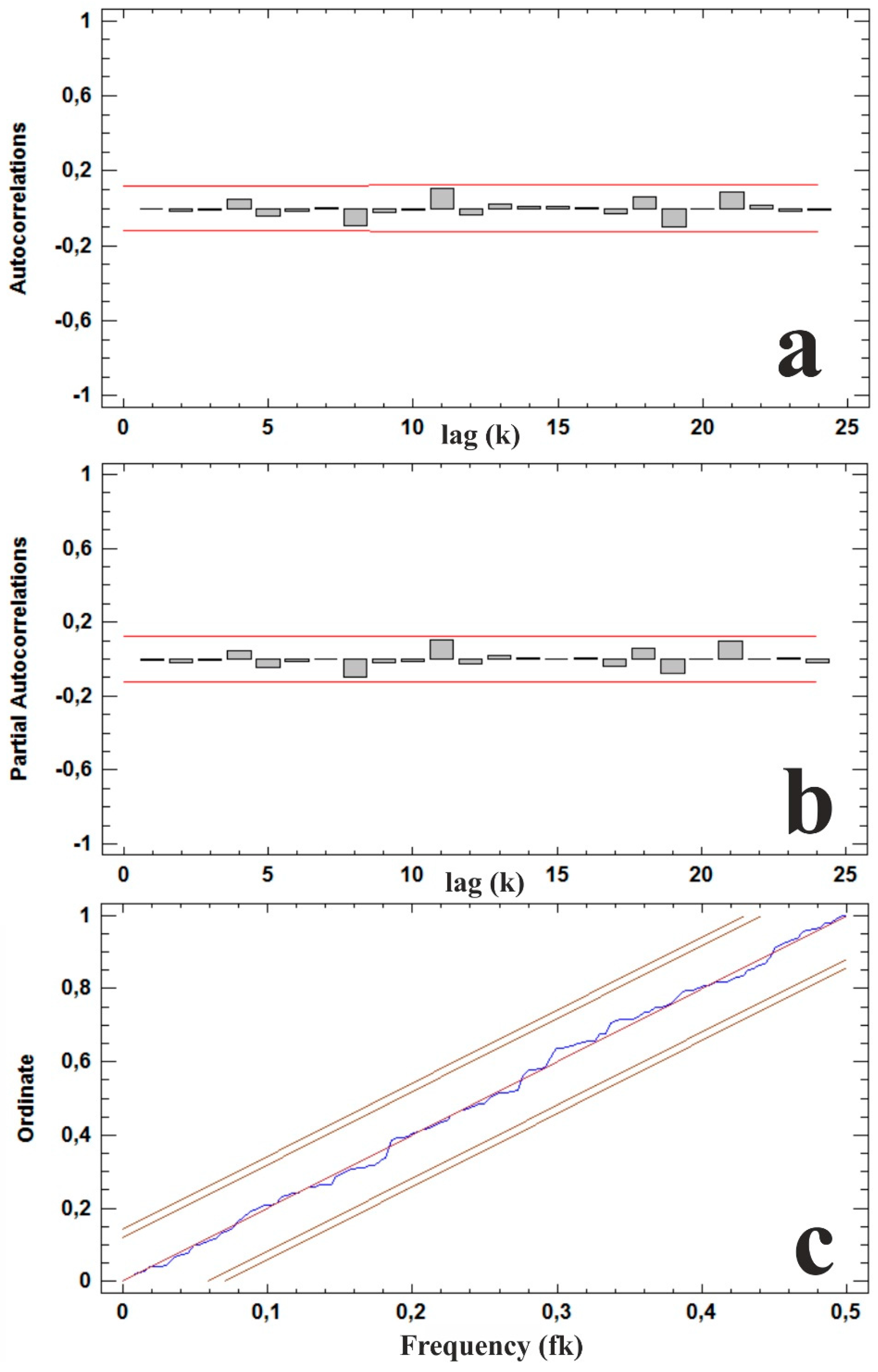
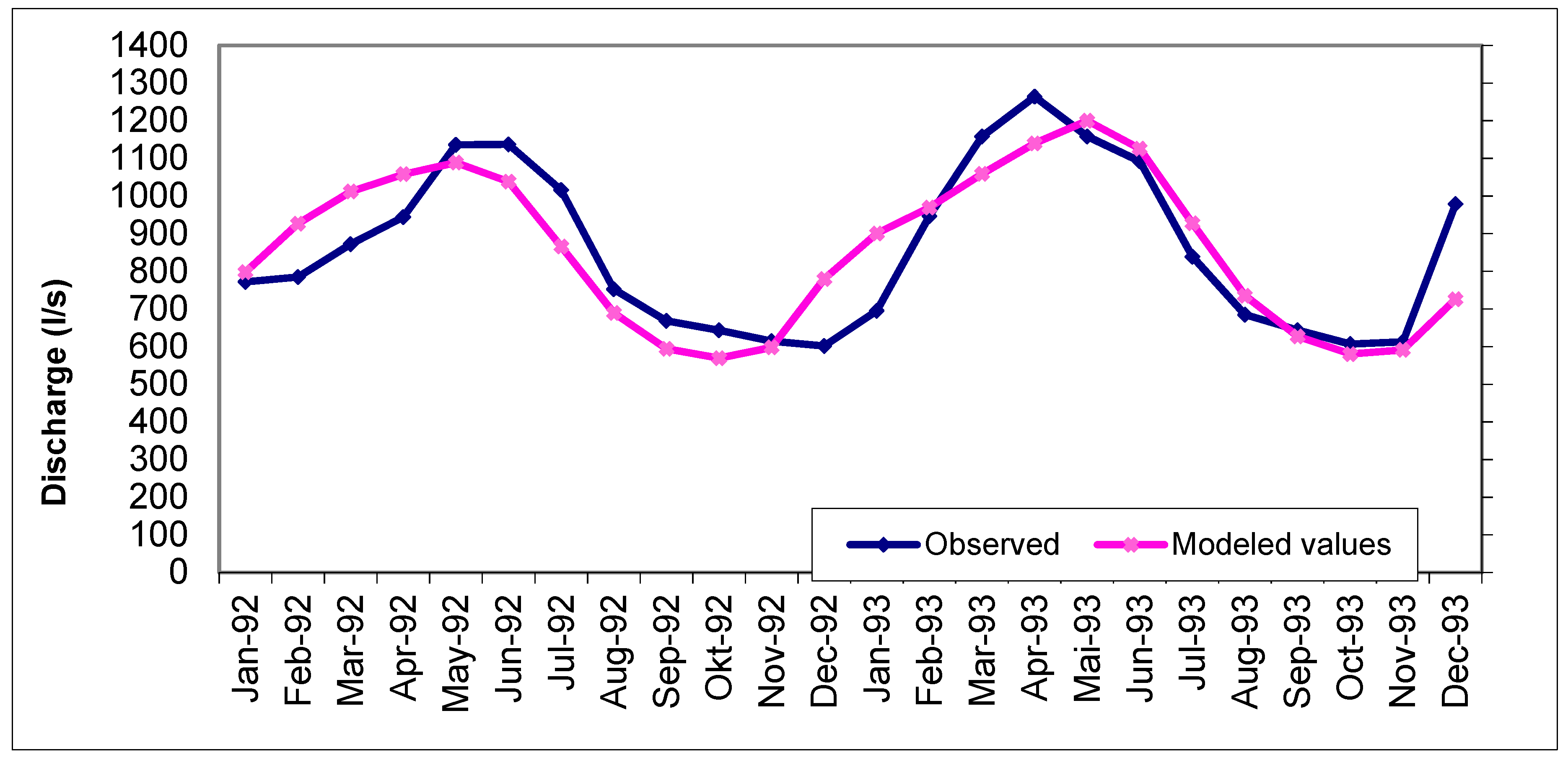
3.3. SARIMA Model
3.4. Research Challenges
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ford, D.C.; Williams, P.W. Karst Geomorphology and Hydrology; Unwin Hyman: London, UK, 1989; Volume 601, ISBN 9401177805. [Google Scholar]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Stevanović, Z. Karst Aquifers—Characterization and Engineering; Springer International Publishing: Basel, Switzerland, 2015. [Google Scholar]
- Daskalaki, P.; Voudouris, K. Groundwater quality of porous aquifers in Greece: A synoptic review. Environ. Geol. 2008, 54, 505–513. [Google Scholar] [CrossRef]
- Kazakis, N.; Chalikakis, K.; Mazzilli, N.; Ollivier, C.; Manakos, A.; Voudouris, K. Management and research strategies of karst aquifers in Greece: Literature overview and exemplification based on hydrodynamic modelling and vulnerability assessment of a strategic karst aquifer. Sci. Total Environ. 2018, 643, 592–609. [Google Scholar] [CrossRef]
- Perrin, J.; Jeannin, P.Y.; Zwahlen, F. Epikarst storage in a karst aquifer: A conceptual model based on isotopic data, milandre test site, Switzerland. J. Hydrol. 2003, 279, 106–124. [Google Scholar] [CrossRef]
- Goldscheider, N.; Drew, D. Methods in Karst Hydrogeology; CRC Press: London, UK, 2007; ISBN 9780415428736. [Google Scholar]
- Knez, M.; Petrič, M.; Slabe, T.; Šebela, S. The Beka-Ocizla Cave System, Karstological Railway Planning in Slovenia; Springer International Publishing: Basel, Switzerland, 2015. [Google Scholar]
- Ficco, K.K.; Sasowsky, I.D. An interdisciplinary framework for the protection of karst aquifers. Environ. Sci. Policy 2018, 89, 41–48. [Google Scholar] [CrossRef]
- Patrikaki, O.; Kazakis, N.; Voudouris, K. Vulnerability map: A useful tool for groundwater protection: An example from Mouriki basin, North Greece. Fresenius Environ. Bull. 2012, 21, 2516–2521. [Google Scholar]
- Kazakis, N.; Spiliotis, M.; Voudouris, K.; Pliakas, F.K.; Papadopoulos, B. A fuzzy multicriteria categorization of the GALDIT method to assess seawater intrusion vulnerability of coastal aquifers. Sci. Total Environ. 2018, 621, 552–566. [Google Scholar] [CrossRef]
- Dörfliger, N.; Plagnes, V.; Kavouri, K. PaPRIKa a multicriteria vulnerability method as a tool for sustainable management of karst aquifers, example of application on a test site in SW France. In Proceedings of the International Interdisciplinary Scientific Conference “Sustainability of the Karst Environment: Dinaric Karst and Other Karst Regions”, Plitvice Lakes, Croatia, 23–26 September 2009. [Google Scholar]
- Dörfliger, N.; Plagnes, V.; Kavouri, K.; Balayre, S.; Paris, C.; Muet, P.; Subias, C.; Jaunat, J.; Huneau, F.; Prévost, V.; et al. PaPRIKa, une méthode multicritère de cartographie de la vulnérabilité pour une gestion des ressources et des captages en milieu karstique: Exemples d’application dans le Sud-Ouest de la France. Géologues 2009, 163, 86–92. [Google Scholar]
- Dörfliger, N. Advances in Karst Groundwater Protection Strategy Using Artificial Tracer Tests Analysis and Multiattribute Vulnerability Mapping (EPIK Method). Ph.D. Thesis, Neuchatel University, Neuchatel, Switzerland, 1996. [Google Scholar]
- Goldscheider, N.; Klute, M.; Sturm, S.; Hötzl, H. The PI method—A GIS-based approach to mapping groundwater vulnerability with special consideration of karst aquifers. Z. Angew. Geol. 2000, 46, 157–166. [Google Scholar]
- Daly, D.; Dassargues, A.; Drew, D.; Dunne, S.; Goldscheider, N.; Neale, S.; Popescu, I.; Zwahlen, F. Main concepts of the “European approach” to karst groundwater-vulnerability assessment and mapping. Hydrogeol. J. 2002, 10, 340–345. [Google Scholar] [CrossRef]
- Jeannin, P.Y.; Cornaton, F.; Zwahlen, F.; Perrochet, P. VULK: A tool for intrinsic vulnerability assessment and validation. Sci. Tech. L’environ. Mém. Hors-Sér. 2001, 13, 185–190. [Google Scholar]
- Vias, J.M.; Andreo, B.; Perles, M.J.; Carrasco, F.; Vadillo, I.; Jimenez, P. Proposed method for groundwater vulnerability mapping in carbonate (karstic) aquifers: The COP method. Hydrogeol. J. 2006, 14, 912–925. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, Revised ed.; Holden Day, Inc.: San Francisco, CA, USA, 1976; p. 532. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994; Volume 45, p. 1013. [Google Scholar]
- Ahn, H.; Salas, J.D. Groundwater head sampling based on stochastic analysis. Water Resour. Res. 1997, 33, 2769–2780. [Google Scholar] [CrossRef]
- Manakos, A. Hydrogeological Behavior and Stochastic Simulation of Krania Elassona Karstic Aquifer Thessaly. Ph.D. Thesis, Aristotle University of Thessaloniki, Thessaloniki, Greece, 1999. [Google Scholar]
- Papamichail, D.M.; Antonopoulos, V.Z.; Georgiou, P.E. Stochastic models for Strymon river flow and water quality parameters. In Proceedings of the International Conference Protection and Restoration of the Environment V, Thassos, Greece, 2–6 July 2000; pp. 219–226. [Google Scholar]
- Papamichail, D.M.; Georgiou, P.E. Seasonal ARIMA inflow models for reservoir sizing. J. Am. Water Resour. Assoc. 2001, 37, 877–885. [Google Scholar] [CrossRef]
- Manakos, A.; Dimopoulos, G. Contribution of stochastic models to the sustainable water management. The example of Krania Elassona karstic aquifer in Thessaly. In Proceedings of the 10th International Conference of Greek Geol. Society, Thessaloniki, Greece, 15–17 April 2004; pp. 361–368. [Google Scholar]
- Manakos, A.; Georgiou, P. Time series modeling of groundwater head using seasonal stochastic models SARIMA. In Proceedings of the common Conference of the 11th Hellenic Hydrotechnical Society and of the 7th Conference of the Hellenic Committee of Water Management, Volos, Greece, 27–30 May 2009; pp. 709–716. [Google Scholar]
- Voudouris, K.; Georgiou, P.; Stiakakis, E.; Monopolis, D. Comparative analysis of stochastic models for simulation of discharge and chloride concentration in Almyros Karstic Spring in Greece. In Proceedings of the 14th Annual Conference of the International Association of Mathematical Geo-sciences, IAMG, Budapest, Hungary, 10–16 August 2010; p. 15. [Google Scholar]
- Manakos, A.; Georgiou, P.; Mouratidis, I. Application of stochastic models to rational management of water resources at the Damasi Titanos karstic aquifer in Thessaly Greece. In Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1, pp. 435–442. ISBN 978-3-642-19901. [Google Scholar]
- Manakos, A.; Tasios, N. Hydrogeological Research of Large Carbonated Masses in Thessaly; Krania Karstic Aquifer, Institouto Geologikon Kai Metalleftikon Erevnon (I.G.M.E.): Thessaloniki, Greece, 1999. [Google Scholar]
- Triantafyllis, E. Geological Maps of Greece, Scale 1:50000, Sheets: Elassona, Deskati; I.G.M.E.: Thessaloniki, Greece, 1982. [Google Scholar]
- Mohan, S.; Vedula, S. Multiplicative seasonal arima model for longterm forecasting of inflows. Water Resour. Manag. 1995, 9, 115–126. [Google Scholar] [CrossRef]
- Box, G.E.P.; Pierce, D.A. Distribution of autocorrelations in autoregressive integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Katsikatsos, G.; Migiros, G.; Triantaphyllis, M.; Mettos, A. Geological structure of internal Hellenides (E. Thessaly—SW. Macedonia, Euboea—Attica—Northern Cyclades islands and Lesvos). Geol. Geophys. Res. Spec. Issue 1986, 191–212. [Google Scholar]
- Stamatis, A.; Migiros, G. Das tektonische Fenster von Kranea-Elasson (NW Thessalien/Griechenland), Neues Jahrbuch für Geologie und Paläontologie. 1993; 49–64. [Google Scholar]
- Kilias, A.; Mountrakis, D. The Pelagonian Nappe. Tectonics, metamorphism and magmatism. In Proceedings of the 4th Congress of the Geological Society of Greece XXIII, Athens, Greece, 25–27 May 1988; pp. 16–38. [Google Scholar]
- Voudouris, K.; Mandrali, P.; Kazakis, N. Preventing Groundwater Pollution Using Vulnerability and Risk Mapping: The Case of the Florina Basin, NW Greece. Geosciences 2018, 8, 129. [Google Scholar] [CrossRef]
- Nanou, E.A.; Zagana, E. Groundwater vulnerability to pollution map for karst aquifer protection (Ziria Karst System, Southern Greece). Geosciences 2018, 8, 125. [Google Scholar] [CrossRef]
- Kavouri, K.P.; Karatzas, G.P.; Plagnes, V. A coupled groundwater-flow-modelling and vulnerability-mapping methodology for karstic terrain management. Hydrogeol. J. 2017, 25, 1301–1307. [Google Scholar] [CrossRef]
- Kazakis, N.; Oikonomidis, D.; Voudouris, K. Groundwater vulnerability and pollution risk assessment with disparate models in karstic, porous and fissured rock aquifers using remote sensing techniques and GIS in Anthemountas basin, Greece. Environ. Earth Sci. 2015, 74, 6199–6209. [Google Scholar] [CrossRef]
- Panagopoulos, G.; Lambrakis, N. The contribution of TSA to the study of the hydrodynamic characteristics of the karst systems: Application on two typical karst aquifers of Greece (Trifilia, Almyros Crete). Hydrol. J. 2006, 329, 368–376. [Google Scholar] [CrossRef]
- Mazzilli, N.; Guinot, V.; Jourde, H.; Lecoq, N.; Labat, D.; Arfib, B.; Baudement, C.; Danquigny, C.; Dal Soglio, L.; Bertin, D. KarstMod: A modelling platform for rainfall—discharge analysis and modelling dedicated to karst systems. Environ. Model. Softw. 2017. In Press, Corrected Proof. [Google Scholar] [CrossRef]
- Vacher, H.L.; Mylroie, J.E. Eogenetic Karst from the Perspective of an Equivalent Porous Medium. Carbonates Evaporites 2002, 17, 182–196. [Google Scholar] [CrossRef]
- Mylroie, J.E.; Carew, J.L. Karst development on carbonate islands. Speleogenesis and Evolution of Karst Aquifers. Virtual Sci. J. 2003, 1, 1–21. [Google Scholar]
- Langston, A.L.; Screaton, E.J.; Martin, J.B.; Vincent, B.C. Interactions of diffuse and focused allogenic recharge in an eogenetic karst aquifer (Florida, USA). Hydrogeol. J. 2012, 20, 767–781. [Google Scholar] [CrossRef]
- Gill, L.W.; Babechuk, M.G.; Kamber, B.S.; McCormack, T.; Murphy, C. Use of trace and rare earth elements to quantify autogenic and allogenic inputs within a lowland karst network. Appl. Geochem. 2018, 90, 101–114. [Google Scholar] [CrossRef]



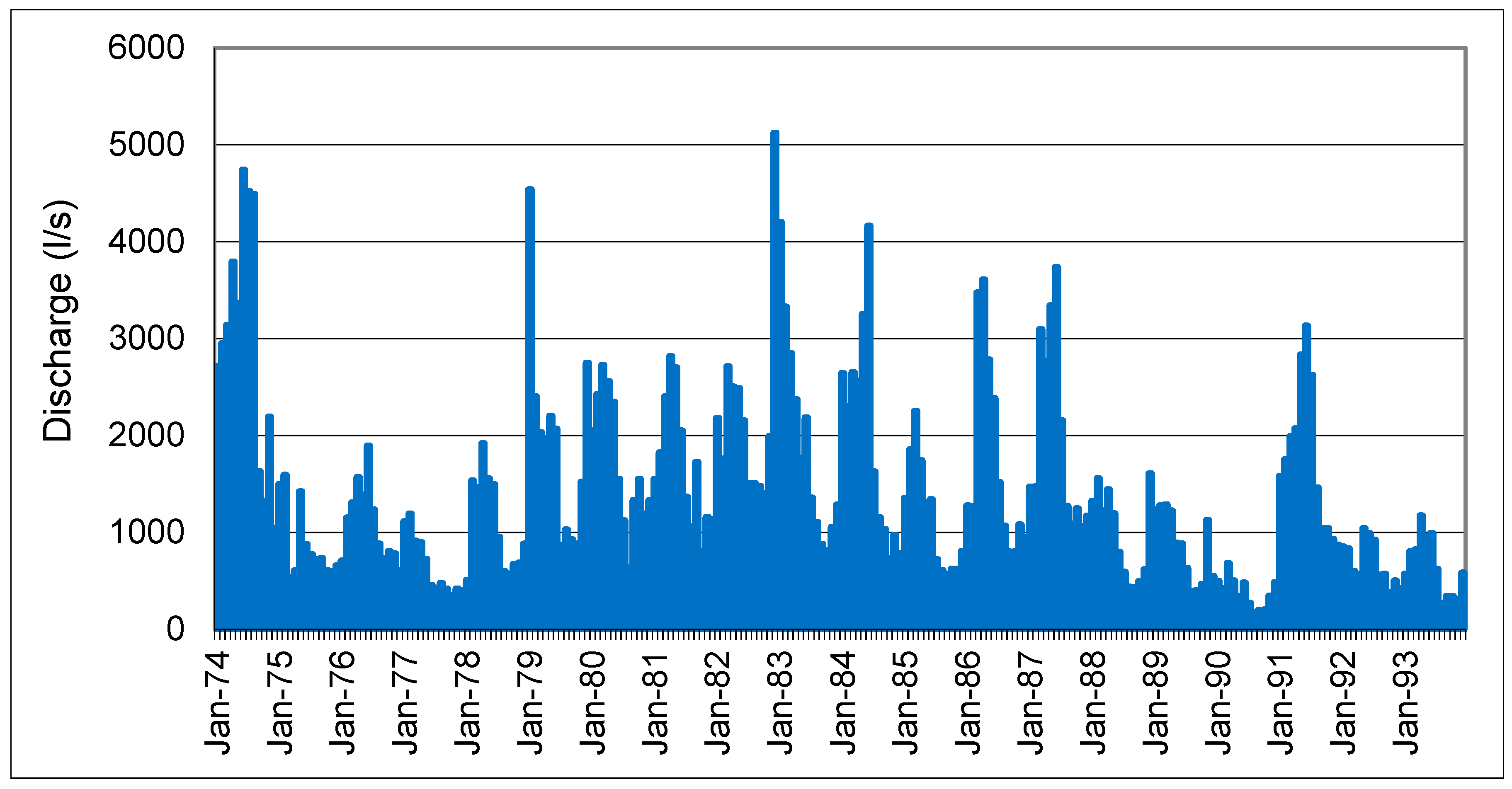
| Hydrological Year | Mean Annual Discharge [Qj] lit/sec | Max. Discharge [Qmax] lit/sec | Min. Discharge [Qmin] lit/sec | Mean Annual Temperature T [°C] | Ratio of Min./Max. Discharge Qmax/Qmin |
|---|---|---|---|---|---|
| 1988/1989 | 843 | 1891 | 479 | 12.5 | 3.80 |
| 1989/1990 | 544 | 893 | 259 | 14.1 | 3.45 |
| 1990/1991 | 1878 | 3210 | 316 | 11.7 | 10.16 |
| 1991/1992 | 721 | 1148 | 515 | 13.2 | 2.23 |
| 1992/1993 | 830 | 1301 | 334 | 12.3 | 3.90 |
| Mean | 963 | 1689 | 381 | 12.8 | 4.71 |
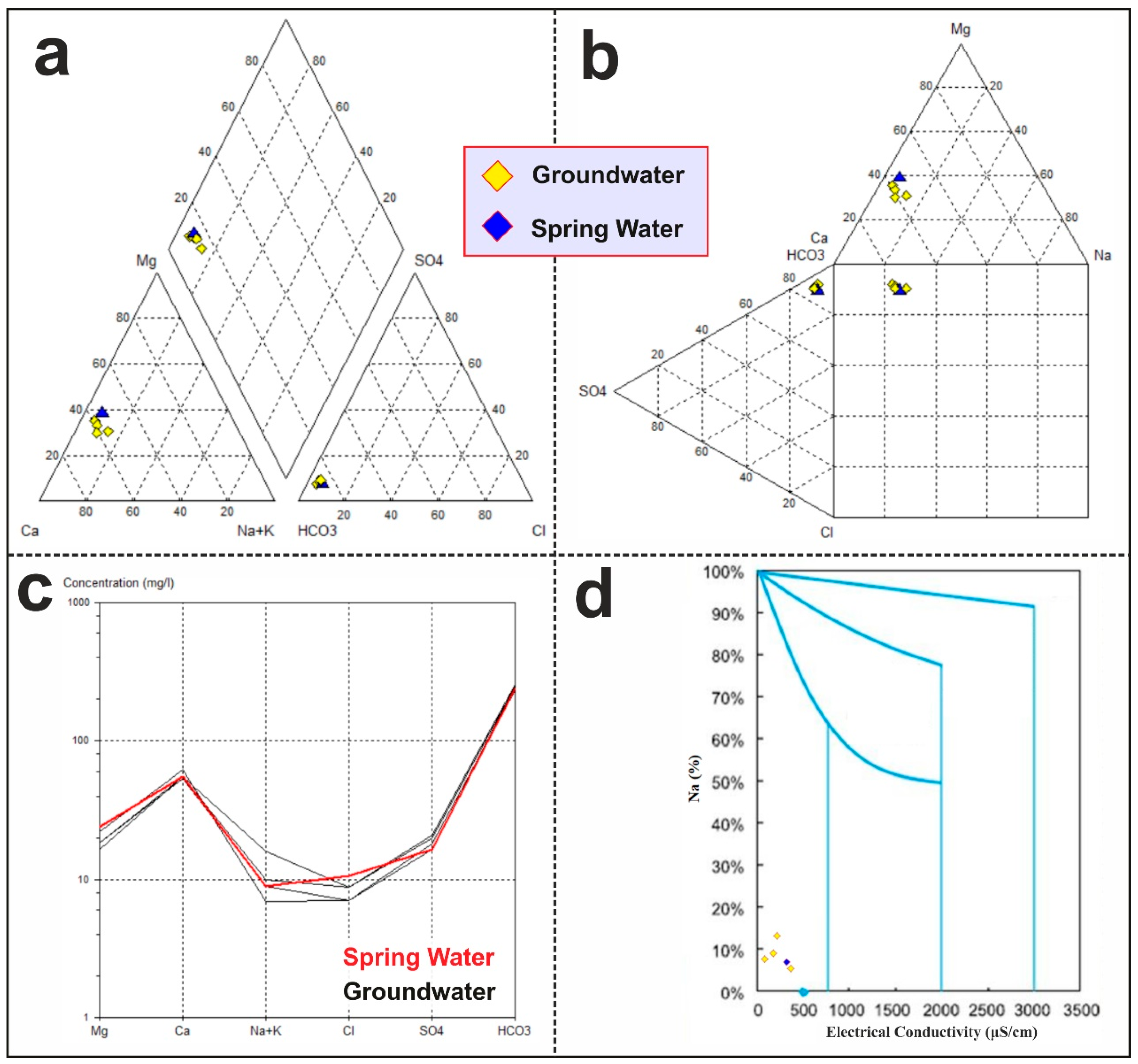
| Sample | Type | pH | EC (μS/cm) | TDS (mg/L) | Ca (mg/L) | Mg (mg/L) | Na (mg/L) | K (mg/L) | HCO3 (mg/L) | Cl (mg/L) | SO4 (mg/L) | NO3 (mg/L) | NO2 (mg/L) | NH4 (mg/L) | Ca+Mg/HCO3 | Mg/Ca | Na/Cl |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ELP1 | Spring | 7.80 | 420 | 359 | 59 | 16 | 10 | 2 | 239 | 5 | 17 | 10 | 0.002 | 0.001 | 1.1 | 0.4 | 2.9 |
| ELR1 | Surface water | 7.48 | 425 | 345 | 46 | 13 | 22 | 5 | 190 | 21 | 41 | 7 | 0.005 | 0.001 | 1.1 | 0.5 | 1.6 |
| ELR2 | Surface water | 7.60 | 477 | 399 | 69 | 16 | 10 | 2 | 248 | 12 | 30 | 13 | 0.006 | 0.001 | 1.2 | 0.4 | 1.2 |
| ELR3 | Surface water | 7.24 | 297 | 225 | 30 | 10 | 11 | 7 | 87 | 16 | 43 | 21 | <DL | 0.113 | 1.6 | 0.5 | 1.1 |
| ELR4 | Surface water | 8.24 | 710 | 471 | 60 | 25 | 30 | 4 | 244 | 21 | 78 | 9 | 0.002 | 0.05 | 1.3 | 0.7 | 2.2 |
| ERL5 | Surface water | 8.06 | 480 | 337 | 51 | 15 | 12 | 2 | 215 | 7 | 26 | 9 | 0.012 | 0.022 | 1.1 | 0.5 | 2.6 |
| B-25 | Groundwater | 7.70 | 470 | 372 | 62 | 22 | 6 | 1 | 249 | 7 | 16 | 9 | <DL | 0.018 | 1.2 | 0.6 | 1.3 |
| B-6 | Groundwater | 7.76 | 414 | 351 | 54 | 18 | 7 | 2 | 232 | 11 | 18 | 9 | 0.01 | 0.001 | 1.1 | 0.6 | 1.0 |
| PZ37/90 | Groundwater | 7.90 | 433 | 365 | 55 | 17 | 9 | 1 | 245 | 9 | 20 | 9 | 0.004 | 0.059 | 1.0 | 0.5 | 1.6 |
| PZ45/90 | Groundwater | 8.00 | 441 | 382 | 55 | 18 | 14 | 2 | 253 | 9 | 21 | 10 | <DL | 0.044 | 1.0 | 0.6 | 2.4 |
| Min. | 7.20 | 297 | 225 | 30 | 10 | 6 | 1 | 87 | 5 | 16 | 7 | 0.002 | 0.001 | 1.0 | 0.4 | 1.0 | |
| Max. | 8.20 | 710 | 471 | 69 | 25 | 30 | 7 | 253 | 21 | 78 | 21 | 0.012 | 0.113 | 1.6 | 0.7 | 2.9 | |
| SD | 0.30 | 103 | 61.3 | 10.4 | 4.4 | 7.4 | 1.9 | 50.6 | 5.8 | 19.1 | 3.8 | 0.004 | 0.036 | 0.2 | 0.1 | 0.7 | |
| Mean | 7.80 | 456.7 | 360 | 54.2 | 17.0 | 13.1 | 2.8 | 220.1 | 11.9 | 31.0 | 10.6 | 0.0 | 0.0 | 1.2 | 0.5 | 1.8 | |
| CN | Model | AIC | PP | n | σe2 | Qp |
|---|---|---|---|---|---|---|
| 1 | (1,0,1)(0,1,1)12 | 229,1551 | 272,9079 | 5 | 0,0536982 | 13,2792 |
| 2 | (2,0,0)(0,1,1)12 | 235,7214 | 270,7234 | 4 | 0,0558706 | 17,9667 |
| 3 | (4,1,0)(1,1,1)12 | 232,4000 | 328,656 | 11 | 0,0515653 | 10,0651 |
| 4 | (3,1,0)(1,1,1)12 | 232,5456 | 311,3006 | 9 | 0,0525644 | 16,1979 |
| 5 | (4,1,1) (1,1,1)12 | 227,4535 | 297,4580 | 13 | 0,0518173 | 9,95088 |
| 6 | (4,1,0)(1,1,2)12 | 235,2279 | 340,2346 | 12 | 0,0517632 | 10,1882 |
| Model Parameter | Parameter Value | Confidence Interval (95%) | Standard Error | T-Value | P-Value |
|---|---|---|---|---|---|
| φ1 | 0.42862 | 0.29648–0.56076 | 0.06704 | 6.39365 | 0.00000 |
| φ2 | −0.39013 | −0.53080–0.24946 | 0.07137 | −5.46654 | 0.00000 |
| φ3 | 0.23333 | 0.09215–0.37451 | 0.71630 | 3.25745 | 0.00130 |
| φ4 | −0.15361 | −2.28582–0.02140 | 0.67080 | −2.29012 | 0.02296 |
| Φ1 | −0.13274 | −1.97641–1.71093 | 0.09354 | −1.41910 | 0.15728 |
| θ1 | −0.17472 | −1.06035–0.71091 | 0.44933 | −0.38884 | 0.69781 |
| Θ1 | 0.66286 | 0.53221–0.79351 | 0.07198 | 9.20902 | 0.00000 |
| Modelling Efficiency | Index of Agreement | |
|---|---|---|
| Observed | 859.37 | 215.42 |
| Forecasted | 858.40 | 205.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manakos, A.; Ntona, M.M.; Kazakis, N.; Chalikakis, K. Enhanced Characterization of the Krania–Elassona Structure and Functioning Allogenic Karst Aquifer in Central Greece. Geosciences 2019, 9, 15. https://doi.org/10.3390/geosciences9010015
Manakos A, Ntona MM, Kazakis N, Chalikakis K. Enhanced Characterization of the Krania–Elassona Structure and Functioning Allogenic Karst Aquifer in Central Greece. Geosciences. 2019; 9(1):15. https://doi.org/10.3390/geosciences9010015
Chicago/Turabian StyleManakos, Antonios, Maria Margarita Ntona, Nerantzis Kazakis, and Konstantinos Chalikakis. 2019. "Enhanced Characterization of the Krania–Elassona Structure and Functioning Allogenic Karst Aquifer in Central Greece" Geosciences 9, no. 1: 15. https://doi.org/10.3390/geosciences9010015
APA StyleManakos, A., Ntona, M. M., Kazakis, N., & Chalikakis, K. (2019). Enhanced Characterization of the Krania–Elassona Structure and Functioning Allogenic Karst Aquifer in Central Greece. Geosciences, 9(1), 15. https://doi.org/10.3390/geosciences9010015






