1. Introduction
The increasing global population leads to an increasing amount of municipal waste that must be a) recycled, b) burned, or c) deposited [
1]. The latter option requires legally-fixed environmental and technical standards. Therefore, the German Landfill Directive, which was enacted in 2009, includes the essential qualitative criteria for engineered barriers [
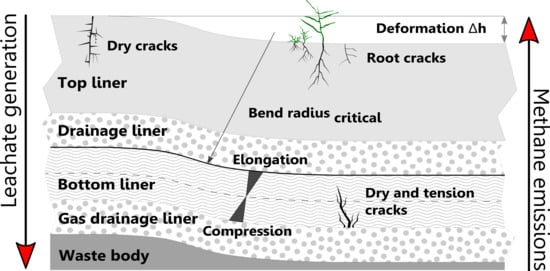
2]. Landfill capping systems are essential to protect the immediate environment of the waste body that can include aromatic hydrocarbons, carbolic acids, or heavy metals (i.e., arsenic).
Therefore, capping systems are purposed to (a) protect the groundwater against potentially leaking bottom liners through leachate minimizing and (b) inhibit the diffusive emission of greenhouse gases (i.e., methane) [
3]. The top and bottom liner of landfills are often constructed by natural materials (i.e., clay, boulder marl) that should fulfil the technical requirements of technical guidelines [
1,
2]. Natural materials can be installed in combination with geotextiles or geomembranes, although their application is restricted due to the high cost factor, especially in financially less powerful regions (i.e., Romania) as stated by reference [
4]. Consequently, high engineering demands are placed on the material. Considering the legally-fixed standards, (a) plant available water capacity (AWC ≥ 0.14 cm
3/cm
3), (b) saturated hydraulic conductivity (Ks value ≤ 5 × 10
9 m/s equal to 0.5 m thickness and a hydraulic gradient of i = 0.3), (c) air capacity (AC ≥ 0.08 cm
3/cm
3), and (d) low shrinkage tendency (volume shrinkage index < 5%) are essential soil physical properties of mineral landfill liner [
5,
6]. These properties were regularly affected by the degree of compaction and the water content during liner installation considering potential changes in the pore size distribution (PSD) [
6,
7].
The study is focused on the Rastorf landfill (Northern Germany), because the temporary installed capping system with a maximum duration of up to 10 years must be transferred into a final capping system according to the statutory requirements as mentioned before. Therefore, it was the task of the authors to estimate the soil chemical and physical characteristics of locally available and sustainable material and its possible use as landfill top and bottom liner [
5]. In this case, boulder marl (bm) and marsh clay (mc) were chosen, while bm was also an integral part of the temporary capping system that, if suitable, could be continued to be used. Both substrates are also common for its use as landfill liners, even in combination with elastic polymers, depending on the hazardousness of the stored waste [
1].
Proctor compaction tests [
8] are requested before installation of mineral landfill liner to determine the effect of compaction on the soil water retention curve (SWRC) characteristics including AWC, AC, as well as the Ks values due to the statutory requirements in Germany. For a more accurate description of the SWRC in the near-saturated soil water content, the standard unimodal approach [
9] assuming a single-porosity could be used to fit observed data from fine-textured soils, or if bimodal approaches [
10] could better represent any modality of the PSD induced by soil mechanical processes in compacted liners. The impact soil shrinkage on the long-term sealing effect of mineral landfill liner was described in a previous study [
6] and is excluded from the current study, but the opportunity of PSD as an indicator for the shrinkage-dependent volume change was tested for both materials.
In this context, the estimated fitting parameter (i.e., van Genuchten parameter), especially for heavily compacted soils (>1.8 g/cm
3) are a useful addition towards commonly used data [
11] in case of landfill engineering and modelling. The modelling process including the water and solute transport in the vadose zone, and therefore the fitting parameter, are essential to improve the modelling performance of the Rastorf landfill as mentioned by [
12]. This step is necessary to make essential adjustments to the existing temporary capping system before transferring part of it into the final capping system and to construct a final capping system with proven efficiency with respect to the statutory requirements. The adjustments include, among other things, the application of compost to the chosen substrates, since its ability as soil conditioner was proven in several field and laboratory studies (i.e., [
13]).
The first objective of this study was to determine the effect of compaction on the soil physical properties of boulder marl (bm) and marsh clay (mc) and its suitability as landfill liner materials considering experimental Proctor compaction tests. The second objective was to investigate the effect of compaction on the pore size distribution, and therefore the modality, to find the optimum model (unimodal or bimodal) for further water flow transport modelling of landfill liner systems. Additionally, the effect of compost application on SWRC characteristics of boulder marl was also tested to answer the question whether and how can compost improve the water holding capacity of landfills’ top liner.
The authors hypothesized that the degree of compaction affects (i) the pore size distribution and (ii) the modality of the SWRC, and therefore the soil physical properties of both materials, and that (iii) compost application positively affects the SWRC characteristics of boulder marl.
This study intends to provide knowledge on soil chemical and physical properties of alternative materials for engineering landfill capping systems.
2. Materials and Methods
The boulder marl derived from a pit located in the young moraine landscape (Rastorf: lat 54°16′ N, long 10°19′ E) and the marsh clay from decalcified marshland (Barlt: lat 54°28′ N, long 9°18′ E) in the state of Schleswig-Holstein in Northern Germany. Both materials were used for the Proctor compaction test (ASTM D-698).
In June 2013, as a result of erosion damage and less pronounced vegetative growth, approximately 100 m
3 of compost, produced in the local compost facility (Rastorf, Northern Germany) consisting of tree and shrub chippings and debris, was applicated by milling machine to the upper 0.2 m of the top liner (same boulder marl for Proctor compaction tests) of the Rastorf landfill on approximately 1000 m
2 [
14,
15]. The basic material was mechanically shredded and frayed and then stored in a composting plant for nearly 9 months to enhance the biochemical processes of composting between 70 °C and 100 °C. In 2013 (without compost: wco) and 2015 (compost: co), more than 80 undisturbed soil cores (diameter: 0.055 m, height: 0.04 m) were collected from a pit in the northeast part of the landfill (lat 54°28′ N, long 10°32′ E) in depths between 0.1 m and 0.2 m.
2.1. Standard Proctor Compaction Tests
Disturbed and homogenized bm and mc material was used for four standard Proctor compaction tests (ASTM D-698), respectively. Therefore, the material was moistened and then compacted to estimate a) the optimum dry bulk density (ρ
topt) and b) the optimum water content (w
opt) including two different stages at the dry side (bm1, bm2, mc1, mc2) and wet side (bm4, bm5, mc4, mc5) of the optimum water content (bm3, mc3) as mentioned following reference [
6].
As result, 20 soil cores (diameter: 5.5 cm, height: 4 cm) per Proctor stage (1–5) were prepared with standard method by a load frame through a stamp (diameter: 5.5 cm) with a static load of 50 kN (Instron, Norwood, MA, USA) to estimate AC, AWC, and Ks values of both materials, respectively.
2.2. Laboratory Analyses of Soil Properties
Disturbed bm, mc, wco, and co material was used to estimate the organic carbon content (OC) with coulometry, soil texture (sieve and pipette method), soil pH (pH meter, CaCl
2), particle density (ρ
s) (pycnometer method), and dry bulk density (ρ
t) (core method) with 4 replications per Proctor stage, respectively, based on standard laboratory experiments as mentioned in the following literature [
16]. The Ks values were determined by the falling-head method [
17] with 5 to 10 undisturbed soil cores for each Proctor stage, wco and co, respectively.
The SWRC characteristics were measured from undisturbed soil cores (5 to 10 per Proctor stage, wco, co) by a combined pressure plate (quasi-saturated, −30, −60, −150, −300, −500, −1000 hPa) and −15,000 hPa ceramic vacuum outflow method as well as oven-dried for 16 h at 105 °C [
16].
The total porosity was calculated from the ratio between bulk, ρ
t, and solid particle density, ρ
s (bm: 2.63–2.64 g/cm
3, mc: 2.67–2.68 g/cm
3); the air capacity (AC) and the plant available water capacity (AWC) were calculated as follows:
where θ is the volumetric water content (cm
3/cm
3), θ
s is the saturated volumetric water content (cm
3/cm
3), and θ
r (cm
3/cm
3) is the residual water content, subscripts FC (field capacity) and PWP (permanent wilting point) indicate the water content at −60 hPa and −15,000 hPa, respectively.
2.3. Descriptions of the Soil Water Retention Curve
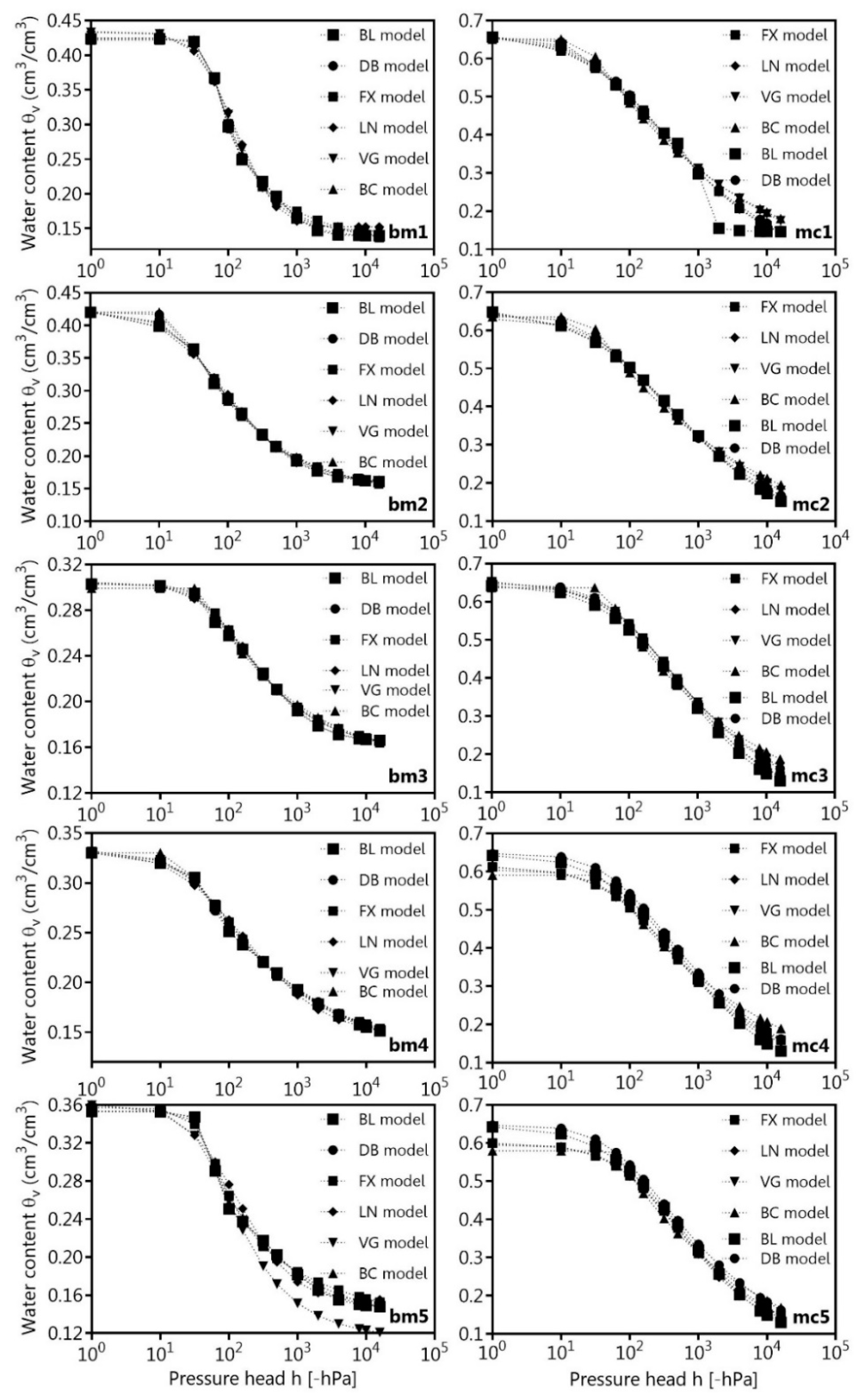
The software SWRC FIT [
10] was used to fit the observed soil water retention data based on a Levenberg–Marquardt optimization method with the following unimodal and bimodal models: Brooks–Corey (BC) model [
18], van Genuchten (VG) model [
9], Fredlund and Xing (FX) model [
19], Kosugi (LN) model [
20], Durner (DB) model [
21], and Seki (BL) model [
10]. The effective water saturation, S
e, is defined as follows:
The Brooks–Corey (BC) model is expressed as follows [
18]:
where h is the pressure head (hPa) and h
b is the pressure head value (hPa) at air-entry.
The van Genuchten (VG) model is defined as [
9]:
where α is a scale parameter inversely proportional to pore diameter (1/cm), n is related to the pore size distribution with n ≥ 1, and m is the Mualem coefficient and defined as m = 1 − 1/n with 0 < m < 1.
The Fredlund and Xing (FX) model described was used as follows [
19]:
where α is related to the air entry value of the soil (hPa), n is related to the maximum slope of the soil, m is related to the curvature of the slope, e is the Euler’s number (of natural exponential function), and C(h) is the correction factor that extends the range of pressure head up to 1 × 10
7 hPa.
The linear Kosugi (LN) model [
20] was used in the following form:
where h
m is the capillary pressure head (hPa) related to the median pore radius (cm), σ is a dimensionless parameter related to the width of the pore radius distribution, and Q is related to the complementary error function (erfc) as follows:
where x describes the term in brackets in Equation (6).
The bimodal Durner (DB) model includes the weight term w for two VG soil water retention functions in the following formulation [
21]:
The bimodal Seki (BL) model [
10] also includes a weight term as proposed follows reference [
22]:
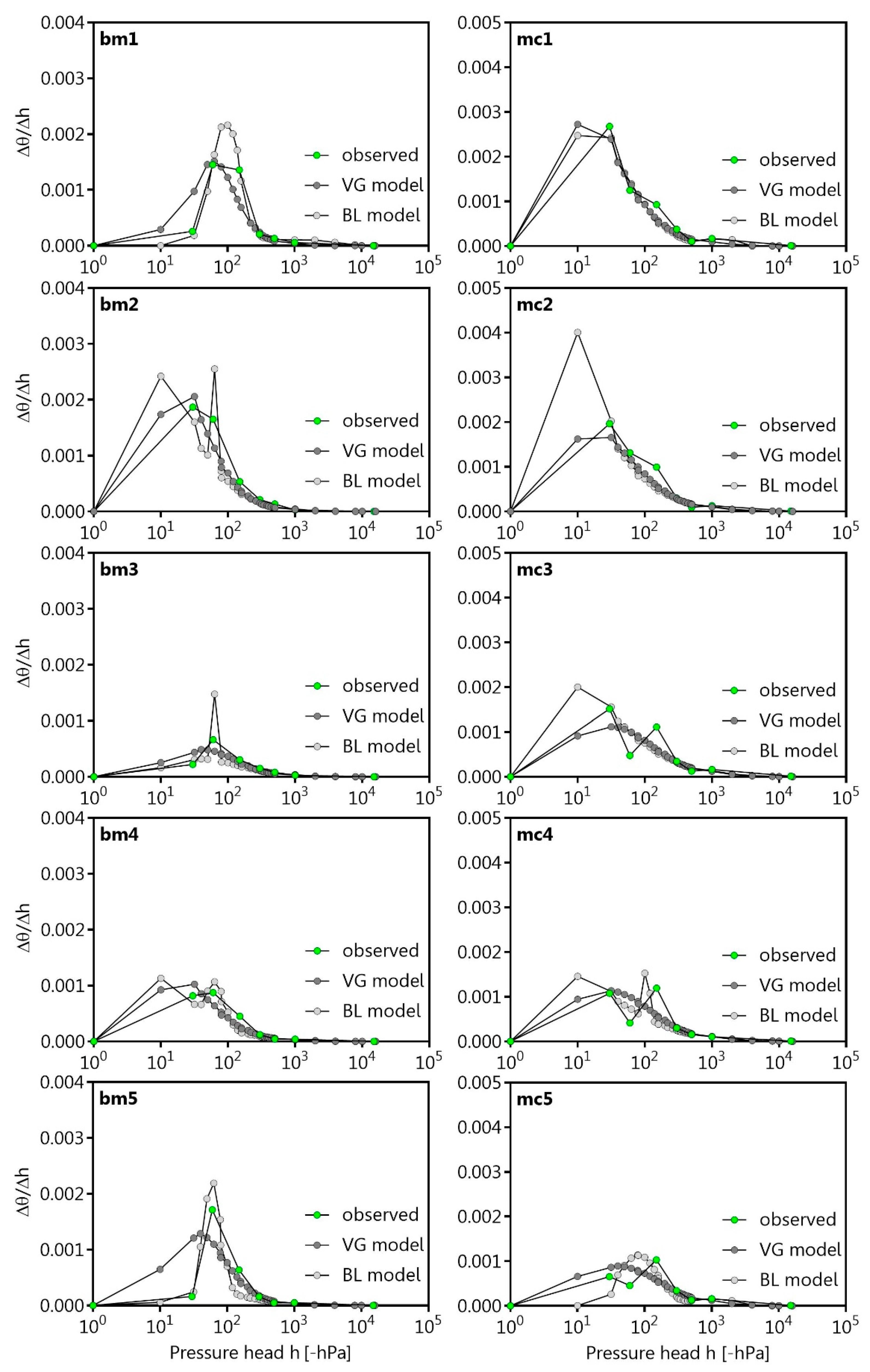
In this study, the differential function for the SWRC was directly regarded as the soil PSD in form of the slope of the SWRC [
23]:
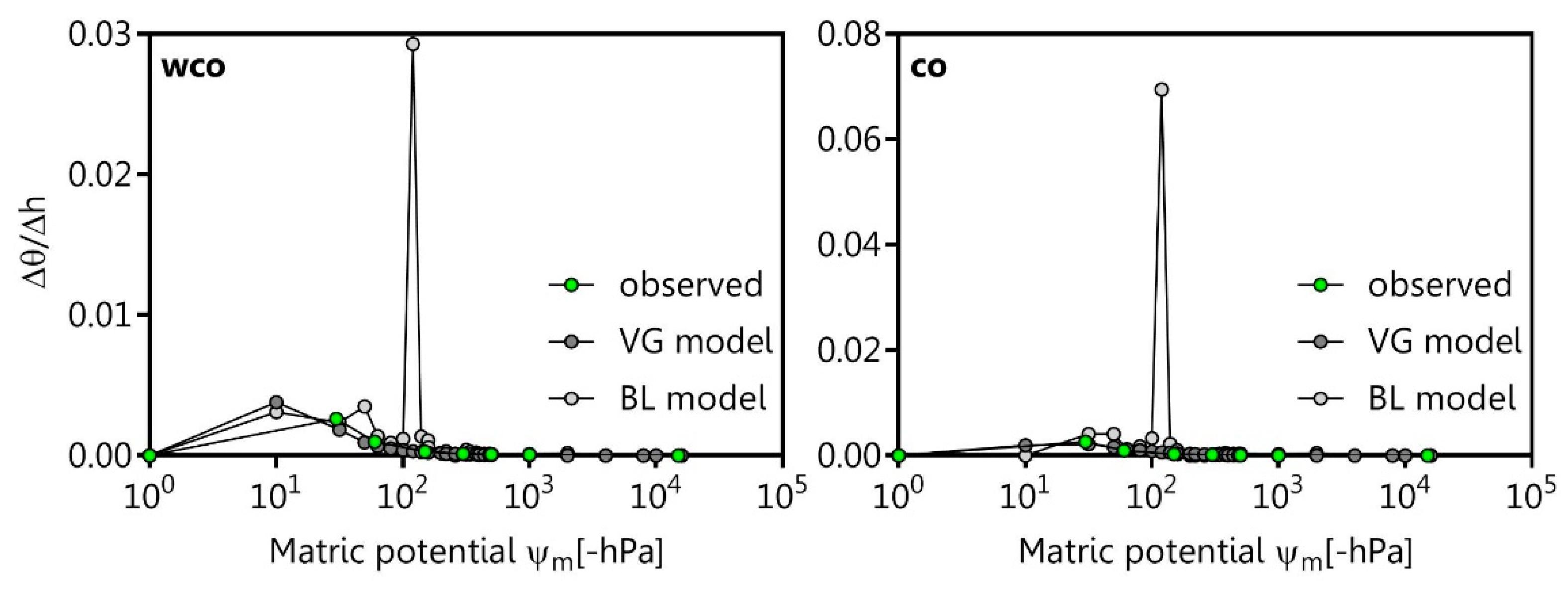
According to reference [
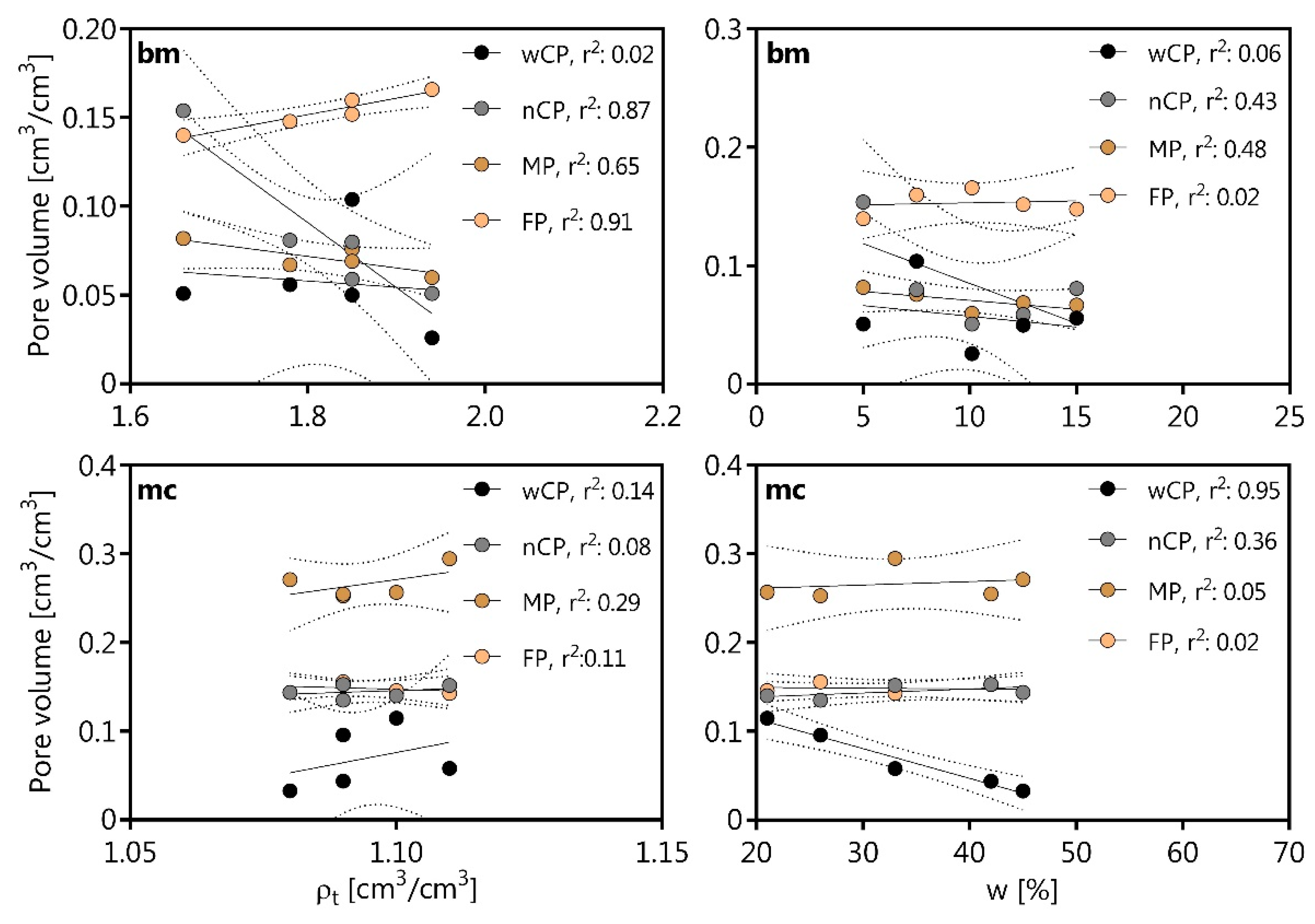
20], the boundary between the macro-pores and the structural pores (wide coarse pores, wCP) was assumed between 0 hPa and −10 hPa, while the first peak is described by the wCP; the second or third peak (matric peak) is described by textural pores (narrow coarse pores: nCP, medium pores: MP, fine pores: FP) as proposed follows reference [
23].
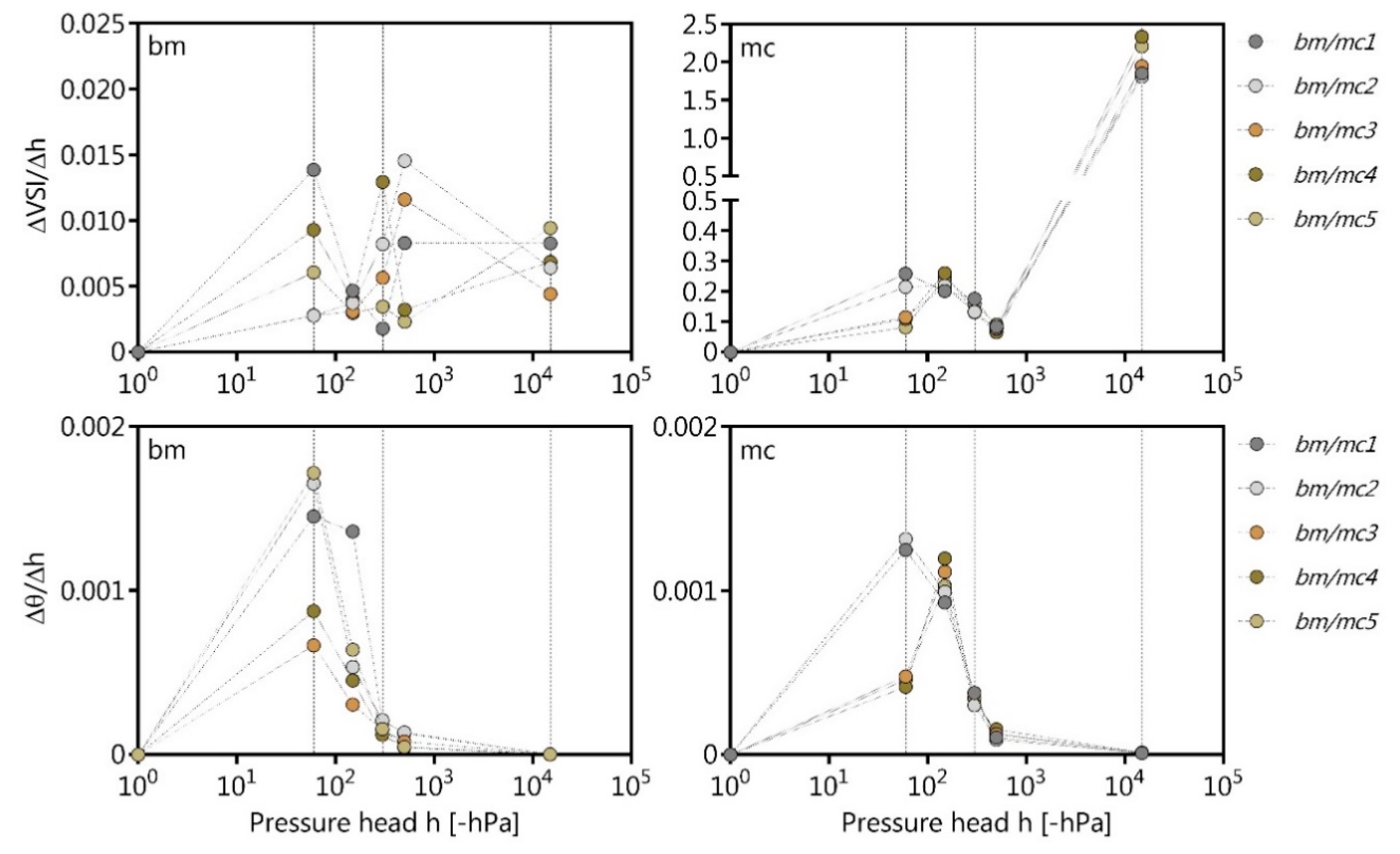
2.4. Shrinkage Behaviour and Volume Shrinkage Index
In addition to the SWRC characteristics, the soil volume change at the different drying stages as mentioned before was estimated with the laser triangulation method as detailed described in a previous study following reference [
6]. The volume shrinkage index (VSI) was also used to describe the pore size dependent shrinkage tendency defined as follows (wide coarse pores, >50 µm, 0 to −60 hPa), nCP (narrow coarse pores, 50–10 µm, −60 to −300 hPa), medium pores (MP, 10–2 µm, −300 to −15,000 hPa), and fine pores (<2 µm, <−15,000 hPa).
where ∆V
t is the soil volume in relation to the drained water-filled pore volume (∆V
p) and i corresponds to the pore size (coarse, medium, and fine pores) of the respective drying stage.
In this study, the differential function of the VSI was directly compared to the soil PSD in the following form:
2.5. Statistical Analysis
The mean values and standard deviations for each sampling depth and the correlation coefficient (r
2) as index of goodness of fit were calculated. The second-order Akaike Information Criterion (AIC
c) for small sample sizes [
24]:
where n is the effective sample size and K is the number of estimated parameters. For a specified data set, the model with the lowest AIC
c will be the “best” model among all models [
25]. The statistical quality criteria were used to represent the deviations between the fitted (x
sim) and the observed (x
obs) volumetric water contents. Therefore, the higher the arithmetic mean of the absolute error, the higher is the root mean square error (RMSE
θ):
5. Conclusions
This study was focused on the effect and improvement potential of soil compaction on the soil water retention curve characteristics or rather the pore size distribution of the differently-textured boulder marl and marsh clay. The used unimodal and bimodal models fitted the soil water retention curve reasonably well, but the bimodal DB and BL models enabled a better description of the soil water retention curve characteristics than the unimodal models.
The mono- or bi-modality of the observed and modelled pore size distributions, and thus the changes in the pore size distribution were found to be related to (i) the degree of compaction and (ii) the initial water content considering the different Proctor stages. The progress of the pore size distribution curve is also a promising indicator for the shrinkage-dependent volume change, although more research is needed with differently textured soils.
In conclusion, if considering the tested materials for a prospective use as a top and bottom liner material, especially a) the available water capacity must be improved (boulder marl) and b) the Ks values must be lowered (marsh clay). The former objective can be reached through compost application, while further investigations are needed to improve the material properties of the marsh clay.