Identifying Karst Aquifer Recharge Areas using Environmental Isotopes: A Case Study in Central Italy
Abstract
1. Introduction
2. Geological and Hydrogeological Setting
3. Materials and Methods
4. Results and Discussions
4.1. Oxygen and Hydrogen Isotope Composition
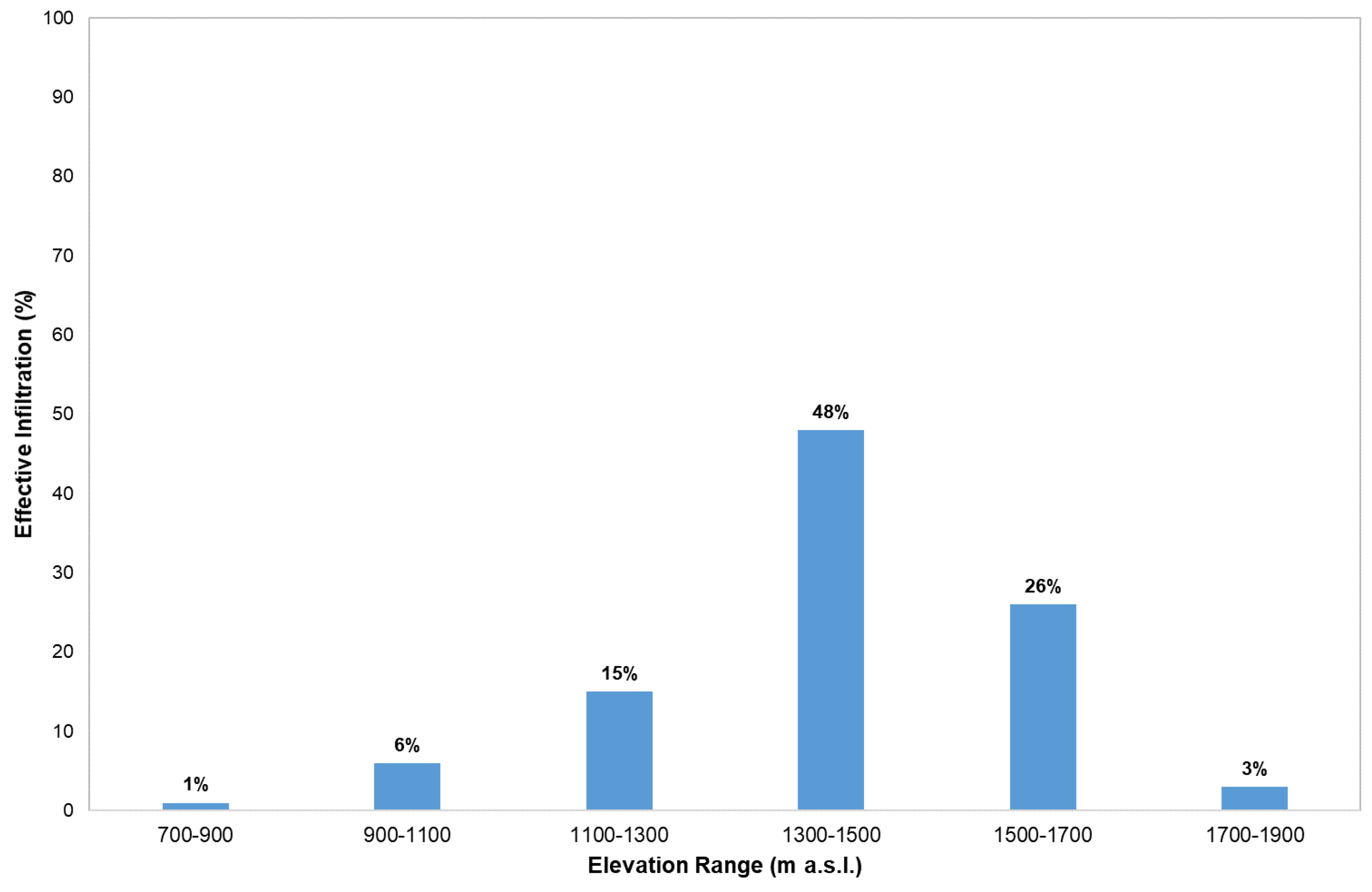
4.2. Spring Recharge Area Identification Using Isotope Analysis
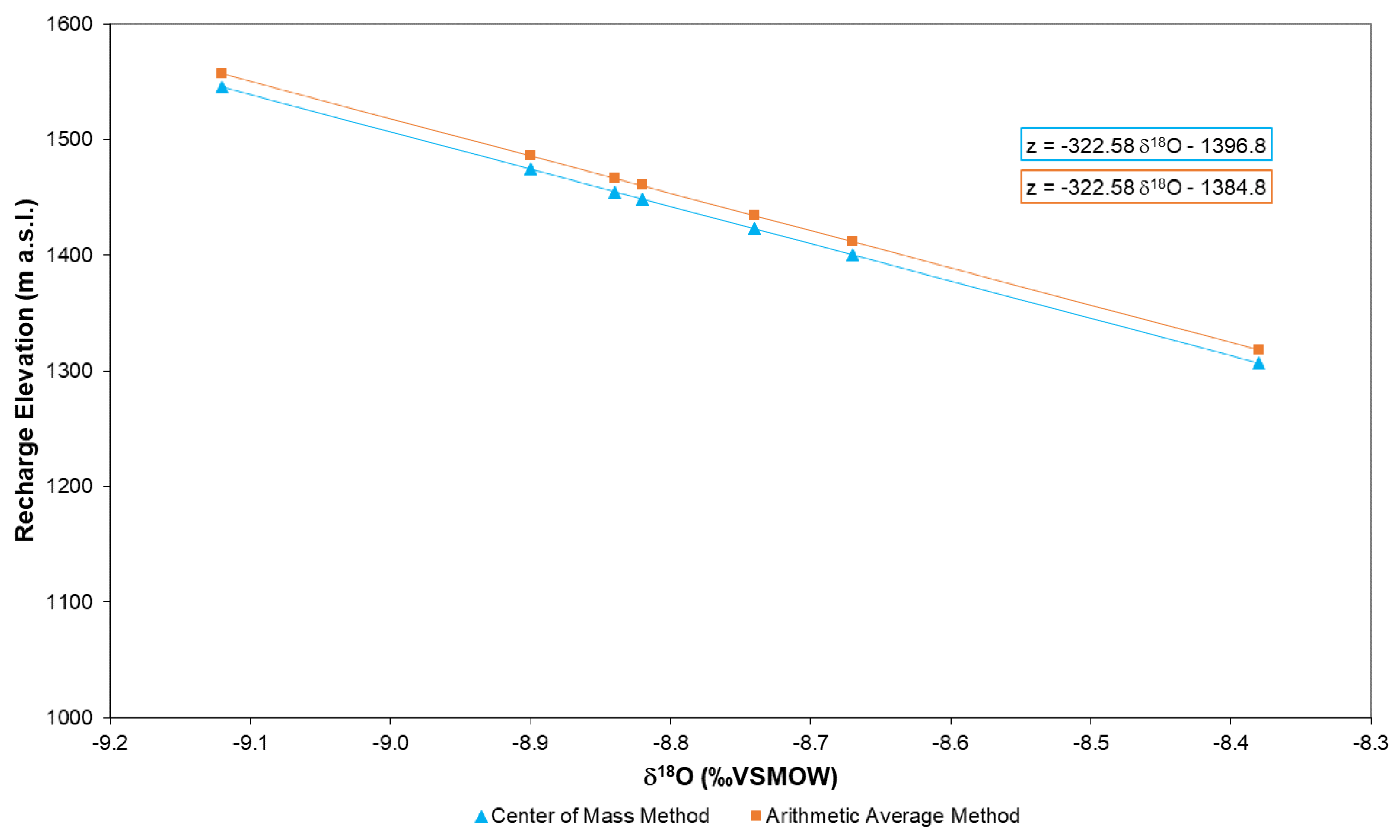
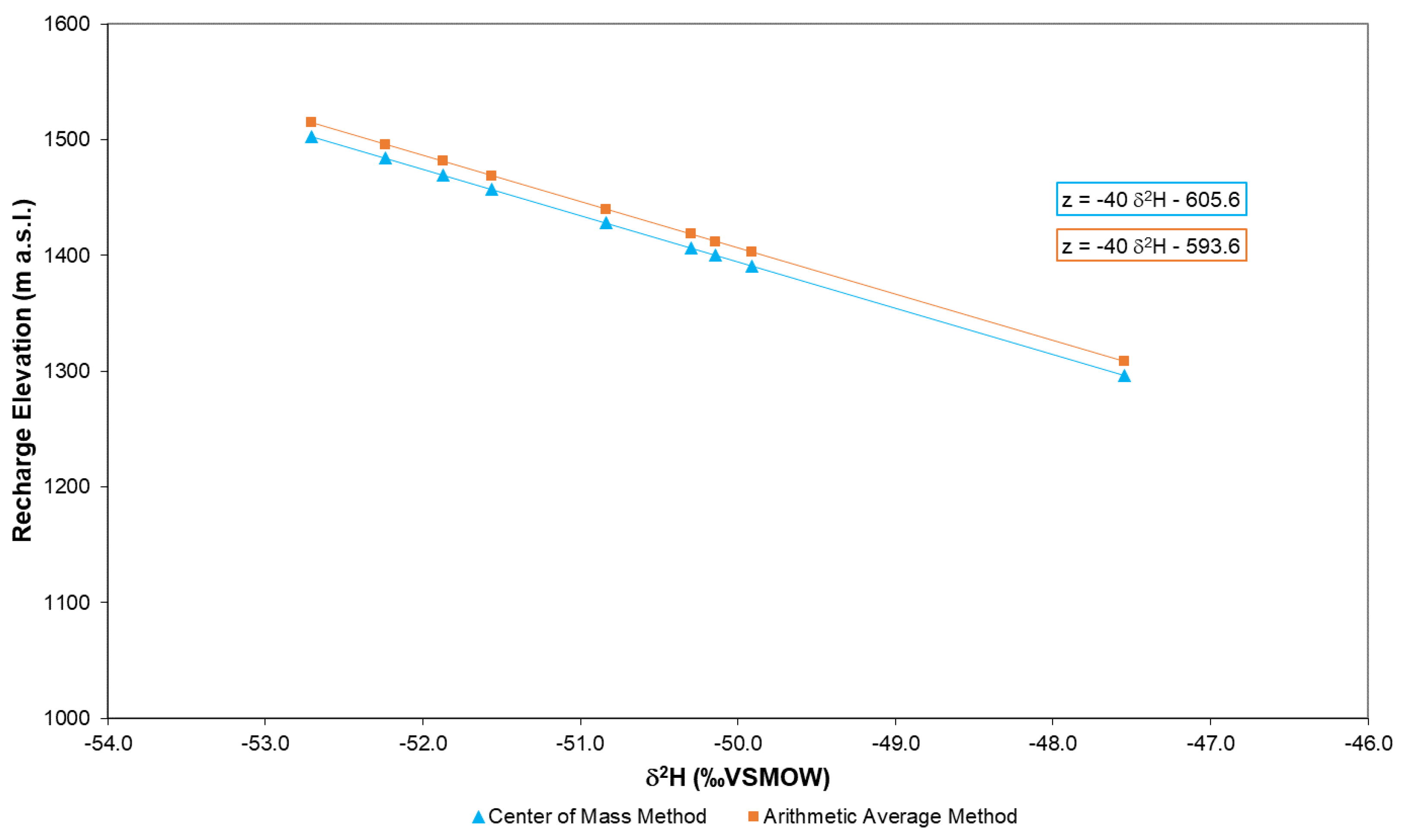
4.2.1. Center of Mass Method
4.2.2. The Arithmetic Average Method
4.2.3. Comparison of Recharge Area Identification Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sappa, G.; Ferranti, F.; Ergul, S.; Ioanni, G. Evaluation of the groundwater active recharge trend in the coastal plain of Dar Es Salaam (Tanzania). J. Chem. Pharm. Res. 2013, 5, 548–552. [Google Scholar]
- Foster, S.; Hirata, R.; Andreo, B. The aquifer pollution vulnerability concept: Aid or impediment in promoting groundwater protection? Hydrogeol. J. 2013, 21, 1389–1392. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Cozma, A.I.; Baciu, C.; Moldovan, M.; Pop, I.C. Using natural tracers to track the groundwater flow in a mining area. Procedia Environ. Sci. 2016, 32, 211–220. [Google Scholar] [CrossRef]
- Leibundgut, C.; Maloszewski, P.; Kulls, C. Tracer in Hydrology, 1st ed.; Wiley-Blackwell: Chichester, UK, 2009; p. 432. [Google Scholar]
- Barbieri, M.; Nigro, A.; Petitta, M. Groundwater mixing in the discharge area of San Vittorino Plain (Central Italy): Geochemical characterization and implication for drinking uses. Environ. Earth Sci. 2017, 76, 393. [Google Scholar] [CrossRef]
- Massmann, G.; Sültenfuß, J.; Dünnbier, U.; Knappe, A.; Taute, T.; Pekdeger, A. Investigation of groundwater residence times during bank filtration in Berlin: A multi-tracer approach. Hydrol. Process. 2008, 22, 788–801. [Google Scholar] [CrossRef]
- Petitta, M.; Scarascia Mugnozza, G.; Barbieri, M.; Bianchi Fasani, G.; Esposito, C. Hydrodynamic and isotopic investigations for evaluating the mechanisms and amount of groundwater seepage through a rockslide dam. Hydrol. Process. 2010, 24, 3510–3520. [Google Scholar] [CrossRef]
- Gasser, G.; Pankratov, I.; Elhanany, S.; Glazman, H.; Lev, O. Calculation of wastewater effluent leakage to pristine water sources by the weighted average of multiple tracer approach. Water Resour. Res. 2014, 50, 4269–4282. [Google Scholar] [CrossRef]
- Moeck, C.; Radny, D.; Popp, A.; Brennwald, M.; Stoll, S.; Auckenthaler, A.; Berg, M.; Schirmer, M. Characterization of a managed aquifer recharge system using multiple tracers. Sci. Total Environ. 2017, 609, 701–714. [Google Scholar] [CrossRef] [PubMed]
- Nigro, A.; Sappa, G.; Barbieri, M. Application of boron and tritium isotopes for tracing landfill contamination in groundwater. J. Geochem. Explor. 2017, 172, 101–108. [Google Scholar] [CrossRef]
- Sappa, G.; Ferranti, F.; De Filippi, F.M.; Cardillo, G. Mg2+-based method for the Pertuso spring discharge evaluation. Water 2017, 9, 67. [Google Scholar] [CrossRef]
- Coplen, T.B.; Herczeg, A.L.; Barnes, C. Isotope engineering—Using stable isotopes of the water molecule to solve practical problems. In Environmental Tracers in Subsurface Hydrology; Cook, P., Herczeg, A.L., Eds.; Kluwer Academic Publishers: South Holland, The Nerthelands, 2000; pp. 79–110. [Google Scholar]
- Barbieri, M.; Boschetti, T.; Petitta, M.; Tallini, M. Stable Isotopes (2H, 18O and 87Sr/86Sr) and Hydrochemistry Monitoring for Groundwater Hydrodynamics Analysis in a Karst Aquifer (Gran Sasso, Central Italy). Appl. Geochem. 2005, 20, 2063–2081. [Google Scholar] [CrossRef]
- Sappa, G.; Ergul, S.; Ferranti, F. Water Quality Assessment Of Carbonate Aquifers In Southern Latium Region, Central Italy: A Case Study For Irrigation And Drinking Purposes. Appl. Water Sci. 2014, 4, 115–128. [Google Scholar] [CrossRef]
- Gat, J.R. Oxygen and hydrogen isotopes in the hydrological cycle. Annu. Rev. Earth Planet. Sci. 1996, 24, 225–262. [Google Scholar] [CrossRef]
- Rozanski, K.; Araguas-Araguas, L.; Gonfiantini, R. Isotopic patterns in modern global precipitation. In Climate Change in Continental Isotopic Records; Swart, P.K., Lohmann, K.C., McKenzie, J., Savin, S., Eds.; American Geophysical Union: Washington, DC, USA, 1993; Volume 78, pp. 1–36. [Google Scholar]
- Song, C.; Wang, G.; Liu, G.; Mao, T.; Sun, X.; Chen, X. Stable isotope variations of precipitation and streamflow reveal the young water fraction of a permafrost watershed. Hydrol. Process. 2017, 31, 935–947. [Google Scholar] [CrossRef]
- Kirchner, J.W. Aggregation in environmental systems-Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments. Hydrol. Earth Syst. Sci. 2016, 20, 279–297. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, XVI, 436–468. [Google Scholar]
- Gat, J.R.; Gonfiantini, R. Stable Isotope Hydrology. Deuterium and Oxygen-18 in the Water Cycle; Series No. 210; Technical Reports for International Atomic Energy Agency (IAEA): Vienna, Austria, 1981; p. 356. [Google Scholar]
- Gonfiantini, R.; Roche, M.-A.; Olivry, J.-C.; Fontes, J.-C.; Zuppi, G.M. The altitude effect on the isotopic composition of tropical rains. Chem. Geol. 2001, 181, 147–167. [Google Scholar] [CrossRef]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrogeology; CRC Press/Lewis Publishers: Palm Beach County, FL, USA, 1997; p. 342. [Google Scholar]
- Civita, M.; De Maio, M. Average Groundwater Recharge in Carbonate Aquifers: A GIS Processed Numerical Model. In Proceedings of the VII Conference on Limestone Hydrology and Fissured Media, Besancon, France, 20–22 September 2001; Université de Franche-Comté, Sciences & Techniques de l’Environnement: Besançon, France, 2001. [Google Scholar]
- Devoto, G. Note Geologiche Sul Settore Centrale Dei Monti Simbruini Ed Ernici (Lazio Nord-Orientale); Stabilimento Tipografico G. Genovese: Naples, Italy, 1967; pp. 1–112. [Google Scholar]
- Devoto, G. Sguardo geologico dei Monti Simbruini (Lazio nord-orientale). Geol. Rom. 1970, 9, 127–136. [Google Scholar]
- Devoto, G.; Parotto, M. Note geologiche sui rilievi tra Monte Crepacuore e Monte Ortara (Monti Ernici-Lazio nord-orientale). Geol. Rom. 1967, 6, 145–163. [Google Scholar]
- Accordi, G.; Carbone, F. Sequenze carbonatiche meso-cenozoiche. Note illustrative alla Carta delle Litofacies del Lazio-Abruzzo ed aree limitrofe. Quad. Ric. Scient. 1988, 114, 11–92. [Google Scholar]
- Damiani, A.V. Studi sulla piattaforma laziale-abruzzese. Nota I. Considerazioni e problematiche sull’assetto tettonico e sulla paleogeologia dei Monti Simbruini. In Memorie. Della Descrittive Carta Geologica D’Italia; Istituto Superiore per la Protezione e la Ricerca Ambientale: Roma, Italy, 1990; Volume 38, pp. 145–176. [Google Scholar]
- Bono, P.; Percopo, C. Flow dynamics and erosion rate of a representative karst basin (Upper Aniene River, Central Italy). Environ. Geol. 1996, 27, 210–218. [Google Scholar] [CrossRef]
- Ventriglia, U. Idrogeologia della Provincia di Roma, IV, Regione Orientale. In Hydrogeology of the Province of Rome, IV, Eastern Region; Amministrazione provinciale di Roma: Roma, Italy, 1990. [Google Scholar]
- Penta, F. Indagini Nella Zona delle Sorgenti del Simbrivio, Istituto di Giacimenti Minerari e Geologia Applicata; Sapienza University of Rome: Roma, Italy, 1956. [Google Scholar]
- Sappa, G.; Ferranti, F. An integrated approach to the Environmental Monitoring Plan of the Pertuso Spring (Upper Valley of Aniene River). Ital. J. Groundw. 2014, 3, 47–55. [Google Scholar] [CrossRef]
- White, W.B. Geomorphology and Hydrology of Karst Terrains; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- White, W.B. Karst hydrology: recent developments and open questions. Eng. Geol. 2002, 65, 85–105. [Google Scholar] [CrossRef]
- Longinelli, A.; Selmo, E. Isotopic Composition of Precipitation in Italy: A First Overall Map. J. Hydrol. 2003, 270, 75–88. [Google Scholar]
- Gourcy, L.L.; Groening, M.; Aggarwal, P.K. Stable oxygen and hydrogen isotopes in precipitation. In Isotopes in the Water Cycle: Past, Present and Future of Developing Science; Aggarwal, P.K., Gat, J.R., Froehlich, K.F.O., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 39–51. [Google Scholar]
- Gat, J.R.; Carmi, I. Evolution of the isotopic composition of atmospheric waters in the Mediterranean Sea Area. J. Geophys. Res. 1970, 75, 3039–3048. [Google Scholar] [CrossRef]
- Cappa, C.D.; Hendricks, M.B.; DePaolo, D.J.; Cohen, R.C. Isotopic fractionation of water during evaporation. J. Geophys. Res. 2003, 108, D16. [Google Scholar] [CrossRef]
- Gat, J.R.; Matsui, E. Atmospheric water balance in the Amazon Basin: an isotopic evapotranspiration model. J. Geophys. Res. Atmos. 1991, 96, 13179–13188. [Google Scholar] [CrossRef]
- Cox, K.A.; Rohling, E.J.; Schmidt, G.A.; Schiebel, R.; Bacon, S.; Winter, D.A.; Bolshaw, M.; Spero, H.J. New constraints on the Eastern Mediterranean δ18O:δD relationship. Ocean Sci. Discuss. 2011, 1, 39–53. [Google Scholar] [CrossRef]
- Gat, J.R.; Klein, B.; Kushnir, Y.; Roether, W.; Wernli, H.; Yam, R.; Shemesh, A. Isotope composition of air moisture over the Mediterranean Sea: an index of the air-sea interaction pattern. Tellus B Chem. Phys. Meteorol. 2003, 55, 953–965. [Google Scholar] [CrossRef]
- Bortolami, G.C.; Ricci, B.; Susella, G.F.; Zuppi, G.M. Isotope hydrology of the Val Corsaglia, Maritime Alps, Piedmont, Italy. In Isotope Hydrology; International Atomic Energy Agency IAEA: Vienna, Austria, 1978; pp. 27–350. [Google Scholar]
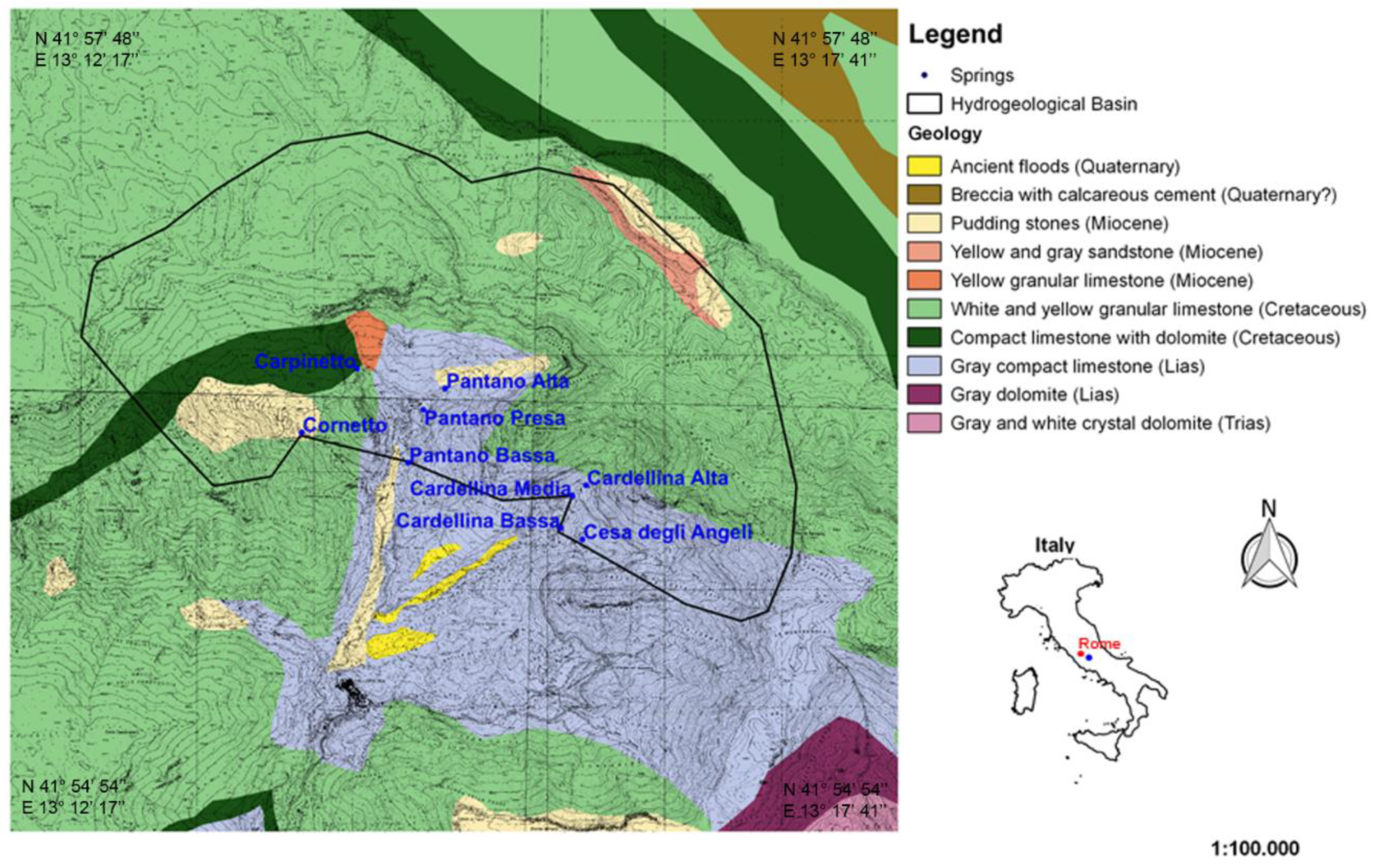
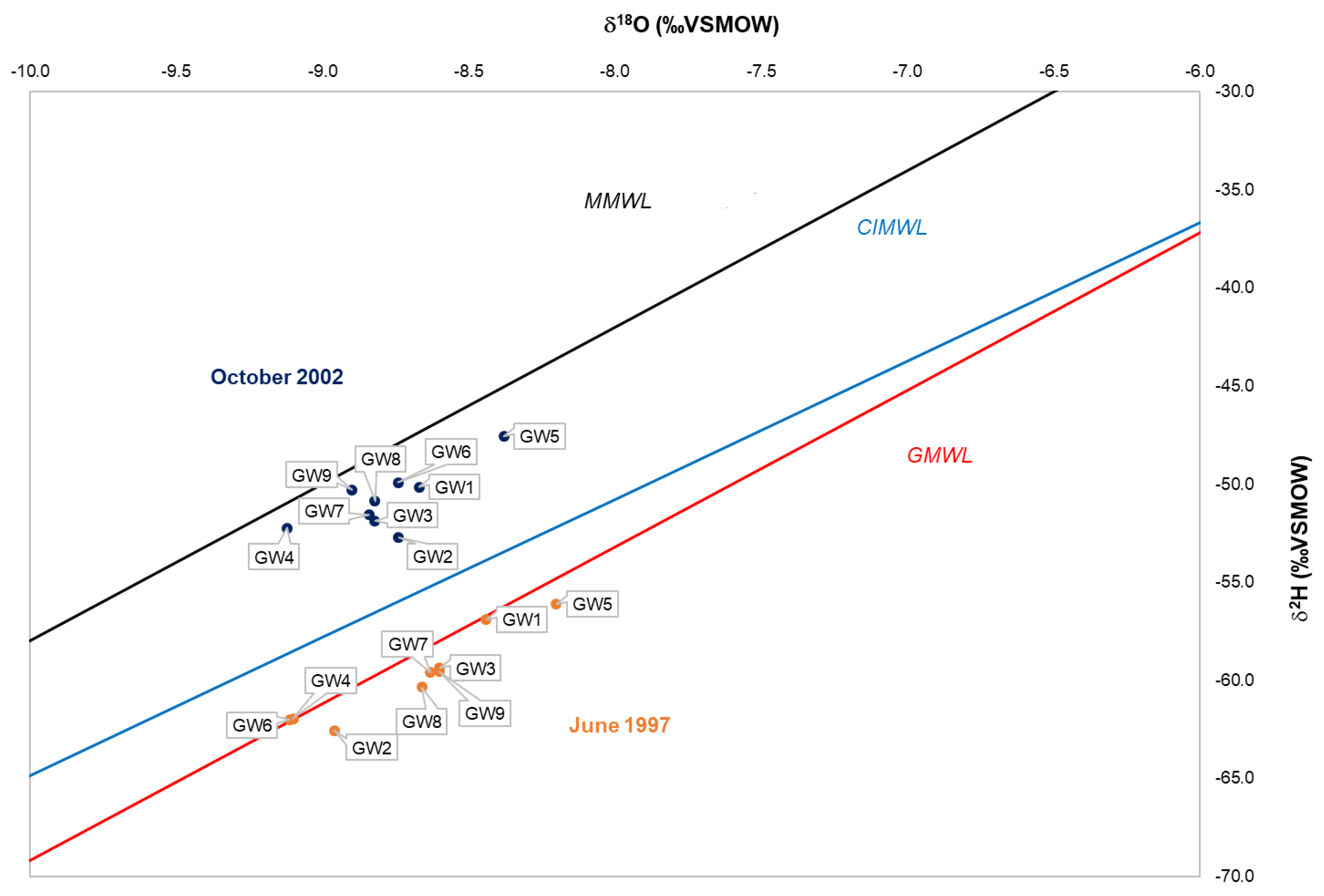
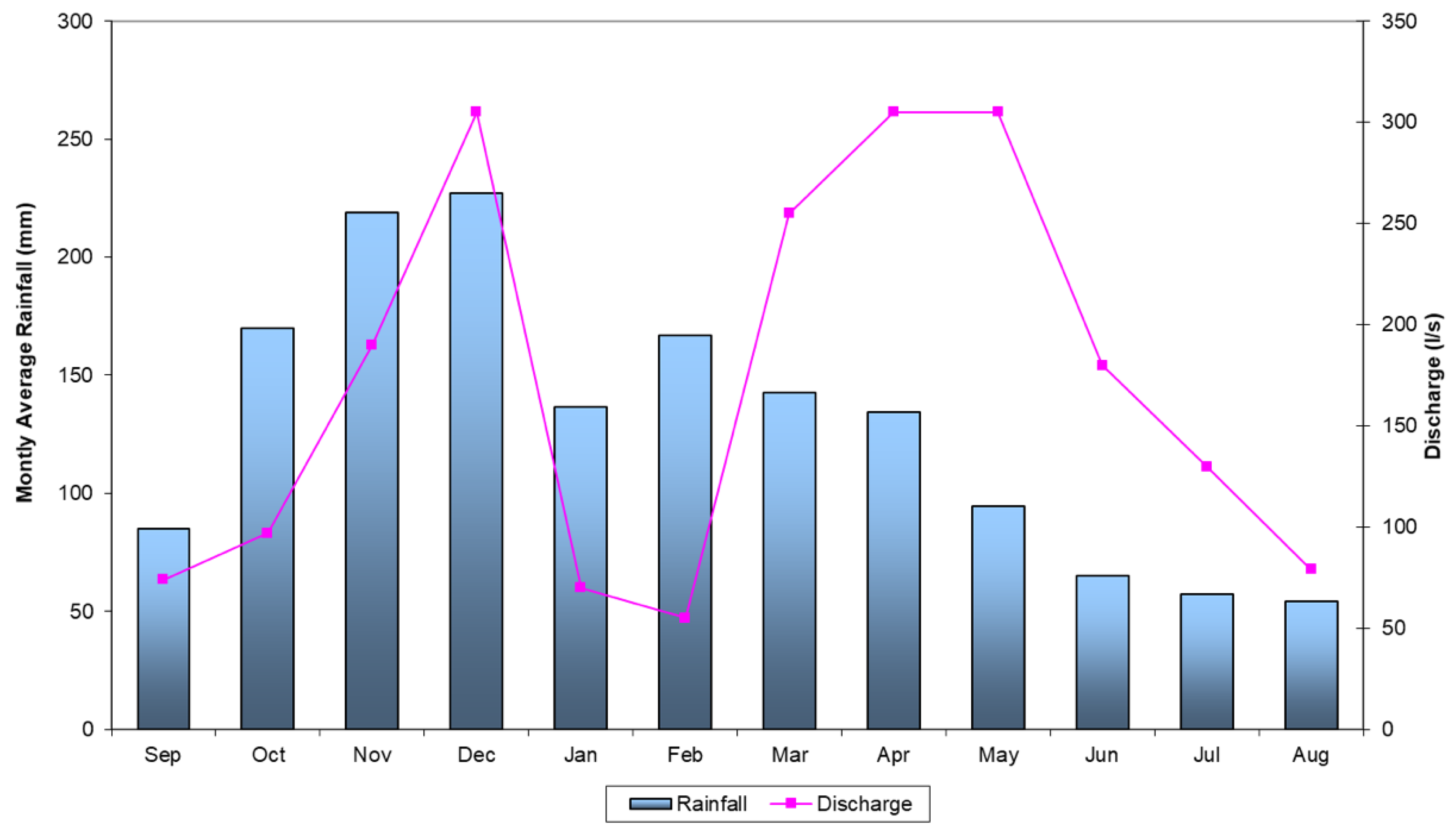
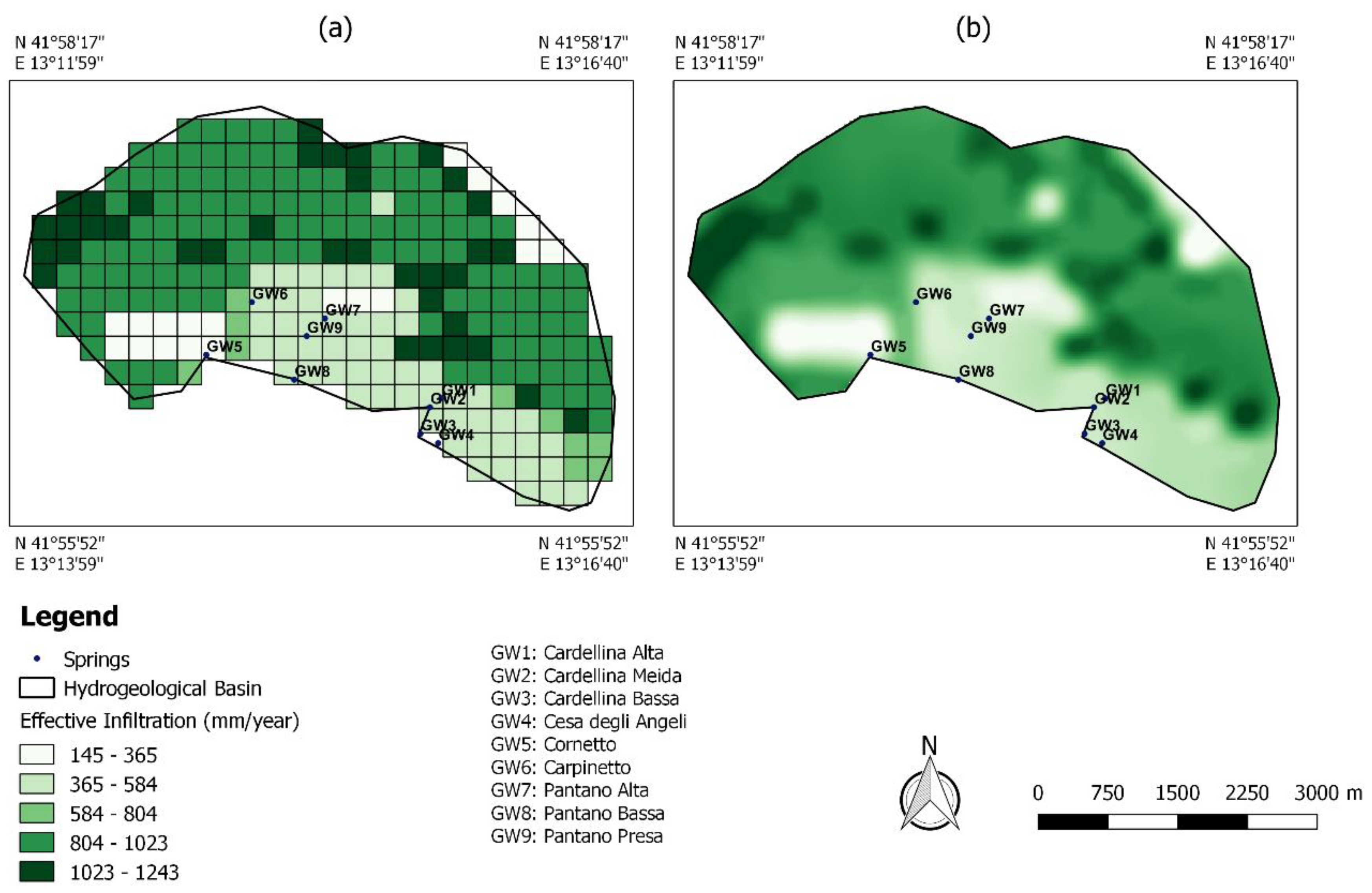
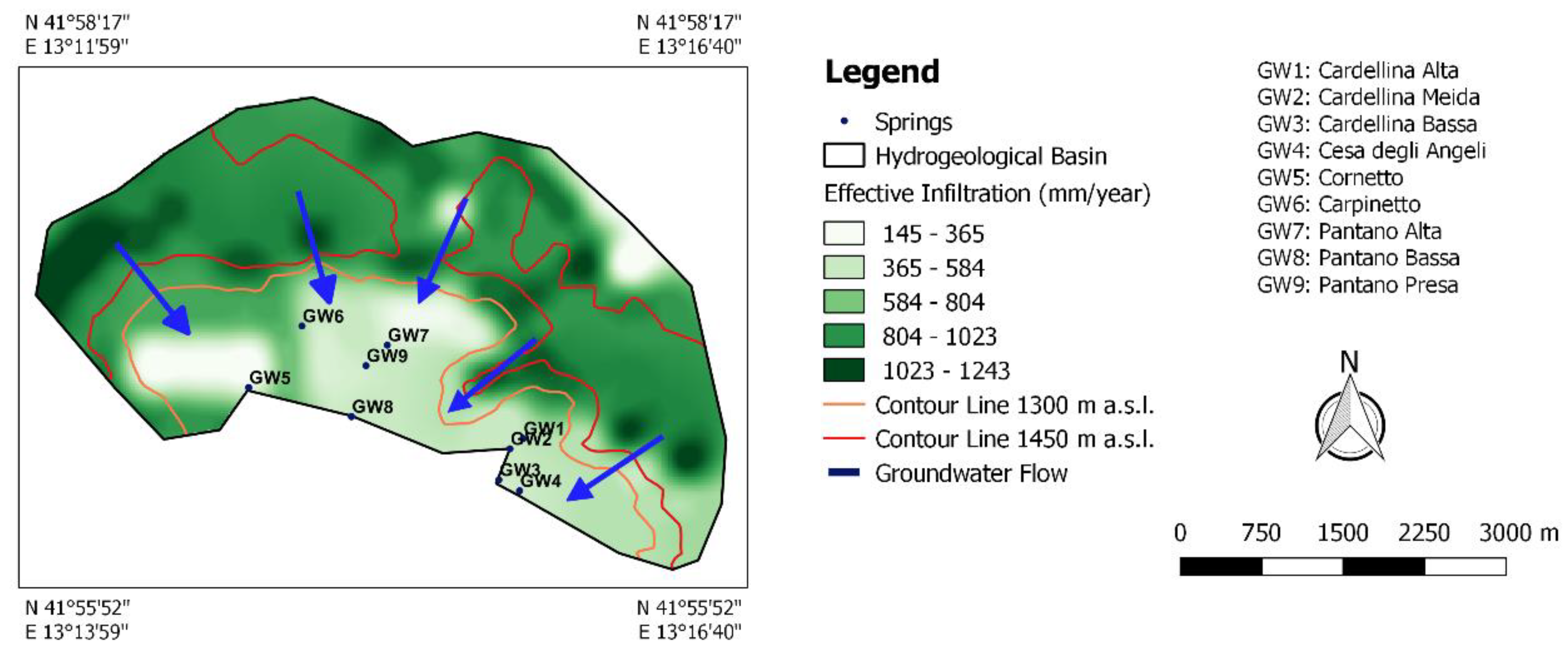
| Sample Codes | Spring | Lng (m) | Lat (m) | Elevation (m a.s.l.) |
|---|---|---|---|---|
| GW1 | Cardellina Alta | 4,645,069 | 355,391 | 1057 |
| GW2 | Cardellina Media | 4,644,978 | 355,274 | 989 |
| GW3 | Cardellina Bassa | 4,644,703 | 355,176 | 939 |
| GW4 | Cesa degli Angeli | 4,644,606 | 355,359 | 940 |
| GW5 | Cornetto | 4,645,520 | 352,959 | 945 |
| GW6 | Carpinetto | 4,646,065 | 353,431 | 960 |
| GW7 | Pantano Alta | 4,645,896 | 354,187 | 952 |
| GW8 | Pantano Bassa | 4,645,547 | 354,012 | 901 |
| GW9 | Pantano Presa | 4,645,714 | 353,999 | 830 |
| Sample Codes | June 1997 | October 2002 | ||||
|---|---|---|---|---|---|---|
| δ18O (‰VSMOW) | δ2H (‰VSMOW) | dexcess (‰) | δ18O (‰VSMOW) | δ2H (‰VSMOW) | dexcess (‰) | |
| GW1 | −8.4 | −57 | 10.6 | −8.7 | −50 | 19.2 |
| GW2 | −9.0 | −63 | 9.1 | −8.7 | −53 | 17.2 |
| GW3 | −8.6 | −59 | 9.4 | −8.8 | −52 | 18.7 |
| GW4 | −9.1 | −62 | 10.8 | −9.1 | −52 | 20.7 |
| GW5 | −8.2 | −56 | 9.5 | −8.4 | −48 | 19.5 |
| GW6 | −9.1 | −62 | 10.9 | −8.7 | −50 | 20.0 |
| GW7 | −8.6 | −60 | 9.4 | −8.8 | −52 | 19.1 |
| GW8 | −8.6 | −60 | 8.9 | −8.9 | −50 | 19.7 |
| GW9 | −8.7 | −60 | 9.2 | −8.8 | −51 | 20.9 |
| Sample Codes | Spring | Average Elevation (m a.s.l.) | δ18O (‰VSMOW) | δ2H (‰VSMOW) |
|---|---|---|---|---|
| GW1 | Cardellina Alta | 1400 | −8.67 | −50.14 |
| Sample Codes | Recharge Elevation (m a.s.l.) δ18O (‰VSMOW) | Recharge Elevation (m a.s.l.) δ2H (‰VSMOW) | Average Recharge Elevation (m a.s.l.) |
|---|---|---|---|
| GW1 | 1400 | 1400 | 1400 |
| GW2 | 1423 | 1503 | 1463 |
| GW3 | 1448 | 1469 | 1459 |
| GW4 | 1545 | 1484 | 1515 |
| GW5 | 1306 | 1296 | 1301 |
| GW6 | 1423 | 1391 | 1407 |
| GW7 | 1455 | 1457 | 1456 |
| GW8 | 1448 | 1428 | 1438 |
| GW9 | 1474 | 1406 | 1440 |
| Sample Codes | Spring | Average Elevation (m a.s.l.) | δ18O (‰VSMOW) | δ2H (‰VSMOW) |
|---|---|---|---|---|
| GW1 | Cardellina Alta | 1412 | −8.67 | −50.14 |
| Sample Codes | Recharge Elevation (m a.s.l.) δ18O (‰VSMOW) | Recharge Elevation (m a.s.l.) δ2H (‰VSMOW) | Average Recharge Elevation (m a.s.l.) |
|---|---|---|---|
| GW1 | 1412 | 1412 | 1412 |
| GW2 | 1435 | 1515 | 1475 |
| GW3 | 1460 | 1481 | 1471 |
| GW4 | 1557 | 1496 | 1527 |
| GW5 | 1318 | 1308 | 1313 |
| GW6 | 1435 | 1403 | 1419 |
| GW7 | 1467 | 1469 | 1468 |
| GW8 | 1460 | 1440 | 1450 |
| GW9 | 1486 | 1418 | 1452 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sappa, G.; Vitale, S.; Ferranti, F. Identifying Karst Aquifer Recharge Areas using Environmental Isotopes: A Case Study in Central Italy. Geosciences 2018, 8, 351. https://doi.org/10.3390/geosciences8090351
Sappa G, Vitale S, Ferranti F. Identifying Karst Aquifer Recharge Areas using Environmental Isotopes: A Case Study in Central Italy. Geosciences. 2018; 8(9):351. https://doi.org/10.3390/geosciences8090351
Chicago/Turabian StyleSappa, Giuseppe, Stefania Vitale, and Flavia Ferranti. 2018. "Identifying Karst Aquifer Recharge Areas using Environmental Isotopes: A Case Study in Central Italy" Geosciences 8, no. 9: 351. https://doi.org/10.3390/geosciences8090351
APA StyleSappa, G., Vitale, S., & Ferranti, F. (2018). Identifying Karst Aquifer Recharge Areas using Environmental Isotopes: A Case Study in Central Italy. Geosciences, 8(9), 351. https://doi.org/10.3390/geosciences8090351






