The Influence of Crude Oil on Mechanistic Detachment Rate Parameters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Analysis of Erodibility Parameters in Persence of Crude Oil
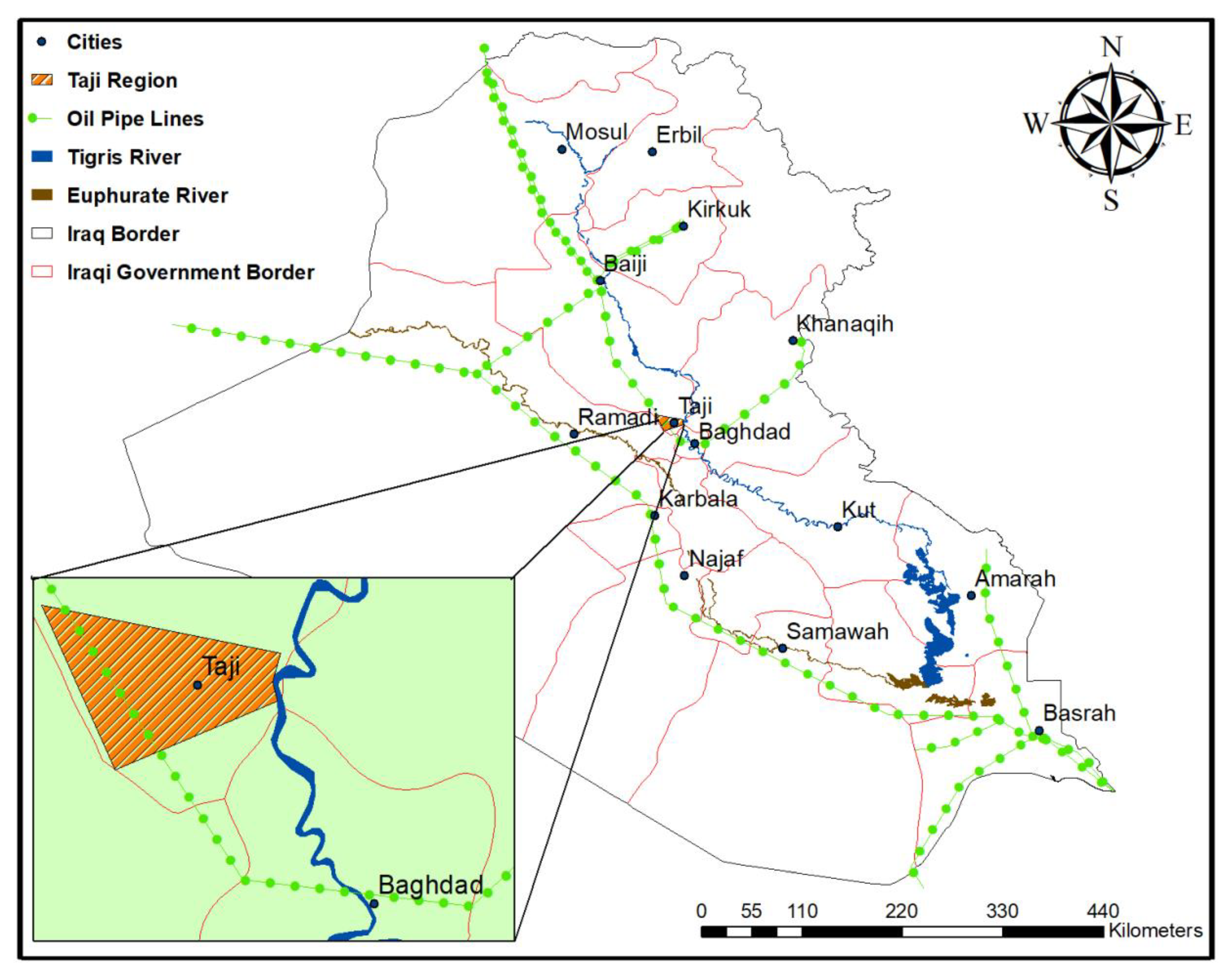
2.2. Materials and Experimental Procedure
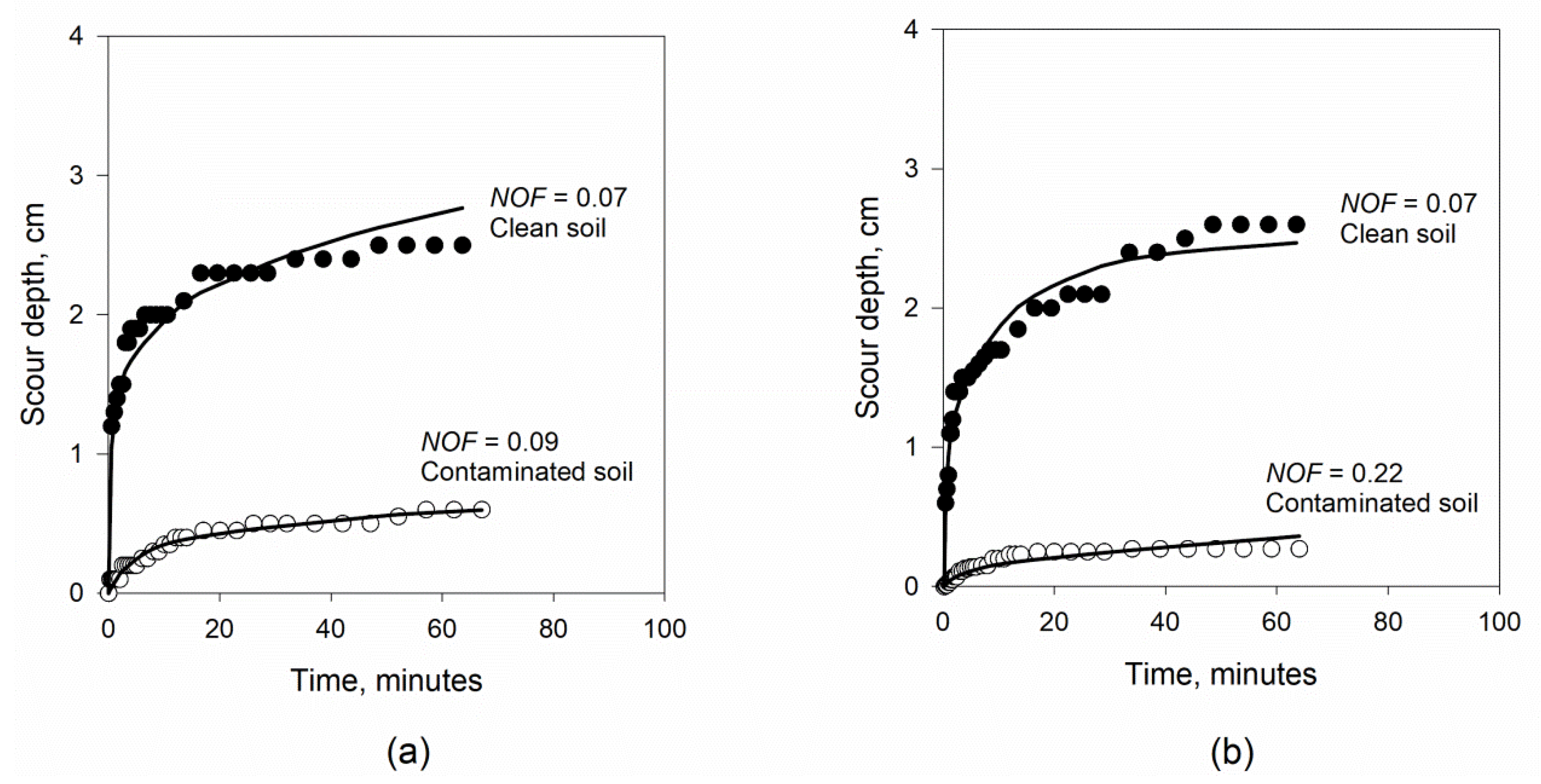
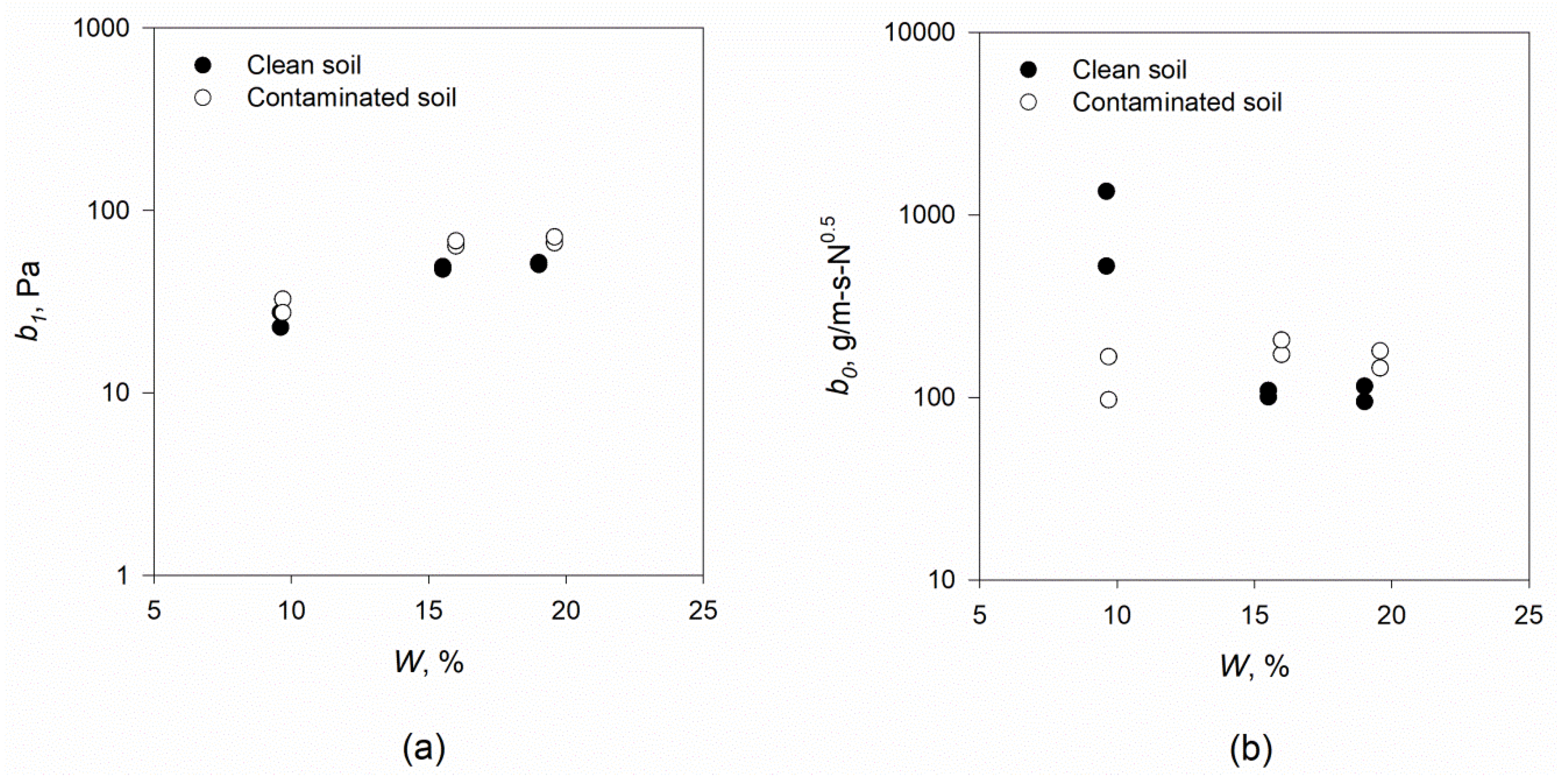
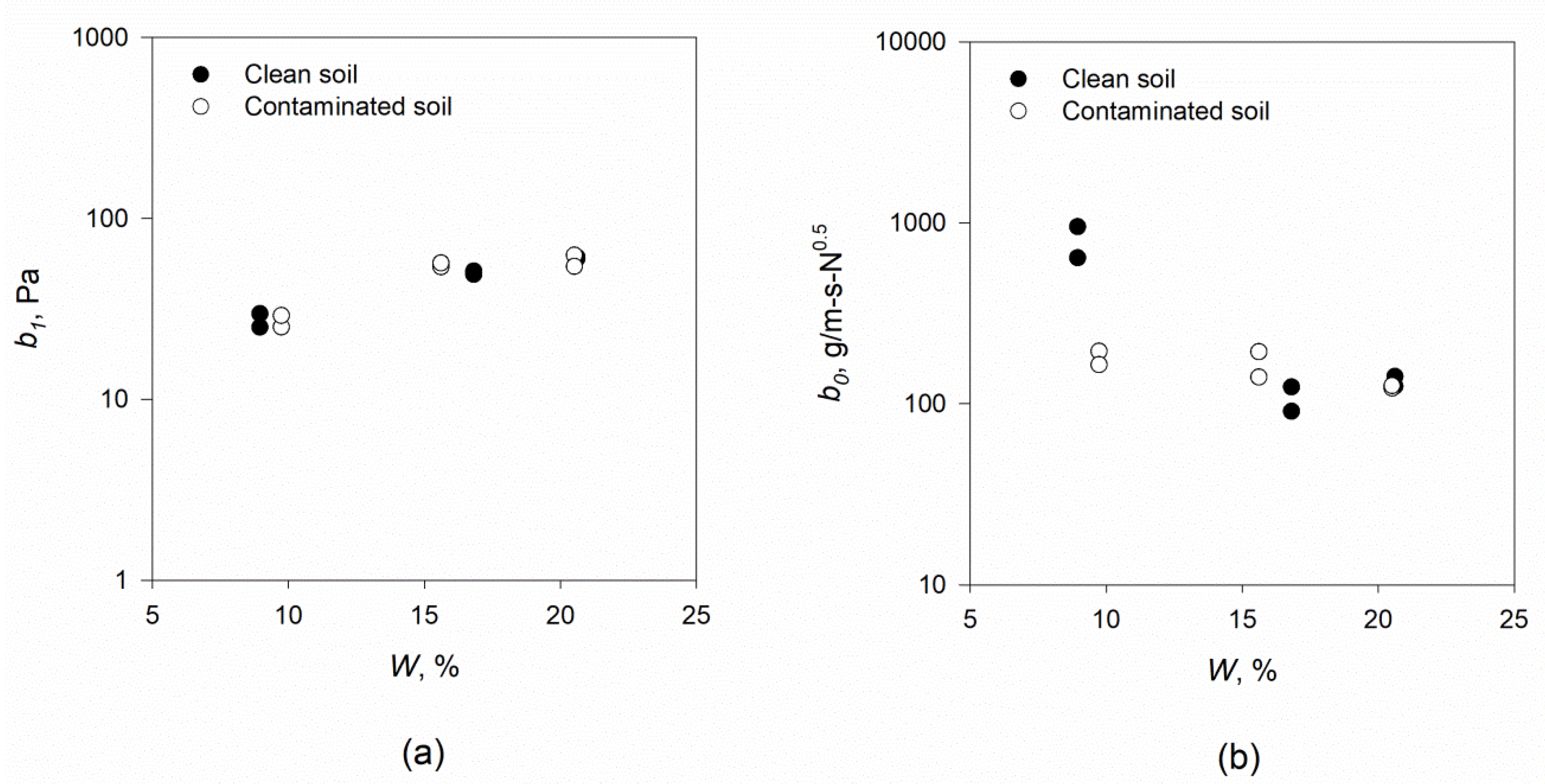
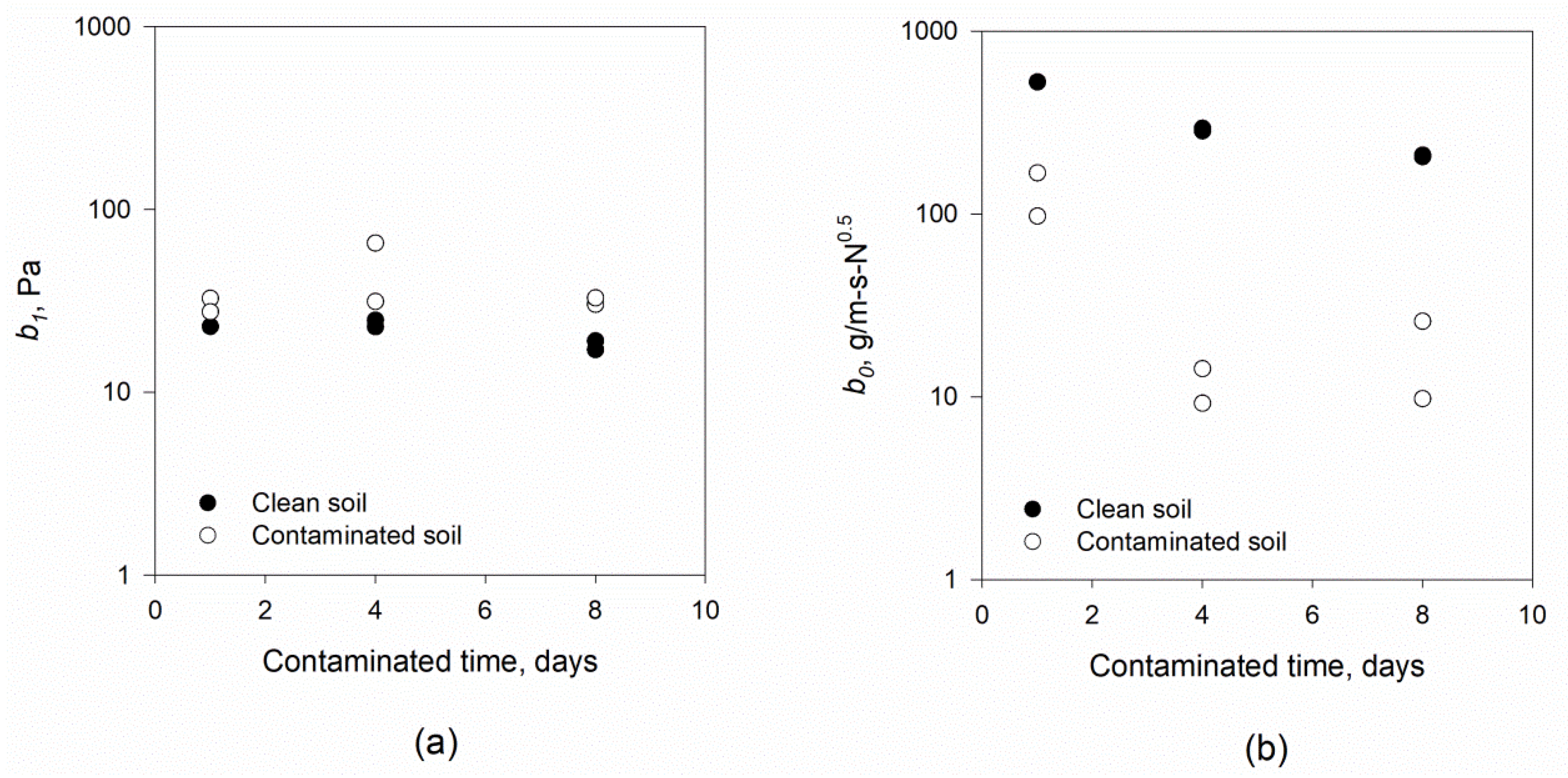
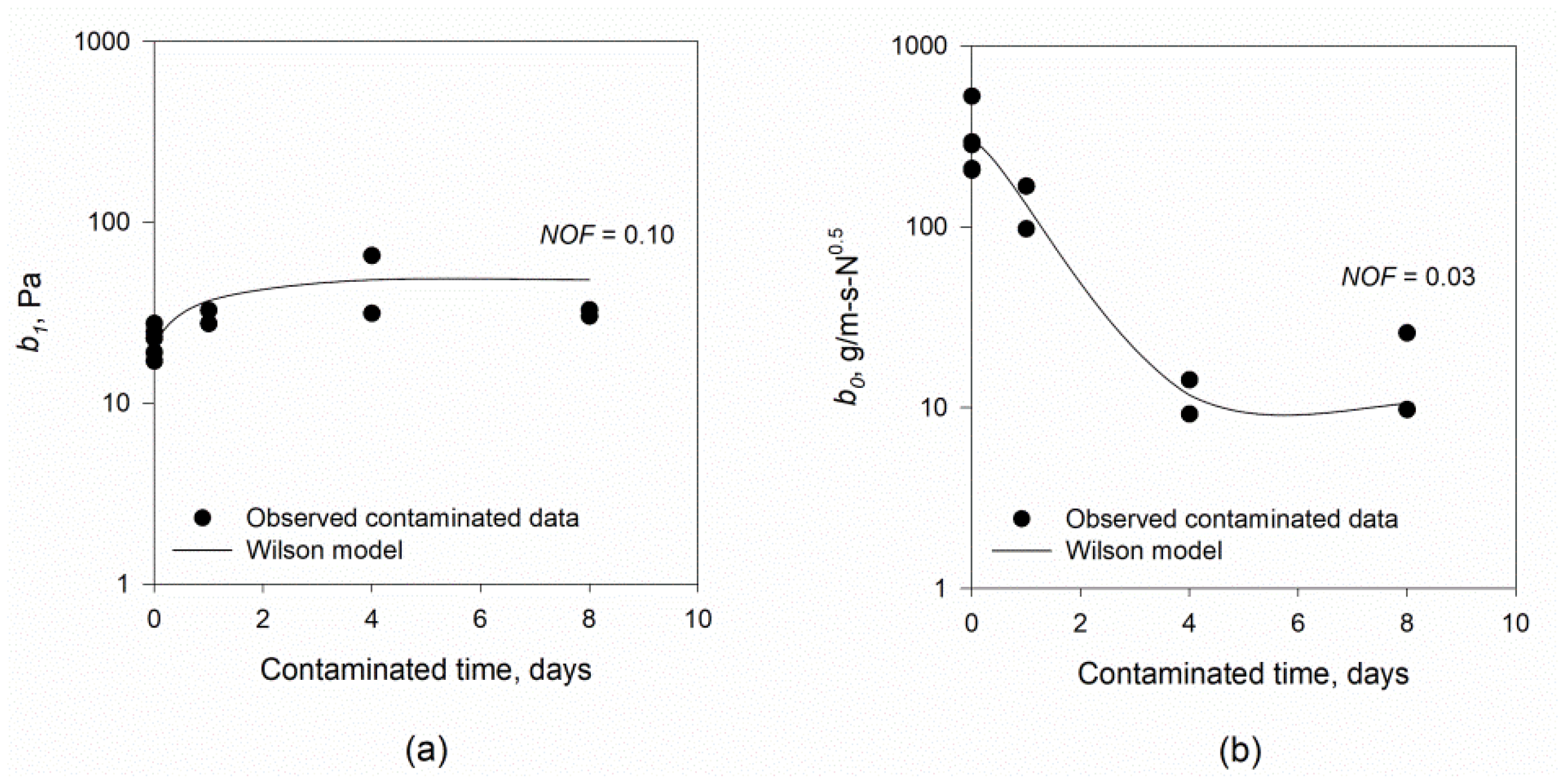
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Briaud, J.L.; Ting, C.K.; Chen, H.C.; Han, S.W.; Kwak, K.W. Erosion function apparatus for scour rate predictions. J. Geotech. Geoenviron. Eng. 2001, 127, 105–113. [Google Scholar] [CrossRef]
- Hanson, G.J. Surface erodibility of earthen channels at high stresses part ii-developing an in situ testing device. Trans. ASAE 1990, 33, 132–137. [Google Scholar] [CrossRef]
- Hanson, G.J.; Cook, K.R. Apparatus, test procedures, and analytical methods to measure soil erodibility in situ. Appl. Eng. Agric. 2004, 20, 455–462. [Google Scholar] [CrossRef]
- Wan, C.F.; Fell, R. Laboratory tests on the rate of piping erosion of soils in embankment dams. Geotech. Test. J. 2004, 27, 295–303. [Google Scholar]
- Khanal, A.; Fox, G.A.; Al-Madhhachi, A.T. Variability of erodibility parameters from laboratory mini jet erosion tests. J. Hydrol. Eng. 2016, 21, 04016030. [Google Scholar] [CrossRef]
- Abbas, M.N.; Al-Madhhachi, A.T.; Esmael, S.A. Quantifying soil erodibility parameters due to wastewater chemicals. Int. J. Hydrol. Sci. Technol. 2018, in press. [Google Scholar]
- Al-Madhhachi, A.T.; Hasan, M.B. Influence of in-situ scaling on variability of polluted soil erodibility parameters. Pollution 2018. [Google Scholar] [CrossRef]
- Mutter, G.M.; Al-Madhhachi, A.T.; Rashed, R.R. Influence of soil stabilizing materials on lead polluted soils using jet erosion tests. Int. J. Integr. Eng. 2017, 9, 28–38. [Google Scholar]
- Salah, M.M.; Al-Madhhachi, A.T. Influence of lead pollution on cohesive soil erodibility using jet erosion tests. Environ. Nat. Resour. Res. 2016, 6, 88–98. [Google Scholar] [CrossRef]
- Shayannejad, M.; Ostad-Ali-Askari, K.; Ramesh, A.; Singh, V.P.; Eslamian, S. Wastewater and magnetized wastewater effects on soil erosion in furrow irrigation. Int. J. Res. Stud. Agric. Sci. 2017, 3, 1–14. [Google Scholar]
- Quyum, A.; Achari, G.; Goodman, R.H. Effect of wetting and drying and dilution on moisture migration through oil contaminated hydrophobic soils. Sci. Total Environ. 2002, 296, 77–87. [Google Scholar] [CrossRef]
- Tsai, T.T.; Kao, C.M. Treatment of petroleum-hydrocarbon contaminated soils using hydrogen peroxide oxidation catalyzed by waste basic oxygen furnace slag. J. Hazard. Mater. 2009, 170, 466–472. [Google Scholar] [CrossRef] [PubMed]
- Anoliefo, G.O.; Vwioko, D.E. Effects of spent lubrication oil on the growth of Capsicum anumL and Hycopersiconesculentum Miller. Environ. Pollut. 1995, 88, 361–364. [Google Scholar] [CrossRef]
- Tigris Oil Spill Pollutes Iraq Water Supplyitle of Site. Available online: https://www. oilandgasmiddleeast.com/article-12343-tigris-oil-spill-pollutes-iraq-water-supply (accessed on 24 April 2014).
- Al-Madhhachi, A.T. Variability in soil erodibility parameters of tigris riverbanks using linear and non-linear models. Nahrain J. Eng. Sci. 2017, 20, 959–969. [Google Scholar]
- Al-Madhhachi, A.T.; Hanson, G.J.; Fox, G.A.; Tyagi, A.K.; Bulut, R. Measuring soil erodibility using a laboratory “mini” jet. Trans. ASABE 2013, 56, 901–910. [Google Scholar]
- Al-Madhhachi, A.T.; Hanson, G.J.; Fox, G.A.; Tyagi, A.K.; Bulut, R. Deriving parameters of a fundamental detachment model for cohesive soils from flume and jet erosion tests. Trans. ASABE 2013, 56, 489–504. [Google Scholar] [CrossRef]
- Daly, E.R.; Fox, G.A.; Miller, R.B.; Al-Madhhachi, A.T. A scour depth approach for deriving erodibility parameters from jet erosion tests. Trans. ASABE 2013, 56, 1343–1351. [Google Scholar]
- Daly, E.R.; Fox, G.A.; Al-Madhhachi, A.T.; Storm, D.E. Variability of fluvial erodibility parameters for streambanks on a watershed scale. Geomorphology 2015, 231, 281–291. [Google Scholar] [CrossRef]
- Hanson, G.J.; Hunt, S.L. Lessons learned using laboratory jet method to measure soil erodibility of compacted soils. Trans. ASABE 2007, 23, 305–312. [Google Scholar]
- Cleaver, J.W.; Yates, B. Mechanism of detachment of colloidal particles from a flat substrate in a turbulent flow. J. Colloid Interface Sci. 1973, 44, 464–474. [Google Scholar] [CrossRef]
- Nearing, M.A. A probabilistic model of soil detachment by shallow turbulent flow. Trans. ASAE 1991, 34, 81–85. [Google Scholar] [CrossRef]
- Sharif, A.R.; Atkinson, J.F. Model for surface erosion of cohesive soils. J. Hydraul. Eng. 2012, 138, 581–590. [Google Scholar] [CrossRef]
- Al-Madhhachi, A.T.; Hanson, G.; Fox, G.; Tyagi, A.; Bulut, R. Mechanistic detachment rate model to predict soil erodibility due to fluvial and seepage forces. J. Hydraul. Eng. ASCE 2014, 140, 04014010. [Google Scholar] [CrossRef]
- Al-Madhhachi, A.T.; Fox, G.A.; Hanson, G.J. Quantifying the erodibility of streambanks and hillslopes due to surface and subsurface forces. Trans. ASABE 2014, 57, 1057–1069. [Google Scholar]
- Wilson, B.N. Development of a fundamentally based detachment model. Trans. ASAE 1993, 36, 1105–1114. [Google Scholar] [CrossRef]
- Wilson, B.N. Evaluation of a fundamentally based detachment model. Trans. ASAE 1993, 36, 1115–1122. [Google Scholar] [CrossRef]
- Khanal, A.; Fox, G.A. Detachment characteristics of root-permeated soils from laboratory jet erosion tests. Ecol. Eng. 2017, 100, 335–343. [Google Scholar] [CrossRef]
- Criswell, D.T.; Fox, G.A.; Miller, R.B.; Daly, E.R.; Al-Madhhachi, A.T. Flume experiments to determine the erodibility of gravel streambank soils. In Proceedings of the American Society of Agricultural and Biological Engineers Annual International Meeting 2013, Kansas City, MO, USA, 21–24 July 2013. [Google Scholar]
- Criswell, D.T.; Al-Madhhachi, A.T.; Fox, G.A.; Miller, R.B. Deriving erodibility parameters of a mechanistic detachment model for gravels. Trans. ASABE 2016, 59, 145–151. [Google Scholar]
- Chepil, W. Equilibrium of soil grains at the threshold of movement by wind 1. Soil Sci. Soc. Am. J. 1959, 23, 422–428. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; USDA Soil Conservation: Washington, DC, USA, 1950; Volume 1026. [Google Scholar]
- Partheniades, E. Erosion and deposition of cohesive soils. J. Hydraul. Div. ASCE 1965, 91, 105–139. [Google Scholar]
- Einstein, H.A.; El-Samni, E.-S.A. Hydrodynamic forces on a rough wall. Rev. Mod. Phys. 1949, 21, 520–524. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Upper Saddle River, NJ, USA, 1979. [Google Scholar]
- Ibrahem, M.M.; Mohammed, A.A.; Jar-Allah, A.T. Kinetics of sulfur, vanadium and nickel removal from basra crude oil hydro treating. Tikrit J. Eng. Sci. 2010, 17, 1–14. [Google Scholar]
- Al-Madhhachi, A.T.; Hanson, G.; Fox, G.; Tyagi, A.; Bulut, R. Measuring erodibility of cohesive soils using laboratory jet erosion tests. Presented at the World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability, Palm Springs, CA, USA, 22–26 May 2011; ASCE: Reston, VA, USA, 2011. [Google Scholar]
- Wang, Y.; Feng, J.; Lin, Q.; Lyu, X.; Wang, X.; Wang, G. Effects of crude oil contamination on soil physical and chemical properties in momoge wetland of china. Chin. Geogr. Sci. 2013, 23, 708–715. [Google Scholar] [CrossRef]
- Richardson, V.; Herath, G.; Kalpage, C.; Jinadasa, K. Physico-chemical characteristic of a petroleum contaminated soil from the spill site of jaffna district. In Proceedings of the 6th International Conference on Structural Engineering and Construction Management, Kandy, Sri Lanka, 11–13 December 2015. [Google Scholar]
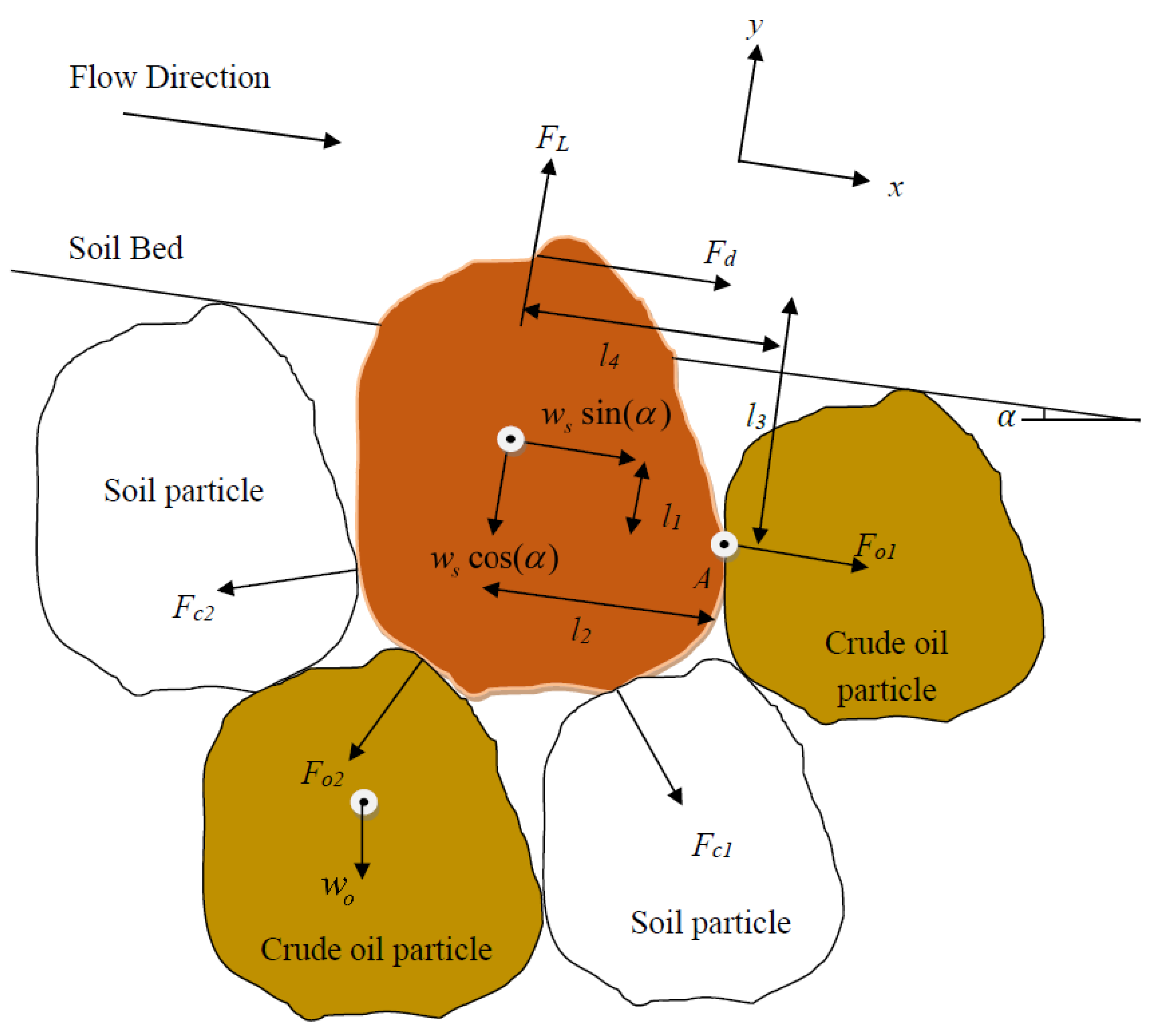

| Symbols | Description | Value or Equation | Reference |
|---|---|---|---|
| C | Discharge jet coefficient | 0.65 | Mutter et al. [8] |
| CD | Drag coefficient | 0.2 | Einstein and El-Samni [34] |
| cd | Diffusion constant | 6.3 | Hanson and Cook [3] |
| Cf | Coefficient of friction | 0.00416 | Hanson and Cook [3] |
| d | Equivalent particle diameter equivalent to d50 | 0.03 mm | Experiments in this study |
| do | Oil particle diameter | 0.03 mm | Experiments in this study |
| Coefficient of variation | 0.35 | Einstein and El-Samni [34] | |
| fco | Dimensionless parameter based on soil and oil cohesions | Ranges from 81 to 140 | Experiments in this study |
| h | Pressure head for JET | 90 cm | Experiments in this study |
| Ji | Jet nozzle height | 32 mm | Experiments in this study |
| Jp | Potential core of jet nozzle | cd do | Hanson and Cook [3] |
| Ke | Exposure of lower particle parameter | Based on Wilson model parameter b0 | Experiments in this study |
| Kf | Ratio of projected area drag and lift forces | 0.92 for equal radii of a spherical particle | Wilson [27] |
| KL | Ratio of drag and lift coefficients along with the ratio of velocities | 1 | Wilson [27] |
| Kt | Factor of cumulating of instantaneous fluid forces | 2.5 | Chepil [31] |
| ka | Area constant of a spherical particle | π/4 for the spherical particle | Wilson [27] |
| kdd | Detachment distance parameter | 2 | Einstein [32] |
| kr | Geometry ratio for a spherical particle | kv/ka = 2/3 for the spherical particle | Wilson [27] |
| kv | Volume constant of a spherical particle | π/6 for the spherical particle | Wilson [27] |
| l1 | Moment length of gravity downslope | 0.86 d/2 | Wilson [27] |
| l3 | Moment length of drag force | 1.18 d/2 | Wilson [27] |
| r | Jet radius upon maximum jet velocity works | 0.13 Ji | Al-Madhhachi et al. [17] |
| Uo | Velocity of jet at the orifice | Hanson and Cook [3] | |
| ws | Submerged particle weight | Wilson [26,27] | |
| wo | Submerged particle weight | Proposed in this study | |
| yp | Pivot point a spherical particle | − d/2 − l1 | Al-Madhhachi et al. [17] |
| zd | Height that the drag velocity is acting upon | l3 + yp | Al-Madhhachi et al. [17] |
| Crude oil coefficient ratio | Ranges from 18 to 23 | Experiments in this study | |
| Particle density | 2.65 Mg/m3 | Freeze and Cherry [35] | |
| Crude oil density | 0.88 Mg/m3 | Al-Madhhachi and Hasan [7], Ibrahem et al. [36] | |
| Water density | 1 Mg/m3 | - |
| Soil Texture | Atterberg Limits | Standard Compaction | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Source | USCS classification | Sand (%) | Silt (%) | Clay (%) | Liquid limit | Plastic limit | Plasticity index | Maximum Density, g/cm3 | Optimum water content (%) |
| Al-Taji, northwest Baghdad | Lean Clay | 15 | 55 | 30 | 38 | 26 | 14 | 1.88 | 16.00 |
| American Petroleum Institute (API°) Density * | Kinematic Viscosity * at 40 °C, mm2/s | Conradson Carbon Content *, % | Sulfur Content *, % | Vanadium Content *, ppm | Nickel Content *, ppm | Ash *, % |
|---|---|---|---|---|---|---|
| 33.60 | 6.90 | 4.10 | 1.95 | 23.90 | 16.41 | 0.01 |
| Contamination Time, Days | pH | Electrical Conductivity (EC), ds/m | Pb2, ppm | Total Organic Matter, % | Organic Carbon, % |
|---|---|---|---|---|---|
| 0 (Clean soil) | 7.14 | 23.78 | 46 | 1.27 | 0.74 |
| 1 | 7.18 | 17.40 | 89 | 1.50 | 0.87 |
| 4 | 7.31 | 19.50 | 102 | 1.56 | 0.91 |
| 8 | 7.81 | 19.80 | 135 | 1.69 | 0.98 |
| Median Values (IQR) a of Wilson Model Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| Clean Soil | Contaminated Soil | |||||||
| Contamination Time, Days | fco | b1, Pa | b0, g/m-s-N0.5 | b1, Pa | b0, g/m-s-N0.5 | p-Value of b1 | p-Value of b0 | |
| 1 | 81.00 | 18.67 | 25.5 (4.7) | 942.5 (827.2) | 30.4 (5.2) | 133.4 (70.7) | 0.505 | 0.278 |
| 4 | 140.00 | 23.03 | 24.1 (2.0) | 290.8 (10.0) | 48.9 (34.3) | 11.8 (5.1) | 0.402 | 0.006 |
| 8 | 140.00 | 23.04 | 18.3 (2.0) | 208.8 (4.0) | 31.9 (2.6) | 18.0 (16.3) | 0.013 | 0.021 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.B.; Al-Madhhachi, A.-S.T. The Influence of Crude Oil on Mechanistic Detachment Rate Parameters. Geosciences 2018, 8, 332. https://doi.org/10.3390/geosciences8090332
Hasan MB, Al-Madhhachi A-ST. The Influence of Crude Oil on Mechanistic Detachment Rate Parameters. Geosciences. 2018; 8(9):332. https://doi.org/10.3390/geosciences8090332
Chicago/Turabian StyleHasan, Manar B., and Abdul-Sahib T. Al-Madhhachi. 2018. "The Influence of Crude Oil on Mechanistic Detachment Rate Parameters" Geosciences 8, no. 9: 332. https://doi.org/10.3390/geosciences8090332
APA StyleHasan, M. B., & Al-Madhhachi, A.-S. T. (2018). The Influence of Crude Oil on Mechanistic Detachment Rate Parameters. Geosciences, 8(9), 332. https://doi.org/10.3390/geosciences8090332






