A Multi-Scale Conceptual Model of Flood-Tide Delta Morphodynamics in Micro-Tidal Estuaries
Abstract
:1. Introduction
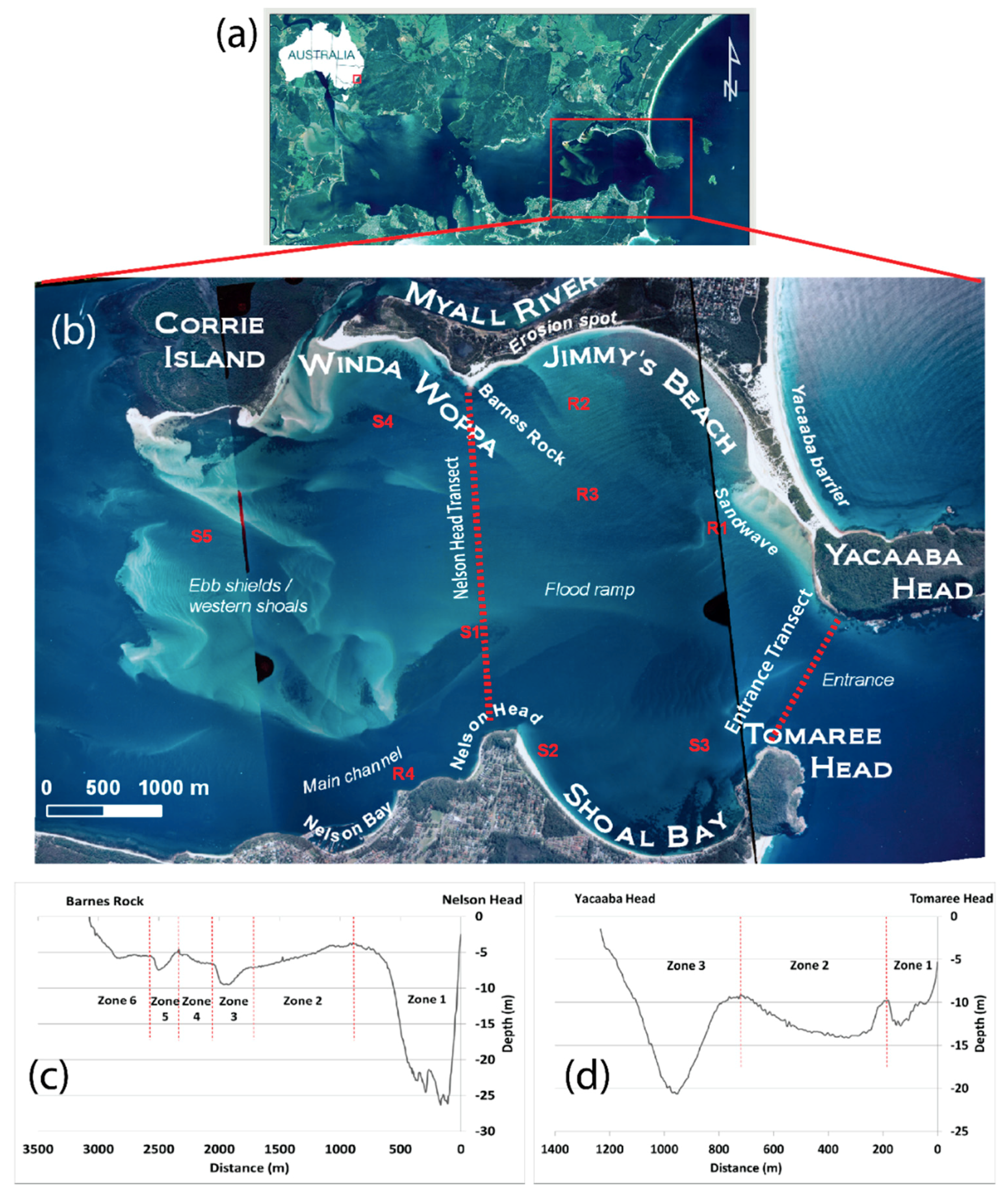
2. Study Area
3. Methods
3.1. Wave and Wind Climate
3.2. Flood Tide Delta Hydrodynamics
3.2.1. Bottom Mounted Measurements
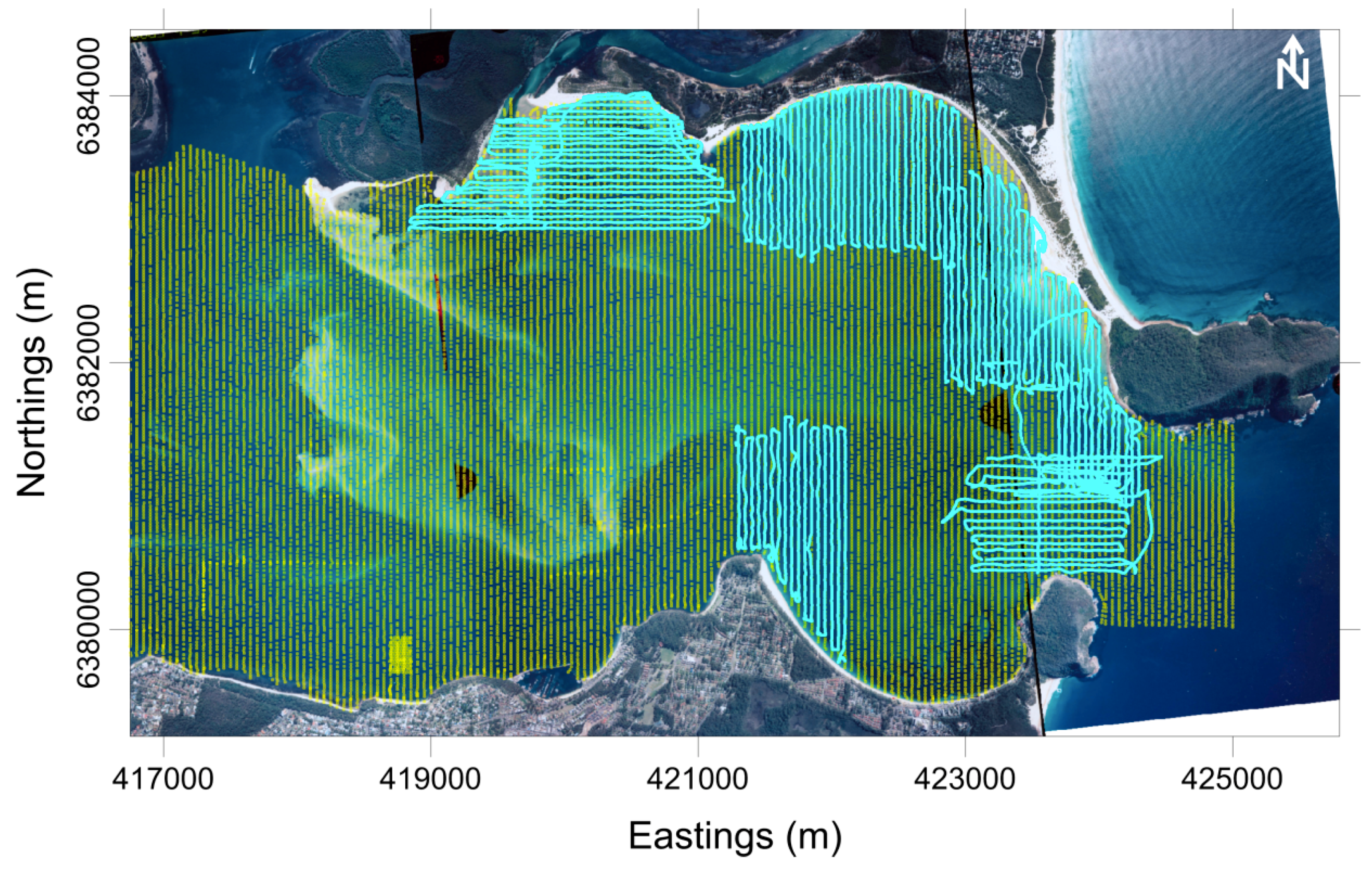
3.2.2. Vessel-Mounted Transect Measurements
- From south to north, we identified six zones in the Nelson Head transect (Figure 1c). Zone 1 is a 700 m wide, >25 m deep “U” shaped channel. Zone 2 represents the ebb shield and gradually deepens from ~3 m adjacent to the channel to ~7 m. Zone 3 is a narrow (300 m) and shallow (2 m) channel. Zone 4 is a gradual shallowing shoal from 7 m to 5 m. Zone 5 is another small channel of approximately 2 m depth and 200 m width. Zone 6 represents a gradual shallowing to the shoreline over approximately 500 m.
- From south to north, we identified three zones in the entrance transect (Figure 1d). Zone 1 is a 200 m wide channel, reaching a depth of 12 m. Zone 2 is characterised by a gentle depression that covers approximately 600 m and reaches a depth of approximately 14 m before rising to about 8 m. Zone 3 is a 400 m wide, >20 m deep “V” shaped channel.
3.3. Bathymetric Measurements
4. Results
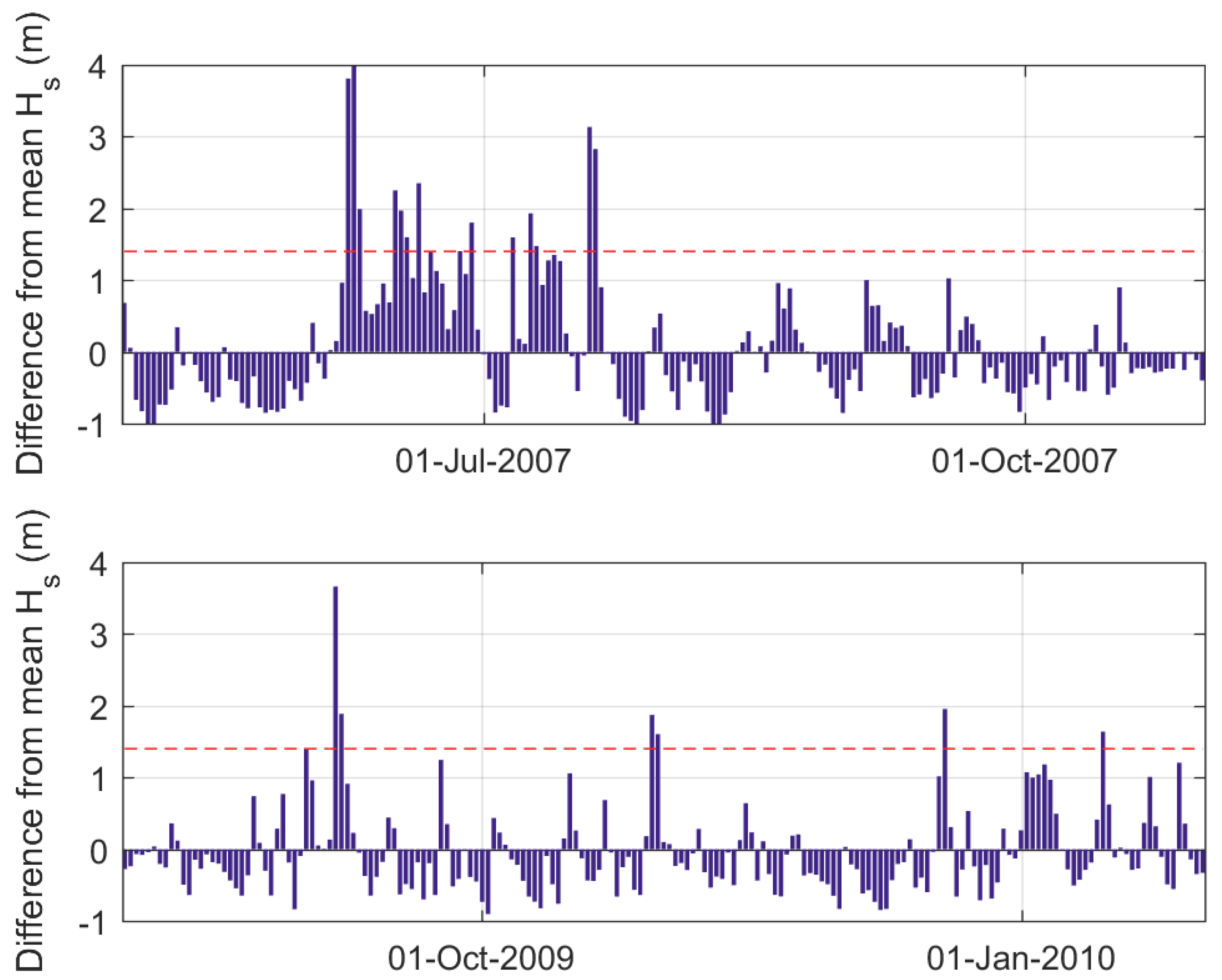
4.1. Wind and Wave Climate
4.2. Spring Tidal Cycle Circulation
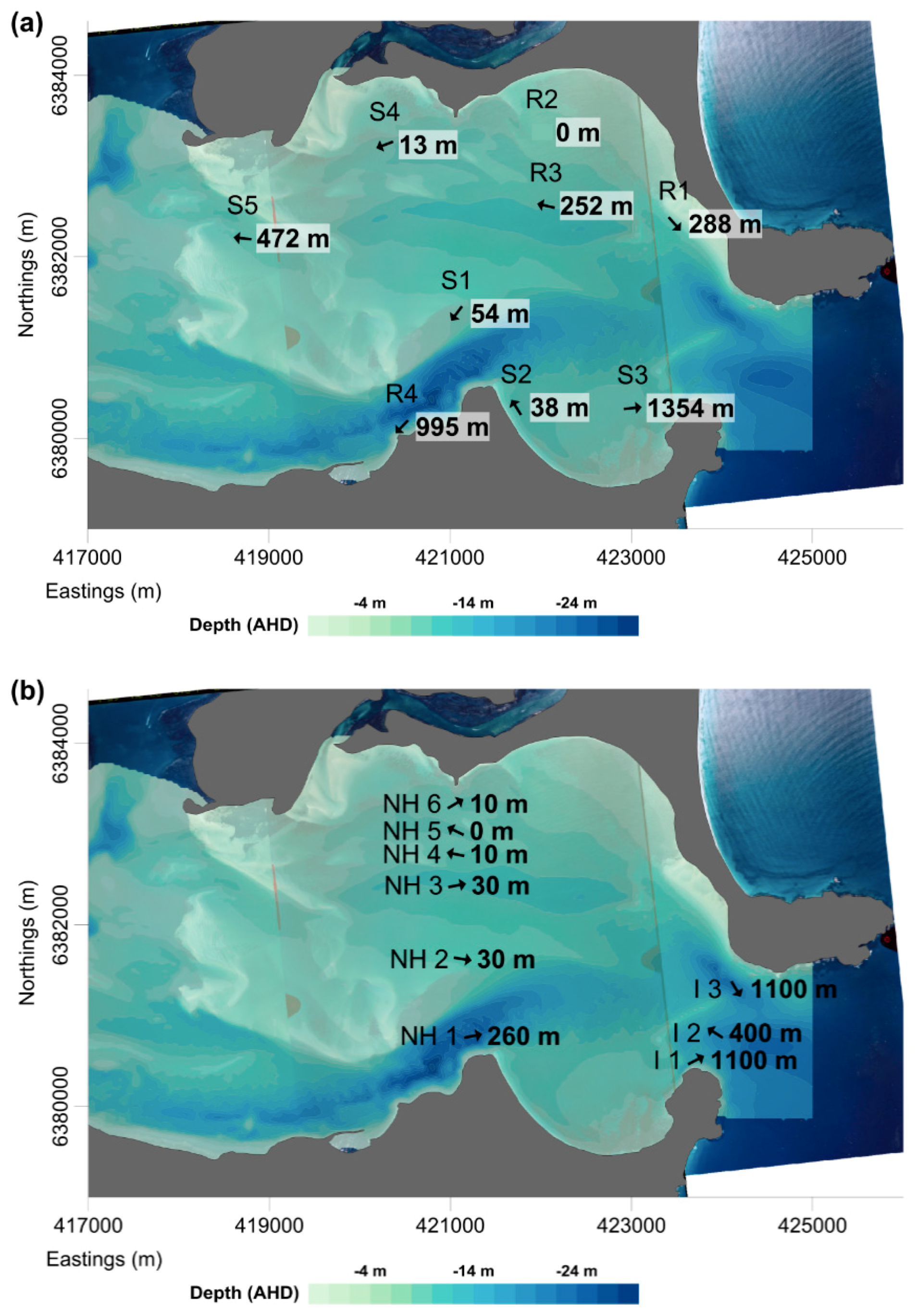
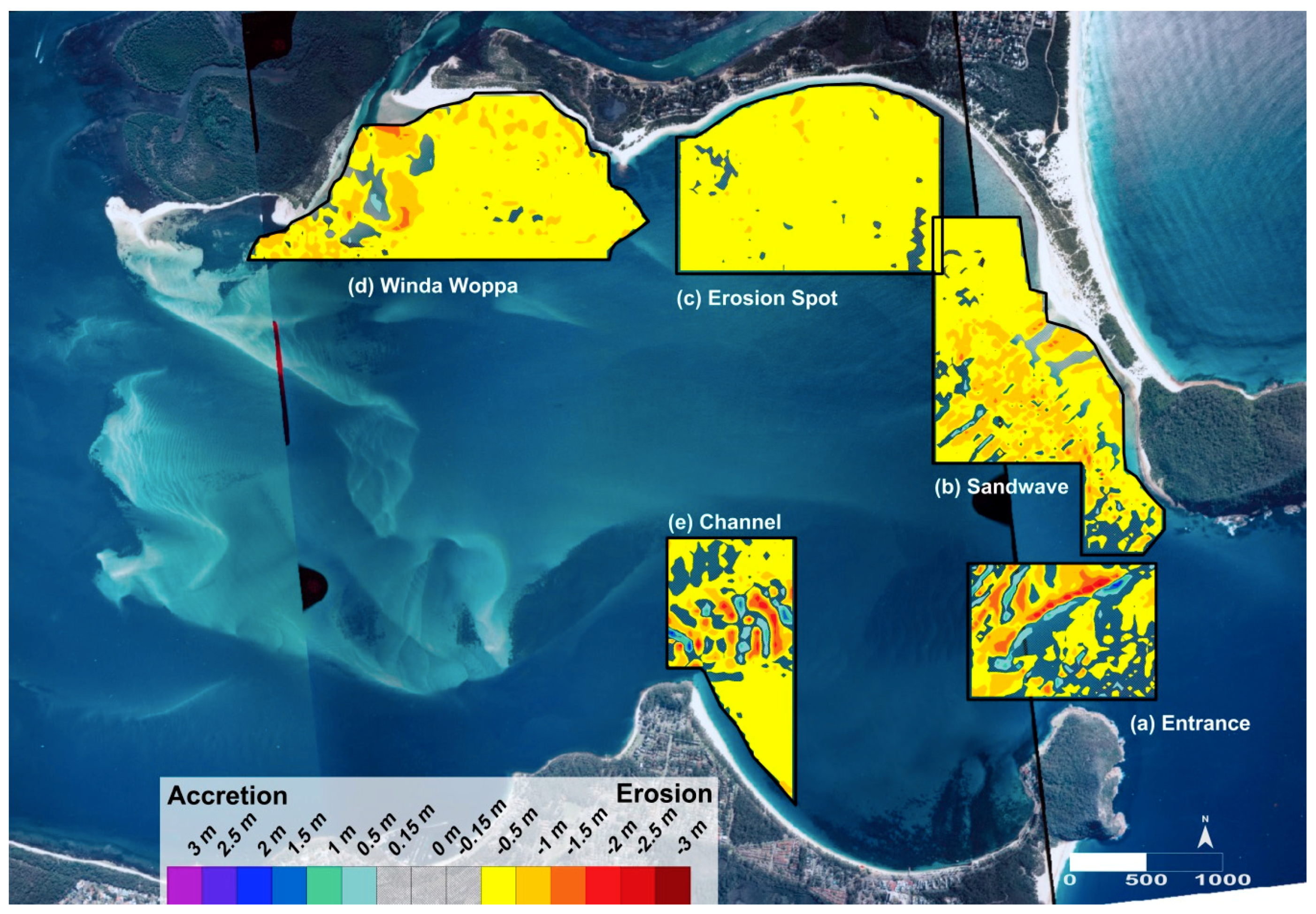
4.3. Bathymetric Changes
4.3.1. Entrance Shoal Survey Section
4.3.2. Sand Wave Survey Section
4.3.3. Jimmy’s Beach Erosion Survey Section
4.3.4. Winda Woppa Survey Section
4.3.5. Nelson Head Channel/Western Shoal Bay Survey Section
5. Discussion
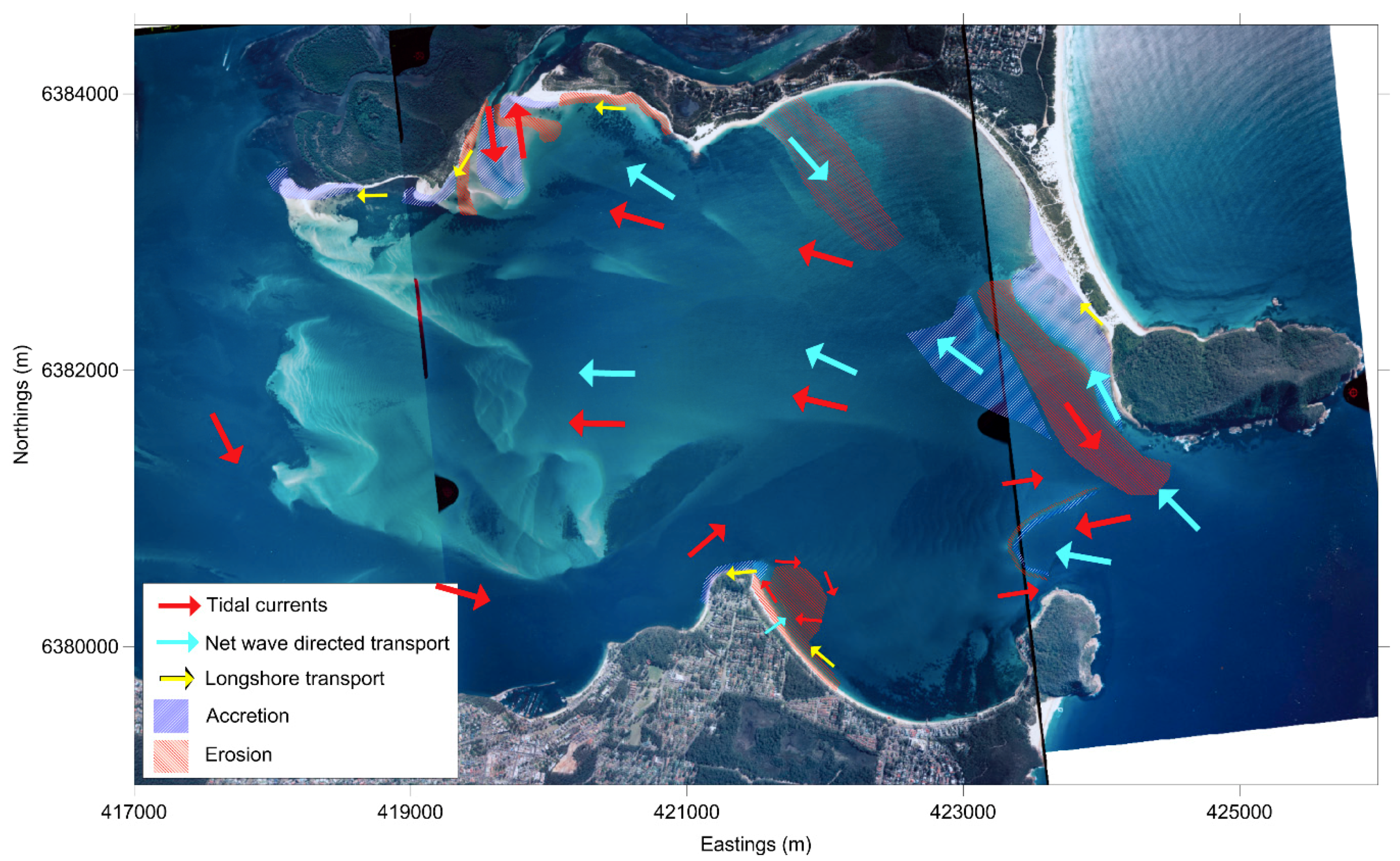
5.1. Port Stephens Estuary Function
5.2. Conceptual Model
- (1)
- Fetch limited estuary.
- (2)
- A relatively wide (hundreds of meters) fixed-width entrance.
- (3)
- Absence of large offshore sediment sources.
- (4)
- Absence (or underdeveloped) of an ebb-tidal delta.
- (5)
- Deep entrance channel with adjacent shallow regions.
- (6)
- Estuarine beaches are present along the estuary shorelines adjacent to the entrance.
- (7)
- Presence of a FTD of the general form described by Hayes [7].
- (8)
- Presence of a FTD adjacent main channel that connects with the entrance.
5.2.1. Fair Weather Conditions
5.2.2. Storm Conditions
5.2.3. Overall Evolution-Linking Timescales
- Entrance shoals maintain their approximate location and volume undergoing seaward migration under fair weather conditions (due to tidal current dominance), and up-estuary migration under storm conditions due to wave dominance.
- Shorelines undergo erosion due to storm conditions transporting sediment both along-shore and to the FTD, which is not returned during fair weather conditions, which have insufficient energy to act on the eroded sediment and/or which is affected by asymmetric tidal currents.
- Sediment from the flood ramp is transported up-estuary resulting in net lowering of the flood ramp (erosion) and up-estuary migration of the ebb shield.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Roy, P.S. New South Wales estuaries—Their origin and evolution. In Coastal Geomorphology in Australia; Academic Press: New York, NY, USA, 1984; pp. 99–121. [Google Scholar]
- Sloss, C.R.; Murray-Wallace, C.V.; Jones, G. Holocene Sea-Level Change on the Southeast Coast of Australia: A Review. Holocene 2007, 17, 999–1014. [Google Scholar] [CrossRef]
- Roy, P.S.; Williams, R.J.; Jones, A.R.; Yassini, I.; Gibbs, P.J.; Coates, B.; West, R.J.; Scanes, P.R.; Hudson, J.P.; Nichol, S. Structure and function of South-east Australian Estuaries. Estuar. Coast. Shelf Sci. 2001, 53, 351–384. [Google Scholar] [CrossRef]
- Boothroyd, J.C. Tidal inlets and tidal deltas. In Coastal Sedimentary Environment; Davis, R.A., Ed.; Springer-Verlag: New York, NY, USA, 1985; pp. 445–532. [Google Scholar]
- Coleman, J.M. Deltas: Processes of Deposition and Models for Exploration, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1982; p. 124. [Google Scholar]
- Hayes, M.O. General morphology and sediment patterns in tidal inlets. Sed. Geol. 1980, 26, 18. [Google Scholar] [CrossRef]
- Hayes, M.O. Morphology of sand accumulation in estuaries. In Estuarine Research; Cronin, L.E., Ed.; Academic Press: New York, NY, USA, 1975; p. 24. [Google Scholar]
- Nichols, M.M.; Biggs, R.B. Estuaries. In Coastal Sedimentary Environments; Davis, R.A., Ed.; Springer-Verlag: New York, NY, USA, 1985; pp. 77–186. [Google Scholar]
- Hayes, M.O. Barrier island morphology as a function of tidal and wave regime. In Barrier Islands from the Gulf of St Lawrence to the Gulf of Mexico; Leatherman, S.P., Ed.; Academic Press: New York, NY, USA, 1979; pp. 1–27. [Google Scholar]
- Moslow, T.F.; Heron, S.D. Relict inlets; preservation and occurrence in the Holocene stratigraphy of southern core banks, North Carolina. J. Sed. Res. 1978, 48, 1275–1286. [Google Scholar]
- FitzGerald, D.M. Geomorphic variability and morphologic and sedimentologic controls on tidal inlets. J. Coast. Res. 1996, 23, 47–71. [Google Scholar]
- Pacheco, A.; Williams, J.J.; Ferreira, Ó.; Dias, J.A. Evaluation of shear stress computation at a tidal inlet using different methods. J. Coast. Res. 2009, 56, 5. [Google Scholar]
- Vila-Concejo, A.; Ferreira, Ó.; Matias, A.; Dias, J.M.A. The first two years of an inlet: Sedimentary dynamics. Cont. Shelf Res. 2003, 23, 1425–1445. [Google Scholar] [CrossRef]
- Vila-Concejo, A.; Matias, A.; Ferreira, Ó.; Duarte, C.; Dias, J.M.A. Recent evolution of the natural inlets of a barrier island system in Southern Portugal. J. Coast. Res. 2002, 36, 741–752. [Google Scholar] [CrossRef]
- Adams, P.N.; Keough, K.M.; Olabarrieta, M. Beach Morphodynamics influenced by an ebb-tidal delta on the north Florida Atlantic coast. Earth Surf. Process. Landf. 2016, 41, 936–950. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Luijendijk, A.; Walstra, D.; Roelvink, D. Assessing climate change impacts on the stability of small tidal inlets: Part 1-Data poor environments. Mar. Geol. 2017, 390, 331–346. [Google Scholar] [CrossRef]
- Duong, T.M.; Ranasinghe, R.; Thatcher, M.; Mahanama, S.; Zheng, B.W.; Dissanayake, P.K.; Hemer, M.; Luijendijk, A.; Bamunawala, J.; Roelvink, D.; et al. Assessing climate change impacts on the stability of small tidal inlets: Part 2-Data rich environments. Mar. Geol. 2018, 395, 65–81. [Google Scholar] [CrossRef] [PubMed]
- FitzGerald, D.M. Interactions between the ebb-tidal delta and landward shoreline: Price Inlet, South Carolina. J. Sediment. Petrol. 1984, 54, 1303–1318. [Google Scholar]
- Hubbard, D.K.; Oertel, G.; Nummedal, D. The role of waves and tidal currents in the development of tidal-inlet sedimentary structures and sand body geometry; examples from North Carolina, South Carolina, and Georgia. J. Sediment. Res. 1979, 49, 1073–1091. [Google Scholar]
- Austin, T.P.; Short, A.D.; Hughes, M.G.; Vila-Concejo, A.; Ranasinghe, R. Tidal hydrodynamics of a micro-tidal, wave dominated flood-tide delta: Port Stephens, Australia. J. Coast. Res. 2009, 56, 693–697. [Google Scholar]
- Jackson, N.L. Wind and waves: Influence if local and non-local waves on mesoscale beach behaviour in estuarine environments. Annal. Assoc. Am. Geogr. 1995, 85, 21–37. [Google Scholar]
- Nordstrom, K.F. Estuarine Beaches; Elsevier Science Publishers Ltd.: Essex, UK, 1992; p. 225. [Google Scholar]
- Vila-Concejo, A.; Hughes, M.G.; Short, A.D.; Ranasinghe, R. Estuarine shoreline processes in a dynamic low-energy system. Ocean Dyn. 2010, 60, 285–298. [Google Scholar] [CrossRef]
- Costas, S.; Alejo, I.; Vila-Concejo, A.; Nombela, M.A. Persistence of storm-induced morphology on a modal low-energy beach: A case study from NW-Iberian Peninsula. Mar. Geol. 2005, 224, 43–56. [Google Scholar] [CrossRef]
- Easton, A.K. The Tides of the Continent of Australia, in Horace Lamb Centre for Oceanographical Research; Flinders University of South Australia: Bedford Park, Australia, 1970; p. 326. [Google Scholar]
- Jiang, A.W.; Ranasinghe, R.; Cowell, P. Hydrodynamic variability along a low-energy estuarine beach located in an open estuary. Aust. J. Civ. Eng. 2011, 9, 113–128. [Google Scholar] [CrossRef]
- Vila-Concejo, A.; Short, A.D.; Hughes, M.G.; Ranasinghe, R. Flood-tide delta morphodynamics and management implications, Port Stephens, Australia. J. Coast. Res. 2007, 50, 705–709. [Google Scholar]
- Benavente, J.; Harris, D.L.; Austin, T.P.; Vila-Concejo, A. Medium term behaviour and evolution of a beach cusps system in a low energy beach, Port Stephens, NSW, Australia. J. Coast. Res. 2011, 64, 170–174. [Google Scholar]
- DPWS, MHL. Port Stephens/Myall Lakes Estuary Processes Study; Report for Manly Hydraulics Laboratory: Manly Vale, NSW, Australia, 1999; pp. 110–115. [Google Scholar]
- Short, A.D.; Trenaman, N.L. Wave Climate of the Sydney Region, an Energetic and Highly Variable Ocean Wave Regime. Aust. J. Mar. Freshw. Res. 1992, 43, 26. [Google Scholar] [CrossRef]
- Malone, J.D.; Eagle, R.J. Jimmys Beach Erosion Study; Public Works Coastal Branch: Sydney, Australia, 1987; p. 340. [Google Scholar]
- Dewar, R. Stage 1: Analysis and review of existing information. In Port Stephens Flood Study; Report for Manly Hydraulics Laboratory: Manly Vale, NSW, Australia, 1993; p. 35. [Google Scholar]
- Anonymous, A. Coastline Management Manual. Report for Hydraulic Engineering Reports; NSW Government: Sydney, Australia, 1990. [Google Scholar]
- Shand, T.D.; Goodwin, I.D.; Mole, M.A.; Carley, J.T.; Browning, S.; Coghlan, I.G.; Harley, M.D.; Peirson, W.L.; You, Z.-J.; Kulmar, M.A. NSW Coastal Storms and Extreme Waves; Technical Report for Water Research Laborator; University of New South Wales: Sydney, Australia, 2010. [Google Scholar]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. Interannual variability and controls of the Sydney wave climate. Int. J. Climatol. 2010, 30, 1322–1335. [Google Scholar] [CrossRef]
- Woods Hole Coastal and Marine Science Center. Fetch- and depth-limited wave calculations. In Shore Protection Manual; Army Corps of Engineers; Waterways Experiment Station: Vicksburg, MS, USA, 1984. [Google Scholar]
- USACE. Shore Protection Maunal; USACE: Washington, DC, USA, 1984. [Google Scholar]
- Soulsby, R.L. Dynamics of Marine Sands; Thomas Telford Ltd.: Sotland, UK, 1997; p. 249. [Google Scholar]
- Black, K.P.; Healy, T.R.; Hunter, M.G. Sediment dynamics in the lower section of a mixed sand and shell-lagged Tidal Estuary, New Zealand. J. Coast. Res. 1989, 5, 503–521. [Google Scholar]
- Acoustic Doppler Profiler (ADP) Principles of Operation, version 6.24; SonTek: San Diego, CA, USA, 1997; p. 12.
- Burningham, H. Contrasting geomorphic response to structural control: The Loughros estuaries, northwest Ireland. Geomorphology 2008, 97, 300–320. [Google Scholar] [CrossRef]
- Dewar, R. Stage 2: Design water levels and wave climate. In Port Stephens Flood Study; Port Stephens Council: Port Stephens, Australia, 1996; p. 55. [Google Scholar]
- Fenster, M.S.; FitzGerald, D.M. Morphodynamics, stratigraphy, and sediment transport patterns of the Kennebec River estuary, Maine, USA. Sediment. Geol. 1996, 107, 99–120. [Google Scholar] [CrossRef]
- Vila-Concejo, A.; Austin, T.; Harris, D.; Hughes, M.G.; Short, A.D.; Ranasinghe, R. Estuarine beach evolution in relation to a flood-tide delta. J. Coast. Res. 2011, 64, 190–194. [Google Scholar]
- Thom, B.G. Coastal Geomorphology and Quaternary Geology of the Port Stephens-Myall Lakes Area; The Department of Biogeography and Geomorphology, The Australian National University: Canberra, Australia, 1939; pp. 375–391. [Google Scholar]
- Roy, P.S. Wave dominated coasts. In Coastal Evolution: Late Quaternary Shoreline Morphodynamics; Carter, R.W.G., Woodroffe, C.D., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 121–186. [Google Scholar]
- Frolich, M. Recent Morphological Evolution of the Port Stephens Llood-Tide Delta; School of Geosciences, University of Sydney: Sydney, Australia, 2007; p. 110. [Google Scholar]
- Druery, B.M.; Hurrel, G.L. Port Hacking Marine Delta: Management options; Public Works Department: Sydney, Australia, 1986. [Google Scholar]
- Flor-Blanco, G.; Flor, G.; Morales, J.A.; Flor, G.; Morales, J.A.; Pando, L. Hydrodynamic controls of morpho-sedimentary evolution in a rock-bounded mesotidal estuary. Tina Menor (N Spain). J. Iberian Geol. 2015, 41, 315–332. [Google Scholar]
- Morris, B.D.; Davidson, M.A.; Huntley, D.A. Measurements of the response of a coastal inlet using video monitoring techniques. Mar. Geol. 2001, 175, 251–272. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Duong, T.M.; Uhlenbrook, S.; Roelvink, D.; Stive, M. Climate-change impact assessment for inlet-interrupted coastlines. Nat. Clim. Chang. 2012, 3, 83–87. [Google Scholar] [CrossRef]
- Boon, J.D.I.; Byrne, R.J. On basin hyposmetry and the morphodynamic response of coastal inlet systems. Mar. Geol. 1981, 40, 27–48. [Google Scholar] [CrossRef]
- FitzGerald, D.M.; Nummedal, D. Response characteristics of an ebb-dominated tidal inlet channel. J. Sediment. Petrol. 1983, 53, 833–845. [Google Scholar]
- Bird, E.C.F. Coastal Geomorphology: An Introduction; Chichester: New York, NY, USA, 2000; p. 322. [Google Scholar]
- Cooper, J.A.G. Geomorphological variability among microtidal estuaries from the wave-dominated South African coast. Geomorphology 2001, 40, 99–122. [Google Scholar] [CrossRef]
- Green, M.O.; MacDonald, I.T. Processes driving estuary infilling by marine sands on an embayed coast. Mar. Geol. 2001, 178, 11–37. [Google Scholar] [CrossRef]
- Jackson, N.L.; Nordstrom, K.F.; Saini, S.; Smith, D.R. Effects of nourishment on the form and function of an estuarine beach. Ecol. Eng. 2010, 36, 1709–1718. [Google Scholar] [CrossRef]
- Vila-Concejo, A.; Short, A.D.; Hughes, M.G.; Ranasinghe, R. Formation and evolution of a sandwave on an estuarine beach. J. Coast. Res. 2009, 56, 153–157. [Google Scholar]
| Deployment | Deployment Site | Depth (Avg. Water Level Above Instrument (m)) | Deployment Period | Duration (days) |
|---|---|---|---|---|
| 1 | R1 S1 | 4.42/3.73 | 28 November 2007–19 December 2007 | 20 |
| 2 | R2/S2 | 3.72/5.73 | 20 December 2007–14 February 2008 | 56 |
| 3 | R3/S3 | 6.82/3.89 | 14 February 2008–28 March 2008 | 32 |
| 4 | R4 | 15.34 | 10 April 2008–04 May 2008 | 24 |
| 5 | S4 | 5.68 | 18 May 2008–18 September 2008 | 122 |
| 6 | S5 | 5.06 | 10 October 2008–15 December 2008 | 66 |
| Transect | Date | Length (m) | No. Transects | Frequency of Transect (h:mm) | Transect Duration (h:mm) | Avg. Boat Speed (m/s) | Average Ensemble Length (m) |
|---|---|---|---|---|---|---|---|
| Entrance transect | 17 December 2008 | 1250 | 27 | 0:30 | 0:15 | 1.3 | 6.5 |
| Nelson Head transect | 28 January 2010 | 3080 | 12 | 1:00 | 0:30 | 1.6 | 8 |
| 2007 | 2010 | |
|---|---|---|
| No. Storms | 15 | 7 |
| Avg. Duration (hrs) | 23.3 | 19 |
| Avg. Hs (m) | 3.6 | 3.47 |
| Hmax (m) | 14.1 | 12.2 |
| Avg. Tp (s) | 10.4 | 10.6 |
| Dir (°N) | 161 | 163 |
| Avg. Mean Power (kW/m) | 70 | 63 |
| Avg. Peak Power (kW/m) | 109 | 95 |
| Cumulative energy of largest storm (MJh/m2) | 952,000 | 528,000 |
| Total cumulative energy (MJh/m2) | 3,281,000 | 1,086,000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Austin, T.P.; Vila-Concejo, A.; Short, A.D.; Ranasinghe, R. A Multi-Scale Conceptual Model of Flood-Tide Delta Morphodynamics in Micro-Tidal Estuaries. Geosciences 2018, 8, 324. https://doi.org/10.3390/geosciences8090324
Austin TP, Vila-Concejo A, Short AD, Ranasinghe R. A Multi-Scale Conceptual Model of Flood-Tide Delta Morphodynamics in Micro-Tidal Estuaries. Geosciences. 2018; 8(9):324. https://doi.org/10.3390/geosciences8090324
Chicago/Turabian StyleAustin, Timothy P, Ana Vila-Concejo, Andrew D Short, and Roshanka Ranasinghe. 2018. "A Multi-Scale Conceptual Model of Flood-Tide Delta Morphodynamics in Micro-Tidal Estuaries" Geosciences 8, no. 9: 324. https://doi.org/10.3390/geosciences8090324
APA StyleAustin, T. P., Vila-Concejo, A., Short, A. D., & Ranasinghe, R. (2018). A Multi-Scale Conceptual Model of Flood-Tide Delta Morphodynamics in Micro-Tidal Estuaries. Geosciences, 8(9), 324. https://doi.org/10.3390/geosciences8090324






