Magnetic Anisotropy in Single Crystals: A Review
Abstract
1. Introduction
2. Theory
2.1. Diamagnetic, Paramagnetic, and Ferromagnetic Anisotropy
2.2. Description of Magnetic Fabrics
2.3. Symmetry Constraints
3. Measurement Methods
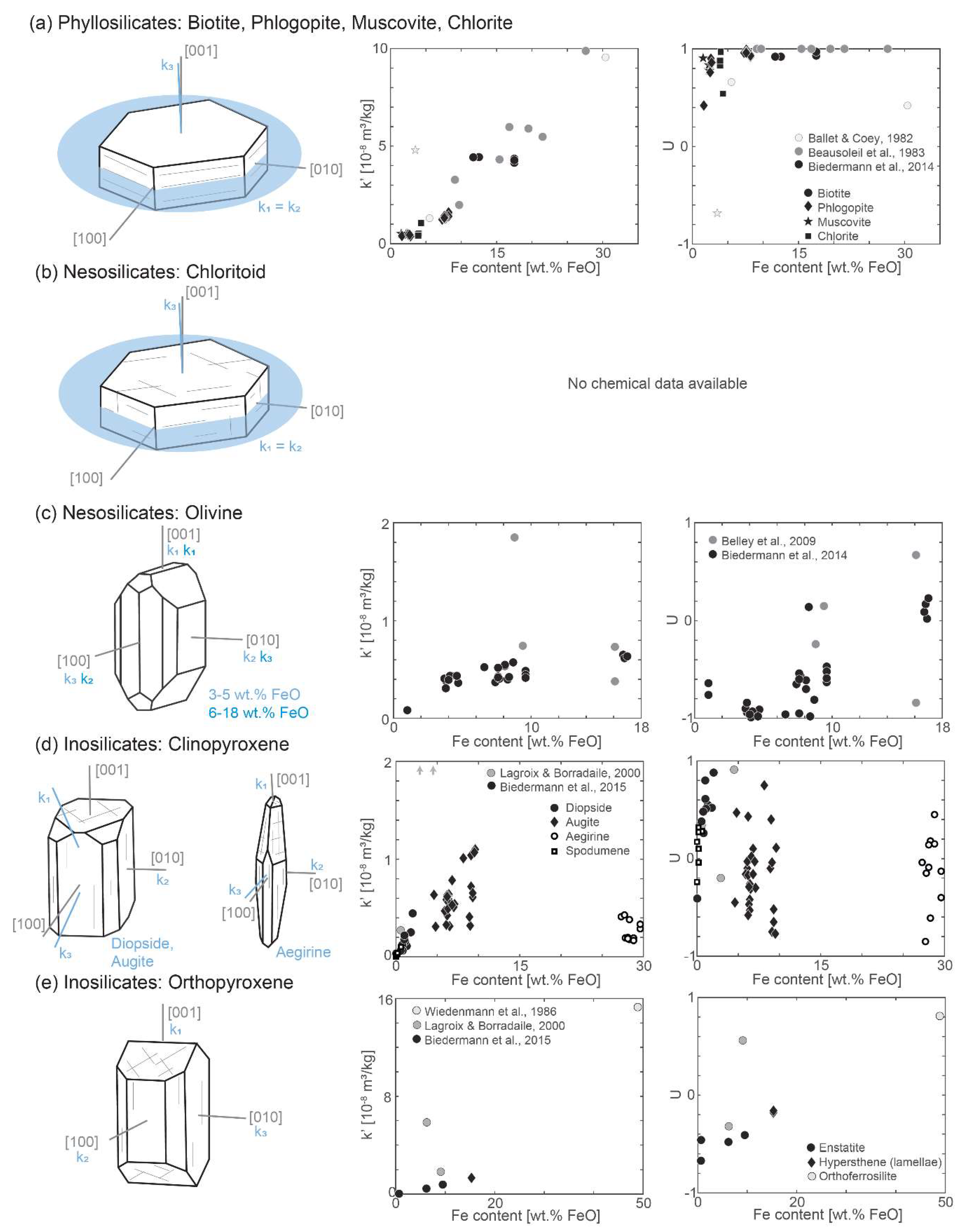
4. Single Crystal Properties of Silicate Minerals
4.1. Phyllosilicates: Mica and Chlorite
4.2. Nesosilicates: Olivine, Chloritoid
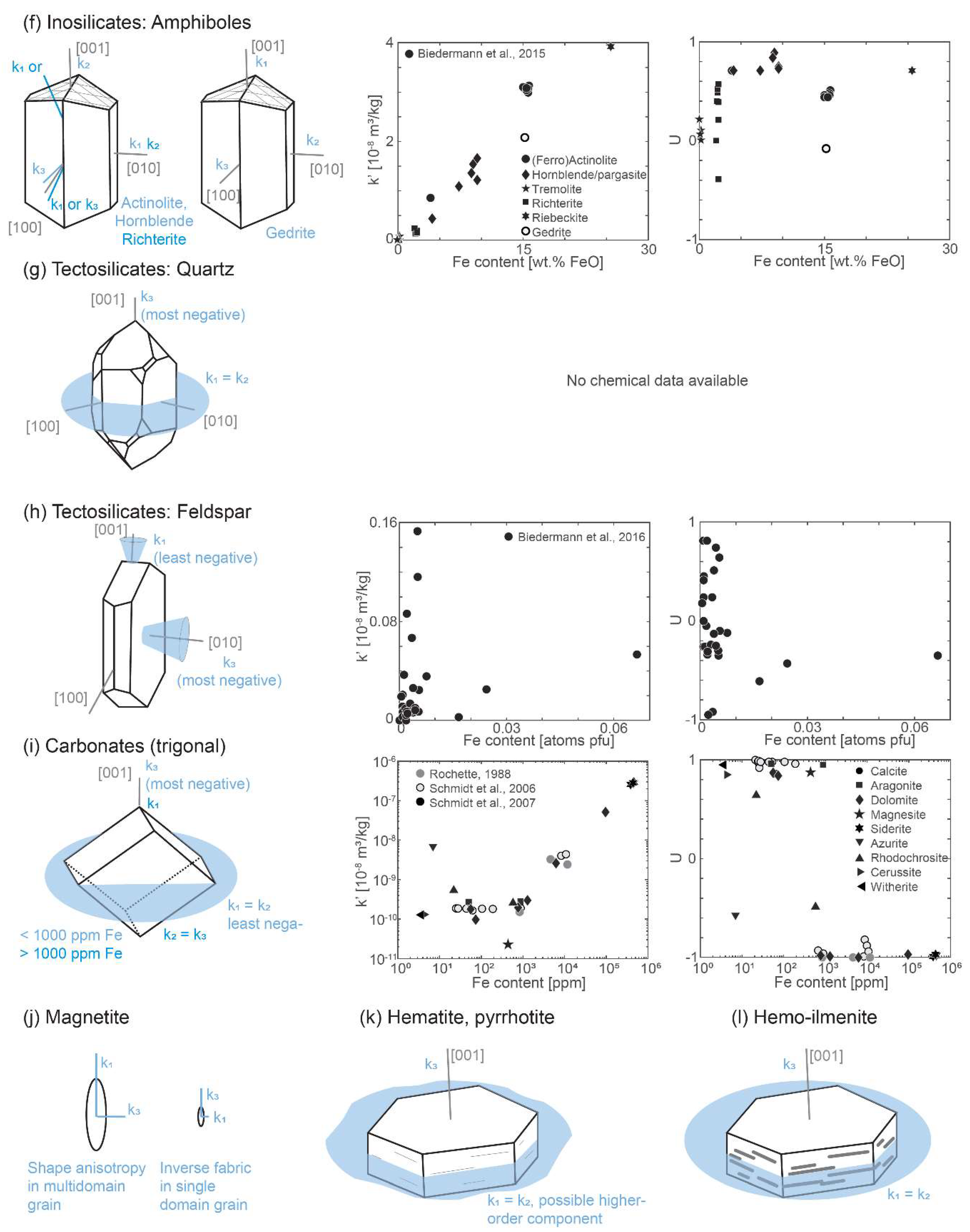
4.3. Inosilicates: Pyroxenes and Amphiboles
4.4. Tectosilicates: Quartz and Feldspar
5. Single Crystal Properties of Carbonate Minerals
6. Ferromagnetic Minerals
7. Application of Single Crystal Magnetic Anisotropy to Fabric Interpretation
8. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- Borradaile, G.J.; Henry, B. Tectonic applications of magnetic susceptibility and its anisotropy. Earth Sci. Rev. 1997, 42, 49–93. [Google Scholar] [CrossRef]
- Borradaile, G.J.; Jackson, M. Structural geology, petrofabrics and magnetic fabrics (AMS, AARM, AIRM). J. Struct. Geol. 2010, 32, 1519–1551. [Google Scholar] [CrossRef]
- Hrouda, F. Magnetic anisotropy of rocks and its application in geology and geophysics. Geophys. Surv. 1982, 5, 37–82. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Lüneburg, C.M.; Aubourg, C.; Jackson, M. Magnetic Fabrics: Methods and Applications; The Geological Society: London, UK, 2004; Volume 238. [Google Scholar]
- Tarling, D.H.; Hrouda, F. The Magnetic Anisotropy of Rocks; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Owens, W.H.; Bamford, D. Magnetic, seismic, and other anisotropic properties of rock fabrics. Philos. Trans. R. Soc. A 1976, 283, 55–68. [Google Scholar] [CrossRef]
- Rochette, P.; Jackson, M.; Aubourg, C. Rock magnetism and the interpretation of anisotropy of magnetic susceptibility. Rev. Geophys. 1992, 30, 209–226. [Google Scholar] [CrossRef]
- Balsley, J.R.; Buddington, A.F. Magnetic susceptibility anisotropy and fabric of some adirondack granites and orthogneisses. Am. J. Sci. 1960, 258, 6–20. [Google Scholar]
- Lüneburg, C.M.; Lampert, S.A.; Lebit, H.D.; Hirt, A.M.; Casey, M.; Lowrie, W. Magnetic anisotropy, rock fabrics and finite strain in deformed sediments of SW Sardinia (Italy). Tectonophysics 1999, 307, 51–74. [Google Scholar] [CrossRef]
- Oliva-Urcia, B.; Rahl, J.M.; Schleicher, A.M.; Pares, J.M. Correlation between the anisotropy of the magnetic susceptibility, strain and X-ray texture goniometry in phyllites from crete, greece. Tectonophysics 2010, 486, 120–131. [Google Scholar] [CrossRef]
- Rathore, J.S. Magnetic susceptibility anisotropy in the cambrian slate belt of north wales and correlation with strain. Tectonophysics 1979, 53, 83–97. [Google Scholar] [CrossRef]
- Richter, C.; Ratschbacher, L.; Frisch, W. Magnetic fabrics, crystallographic preferred orientation, and strain of progressively metamorphosed pelites in the Helvetic Zone of the Central Alps (Quartenschiefer Formation). J. Geophys. Res. Solid Earth 1993, 98, 9557–9570. [Google Scholar] [CrossRef]
- Borradaile, G.J. Magnetic susceptibility, petrofabrics and strain. Tectonophysics 1988, 156, 1–20. [Google Scholar] [CrossRef]
- Hargraves, R.B. Magnetic anisotropy and remanent magnetism in hemo-ilmenite from ore deposits at Allard Lake, Quebec. J. Geophys. Res. 1959, 64, 1565–1578. [Google Scholar] [CrossRef]
- Graham, J.W. Magnetic susceptibility anisotropy, an unexploited petrofabric element. Geol. Soc. Am. Bull. 1954, 65, 1257–1258. [Google Scholar]
- Graham, J.W. Significance of magnetic anisotropy in appalachian sedimentary rocks. In The Earth Beneath the Continents: A Volume of Geophysical Studies in Honor of Merle A. Tuve; Steinhart, J.S., Smith, T.J., Eds.; American Geophysical Union: Washington, DC, USA, 1966; Volume 10, pp. 627–648. [Google Scholar]
- Borradaile, G.J.; Stewart, R.A.; Werner, T. Archean uplift of a subprovince boundary in the canadian shield, revealed by magnetic fabrics. Tectonophysics 1993, 227, 1–15. [Google Scholar] [CrossRef]
- Biedermann, A.R. Magnetic Properties of the Møre-Trøndelag Fault Complex. Master’s Thesis, ETH Zurich, Zurich, Switzerland, 2010. [Google Scholar]
- Biedermann, A.R.; Kunze, K.; Hirt, A.M. Interpreting magnetic fabrics in amphibole-bearing rocks. Tectonophysics 2018, 722, 566–576. [Google Scholar] [CrossRef]
- Kligfield, R.; Lowrie, W.; Dalziel, W.D. Magnetic susceptibility anisotropy as a strain indicator in the Sudbury Basin, Ontario. Tectonophysics 1977, 40, 287–308. [Google Scholar] [CrossRef]
- Kligfield, R.; Owens, W.H.; Lowrie, W. Magnetic susceptibility anisotropy, strain, and progressive deformation in Permian sediments from the Maritime Alps (France). Earth Planet. Sci. Lett. 1981, 55, 181–189. [Google Scholar] [CrossRef]
- Hirt, A.M.; Lowrie, W.; Clendenen, W.S.; Kligfield, R. The correlation of magnetic anisotropy with strain in the Chelmsford Formation of the Sudbury Basin, Ontario. Tectonophysics 1988, 145, 177–189. [Google Scholar] [CrossRef]
- Hirt, A.M.; Lowrie, W.; Clendenen, W.S.; Kligfield, R. Correlation of strain and the anisotropy of magnetic susceptibility in the Onaping Formation: Evidence for a near-circular origin of the Sudbury basin. Tectonophysics 1993, 225, 231–254. [Google Scholar] [CrossRef]
- Borradaile, G.J. Correlation of strain with anisotropy of magnetic susceptibility (AMS). Pure Appl. Geophys. 1991, 135, 15–29. [Google Scholar] [CrossRef]
- Cogné, J.P.; Perroud, H. Anisotropy of magnetic susceptibility as a strain gauge in the Flamanville granite, NW France. Phys. Earth Planet. Inter. 1988, 51, 264–270. [Google Scholar] [CrossRef]
- Hrouda, F. Theoretical models of magnetic anisotropy to strain relationship revisited. Phys. Earth Planet. Inter. 1993, 77, 237–249. [Google Scholar] [CrossRef]
- Kneen, S.J. The relationship between the magnetic and strain fabrics of some haematite-bearing slates. Earth Planet. Sci. Lett. 1976, 31, 413–416. [Google Scholar] [CrossRef]
- Wood, D.S.; Oertel, G.; Singh, J.; Bennett, H.F. Strain and anisotropy in rocks. Philos. Trans. R. Soc. A 1976, 283, 27–42. [Google Scholar] [CrossRef]
- Housen, B.A.; van der Pluijm, B.A. Chlorite control of correlations between strain and anisotropy of magnetic susceptibility. Phys. Earth Planet. Inter. 1990, 61, 315–323. [Google Scholar] [CrossRef]
- Borradaile, G. Anisotropy of magnetic susceptibility: Rock composition versus strain. Tectonophysics 1987, 138, 327–329. [Google Scholar] [CrossRef]
- Chadima, M.; Hansen, A.; Hirt, A.M.; Hrouda, F.; Siemens, H. Phyllosilicate preferred orientation as a control of magnetic fabric: Evidence from neutron texture goniometry and low and high-field magnetic anisotropy (SE Rhenohercynian Zone of Bohemian Massif). In Magnetic Fabric: Methods and Applications; Martín-Hernández, F., Lüneburg, C.M., Aubourg, C., Jackson, M., Eds.; The Geological Society: London, UK, 2004; Volume 238, pp. 361–380. [Google Scholar]
- Hirt, A.M.; Evans, K.F.; Engelder, T. Correlation between magnetic anisotropy and fabric for Devonian shales on the Appalachian Plateau. Tectonophysics 1995, 247, 121–132. [Google Scholar] [CrossRef]
- Hrouda, F.; Schulmann, K.; Suppes, M.; Ullemeyer, K.; de Wall, H.; Weber, K. Quantitative relationship between low-field AMS and phyllosilicate fabric: A review. Phys. Chem. Earth 1997, 22, 153–156. [Google Scholar] [CrossRef]
- Siegesmund, S.; Ullemeyer, K.; Dahms, M. Control of magnetic rock fabrics by mica preferred orientation—A quantitative approach. J. Struct. Geol. 1995, 17, 1601–1613. [Google Scholar] [CrossRef]
- Schmidt, V.; Hirt, A.M.; Leiss, B.; Burlini, L.; Walter, J.M. Quantitative correlation of texture and magnetic anisotropy of compacted calcite–muscovite aggregates. J. Struct. Geol. 2009, 31, 1062–1073. [Google Scholar] [CrossRef]
- Grégoire, V.; De Saint-Blanquat, M.; Nédélec, A.; Bouchez, J.-L. Shape anisotropy versus magnetic interactions of magnetite grains: Experiments and application to AMS in granitic rocks. Geophys. Res. Lett. 1995, 22, 2765–2768. [Google Scholar] [CrossRef]
- Grégoire, V.; Darrozes, P.; Gaillot, P.; Nédélec, A. Magnetite grain shape fabric and distribution anisotropy vs rock magnetic fabric: A three-dimensional case study. J. Struct. Geol. 1998, 20, 937–944. [Google Scholar] [CrossRef]
- Hargraves, R.B.; Johnson, D.; Chan, C.Y. Distribution anisotropy: The cause of ams in igneous rocks? Geophys. Res. Lett. 1991, 18, 2193–2196. [Google Scholar] [CrossRef]
- Stephenson, A. Distribution anisotropy: Two simple models for magnetic lineation and foliation. Phys. Earth Planet. Inter. 1994, 82, 49–53. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Kunze, K.; Julivert, M.; Hirt, A.M. Mathematical simulations of anisotropy of magnetic susceptibility on composite fabrics. J. Geophys. Res. 2005, 110, B06102. [Google Scholar] [CrossRef]
- Owens, W.H. Mathematical model studies on factors affecting the magnetic anisotropy of deformed rocks. Tectonophysics 1974, 24, 115–131. [Google Scholar] [CrossRef]
- Biedermann, A.R.; Kunze, K.; Zappone, A.S.; Hirt, A.M. Origin of magnetic fabric in ultramafic rocks. IOP Conf. Ser.: Mater. Sci. Eng. 2015, 82, 012098. [Google Scholar] [CrossRef]
- Mainprice, D.; Hielscher, R.; Schaeben, H. Calculating anisotropic physical properties from texture data using the MTEX open-source package. Geol. Soc. Lond. Spec. Publ. 2011, 360, 175–192. [Google Scholar] [CrossRef]
- Hrouda, F. Modelling relationship between bulk susceptibility and AMS in rocks consisting of two magnetic fractions represented by ferromagnetic and paramagnetic minerals—Implications for understanding magnetic fabrics in deformed rocks. J. Geol. Soc. India 2010, 75, 254–266. [Google Scholar] [CrossRef]
- Tyndall, J. Ueber diamagnetismus und magnekrystallinische wirkung. Ann. Phys. 1851, 159, 384–416. [Google Scholar] [CrossRef]
- Stenger, F. Ueber das verhalten des kalkspaths im homogenen magnetischen felde. Ann. Phys. 1883, 256, 304–326. [Google Scholar] [CrossRef][Green Version]
- König, W. Magnetische untersuchungen an krystallen. Ann. Phys. 1887, 267, 273–302. [Google Scholar] [CrossRef]
- Stenger, F. Ueber die gesetze des krystallmagnetismus. Ann. Phys. 1888, 271, 331–353. [Google Scholar] [CrossRef]
- Tyndall, J. Researches on Diamagnetism and Magne-Crystallic Action: Including the Question of Diamagnetic Polarity; Longmans, Green & Co.: London, UK, 1888; 288p. [Google Scholar]
- Voigt, W.; Kinoshita, S. Bestimmung absoluter werte von magnetisierungszahlen insbesondere für kristalle. Ann. Phys. 1907, 24, 492–514. [Google Scholar] [CrossRef]
- Finke, W. Magnetische Messungen an Platinmetallen und monoklinen Kristallen, insbesondere der Eisen-, Kobalt-und Nickelsalze. Ann. Phys. 1909, 336, 149–168. [Google Scholar] [CrossRef]
- Krishnan, K.S.; Guha, B.C.; Banerjee, S. Investigations on magne-crystallic action. Part I: Diamagnetics. Philos. Trans. R. Soc. A 1933, 231, 235–262. [Google Scholar] [CrossRef]
- Rowland, H.A. On the diamagnetic constants of bismuth and calc-spar in absolute measure. Am. J. Sci. 1879, 18, 360–371. [Google Scholar] [CrossRef]
- Pauling, L. The diamagnetic anisotropy of aromatic molecules. J. Chem. Phys. 1936, 4, 673–677. [Google Scholar] [CrossRef]
- Banerjee, S. The magnetic anisotropies of some organic crystals in relation to their structures. Z. Krist. 1939, 100, 316–355. [Google Scholar] [CrossRef]
- Krishnan, K.S.; Ganguli, N. Temperature variation of the magnetic anisotropy of graphite. Z. Krist. 1939, 100, 530–536. [Google Scholar] [CrossRef]
- Zapletal, K. Low-field susceptibility anisotropy of some biotite crystals. Phys. Earth Planet. Inter. 1990, 63, 85–97. [Google Scholar] [CrossRef]
- Borradaile, G.; Keeler, W.; Alford, C.; Sarvas, P. Anisotropy of magnetic susceptibility of some metamorphic minerals. Phys. Earth Planet. Inter. 1987, 48, 161–166. [Google Scholar] [CrossRef]
- Wagner, J.-J.; Hedley, I.G.; Steen, D.; Tinkler, C.; Vuagnat, M. Magnetic anisotropy and fabric of some progressively deformed ophiolitic gabbros. J. Geophys. Res. 1981, 86, 307–315. [Google Scholar] [CrossRef]
- Lagroix, F.; Borradaile, G.J. Magnetic fabric interpretation complicated by inclusions in mafic silicates. Tectonophysics 2000, 325, 207–225. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Hirt, A.M. The anisotropy of magnetic susceptibility in biotite, muscovite and chlorite single crystals. Tectonophysics 2003, 367, 13–28. [Google Scholar] [CrossRef]
- Biedermann, A.R.; Bender Koch, C.; Pettke, T.; Hirt, A.M. Magnetic anisotropy in natural amphibole crystals. Am. Mineral. 2015, 100, 1940–1951. [Google Scholar] [CrossRef]
- Biedermann, A.R.; Pettke, T.; Bender Koch, C.; Hirt, A.M. Magnetic anisotropy in clinopyroxene and orthopyroxene single crystals. J. Geophys. Res. Solid Earth 2015, 120, 1431–1451. [Google Scholar] [CrossRef]
- Schmidt, V.; Günther, D.; Hirt, A.M. Magnetic anisotropy of calcite at room-temperature. Tectonophysics 2006, 418, 63–73. [Google Scholar] [CrossRef]
- Ballet, O.; Coey, J.M.D. Magnetic properties of sheet silicates; 2:1 layer minerals. Phys. Chem. Miner. 1982, 8, 218–229. [Google Scholar] [CrossRef]
- Coey, J.M.D.; Ballet, O.; Moukarika, A.; Soubeyroux, J.L. Magnetic properties of sheet silicates; 1:1 layer minerals. Phys. Chem. Miner. 1981, 7, 141–148. [Google Scholar] [CrossRef]
- Beausoleil, N.; Lavallee, P.; Yelon, A.; Ballet, O.; Coey, J.M.D. Magnetic properties of biotite micas. J. Appl. Phys. 1983, 54, 906–915. [Google Scholar] [CrossRef]
- Ballet, O.; Coey, J.M.D.; Burke, K.J. Magnetic properties of sheet silicates; 2:1:1 layer minerals. Phys. Chem. Miner. 1985, 12, 370–378. [Google Scholar] [CrossRef]
- Pares, J.M.; van der Pluijm, B.A. Phyllosilicate fabric characterization by low-temperature anisotropy of magnetic susceptibility (LT-AMS). Geophys. Res. Lett. 2002, 29, 68:1–68:4. [Google Scholar] [CrossRef]
- Biedermann, A.R.; Bender Koch, C.; Lorenz, W.E.A.; Hirt, A.M. Low-temperature magnetic anisotropy in micas and chlorite. Tectonophysics 2014, 629, 63–74. [Google Scholar] [CrossRef]
- Müller, R.; Fuess, H.; Brown, P.J. Magnetic properties of synthetic fayalite (α-FE2SiO4). J. Phys. Colloq. 1982, 43, 249–252. [Google Scholar] [CrossRef]
- Belley, F.; Ferré, E.C.; Martín-Hernández, F.; Jackson, M.J.; Dyar, M.D.; Catlos, E.J. The magnetic properties of natural and synthetic (Fex, Mg1−x)2 SiO4 olivines. Earth Planet. Sci. Lett. 2009, 284, 516–526. [Google Scholar] [CrossRef]
- Biedermann, A.R.; Pettke, T.; Reusser, E.; Hirt, A.M. Anisotropy of magnetic susceptibility in natural olivine single crystals. Geochem. Geophys. Geosyst. 2014, 15, 3051–3065. [Google Scholar] [CrossRef]
- Ferré, E.C.; Tikoff, B.; Jackson, M. The magnetic anisotropy of mantle peridotites: Example from the Twin Sisters Dunite, Washington. Tectonophysics 2005, 398, 141–166. [Google Scholar] [CrossRef]
- Parry, G.R. The Magnetic anisotropy of some deformed rocks. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 1971. [Google Scholar]
- Wiedenmann, A.; Regnard, J.-R.; Fillion, G.; Hafner, S.S. Magnetic properties and magnetic ordering of the orthopyroxenes FexMg1−xSiO3. J. Phys. C Solid State Phys. 1986, 19, 3683–3695. [Google Scholar] [CrossRef]
- Ballet, O.; Fuess, H.; Wacker, K.; Untersteller, E.; Treutmann, W.; Hellner, E.; Hosoya, S. Magnetisation measurements of the synthetic olivine single crystals A2SiO4 with A = Mn, Fe or Co. J. Phys. Condens. Matter 1989, 1, 4955–4970. [Google Scholar] [CrossRef]
- Ehrenberg, H.; Fuess, H. Analytical interpretation and simulation of the static magnetic properties of synthetic alpha-Fe2SiO4. J. Phys. Condens. Matter 1993, 5, 3663–3672. [Google Scholar] [CrossRef]
- Feinberg, J.M.; Wenk, H.-R.; Renne, P.R.; Scott, G.R. Epitaxial relationships of clinopyroxene-hosted magnetite determined using electron backscatter diffraction (EBSD) technique. Am. Mineral. 2004, 89, 462–466. [Google Scholar] [CrossRef]
- Feinberg, J.M.; Scott, G.R.; Renne, P.R.; Wenk, H.-R. Exsolved magnetite inclusions in silicates: Features determining their remanence behavior. Geology 2005, 33, 513–516. [Google Scholar] [CrossRef]
- Feinberg, J.M.; Harrison, R.J.; Kasama, T.; Dunin-Borkowski, R.E.; Scott, G.R.; Renne, P.R. Effects of internal mineral structures on the magnetic remanence of silicate-hosted titanomagnetite inclusions: An electron holography study. J. Geophys. Res. 2006, 111, B12S15. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Hirt, A.M. Separation of ferrimagnetic and paramagnetic anisotropies using a high-field torsion magnetometer. Tectonophysics 2001, 337, 209–221. [Google Scholar] [CrossRef]
- Ferré, E.C.; Martin-Hernandez, F.; Teyssier, C.; Jackson, M. Paramagnetic and ferromagnetic anisotropy of magnetic susceptibility in migmatites: Measurements in high and low fields and kinematic implications. Geophys. J. Int. 2004, 157, 1119–1129. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Hirt, A.M. A method for the separation of paramagnetic, ferrimagnetic and haematite magnetic subfabrics using high-field torque magnetometry. Geophys. J. Int. 2004, 157, 117–127. [Google Scholar] [CrossRef]
- Martín-Hernández, F.; Ferré, E.C. Separation of paramagnetic and ferrimagnetic anisotropies: A review. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Kelso, P.R.; Tikoff, B.; Jackson, M.; Sun, W. A new method for the separation of paramagnetic and ferromagnetic susceptibility anisotropy using low field and high field methods. Geophys. J. Int. 2002, 151, 345–359. [Google Scholar] [CrossRef]
- Richter, C.; van der Pluijm, B.A. Separation of paramagnetic and ferrimagnetic susceptibilities using low-temperature magnetic susceptibilities and comparison with high-field methods. Phys. Earth Planet. Inter. 1994, 82, 113–123. [Google Scholar] [CrossRef]
- Schmidt, V.; Hirt, A.M.; Hametner, K.; Gunther, D. Magnetic anisotropy of carbonate minerals at room temperature and 77 k. Am. Mineral. 2007, 92, 1673–1684. [Google Scholar] [CrossRef]
- Uyeda, S.; Fuller, M.D.; Belshe, C.; Girdler, R.W. Anisotropy of magnetic susceptibility of rocks and minerals. J. Geophys. Res. 1963, 68, 279–291. [Google Scholar] [CrossRef]
- Cañón-Tapia, E. Factors affecting the relative importance of shape and distribution anisotropy in rocks: Theory and experiments. Tectonophysics 2001, 340, 117–131. [Google Scholar] [CrossRef]
- De Wall, H.; Worm, H.-U. Field dependence of magnetic anisotropy in pyrrhotite: Effects of texture and grain shape. Phys. Earth Planet. Inter. 1993, 76, 137–149. [Google Scholar] [CrossRef]
- Martin-Hernandez, F.; Dekkers, M.J.; Bominaar-Silkens, I.M.A.; Maan, J.C. Magnetic anisotropy behaviour of pyrrhotite as determined by low- and high-field experiments. Geophys. J. Int. 2008, 174, 42–54. [Google Scholar] [CrossRef]
- Martin-Hernandez, F.; Guerrero-Suarez, S. Magnetic anisotropy of hematite natural crystals: High field experiments. Int. J. Earth Sci. 2012, 101, 637–647. [Google Scholar] [CrossRef]
- Guerrero-Suarez, S.; Martin-Hernandez, F. Magnetic anisotropy of hematite natural crystals: Increasing low-field strength experiments. Int. J. Earth Sci. 2012, 101, 625–636. [Google Scholar] [CrossRef]
- Hrouda, F. Low-field variation of magnetic susceptibility and its effect on the anisotropy of magnetic susceptibility of rocks. Geophys. J. Int. 2002, 150, 715–723. [Google Scholar] [CrossRef]
- Borradaile, G.; Mothersill, J.; Tarling, D.; Alford, C. Sources of magnetic susceptibility in a slate. Earth Planet. Sci. Lett. 1986, 76, 336–340. [Google Scholar] [CrossRef]
- Hounslow, M.W. Magnetic fabric arising from paramagnetic phyllosilicate minerals in mudrocks. J. Geol. Soc. 1985, 142, 995–1006. [Google Scholar] [CrossRef]
- Rochette, P. Magnetic susceptibility of the rock matrix related to magnetic fabric studies. J. Struct. Geol. 1987, 9, 1015–1020. [Google Scholar] [CrossRef]
- Rochette, P.; Vialon, P. Development of planar and linear fabrics in Dauphinois shales and slates (French Alps) studied by magnetic anisotropy and its mineralogical control. J. Struct. Geol. 1984, 6, 33–38. [Google Scholar] [CrossRef]
- Hrouda, F.; Chadima, M.; Jezek, J.; Pokorny, J. Anisotropy of out-of-phase magnetic susceptibility of rocks as a tool for direct determination of magnetic subfabrics of some minerals: An introductory study. Geophys. J. Int. 2016, 208, 385–402. [Google Scholar] [CrossRef]
- Jackson, M.; Tauxe, L. Anisotropy of magnetic susceptibility and remanence: Developments in the characterization of tectonic, sedimentary, and igneous fabric. Rev. Geophys. 1991, 29, 371–376. [Google Scholar] [CrossRef]
- Jelinek, V. The Statistical Theory of Measuring Anisotropy of Magnetic Susceptibility of Rocks and Its Application; Geofyzika: Brno, Czech Republic, 1977. [Google Scholar]
- Flanders, P.J.; Remeika, J.P. Magnetic properties of hematite single crystals. Philos. Mag. 1965, 11, 1271–1288. [Google Scholar] [CrossRef]
- Jelinek, V. Characterization of the magnetic fabric of rocks. Tectonophysics 1981, 79, T63–T67. [Google Scholar] [CrossRef]
- Jelinek, V. On a mixed quadratic invariant of the magnetic susceptibility tensor. J. Geophys. 1984, 56, 58–60. [Google Scholar]
- Neumann, F.E. Vorlesungen über die Theorie der Elastizität der Festen Körper und des Lichtäthers; B.G. Teubner Verlag: Leipzig, Germany, 1885. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Clarendon Press: Oxford, UK, 1957; 322p. [Google Scholar]
- Jelinek, V. Measuring Anisotropy of Magnetic Susceptibility on a Slowly Spinning Specimen—Basic Theory; AGICO Print No. 10; AGICO: Brno, Czech Republic, 1996. [Google Scholar]
- Schmidt, V.; Hirt, A.M.; Rosselli, P.; Martín-Hernández, F. Separation of diamagnetic and paramagnetic anisotropy by high-field, low-temperature torque measurements. Geophys. J. Int. 2007, 168, 40–47. [Google Scholar] [CrossRef]
- Jackson, M.J. Anisotropy of magnetic remanence: A brief review of mineralogical sources, physical origins, and geological applications, and comparison with susceptibility anisotropy. Pure Appl. Geophys. 1991, 136, 1–28. [Google Scholar] [CrossRef]
- Potter, D.K. A comparison of anisotropy of magnetic remanence methods—A user’s guide for application to paleomagnetism and magnetic fabric studies. In Magnetic Fabrics: Methods and Applications; Martín-Hernández, F., Lüneburg, C.M., Aubourg, C., Jackson, M., Eds.; The Geological Society: London, UK, 2004; Volume 238, pp. 21–35. [Google Scholar]
- Fleet, M.E. Micas, 2nd ed.; The Geological Society: London, UK, 2003; 758p. [Google Scholar]
- Deer, W.A.; Howie, R.A.; Zussman, J. Layered Silicates Excluding Micas and Clay Minerals, 2nd ed.; The Geological Society: London, UK, 2009; Volume 3B. [Google Scholar]
- Deer, W.A.; Howie, R.A.; Zussman, J. Orthosilicates, 2nd ed.; The Geological Society: London, UK, 1997; 919p. [Google Scholar]
- Haerinck, T.; Debacker, T.N.; Sintubin, M. Magnetic anisotropy in chloritoid. J. Geophys. Res. Solid Earth 2013, 118, 3886–3898. [Google Scholar] [CrossRef]
- Ballet, O.; Fuess, H.; Fritzsche, T. Magnetic structure and cation distribution in (Fe,Mn)2SiO4 (olivine) by neutron diffraction. Phys. Chem. Miner. 1987, 15, 54–58. [Google Scholar] [CrossRef]
- Ferré, E.C.; Tikoff, B.; Jackson, M. Corrigendum to “the magnetic anisotropy of mantle peridotites: Example from the Twin Sisters dunite, Washington” [tectonophysics 398 (2005) 141–166]. Tectonophysics 2005, 405, 233. [Google Scholar] [CrossRef]
- Deer, W.A.; Howie, R.A.; Zussman, J. Single-Chain Silicates; Longman Group Ltd.: London, UK, 1978; Volume 2A, 668p. [Google Scholar]
- Deer, W.A.; Howie, R.A.; Zussman, J. Double-Chain Silicates, 2nd ed.; The Geological Society: London, UK, 1997; 764p. [Google Scholar]
- Povarennykh, A.S. On the magnetic properties of minerals. In Aspects of Theoretical Mineralogy in the U.S.S.R.—A Collection of Papers; Battey, M.H., Tomkeieff, S.I., Eds.; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Biedermann, A.R.; Pettke, T.; Angel, R.J.; Hirt, A.M. Anisotropy of magnetic susceptibility in alkali feldspar and plagioclase. Geophys. J. Int. 2016, 205, 479–489. [Google Scholar] [CrossRef]
- Rochette, P. Inverse magnetic fabric in carbonate-bearing rocks. Earth Planet. Sci. Lett. 1988, 90, 229–237. [Google Scholar] [CrossRef]
- Foex, M.G. Recherches sur le paramagnétisme. Ann. Physiq. 1921, 16, 174–305. [Google Scholar] [CrossRef]
- Krishnan, K.S.; Banerjee, S. Magnetic studies on rhodochrosite, MnCO3. Z. Krist. 1938, 99, 499–508. [Google Scholar] [CrossRef]
- Rochette, P.; Aubourg, C.; Perrin, M. Is this magnetic fabric normal? A review and case studies in volcanic formations. Tectonophysics 1999, 307, 219–234. [Google Scholar] [CrossRef]
- De Wall, H. The field dependence of ac susceptibility in titanomagnetites: Implications for the anisotropy of magnetic susceptibility. Geophys. Res. Lett. 2000, 27, 2409–2411. [Google Scholar] [CrossRef]
- Jackson, M.; Moskowitz, B.; Rosenbaum, J.; Kissel, C. Field-dependence of ac susceptibility in titanomagnetites. Earth Planet. Sci. Lett. 1998, 157, 129–139. [Google Scholar] [CrossRef]
- Fuller, M.D. Magnetic anisotropy and paleomagnetism. J. Geophys. Res. 1963, 68, 293–309. [Google Scholar] [CrossRef]
- Robinson, P.; Heidelbach, F.; Hirt, A.M.; McEnroe, S.A.; Brown, L.L. Crystallographic-magnetic correlations in single-crystal haemo-ilmenite: New evidence for lamellar magnetism. Geophys. J. Int. 2006, 165, 17–31. [Google Scholar] [CrossRef][Green Version]
- Hrouda, F.; Siemes, H.; Herres, N.; Hennig-Michaeli, C. The relationship between the magnetic anisotropy and the c-axis fabric in a massive hematite ore. J. Geophys. 1985, 56, 174–182. [Google Scholar]
- Flanders, P.J.; Schuele, W.J. Anisotropy in the basal plane of hematite single crystals. Philos. Mag. 1964, 9, 485–490. [Google Scholar] [CrossRef]
- Worm, H.-U. Magnetic stability of oceanic gabbros from ODP hole 735B. Earth Planet. Sci. Lett. 2001, 193, 287–302. [Google Scholar] [CrossRef]
- Mainprice, D.; Humbert, M. Methods of calculating petrophysical properties from lattice preferred orientation data. Surv. Geophys. 1994, 15, 575–592. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biedermann, A.R. Magnetic Anisotropy in Single Crystals: A Review. Geosciences 2018, 8, 302. https://doi.org/10.3390/geosciences8080302
Biedermann AR. Magnetic Anisotropy in Single Crystals: A Review. Geosciences. 2018; 8(8):302. https://doi.org/10.3390/geosciences8080302
Chicago/Turabian StyleBiedermann, Andrea R. 2018. "Magnetic Anisotropy in Single Crystals: A Review" Geosciences 8, no. 8: 302. https://doi.org/10.3390/geosciences8080302
APA StyleBiedermann, A. R. (2018). Magnetic Anisotropy in Single Crystals: A Review. Geosciences, 8(8), 302. https://doi.org/10.3390/geosciences8080302




