Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site
Abstract
:1. Introduction
2. Study Area: The Euroseistest Site
3. Methods
4. Results for Hard Rock Hazard
4.1. Rock Target Hazard
4.2. Host-to-Target Adjustments
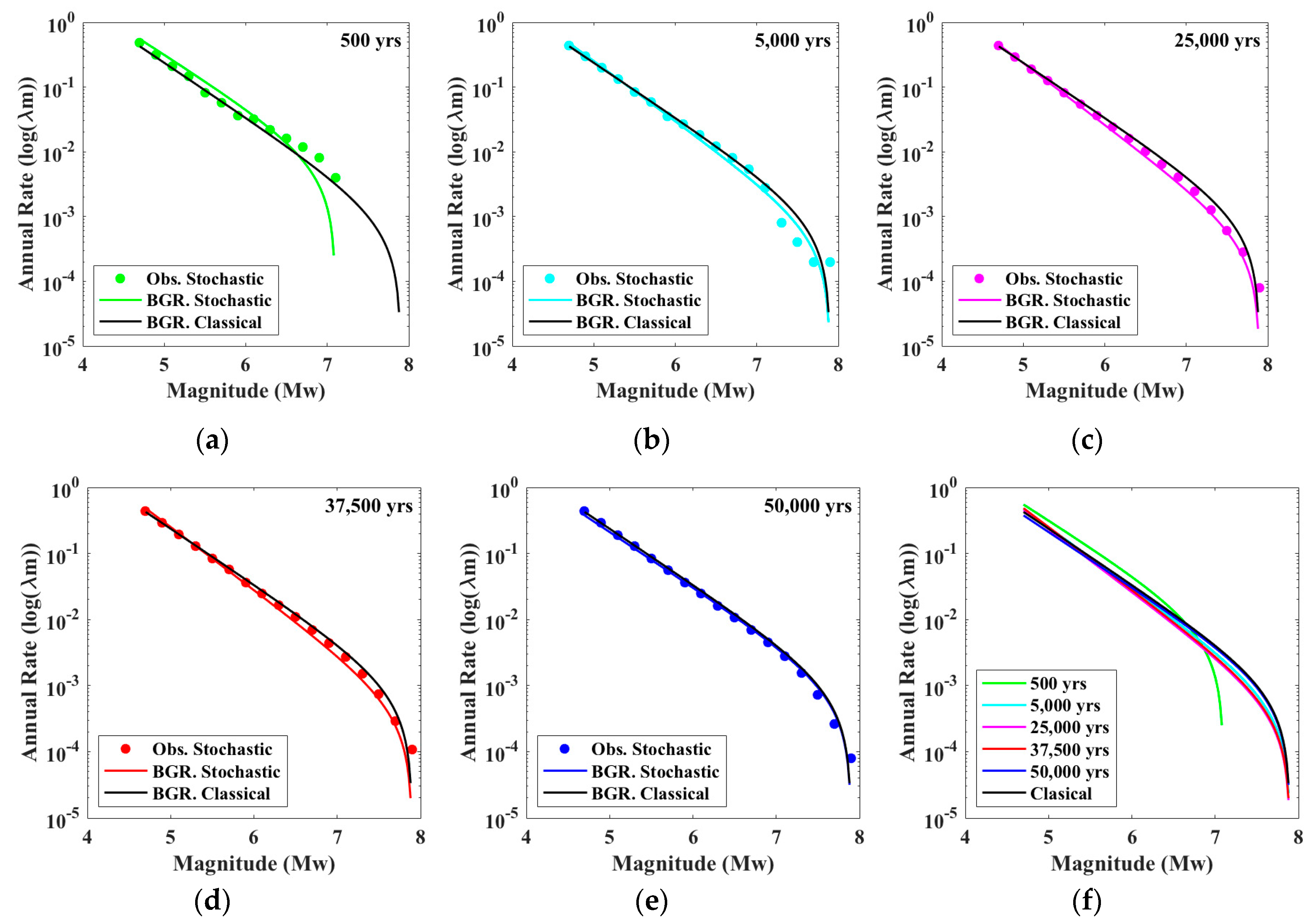
4.3. Synthetic Earthquake Catalog
4.4. Synthetic Time Histories on Rock
5. Results for Soft Soil Hazard
5.1. Synthetic Time Histories on Soil
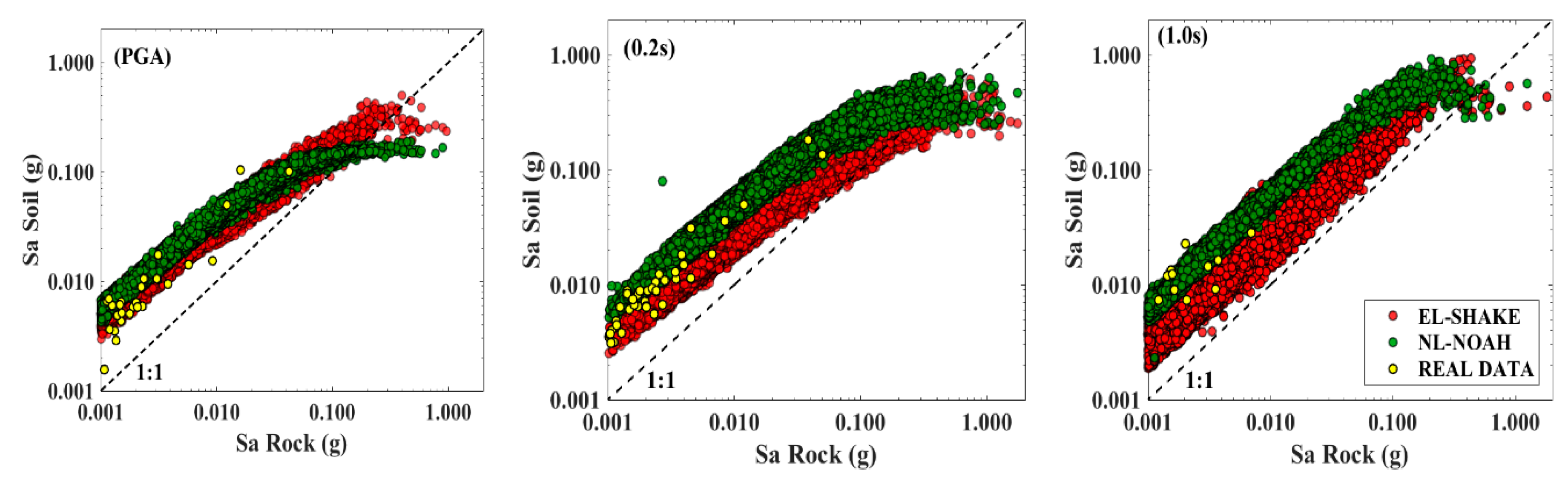
5.1.1. Focus on Nonlinear Ground Motion Saturation
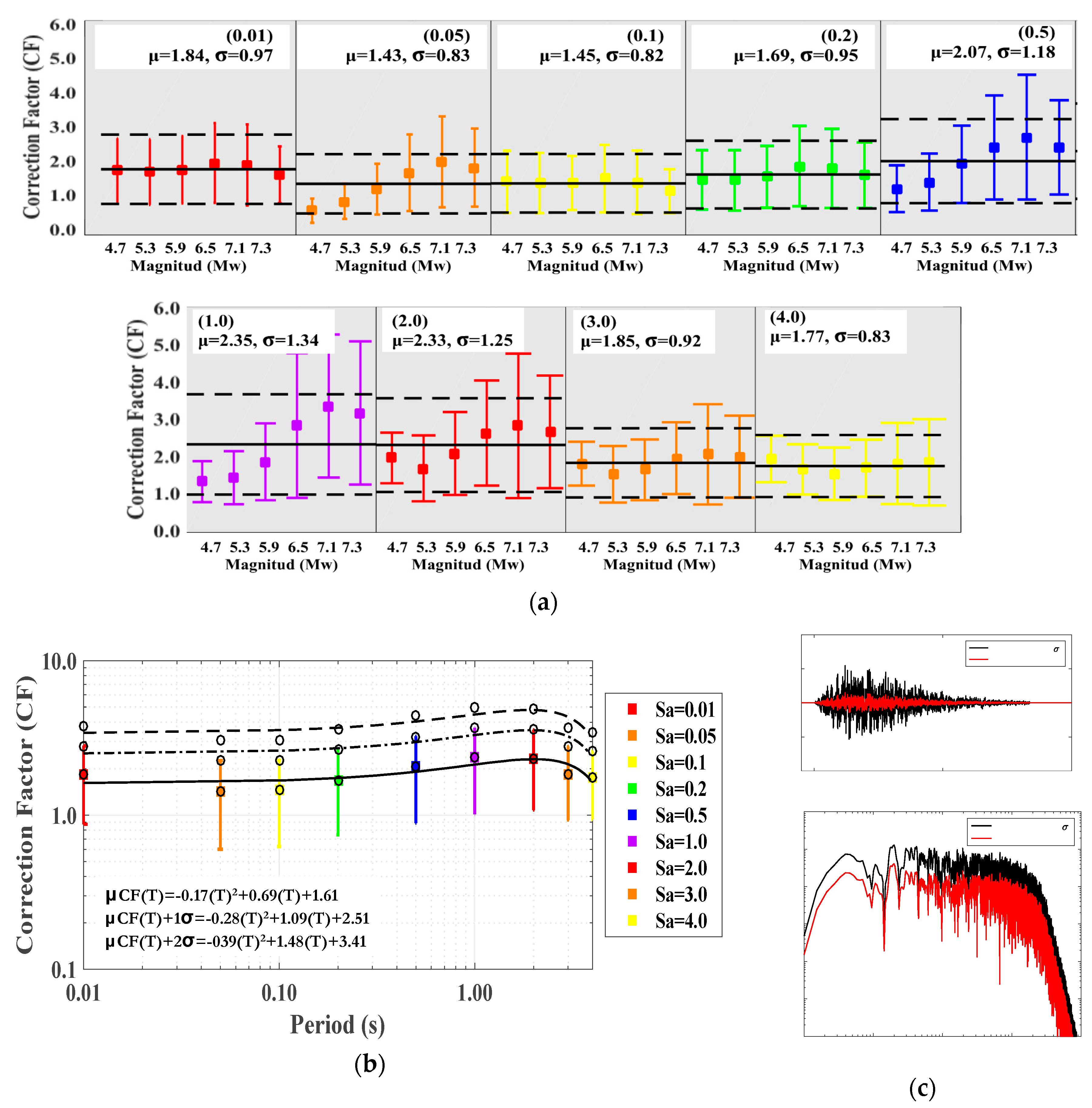
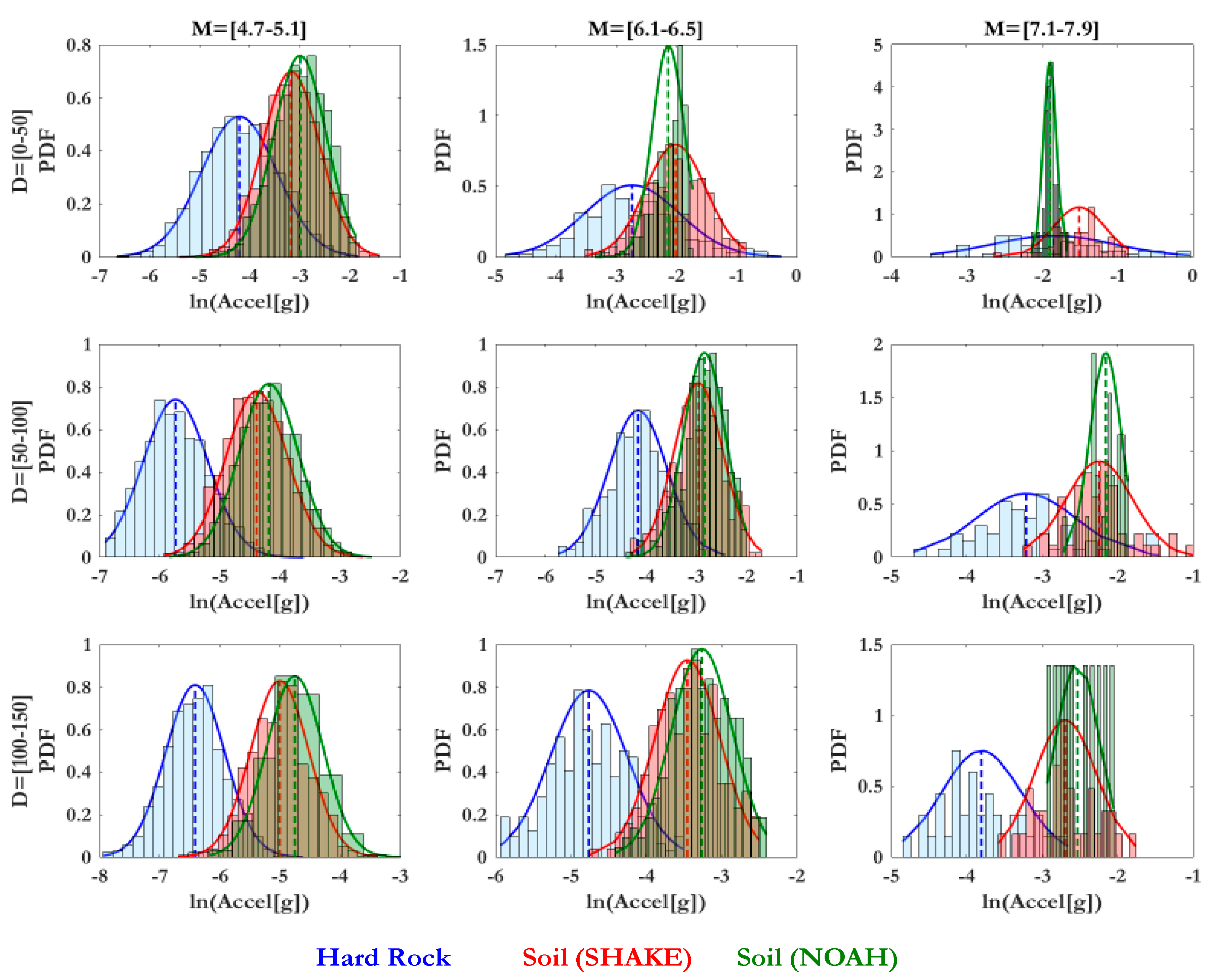
5.1.2. Ground Motion Variability
5.2. Full Probabilistic Stochastic Method (SM)
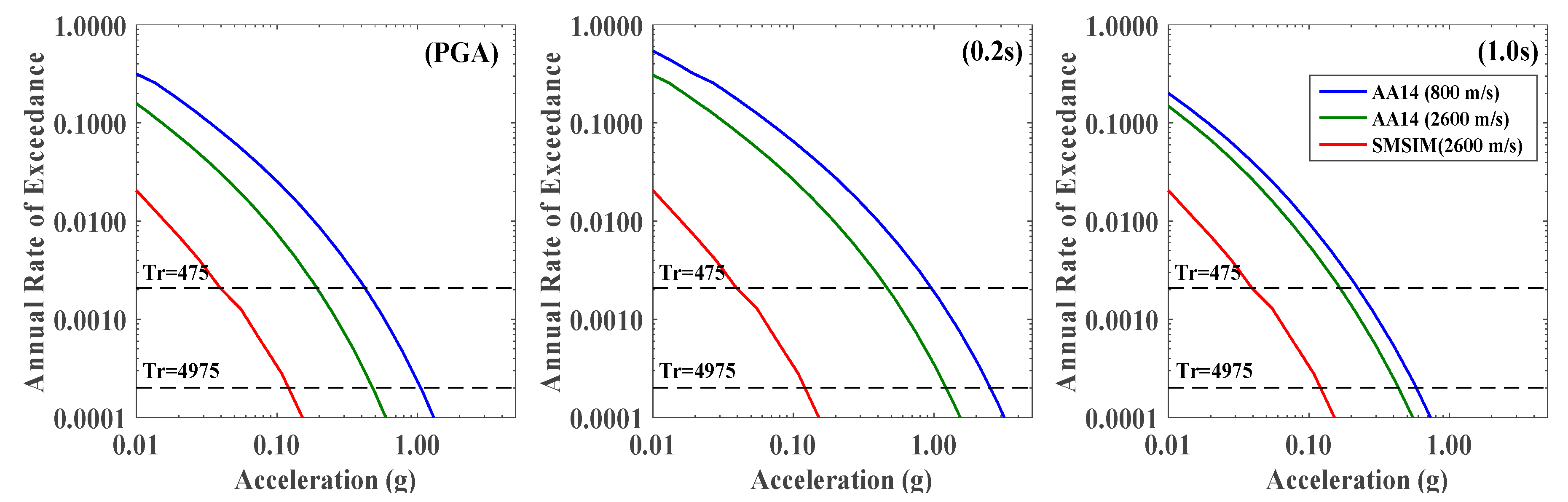
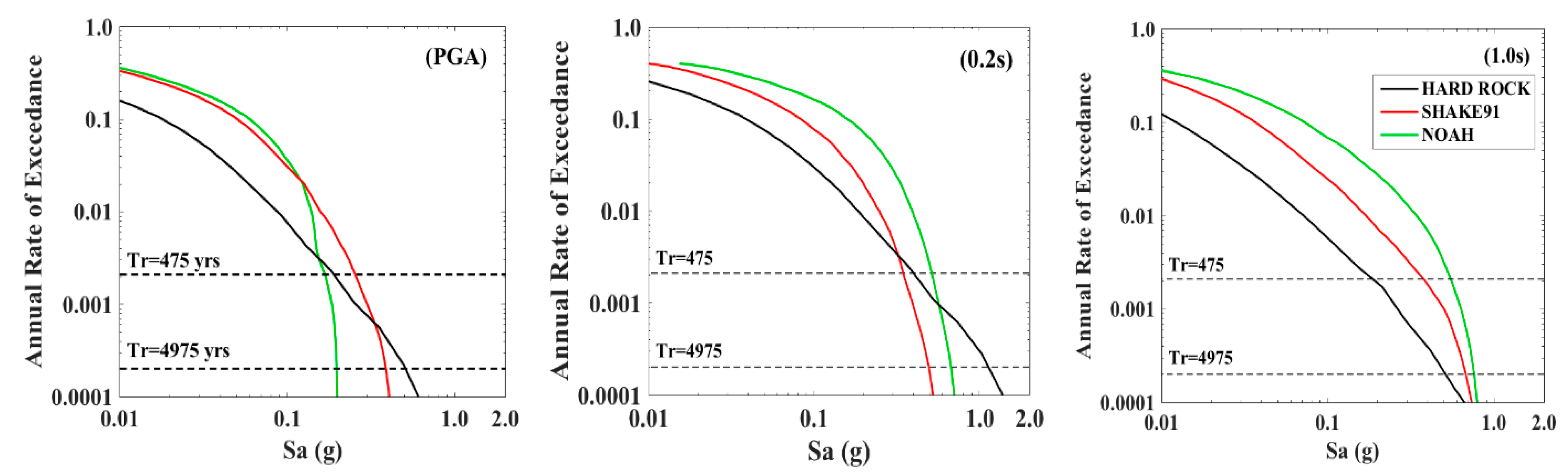
5.2.1. SM Results for Hard Rock
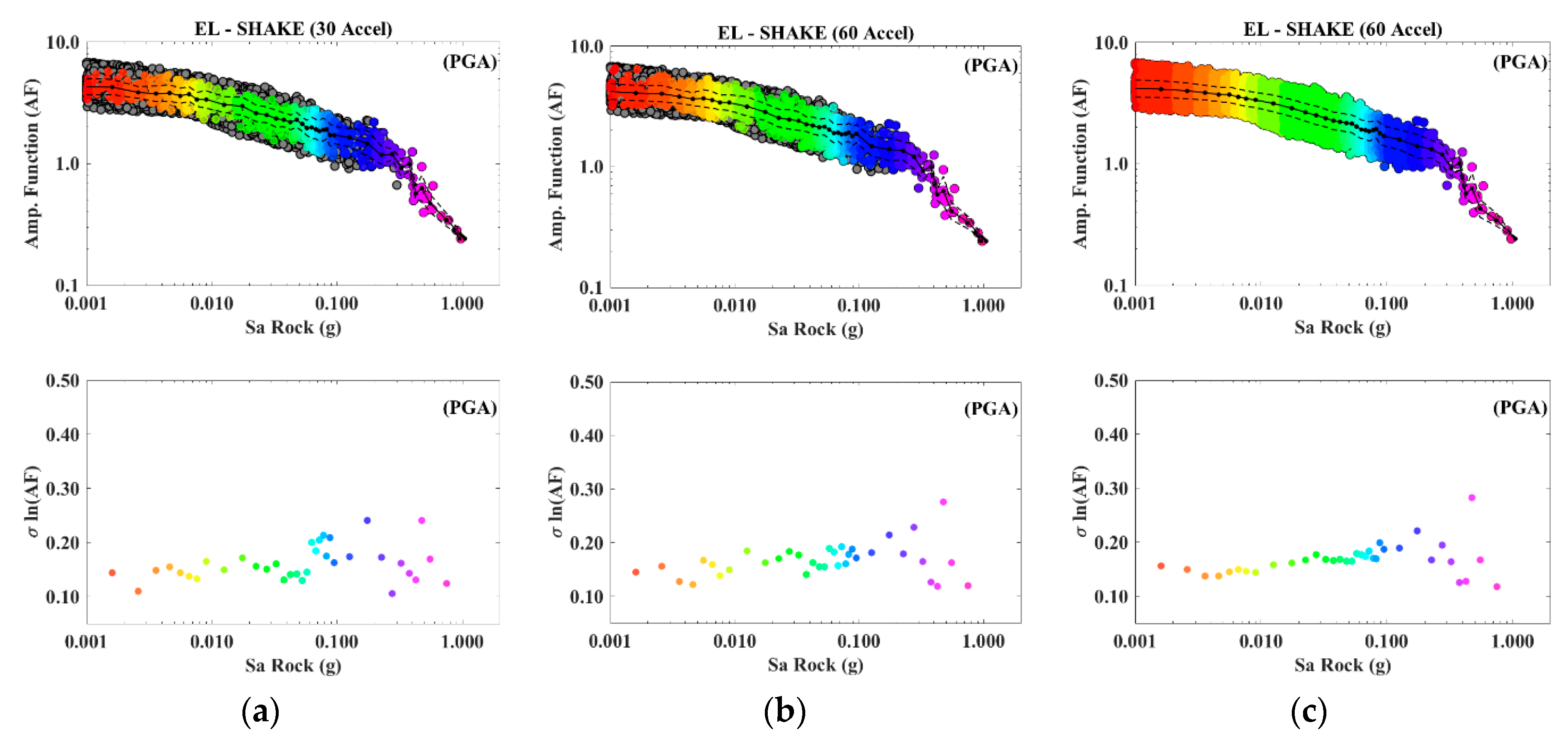
5.2.2. SM Results for Soft Soil Using SHAKE91
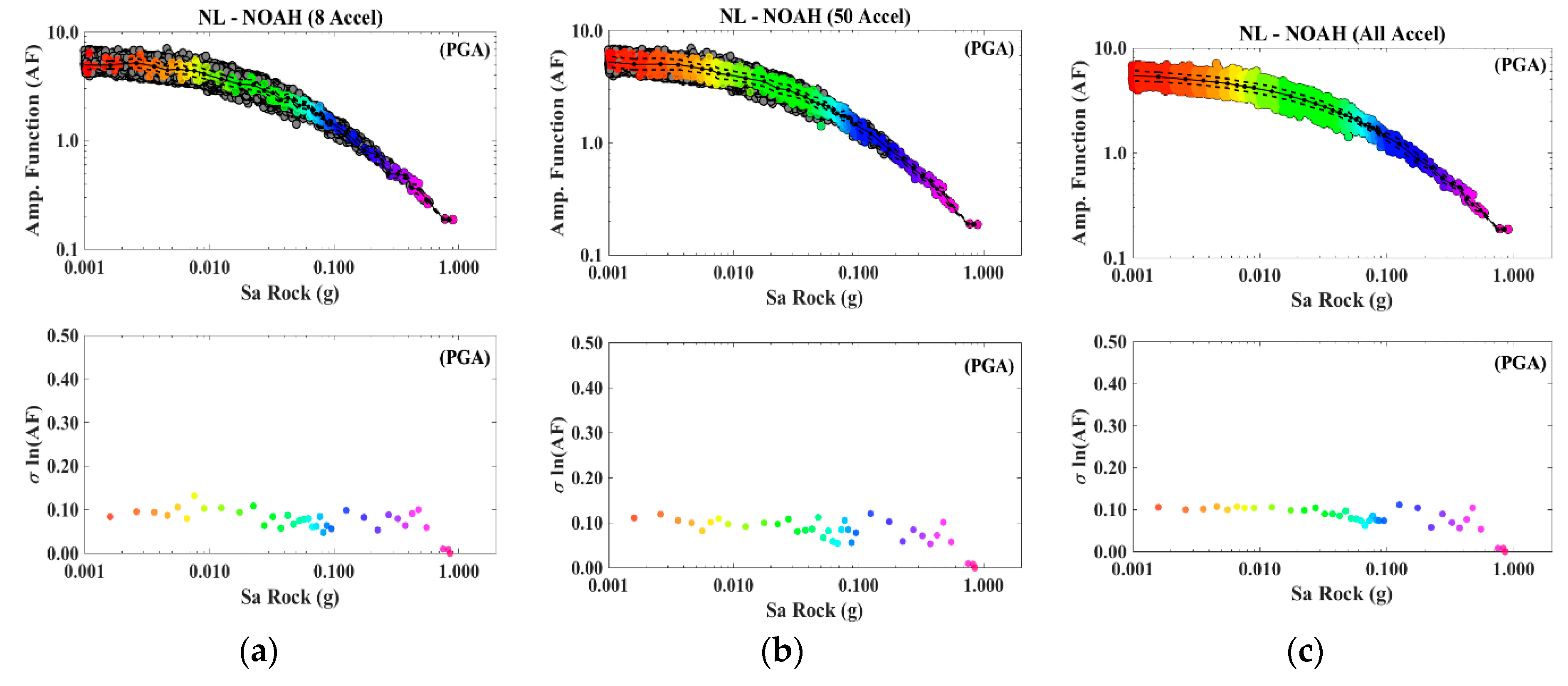
5.2.3. SM Results for Soft Soil Using NOAH
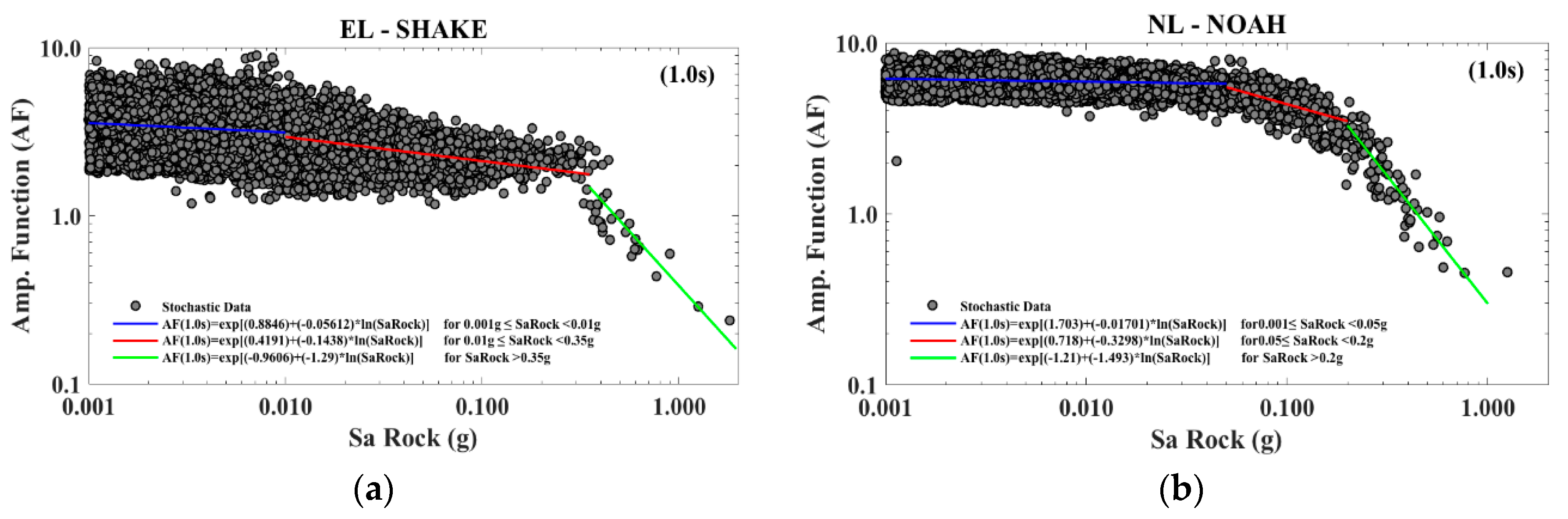
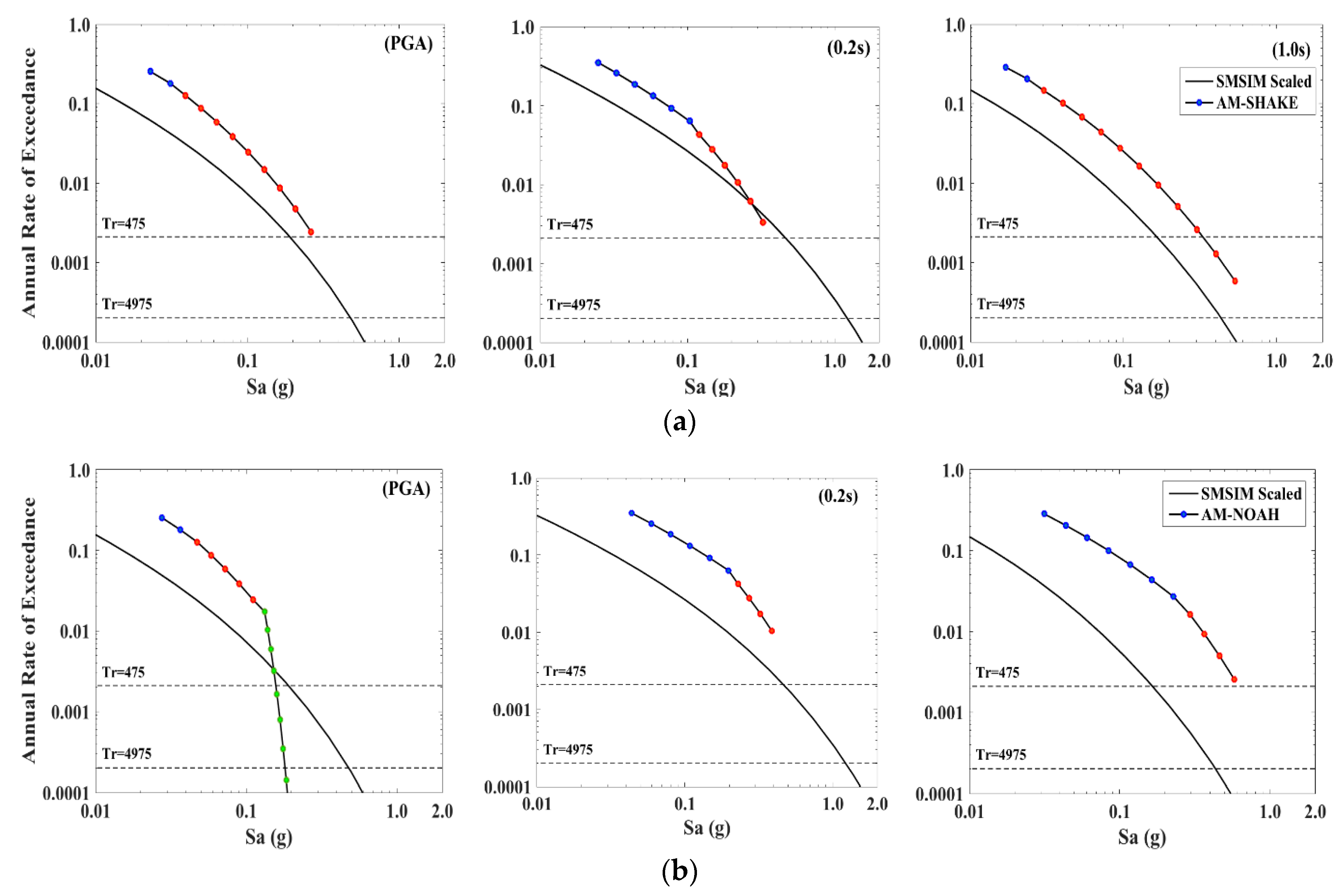
5.3. Analytical Approximation of the Full Convolution Method (AM)
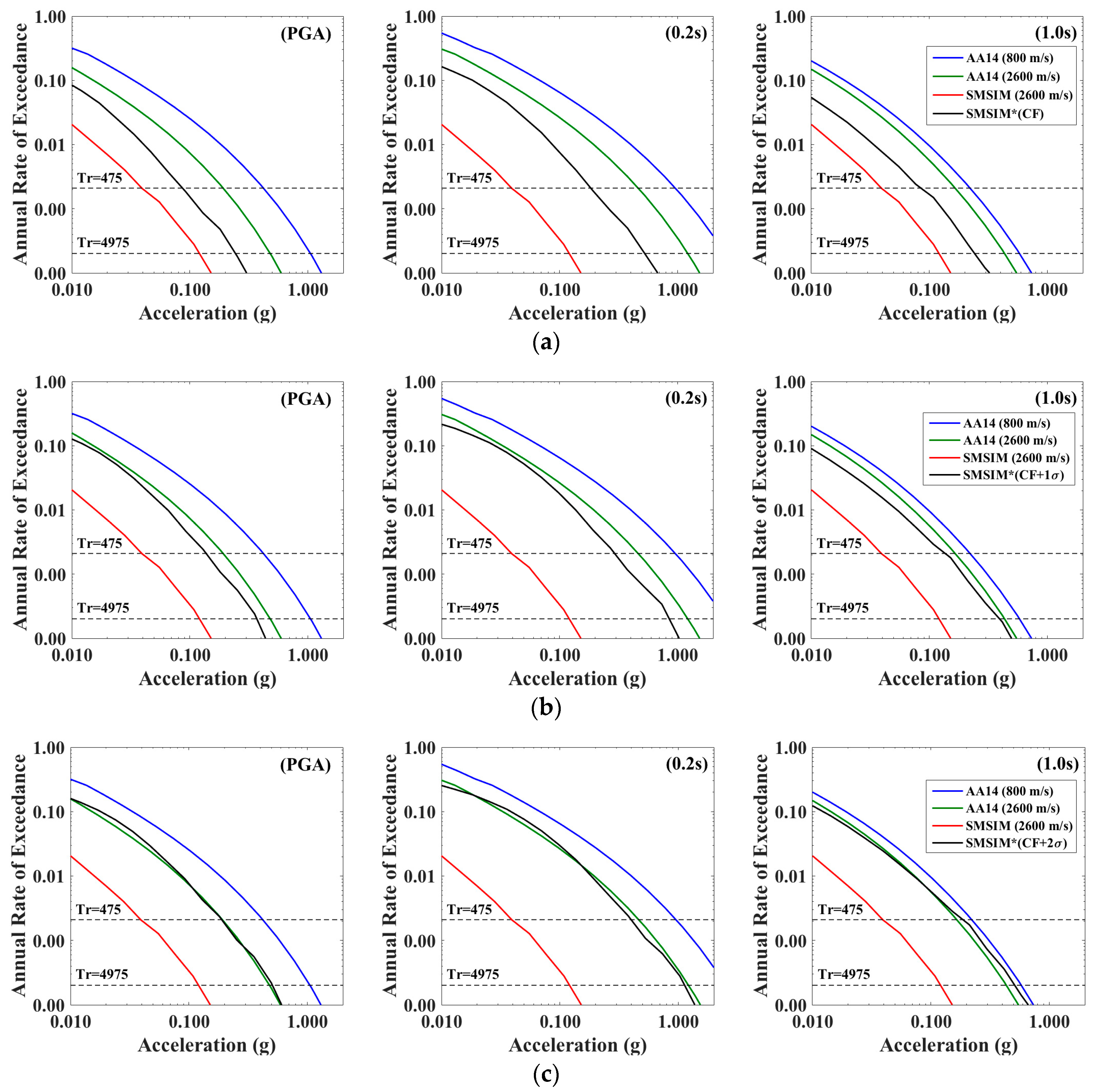
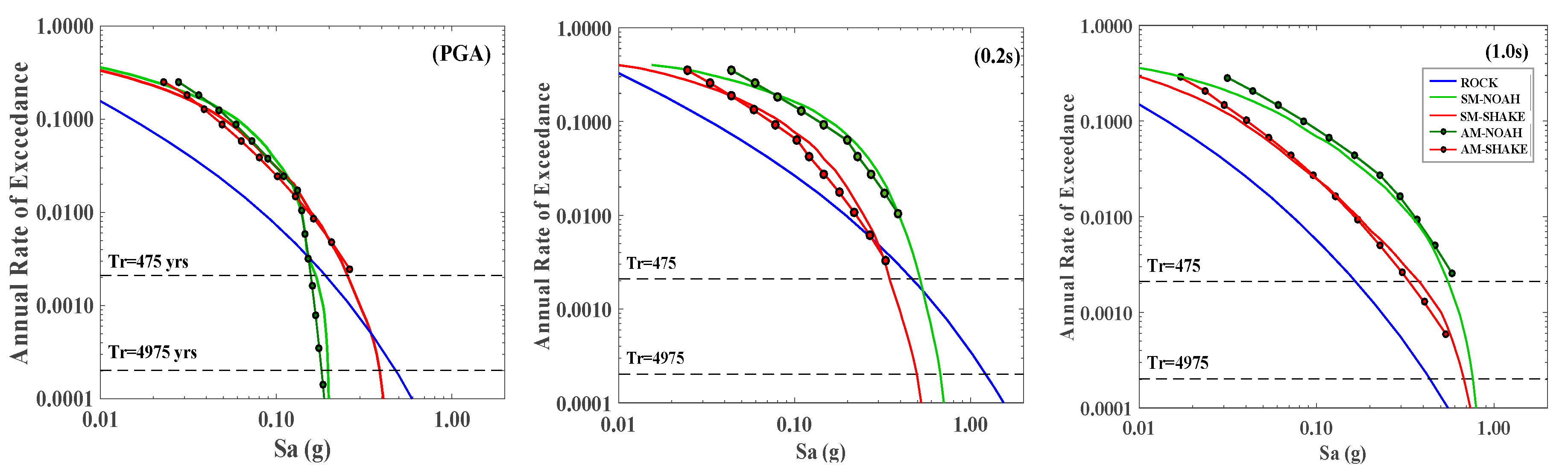
5.4. Robustness of the Prediction
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: New York, NY, USA, 1996. [Google Scholar]
- Bazzurro, P. Probabilistic Seismic Damage Analysis. Ph.D. Thesis, Stanford University, Stanford, CA, USA, August 1998. [Google Scholar]
- Bazzurro, P.; Cornell, C.A.; Shome, N.; Carballo, J.E. Three proposals for characterizing MDOF nonlinear seismic response. J. Struct. Eng. 1998, 124, 1281–1289. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Vector-valued probabilistic seismic hazard analysis (VPSHA). In Proceedings of the 7th US National Conference on Earthquake Engineering, Boston, MA, USA, 21–25 July 2002; pp. 21–25. [Google Scholar]
- Lee, R.; Silva, W.J.; Cornell, C.A. Alternatives in evaluating soil-and rock-site seismic hazard. Seismol. Res. Lett. 1998, 69, 81. [Google Scholar]
- Lee, R.C. A Methodology to Integrate Site Response into Probabilistic Seismic Hazard Analysis; Site Geotechnical Services: Savannah, GA, USA, 2000. [Google Scholar]
- Tsai, C.C.P. Probabilistic seismic hazard analysis considering nonlinear site effect. Bull. Seismol. Soc. Am. 2000, 90, 66–72. [Google Scholar] [CrossRef]
- Cramer, C.H. Site-specific seismic-hazard analysis that is completely probabilistic. Bull. Seismol. Soc. Am. 2003, 93, 1841–1846. [Google Scholar] [CrossRef]
- Cramer, C.H. Erratum: Site-Specific Seismic-Hazard Analysis that is Completely Probabilistic. Bull. Seismol. Soc. Am. 2005, 95, 2026. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Ground-motion amplification in nonlinear soil sites with uncertain properties. Bull. Seismol. Soc. Am. 2004, 94, 2090–2109. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, C.A. Nonlinear soil-site effects in probabilistic seismic-hazard analysis. Bull. Seismol. Soc. Am. 2004, 94, 2110–2123. [Google Scholar] [CrossRef]
- Papaspiliou, M.; Kontoe, S.; Bommer, J.J. An exploration of incorporating site response into PSHA—Part I: Issues related to site response analysis methods. Soil Dyn. Earthq. Eng. 2012, 42, 302–315. [Google Scholar] [CrossRef]
- Papaspiliou, M.; Kontoe, S.; Bommer, J.J. An exploration of incorporating site response into PSHA—Part II: Sensitivity of hazard estimates to site response approaches. Soil Dyn. Earthq. Eng. 2012, 42, 316–330. [Google Scholar] [CrossRef]
- Aristizábal, C.; Bard, P.Y.; Beauval, C. Site-specific PSHA: Combined effects of single station sigma, host-o-target adjustments and non-linear behavior. In Proceedings of the World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Aristizábal, C. Integration of Site Effects into Probabilistic Seismic Hazard Methods. Ph.D. Thesis, Université Grenoble Alpes, Grenoble, France, 2018. [Google Scholar]
- Campbell, K.W. Prediction of strong ground motion using the hybrid empirical method and its use in the development of ground-motion (attenuation) relations in eastern North America. Bull. Seismol. Soc. Am. 2003, 93, 1012–1033. [Google Scholar] [CrossRef]
- Pitilakis, K.; Roumelioti, Z.; Raptakis, D.; Manakou, M.; Liakakis, K.; Anastasiadis, A.; Pitilakis, D. The EUROSEISTEST Strong-Motion Database and Web Portal. Seismol. Res. Lett. 2013, 84, 796–804. [Google Scholar] [CrossRef]
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European seismic hazard model: Key components and results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar]
- Liotier, Y. Modelisation des Ondes de Volume des Seismes de L’arc Ageen; DEA de l’Universite Joseph Fourier: Grenoble, France, 1989. [Google Scholar]
- Carver, D.; Bollinger, G.A. Aftershocks of the June 20, 1978, Greece earthquake: A multimode faulting sequence. Tectonophysics 1981, 73, 343–363. [Google Scholar] [CrossRef]
- Mountrakis, D.; Psilovikos, A.; Papazachos, B. The geotectonic regime of the 1978 Thessaloniki earthquakes. In The Thessaloniki, Northern Greece, Earthquake of June 20, 1978 and Its Seismic Sequence; Papazachos, B.C., Carydis, P.G., Eds.; Technical Chamber of Greece: Thessaloniki, Greece, 1983; pp. 11–27. [Google Scholar]
- Jongmans, D.; Pitilakis, K.; Demanet, D.; Raptakis, D.; Riepl, J.; Horrent, C.; Tsokas, G.; Lontzetidis, K.; Bard, P.Y. EURO-SEISTEST: Determination of the geological structure of the Volvi basin and validation of the basin response. Bull. Seismol. Soc. Am. 1998, 88, 473–487. [Google Scholar]
- Raptakis, D.; Chávez-Garcıa, F.J.; Makra, K.; Pitilakis, K. Site effects at Euroseistest—I. Determination of the valley structure and confrontation of observations with 1D analysis. Soil Dyn. Earthq. Eng. 2000, 19, 1–22. [Google Scholar] [CrossRef]
- Chávez-Garcıa, F.J.; Raptakis, D.; Makra, K.; Pitilakis, K. Site effects at Euroseistest—II. Results from 2D numerical modeling and comparison with observations. Soil Dyn. Earthq. Eng. 2000, 19, 23–39. [Google Scholar] [CrossRef]
- Manakou, M.V.; Raptakis, D.G.; Chávez-García, F.J.; Apostolidis, P.I.; Pitilakis, K.D. 3D soil structure of the Mygdonian basin for site response analysis. Soil Dyn. Earthq. Eng. 2010, 30, 1198–1211. [Google Scholar] [CrossRef]
- Pitilakis, K.; Raptakis, D.; Lontzetidis, K.; Tika-Vassilikou, T.; Jongmans, D. Geotechnical and Geophysical Description of Euro-Seistest, Using Field, Laboratory Tests and Moderate Strong Motion Recordings. J. Earthq. Eng. 1999, 3, 381–409. [Google Scholar] [CrossRef]
- Riepl, J.; Bard, P.Y.; Hatzfeld, D.; Papaioannou, C.; Nechtschein, S. Detailed evaluation of site-response estimation methods across and along the sedimentary valley of Volvi (EURO-SEISTEST). Bull. Seismol. Soc. Am. 1998, 88, 488–502. [Google Scholar]
- Maufroy, E.; Chaljub, E.; Hollender, F.; Kristek, J.; Moczo, P.; Klin, P.; Priolo, E.; Iwaki, A.; Iwata, T.; Etienne, V.; et al. Earthquake ground motion in the Mygdonian basin, Greece: The E2VP verification and validation of 3D numerical simulation up to 4 Hz. Bull. Seismol. Soc. Am. 2015, 105, 1398–1418. [Google Scholar] [CrossRef]
- Maufroy, E.; Chaljub, E.; Hollender, F.; Bard, P.Y.; Kristek, J.; Moczo, P.; De Martin, F.; Theodoulidis, N.; Manakou, M.; Guyonnet-Benaize, C.; et al. 3D numerical simulation and ground motion prediction: Verification, validation and beyond—Lessons from the E2VP project. Soil Dyn. Earthq. Eng. 2016, 91, 53–71. [Google Scholar]
- Maufroy, E.; Chaljub, E.; Theodoulidis, N.P.; Roumelioti, Z.; Hollender, F.; Bard, P.Y.; De Martin, F.; Guyonnet-Benaize, C.; Margerin, L. Source-Related Variability of Site Response in the Mygdonian Basin (Greece) from Accelerometric Recordings and 3D Numerical Simulations. Bull. Seismol. Soc. Am. 2017, 107, 787–808. [Google Scholar] [CrossRef]
- Cotton, F.; Scherbaum, F.; Bommer, J.J.; Bungum, H. Criteria for selecting and adjusting ground-motion models for specific target regions: Application to central Europe and rock sites. J. Seismol. 2006, 10, 137–156. [Google Scholar]
- Van Houtte, C.; Drouet, S.; Cotton, F. Analysis of the origins of κ (kappa) to compute hard rock to rock adjustment factors for GMPEs. Bull. Seismol. Soc. Am. 2011, 101, 2926–2941. [Google Scholar] [CrossRef]
- Delavaud, E.; Scherbaum, F.; Kuehn, N.; Allen, T. Testing the global applicability of ground-motion prediction equations for active shallow crustal regions. Bull. Seismol. Soc. Am. 2012, 102, 707–721. [Google Scholar] [CrossRef]
- Biro, Y.; Renault, P. Importance and impact of host-to-target conversions for ground motion prediction equations in PSHA. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Anderson, J.G.; Hough, S.E. A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies. Bull. Seismol. Soc. Am. 1984, 74, 1969–1993. [Google Scholar]
- Akkar, S.; Sandıkkaya, M.A.; Bommer, J.J. Empirical ground-motion models for point-and extended-source crustal earthquake scenarios in Europe and the Middle East. Bull. Earthq. Eng. 2014, 12, 359–387. [Google Scholar]
- Laurendeau, A.; Bard, P.-Y.; Hollender, F.; Perron, V.; Foundotos, L.; Ktenidou, O.J.; Hernandez, B. Derivation of consistent hard rock (1000 <VS <3000 m/s) GMPEs from surface and down-hole recordings: Analysis of KiK-net data. Bull. Earthq. Eng. 2018, 16, 2253–2284. [Google Scholar]
- Bard, P.-Y.; Bora, S.S.; Hollender, F.; Laurendeau, A.; Traversa, P. Are the standard Vs30-kappa host-to-target adjustments the best way to get consistent hard-rock ground motion prediction? In Proceedings of the 2nd International Workshop on “Best Practices in Physics-Based Fault Rupture Models for Seismic Hazard Assessment of Nuclear Installations: Issues and challenges towards Full Seismic Risk Analysis”, Cadarache-Château, France, 14–16 May 2018.
- Pagani, M.; Monelli, D.; Weatherill, G.; Danciu, L.; Crowley, H.; Silva, V.; Henshaw, P.; Butler, L.; Nastasi, M.; Panzeri, L.; et al. OpenQuake engine: An open hazard (and risk) software for the global earthquake model. Seismol. Res. Lett. 2014, 85, 692–702. [Google Scholar] [CrossRef]
- Boore, D.M. Simulation of ground motion using the stochastic method. In Seismic Motion, Lithospheric Structures, Earthquake and Volcanic Sources; Birkhäuser: Basel, Switzerland, 2006; pp. 635–676. [Google Scholar]
- Boore, D.M. SMSIM: Fortran Programs for Simulating Ground Motions from Earthquakes; version 2.3; US Department of the Interior: Washington, DC, USA; US Geological Survey: Reston, VA, USA, 2005.
- Schnabel, P.B. SHAKE a Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; EERC Report; University of California: Berkeley, CA, USA, 1972. [Google Scholar]
- Idriss, I.M.; Sun, J.I. User’s Manual for SHAKE91: A Computer Program for conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits; Center for Geotechnical Modeling, Department of Civil and Environmental Engineering, University of California: Davis, CA, USA, 1993. [Google Scholar]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE-91: Equivalent Linear Seismic Response Analysis of Horizontally Layered Soil Deposits; The Earthquake Engineering Online Archive NISEE E-Library: Berkeley, CA, USA, 1993. [Google Scholar]
- Bonilla, L.F. NOAH: Users Manual; Institute for Crustal Studies, University of California: Santa Barbara, CA, USA, 2001. [Google Scholar]
- Régnier, J.; Bonilla, L.F.; Bard, P.Y.; Bertrand, E.; Hollender, F.; Kawase, H.; Sicilia, D.; Arduino, P.; Amorosi, A.; Asimaki, D.; et al. International benchmark on numerical simulations for 1D, non-linear site response (PRENOLIN): Verification phase based on canonical cases. Bull. Seismol. Soc. Am. 2016, 106, 2112–2135. [Google Scholar] [CrossRef]
- Régnier, J.; Bonilla, L.F.; Bard, P.Y.; Bertrand, E.; Hollender, F.; Kawase, H.; Sicilia, D.; Arduino, P.; Amorosi, A.; Asimaki, D.; et al. PRENOLIN: International Benchmark on 1D Nonlinear Site-Response Analysis—Validation Phase Exercise. Bull. Seismol. Soc. Am. 2018, 108, 876–900. [Google Scholar] [CrossRef]
- Global Earthquake Model. The OpenQuake-Engine User Manual; Technical Report; GEM: Pavia, Italy, 2017. [Google Scholar]
- Ktenidou, O.J.; Abrahamson, N.A. Empirical estimation of high-frequency ground motion on hard rock. Seismol. Res. Lett. 2016, 87, 1465–1478. [Google Scholar] [CrossRef]
- Kottke, A.R. VS30-k0 relationship implied by ground motion models? In Proceedings of the 16th World Conference on Earthquake Engineering, Santiago, Chile, 9–13 January 2017.
- Al Atik, L.; Kottke, A.; Abrahamson, N.; Hollenback, J. Kappa (κ) scaling of ground-motion prediction equations using an inverse random vibration theory approach. Bull. Seismol. Soc. Am. 2014, 104, 336–346. [Google Scholar] [CrossRef]
- Okada, Y.; Kasahara, K.; Hori, S.; Obara, K.; Sekiguchi, S.; Fujiwara, H.; Yamamoto, A. Recent progress of seismic observation networks in Japan—Hi-net, F-net, K-NET and KiK-net—. Earth Planets Space 2004, 56, 15–28. [Google Scholar] [CrossRef]
- Ktenidou, O.J.; Abrahamson, N.A.; Drouet, S.; Cotton, F. Understanding the physics of kappa (κ): Insights from a downhole array. Geophys. J. Int. 2015, 203, 678–691. [Google Scholar]
- Atkinson, G.M.; Boore, D.M. Ground-motion relations for eastern North America. Bull. Seismol. Soc. Am. 1995, 85, 17–30. [Google Scholar]
- Zandieh, A.; Pezeshk, S.; Campbell, K.W. An Equivalent Point-Source Stochastic Simulation of the NGA-West2 Ground-Motion Prediction Equations. Bull. Seismol. Soc. Am. 2018, 108, 815–835. [Google Scholar] [CrossRef]
- Silva, W.J.; Lee, R.; McGuire, R.K.; Cornell, C.A. A comparison of methodologies to achieve a site-specific PSHA. Seismol. Res. Lett. 2000, 71, 247. [Google Scholar]
- Abrahamson, N.A.; Sykora, D. Variations of ground motions across individual sites. In Proceedings of the DOE Natural Phenomena Hazards Mitigation Conference, Atlanta, GA, USA, 19–22 October 1993; pp. 192–198. [Google Scholar]
- Toro, G.R.; Abrahamson, N.A.; Schneider, J.F. Model of strong ground motions from earthquakes in central and eastern North America: Best estimates and uncertainties. Seismol. Res. Lett. 1997, 68, 41–57. [Google Scholar] [CrossRef]
- Al Atik, L.; Abrahamson, N. Nonlinear site response effects on the standard deviations of predicted ground motions. Bull. Seismol. Soc. Am. 2010, 100, 1288–1292. [Google Scholar] [CrossRef]
- Stafford, P.J.; Rodriguez-Marek, A.; Edwards, B.; Kruiver, P.P.; Bommer, J.J. Scenario Dependence of Linear Site-Effect Factors for Short-Period Response Spectral Ordinates. Bull. Seismol. Soc. Am. 2017, 107, 2859–2872. [Google Scholar]
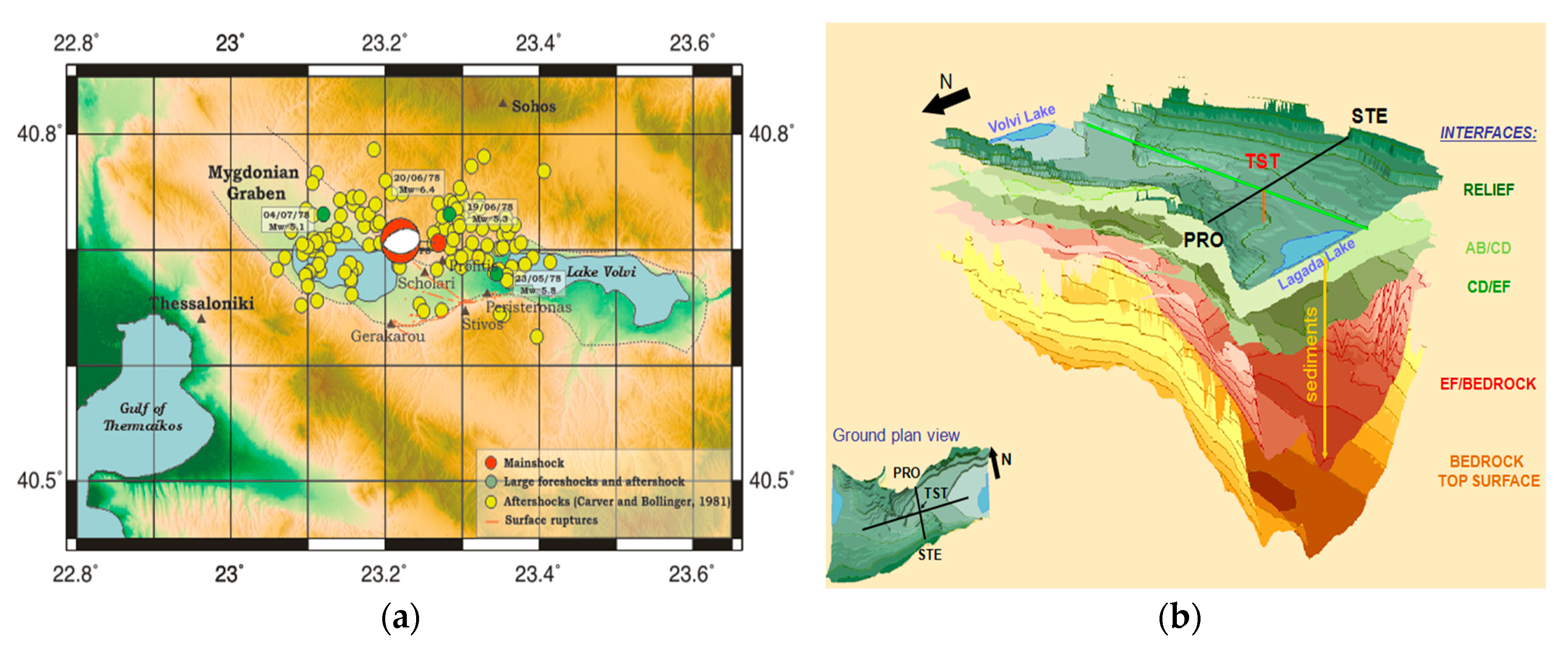
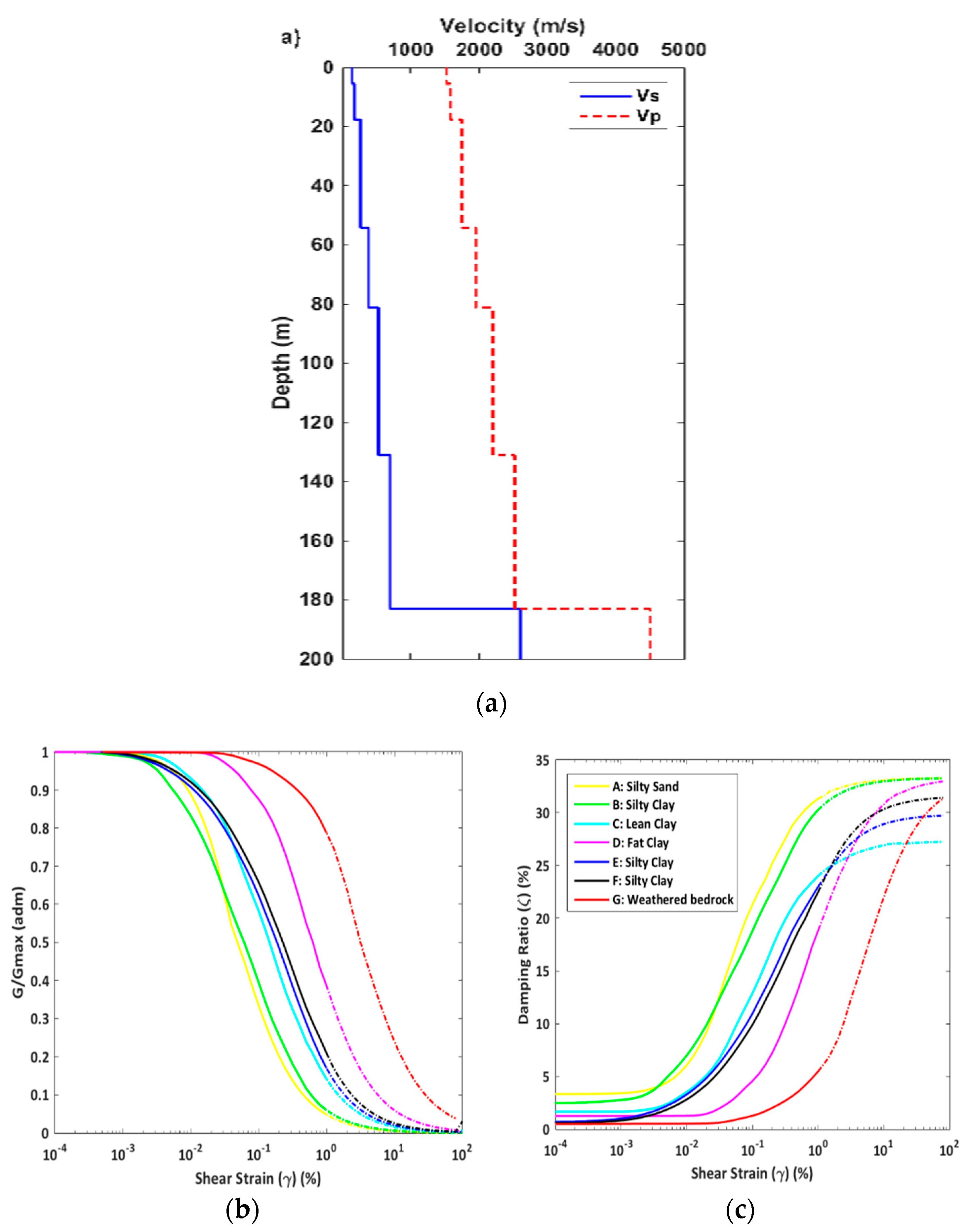
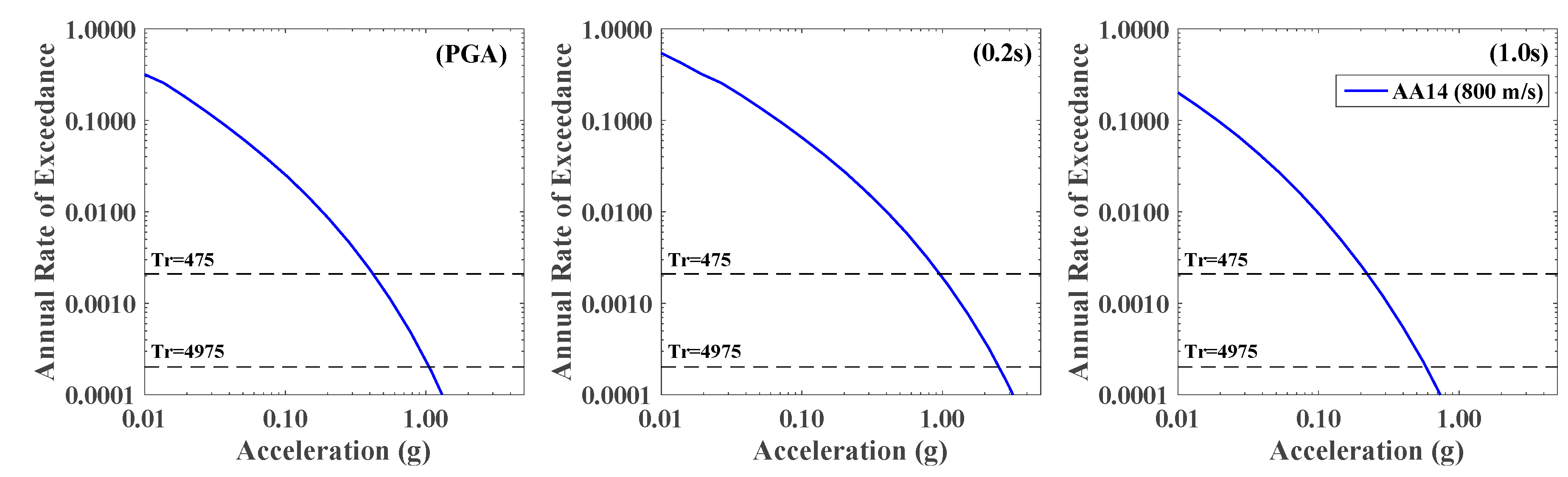
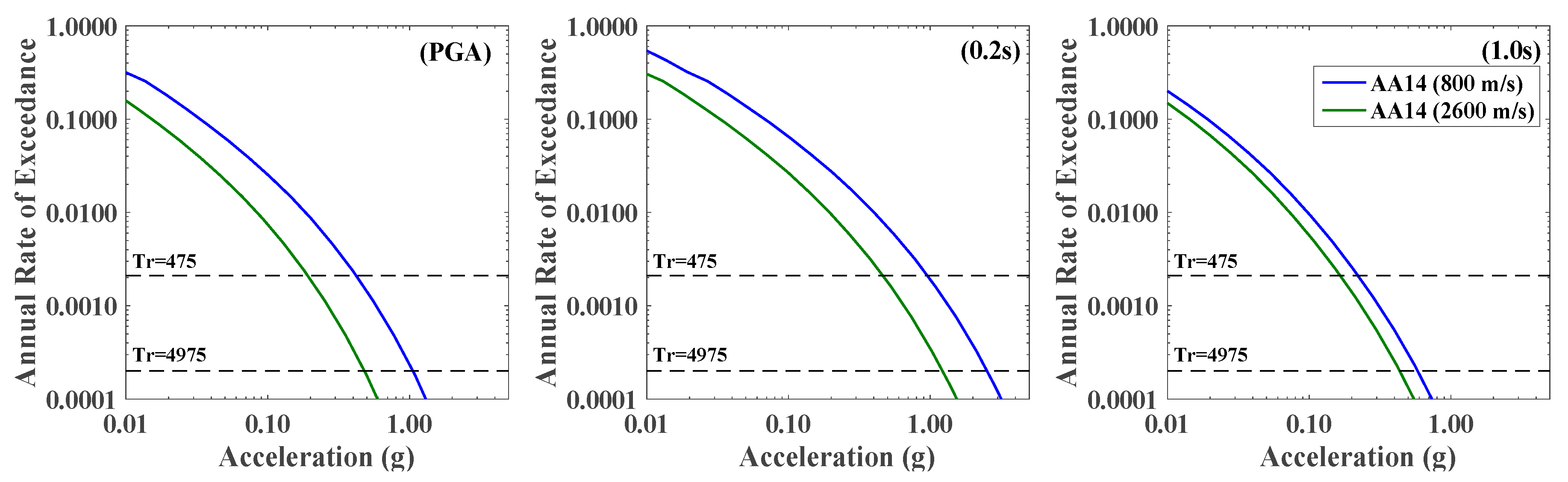

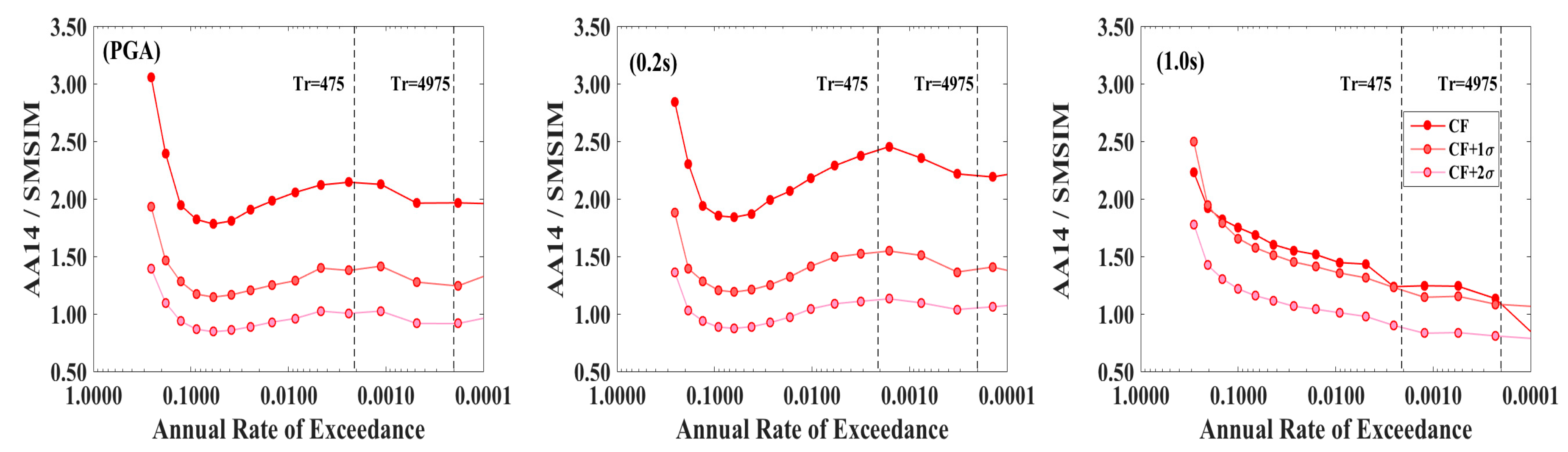
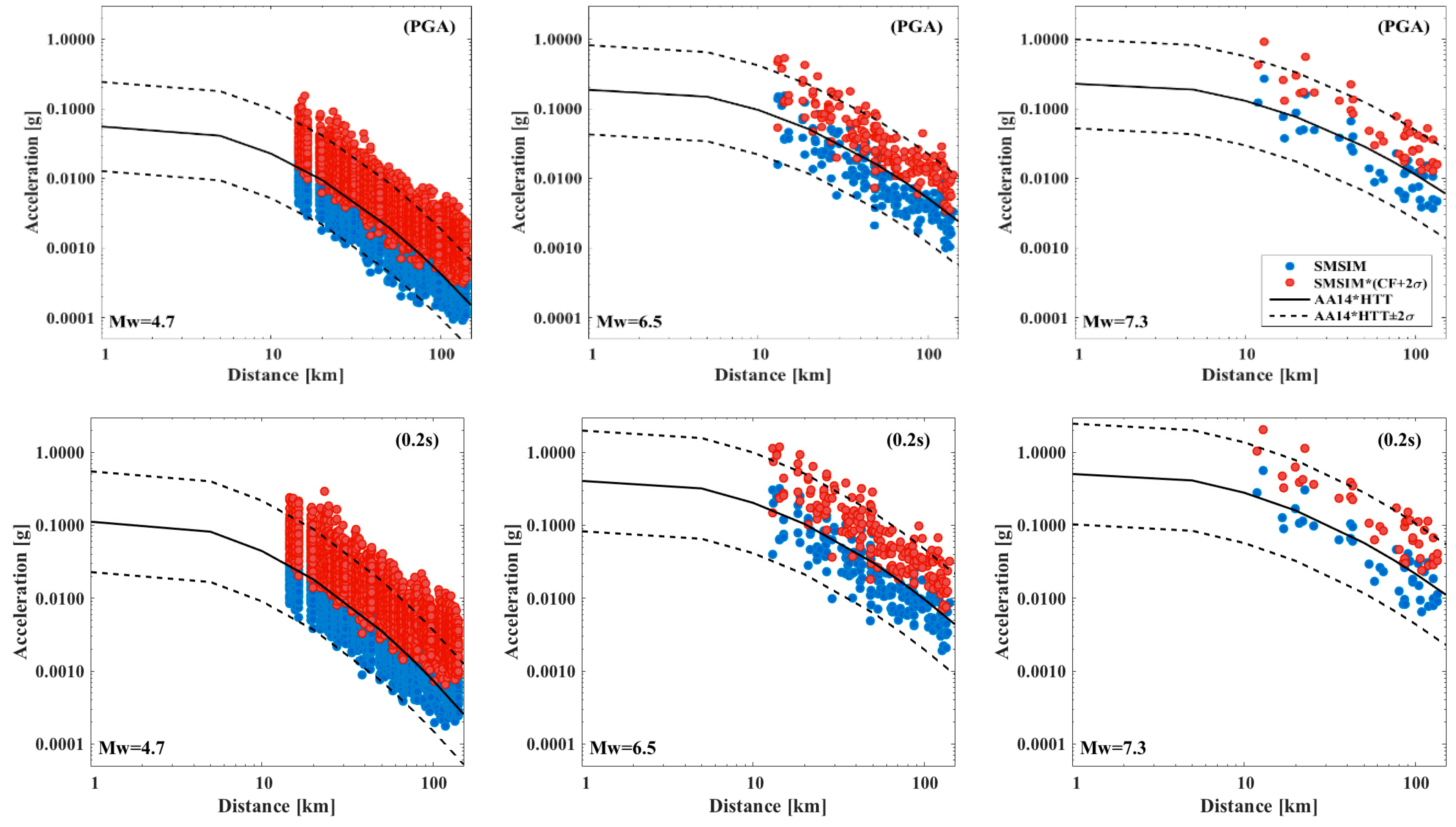
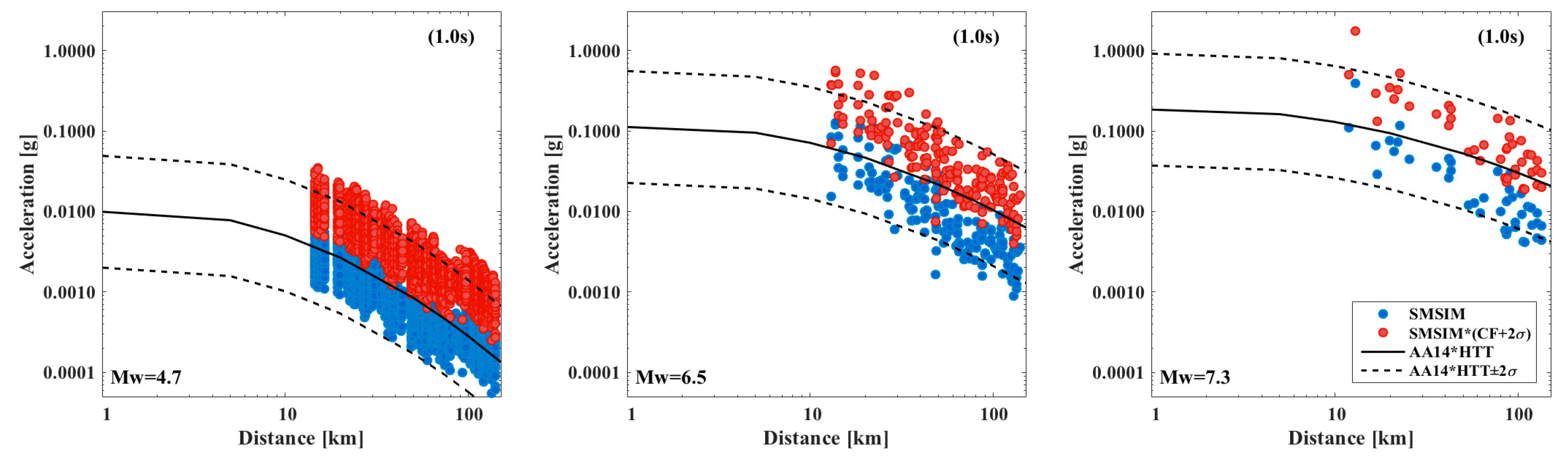
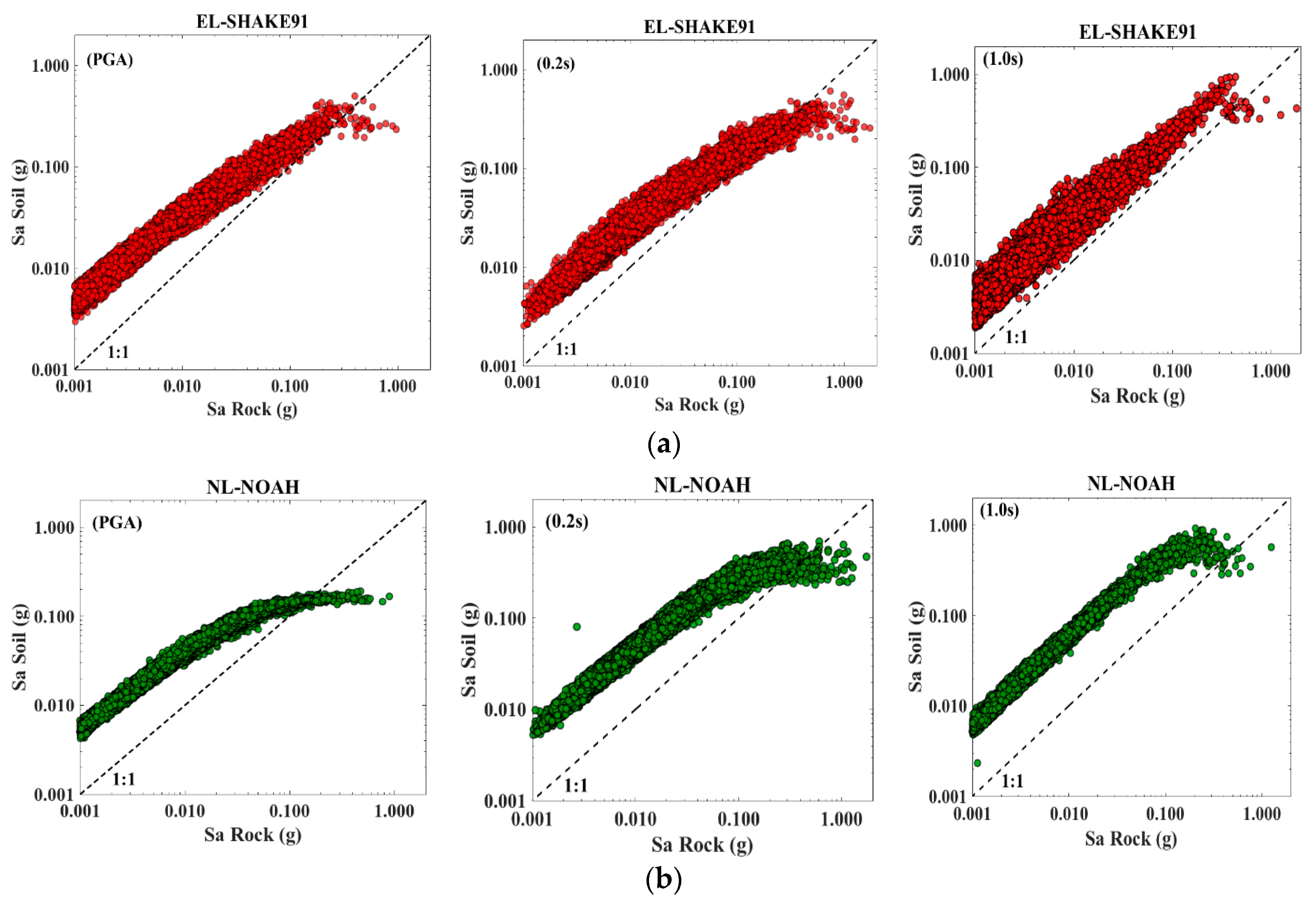


| Layer | Soil Type | Depth (m) | Vs (m/s) | Vp (m/s) | ρ (kg/m3) | Q | ϕ (°) | Ko (adm) |
|---|---|---|---|---|---|---|---|---|
| 1 | Silty Clay Sand | 0.0 | 144 | 1524 | 2077 | 14.4 | 47 | 0.26 |
| 2 | Silty Sand* | 5.5 | 177 | 1583 | 2083 | 17.7 | 19 | 0.67 |
| 3 | Lean Clay | 17.6 | 264 | 1741 | 2097 | 26.4 | 19 | 0.68 |
| 4 | Fat Clay | 54.2 | 388 | 1952 | 2117 | 38.8 | 27 | 0.54 |
| 5 | Silty Clay | 81.2 | 526 | 2200 | 2151 | 52.6 | 42 | 0.33 |
| 6 | Weathered Rock | 131.1 | 701 | 2520 | 2215 | 70.1 | 69 | 0.07 |
| 7 | Hard Rock | 183.0 | 2600 | 4500 | 2446 | - | - | - |
| Spectral Period (s) | PGA | 0.05 | 0.1 | 0.2 | 0.5 | 1.0 | 2.0 |
|---|---|---|---|---|---|---|---|
| HTT Adjustment Factors | 0.47 | 0.45 | 0.38 | 0.51 | 0.70 | 0.78 | 0.86 |
| Spectral Period (s) | Piecewise-Linear Models | SHAKE91 | NOAH | ||||
|---|---|---|---|---|---|---|---|
| C0 | C1 | C0 | C1 | ||||
| PGA | PLM 1 (Blue) | 0.7487 | −0.1089 | 0.15 | 0.5585 | −0.1833 | 0.11 |
| PLM 2 (Red) | −0.1202 | −0.2906 | 0.19 | −0.2539 | −0.3649 | 0.08 | |
| PLM 3 (Green) | −1.3990 | −1.2140 | 0.19 | −1.6390 | −0.8594 | 0.08 | |
| (0.2) | PLM 1 (Blue) | 0.2855 | −0.1475 | 0.19 | 1.0730 | −0.1020 | 0.12 |
| PLM 2 (Red) | −0.5356 | −0.4043 | 0.18 | −0.0906 | −0.4789 | 0.13 | |
| PLM 3 (Green) | −1.1360 | −1.1970 | 0.27 | −0.9453 | −1.1172 | 0.35 | |
| (1.0) | PLM 1 (Blue) | 0.8846 | −0.0561 | 0.27 | 1.7030 | −0.0170 | 0.11 |
| PLM 2 (Red) | 0.4191 | −0.1438 | 0.14 | 0.7180 | −0.3298 | 0.22 | |
| PLM 3 (Green) | 0.9606 | −1.2900 | 0.08 | 2.2100 | −1.4930 | 0.26 | |
| Code | n, (PGA) | n, (0.2 s) | n, (1.0 s) |
|---|---|---|---|
| SHAKE91 | 30 | 60 | 50 |
| NOAH | 8 | 50 | 30 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aristizábal, C.; Bard, P.-Y.; Beauval, C.; Gómez, J.C. Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site. Geosciences 2018, 8, 285. https://doi.org/10.3390/geosciences8080285
Aristizábal C, Bard P-Y, Beauval C, Gómez JC. Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site. Geosciences. 2018; 8(8):285. https://doi.org/10.3390/geosciences8080285
Chicago/Turabian StyleAristizábal, Claudia, Pierre-Yves Bard, Céline Beauval, and Juan Camilo Gómez. 2018. "Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site" Geosciences 8, no. 8: 285. https://doi.org/10.3390/geosciences8080285
APA StyleAristizábal, C., Bard, P.-Y., Beauval, C., & Gómez, J. C. (2018). Integration of Site Effects into Probabilistic Seismic Hazard Assessment (PSHA): A Comparison between Two Fully Probabilistic Methods on the Euroseistest Site. Geosciences, 8(8), 285. https://doi.org/10.3390/geosciences8080285





