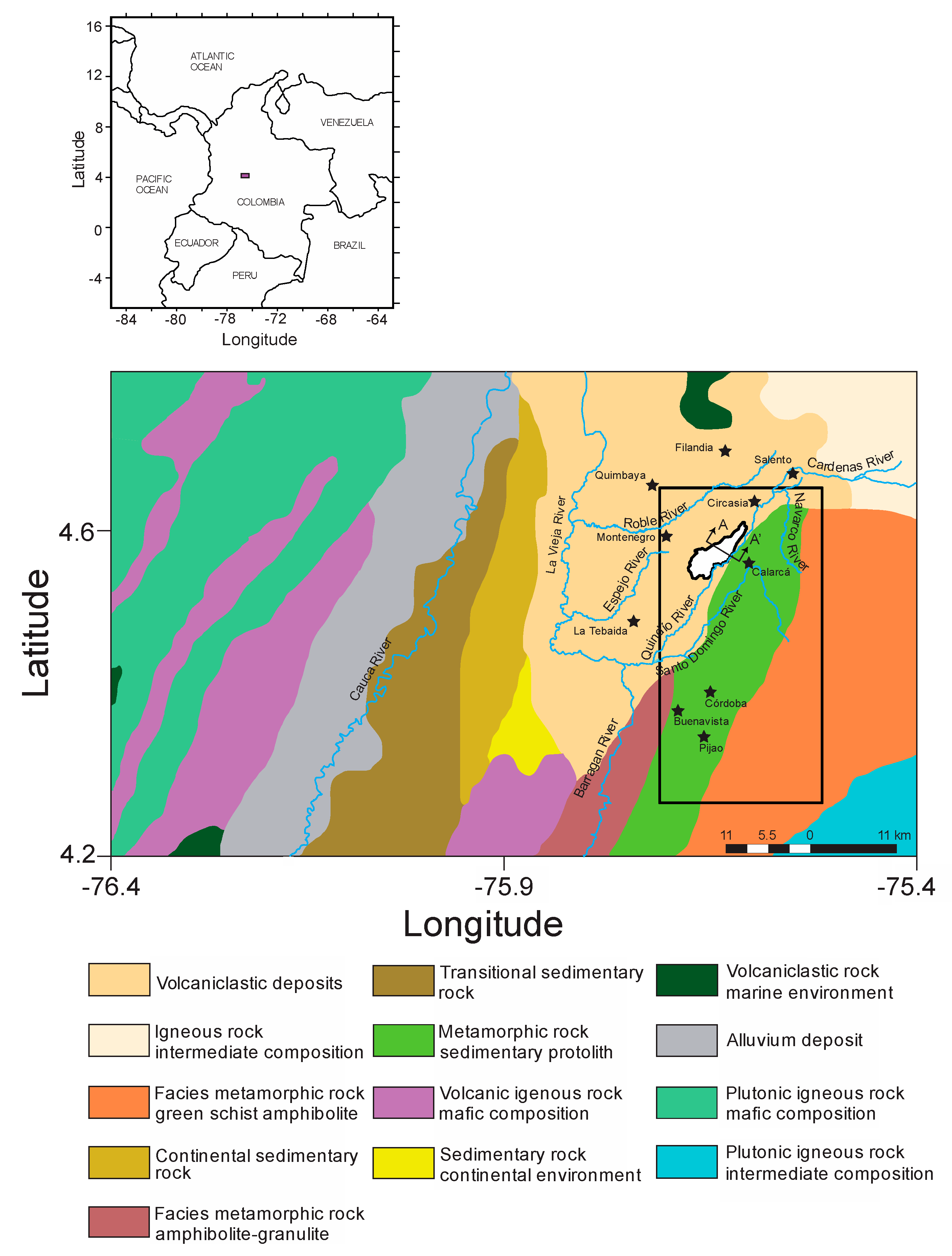
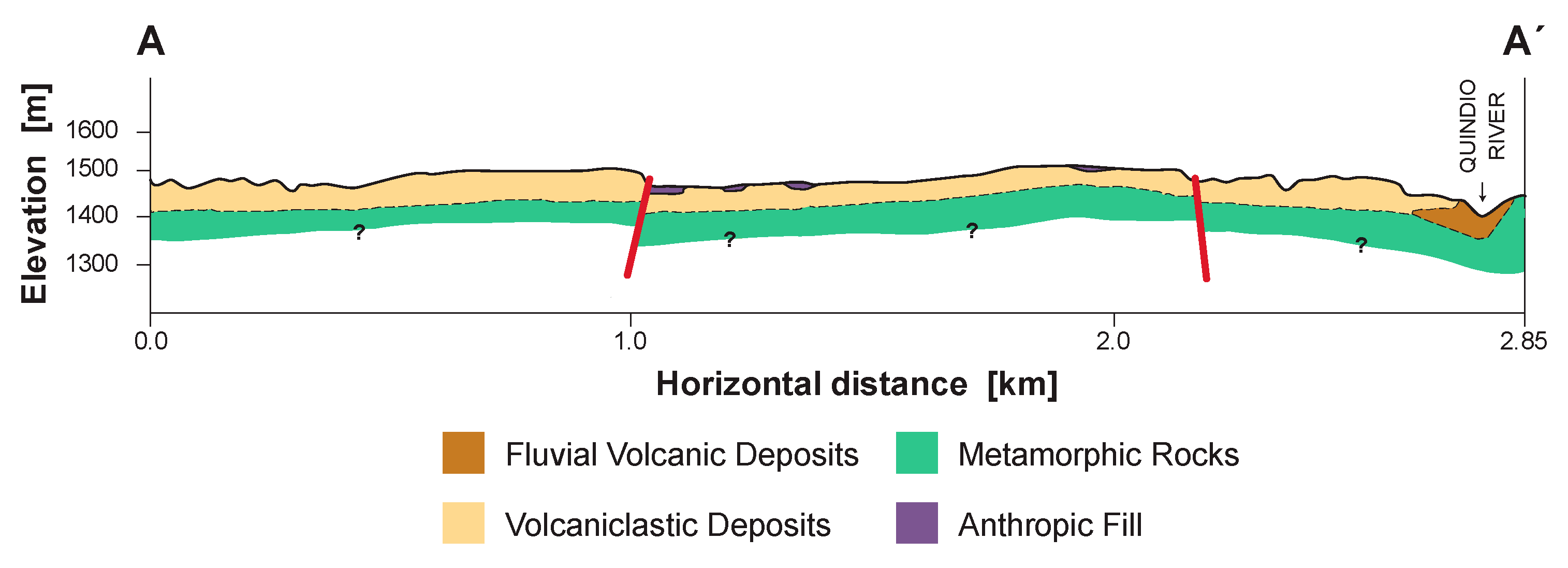
4. Results
Fourier amplitude spectra computed for our earthquake records were used to estimate amplification using SSR and HVSR. A time window of 20 s was used. For many events, this comprised the complete records (e.g.,
Figure 4). The traces had their average value removed, as well as any possible linear trend in the record. A Hanning taper over 5% of the window duration was applied at each end. Fourier amplitude spectra were smoothed using the window proposed in [
22], with a b-parameter of 40.
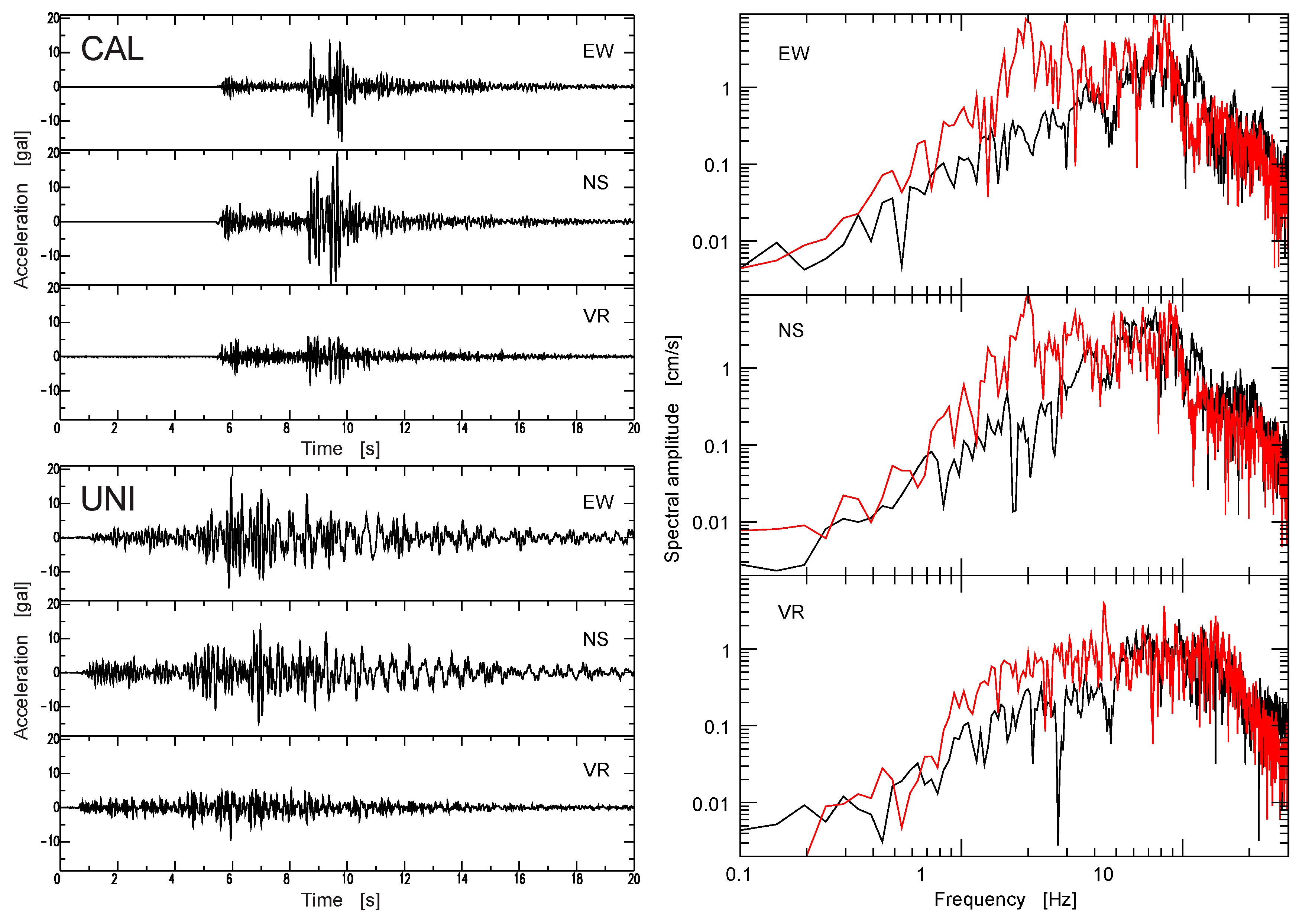
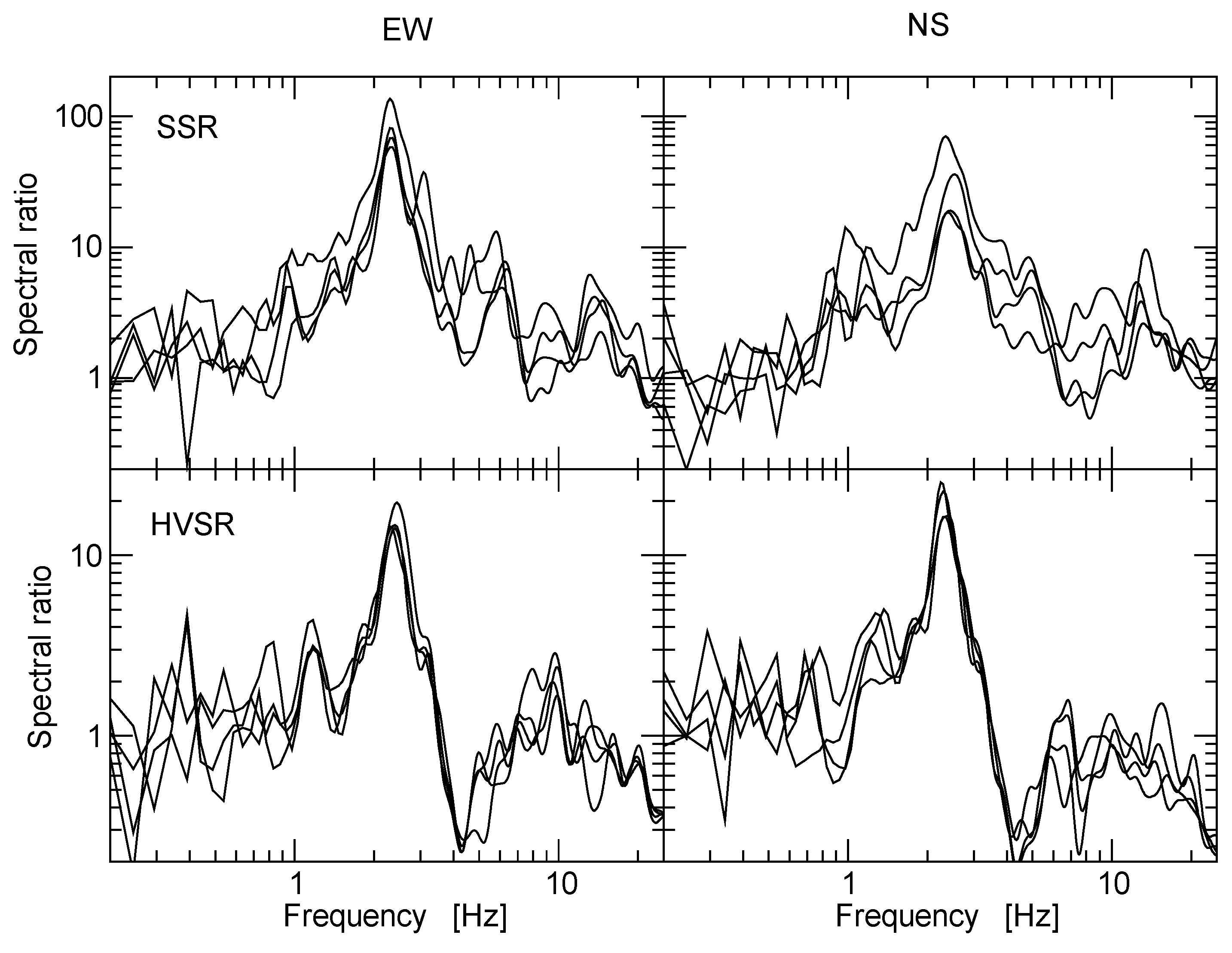
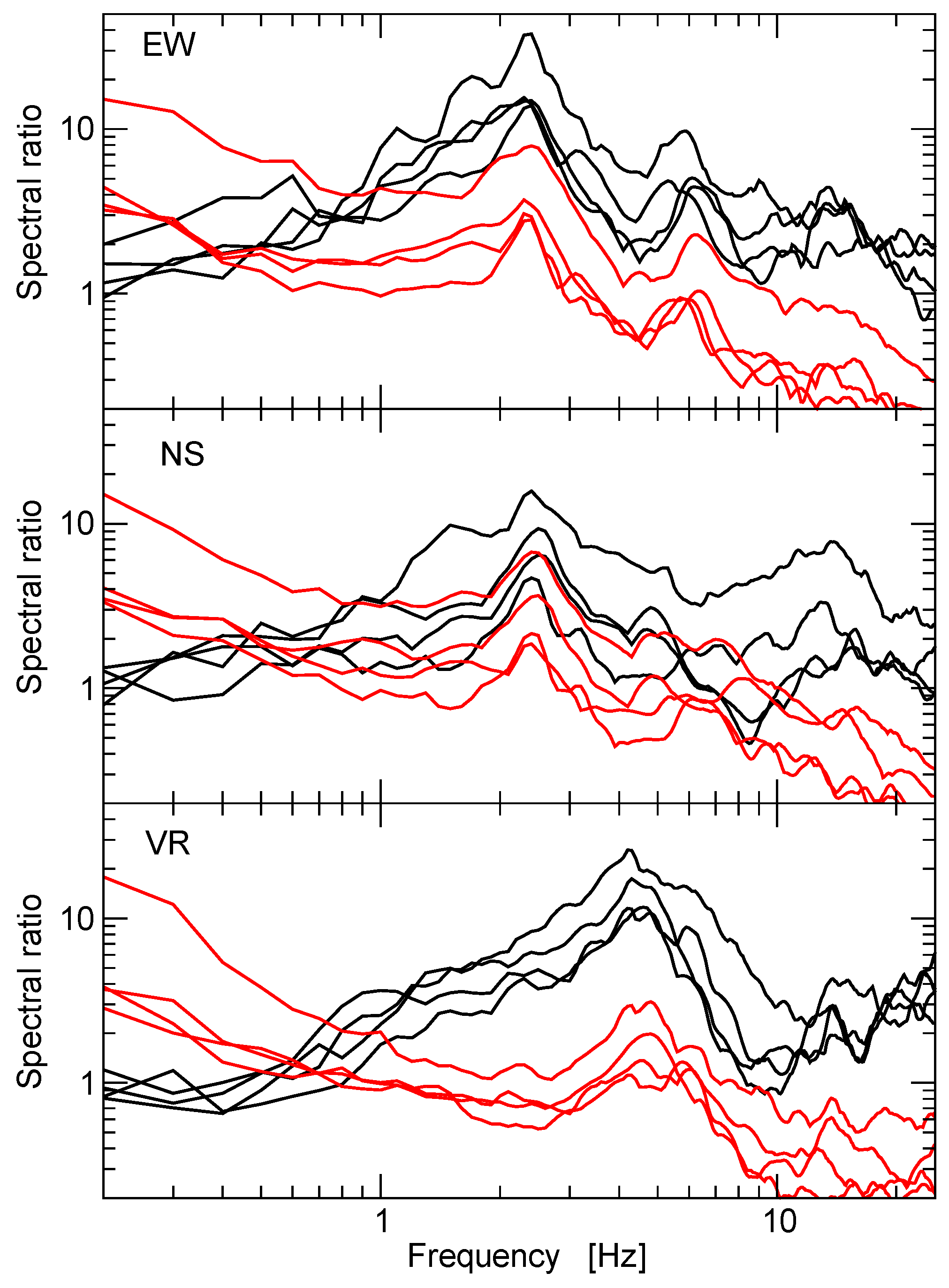
Figure 5 shows an example of the results. This figure shows SSR and HVSR for the four aftershocks recorded by station EST. Station CAL is the reference station for SSR. A very prominent amplification peak is observed between 2 Hz and 3 Hz for both SSR and HVSR. The shapes of the curves are very similar for both techniques. However, amplitudes of SSR transfer functions are almost an order of magnitude larger than the results for HVSR. That is, station CAL seems not to be affected by a local amplification function that would affect the shape of the SSR, but its amplitudes are small and, consequently, SSR relative to CAL have large amplitudes. Earthquake HVSR curves show a smaller scatter than SSR curves, giving a more precise image of the transfer function at EST.
SSR requires that the propagation path be similar between the source and the soft soil and reference sites. This may not be satisfied in our data (
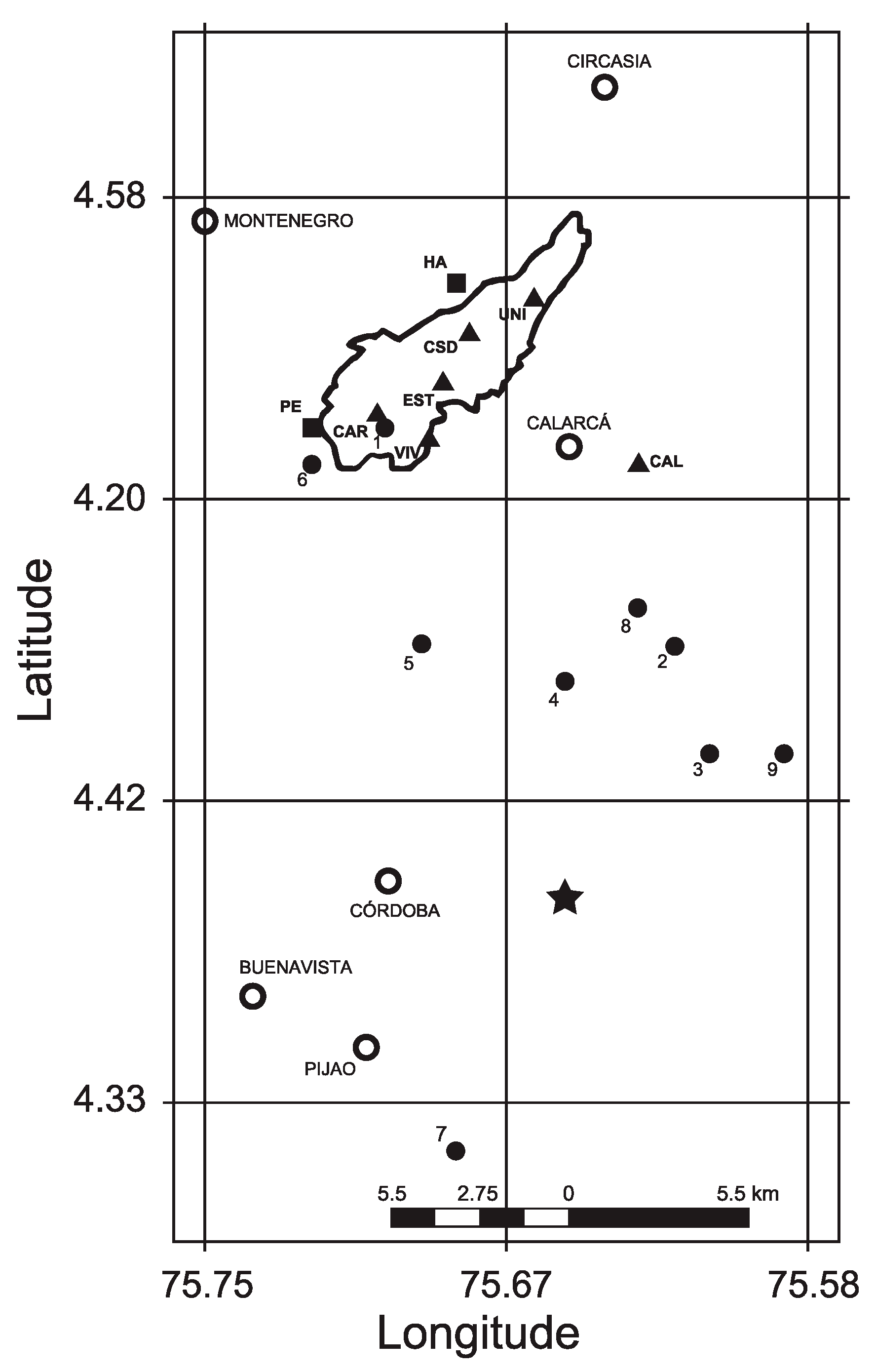
Figure 3) given the short epicentral distances and the consequent azimuth differences between the source and recording stations. We corrected Fourier amplitude spectra for geometrical spreading and recomputed SSR. The scatter among SSR curves for each station did not decrease and, at some stations, increased significantly (therefore, results shown correspond to SSR uncorrected by geometrical spreading). We conclude that even small location errors may significantly change the computed epicentral distances and azimuths for aftershocks that were recorded at distances as small as 1.1 km. Clearly, SSR indicates that site effects are very significant. However, this technique is unable to provide a precise estimate of amplification because amplitudes of ground motion recorded at CAL seem to be unnaturally small, by a factor that is independent of frequency. A possible explanation would be large differences in the radiation pattern from the source to CAL relative to our other stations.
Average results for station EST are shown in
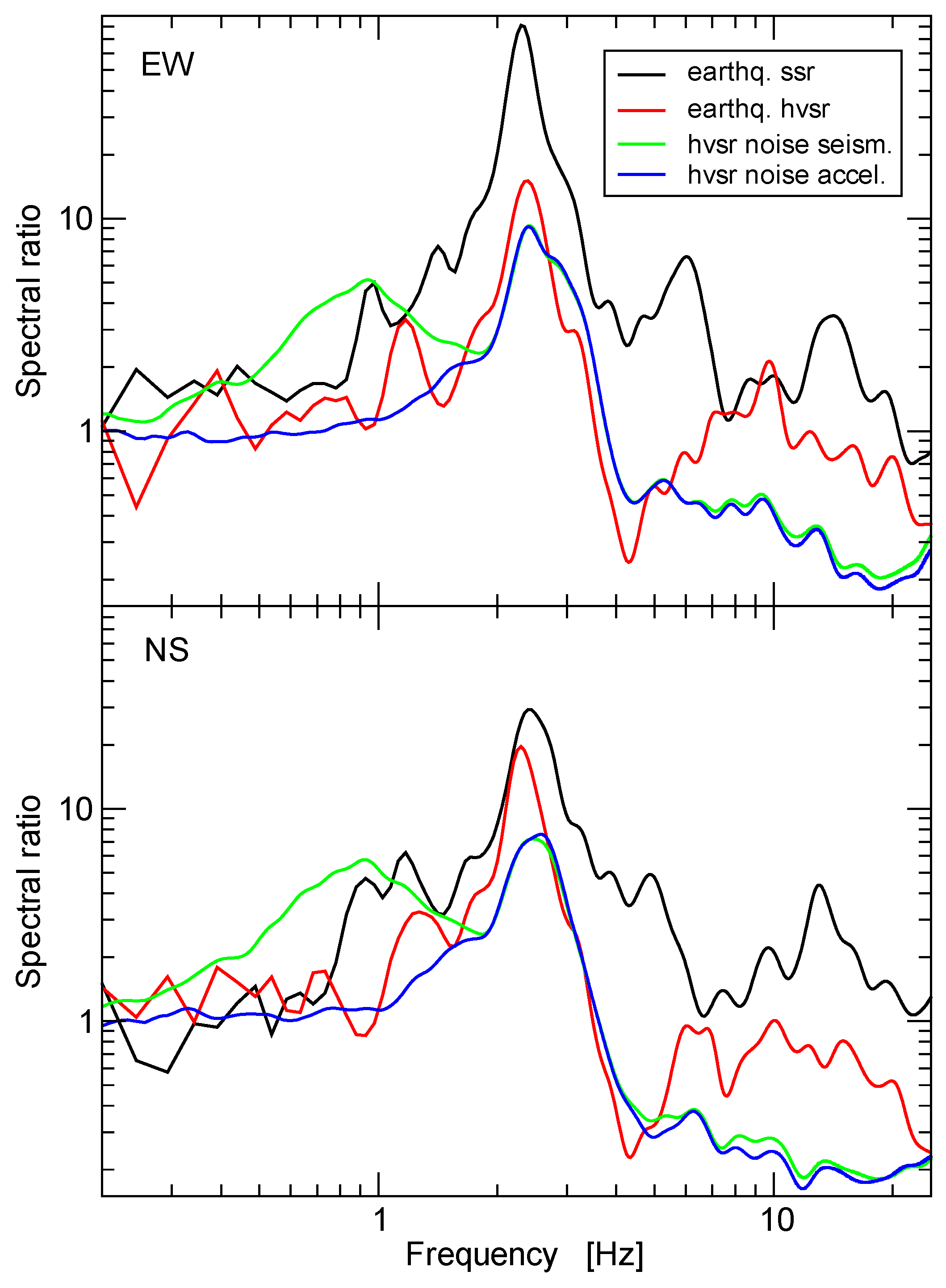
Figure 6. This figure shows average earthquake SSR and HVSR results together. Two additional curves in this figure show the results of HVSR of ambient noise recorded at station EST using the broad band seismometer and the FBA accelerometer. Results for ambient noise indicate that there are some differences between the seismograph and the accelerograph records. However, they appear at frequencies below 2 Hz, outside the frequency range where ground motion is amplified at this site. For frequencies above 2 Hz, the results for seismic noise recorded using a seismograph or an accelerograph are undistinguishable (the same was observed for all other five stations). All the curves in
Figure 6 show a large amplification peak between 2 Hz and 3 Hz. However, the amplitudes display a large scatter, between 9 and 80 for the EW component and between 7 and 30 for the NS component. Earthquake data SSR show larger amplification than all other estimates. Earthquake data HVSR are closer to amplification estimates from ambient noise data, which show the smallest amplitudes of the resonant peak. However, it is well known (e.g., [
28,
31]) that HVSR of ambient noise usually underestimate local amplification. For this reason, we qualify the results in
Figure 6 as in good agreement, despite the small differences between HVSR of earthquake and ambient noise data.
In addition to the resonance peak between 2 Hz and 3 Hz, broad band seismograph HVSR in
Figure 6 show a broad, smaller amplitude peak at about 1 Hz. This peak is absent from the earthquake data curves and from accelerometer ambient noise HVSR.
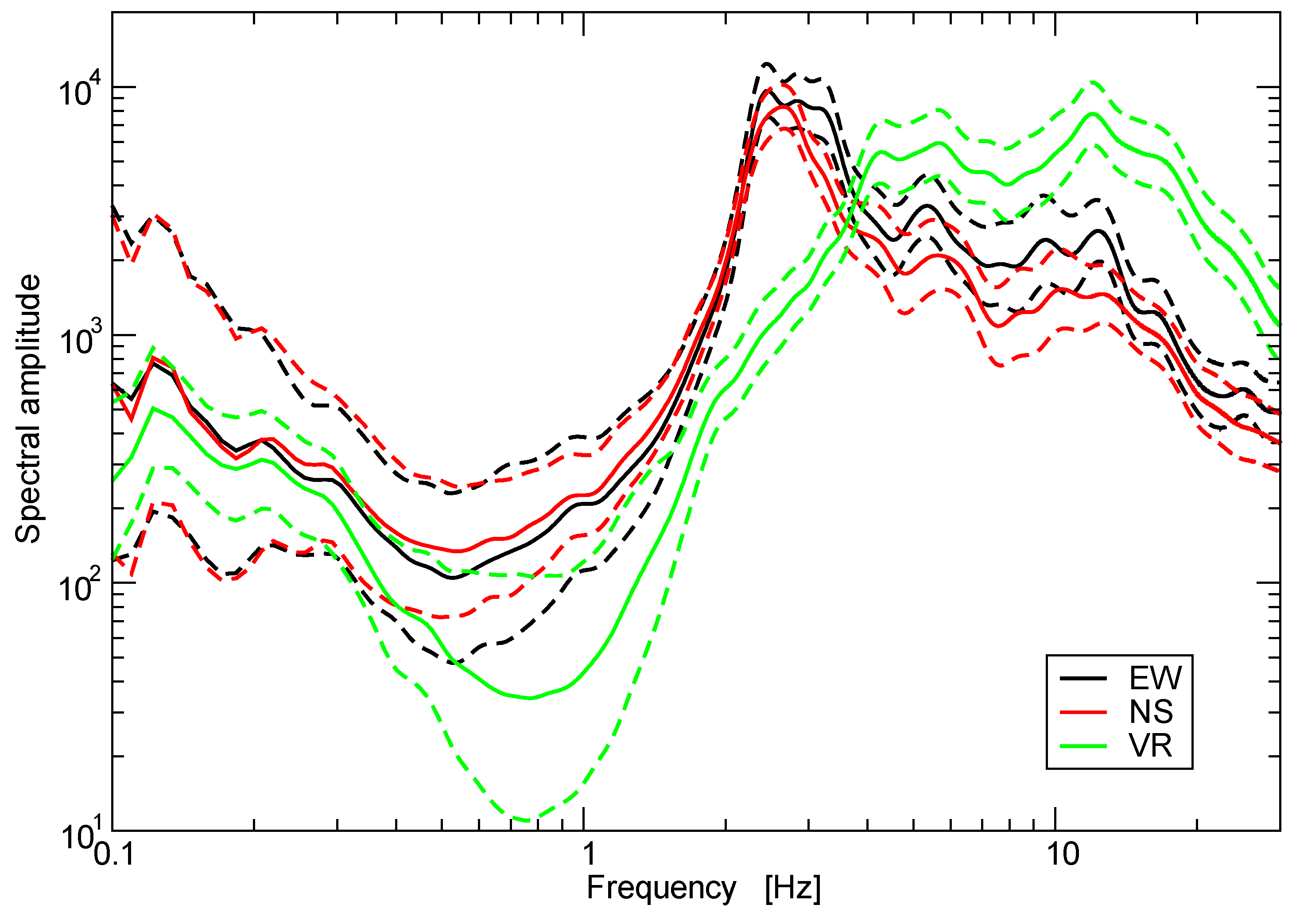
Figure 7 shows average Fourier amplitude spectra of ambient noise recorded at station EST using the broad band seismometer (average for 236 windows of 60 s duration). Solid lines show average values. The dashed lines indicate average plus or minus one standard deviation. The broad peak at 1 Hz results from anomalous low amplitude of the vertical component. However, the resonant peak between 2 Hz and 3 Hz stands out in both horizontal components and the three components show very small scatter in that frequency range.
The results shown in
Figure 5 and
Figure 6 show that SSR computed using CAL as a reference station estimates correctly the fundamental frequency, but overestimates significantly the maximum amplification by a factor that seems independent of frequency.
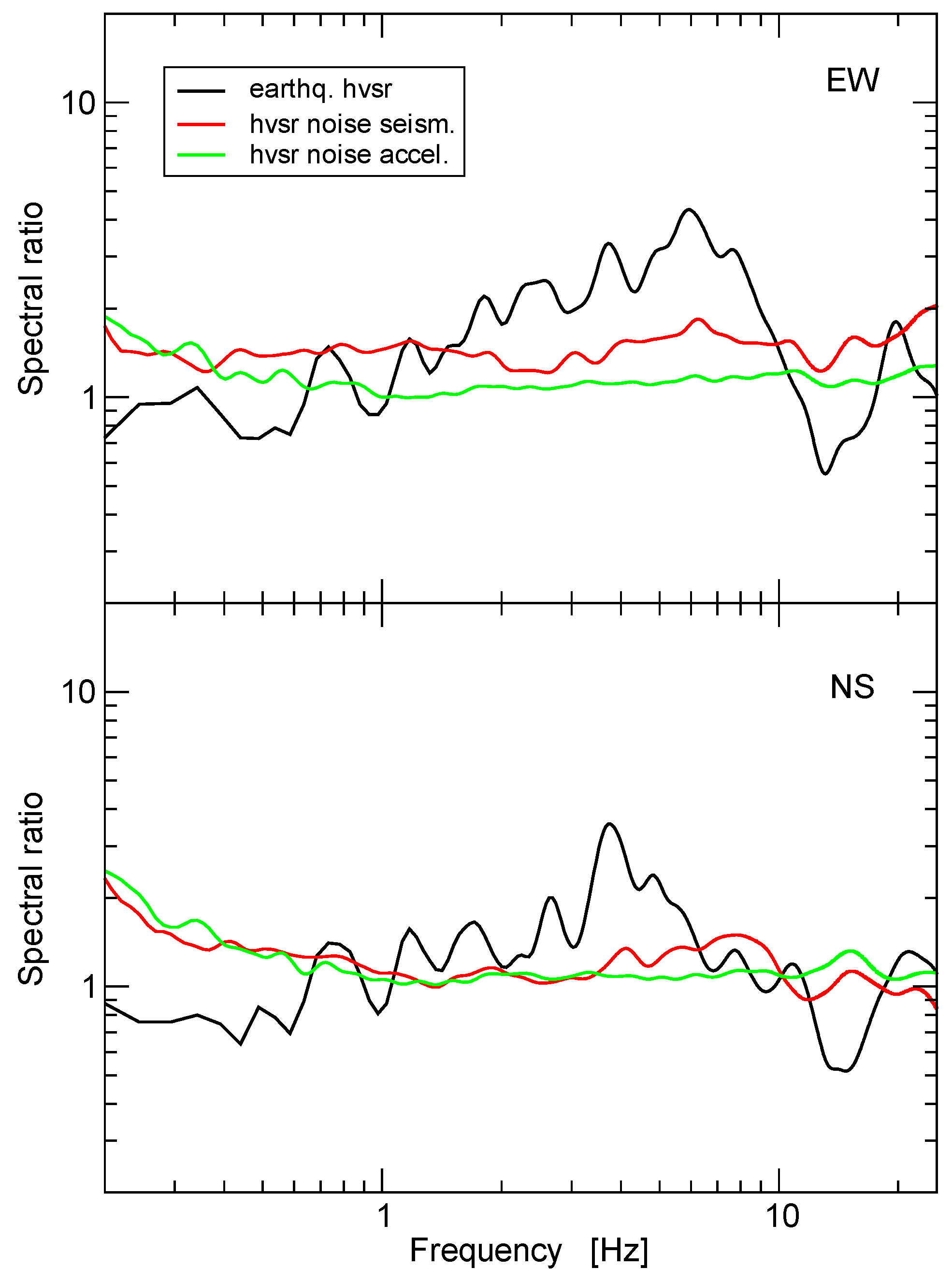
Figure 8 shows HVSR results for CAL using both earthquake and ambient noise data. Results for ambient noise do not show evidence of sub-surface resonance, in terms of HVSR peak frequencies. The weak-motion HVSR show some small amplification between 3 and 8 Hz, which is in good agreement with the geological description of the site at this station (a thin weathered layer overlying metamorphic rock). This indicates that SSR does not fail to provide a precise estimate of site effects in Armenia because of local resonances at CAL. We hypothesize that because the source locations are close to the recording stations, differences in radiation pattern decrease significantly the amplitudes of the earthquake recorded at station CAL. Unfortunately, we do not have the data to test this hypothesis.
Figure 9 shows results computed using response spectra. For each aftershock, black solid lines show the ratios of response spectra computed for the records at station EST divided by the corresponding response spectra of the records at the reference station, CAL. As mentioned above for SSR, we did not correct for geometric expansion as this correction did not improve the results. We also computed ratios of response spectra, using as the reference the predicted response spectra at each site computed using the program, SMSIM (see the detailed description in [
39,
40]). For each earthquake record, we simulated the response spectrum predicted by the stochastic method using a point source ω-square model and varying only the magnitude and distance. A factor of 0.71 is used to account for the partitioning of energy into two horizontal components, and an average radiation factor of 0.55 is assumed. The red lines in
Figure 9 show RSR relative to the SMSIM simulated response spectra. The shape of the estimated amplification functions are very similar between the black and red lines. Both predict an amplification peak at a frequency that is very similar to that obtained from SSR. Moreover, RSR relative to CAL show very similar amplitudes with those obtained using earthquake HVSR. Results for the vertical component indicate amplification at a frequency that is larger by about a factor of 2 relative to the frequency for which we observe amplification of the horizontal components in
Figure 9. This is to be expected if amplification for both vertical and horizontal components is produced by the velocity contrast for the P and S wave velocities (
Vp and
Vs) at the base of a single layer over the halfspace model (assuming vertical plane wave incidence). The ratio between fundamental frequencies for vertical and horizontal ground motion corresponds in that model to the ratio between
Vp and
Vs. The amplitude of amplification of RSR relative to CAL is significantly different from that observed in the ratios of response spectra relative to SMSIM predictions, which are very small. This suggests that SMSIM simulations overestimate response spectra at CAL, which is consistent with the hypothesis stated above of a small radiation pattern affecting records at CAL. In addition to a frequency independent difference between the black and red lines in
Figure 9, we observe that the red lines decrease faster with frequency than the black lines at high frequencies. This suggests that SMSIM simulations underestimate anelastic attenuation along the path source-receiver.
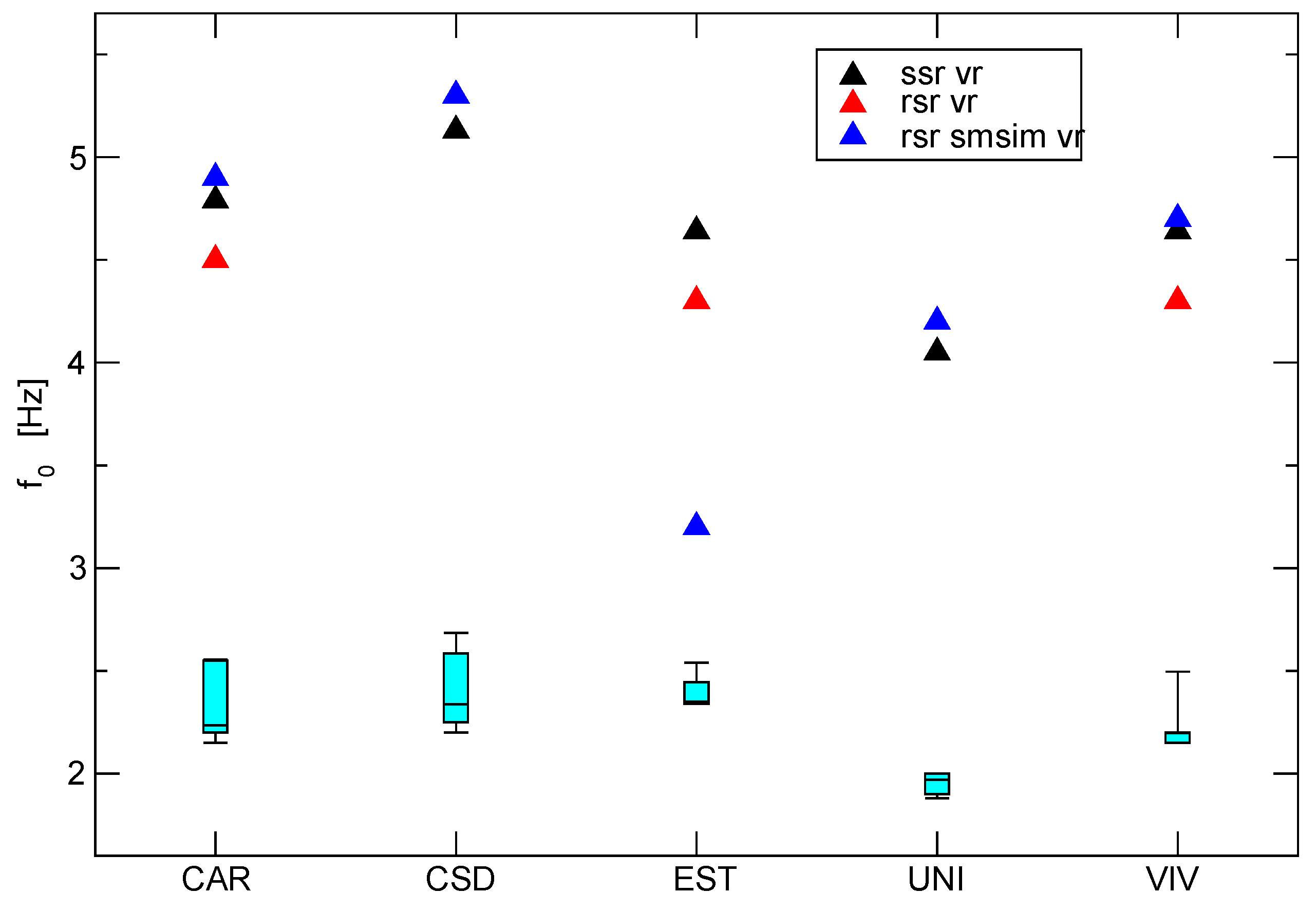
Let us now compare the values of fundamental frequency estimated at the five instrumented sites inside Armenia.
Figure 10 shows together the fundamental frequency values for horizontal and vertical components obtained from our different estimates of site response using a standard box plot. We averaged together the NS and EW components for each estimate. We observe very small variations throughout the city, as fundamental frequencies for horizontal ground motion vary less than 0.5 Hz. The differences in horizontal fundamental frequency among the five stations are echoed by the vertical component fundamental frequencies, where variations are larger, but of the same order as those for the horizontal component (about 20%). For the vertical component, it is only the estimate obtained from the ratios of observed response spectra relative to the response spectra, simulated using SMSIM at station EST, that diverges from the other estimates. A Poisson ratio of 0.25 implies a factor between
Vp and
Vs of
. The differences between the fundamental frequencies in the horizontal and vertical components suggest a ratio between
Vp and
Vs of the order of a factor 2, indicating a Poisson ratio in the layer at the origin of the amplification slightly larger than 0.25.
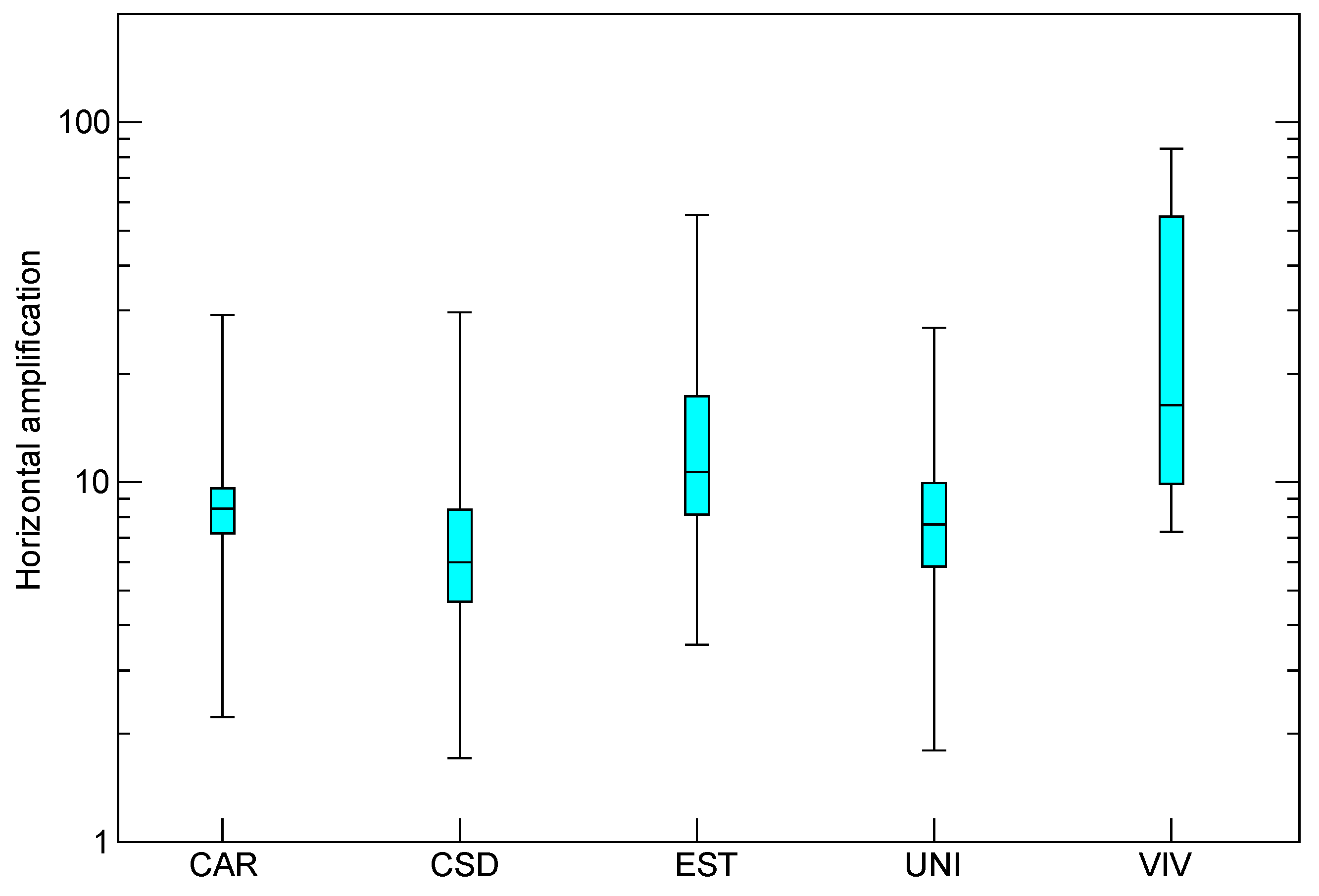
Similar to
Figure 10,
Figure 11 compiles horizontal amplification from the different techniques used to estimate site response, again using a box plot. As expected, the scatter is significantly larger than that for the fundamental frequency. The median value varies between 6 for CSD and 16.4 for VIV, a variation slightly larger than the usual uncertainty factor of 2 [
8,
41,
42]. This suggests that maximum amplification shows mild variations in Armenia. The upper extreme values correspond to SSR for all the stations, and, as stated above, they may be biased by unnaturally small amplitudes at the reference station CAL. If we make an abstraction of the upper and lower extreme values, the maximum amplification in Armenia may be considered relatively constant, around a factor of 8 or 9, and would have an associated uncertainty smaller than a factor of 2.
The results for the aftershocks suggest that site response does not vary significantly within Armenia. However, earthquake data gives us information on site response only at five sites. Consider now the additional ambient noise measurements made at 29 sites within the city in 2002. As a different instrument was used, it is first necessary to compare the 2002 measurements with those made recently at the five sites where aftershocks were recorded.
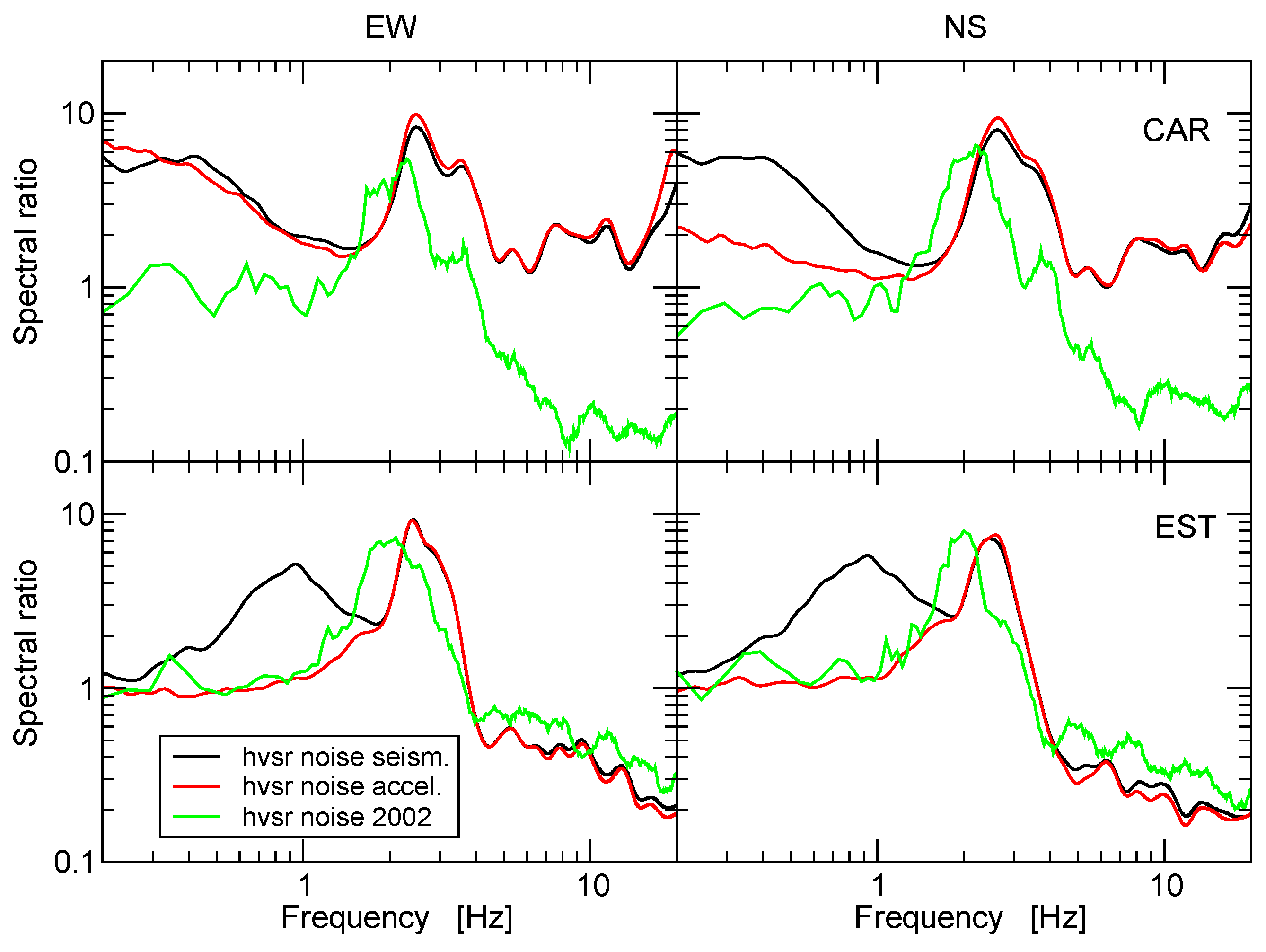
Figure 12 shows this comparison for two stations, CAR and EST. Together with the results for HVSR from ambient noise recorded during August 2017, we plot the results of HVSR at the closest points, measured in 2002 using the Sprengnether DR100 and 5-s period seismometers. We would have preferred to compare measurements at exactly the same location. Unfortunately, in 2017, we borrowed the instruments used, which were returned to their owner before we had the map with the locations of the sites measured in 2002. The distance between CAR and point P27 is 87 m, while that between EST and P14 is 582 m. The fundamental frequency value varies a little between measurements made in 2002 and 2017. However, the difference are small in both cases, and are larger between EST and P14 than between CAR and P27, in agreement with the corresponding distances between the measurement points. The maximum amplitudes of HVSR are very similar. This suggests that it is possible to add the results of the measurements made in 2002 to those obtained at the five accelerographic stations.
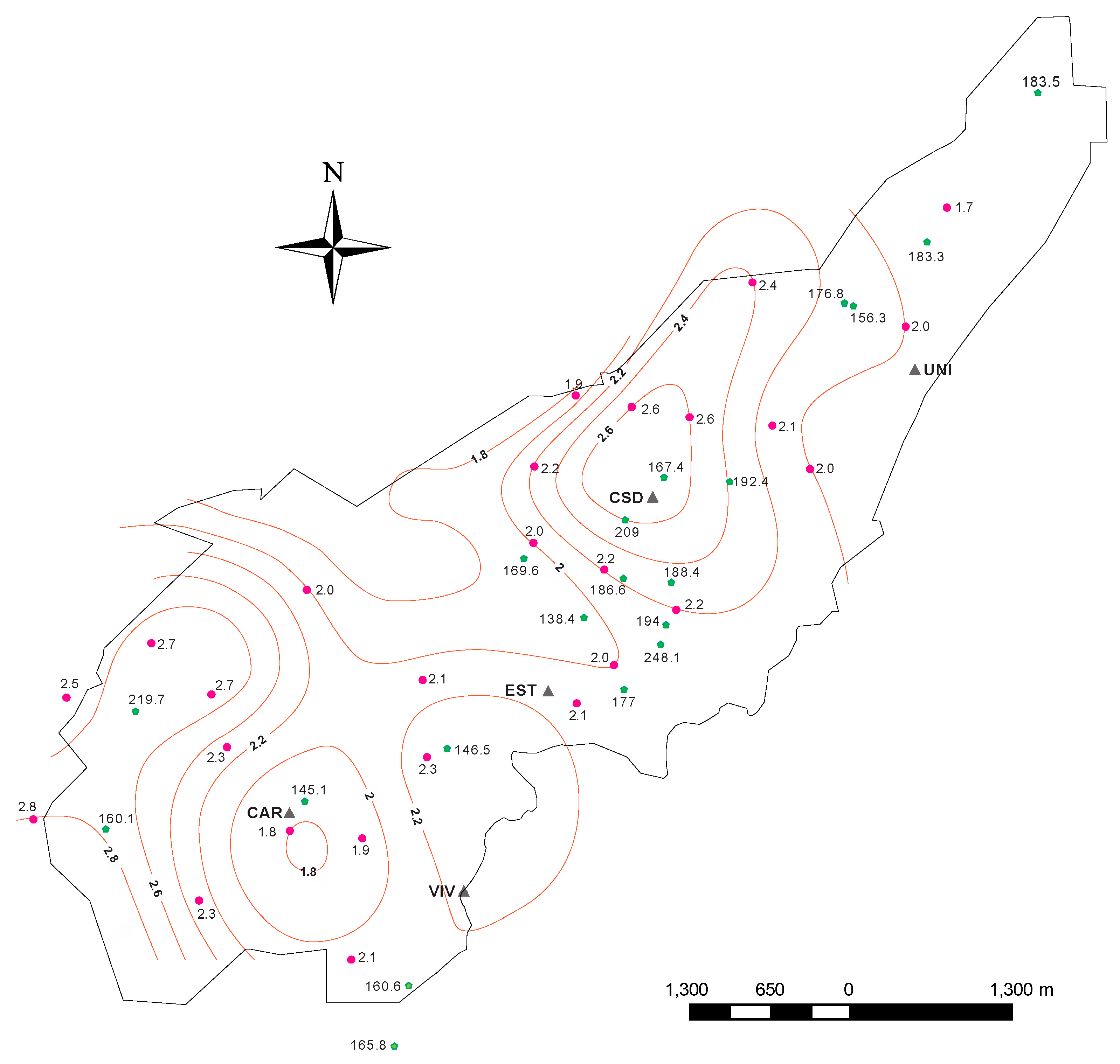
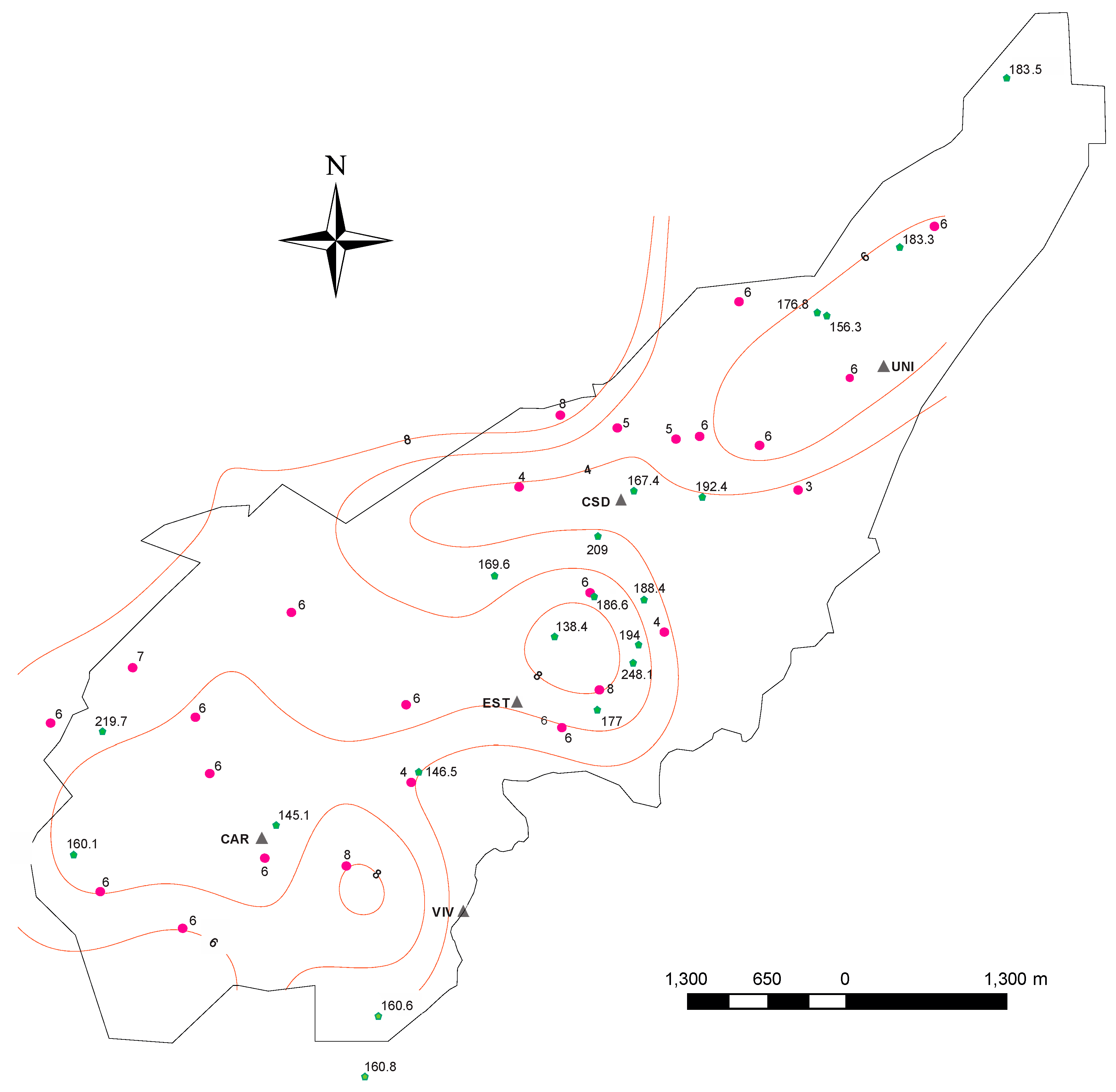
Figure 13 shows the final map of the fundamental frequency obtained from HVSR of ambient noise. Fundamental frequency within the city varies between 1.7 Hz and 2.8 Hz. The corresponding contours of the maximum amplification, computed as the average for both horizontal components, are shown in
Figure 14. The observed amplification varies between 4 and 8 (only a single point shows an amplification of 3). These values are somewhat smaller than those shown in
Figure 11. However, it is well known (e.g., [
28,
31]) that ambient noise HVSR underestimate local amplification relative to that estimated using earthquake data. Thus, we may consider that
Figure 11 and
Figure 14 show very good agreement. The shape of the contours in
Figure 14 shows no relation with that of the contours in
Figure 13.
Figure 13 and
Figure 14 also show the values of average velocity determined at 21 sites within Armenia using the seismic cone, in the frame of a microzonification project. The depth of investigation varied between 11 m and 30 m, with an average depth of 17 m, and, therefore, these measurements sample only the shallowest layers. We averaged the results at each site using the relation:
where
hi and
Vsi are the thickness and shear wave velocity of the n-layers determined at each site, and
Vs is the average shear wave velocity, indicated at each measurement point in
Figure 13 and
Figure 14. Average shear wave velocities varied between 140 m/s and 250 m/s. However, we observe no relation between these values and the contours of the maximum amplification, or between those values and the contours of the fundamental frequency. Fundamental frequency is closely related with the average shear wave velocity of the soft layers and their thickness. The fact that contours of the fundamental frequency show no relation with the distribution of
Vs determined from seismic cone tests suggests that shallow
Vs values do not reflect the average shear wave velocity for the thickness of sediments at the origin of the fundamental frequency value. This is supported by the lack of correlation between the contours of maximum amplification and the same
Vs values. Amplification is related to impedance contrast at the base of the sedimentary layers. If the variations in shallow
Vs were representative of
Vs for the sedimentary layers at the origin of site effects, we should observe some correlation of those
Vs values with the contours of maximum amplification.
Figure 13 and
Figure 14 suggest together that shallow variations of
Vs are not representative of the average velocity for the sedimentary layers at the origin of site effects, that those sedimentary layers have a rather homogeneous average
Vs, and that the impedance contrast between average
Vs for the soft deposits and the underlying bedrock is relatively constant.
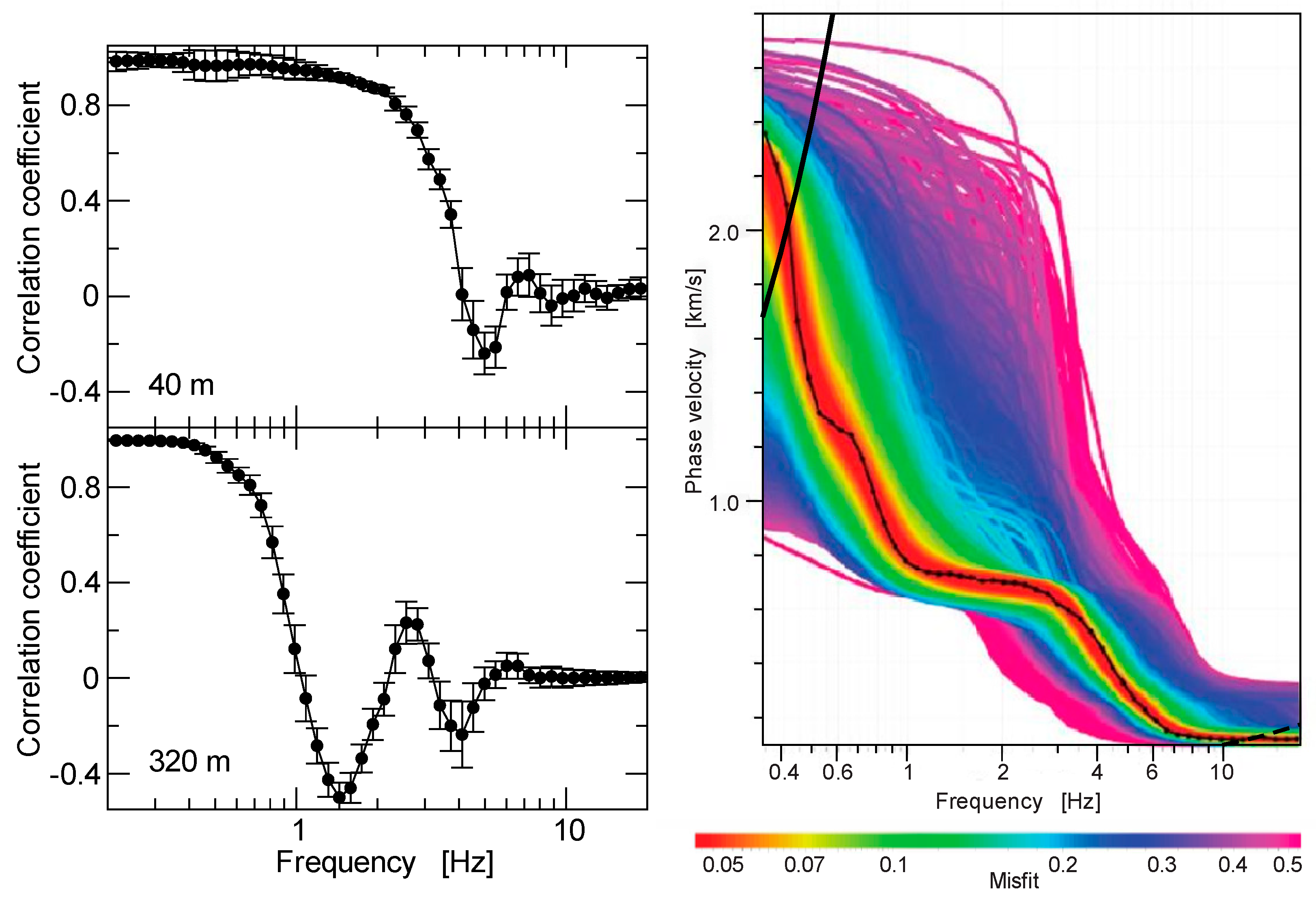
Finally, we consider the results of the SPAC method applied to the ambient noise data recorded by linear arrays of seismographs at the sites, HA and PE (
Figure 3).
Figure 15 shows two examples of correlation coefficients (K. Aki (1957) [
33] used this term to refer to normalized, averaged cross-correlation of seismic noise at a fixed distance; see also [
34,
35,
36]) as a function of frequency. According to the theory of the SPAC method, correlation coefficients should take the form of a Bessel function of first class and order zero. Its argument is frequency times the distance between stations divided by the phase velocity (of Rayleigh waves for the case of cross-correlation of vertical components). The two plots on the left of
Figure 15 show correlation coefficients computed for station pairs, separated by distances of 40 and 320 m at the PE site (
Figure 3). Our correlation coefficients take the form of a Bessel function, allowing us to estimate the phase velocity of Rayleigh waves as a function of the frequency. The correlation coefficients for the sites, PE and HA, were inverted to estimate phase velocity dispersion curves, which were in turn inverted to obtain shear wave velocity profiles at those sites. The diagram on the right in
Figure 15 shows the result for the PE site, computed using GEOPSY [
37]. The solid black line shows the phase velocity dispersion curve estimated from all correlation coefficients at site PE. All other lines show the dispersion curves determined from the inversion of the observed phase velocity dispersion using the neighborhood algorithm. The color of each dispersion curve corresponds to the misfit scale shown at the bottom. The thin red band around the observed dispersion curve indicates the inverted dispersion corresponding to the smallest misfit values and is a measure of the uncertainty of the results. Although it is not possible to estimate precisely, a frequency range for which our phase velocity dispersion is a curve is well determined and B. L. N. Kennet (1983) [
43] proposed that correlation coefficients are valid in the wavelength range from 2
r to 15
r, where
r is the inter-station distance. The right diagram in
Figure 15 shows lines corresponding to 15
r for our largest distance (320 m) and 2
r for our smallest distance (5 m). We observe that almost all the frequency range shown in
Figure 15 may be considered valid according to this criterion.
The final models determined for the two observation sites are given in
Table 2. A fixed ratio of
Vp to
Vs of
was used. We checked that the results did not change assuming
Vp/
Vs = 2, as argued above. It is well known that phase velocity dispersion curves are not sensitive to
Vp values (or, conversely, to Poisson ratio values). These results coincide with the geological information: The topmost layer fits the volcanic ash deposits and the second layer fits the underlying silt and silty clay layer that resulted from the weathering of the underlying pyroclastic flows. The latter would correspond to the halfspace in
Table 2. The observed dispersion curve extends to values larger than the 800 m/s chosen to represent the bedrock. We did not invert deeper layers because it becomes difficult to fit the observed dispersion at small frequencies. In addition, although observed phase dispersion suggests that the shear-wave velocity of the bedrock is in excess of 2 km/s, the increase in velocity occurs over a large depth interval and without large impedance contrasts at single interfaces. This is supported by the lack of amplification at small frequencies in our results.
We have used the soil profiles given in
Table 2 to compute the expected amplification in Armenia for the vertical incidence of plane shear-waves using the reflectivity method [
44].
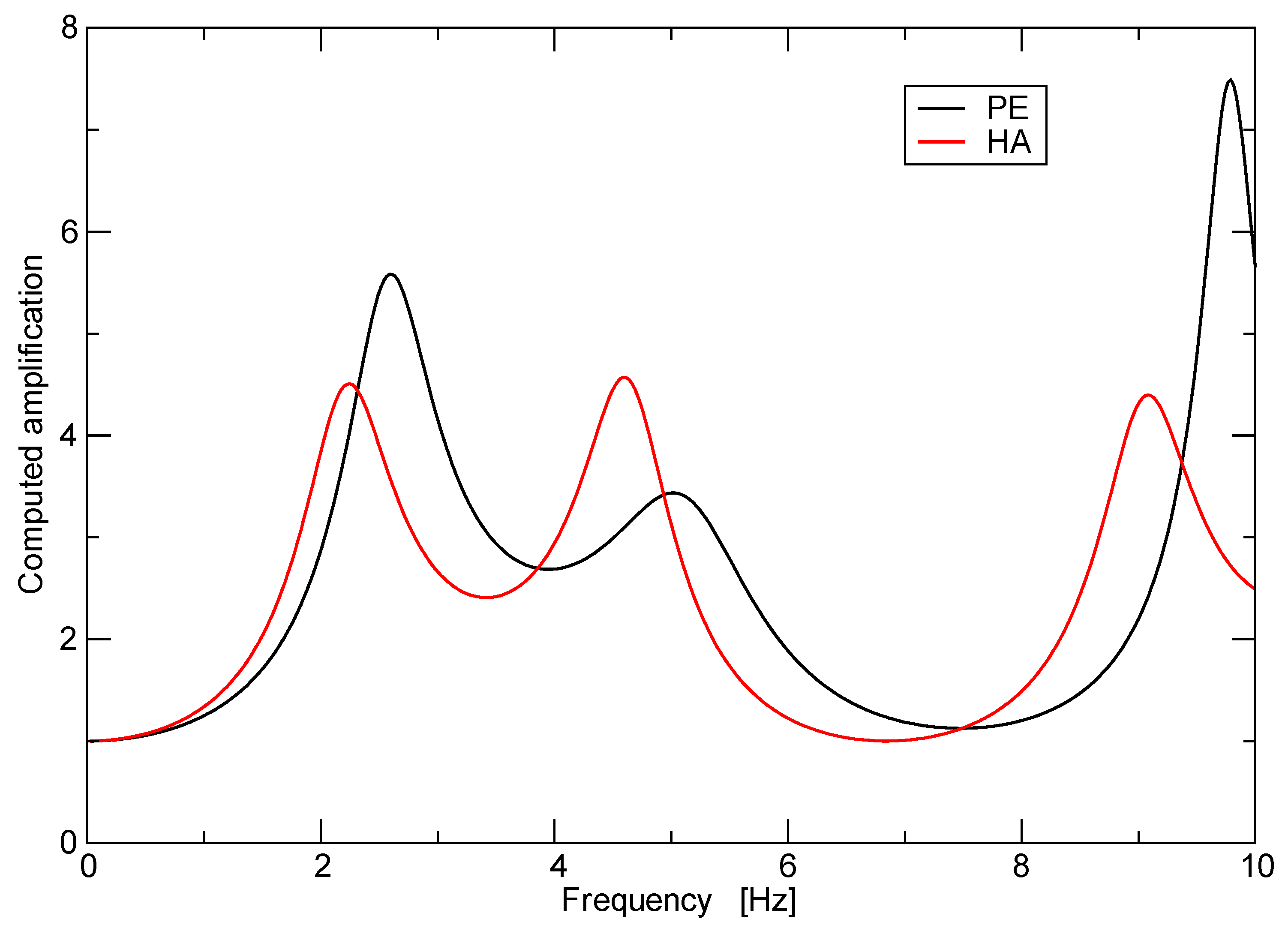
Figure 16 shows the resulting transfer functions. Lacking data, anelastic attenuation was neglected in this simulation. However, attenuation becomes increasingly significant with increasing frequency, and its effects at the fundamental frequency are minor for reasonable values of the Q factor. Thus, neglecting attenuation has a small effect on our comparisons between observations and modelling, centered on the frequency of the first resonant peak.
Figure 16 shows that the maximum amplification is 5.6 for the PE site at 2.6 Hz, and 4.5 for the HA site at 2.3 Hz. The fundamental frequencies coincide with all other estimates, but maximum amplification is underestimated.
5. Discussion
Our study on site effects in Armenia has included previous results and data that were available only in internal reports, as well as new data. Moreover, efforts were made to contrast the different estimates of the site amplification and relate them to available data on the subsoil structure. Thus, for the first time, we may confidently use these results to push for an official seismic microzonation of the city. The use of different data types and different analysis techniques gives us confidence that our amplification estimates are robust, even as amplification values show the usual minimum uncertainty of a factor, 2. Although a seismic microzonation of Armenia is required by law, to date, the lack of an integrated analysis and validation of results has precluded the publication of a microzonation map.
It is not surprising that the site effects in Armenia are significant. The shear wave velocity contrast between the surficial volcanic ash deposits and the underlying pyroclastic flows accounts for computed amplification factors between 4 and 6. This value is slightly smaller than the amplification values estimated from earthquake data, about a factor of 10. We speculate that the value determined for the shear-wave velocity of the bedrock may be underestimated, especially given that the shear-wave velocity values determined for the shallowest layers from the inversion of dispersion curves coincide with the values observed in the seismic cone tests.
Fundamental frequencies vary mainly between 2 Hz and 2.8 Hz (only two points show fundamental frequencies of 1.9 and 1.7 Hz). This is a relatively small range of variation. The shear wave velocity contrast between the surficial deposits and the underlying basement is large enough to render meaningless the variations of shear wave velocity of the topmost layers (between 140 m/s and 250 m/s). In terms of local amplification, it is not worthwhile to differentiate microzones in Armenia, with the available data. Site amplification, which is substantial, varies within the usual minimum uncertainty of a factor of 2. However, because their variations within Armenia are small, our results suggest that site effects are not enough to explain the irregular damage distribution caused by the 1999 event.
We have shown that it is useful to compare different types of data and different techniques of analysis to estimate site effects, even if the results may show some minor discrepancies. For example, the use of response spectral ratios relative to SMSIM simulations of response spectra provide surprisingly good estimates of the observed transfer function, even if average amplification values are underestimated. This is a promising result considering the very little data used to constrain the SMSIM simulations. Moreover, RSR relative to SMSIM provide a better estimate of the amplification than spectral ratios relative to a reference site (SSR). Empirical transfer functions determined using SSR show the same shape as those obtained from earthquake HVSR or RSR, but the amplification is significantly overestimated. We believe that the reason SSR fails to estimate the amplification correctly are unnaturally small amplitudes of earthquake records at our reference station, CAL. Because SSR have the same shape as other estimates, the factor that affects amplitudes at CAL seems to be independent of the frequency. We hypothesize that, because the source locations are close to the recording stations, differences in radiation patterns may decrease significantly the amplitudes of the earthquake recorded at station CAL. Unfortunately, we do not have the data to test this hypothesis. Despite this, our final results show a good agreement between the experimental estimates of site effects and the computed site response, even if computations would be improved by including anelastic attenuation.
We are convinced that the best approach to a microzonation map in Armenia city for the time being, in terms of local amplification, is to consider homogeneous site effects. However, this is in stark contradiction with the observed irregular damage distribution during the 1999 earthquake. This calls for a similarly detailed analysis of the distribution of the vulnerability of the building stock in Armenia. This is the subject of a companion paper that is currently under preparation.