PHOTOSED—PHOTOgrammetric Sediment Erosion Detection
Abstract
1. Introduction
2. Materials and Methods
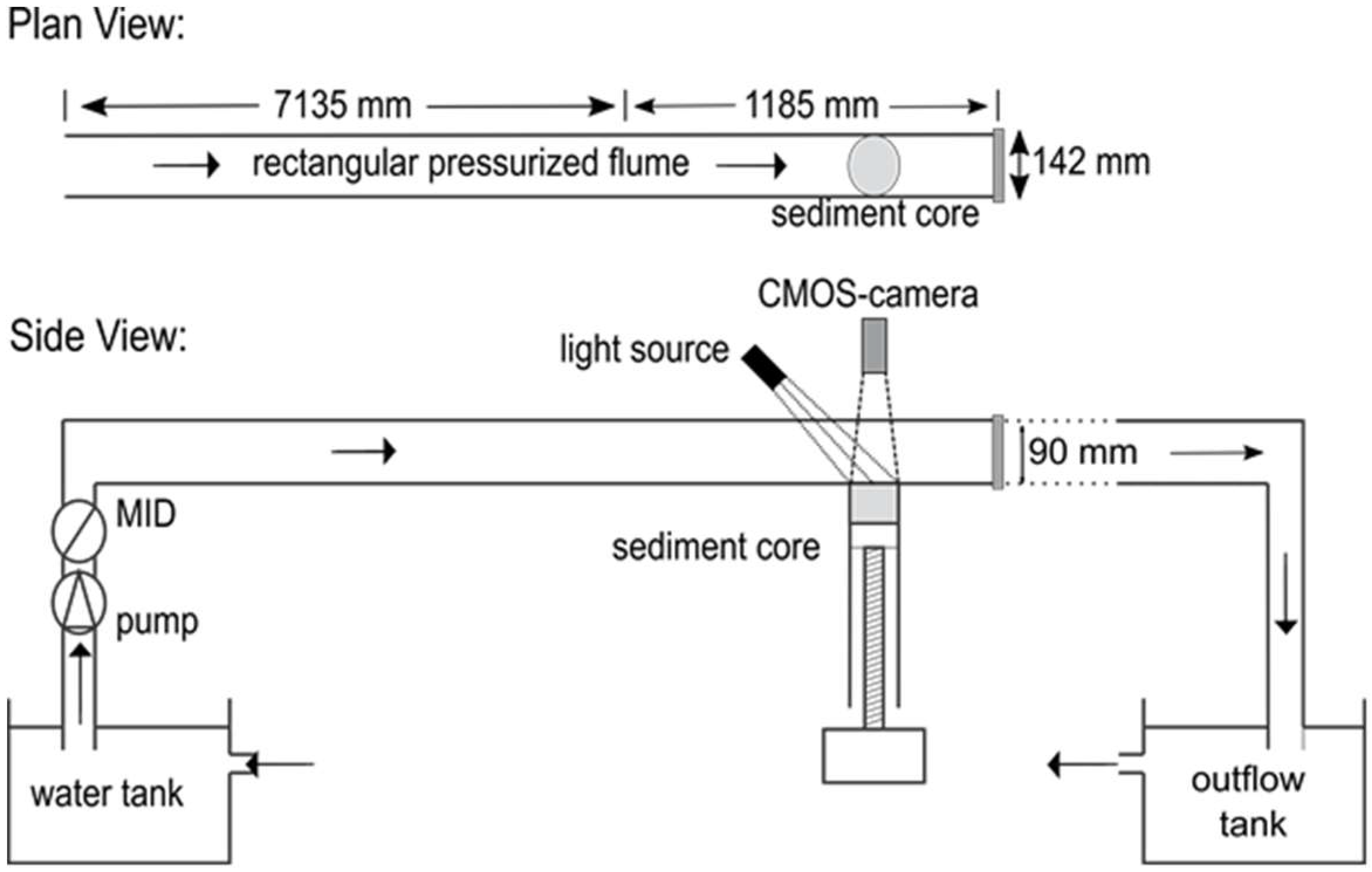
2.1. Experiments in the Erosion Flume—SETEG
2.2. PHOTOSED—PHOTOgrammetric SEDiment Erosion Detection
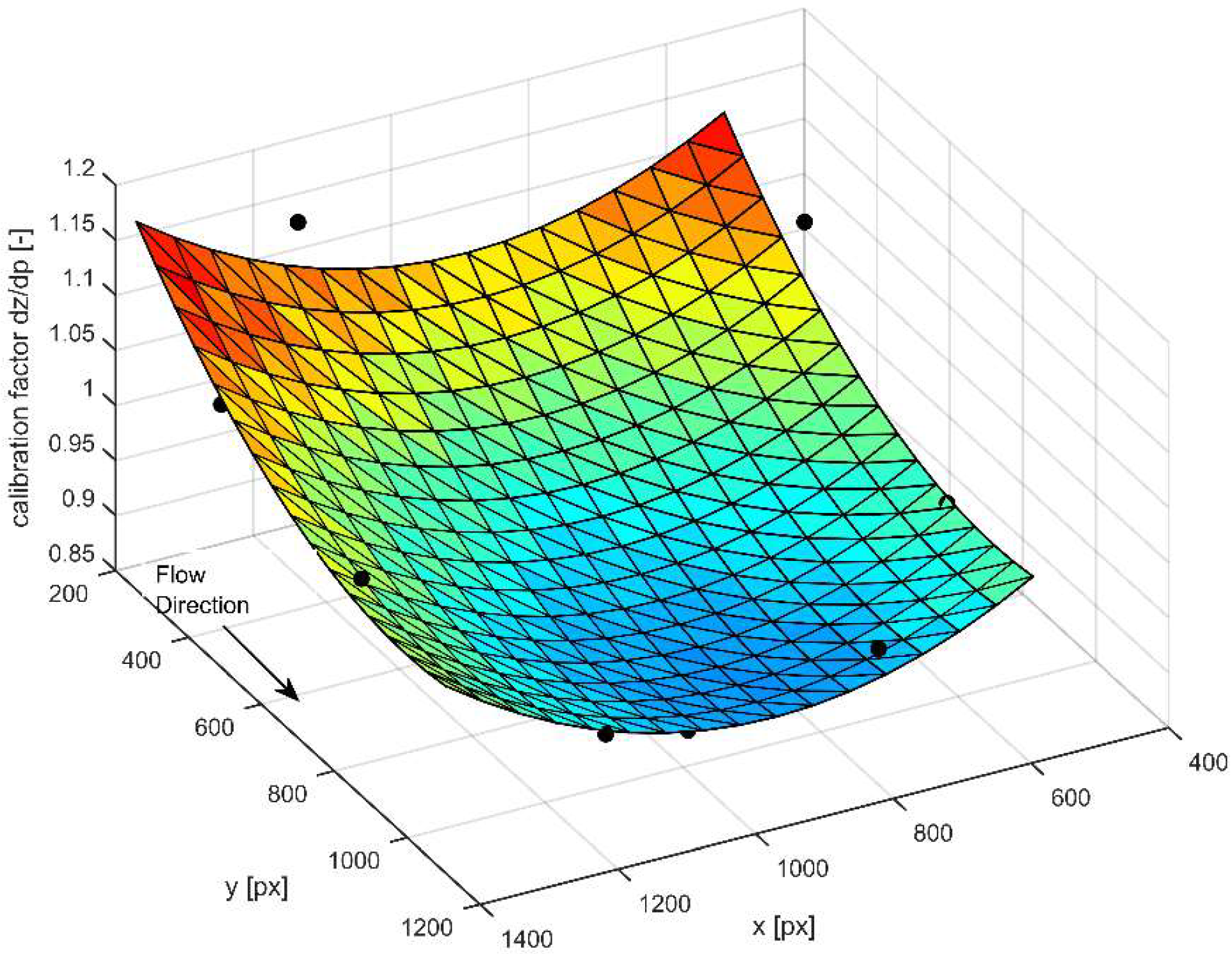
2.3. Calibration and Verification Method
3. Results and Discussion
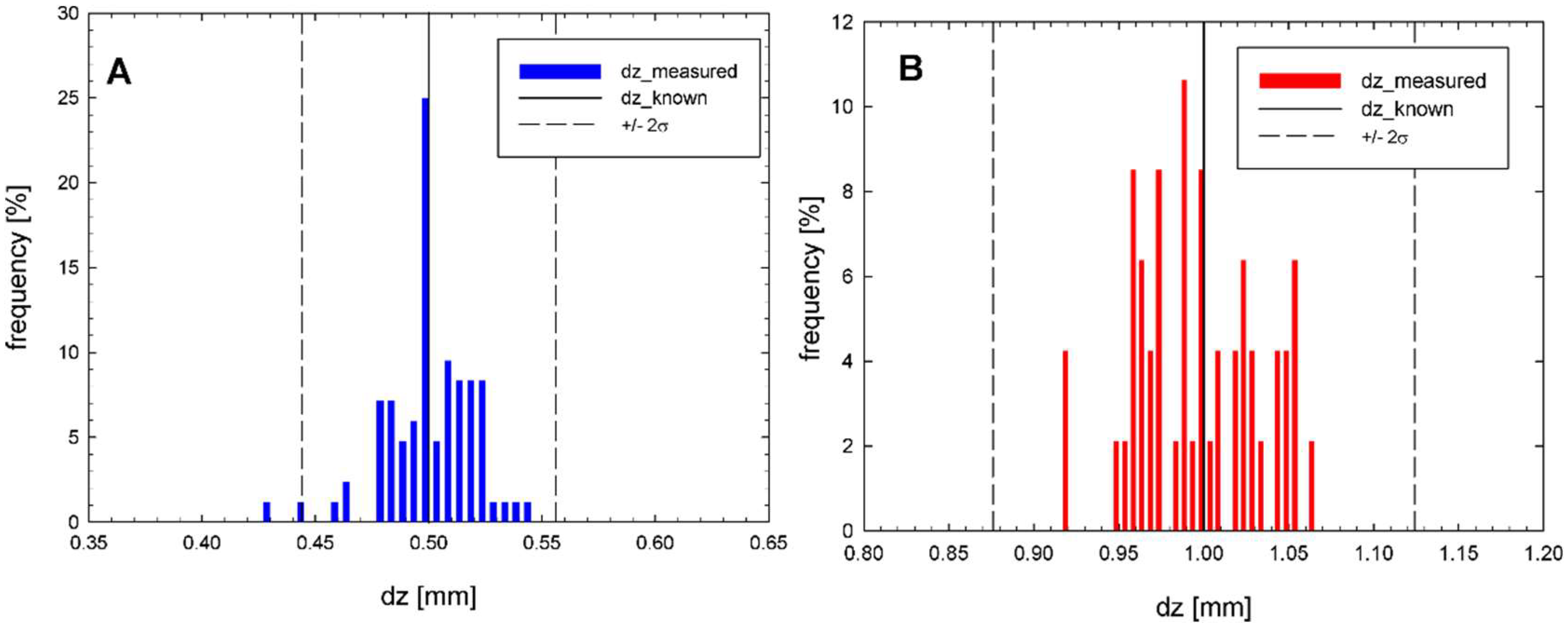
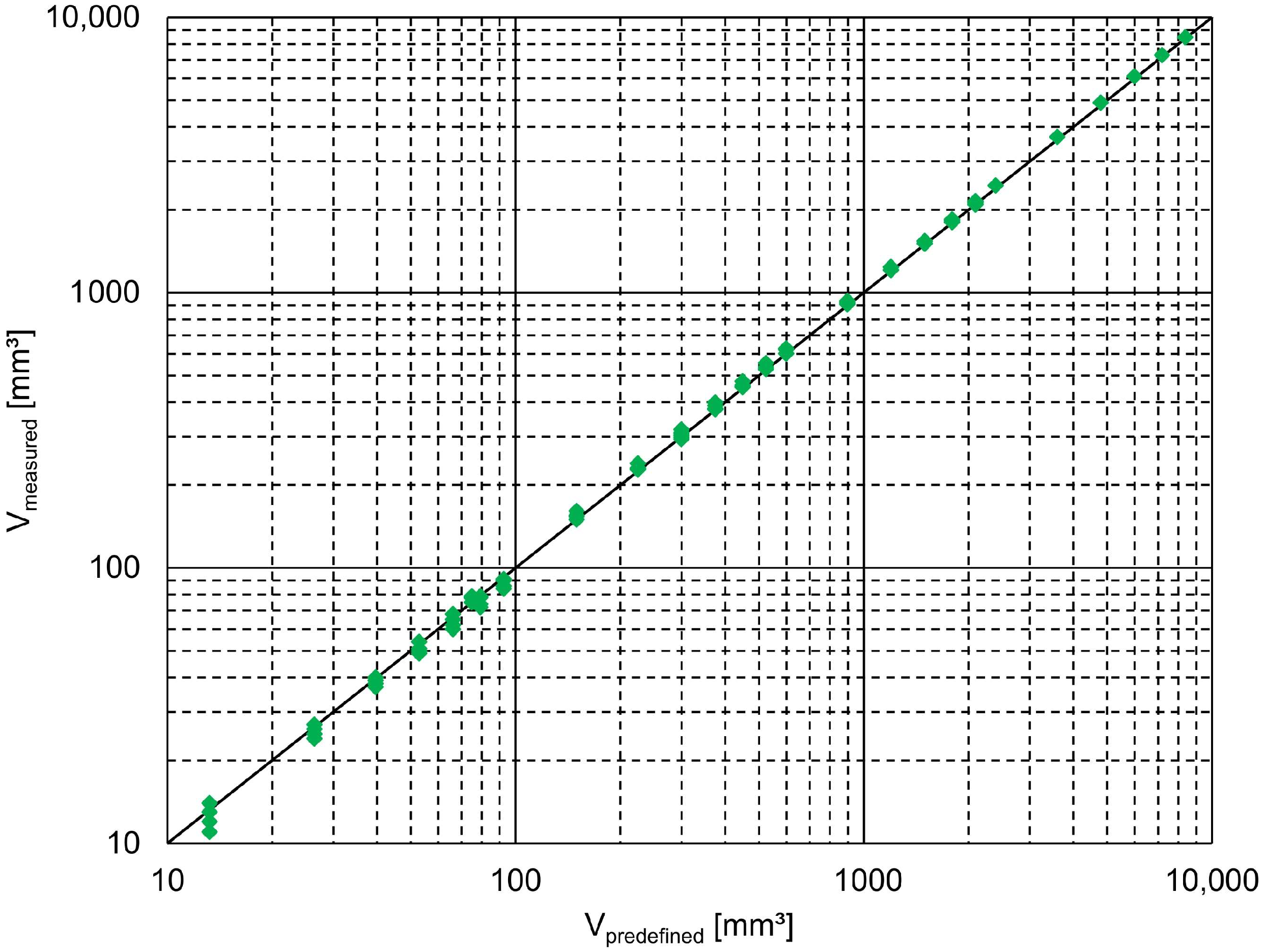
3.1. Calibration and Verification
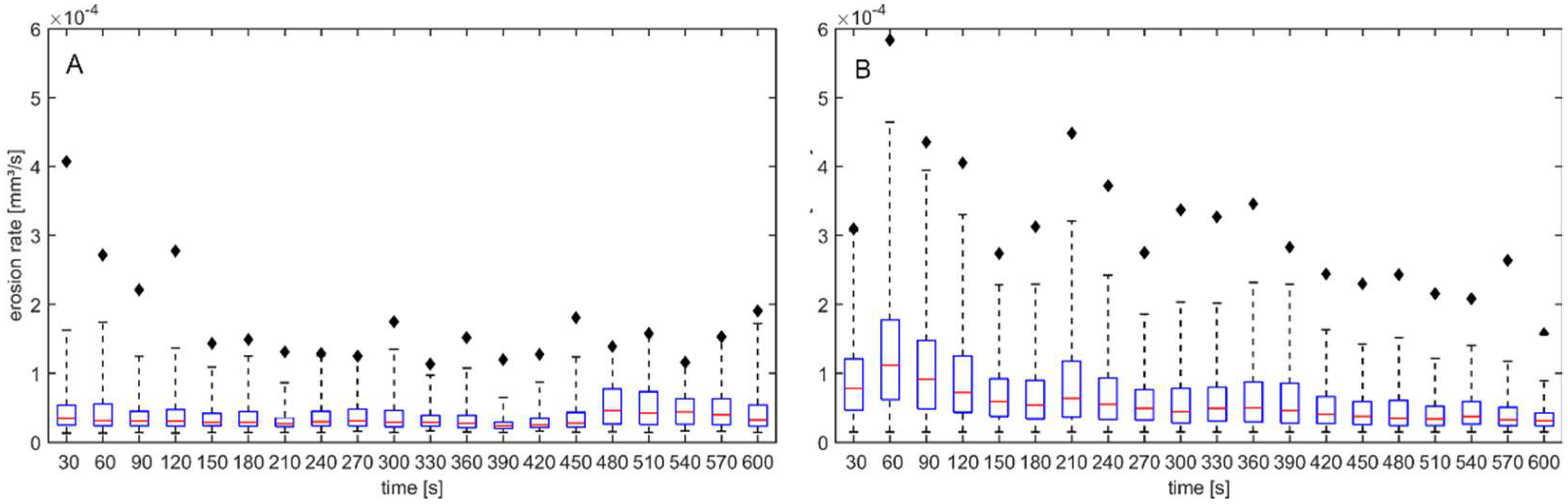
3.2. Accuracy of PHOTOSED
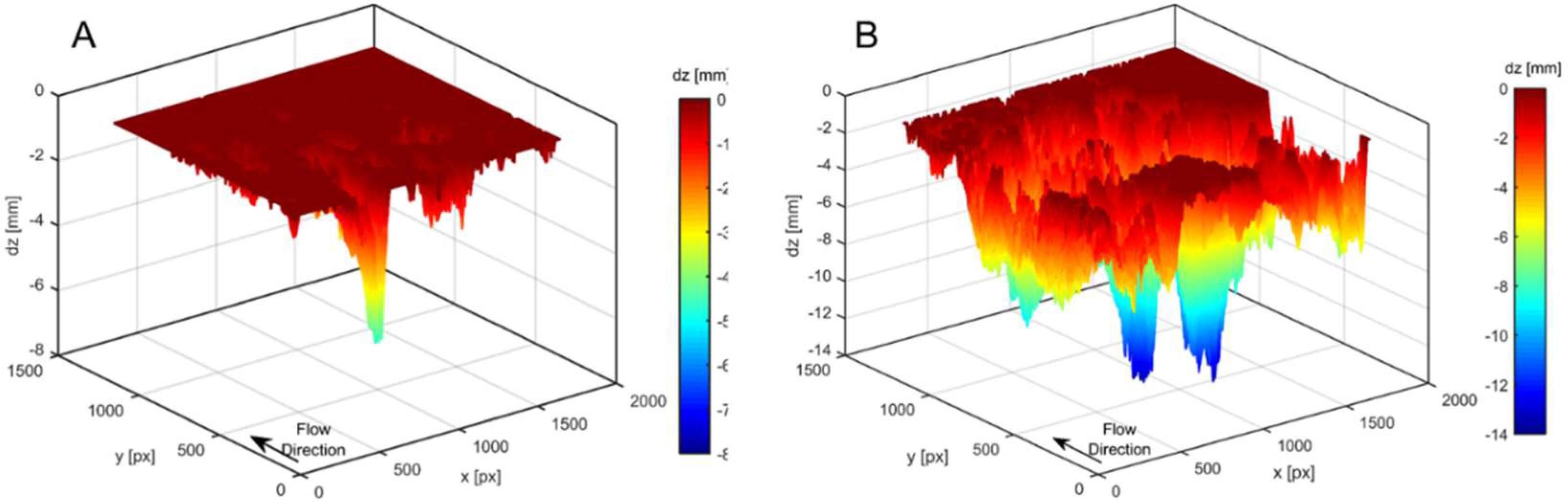
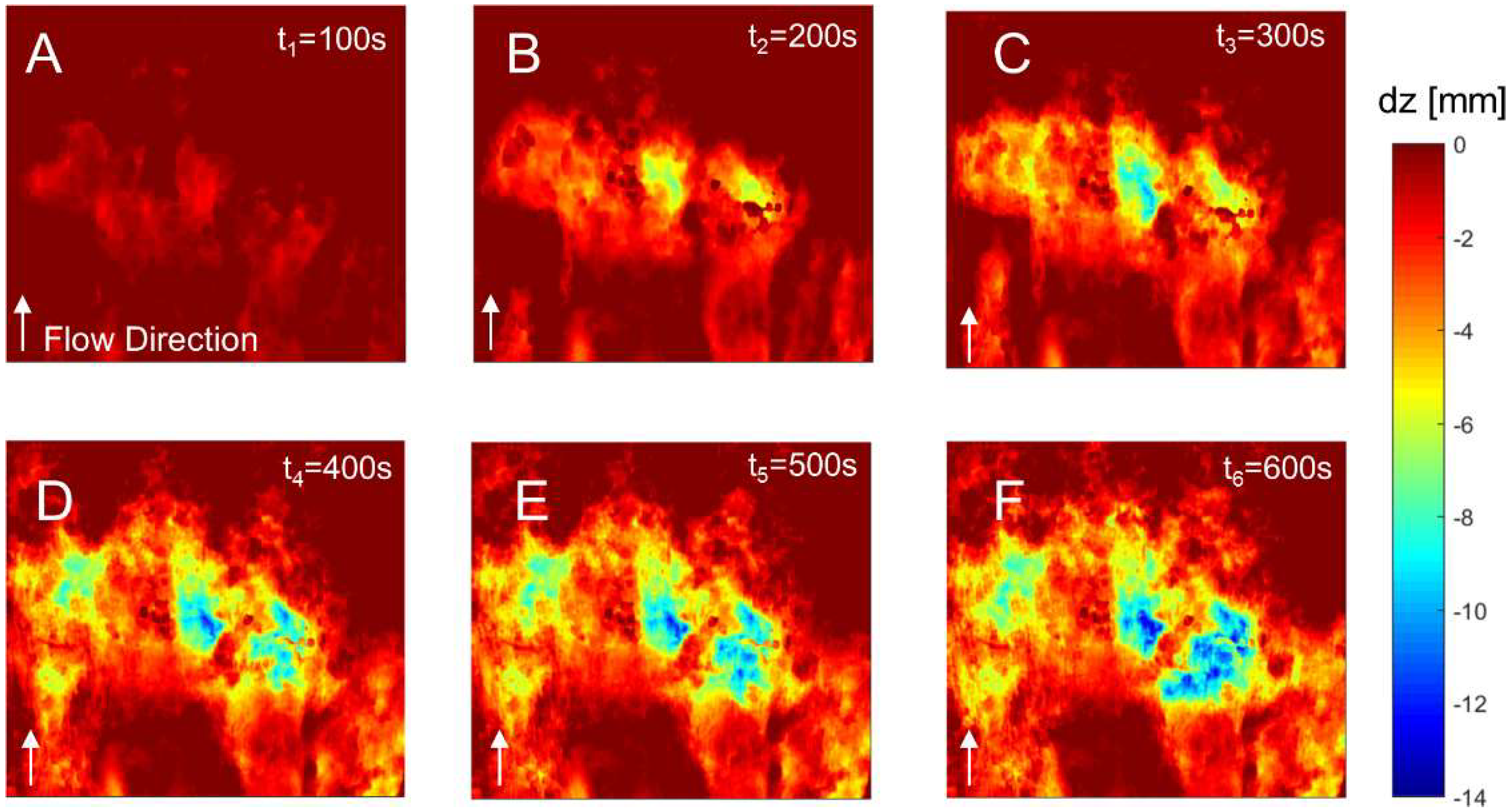
3.3. Exemplary Erosion Experiments
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mirtskhoulava, T.E. Scouring by flowing water of cohesive and noncohesive beds. J. Hydraul. Res. 1991, 29, 341–354. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Jain, R.K. Erosion characteristics of cohesive sediment mixtures. In River Flow 2010: Proceedings of the 5th International Conference on Fluvial Hydraulics (Vol. 1); Braunschweig, Germany, 8–10 September 2010; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2010. [Google Scholar]
- Wu, W.; Perera, C.; Smith, J.; Sanchez, A. Critical shear stress for erosion of sand and mud mixtures. J. Hydraul. Res. 2017, 56, 1–15. [Google Scholar] [CrossRef]
- Paterson, D.M.; Black, K.S. Water flow, sediment dynamics and benthic biology. Adv. Ecol. Res. 1999, 29, 155–196. [Google Scholar] [CrossRef]
- Parchure, T.M.; Mehta, A.J. Erosion of Soft Cohesive Sediment Deposits. J. Hydraul. Eng. 1985, 111, 1308–1326. [Google Scholar] [CrossRef]
- Mitchener, H.; Torfs, H. Erosion of mud/sand mixtures. Coast. Eng. 1996, 29, 1–25. [Google Scholar] [CrossRef]
- Sanford, L.P.; Maa, J.P.-Y. A unified erosion formulation for fine sediments. Mar. Geol. 2001, 179, 9–23. [Google Scholar] [CrossRef]
- Van Prooijen, B.C.; Winterwerp, J.C. A stochastic formulation for erosion of cohesive sediments. J. Geophys. Res. 2010, 115, C01005. [Google Scholar] [CrossRef]
- Walder, J.S. Dimensionless erosion laws for cohesive sediment. J. Hydraul. Eng. 2015, 142. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, J.; Liao, H.; Wang, J.; Fan, B.; Yao, S. Research on cohesive sediment erosion by flow: An overview. Sci. China Ser. E Technol. Sci. 2008, 51, 2001–2012. [Google Scholar] [CrossRef]
- Berlamont, J.; Ockenden, M.; Toorman, E.; Winterwerp, J.C. The characterisation of cohesive sediment properties. Coast. Eng. 1993, 21, 105–128. [Google Scholar] [CrossRef]
- Black, K.S.; Tolhurst, T.J.; Paterson, D.M.; Hagerthey, S.E. Working with natural cohesive sediments. J. Hydraul. Eng. 2002, 128, 2–8. [Google Scholar] [CrossRef]
- Aberle, J.; Nikora, V.; Walters, R. Effects of bed material properties on cohesive sediment erosion. Mar. Geol. 2004, 207, 83–93. [Google Scholar] [CrossRef]
- Gerbersdorf, S.U.; Jancke, T.; Westrich, B. Physico-chemical and biological sediment properties determining erosion resistance of contaminated riverine sediments—Temporal and vertical pattern at the lauffen reservoir/river neckar, Germany. Limnol.-Ecol. Manag. Inland Waters 2005, 35, 132–144. [Google Scholar] [CrossRef]
- Grabowski, R.C.; Droppo, I.G.; Wharton, G. Erodibility of cohesive sediment: The importance of sediment properties. Earth-Sci. Rev. 2011, 105, 101–120. [Google Scholar] [CrossRef]
- Mehta, A.J.; Partheniades, E. Resuspension of deposited cohesive sediment beds. Coast. Eng. Proc. 1982, 1, 1569–1588. [Google Scholar]
- Aberle, J. Measurement techniques for the estimation of cohesive sediment erosion. In Hydraul. Methods for Catastrophes: Floods, Droughts, Environmental Disasters; Rowiński, P.M., Ed.; Publications of the Institute of Geophysics, Polish Academy of Sciences: Warsaw, Poland, 2008; Volume 406, pp. 5–20. [Google Scholar]
- Maa, J.P.-Y.; Wright, L.D.; Lee, C.-H.; Shannon, T.W. VIMS sea carousel: A field instrument for studying sediment transport. Mar. Geol. 1993, 115, 271–287. [Google Scholar] [CrossRef]
- Bale, A.J.; Widdows, J.; Harris, C.B.; Stephens, J.A. Measurements of the critical erosion threshold of surface sediments along the Tamar Estuary using a mini-annular flume. Cont. Shelf Res. 2006, 26, 1206–1216. [Google Scholar] [CrossRef]
- McNeil, J.; Taylor, C.; Lick, W. Measurements of erosion of undisturbed bottom sediments with depth. J. Hydraul. Eng. 1996, 122, 316–324. [Google Scholar] [CrossRef]
- Roberts, J.D.; Jepsen, R.A.; James, S.C. Measurements of sediment erosion and transport with the adjustable shear stress erosion and transport flume. J. Hydraul. Eng. 2003, 129, 862–871. [Google Scholar] [CrossRef]
- Noack, M.; Gerbersdorf, S.U.; Hillebrand, G.; Wieprecht, S. Combining field and laboratory measurements to determine the erosion risk of cohesive sediments best. Water 2015, 7, 5061–5077. [Google Scholar] [CrossRef]
- Wan, C.F.; Fell, R. Investigation of rate of erosion of soils in embankment dams. J. Geotech. Geoenviron. Eng. 2004, 130, 373–380. [Google Scholar] [CrossRef]
- Gust, G.; Muller, V. Interfacial hydrodynamics and entrainment functions of currently used erosion devices. In Cohesive Sediments; Burt, N., Parker, R., Watts, J., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 1997; pp. 149–174. [Google Scholar]
- Tolhurst, T.J.; Black, K.S.; Paterson, D.M.; Mitchener, H.J.; Termaat, G.R.; Shayler, S.A. A comparison and measurement standardisation of four in situ devices for determining the erosion shear stress of intertidal sediments. Cont. Shelf Res. 2000, 20, 1397–1418. [Google Scholar] [CrossRef]
- Witt, O.; Westrich, B. Qunatification of erosion rates for undistrubed contaminated cohesive sediment cores by image analysis. Hydrobiologia 2003, 494, 271–276. [Google Scholar] [CrossRef]
- Kern, U.; Haag, I.; Schürlein, V.; Holzwarth, M.; Westrich, B. Ein strömungskanal zur ermittlung der tiefenabhängigen erosionsstabilität von gewässersedimente. Wasserwirtschaft 1999, 89, 72–77. [Google Scholar]
- Debnath, K.; Nikora, V.; Aberle, J.; Westrich, B.; Muste, M. Erosion of cohesive sediments resuspension, bed load, and erosion patterns from field experiments. J. Hydraul. Eng. 2007, 133, 508–520. [Google Scholar] [CrossRef]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981. [Google Scholar]
- Farnebäck, G. Two-frame motion estimation based on polynomial expansion. In Image Analysis; Lecture Notes in Computer Science; Springer: Berlin, Heidelberg, 2003; pp. 363–370. [Google Scholar]
- Noack, M.; Hillebrand, G.; Seidenkranz, U.; Wieprecht, S. Investigation on the erosion stability of cohesive sediment deposits in the weir channel of the barrage Iffezheim, river rhine. Hydrol. Wasserbewirtsch. 2016, 60, 164–175. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noack, M.; Schmid, G.; Beckers, F.; Haun, S.; Wieprecht, S. PHOTOSED—PHOTOgrammetric Sediment Erosion Detection. Geosciences 2018, 8, 243. https://doi.org/10.3390/geosciences8070243
Noack M, Schmid G, Beckers F, Haun S, Wieprecht S. PHOTOSED—PHOTOgrammetric Sediment Erosion Detection. Geosciences. 2018; 8(7):243. https://doi.org/10.3390/geosciences8070243
Chicago/Turabian StyleNoack, Markus, Gerhard Schmid, Felix Beckers, Stefan Haun, and Silke Wieprecht. 2018. "PHOTOSED—PHOTOgrammetric Sediment Erosion Detection" Geosciences 8, no. 7: 243. https://doi.org/10.3390/geosciences8070243
APA StyleNoack, M., Schmid, G., Beckers, F., Haun, S., & Wieprecht, S. (2018). PHOTOSED—PHOTOgrammetric Sediment Erosion Detection. Geosciences, 8(7), 243. https://doi.org/10.3390/geosciences8070243




