Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data
Abstract
1. Introduction
2. The 2011–2015 Etna Lava Fountains
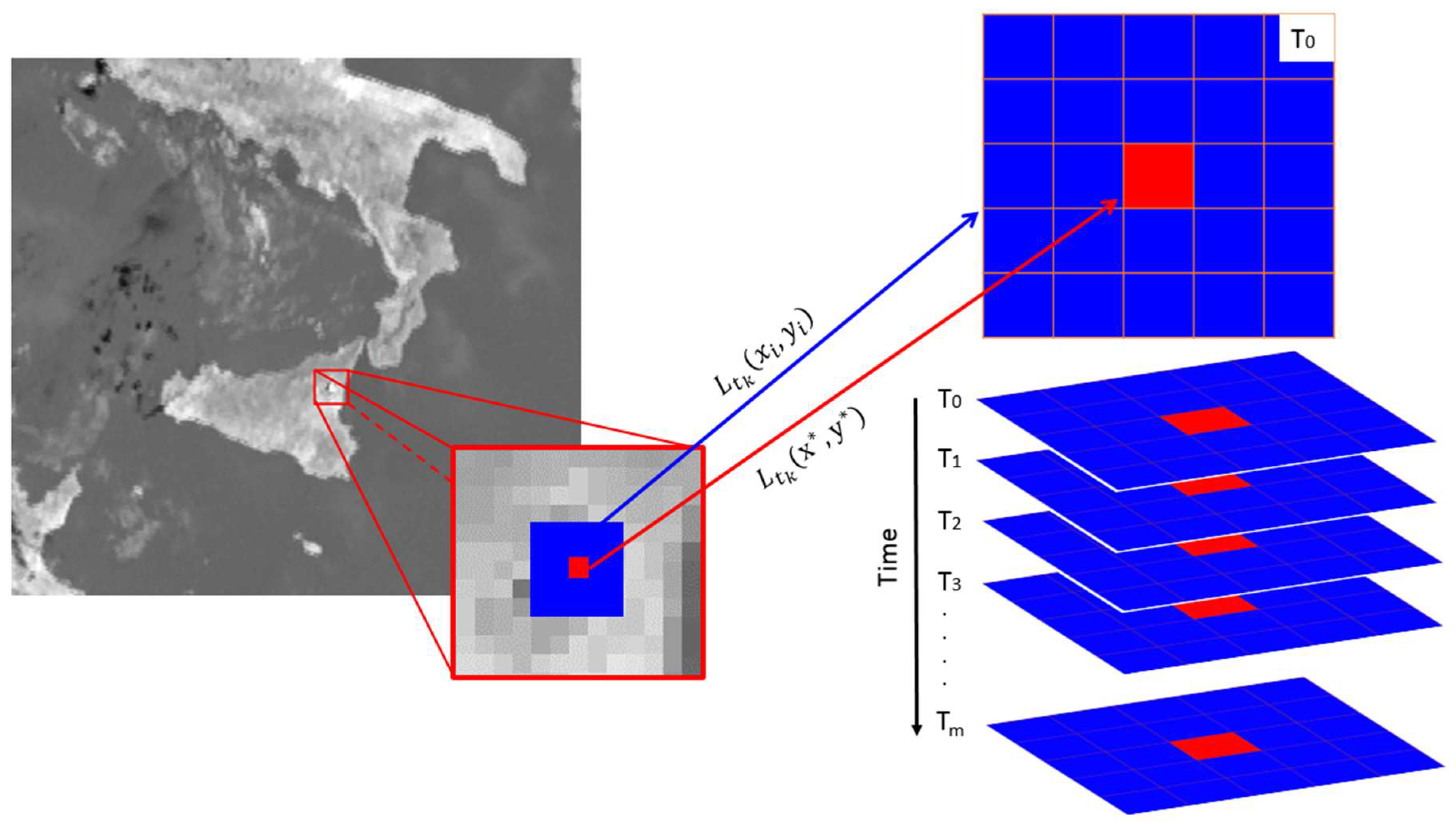
3. Proximal Monitoring of Volcanic Eruptions
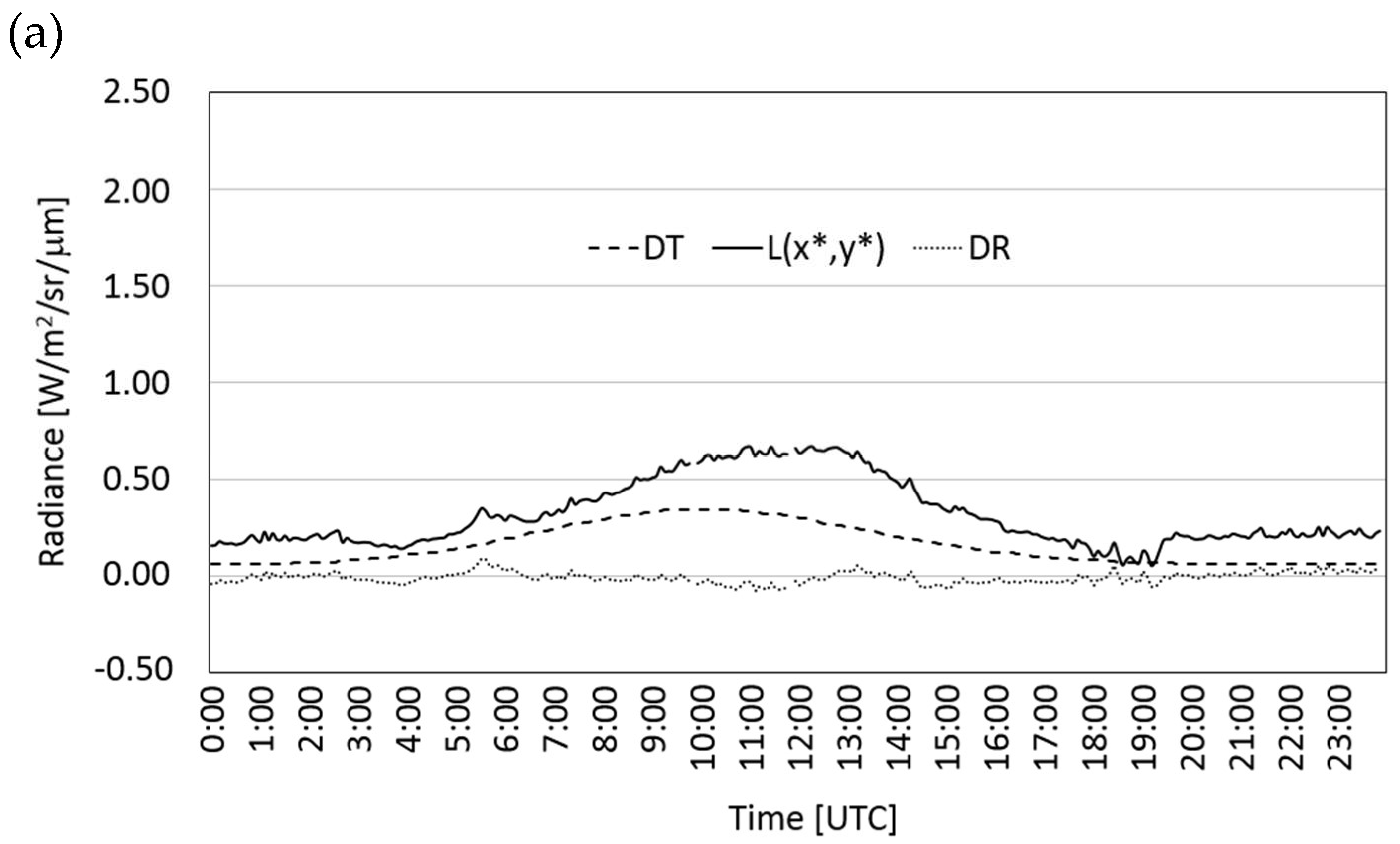
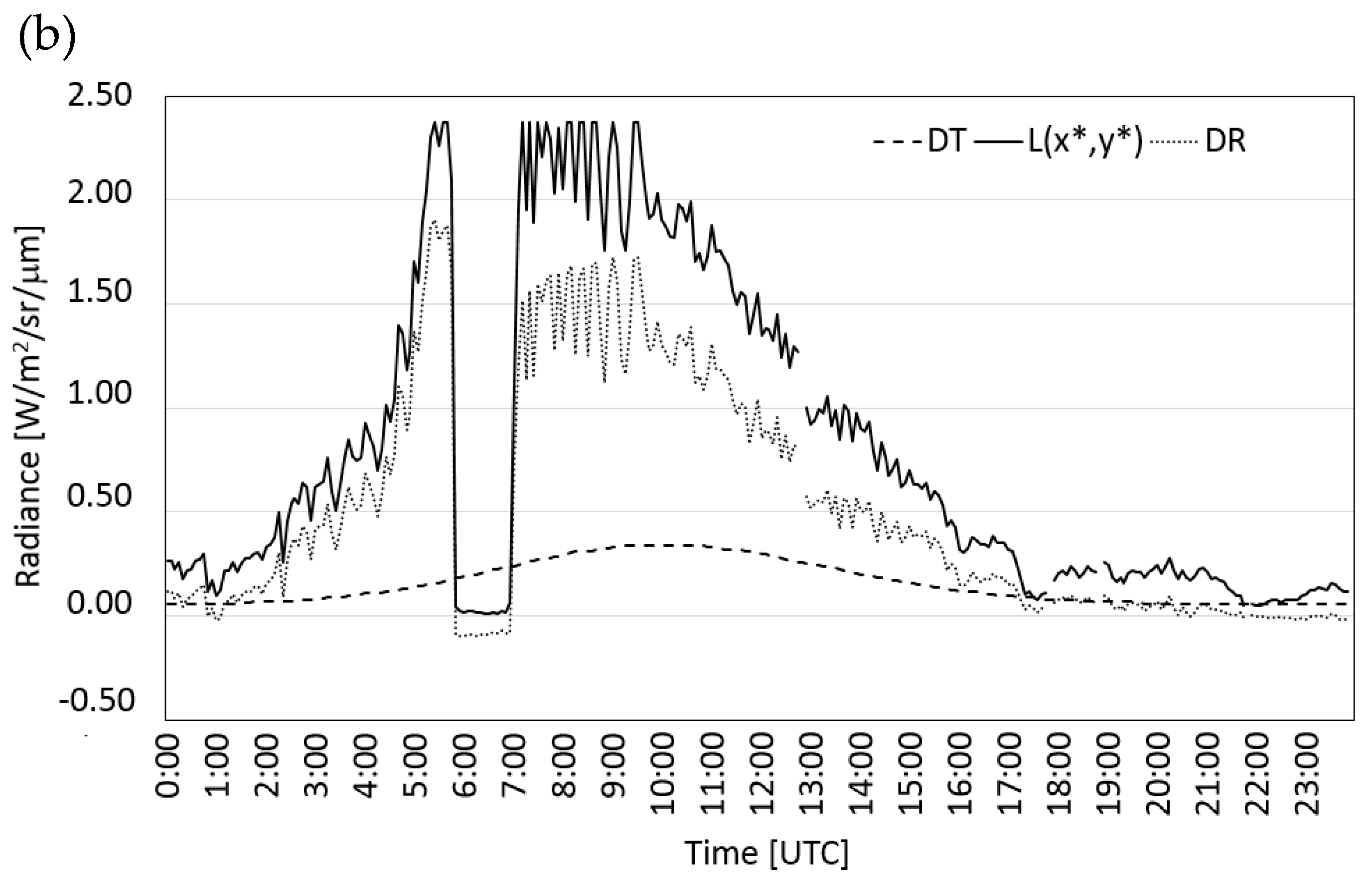
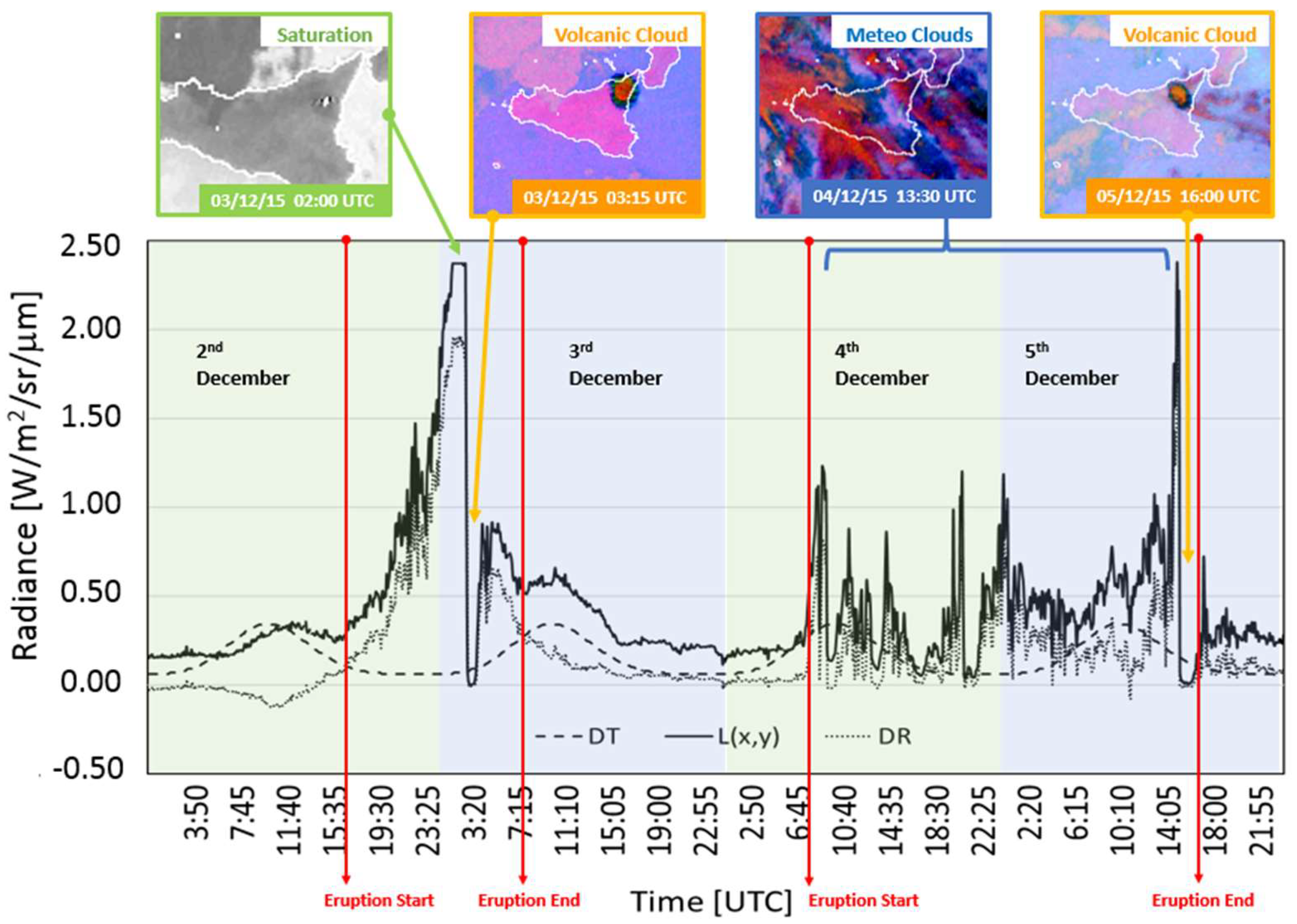
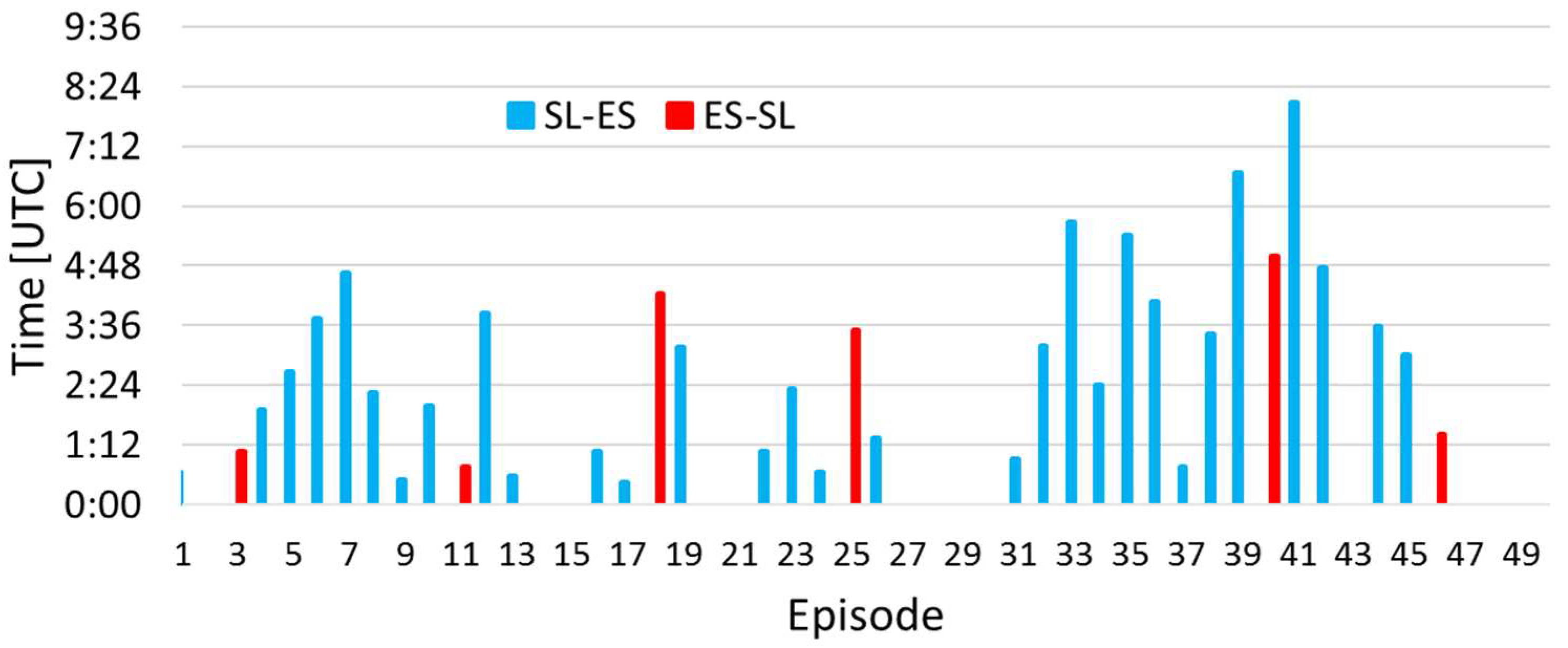
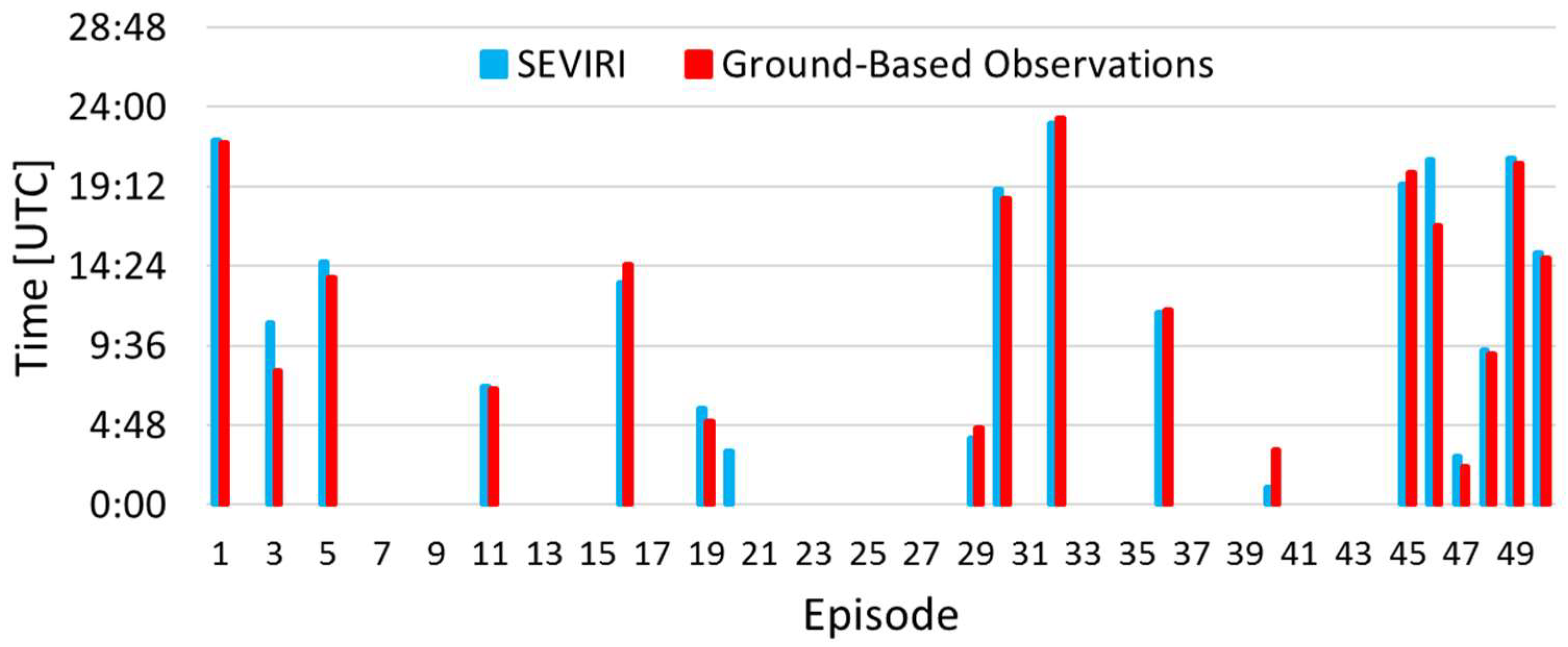
3.1. Eruption Start and Duration
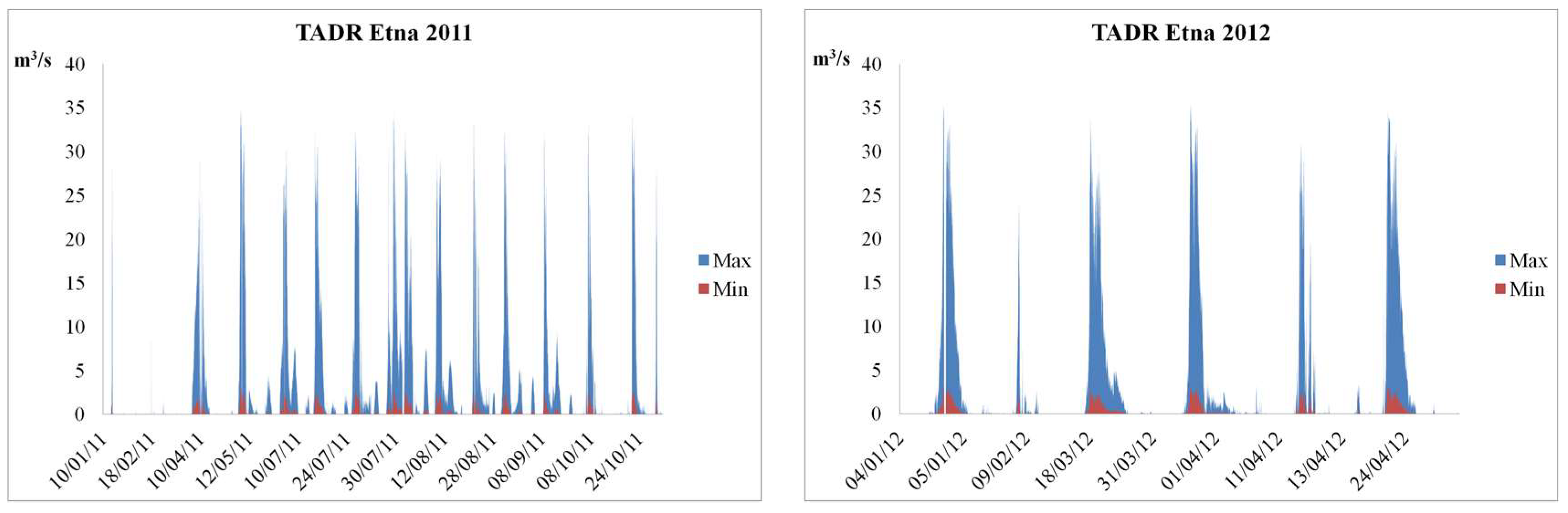
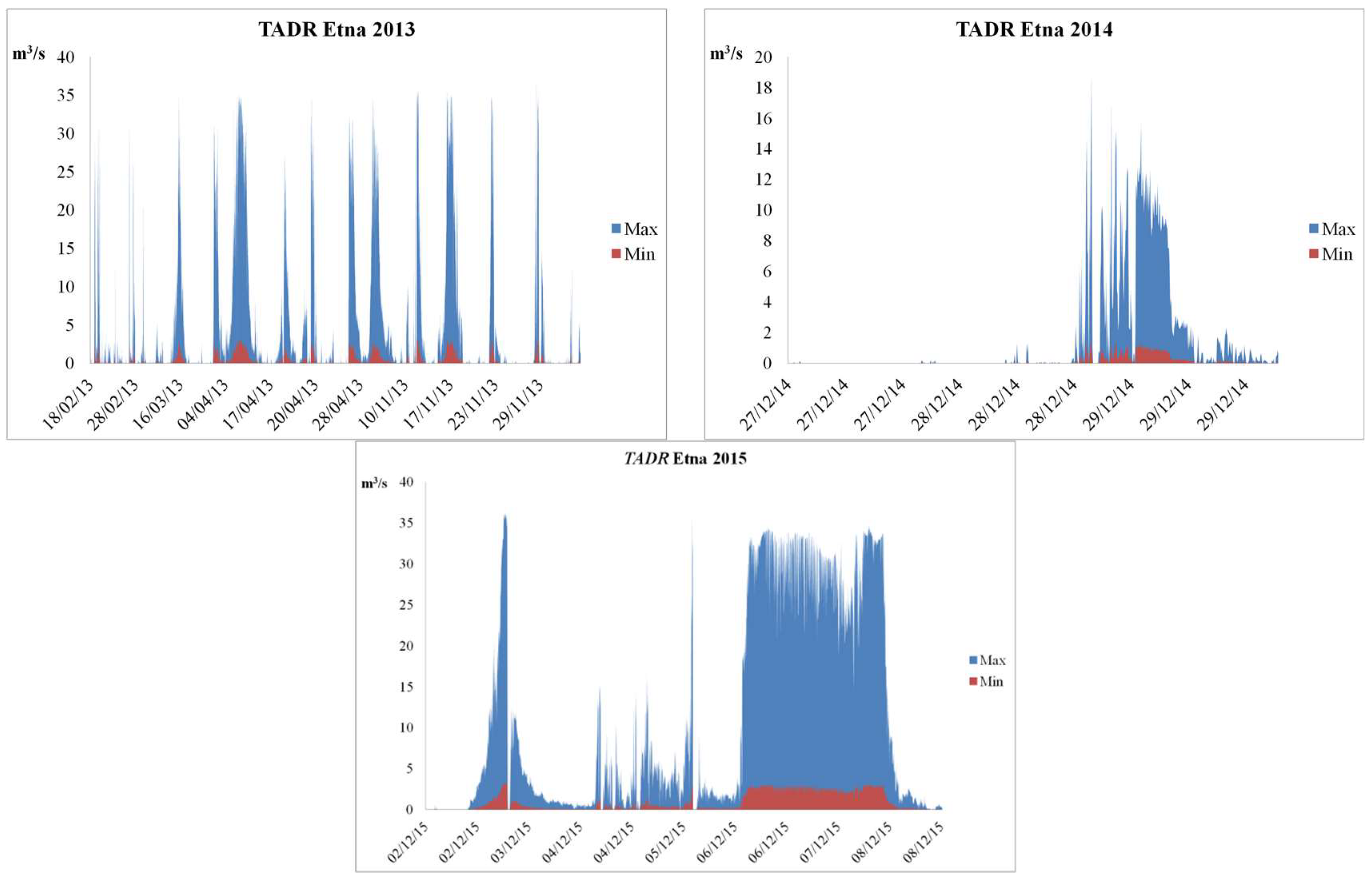
3.2. Lava Discharge during Etna’s Lava Fountains
3.3. Volcanic Plume Top Height
4. Results
5. Validation
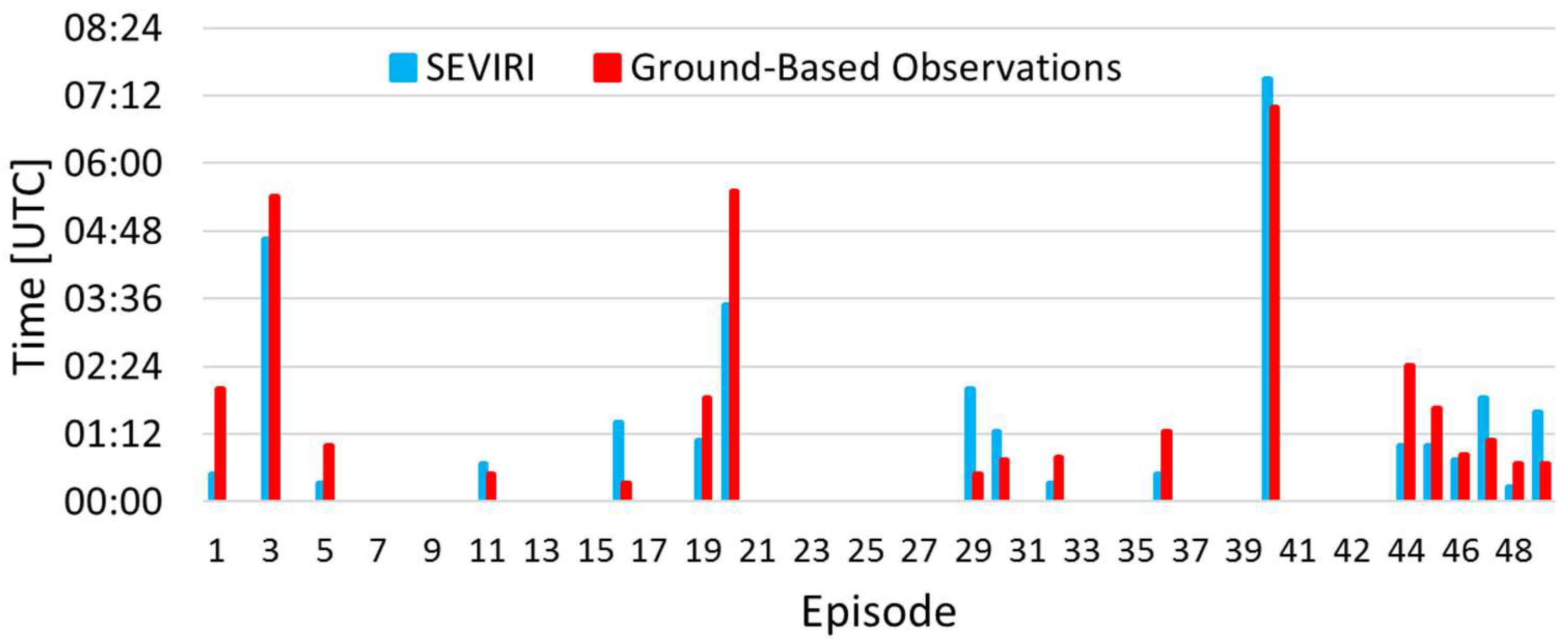
5.1. Eruption and Fountains Start and Duration
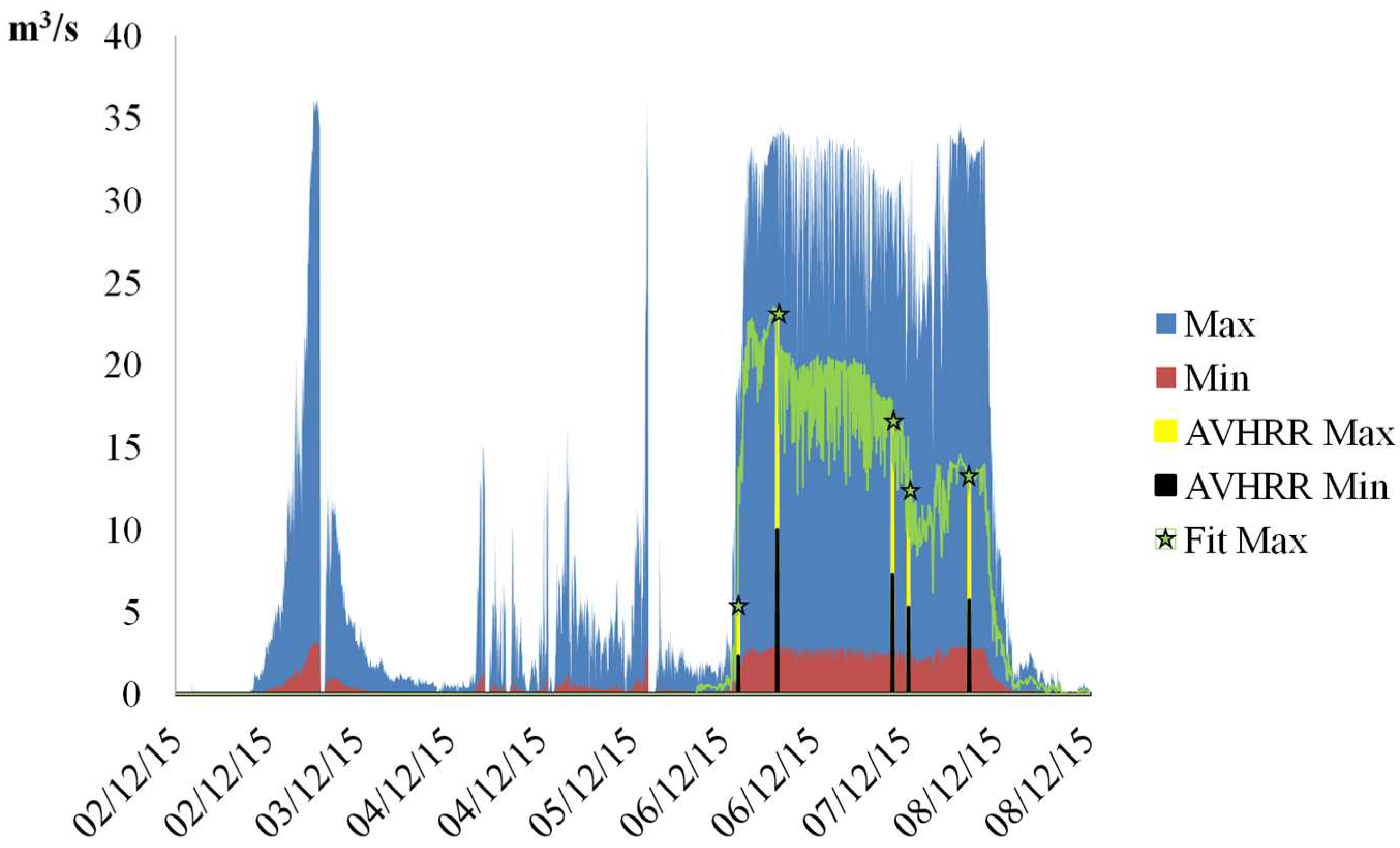
5.2. TADR Improvement Using AVHRR Data
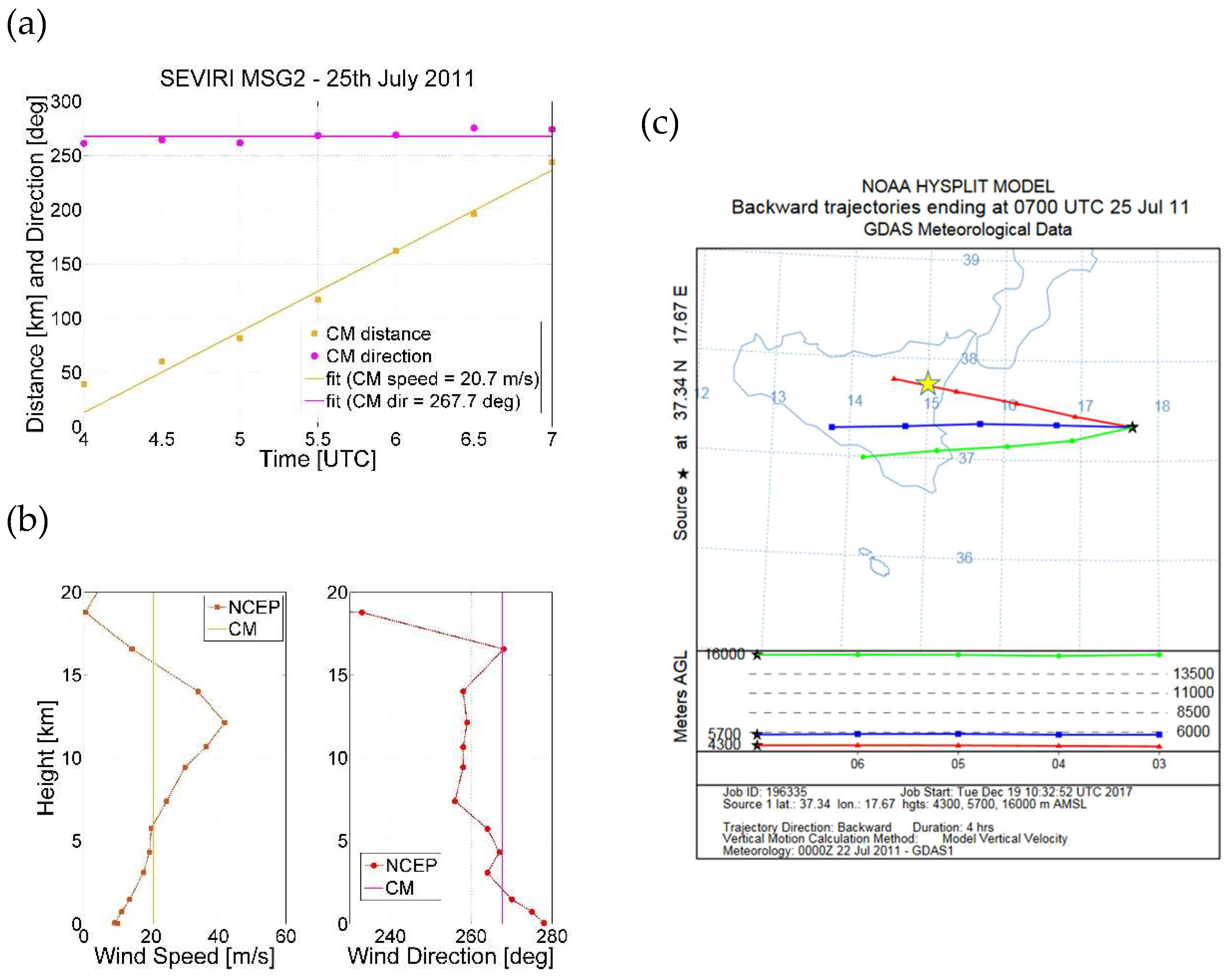
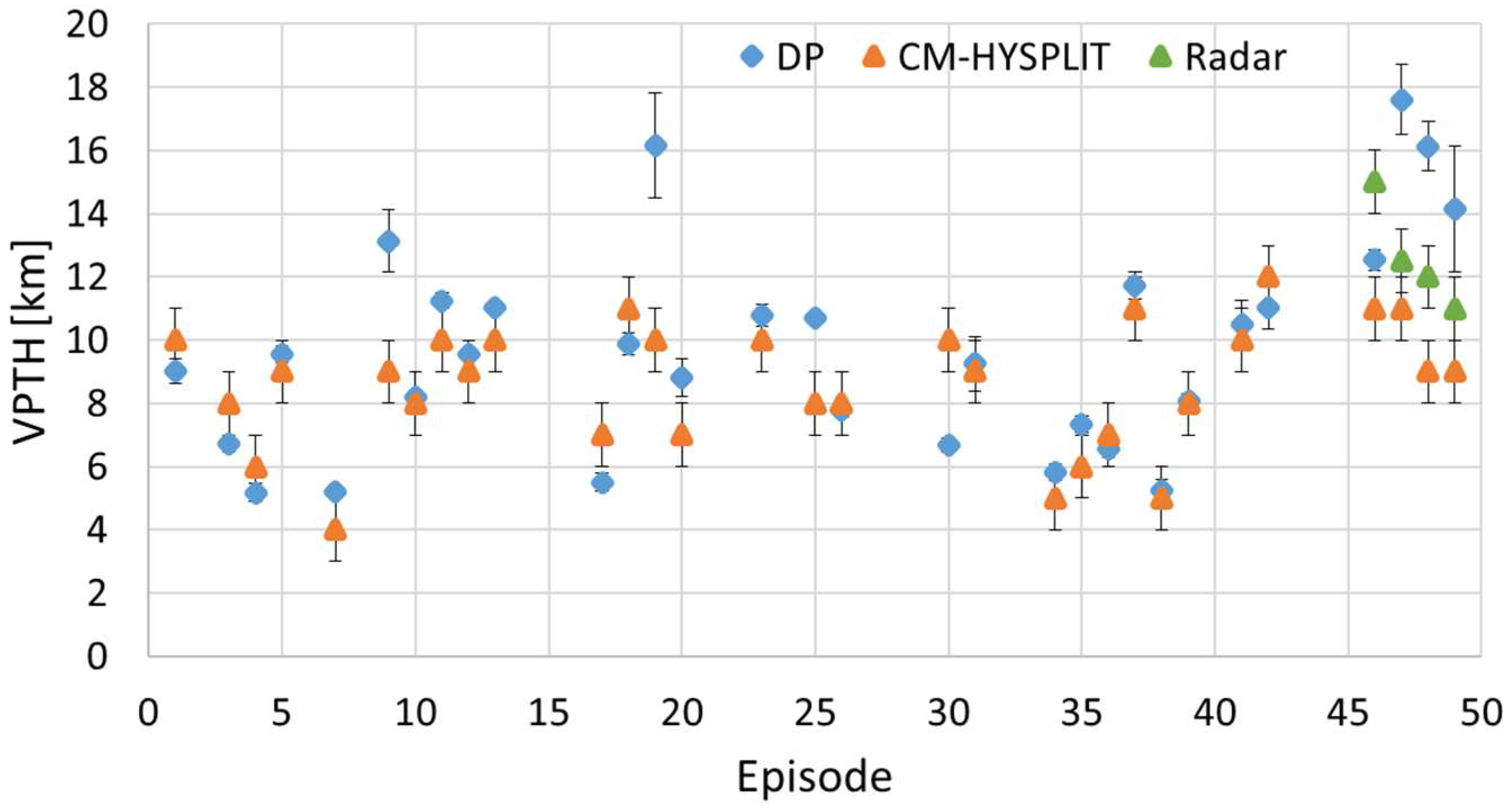
5.3. VPTH by Using the Tracking of the Ash Cloud Center of Mass and HYSPLIT Backtrajectories
- retrieval of the ash abundance map from a given SEVIRI image [34];
- identification of the ash cloud centre of mass;
- computation of the ash centre of mass distance from the top of the volcano and the angle relative to the North.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Corradini, S.; Montopoli, M.; Guerrieri, L.; Ricci, M.; Scollo, S.; Merucci, L.; Marzano, F.S.; Pugnaghi, S.; Prestifilippo, M.; Ventress, L.J.; et al. Multi-Sensor Approach for Volcanic Ash Cloud Retrieval and Eruption Characterization: The 23 November 2013 Etna Lava Fountain. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Merucci, L.; Zakšek, K.; Carboni, E.; Corradini, S. Stereoscopic estimation of volcanic cloud-top height from two geostationary satellites. Remote Sens. 2016, 8, 206. [Google Scholar] [CrossRef]
- Prata, A.J.; Kerkmann, J. Simultaneous retrieval of volcanic ash and SO2 using MSG-SEVIRI measurements. Geophys. Res. Lett. 2007, 34, L05813. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Prata, A.J. Retrieval of SO2 from Thermal Infrared Satellite Measurements: Correction Procedures for the Effects of Volcanic Ash. Atmos. Meas. Tech. 2009, 2, 177–191. [Google Scholar] [CrossRef]
- Merucci, L.; Burton, M.; Corradini, S.; Salerno, G. Reconstruction of SO2 flux emission chronology from space-based measurements. J. Volcanol. Geotherm. Res. 2011. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Blake, S.; Rothery, D.A.; Stevens, N.F. A chronology of the 1991 to 1993 Etna eruption using AVHRR data: Implications for real time thermal volcano monitoring. J. Geophys. Res. 1997, 102, 7985–8003. [Google Scholar] [CrossRef]
- Wooster, M.J.; Rothery, D.A. Time series analysis of effusive volcanic activity using the ERS along track scanning radiometer: The 1995 eruption of Fernandina volcano, Galapagos Island. Remote Sens. Environ. 1997, 69, 109–117. [Google Scholar] [CrossRef]
- Ganci, G.; Harris, A.J.L.; Del Negro, C.; Guehenneux, Y.; Cappello, A.; Labazuy, P.; Calvari, S.; Gouhier, M. A year of lava fountaining at Etna: Volumes from SEVIRI. Geophys. Res. Lett. 2012, 39, L06305. [Google Scholar] [CrossRef]
- Scollo, S.; Boselli, A.; Coltelli, M.; Leto, G.; Pisani, G.; Prestifilippo, M.; Spinelli, N.; Wang, X. Volcanic ash concentration during the 12 August 2011 Etna eruption. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Behncke, B.; Branca, S.; Corsaro, R.A.; De Beni, E.; Miraglia, L.; Proietti, C. The 2011–2012 summit activity of Mount Etna: Birth, growth and products of the new SE crater. J. Volcanol. Geotherm. Res. 2014, 270, 10–21. [Google Scholar] [CrossRef]
- Scollo, S.; Prestifilippo, M.; Pecora, E.; Corradini, S.; Merucci, L.; Spata, G.; Coltelli, M. Eruption column height estimation of the 2011–2013 Etna lava fountains. Ann. Geophys. 2014, 57. [Google Scholar] [CrossRef]
- International Civil Aviation Organization (ICAO). Volcanic Ash Contingency Plan—Eur and Nat Regions; EUR Doc 019–NAT Doc 006, Part II; International Civil Aviation Authority: Montreal, QC, Canada, 2010. [Google Scholar]
- Andronico, D.; Scollo, S.; Cristaldi, A. Unexpected hazards from tephra fallouts at Mt Etna: The 23 November 2013 lava fountain. J. Volcanol. Geotherm. Res. 2015, 304, 118–125. [Google Scholar] [CrossRef]
- Bonaccorso, S.; Calvari, S.; Linde, A.; Sacks, S. Eruptive processes leading to the most explosive lava fountain at Etna volcano: The 23 November 2013 episode. Geophys. Res. Lett. 2014, 41, 4912–4919. [Google Scholar] [CrossRef]
- Vulpiani, G.; Ripepe, M.; Valade, S. Mass discharge rate retrieval combining weather radar and thermal camera observations. J. Geophys. Res. Solid Earth 2016, 121, 5679–5695. [Google Scholar] [CrossRef]
- Corsaro, R.A.; Andronico, D.; Behncke, B.; Branca, S.; Caltabiano, T.; Ciancitto, F.; Cristaldi, A.; De Beni, E.; La Spina, A.; Lodato, L.; et al. Monitoring the December 2015 summit eruptions of Mt. Etna (Italy): Implications on eruptive dynamics. J. Volcanol. Geotherm. Res. 2017. [Google Scholar] [CrossRef]
- Matson, M.; Dozier, J. Identification of subresolution high temperature sources using a thermal IR sensor. Photogramm. Eng. Remote Sens. 1981, 47, 1311–1318. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Rothery, D.A.; Francis, P.; Wood, W. Volcano monitoring using short wavelength infrared data from satellite. J. Geophys. Res. 1988, 93, 7993–8008. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Romaguera, M. Land surface temperature retrieval from MSG1-SEVIRI data. Remote Sens. Environ. 2004, 92, 247–254. [Google Scholar] [CrossRef]
- Musacchio, M.; Silvestri, M.; Buongiorno, M.F. Use of radiance value from MSG SEVIRI and MTSAT data: Application for the monitoring on volcanic area. In Proceedings of the 2011 EUMETSAT Meteorological Satellite Conference, Oslo, Norway, 5–9 September 2011. [Google Scholar]
- Musacchio, M.; Silvestri, M.; Buongiorno, M.F. RT Monitoring of active volcanoes: MT Etna. In Proceedings of the Sea Space International Remote Sensing Conference, Seaspace Corporation, San Diego, CA, USA, 21–24 October 2012. [Google Scholar]
- Gouhier, M.; Harris, A.J.L.; Calvari, S.; Labazuy, P.; Guéhenneux, Y.; Donnadieu, F.; Valade, S. Erratum to: Lava discharge during Etna’s January 2011 fire fountain tracked using MSG-SEVIRI. Bull. Volcanol. 2012, 74, 1261. [Google Scholar] [CrossRef][Green Version]
- Wright, R.; Blake, S.; Harris, A.J.L.; Rothery, D. A Simple explanation for the space-based calculation of lava eruptions rates. Earth Planet. Sci. Lett. 2001, 192, 223–233. [Google Scholar] [CrossRef]
- Lombardo, V. AVHotRR: Near-real time routine for volcano monitoring using IR satellite data. Geol. Soc. Lond. 2015, 426. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Baloga, S.M. Lava discharge rates from satellite measured heat flux. Geophys. Res. Lett. 2009, 36, L19302. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Favalli, M.; Steffke, A.; Fornaciai, A.; Boschi, E. A relation between lava discharge rate, thermal insulation, and flow area set using Lidar data. Geophys. Res. Lett. 2010, 37, L20308. [Google Scholar] [CrossRef]
- Ganci, G.; Vicari, A.; Fortuna, L.; Del Negro, C. The HOTSAT volcano monitoring system based on a combined use of SEVIRI and MODIS multispectral data. Ann. Geophys. 2011, 54. [Google Scholar] [CrossRef]
- Hirn, B.; Ferrucci, F.; Di Bartola, C. Near-tactical eruption rate monitoring of Pu’u O’o (Hawaii) 2000–2005 by synergetic merge of payloads ASTER and MODIS. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2007, Barcelona, Spain, 23–28 July 2007; pp. 3744–3747. [Google Scholar] [CrossRef]
- Govaerts, Y.; Arriaga, A.; Schmetz, J. Operational vicarious calibration of the MSG/SEVIRI solar channels. Adv. Space Res. 2001, 28, 21–30. [Google Scholar] [CrossRef]
- Prata, A.J.; Grant, I.F. Retrieval of microphysical and morphological properties of volcanic ash plumes from satellite data: Application to Mt Ruapehu, New Zealand. Q. J. R. Meteorol. Soc. 2001, 127, 2153–2179. [Google Scholar] [CrossRef]
- Corradini, S.; Spinetti, C.; Carboni, E.; Tirelli, C.; Buongiorno, M.F.; Pugnaghi, S.; Gangale, G. Mt. Etna tropospheric ash retrieval and sensitivity analysis using Moderate Resolution Imaging Spectroradiometer measurements. J. Appl. Remote Sens. 2008, 2, 023550. [Google Scholar] [CrossRef]
- De Beni, E.; Behncke, B.; Branca, S.; Nicolosi, I.; Carluccio, R.; D’Ajello Caracciolo, F.; Chiappini, M. The continuing story of Etna’s New Southeast Crater (2012–2014): Evolution and volume calculations based on field surveys and aerophotogrammetry. J. Volcanol. Geotherm. Res. 2015, 303, 175–186. [Google Scholar] [CrossRef]
- Guerrieri, L.; Merucci, L.; Corradini, S.; Pugnaghi, S. Evolution of the 2011 Mt. Etna ash and SO2 lava fountain episodes using SEVIRI data and VPR retrieval approach. J. Volcanol. Geotherm. Res. 2015, 291, 63–71. [Google Scholar] [CrossRef]
- The NCEP/NCAR Reanalysis Project at the NOAA/ESRL Physical Sciences Division. Available online: http://www.esrl.noaa.gov/psd/data/reanalysis/reanalysis.shtml (accessed on 1 December 2017).
- Pardini, F.; Burton, M.; de’ Michieli Vitturi, M.; Corradini, S.; Salerno, G.; Merucci, L.; Di Grazia, G. Retrieval and intercomparison of volcanic SO2 injection height and eruption time from satellite maps and ground-based observations. J. Volcanol. Geotherm. Res. 2016. [Google Scholar] [CrossRef]
- Draxler, R.R. HYSPLIT4 User’s Guide; NOAA Tech. Memo. ERL ARL-230; NOAA Air Resources Laboratory: Silver Spring, MD, USA, 1999.
- Stein, A.F.; Draxler, R.R.; Rolph, G.D.; Stunder, B.J.B.; Cohen, M.D.; Ngan, F. NOAA’s HYSPLIT atmospheric transport and dispersion modeling system. Bull. Am. Meteorol. Soc. 2015, 96, 2059–2077. [Google Scholar] [CrossRef]
- Rolph, G.; Stein, A.; Stunder, B. Real-time Environmental Applications and Display sYstem: READY. Environ. Model. Softw. 2017, 95, 210–228. [Google Scholar] [CrossRef]

| Reference Date | Episode Number | Start Eruption | Start Fountaining | End Fountaining | End Eruption | Duration Lava Emission | Duration Fountaining | VPTH [Km] |
|---|---|---|---|---|---|---|---|---|
| 12/01/2011 | 1 | 12/01/2011 19:30 | 12/01/2011 22:00 | 12/01/2011 22:30 | 13/01/2011 03:00 | 7:30 | 00:30 | 9.0 +/− 0.4 |
| 18/02/2011 | 2 | / | / | / | / | / | / | |
| 10/04/2011 | 3 | 09/04/2011 19:00 | 10/04/2011 11:00 | 10/04/2011 15:40 | 11/04/2011 23:50 | 52:50 | 04:40 | 6.7 +/− 0.3 |
| 12/05/2011 | 4 | 11/05/2011 18:35 | / | / | 12/05/2011 23:50 | 29:15 | / | 5.2 +/− 0.3 |
| 09/07/2011 | 5 | 09/07/2011 09:25 | 09/07/2011 14:40 | 09/07/2011 15:00 | 10/07/2011 11:25 | 26:00 | 00:20 | 9.6 +/− 0.3 |
| 19/07/2011 | 6 | 18/07/2011 20:45 | / | / | 20/07/2011 04:00 | 31:15 | / | / |
| 25/07/2011 | 7 | 24/07/2011 20:50 | / | / | 26/07/2011 02:45 | 29:55 | / | 5.2 +/− 0.3 |
| 30/07/2011 | 8 | 30/07/2011 07.25 | / | / | 31/07/2011 10:40 | 27:15 | / | / |
| 05/08/2011 | 9 | 05/08/2011 19:45 | / | / | 06/08/2011 10:35 | 14:50 | / | 13.1 +/− 1.0 |
| 12/08/2011 | 10 | 12/08/2011 05:50 | / | / | 13/08/2011 08:20 | 26:30 | / | 8.2 +/− 0.3 |
| 20/08/2011 | 11 | 20/08/2011 03:40 | 20/08/2011 07:10 | 20/08/2011 07:50 | 21/08/2011 05:35 | 25:55 | 00:40 | 11.2 +/− 0.3 |
| 29/08/2011 | 12 | 28/08/2011 23:25 | / | / | 29/08/2011 16:20 | 16:55 | / | 9.6 +/− 0.3 |
| 08/09/2011 | 13 | 08/09/2011 06:15 | / | / | 09/09/2011 09:15 | 27:00 | / | 11.0 +/− 0.3 |
| 19/09/2011 | 14 | / | / | / | / | / | / | / |
| 28/09/2011 | 15 | / | / | / | / | / | / | / |
| 08/10/2011 | 16 | 08/10/2011 12:25 | 08/10/2011 13:25 | 08/10/2011 14:50 | 09/10/2011 03:40 | 15:15 | 01:25 | / |
| 23/10/2011 | 17 | 23/10/2011 17:40 | / | / | 24/10/2011 04:30 | 10:50 | / | 5.5 +/− 0.3 |
| 15/11/2011 | 18 | 15/11/2011 10:15 | / | / | 15/11/2011 20:45 | 10:30 | / | 9.9 +/− 0.4 |
| 05/01/2012 | 19 | 05/01/2012 01:10 | 05/01/2012 05:50 | 05/01/2012 06:55 | 05/01/2012 20:15 | 19:05 | 01:05 | 16.2 +/− 1.7 |
| 09/02/2012 | 20 | 08/02/2012 19:00 | 09/02/2012 03:15 | 09/02/2012 06:45 | 09/02/2012 06:15 | 11:15 | 03:30 | 8.8 +/− 0.6 |
| 04/03/2012 | 21 | / | / | / | / | / | / | / |
| 18/03/2012 | 22 | 18/03/2012 04:50 | / | / | 19/03/2012 04:15 | 23:25 | / | 11.0 +/− 0.4 |
| 01/04/2012 | 23 | 31/03/2012 22:40 | / | / | 02/04/2012 01:35 | 26:55 | / | 10.8 +/− 0.4 |
| 12/04/2012 | 24 | 12/04/2012 11:45 | / | / | 12/04/2012 23:30 | 11:45 | / | / |
| 24/04/2012 | 25 | 23/04/2012 03:30 | / | / | 24/04/2012 12:50 | 33:20 | / | 10.7 +/− 0.2 |
| 19/02/2013 | 26 | 19/02/2013 02:30 | / | / | / | / | / | 7.8 +/− 0.3 |
| 20/02/2013 | 27 | / | / | / | / | / | / | / |
| 20/02/2013 | 28 | / | / | / | / | / | / | / |
| 21/02/2013 | 29 | / | 21/02/2013 04:00 | 21/02/2013 06:00 | / | / | 02:00 | / |
| 23/02/2013 | 30 | / | 23/02/2013 19:00 | 23/02/2013 20:15 | 23/02/2013 18:45 | / | 01:15 | 6.7 +/− 0.3 |
| 28/02/2013 | 31 | 28/02/2013 08:45 | / | / | 28/02/2013 23:30 | 13:45 | / | 9.3 +/− 0.9 |
| 05/03/2013 | 32 | 05/03/2013 20:00 | 05/03/2013 23:00 | 05/03/2013 23:20 | 07/03/2013 03:05 | 31:05 | 00:20 | / |
| 16/03/2013 | 33 | 16/03/2013 11:20 | / | / | 17/03/2013 04:45 | 17:25 | / | / |
| 03/04/2013 | 34 | 03/04/2013 10:40 | / | / | 04/04/2013 04:40 | 17:59 | / | 5.8 +/− 0.3 |
| 12/04/2013 | 35 | 11/04/2013 11:15 | / | / | 13/04/2013 04:00 | 40:45 | / | 7.3 +/− 0.3 |
| 18/04/2013 | 36 | 18/04/2013 07:25 | 18/04/2013 11:35 | 18/04/2013 12:05 | 19/04/2013 04:30 | 21:05 | 00:30 | 6.6 +/− 0.3 |
| 20/04/2013 | 37 | 19/04/2013 23:00 | / | / | 21/04/2013 03:05 | 28:05 | / | 11.7 +/− 0.4 |
| 27/04/2013 | 38 | 27/04/2013 13:35 | / | / | 28/04/2013 07:30 | 17:55 | / | 5.2 +/− 0.4 |
| 26/10/2013 | 39 | 25/10/2013 19:20 | / | / | 27/10/2013 21:50 | 50:30 | / | 8.1 +/− 0.3 |
| 11/11/2013 | 40 | 11/11/2013 08:00 | 11/11/2013 01:05 | 11/11/2013 0 7:30 | 12/11/2013 04:40 | 20:40 | 06:25 | |
| 17/11/2013 | 41 | 16/11/2013 15:15 | / | / | 18/11/2013 03:20 | 36:05 | / | 10.5 +/− 0.8 |
| 23/11/2013 | 42 | 23/11/2013 05:15 | / | / | 24/11/2013 01:00 | 19:45 | / | 11.1 +/− 0.7 |
| 28/11/2013 | 43 | 28/11/2013 16:50 | / | / | 29/11/2013 10:30 | 17:40 | / | / |
| 02/12/2013 | 44 | 02/12/2013 17:00 | 02/12/2013 19:20 | 02/12/2013 20:20 | 03/12/2013 17:05 | 24:05 | 01:00 | / |
| 28/12/2014 | 45 | 28/12/2014 18:15 | 28/12/2014 20:50 | 28/12/2014 21:50 | 29/12/2014 16:20 | 22:05 | 01:00 | / |
| 03/12/2015 | 46 | 02/02/2015 16:40 | 03/12/2015 02:55 | 03/12/2015 03:40 | 03/12/2015 09:55 | 17:20 | 00:45 | 12.5 +/− 0.3 |
| 04/12/2015 | 47 | 04/12/2015 07:55 | 04/12/2015 09:20 | 04/12/2015 11:10 | / | / | 01:50 | 17.6 +/− 1.1 |
| 04/12/2015 | 48 | / | 04/12/2015 20:55 | 04/12/2015 21:10 | / | / | 00:15 | 16.1 +/− 0.8 |
| 05/12/2015 | 49 | / | 05/12/2015 15:10 | 05/12/2015 16:45 | 08/02/2015 18:05 | / | 01:35 | 14.1 +/− 2.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corradini, S.; Guerrieri, L.; Lombardo, V.; Merucci, L.; Musacchio, M.; Prestifilippo, M.; Scollo, S.; Silvestri, M.; Spata, G.; Stelitano, D. Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data. Geosciences 2018, 8, 140. https://doi.org/10.3390/geosciences8040140
Corradini S, Guerrieri L, Lombardo V, Merucci L, Musacchio M, Prestifilippo M, Scollo S, Silvestri M, Spata G, Stelitano D. Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data. Geosciences. 2018; 8(4):140. https://doi.org/10.3390/geosciences8040140
Chicago/Turabian StyleCorradini, Stefano, Lorenzo Guerrieri, Valerio Lombardo, Luca Merucci, Massimo Musacchio, Michele Prestifilippo, Simona Scollo, Malvina Silvestri, Gaetano Spata, and Dario Stelitano. 2018. "Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data" Geosciences 8, no. 4: 140. https://doi.org/10.3390/geosciences8040140
APA StyleCorradini, S., Guerrieri, L., Lombardo, V., Merucci, L., Musacchio, M., Prestifilippo, M., Scollo, S., Silvestri, M., Spata, G., & Stelitano, D. (2018). Proximal Monitoring of the 2011–2015 Etna Lava Fountains Using MSG-SEVIRI Data. Geosciences, 8(4), 140. https://doi.org/10.3390/geosciences8040140







