Multiscale and Hierarchical Classification for Benthic Habitat Mapping
Abstract
1. Introduction
2. Materials and Methods
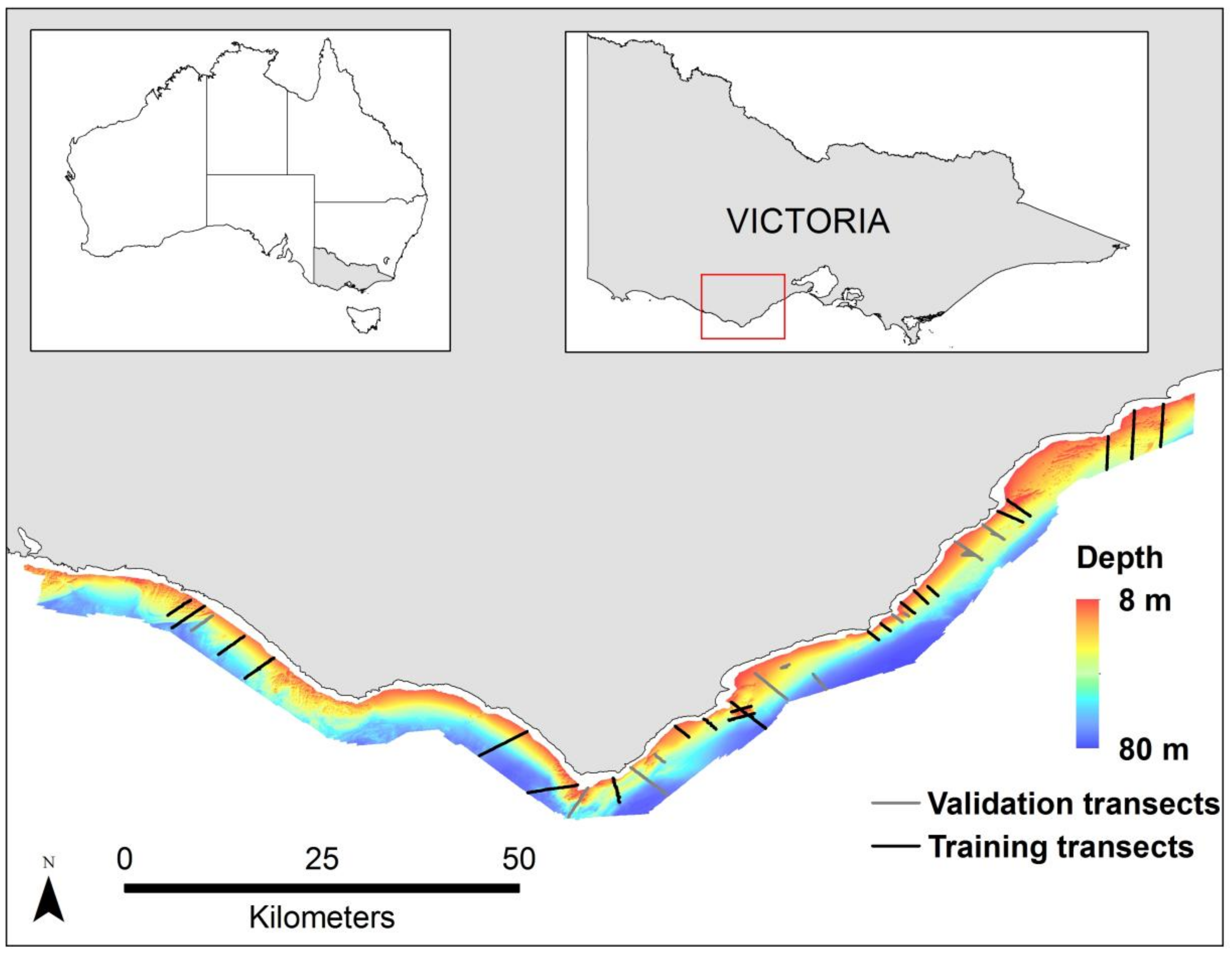
2.1. Study Area
2.2. MBES Data Collection and Processing
2.3. Groundtruth Collection and Classification
2.4. Wave Exposure Model
2.5. Statistical Approaches
2.5.1. Data Analysis
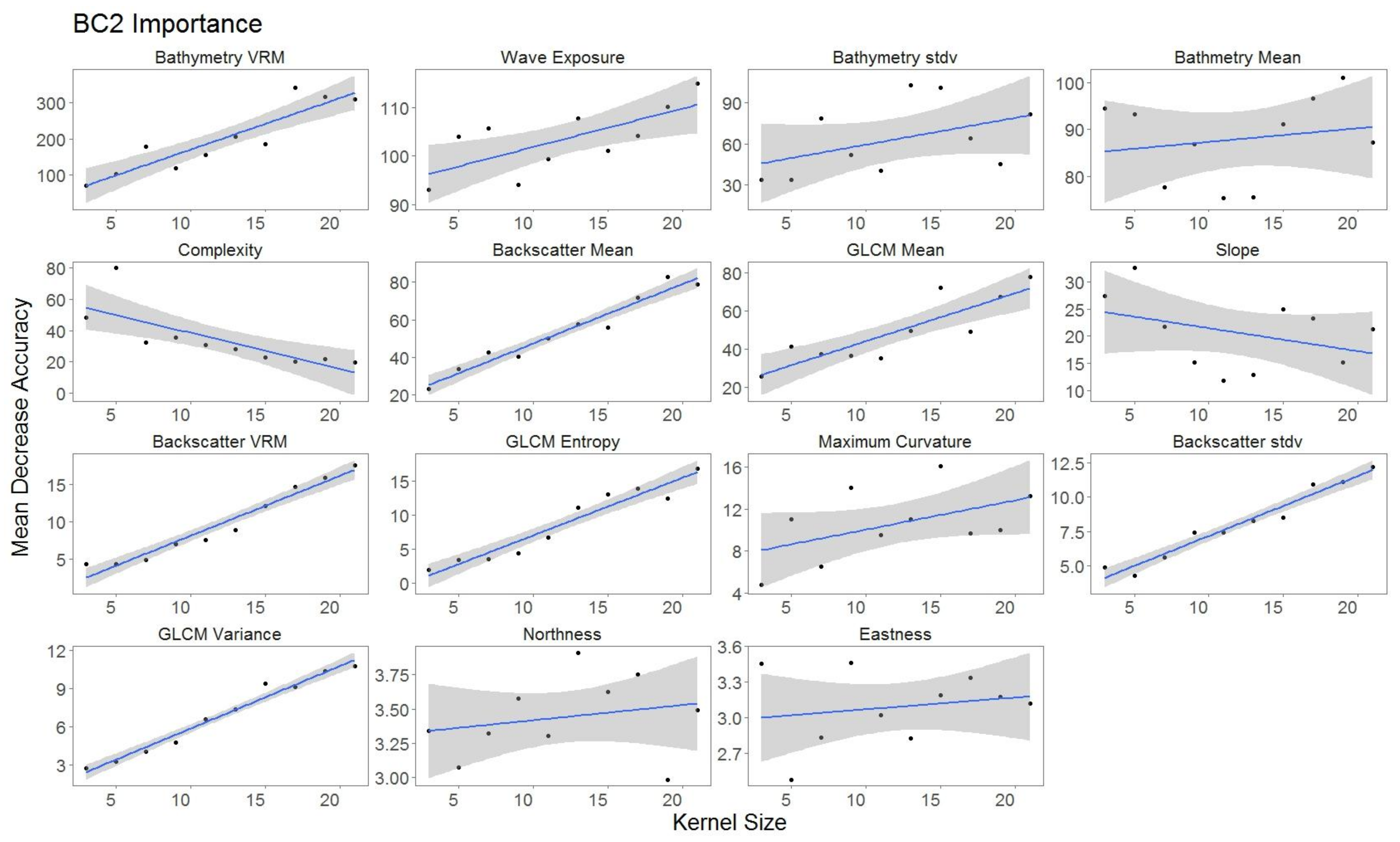
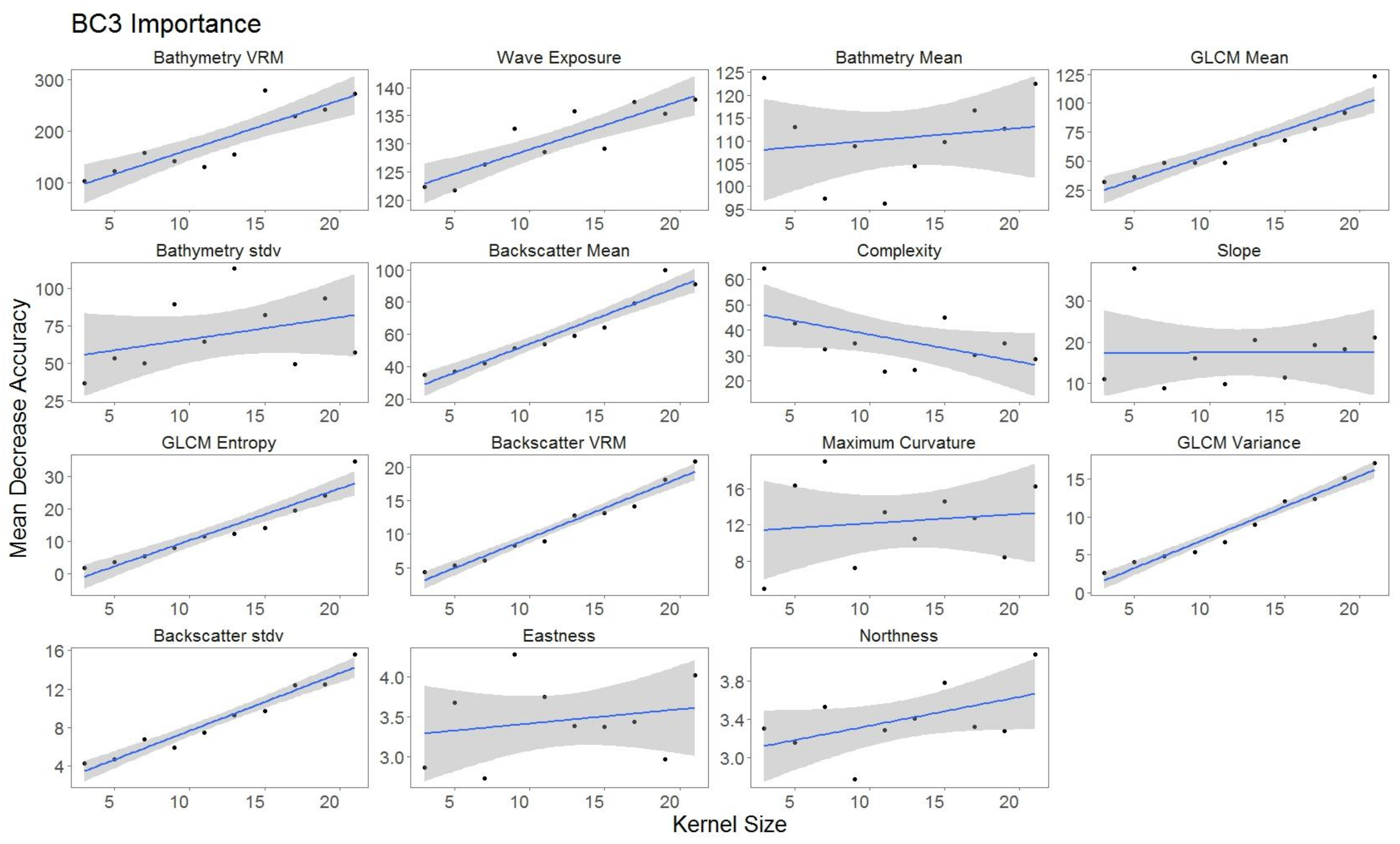
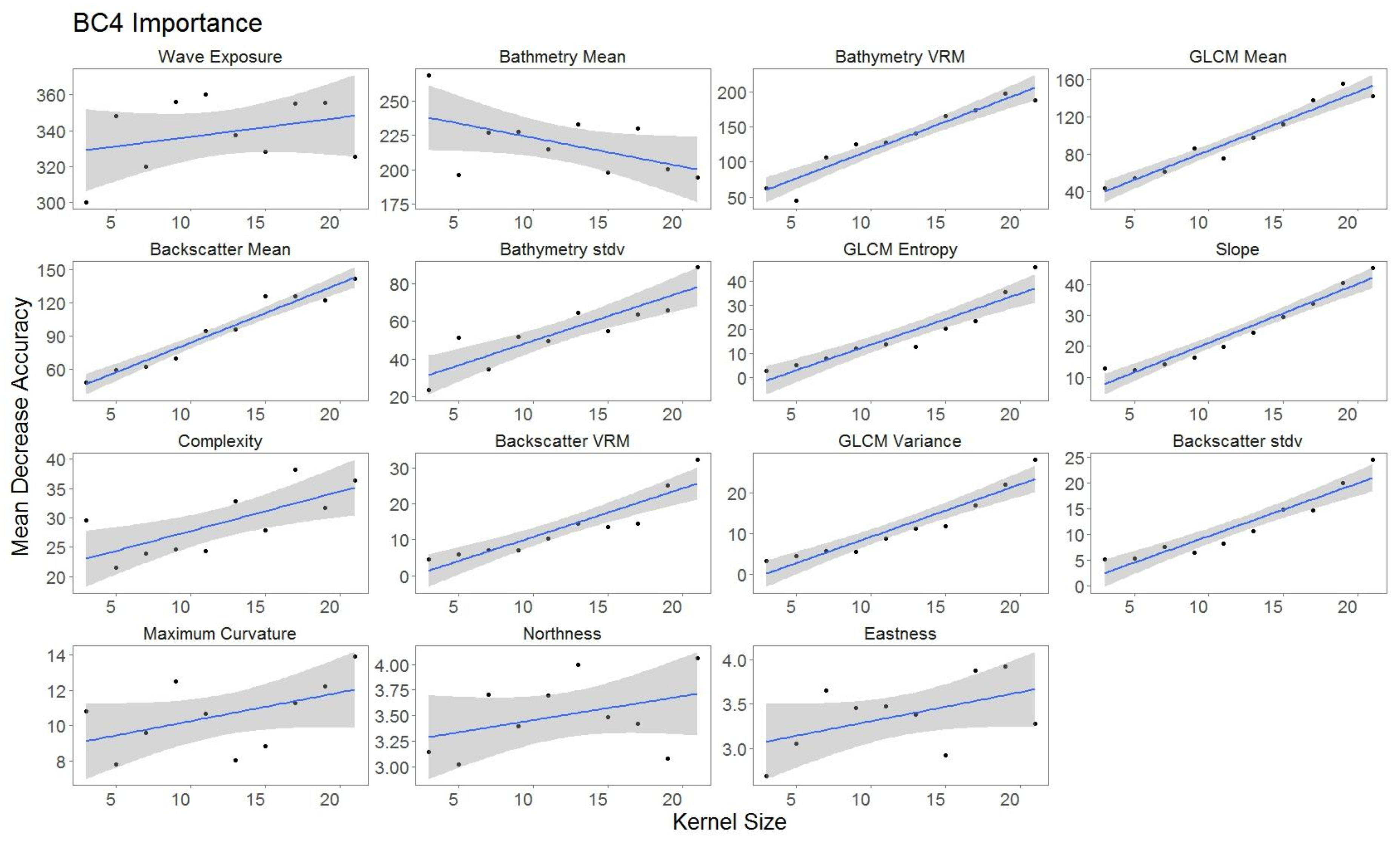
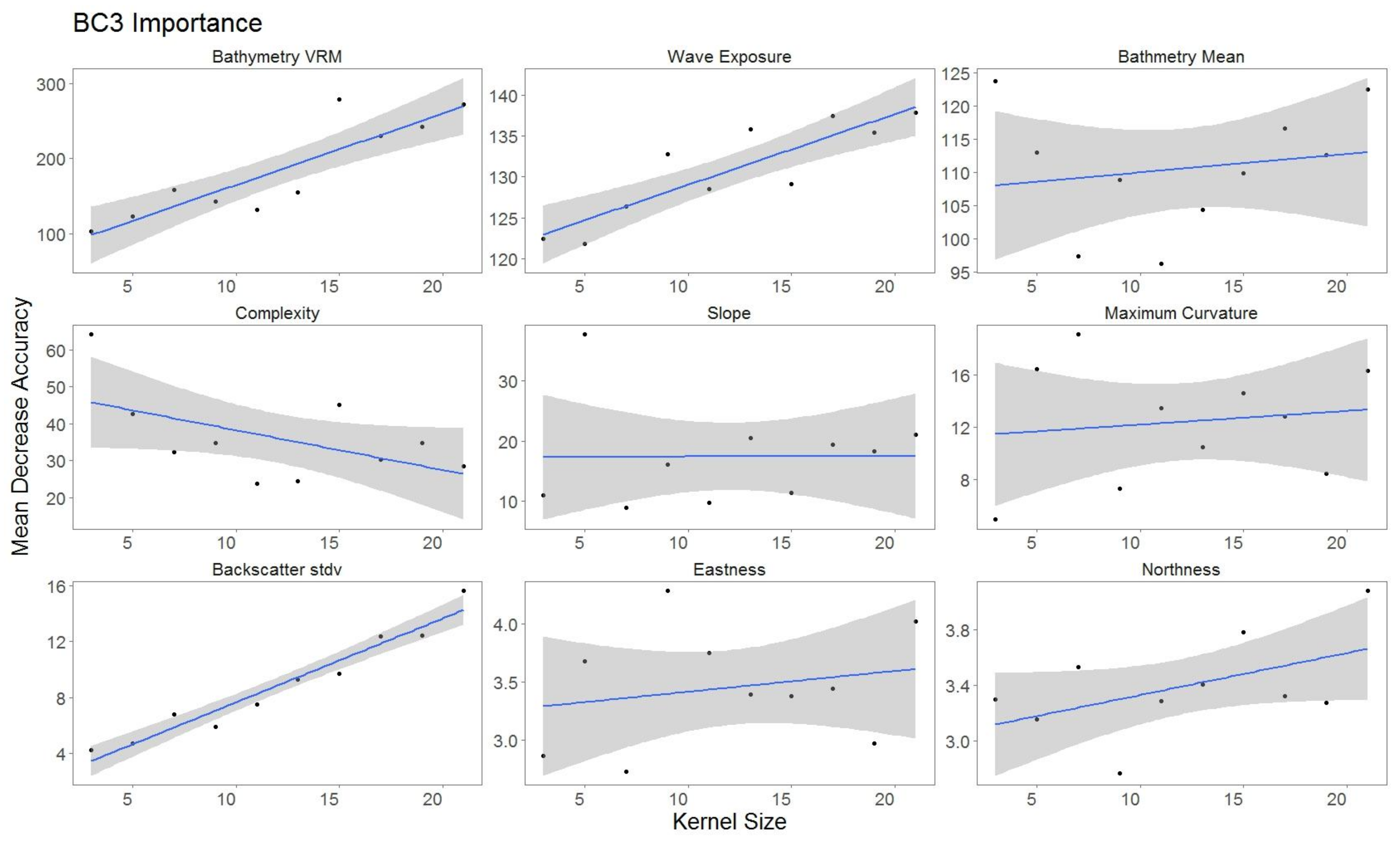
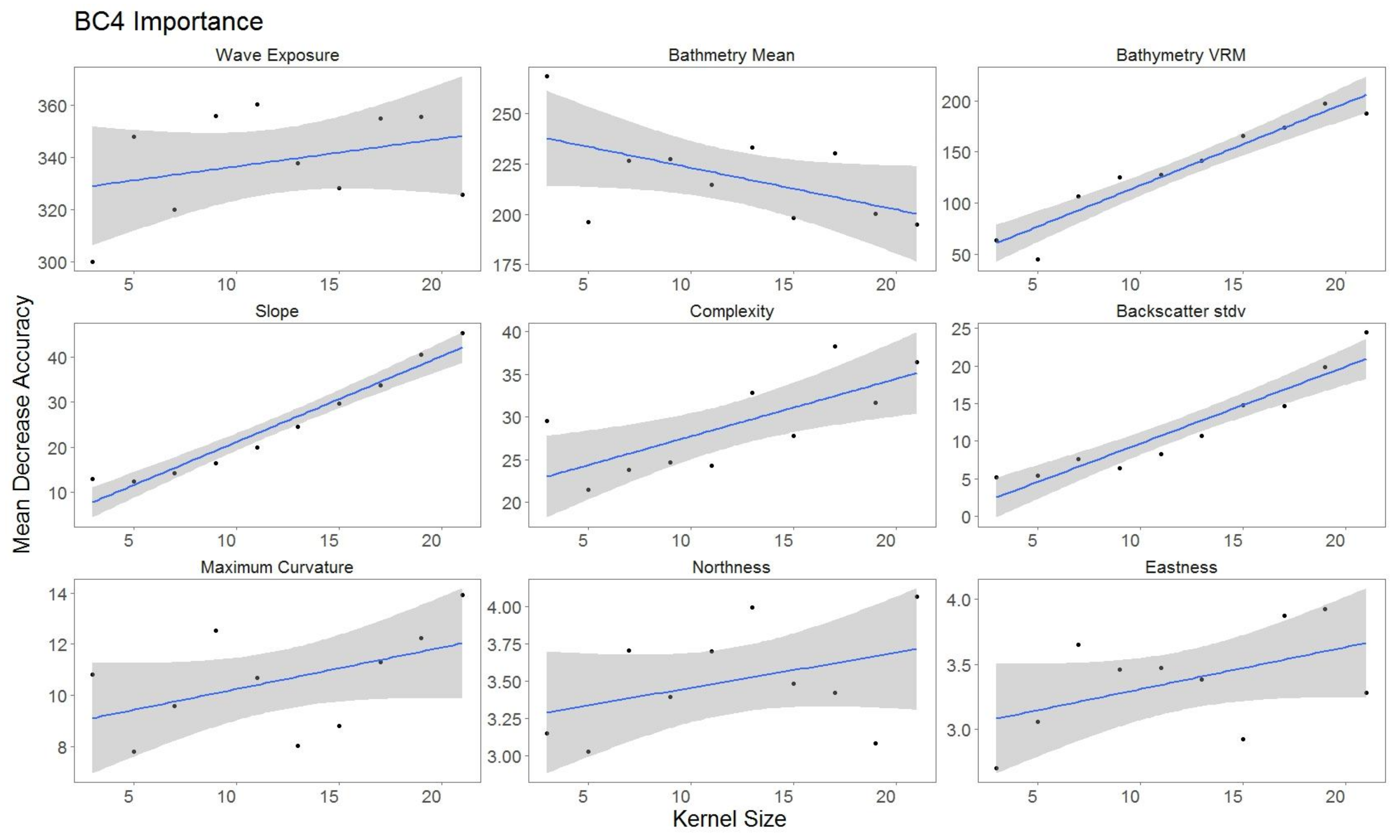
2.5.2. Variable Importance
2.5.3. Predictive Mapping
3. Results
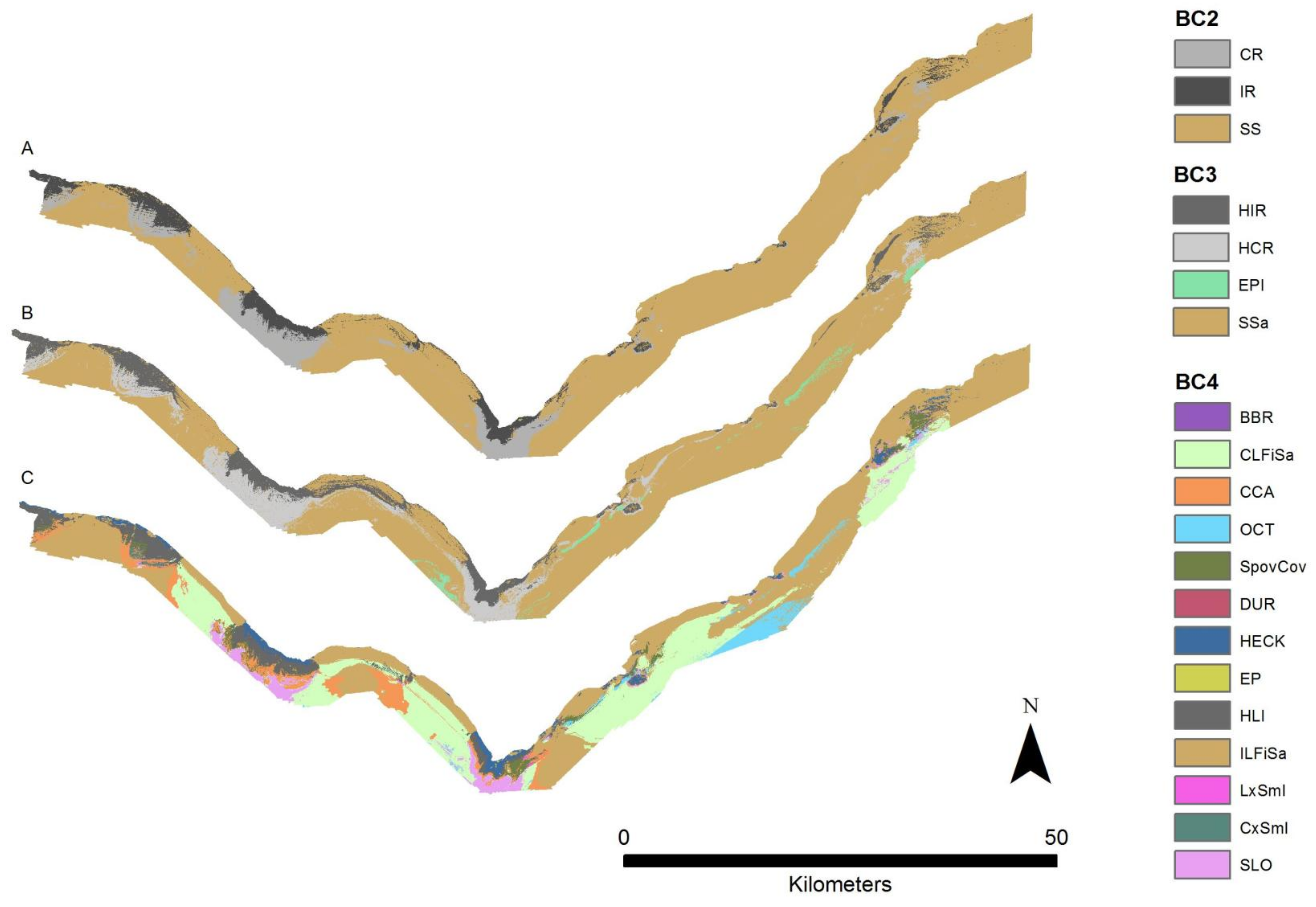
3.1. Habitat Suitability Maps
3.2. Hierarchical Comparison
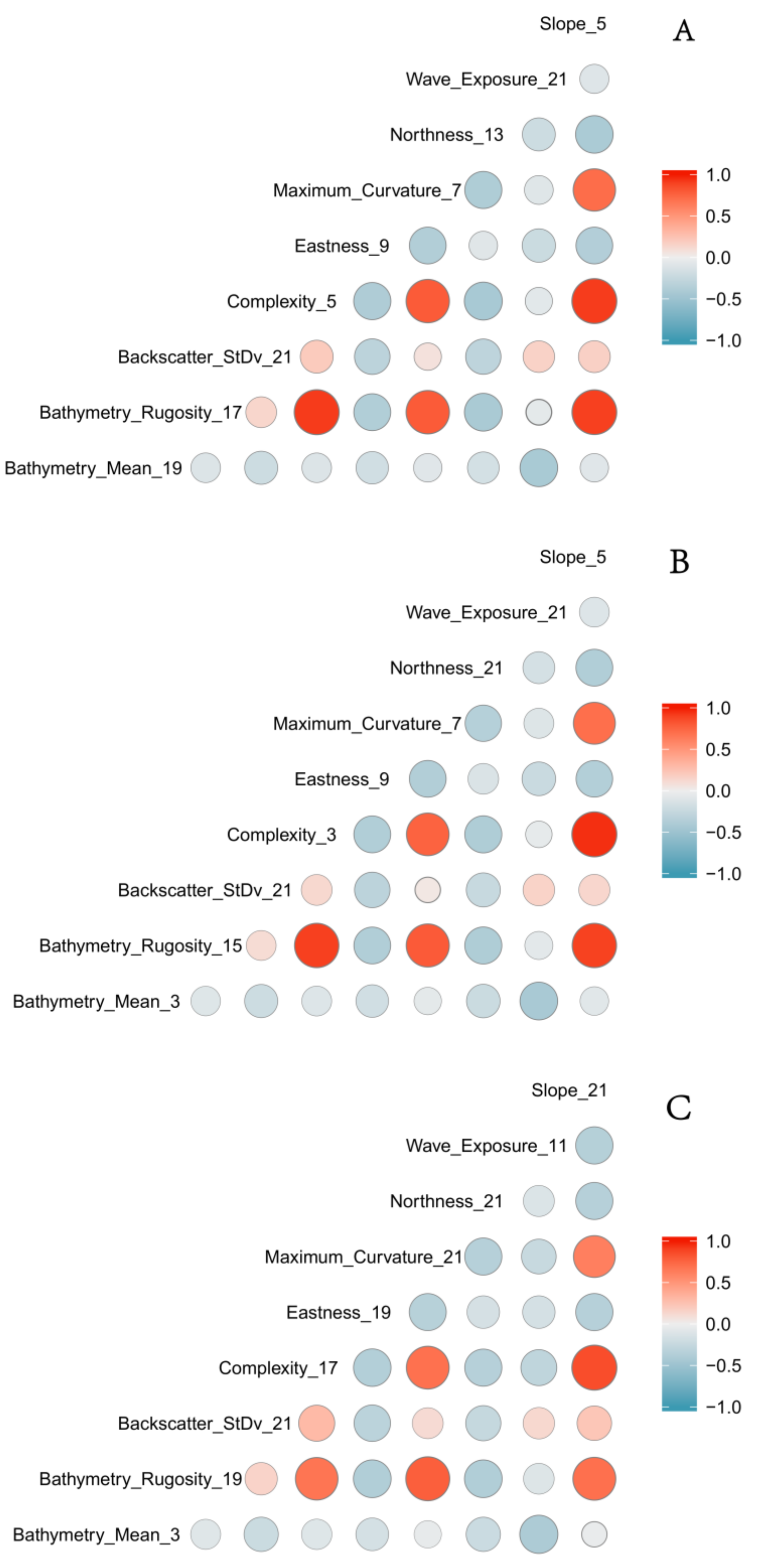
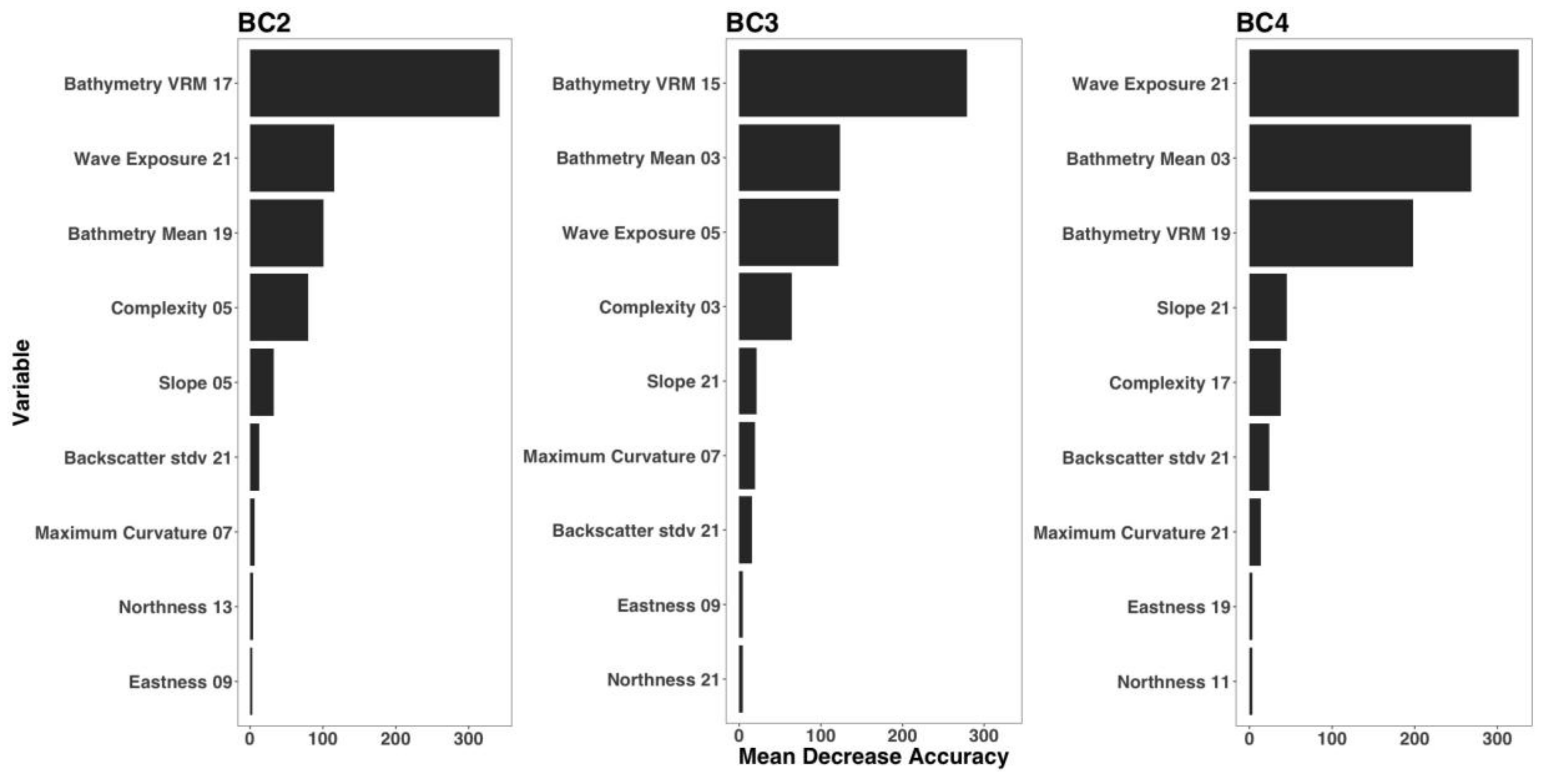
3.3. Variable Importance
4. Discussion
4.1. Impact of Classification Hierarchy on Model Performance
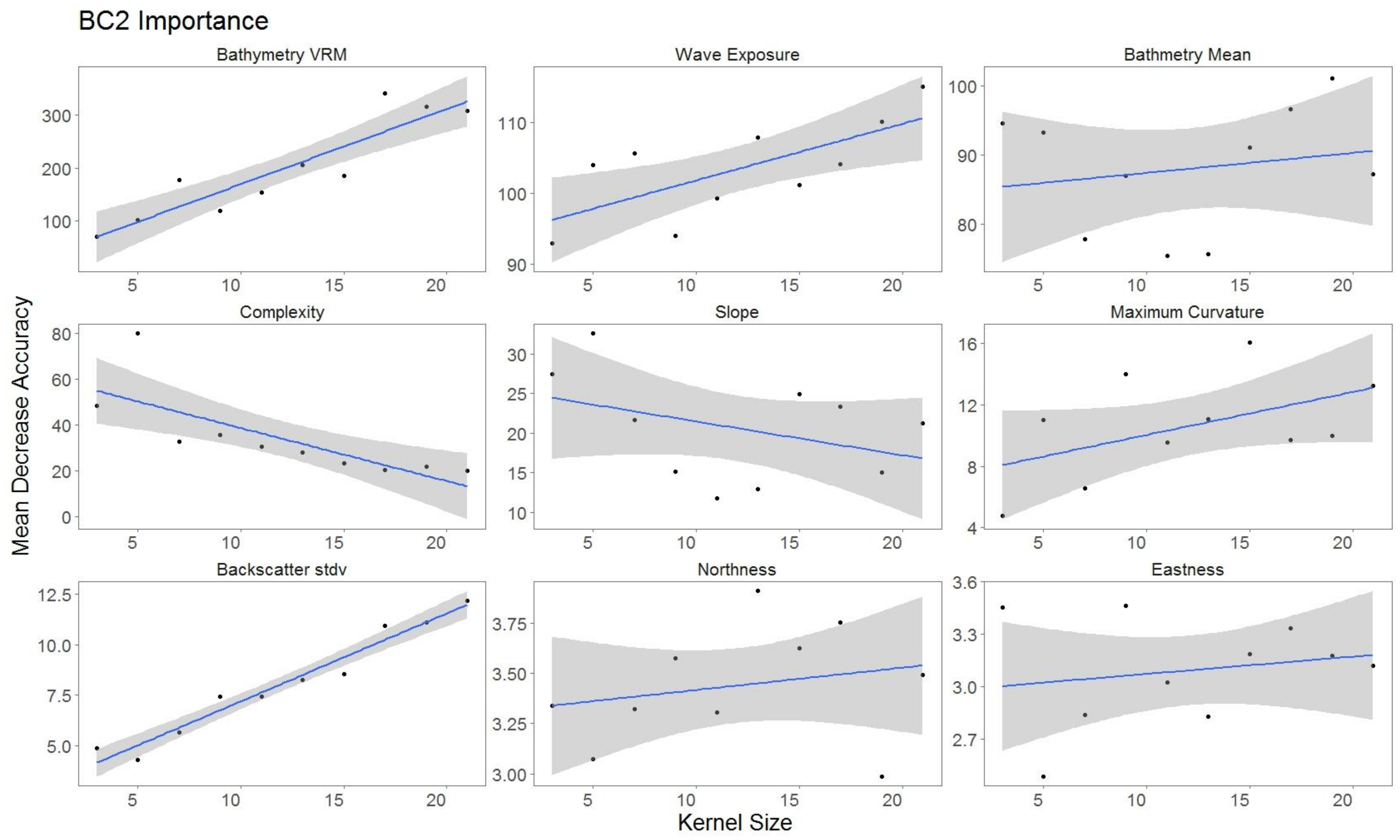
4.2. Impact of Variable Scale
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Schneider, D.; Lucieer, V.; Brown, C.; Edinger, E. Spatial scale and geographic context in benthic habitat mapping: Review and future directions. Mar. Ecol. Prog. Ser. 2015, 535, 259–284. [Google Scholar] [CrossRef]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geodesy 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Diesing, M.; Mitchell, P.; Stephens, D. Image-based seabed classification: What can we learn from terrestrial remote sensing? ICES J. Mar. Sci. J. Cons. 2016, 73, 2425–2441. [Google Scholar] [CrossRef]
- Lemme, M.C.; Koppens, F.H.L.; Falk, A.L.; Rudner, M.S.; Park, H.; Levitov, L.S.; Marcus, C.M. Gate-Activated Photoresponse in a Graphene p–n Junction. Nano Lett. 2011, 11, 4134–4137. [Google Scholar] [CrossRef] [PubMed]
- Engle, V.D.; Summers, J.K. Latitudinal gradients in benthic community composition in Western Atlantic estuaries. J. Biogeogr. 1999, 26, 1007–1023. [Google Scholar] [CrossRef]
- Wernberg, T.; Smale, D.A.; Tuya, F.; Thomsen, M.S.; Langlois, T.J.; de Bettignies, T.; Bennett, S.; Rousseaux, C.S. An extreme climatic event alters marine ecosystem structure in a global biodiversity hotspot. Nat. Clim. Chang. 2013, 3, 78–82. [Google Scholar] [CrossRef]
- Gattuso, J.-P.; Gentili, B.; Duarte, C.M.; Kleypas, J.A.; Middelburg, J.J.; Antoine, D. Light availability in the coastal ocean: Impact on the distribution of benthic photosynthetic organisms and contribution to primary production. Biogeosci. Discuss. 2006, 3, 895–959. [Google Scholar] [CrossRef]
- Anthony, K.; Ridd, P.V.; Orpin, A.R.; Larcombe, P.; Lough, J. Temporal variation of light availability in coastal benthic habitats: Effects of clouds, turbidity, and tides. Limnol. Oceanogr. 2004, 49, 2201–2211. [Google Scholar] [CrossRef]
- Bax, N.; Kloser, R.; Williams, A.; Gowlett-Holmes, K.; Ryan, T. Seafloor habitat definition for spatial management in fisheries: A case study on the continental shelf of southeast Australia. Oceanol. Acta 1999, 22, 705–720. [Google Scholar] [CrossRef]
- Roff, J.C.; Taylor, M.E.; Laughren, J. Geophysical approaches to the classification, delineation and monitoring of marine habitats and their communities. Aquat. Conserv. Mar. Freshw. Ecosyst. 2003, 13, 77–90. [Google Scholar] [CrossRef]
- McArthur, M.A.; Brooke, B.P.; Przeslawski, R.; Ryan, D.A.; Lucieer, V.L.; Nichol, S.; McCallum, A.W.; Mellin, C.; Cresswell, I.D.; Radke, L.C. On the use of abiotic surrogates to describe marine benthic biodiversity. Estuar. Coast. Shelf Sci. 2010, 88, 21–32. [Google Scholar] [CrossRef]
- Kostylev, V.E.; Erlandsson, J.; Ming, M.Y.; Williams, G.A. The relative importance of habitat complexity and surface area in assessing biodiversity: Fractal application on rocky shores. Ecol. Complex. 2005, 2, 272–286. [Google Scholar] [CrossRef]
- Lecours, V.; Devillers, R.; Simms, A.E.; Lucieer, V.L.; Brown, C.J. Towards a framework for terrain attribute selection in environmental studies. Environ. Model. Softw. 2017, 89, 19–30. [Google Scholar] [CrossRef]
- Mitchell, P.J.; Monk, J.; Laurenson, L. Sensitivity of fine-scale species distribution models to locational uncertainty in occurrence data across multiple sample sizes. Methods Ecol. Evol. 2017, 8, 12–21. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Monk, J.; Rattray, A.; Laurenson, L.; Versace, V.L. Comparison of automated classification techniques for predicting benthic biological communities using hydroacoustics and video observations. Cont. Shelf Res. 2011, 31, S28–S38. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Laurenson, L.; Burq, S.; Reston, M. Marine benthic habitat mapping using Multibeam data, georeferencedvideo and image classification techniques in Victoria, Australia. J. Spat. Sci. 2007, 52, 93–104. [Google Scholar] [CrossRef]
- Rattray, A.; Ierodiaconou, D.; Womersley, T. Wave exposure as a predictor of benthic habitat distribution on high energy temperate reefs. Front. Mar. Sci. 2015, 2. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Schimel, A.C.G.; Kennedy, D.; Monk, J.; Gaylard, G.; Young, M.; Diesing, M.; Rattray, A. Combining pixel and object based image analysis of ultra-high resolution multibeam bathymetry and backscatter for habitat mapping in shallow marine waters. Mar. Geophys. Res. 2018. [Google Scholar] [CrossRef]
- Hasan, R.; Ierodiaconou, D.; Monk, J. Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar. Remote Sens. 2012, 4, 3427–3443. [Google Scholar] [CrossRef]
- Siwabessy, P.J.W.; Tran, M.; Picard, K.; Brooke, B.P.; Huang, Z.; Smit, N.; Williams, D.K.; Nicholas, W.A.; Nichol, S.L.; Atkinson, I. Modelling the distribution of hard seabed using calibrated multibeam acoustic backscatter data in a tropical, macrotidal embayment: Darwin Harbour, Australia. Mar. Geophys. Res. 2017. [Google Scholar] [CrossRef]
- De Leo, F.C.; Vetter, E.W.; Smith, C.R.; Rowden, A.A.; McGranaghan, M. Spatial scale-dependent habitat heterogeneity influences submarine canyon macrofaunal abundance and diversity off the Main and Northwest Hawaiian Islands. Deep Sea Res. Part II Top. Stud. Oceanogr. 2014, 104, 267–290. [Google Scholar] [CrossRef]
- Bouchet, P.J.; Meeuwig, J.J.; Salgado Kent, C.P.; Letessier, T.B.; Jenner, C.K. Topographic determinants of mobile vertebrate predator hotspots: Current knowledge and future directions: Landscape models of mobile predator hotspots. Biol. Rev. 2015, 90, 699–728. [Google Scholar] [CrossRef] [PubMed]
- Walbridge, S.; Slocum, N.; Pobuda, M.; Wright, D.J. Unified Geomorphological Analysis Workflows with Benthic Terrain Modeler. Geosciences 2018, 8, 94. [Google Scholar] [CrossRef]
- Le Bas, T.P.; Huvenne, V.A.I. Acquisition and processing of backscatter data for habitat mapping—Comparison of multibeam and sidescan systems. Appl. Acoust. 2009, 70, 1248–1257. [Google Scholar] [CrossRef]
- MacMillan, R.A.; Shary, P.A. Chapter 9 Landforms and Landform Elements in Geomorphometry. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 227–254. ISBN 978-0-12-374345-9. [Google Scholar]
- Lindegarth, M.; Gamfeldt, L. Comparing Categorical and Continuous Ecological Analyses: Effects of “Wave Exposure” on Rocky Shores. Ecology 2005, 86, 1346–1357. [Google Scholar] [CrossRef]
- Bustamante, R.H.; Branch, G.M. Large Scale Patterns and Trophic Structure of Southern African Rocky Shores: The Roles of Geographic Variation and Wave Exposure. J. Biogeogr. 1996, 23, 339–351. [Google Scholar] [CrossRef]
- Hughes, M.G.; Heap, A.D. National-scale wave energy resource assessment for Australia. Renew. Energy 2010, 35, 1783–1791. [Google Scholar] [CrossRef]
- Dartnell, P.; Gardner, J.V. Predicting Seafloor Facies from Multibeam Bathymetry and Backscatter Data. Photogramm. Eng. Remote Sens. 2004, 70, 1081–1091. [Google Scholar] [CrossRef]
- Costello, M. Distinguishing marine habitat classification concepts for ecological data management. Mar. Ecol. Prog. Ser. 2009, 397, 253–268. [Google Scholar] [CrossRef]
- Simboura, N.; Zenetos, A. Benthic indicators to use in Ecological Quality classification of Mediterranean soft bottom marine ecosystems, including a new Biotic Index. Mediterr. Mar. Sci. 2002, 3, 77. [Google Scholar] [CrossRef]
- Guarinello, M.L.; Shumchenia, E.J.; King, J.W. Marine Habitat Classification for Ecosystem-Based Management: A Proposed Hierarchical Framework. Environ. Manag. 2010, 45, 793–806. [Google Scholar] [CrossRef] [PubMed]
- Shumchenia, E.J.; King, J.W. Comparison of methods for integrating biological and physical data for marine habitat mapping and classification. Cont. Shelf Res. 2010, 30, 1717–1729. [Google Scholar] [CrossRef]
- Klijn, F.; de Haes, H.A.U. A hierarchical approach to ecosystems and its implications for ecological land classification. Landsc. Ecol. 1994, 9, 89–104. [Google Scholar] [CrossRef]
- Frissell, C.A.; Liss, W.J.; Warren, C.E.; Hurley, M.D. A hierarchical framework for stream habitat classification: Viewing streams in a watershed context. Environ. Manag. 1986, 10, 199–214. [Google Scholar] [CrossRef]
- Bock, M.; Xofis, P.; Mitchley, J.; Rossner, G.; Wissen, M. Object-oriented methods for habitat mapping at multiple scales—Case studies from Northern Germany and Wye Downs, UK. J. Nat. Conserv. 2005, 13, 75–89. [Google Scholar] [CrossRef]
- Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. Coral reef habitat mapping: How much detail can remote sensing provide? Mar. Biol. 1997, 130, 193–202. [Google Scholar] [CrossRef]
- Department of the Environment and Heritage. A Guide to the Integrated Marine and Coastal Regionalisation of Australia: IMCRA Version 4.0; Australian Government, Department of the Environment and Heritage: Canberra, Australia, 2006; ISBN 978-0-642-55227-3. [Google Scholar]
- Bezore, R.; Kennedy, D.M.; Ierodiaconou, D. The Drowned Apostles: The Longevity of Sea Stacks over Eustatic Cycles. J. Coast. Res. 2016, 75, 592–596. [Google Scholar] [CrossRef]
- ENVI; Exelis Visual Information Solutions: Boulder, CO, USA, 2010.
- ArcGIS; Environmental Systems Research Institute (ESRI): Redlands, CA, USA, 2015.
- Sappington, J.M.; Longshore, K.M.; Thompson, D.B. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. J. Wildl. Manag. 2007, 71, 1419–1426. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Edmunds, M.; Flynn, A. A Victorian Marine Biotope Classification Scheme; Report to Deakin University and Parks Victoria; Australian Marine Ecology Report No. 545; Deakin University: Melbourne, Australia, 2015. [Google Scholar]
- Davies, C.E.; Moss, D.; Hill, M.O. EUNIS Habitat Classification Revised 2004; European Topic Centre on Nature Protection and Biodiversity: Paris, France, 2004; pp. 127–143. [Google Scholar]
- Federal Geographic Data Committee. Coastal and Marine Ecological Classification Standard; FGDC-STD-018-2012; Federal Geographic Data Committee, Marine and Coastal Spatial Data Subcommittee: Reston, VA, USA, 2012. [Google Scholar]
- Eigenraam, M.; McCormick, F.; Contreras, Z. Marine and Coastal Ecosystem Accounting: Port Phillip Bay; State of Victoria Department of Environment, Land, Water and Planning: Victoria, Australia, 2016. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Stephens, D.; Diesing, M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLoS ONE 2014, 9, e93950. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; The R Core Team; et al. Caret: Classification and Regression Training; GitHub, Inc.: San Francisco, CA, USA, 2017. [Google Scholar]
- Freeman, E.; Frescino, T. ModelMap: Modeling and Map Production Using Random Forest and Stochastic Gradient Boosting; USDA Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 2009. [Google Scholar]
- Hallgren, K.A. Computing Inter-Rater Reliability for Observational Data: An Overview and Tutorial. Tutor. Quant. Methods Psychol. 2012, 8, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Lecours, V.; Devillers, R.; Edinger, E.N.; Brown, C.J.; Lucieer, V.L. Influence of artefacts in marine digital terrain models on habitat maps and species distribution models: A multiscale assessment. Remote Sens. Ecol. Conserv. 2017. [Google Scholar] [CrossRef]
- Lecours, V.; Dolan, M.F.J.; Micallef, A.; Lucieer, V.L. A review of marine geomorphometry, the quantitative study of the seafloor. Hydrol. Earth Syst. Sci. 2016, 20, 3207–3244. [Google Scholar] [CrossRef]
- Capolsini, P.; Andréfouët, S.; Rion, C.; Payri, C. A comparison of Landsat ETM+, SPOT HRV, Ikonos, ASTER, and airborne MASTER data for coral reef habitat mapping in South Pacific islands. Can. J. Remote Sens. 2003, 29, 187–200. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.J.; Collier, J.S. Mapping benthic habitat in regions of gradational substrata: An automated approach utilising geophysical, geological, and biological relationships. Estuar. Coast. Shelf Sci. 2008, 78, 203–214. [Google Scholar] [CrossRef]
- Freitas, R.; Rodrigues, A.M.; Quintino, V. Benthic biotopes remote sensing using acoustics. J. Exp. Mar. Biol. Ecol. 2003, 285, 339–353. [Google Scholar] [CrossRef]
- Che Hasan, R.; Ierodiaconou, D.; Laurenson, L. Combining angular response classification and backscatter imagery segmentation for benthic biological habitat mapping. Estuar. Coast. Shelf Sci. 2012, 97, 1–9. [Google Scholar] [CrossRef]
- Galparsoro, I.; Connor, D.W.; Borja, Á.; Aish, A.; Amorim, P.; Bajjouk, T.; Chambers, C.; Coggan, R.; Dirberg, G.; Ellwood, H.; et al. Using EUNIS habitat classification for benthic mapping in European seas: Present concerns and future needs. Mar. Pollut. Bull. 2012, 64, 2630–2638. [Google Scholar] [CrossRef] [PubMed]
- Young, M.; Ierodiaconou, D.; Womersley, T. Forests of the sea: Predictive habitat modelling to assess the abundance of canopy forming kelp forests on temperate reefs. Remote Sens. Environ. 2015, 170, 178–187. [Google Scholar] [CrossRef]
- Graf, R.F.; Bollmann, K.; Suter, W.; Bugmann, H. The Importance of Spatial Scale in Habitat Models: Capercaillie in the Swiss Alps. Landsc. Ecol. 2005, 20, 703–717. [Google Scholar] [CrossRef]
- Kendall, M.; Miller, T.; Pittman, S. Patterns of scale-dependency and the influence of map resolution on the seascape ecology of reef fish. Mar. Ecol. Prog. Ser. 2011, 427, 259–274. [Google Scholar] [CrossRef]
- Hernandez, P.A.; Graham, C.H.; Master, L.L.; Albert, D.L. The Effect of Sample Size and Species Characteristics on Performance of Different Species Distribution Modeling Methods. Ecography 2006, 29, 773–785. [Google Scholar] [CrossRef]
- Kadmon, R.; Farber, O.; Danin, A. A systematic analysis of factors affecting the performance of climatic envelope models. Ecol. Appl. 2003, 13, 853–867. [Google Scholar] [CrossRef]
- Przeslawski, R.; Foster, S. Field Manuals for Marine Sampling to Monitor Australian Waters; National Environmental Science Programme, Marine Biodiversity Hub: Tasmania, Australia, 2018. [Google Scholar]

| Derivative | Software | Description |
|---|---|---|
| Bathymetry Mean | ArcMap 10.4 (Spatial Analyst) | Local mean value of pixel to neighborhood x̅ = (ΣXi)/N |
| Bathymetry Standard Deviation | ArcMap 10.4 (Spatial Analyst) | Local standard deviation value of pixel to neighborhood σX = √(Σ(Xi − X)2/N) |
| Backscatter Mean | ArcMap 10.4 (Spatial Analyst) | Local mean value of pixel to neighborhood x̅ = (ΣXi)/N |
| Backscatter Standard Deviation | ArcMap 10.4 (Spatial Analyst) | Local standard deviation value of pixel to neighborhood σX = √(Σ(Xi − X)2/N) |
| Backscatter Rugosity (VRM) | ArcMap 10.4 (Benthic Terrain Mapper) | Incorporates the heterogeneity of both slope and aspect using three-dimensional dispersion of vectors. See [43] for more details. |
| Bathymetry Rugosity (VRM) | ArcMap 10.4 (Benthic Terrain Mapper) | Incorporates the heterogeneity of both slope and aspect using three-dimensional dispersion of vectors. See [43] for more details. |
| Bathymetry Slope | ENVI 5.3.1 | Change in elevation over designated neighborhood size tan−1(Rise/run) [3] |
| Bathymetry Complexity | ENVI 5.3.1 | Rate of change of slope over designated neighborhood size tan−1(rise(slope)/run(slope)) [3] |
| Maximum Curvature | ENVI 5.3.1 | Steepest curve of convexity for a pixel over designated neighborhood size K(x) = |ex|/(1 + e2x)3/2 |
| Gray-Level Co-Occurrence Matrix (GLCM) Mean Backscatter | ENVI 5.3.1 | Uses a co-occurrence matrix to represent the number of occurrences between a pixel and its neighbor Local mean value of pixel to neighborhood P(i) = probability of each pixel value Ng = Number of distinct gray levels [44] |
| GLCM Standard Deviation Backscatter | ENVI 5.3.1 | As described above Local standard deviation of pixel to neighborhood [44] |
| GLCM Entropy Backscatter | ENVI 5.3.1 | As described above. Statistical measure of randomness of pixel to neighborhood [44] |
| Eastness | ENVI 5.3.1 | The sine of the angle of slope in the analysis window. Equation: sin(aspect) [3] |
| Northness | ENVI 5.3.1 | The cosine of the angle of slope in the analysis window. Equation: cos(aspect) [3] |
| BC2 | BC3 | BC4 | Range (Mean, Standard Deviation) | N |
|---|---|---|---|---|
| Infralittoral rock and other hard substrata (IR) | High energy infralittoral rock (HIR) | High energy Durvillaea potatorum communities (DUR) | 13–16 m (14 m, 1 m) | 10 |
| High energy Ecklonia radiate communities (HECK) | 5–23 m (12 m, 4 m) | 600 | ||
| High energy Ecklonia-Phyllospora comosa communities (EP) | 12–30 m (18 m, 1 m) | 10 | ||
| High energy lower infralittoral zone (HLI) | 18–42 m (31 m, 5 m) | 1617 | ||
| Circalittoral rock and other hard substrata (CR) | High energy open-coast circalittoral rock (HCR) | Bushy bryozoan-dominated communities (BBR) | 32–37 m (36 m, 1 m) | 49 |
| Crustose coralline algal communities with combinations of thallose red algae and scattered sponges on high energy circalittoral rock (CCA) | 33–55 m (42 m, 3 m) | 535 | ||
| High energy circalittoral rock with seabed covering sponges (SpoCov) | 27–45 m (36 m, 5 m) | 516 | ||
| Low complexity circalittoral rock with non-crowded erect sponges (LxSml) | 41–43 m (42 m, 1 m) | 38 | ||
| Moderate to high complexity circalittoral rock with seabed covering sponges (CxSml) | 39–45 m (42 m, 2 m) | 102 | ||
| Sandy low profile reef wave surge communities with sand trapped around sponges (SLO) | 39–45 m (42 m, 11 m) | 558 | ||
| Sublittoral sediment (SS) | Non-reef sediment epibenthos (EPI) | Erect octocorals on sediment (OCT) | 27–71 m (48 m, 13 m) | 239 |
| Sublittoral sand and muddy sand (SSa) | Circalittoral fine sand (CLFiSa) | 29–70 m (48 m, 9 m) | 4078 | |
| Infralittoral fine sand (ILFiSa) | 10–40 m (30 m, 10 m) | 6433 |
| Model | Derivatives | Kernel Size |
|---|---|---|
| BC2 | Bathymetry Mean | 19 |
| Bathymetry Rugosity (VRM) | 17 | |
| Backscatter Standard Deviation | 21 | |
| Complexity | 5 | |
| Eastness | 9 | |
| Maximum Curvature | 7 | |
| Northness | 13 | |
| Slope | 5 | |
| Wave exposure | 21 | |
| BC3 | Bathymetry mean | 3 |
| Bathymetry Rugosity (VRM) | 15 | |
| Backscatter Standard Deviation | 21 | |
| Complexity | 3 | |
| Eastness | 9 | |
| Maximum curvature | 7 | |
| Northness | 21 | |
| Slope | 5 | |
| Wave exposure | 21 | |
| BC4 | Bathymetry Mean | 3 |
| Bathymetry Rugosity (VRM) | 19 | |
| Backscatter Standard Deviation | 21 | |
| Complexity | 17 | |
| Eastness | 19 | |
| Maximum Curvature | 21 | |
| Northness | 21 | |
| Slope | 21 | |
| Wave Exposure | 11 |
| Predicted | Reference | Overall Accuracy = 87.4%, K̂ = 0.59 | |||
| CR | IR | SS | Sensitivity | ||
| CR | 621 | 20 | 279 | 63.6 | |
| IR | 39 | 213 | 218 | 72.7 | |
| SS | 317 | 60 | 5636 | 91.9 | |
| Specificity | 95.4 | 96.4 | 70.3 | ||
| Predicted | Reference | Overall Accuracy = 69.7%, K̂ = 0.31 | ||||
| HIR | HCR | EPI | SSa | Sensitivity | ||
| HIR | 207 | 33 | 0 | 261 | 70.6 | |
| HCR | 20 | 619 | 10 | 404 | 63.4 | |
| EPI | 0 | 6 | 0 | 7 | 0.0 | |
| SSa | 66 | 319 | 1180 | 4234 | 86.3 | |
| Specificity | 95.8 | 93.2 | 99.8 | 36.4 | ||
| Predicted | Reference | Overall Accuracy = 39.94%, K̂ = 0.16 | |||||||||||||
| BBR | CLFiSa | CCA | OCT | SpoCov | DUR | EP | HECK | HLI | ILFiSa | LxSml | CxSml | SLO | Sensitivity | ||
| BBR | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| CLFiSa | 3 | 617 | 0 | 792 | 0 | 0 | 0 | 0 | 0 | 343 | 0 | 9 | 56 | 22.7 | |
| CCA | 0 | 192 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 34 | 0 | 45 | 0 | |
| OCT | 0 | 0 | 0 | 102 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 8.6 | |
| SpoCov | 0 | 46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42 | 0 | 0 | 0 | 0 | |
| DUR | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| EP | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| HECK | 0 | 0 | 0 | 0 | 0 | 11 | 19 | 136 | 0 | 56 | 0 | 0 | 0 | 97.1 | |
| HLI | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 4 | 71 | 83 | 0 | 0 | 3 | 58.2 | |
| ILFiSa | 0 | 1842 | 21 | 296 | 46 | 0 | 0 | 0 | 50 | 1625 | 23 | 7 | 143 | 74.4 | |
| LxSml | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| CxSml | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| SLO | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 26 | 20 | 4 | 277 | 52.8 | |
| Specificity | 99.9 | 72.4 | 96.1 | 99.9 | 98.7 | 100 | 99.9 | 98.8 | 98.6 | 50.4 | 100 | 99.9 | 99.2 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porskamp, P.; Rattray, A.; Young, M.; Ierodiaconou, D. Multiscale and Hierarchical Classification for Benthic Habitat Mapping. Geosciences 2018, 8, 119. https://doi.org/10.3390/geosciences8040119
Porskamp P, Rattray A, Young M, Ierodiaconou D. Multiscale and Hierarchical Classification for Benthic Habitat Mapping. Geosciences. 2018; 8(4):119. https://doi.org/10.3390/geosciences8040119
Chicago/Turabian StylePorskamp, Peter, Alex Rattray, Mary Young, and Daniel Ierodiaconou. 2018. "Multiscale and Hierarchical Classification for Benthic Habitat Mapping" Geosciences 8, no. 4: 119. https://doi.org/10.3390/geosciences8040119
APA StylePorskamp, P., Rattray, A., Young, M., & Ierodiaconou, D. (2018). Multiscale and Hierarchical Classification for Benthic Habitat Mapping. Geosciences, 8(4), 119. https://doi.org/10.3390/geosciences8040119





