Three-Dimensional Growth of Flexural Slip Fault-Bend and Fault-Propagation Folds and Their Geomorphic Expression
Abstract
1. Introduction
2. Characteristics of Isolated Thrust Faults
2.1. Displacement-Length Relationships
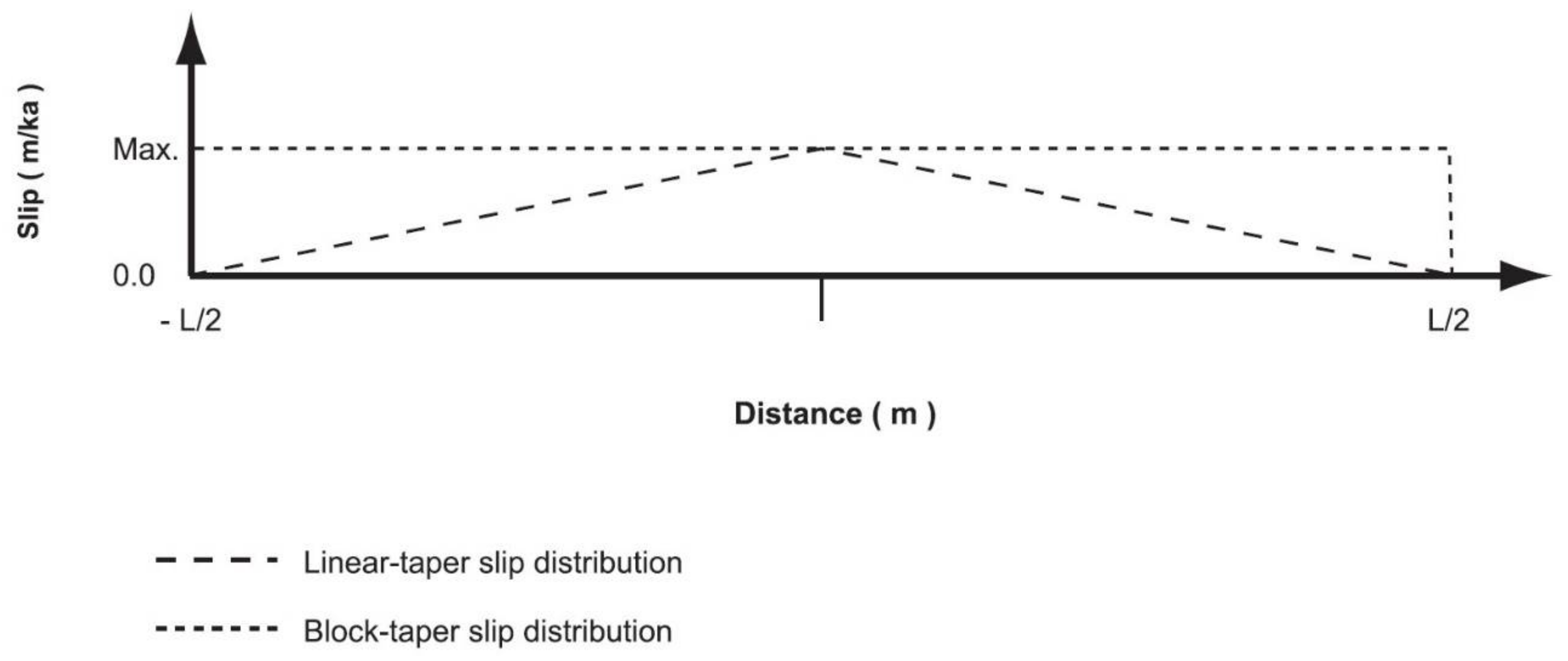
2.2. Lateral Displacement and Slip Distributions
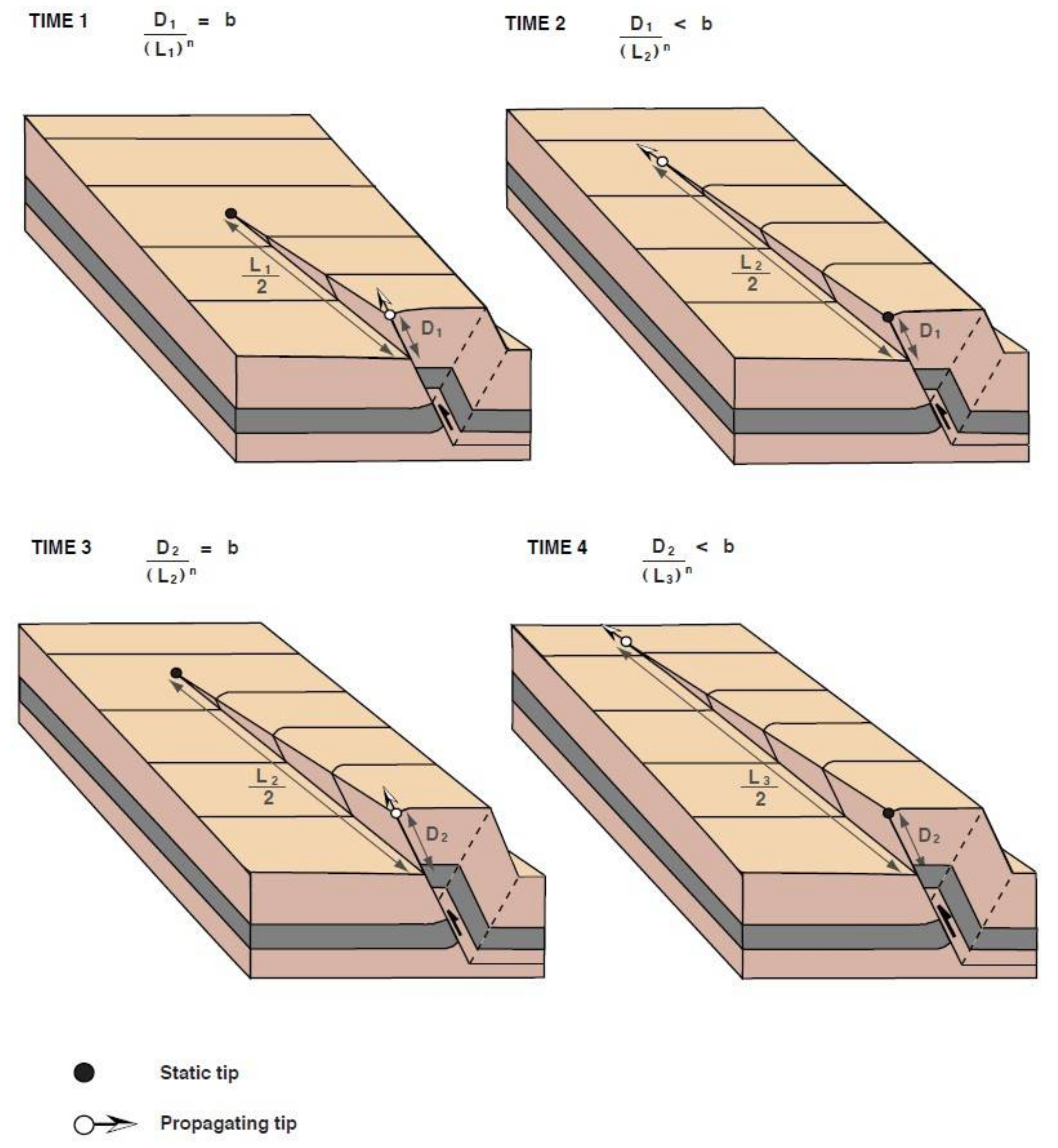
2.3. Rates of Displacement and Lateral Propagation
3. Morphology of Fault-Related Folds
3.1. Three-Dimensional Geometry
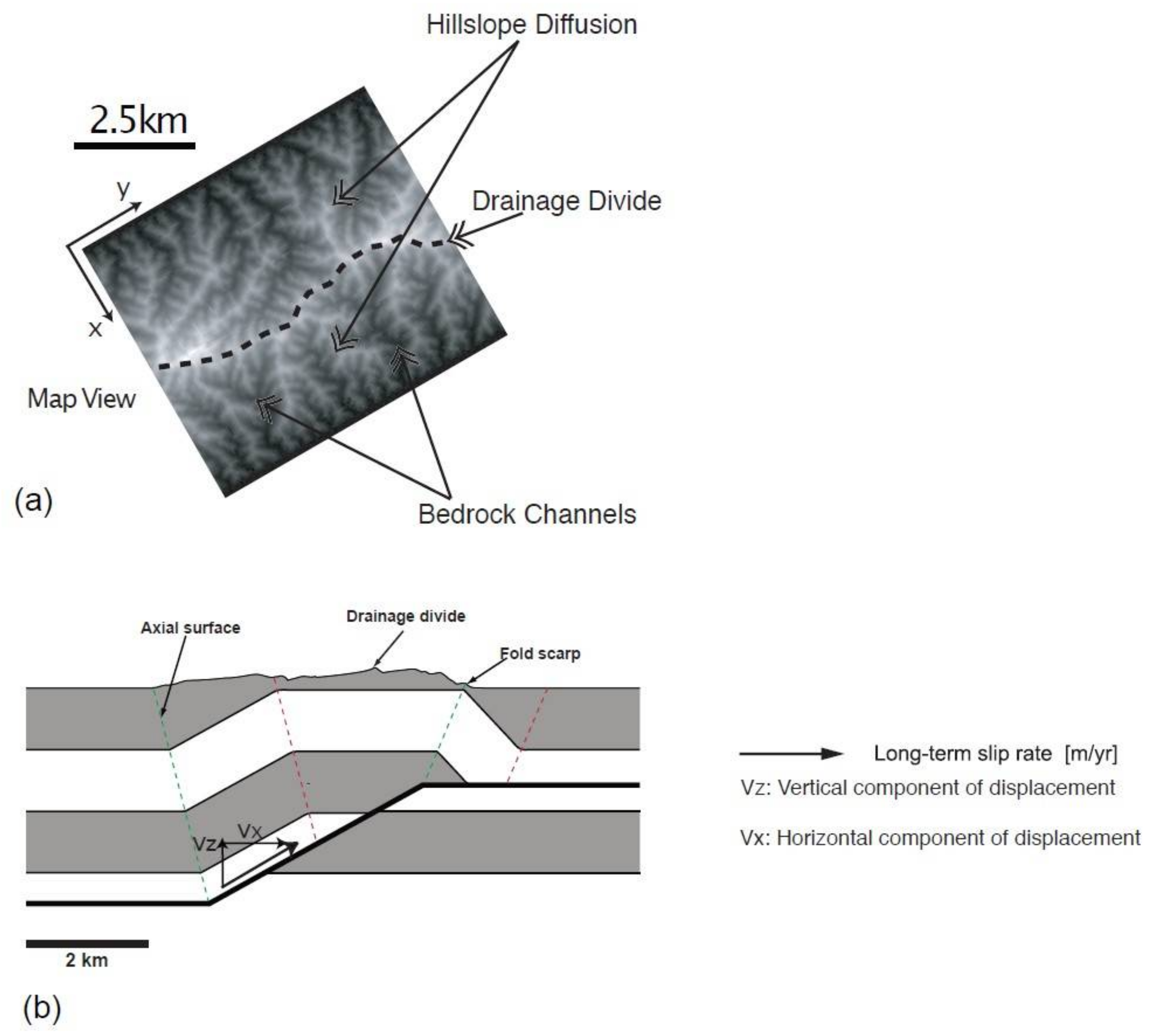
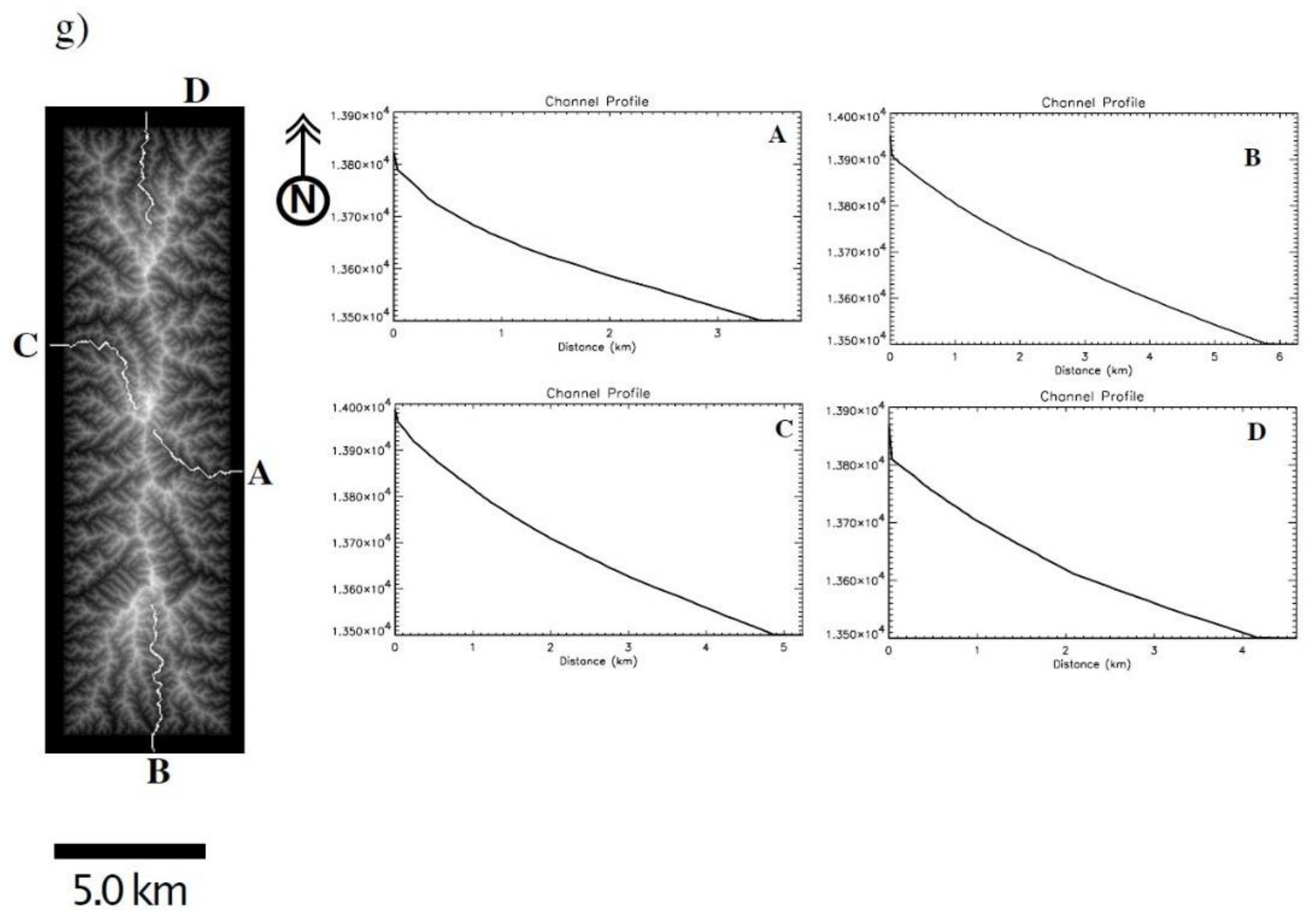
3.2. River Networks Developed above Fault-Related Fold Structures
4. Three Dimensional Modelling of Fault-Related Folding and Surface Processes
4.1. Model Rationale
4.2. Model Overview
4.3. Structural Modelling and Parameters
4.4. Surface Process Modelling and Parameters
4.5. Modelling Scheme
5. Evolution of River Networks above a Simple Uplifting Structure
6. River Networks above Growing Fault-Bend and Fault-Propagation Folds
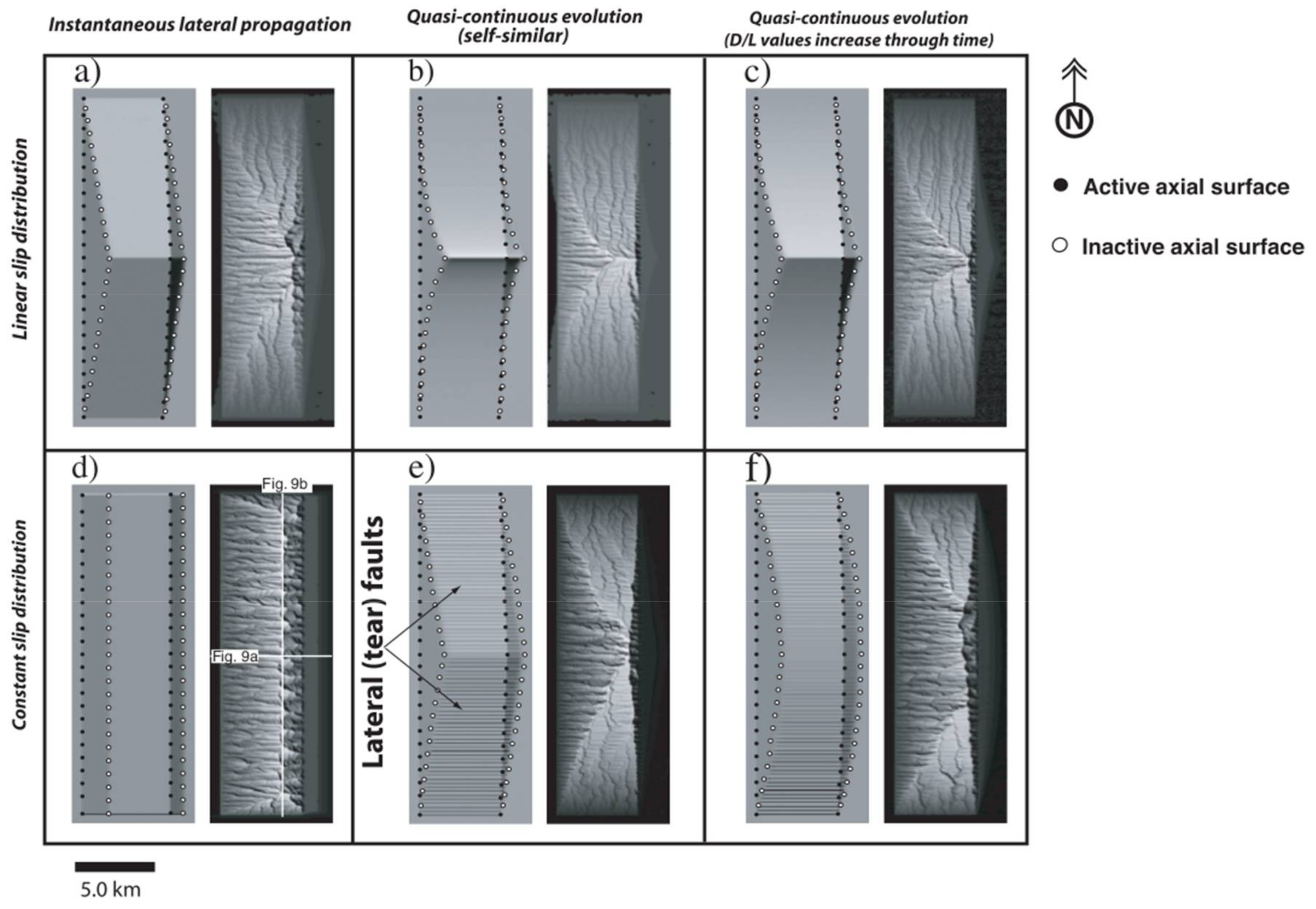
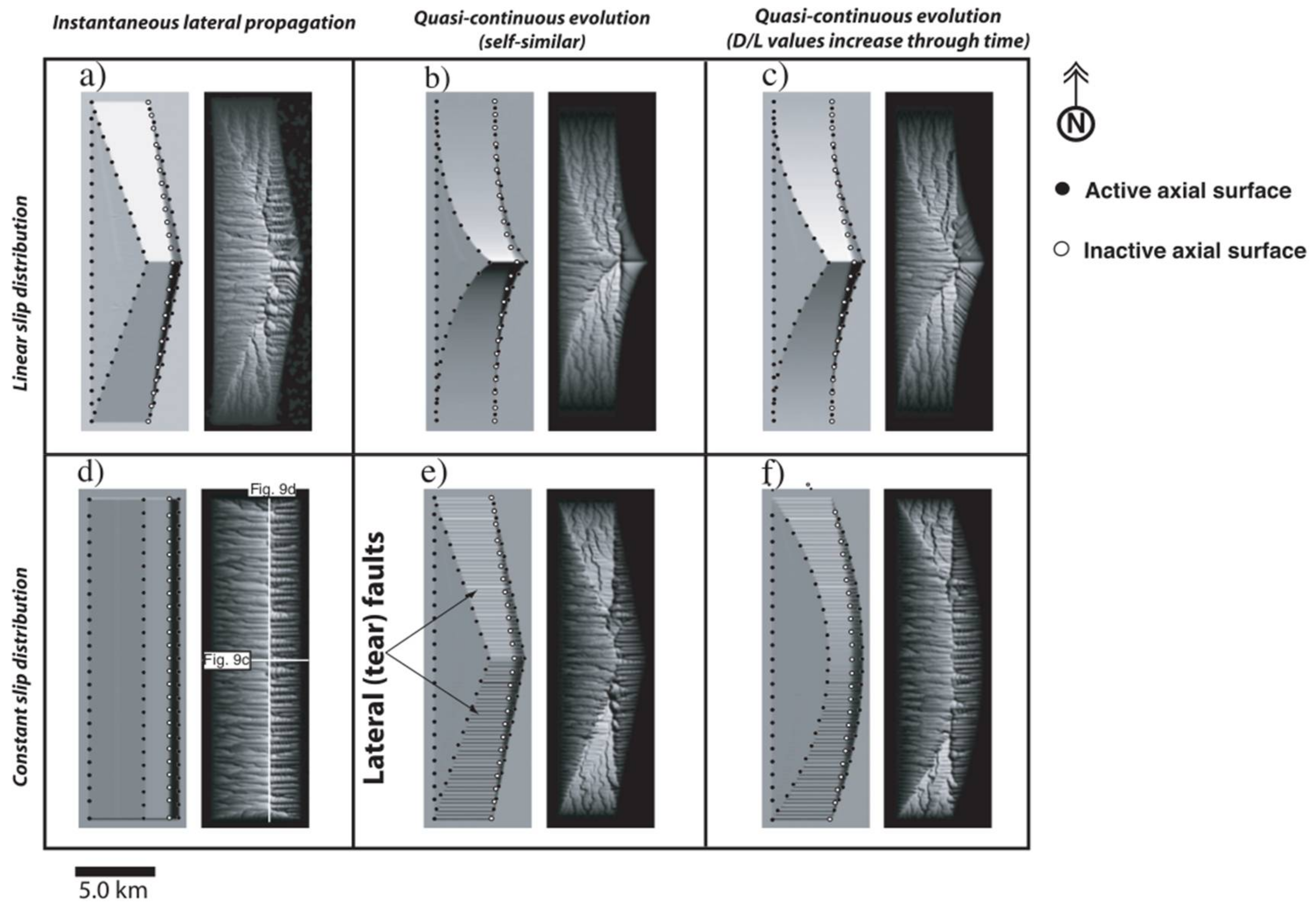
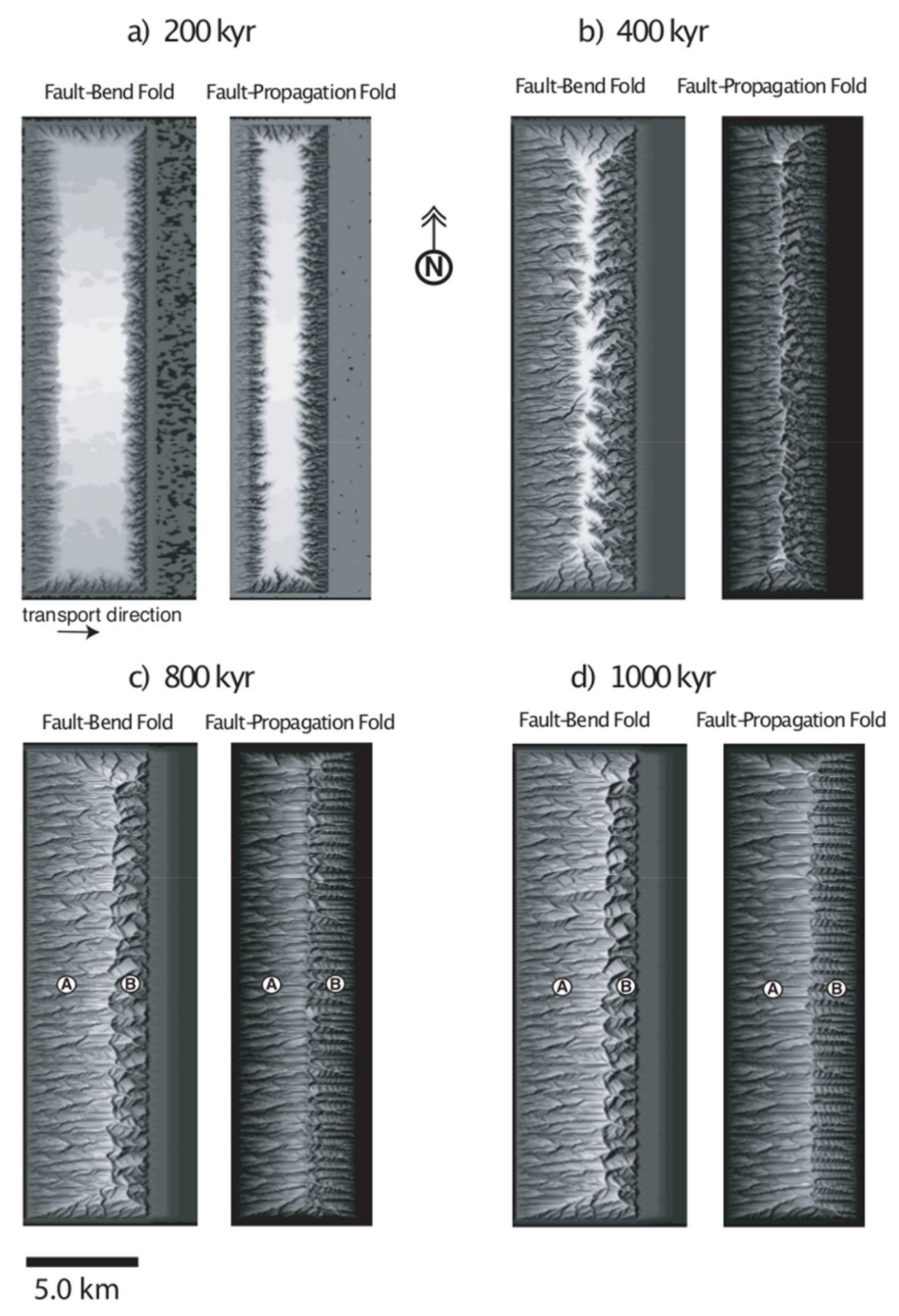
6.1. Final Geometries of River Networks
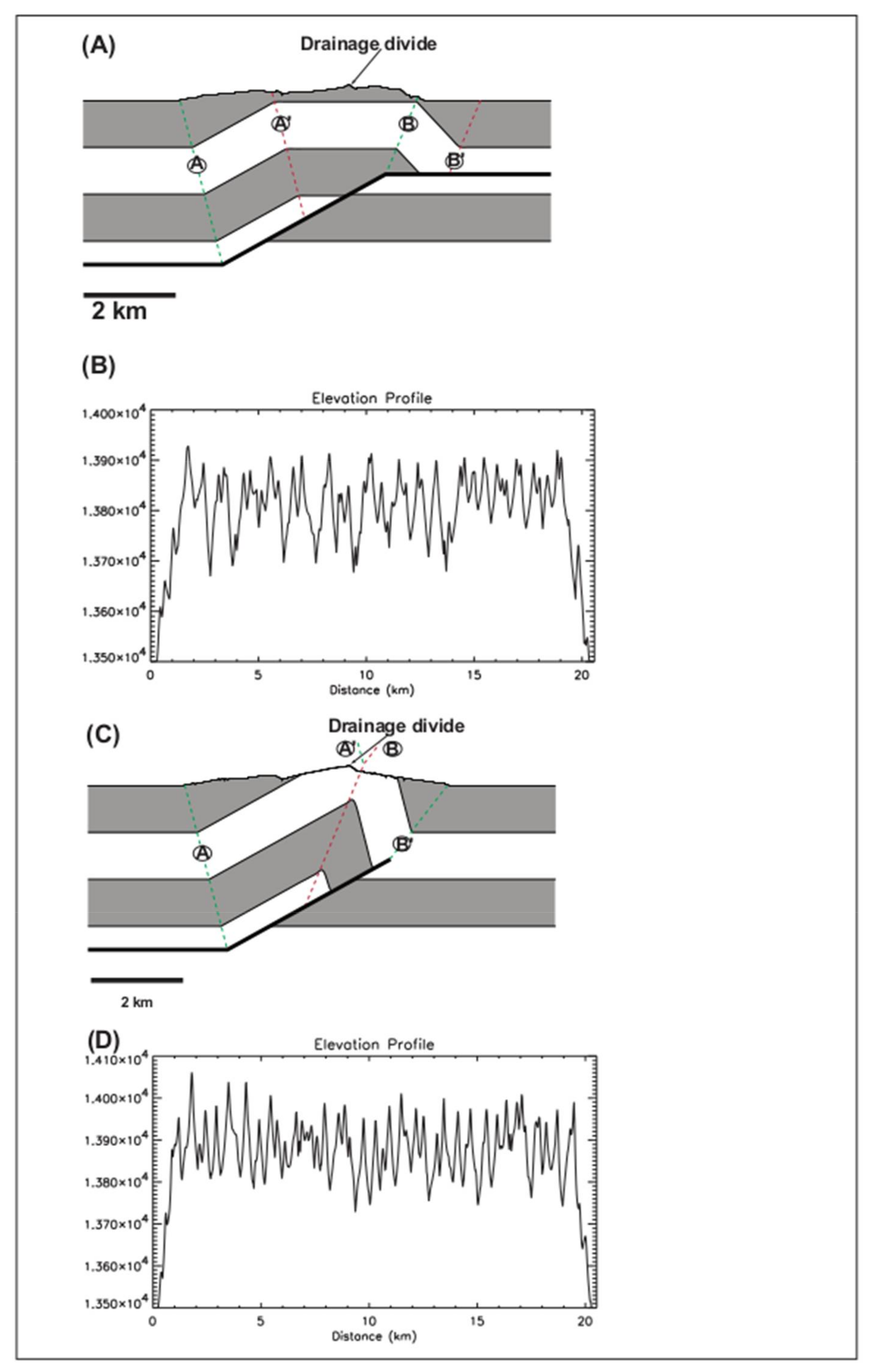
6.2. Final Geometries of Axial Surfaces and Relationship to Drainage Divides
6.3. Temporal Evolution
6.3.1. Instantaneous Lateral Propagation-Constant Slip Distribution
6.3.2. Instantaneous Lateral Propagation-Linear-Taper Slip Distribution
6.3.3. Progressive Lateral Propagation-Constant Slip Distribution
7. Discussion
7.1. Geomorphology of Flexural-Slip Fault-Related Folds
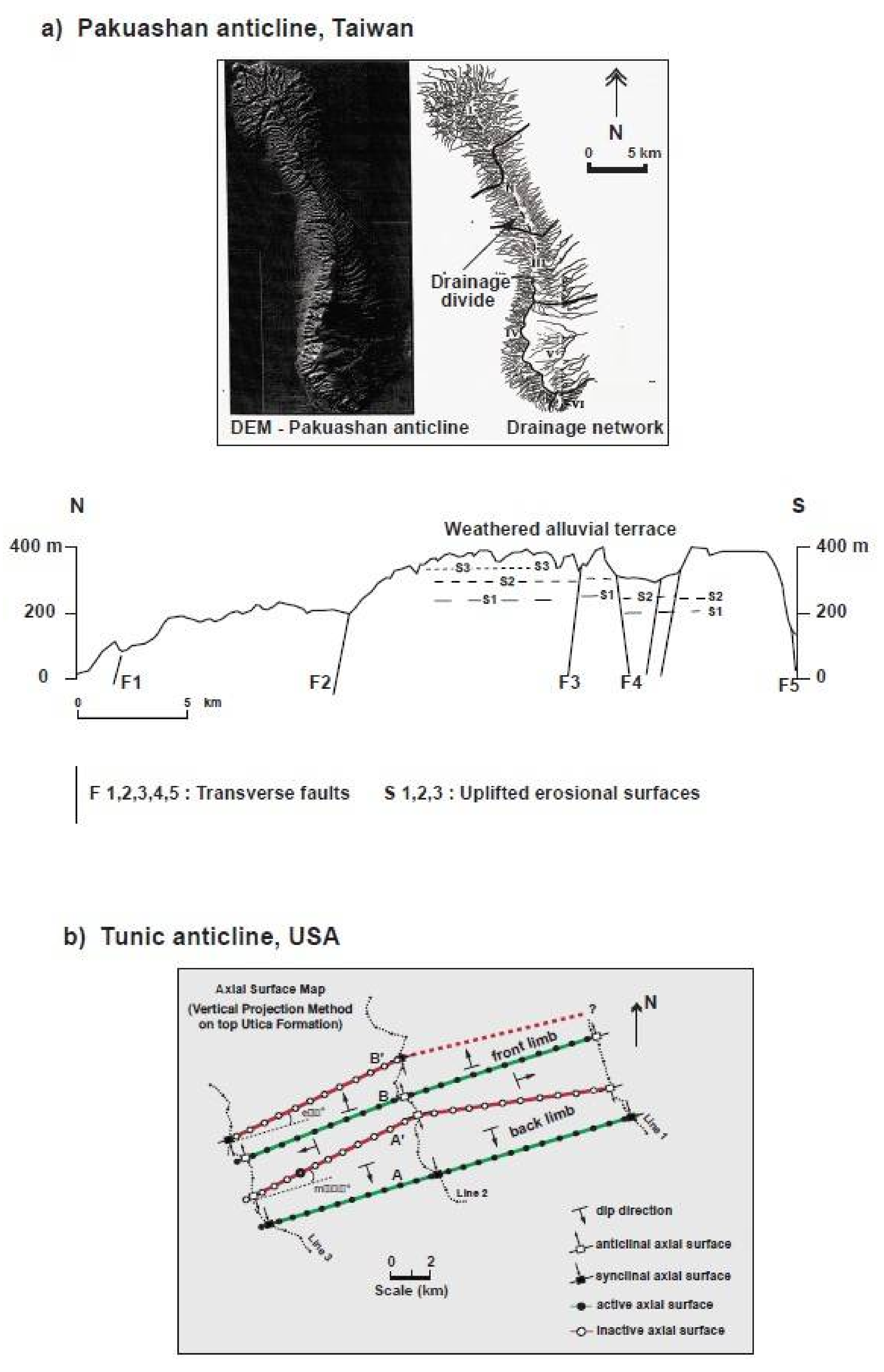
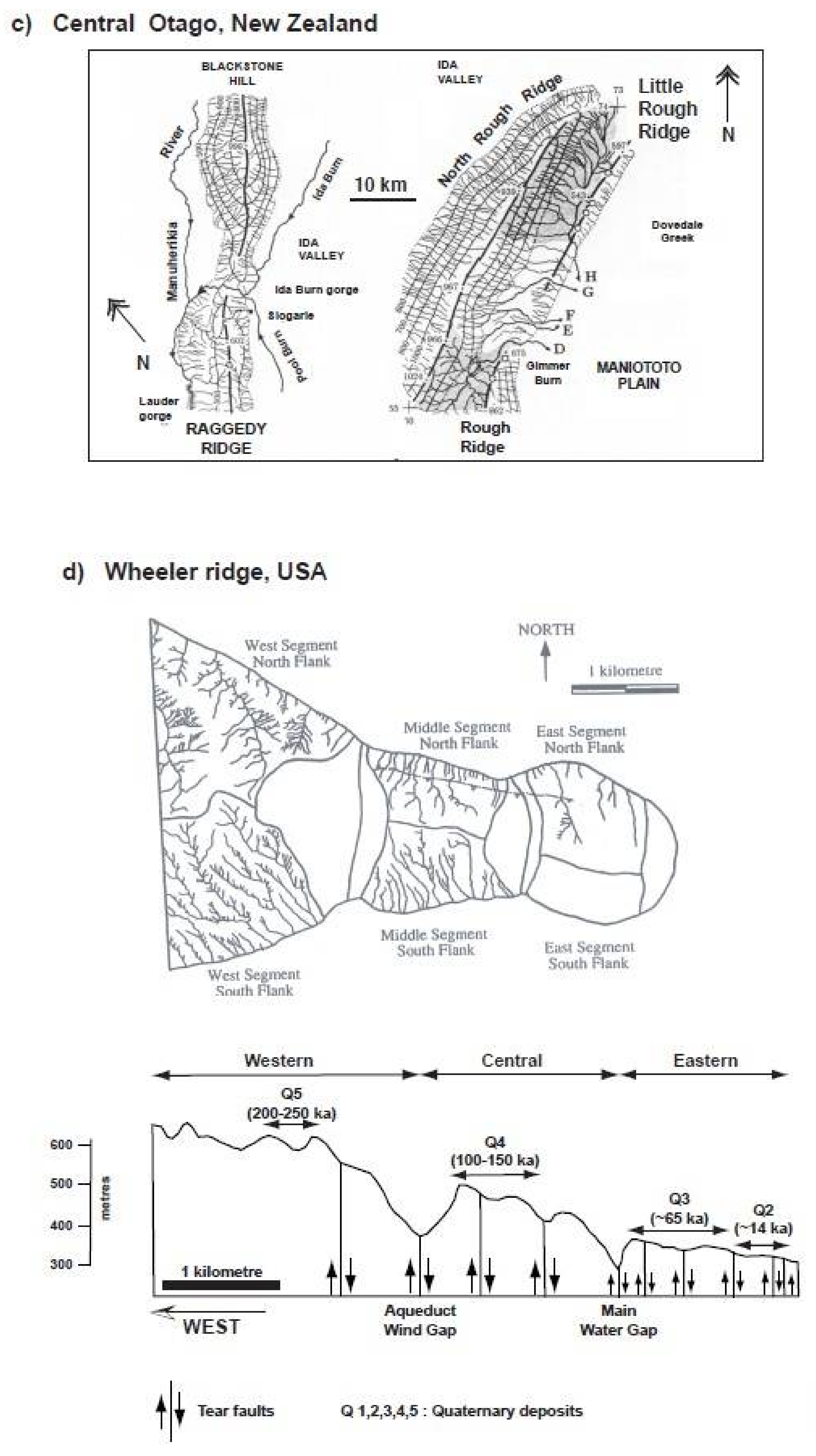
7.2. Comparison with Natural Examples
7.3. Limitations, Assumptions and Improvements
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Grant, L.B.; Mueller, K.J.; Gath, E.M.; Cheng, H.; Edwards, R.L.; Munro, R.; Kennedy, G.L. Late Quaternary uplift and earthquake potential of the San Joaquin Hills, southern Los Angeles basin, California. Geology 1999, 27, 1031–1034. [Google Scholar] [CrossRef]
- Rivero, C.; Shaw, J.H.; Mueller, K. Oceanside and Thirtymile Bank blind thrust: Implications for earthquakes hazards in coastal southern California. Geology 2000, 28, 891–894. [Google Scholar] [CrossRef]
- Allmendinger, R.W.; Shaw, J.H. Estimation of fault propagation distance from fold shape: Implications for earthquake hazard assessment. Geology 2000, 28, 1099–1102. [Google Scholar] [CrossRef]
- Hubert-Ferrari, A.; Suppe, J.; Gonzalez-Mieres, R.; Wang, X. Mechanisms of active folding of the landscape (southern Tian Shan, China). J. Geophys. Res. 2007, 112, B03S09. [Google Scholar] [CrossRef]
- Delcaillau, B.; Carozza, J.-M.; Laville, E.; Amrhar, M.; Sheikholeslami, R. New geomorphic criteria on lateral propagation of blind thrust-related fold growth accommodating oblique convergence. Ann. Geomorphol. 2007, 51, 141–163. [Google Scholar] [CrossRef]
- Talebian, M.; Copley, A.C.; Fattahi, M.; Ghorashi, M.; Jackson, J.A.; Nazari, H.; Sloan, R.A.; Walker, R.T. Active faulting within a megacity: The geometry and slip rate of the Pardisan thrust in central Tehran, Iran. Geophys. J. Int. 2016, 207, 1688–1699. [Google Scholar] [CrossRef]
- Wilkerson, M.S.; Medwedeff, D.A.; Marshak, S. Geometrical modelling of fault-related folds: A pseudo-three-dimensional approach. J. Struct. Geol. 1991, 13, 801–812. [Google Scholar] [CrossRef]
- Jackson, J.; Norris, R.; Youngson, J. The structural evolution of active fault and fold systems in central Otago, New Zealand: Evidence revealed by drainage patterns. J. Struct. Geol. 1996, 18, 217–234. [Google Scholar] [CrossRef]
- Mueller, K.; Talling, P. Geomorphic evidence for tear faults accommodating lateral propagation of an active fault-bend fold, Wheeler Ridge, California. J. Struct. Geol. 1997, 19, 397–411. [Google Scholar] [CrossRef]
- Delcaillau, B.; Deffontaines, B.; Floissac, L.; Angelier, J.; Deramond, J.; Souquet, P.; Chu, H.T.; Lee, J.F. Morphotectonic evidence from lateral propagation of an active frontal fold; Pakvashan anticline, foothills of Taiwan. Geomorphology 1998, 24, 263–290. [Google Scholar] [CrossRef]
- Collignon, M.; Fernandez, N.; Kaus, B.J.P. Influence of surface processes and initial topography on lateral fold growth and fold linkage mode. Tectonics 2015, 34, 1622–1645. [Google Scholar] [CrossRef]
- Poblet, J.; Hardy, S. Reverse modelling of detachment folds; application to the Pico del Aguila anticline in the South Central Pyrenees (Spain). J. Struct. Geol. 1995, 17, 1707–1724. [Google Scholar] [CrossRef]
- Ford, M.; Williams, E.; Artoni, A.; Vergés, J.; Hardy, S. Progressive evolution of a fault-related fold pair from growth strata geometries, Sant Llorenç de Morunys, SE Pyrenees. J. Struct. Geol. 1997, 19, 413–441. [Google Scholar] [CrossRef]
- Suppe, J.; Sabat, F.; Munoz, J.A.; Poblet, J.; Roca, E.; Verges, J. Bed-by-bed fold growth by kink-band migration: Sant Llorenc de Morunys, eastern Pyrenees. J. Struct. Geol. 1997, 19, 443–461. [Google Scholar] [CrossRef]
- Suppe, J.; Mueller, K. Growth of the Wheeler Ridge anticline, California: Geomorphic evidence for fault-bend folding behaviour during earthquakes. J. Struct. Geol. 1997, 19, 383–396. [Google Scholar]
- Casas-Sainz, A.M.; Cortes, A.L.; Maestro, A. Sequential limb rotation and kink-band migration recorded by growth strata, Almazán Basin, North Spain. Sediment. Geol. 2002, 146, 25–45. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.; Rundle, J. The growth of geological structures by repeated earthquakes, 1: Conceptual framework. J. Geohys. Res. 1988, 93, 13307–13318. [Google Scholar] [CrossRef]
- Burbank, D.W.; McLean, J.K.; Bullen, M.; Abdrakhmatov, K.Y.; Miller, M.M. Partitioning of intermontane basins by thrust–related folding, Tien Shan, Kyrgyzstan. Basin Res. 1999, 11, 75–92. [Google Scholar] [CrossRef]
- Keller, E.A.; Gurrola, L.; Tierney, T.E. Geomorphic criteria to determine direction of lateral propagation of reverse faulting and folding. Geology 1999, 27, 515–518. [Google Scholar] [CrossRef]
- Champel, B.; van der Beek, P.; Mugnier, J.-L.; Leturmy, P. Growth and lateral propagation of fault-related folds in the Siwaliks of western Nepal: Rates, mechanisms, and geomorphic signature. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Cooper, K.; Hardy, S.; Gawthorpe, R.L. Stratigraphic and structural expression of the lateral growth of fault-propagation folds: Results and implications from kinematic modelling. Basin Res. 2003, 15, 165–182. [Google Scholar] [CrossRef]
- Gaidzik, K.; Ramirez-Herrera, M.T. Geomorphic indices and relative tectonic uplift in the Guerrero sector of the Mexican forearc. Geosci. Front. 2017, 8, 885–902. [Google Scholar] [CrossRef]
- Talling, P.J.; Sowter, M.J. Drainage network on progressively tilted surfaces with different gradients, Wheeler ridge, California. Earth Surf. Process. Landf. 1999, 24, 809–824. [Google Scholar] [CrossRef]
- Chen, J.; Heermance, R.; Burbank, D.W.; Scharer, K.M.; Miao, J.; Wang, C. Quantification of growth and lateral propagation of the Kashi anticline, southwest Chinese Tian Shan. J. Geophys. Res. 2007, 112, B03S16. [Google Scholar] [CrossRef]
- Ellis, M.A.; Densmore, A.L.; Anderson, R.S. Evolution of mountainous topography in the Basin and Range Province. Basin Res. 1999, 11, 21–42. [Google Scholar] [CrossRef]
- Gawthorpe, R.L.; Leeder, M.R. Tectono-sedimentary evolution of active extensional basins. Basin Res. 2000, 12, 195–218. [Google Scholar] [CrossRef]
- Morewood, N.C.; Roberts, G.P. Surface observations of active normal fault propagation: Implications for growth. J. Geol. Soc. Lond. 2002, 159, 263–272. [Google Scholar] [CrossRef]
- Jackson, J.; Ritz, J.-F.; Siame, L.; Raisbeck, G.; Yiou, F.; Norris, R.; Youngson, J.; Bennett, E. Fault growth and landscape development in Otago, New Zealand, using in situ cosmogenic 10Be. Earth Planet. Sci. Lett. 2002, 195, 185–193. [Google Scholar] [CrossRef]
- Snyder, N.P.; Whipple, K.X.; Tucker, G.E.; Merrits, D.J. Landscape response to tectonic forcing: Digital elevation model analysis of stream profiles in the Mendocino triple junction region, northern California. Geol. Soc. Am. Bull. 2000, 112, 1250–1263. [Google Scholar] [CrossRef]
- Ahmadi, R.; Ouali, J.; Mercier, E.; Mansy, J.L.; Van Vliet Lanoe, B.; Launeau, P.; Hekhiss, F.; Rafini, S. The geomorphologic imprints of hinge migration in the fault-related folds. A case study in southern Tunisian Atlas. J. Struct. Geol. 2006, 28, 721–728. [Google Scholar] [CrossRef]
- Bretis, B.; Bartl, N.; Grasemann, B. Lateral fold growth and linkage in the Zagros fold and thrust belt (Kurdistan, NE Iraq). Basin Res. 2011, 23, 615–630. [Google Scholar] [CrossRef]
- Kirby, E.; Whipple, K.X. Expression of active tectonics in erosional landscapes. J. Struct. Geol. 2012, 44, 54–75. [Google Scholar] [CrossRef]
- Lave, J.; Avouac, J.P. Active folding of fluvial terraces across the Siwalik Hills, Himalayas of central Nepal. J. Geophys. Res. 2000, 105, 5735–5770. [Google Scholar] [CrossRef]
- Kirby, E.; Whipple, K.X. Quantifying differential rock-uplift rates via stream profile analysis. Geology 2001, 29, 415–418. [Google Scholar] [CrossRef]
- Van der Beek, P.; Champel, B.; Mugnier, J.L. Control of detachment dip on drainage development in regions of active fault-propagation folding. Geology 2002, 30, 471–474. [Google Scholar] [CrossRef]
- Thompson, S.C.; Weldon, R.J.; Rubin, C.M.; Abdrakhmatov, K.; Molnar, P.; Berger, G.W. Late Quaternary slip rates across the central Tien Shan, Kyrgyzstan, central Asia. J. Geophys. Res. 2002, 107, 2203. [Google Scholar] [CrossRef]
- Miller, S.; Slingerland, R.L. Topographic advection on fault-bend folds: Inheritance of valley positions and the formation of wind gaps. Geology 2006, 34, 769–772. [Google Scholar] [CrossRef]
- Densmore, A.L.; Ellis, M.A.; Anderson, R.S. Landsliding and the evolution of normal-fault-bounded mountains. J. Geophys. Res. 1998, 103, 15203–15219. [Google Scholar] [CrossRef]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting; Cambridge University Press: Cambridge, MA, USA, 1990; p. 439. [Google Scholar]
- Cowie, P.A.; Scholz, C.H. Displacement-length scaling relationship for faults: Data synthesis and discussion. J. Struct. Geol. 1992, 14, 1149–1156. [Google Scholar] [CrossRef]
- Schultz, R.A.; Okubo, C.H.; Wilkins, S.J. Displacement-length scaling relations for faults on the terrestrial planets. J. Struct. Geol. 2006, 28, 2182–2193. [Google Scholar] [CrossRef]
- Bergen, K.J.; Shaw, J.H. Displacement profiles and displacement-length scaling relationships of thrust faults constrained by seismic-reflection data. GSA Bull. 2010, 122, 1209–1219. [Google Scholar] [CrossRef]
- Dawers, N.H.; Anders, M.H.; Scholz, C.H. Growth of normal faults: Displacement-length scaling. Geology 1993, 21, 1107–1110. [Google Scholar] [CrossRef]
- Clark, R.M.; Cox, S.J.D. A modern regression approach to determining fault displacement-length scaling relationships. J. Struct. Geol. 1996, 18, 147–152. [Google Scholar] [CrossRef]
- Walsh, J.; Watterson, J. Analysis of the relationship between displacement and dimensions of faults. J. Struct. Geol. 1988, 10, 239–247. [Google Scholar] [CrossRef]
- Marrett, R.; Allmendinger, R. Estimates of strain due to brittle faulting: Sampling of fault population. J. Struct. Geol. 1991, 13, 735–738. [Google Scholar] [CrossRef]
- Gillespie, P.A.; Walsh, J.J.; Watterson, J. Limitations of dimension and displacement data from single faults and the consequences for data analysis and interpretation. J. Struct. Geol. 1992, 14, 1157–1172. [Google Scholar] [CrossRef]
- Elliott, D. The energy balance and deformation mechanisms of thrust sheets. Philos. Trans. R. Soc. Lond. A 1976, 283, 289–312. [Google Scholar] [CrossRef]
- Fermor, P. Aspects of the three-dimensional structure of the Alberta Foothills and Front Ranges. Geol. Soc. Amer. Bull. 1999, 111, 317–346. [Google Scholar] [CrossRef]
- Wilkerson, S. Differential transport and continuity of thrust sheets. J. Struct. Geol. 1992, 14, 749–751. [Google Scholar] [CrossRef]
- Mansfield, C.; Cartwright, J. Fault growth by linkage: Observations and implications from analogue models. J. Struct. Geol. 2001, 23, 745–763. [Google Scholar] [CrossRef]
- Ackermann, R.V.; Schlische, R.W.; Withjack, M.O. The geometric and statistical evolution of normal fault systems: An experimental study of the effects of mechanical layer thickness on scaling laws. J. Struct. Geol. 2001, 23, 1803–1819. [Google Scholar] [CrossRef]
- Walsh, J.J.; Nicol, A.; Childs, C. An alternative model for the growth of faults. J. Struct. Geol. 2002, 24, 1669–1675. [Google Scholar] [CrossRef]
- Alvarez, W. Drainage on evolving fold-thrust belts: A study of transverse canyons in the Apennines. Basin Res. 1999, 11, 267–284. [Google Scholar] [CrossRef]
- Pollard, D.D.; Segall, P. Theoretical displacement and stress near fractures in rocks: With application to faults, joints, veins, dikes, and solution surfaces. In Fracture Mechanics of Rocks; Atkinson, B.K., Ed.; Academic Press Geology Series; Academic Press: London, UK, 1987. [Google Scholar]
- Cowie, P.A.; Scholz, C.H. Physical explanation for the displacement-length relationship of faults using a post-yield fracture mechanics model. J. Struct. Geol. 1992, 14, 1133–1148. [Google Scholar] [CrossRef]
- Willemse, E.J.M. Segmented normal faults: Correspondence between three-dimensional mechanical models and field data. J. Geophys. Res. 1997, 102, 675–692. [Google Scholar] [CrossRef]
- Souter, B.J.; Hager, B.H. Faul propagation fold growth during the 1994 Northridge, California, earthquake? J. Geophys. Res. 1997, 112, 11931–11942. [Google Scholar] [CrossRef]
- Ma, K.-F.; Song, T.-R.; Lee, S.-J.; Wu, H.-I. Spatial slip distribution of the September 20, 1999, Chi-Chi, Taiwan, earthquake (Mw 7.6)—Inverted from teleseismic data. Geophys. Res. Lett. 2000, 27, 3417–3420. [Google Scholar] [CrossRef]
- Lin, A.; Ouchi, T.; Chen, A.; Maruyama, T. Co-seismic displacements, folding and shortening structures along the Chelungpu surface rupture zone occurred during the 1999 Chi-Chi (Taiwan) earthquake. Tectonophysics 2001, 330, 225–244. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, J.C.; Ge, L.L.; Ding, X.L.; Chen, Y.L. Determining fault slip distribution of the Chi-Chi Taiwan earthquake with GPS and InSAR data using triangular dislocation elements. J. Geodyn. 2008, 45, 163–168. [Google Scholar] [CrossRef]
- Wan, Y.; Shen, Z.K.; Bürgmann, R.; Sun, J.; Wang, M. Fault geometry and slip distribution of the 2008 Mw 7.9 Wenchuan, China earthquake, inferred from GPS and InSAR measurements. Geophys. J. Int. 2017, 208, 748–766. [Google Scholar] [CrossRef]
- Fukahata, Y.; Hashimoto, M. Simultaneous estimation of the dip angles and slip distribution on the faults of the 2016 Kumamoto earthquake through a weak nonlinear inversion of InSAR data. Earth Planets Space 2016, 68, 204. [Google Scholar] [CrossRef]
- Chen, T.; Akciz, S.O.; Hudnut, K.W.; Zhang, D.Z.; Stock, J.M. Fault-Slip Distribution of the 1999 Mw 7.1 Hector Mine Earthquake, California, Estimated from Postearthquake Airborne LiDAR Data. Bull. Seismol. Soc. Am. 2015, 105, 776–790. [Google Scholar] [CrossRef]
- Chen, J.; Burbank, D.W.; Scharer, K.M.; Sobel, E.; Yin, J.; Rubin, C.; Zhao, R. Magnetochronology of the Upper Cenozoic strata in the Southwestern Chinese Tian Shan: Rates of Pleistocene folding and thrusting. Earth Planet. Sci. Lett. 2002, 195, 113–130. [Google Scholar] [CrossRef]
- Daeron, M.; Avouac, J.P.; Charreau, J.; Dominguez, S. Modeling the shortening history of a fault-tip fold using structural and geomorphic records of deformation. J. Geophys. Res. 2007, 112, B03S13. [Google Scholar] [CrossRef]
- Delcaillau, B. Geomorphic response to growing fault-related folds: Example from the foothills of central Taiwan. Geodin. Acta 2001, 14, 265–287. [Google Scholar] [CrossRef]
- Shaw, J.; Hook, S.; Suppe, J. Structural trend analysis by axial surface mapping. Am. Assoc. Pet. Geol. Bull. 1994, 78, 700–721. [Google Scholar]
- Rowan, M.G.; Linares, R. Fold-evolution matrices and axial surfaces of fault-bend folds: Application to the Medina anticline, Eastern Cordillera, Colombia. Am. Assoc. Pet. Geol. Bull. 2000, 84, 741–763. [Google Scholar]
- Gallango, O.; Novoa, E.; Bernal, A. The petroleum system of the central Perijá fold belt, western Venezuela. Am. Assoc. Pet. Geol. Bull. 2002, 86, 1263–1284. [Google Scholar]
- Goode, J.K.; Burbank, D.W. Kinematic implications of consequent channels on growing folds. J. Geophys. Res. 2011, 116, B04407. [Google Scholar] [CrossRef]
- Keller, E.A.; Zepeda, R.L.; Rockwell, T.K.; Ku, T.L.; Dinklage, W.S. Active tectonics at Wheeler Ridge, southern San Joaquin Valley, California. Geol. Soc. Am. Bull. 1998, 10, 298–310. [Google Scholar] [CrossRef]
- Meigs, A.J.; Brozovic, N.; Johnson, M.L. Steady balanced rates of uplift and erosion of the Santa Monica mountains, California. Basin Res. 1999, 11, 59–73. [Google Scholar] [CrossRef]
- Azor, A.; Keller, E.A.; Yeats, R.S. Geomorphic indicators of active fold growth: South Mountain-Oak Ridge anticline, Ventura basin, southern California. Geol. Soc. Am. Bull. 2002, 114, 745–753. [Google Scholar] [CrossRef]
- Bilotti, F.; Shaw, J.H.; Brennan, P.A. Quantitative structural analysis with stereoscopic remote sensing imagery. Am. Assoc. Pet. Geol. Bull. 2000, 84, 727–740. [Google Scholar]
- Fisher, N.D.; Jordan, T.E.; Brown, L. The structural and stratigraphic evolution of the La Rioja basin, Argentina. J. South Am. Earth Sci. 2002, 15, 141–156. [Google Scholar] [CrossRef]
- Suppe, J. Geometry kinematics of fault-bend folding. Am. J. Sci. 1983, 283, 684–721. [Google Scholar] [CrossRef]
- Suppe, J.; Medwedeff, D.A. Geometry Kinematics of Fault-Propagation Folding. Eclogae Geol. Helvetiae 1990, 83, 409–454. [Google Scholar]
- Stein, R.S.; King, G.C.P. Seismic potential revealed by surface folding: The 1983 Coalinga, California, earthquake. Science 1984, 224, 869–872. [Google Scholar] [CrossRef] [PubMed]
- Niño, F.; Philip, H.; Chery, J. The role of bed-parallel slip in the formation of blind thrust faults. J. Struct. Geol. 1998, 20, 503–516. [Google Scholar] [CrossRef]
- Cardozo, N.; Bhalla, K.; Zehnder, A.T.; Allmendinger, R.W. Mechanical models of fault propagation folds and comparison to the trishear kinematic model. J. Struct. Geol. 2003, 25, 1–18. [Google Scholar] [CrossRef]
- Hardy, S.; Ford, M. Numerical modelling of trishear fault-propagation folding. Tectonics 1997, 16, 841–854. [Google Scholar] [CrossRef]
- Allmendinger, R.W. Inverse and forward numerical modelling of trishear fault propagation folds. Tectonics 1998, 17, 640–656. [Google Scholar] [CrossRef]
- Chester, J.S.; Chester, F.M. Fault-propagation folds above thrust with constant dip. J. Struct. Geol. 1990, 12, 903–910. [Google Scholar] [CrossRef]
- Hardy, S.; Poblet, J. Geometric and numerical model of progressive limb rotation in detachment folds. Geology 1994, 22, 371–374. [Google Scholar] [CrossRef]
- Hardy, S.; Poblet, J. The velocity description of deformation. Paper 2: Sediment geometries associated with fault-bend and fault-propagation folds. Mar. Pet. Geol. 1995, 12, 165–176. [Google Scholar] [CrossRef]
- Whipple, K.X.; Kirby, E.; Brocklehurst, S.H. Geomorphic limits to climate-induced increases in topographic relief. Nature 1999, 401, 39–43. [Google Scholar] [CrossRef]
- Burbank, D.W.; Leland, J.; Fielding, E.; Anderson, R.S.; Brozovic, N.; Reid, M.R.; Duncan, C. Bedrock incision, rock uplift and threshold hillslopes in the northwestern Himalayas. Nature 1996, 379, 505–510. [Google Scholar] [CrossRef]
- Whipple, K.X.; Tucker, G.E. Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs. J. Geophys. Res. 1999, 104, 17661–17674. [Google Scholar] [CrossRef]
- Bernal, A.; Hardy, S. Syn-tectonic sedimentation associated with three-dimensional fault-bend fold structures: A numerical approach. J. Struct. Geol. 2002, 24, 609–635. [Google Scholar] [CrossRef]
- Bernal, A.; Hardy, S.; Gawthorpe, R.L.; Finch, E. Stratigraphic expression of the lateral propagation and growth of isolated fault-related uplifts. Basin Res. 2004, 16, 221–238. [Google Scholar] [CrossRef]
- Bennedetti, L.; Tapponier, P.; King, G.C.P.; Meyer, B.; Manighetti, I. Growth folding and active thrusting in the Montello region, Veneto, northern Italy. J. Geophys. Res. 2000, 105, 739–766. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Sanderson, D.J. The relationship between displacement and length of faults: A review. Earth Sci. Rev. 2005, 68, 317–334. [Google Scholar] [CrossRef]
- Stock, J.D.; Montgomery, D.R. Geologic constraints on bedrock river incision using the stream power law. J. Geophys. Res. 1999, 104, 4983–4993. [Google Scholar] [CrossRef]
- Whipple, K.X.; Snyder, N.P.; Dollenmayer, K. Rates and processes of bedrock incision by the Upper Ukak River since the 1912 Novarupta ash flow in the Valley of Ten Thousand Smokes, Alaska. Geology 2000, 28, 835–838. [Google Scholar] [CrossRef]
- Whipple, K.X.; Hancock, G.S.; Anderson, R.S. River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation. Geol. Soc. Am. Bull. 2000, 112, 490–503. [Google Scholar] [CrossRef]
- Veneziano, D.; Niemann, J.D. Self-similarity and multifractality of fluvial erosion topography, 1, Mathematical conditions and physical origin. Water Resour. Res. 2000, 36, 1923–1936. [Google Scholar] [CrossRef]
- Montgomery, D.R. Predicting landscape-scale erosion rates using digital elevation models. C. R. Geosci. 2003, 335, 1121–1130. [Google Scholar] [CrossRef]
- Howard, A.D. A detachment-limited model of drainage basin evolution. Water Resour. Res. 1994, 30, 2261–2285. [Google Scholar] [CrossRef]
- Hardy, S.; Gawthorpe, R. Normal fault control on sediment supply to extensional basins: Insights from numerical modelling. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Kenyon, P.M.; Turcotte, D.L. Morphology of a delta prograding by bulk sediment transport. Geol. Soc. Am. Bull. 1985, 96, 1457–1465. [Google Scholar] [CrossRef]
- Leeder, M. Sedimentology and Sedimentary Basins: From Turbulence to Tectonics; Blackwell Science Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Leeder, M.R. Denudation, vertical crustal movements and sedimentary fill. Geol. Rundsch. 1991, 80, 441–458. [Google Scholar] [CrossRef]
- Roering, J.J.; Kirchner, J.W.; Sklar, L.S.; Dietrich, W.E. Hillslope evolution by nonlinear creep and landsliding: An experimental approach. Geology 2001, 29, 143–146. [Google Scholar] [CrossRef]
- Colman, S.M.; Watson, K. Ages estimated from a diffusion equation model for scarp degradation. Science 1983, 221, 263–265. [Google Scholar] [CrossRef] [PubMed]
- Avuoac, J.P.; Tapponnier, P.; Bai, M.; You, H.; Wang, G. Active thrusting and folding along the Northern Tien Shan and Late Cenozoic Rotation of the Tarim Relative to Dzungaria and Kazakhstan. J. Geophys. Res. 2001, 98, 6755–6804. [Google Scholar] [CrossRef]
- Martin, Y. Modelling hillslope evolution: Linear and nonlinear transport relations. Geomorphology 2001, 34, 1–21. [Google Scholar] [CrossRef]
- Swan, F.H. Temporal clustering of Paleoseismic events on the Oued Fodda fault, Algeria. Geology 1988, 16, 1092–1095. [Google Scholar] [CrossRef]
- Stein, R.S.; Yeats, R.S. Hidden Earthquakes. Sci. Am. 1989, 260, 48–57. [Google Scholar] [CrossRef]
- Kelson, K.I.; Simpson, G.D.; Vanarsdale, R.B.; Haraden, C.C.; Lettis, W.R. Multiple late Holocene earthquakes along the Reelfoot fault, central New Madrid seismic zone. J. Geophys. Res. 1996, 101, 6151–6170. [Google Scholar] [CrossRef]
- Lague, D.; Crave, A.; Davy, P. Laboratory exp0eriments simulating the geomorphic response to tectonic uplift. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Rigon, R.; Rinaldo, A.; Rodriguez-Iturbe, I. On landscape self-organization. J. Geophys. Res. 1994, 99, 11971–11985. [Google Scholar] [CrossRef]
- Hardy, S.; McClay, K.; Muñoz, J.A. Deformation and fault activity in space and time in high-resolution numerical models of doubly vergent thrust wedges. Mar. Pet. Geol. 2009, 26, 232–248. [Google Scholar] [CrossRef]
- Hardy, S.; Finch, E. Discrete-element modelling of detachment folding. Basin Res. 2005, 17, 507–520. [Google Scholar] [CrossRef]
- Hardy, S. Cover deformation above steep, basement normal faults: Insights from 2D discrete element modeling. Mar. Pet. Geol. 2011, 28, 966–972. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernal, A.; Hardy, S.; Gawthorpe, R.L. Three-Dimensional Growth of Flexural Slip Fault-Bend and Fault-Propagation Folds and Their Geomorphic Expression. Geosciences 2018, 8, 110. https://doi.org/10.3390/geosciences8040110
Bernal A, Hardy S, Gawthorpe RL. Three-Dimensional Growth of Flexural Slip Fault-Bend and Fault-Propagation Folds and Their Geomorphic Expression. Geosciences. 2018; 8(4):110. https://doi.org/10.3390/geosciences8040110
Chicago/Turabian StyleBernal, Asdrúbal, Stuart Hardy, and Robert L. Gawthorpe. 2018. "Three-Dimensional Growth of Flexural Slip Fault-Bend and Fault-Propagation Folds and Their Geomorphic Expression" Geosciences 8, no. 4: 110. https://doi.org/10.3390/geosciences8040110
APA StyleBernal, A., Hardy, S., & Gawthorpe, R. L. (2018). Three-Dimensional Growth of Flexural Slip Fault-Bend and Fault-Propagation Folds and Their Geomorphic Expression. Geosciences, 8(4), 110. https://doi.org/10.3390/geosciences8040110




