Repetitive Rockfall Trajectory Testing
Abstract
1. Introduction
1.1. Previous Rockfall Testing Series
1.2. Laboratory Rockfall Testing
2. Field Test Preparation
2.1. Boundary Conditions
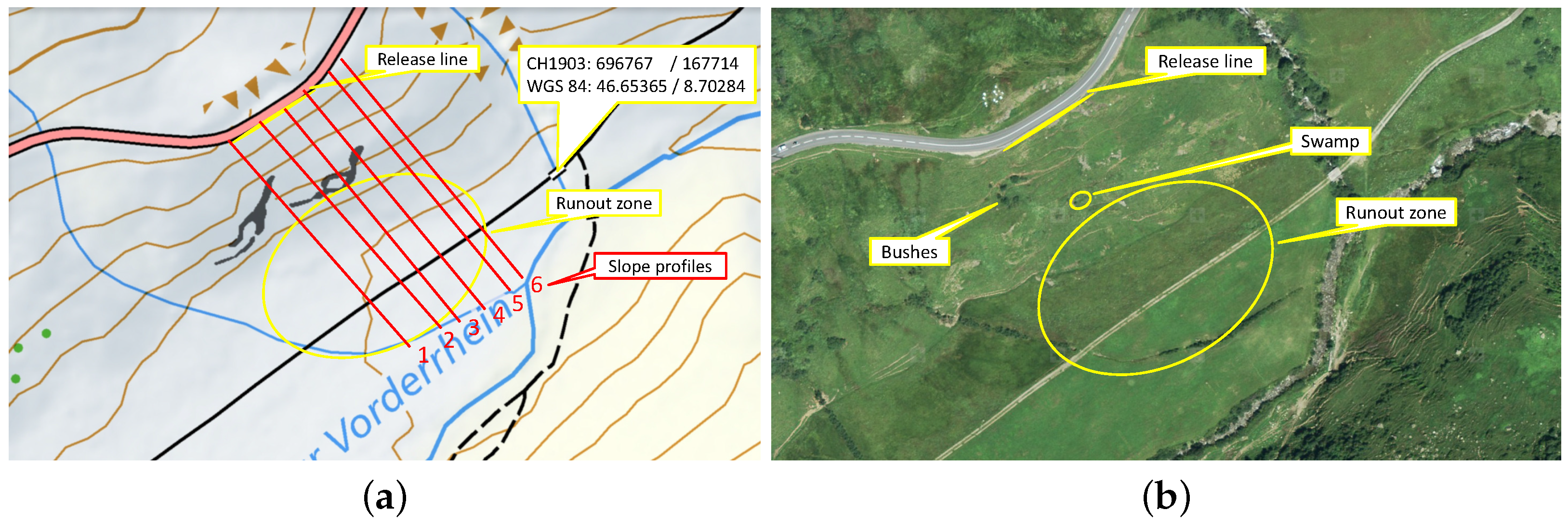
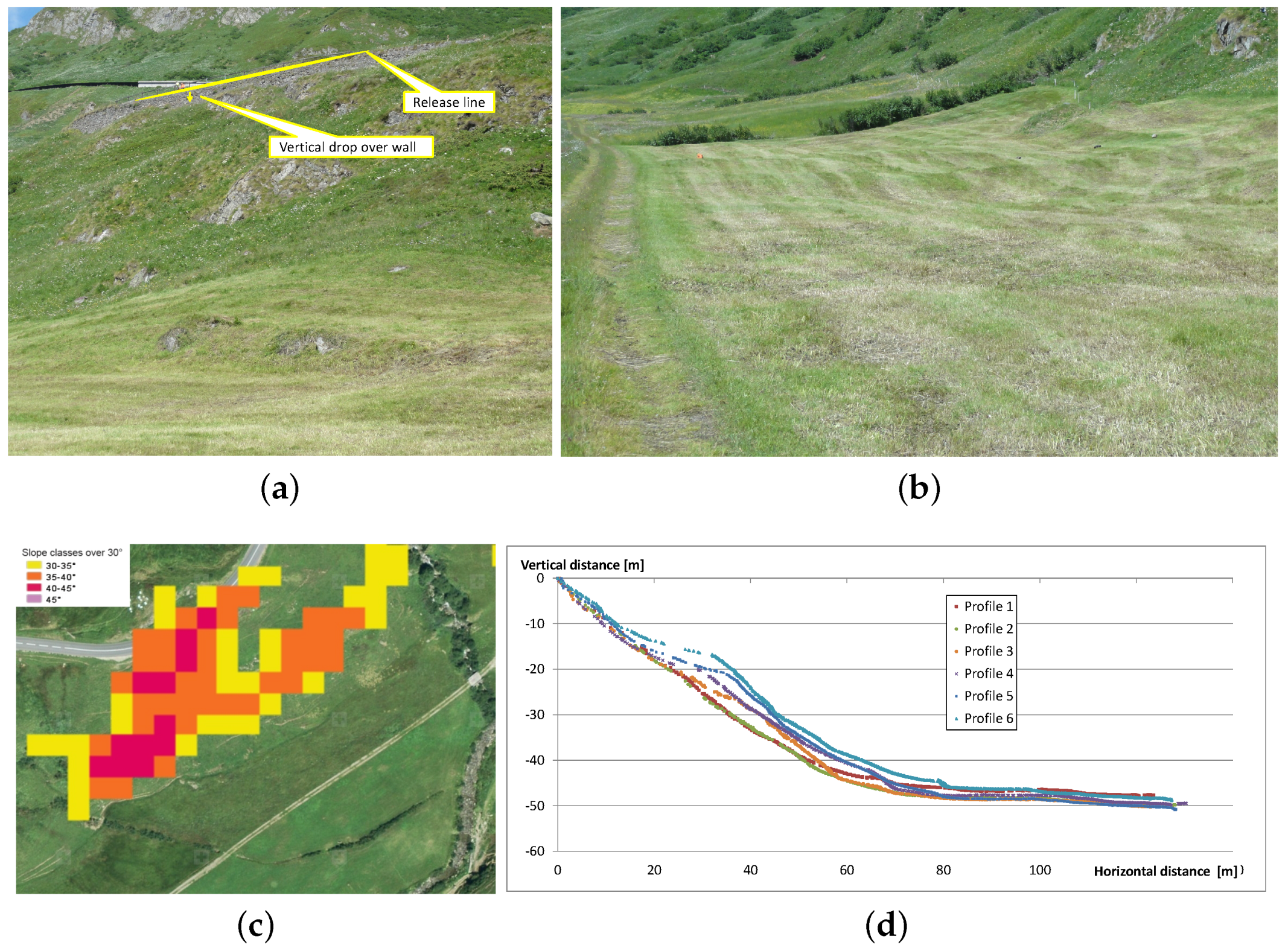
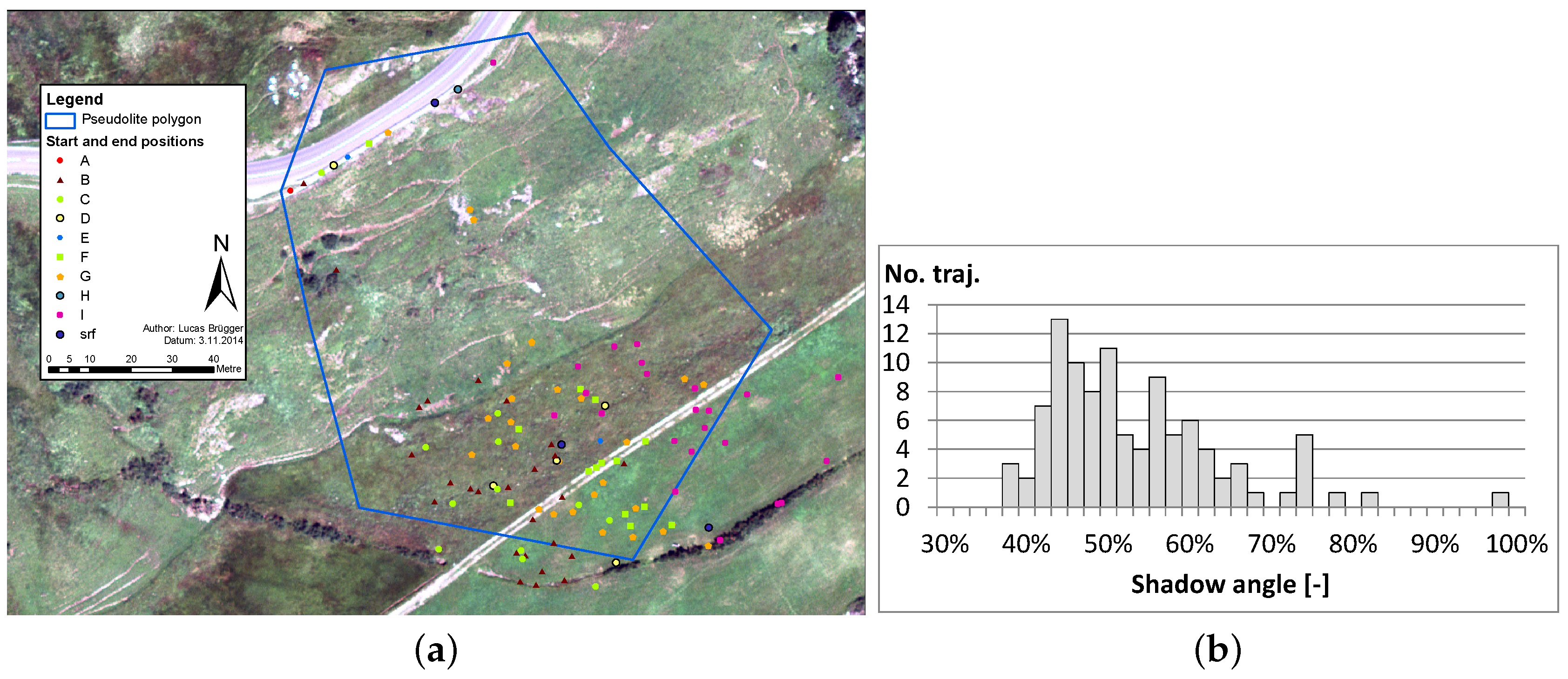
2.2. Test Site Description
2.3. Description of Test Blocks
2.4. Test Site Preparation
2.5. Measurement Instrumentation
3. Overall Test Results
3.1. Standard Test Procedure
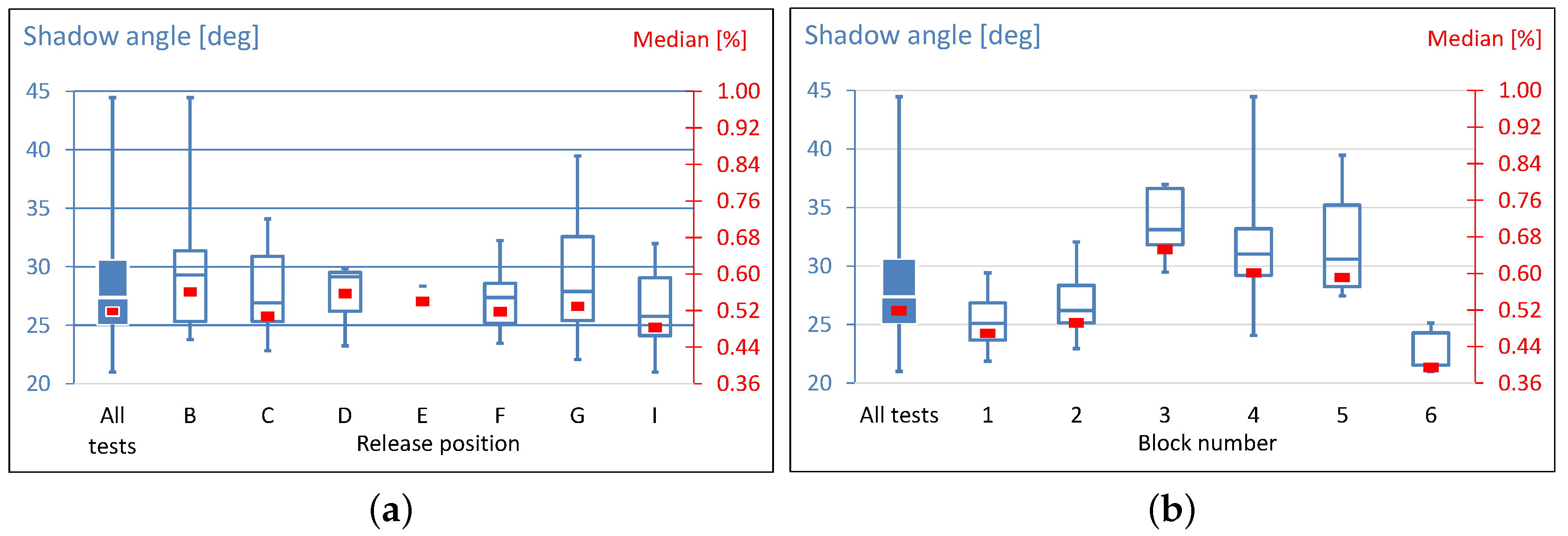
3.2. Test Summary
- More sphere-like shaped blocks lifted off the ground, but only when the terrain served as a ramp.
- The more sphere-like the blocks were shaped the higher their maximum speed.
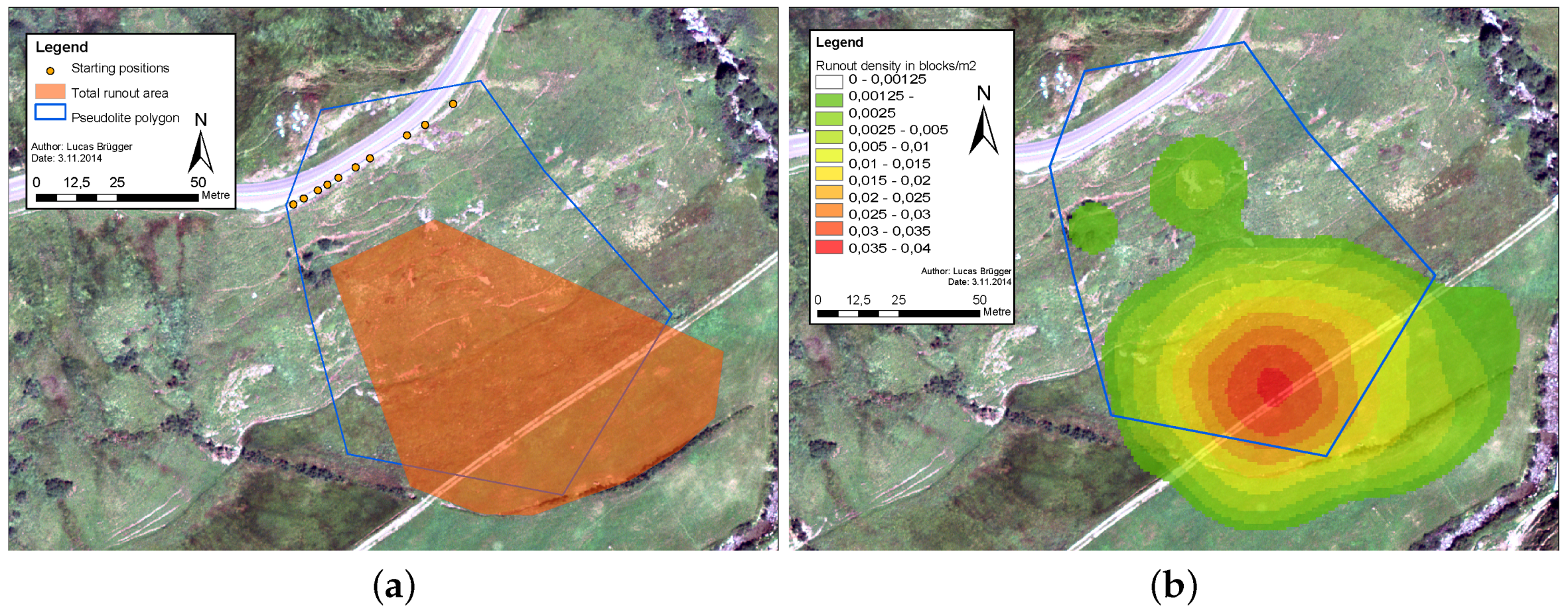
- If a regularly shaped block is thrown from the same start position it stops at the same end position: block no. 6 was thrown three times from start position I and we could see only one single path through the uncut grass in the almost horizontal runout section at the end of the slope. Therefore, we proclaim that the block took the same path three times.
- In the runout zone the terrain is not fully horizontal but slightly inclined to the East (with East being the right side of all aerial figures). All trajectories in this area turned slightly in this direction.
4. Measurement Results
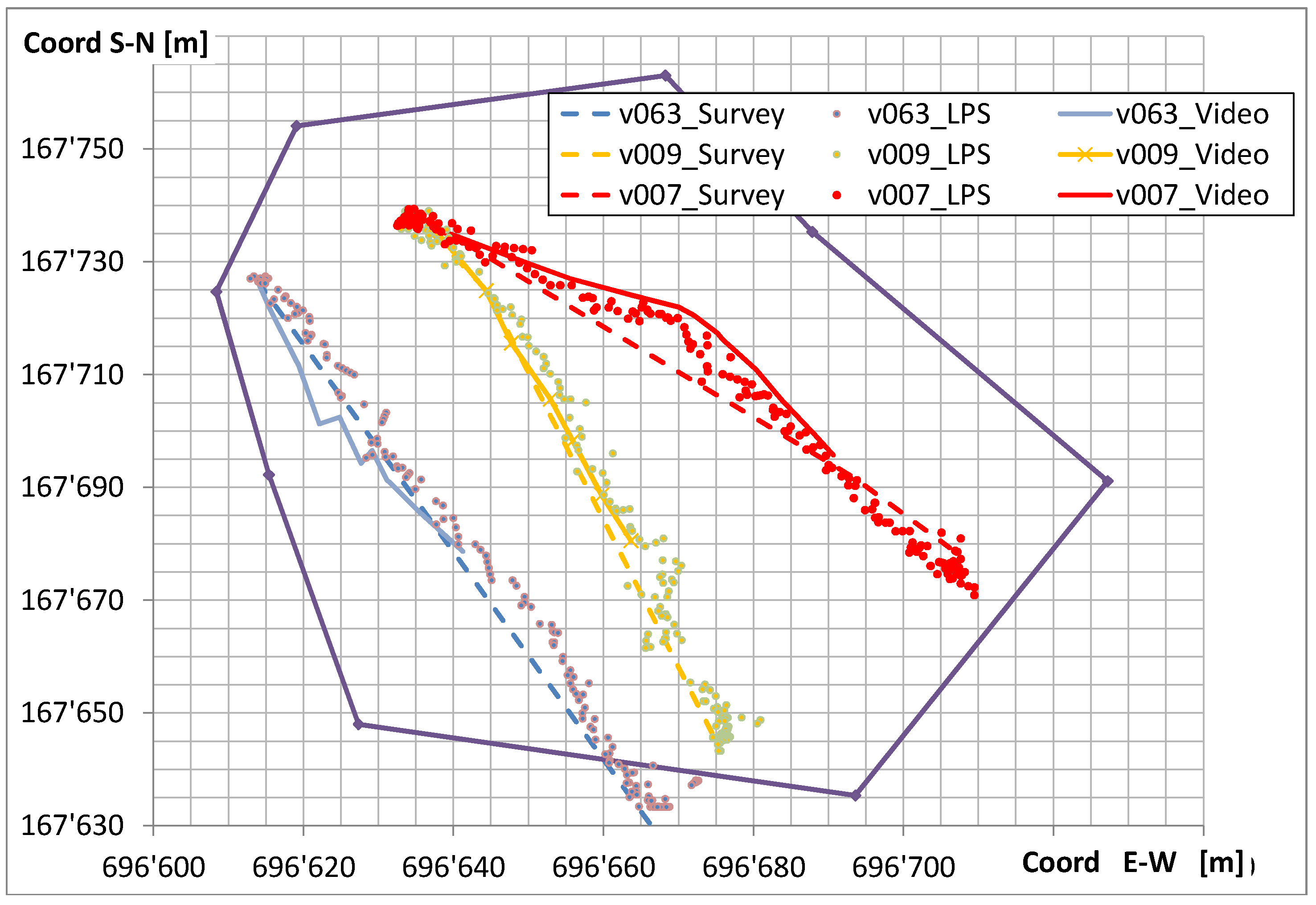
4.1. Surveying
4.2. Digital Elevation Model
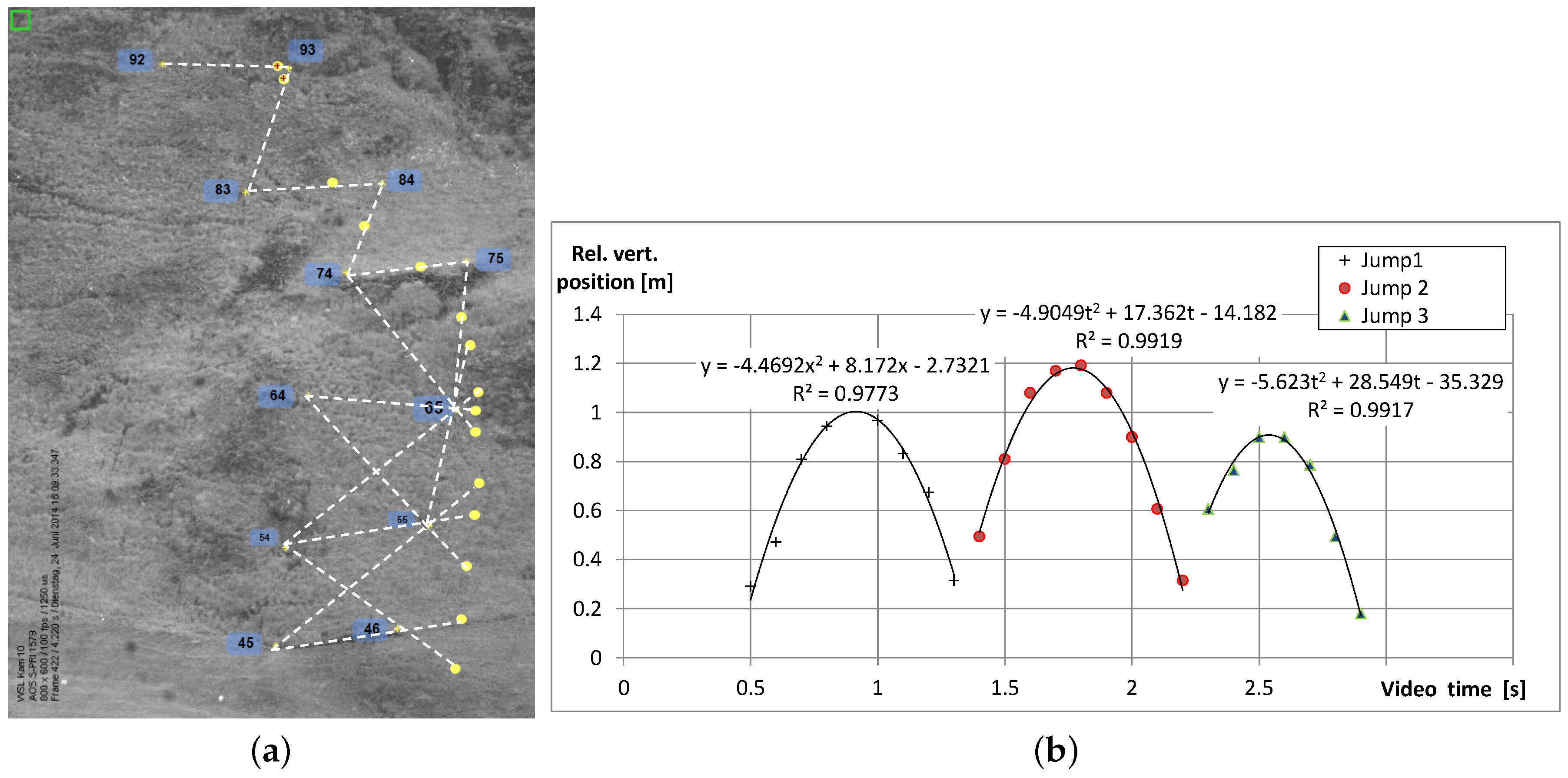
4.3. Video
4.3.1. Trajectory Analysis on the Slope
4.3.2. Trajectory Analysis in the Runout Zone
- During a jump phase of a block the number of images can be counted during which a block completes a full rotation.
- Video analysis allowed the determination of the vertical impact and lift-off velocity before and after an impact with the ground. Their sum divided by the contact time with the ground averages the accelerations acting to the block orthonormal to the ground.
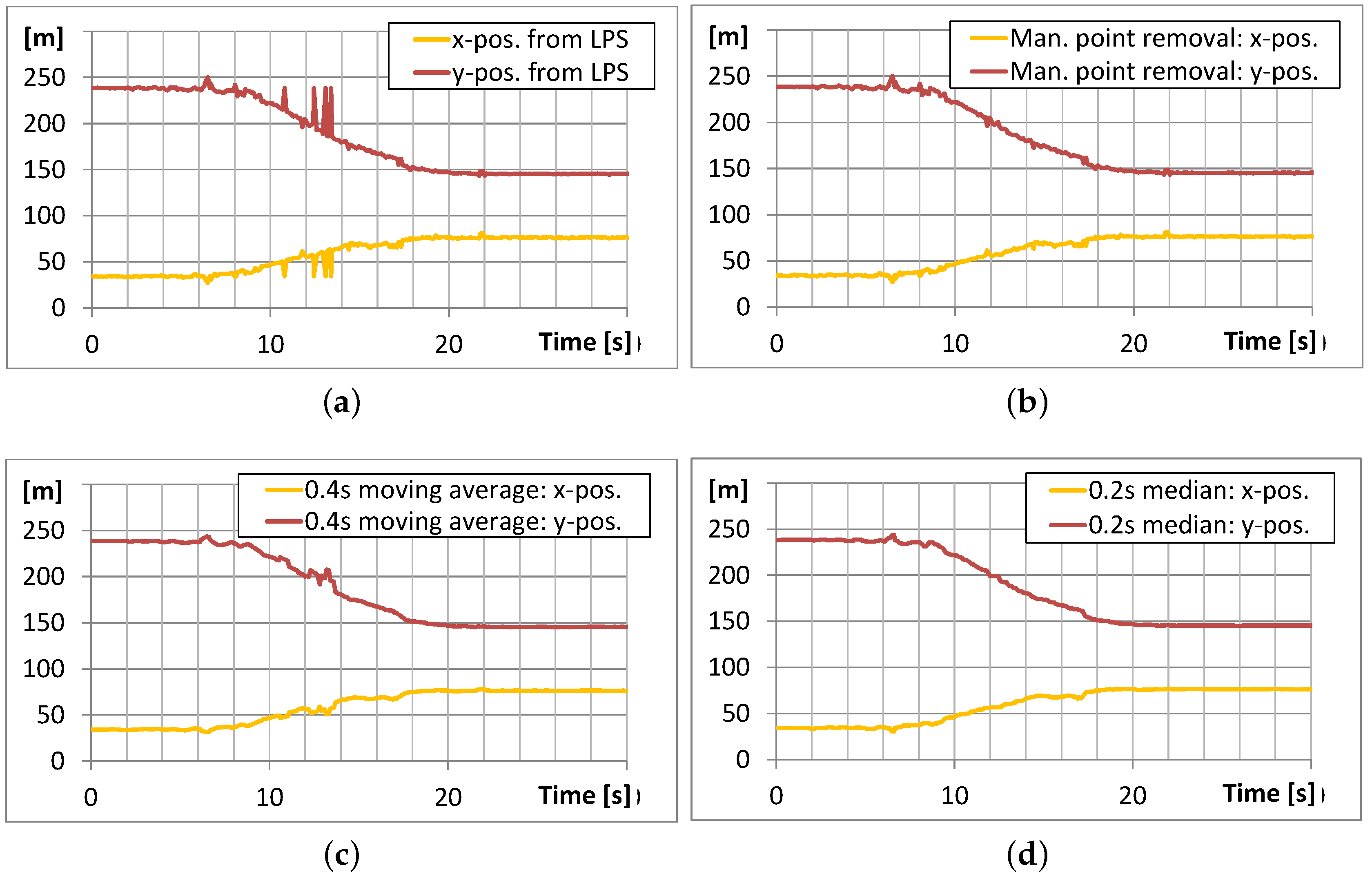
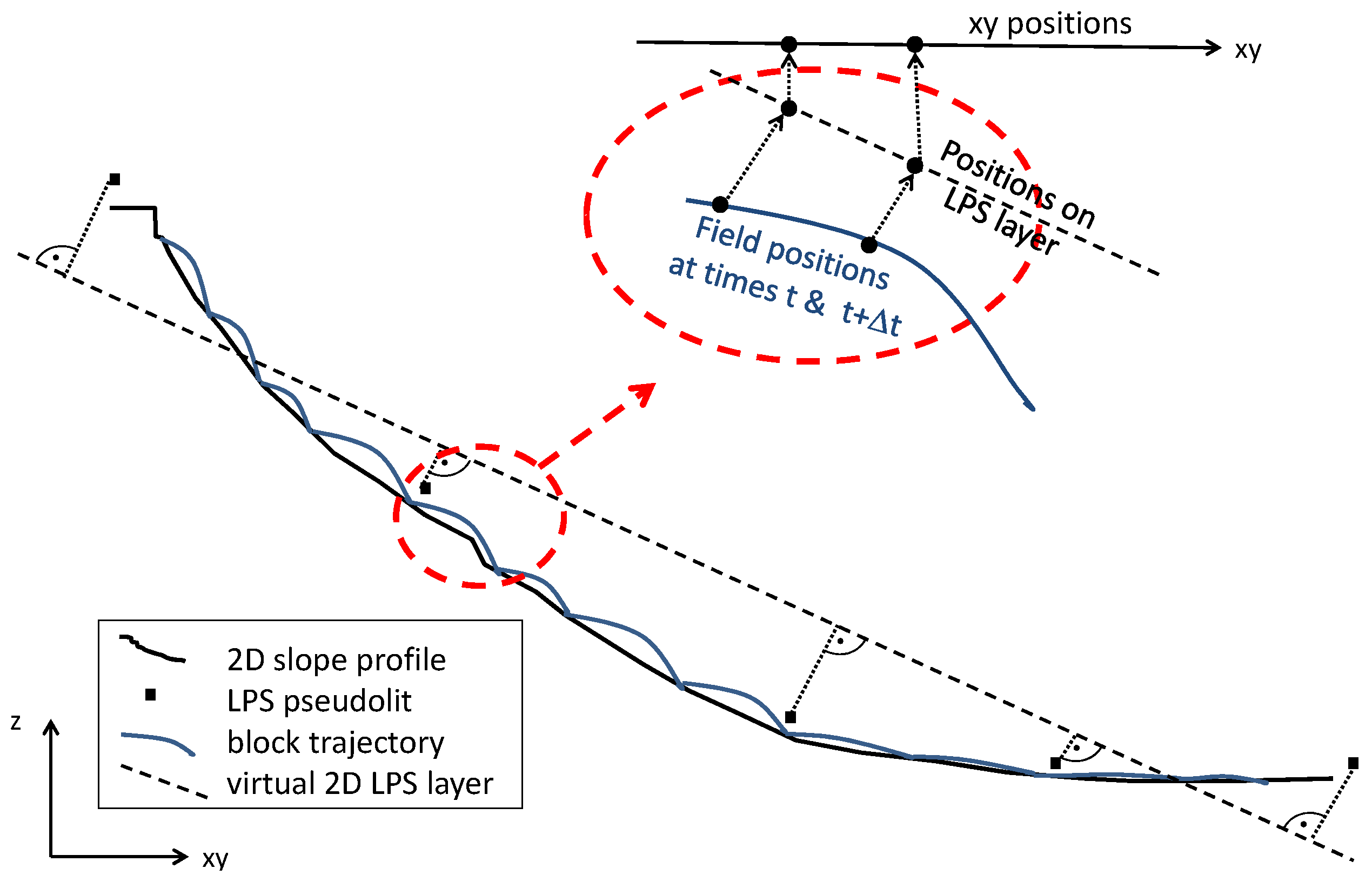
4.4. Local Positioning System
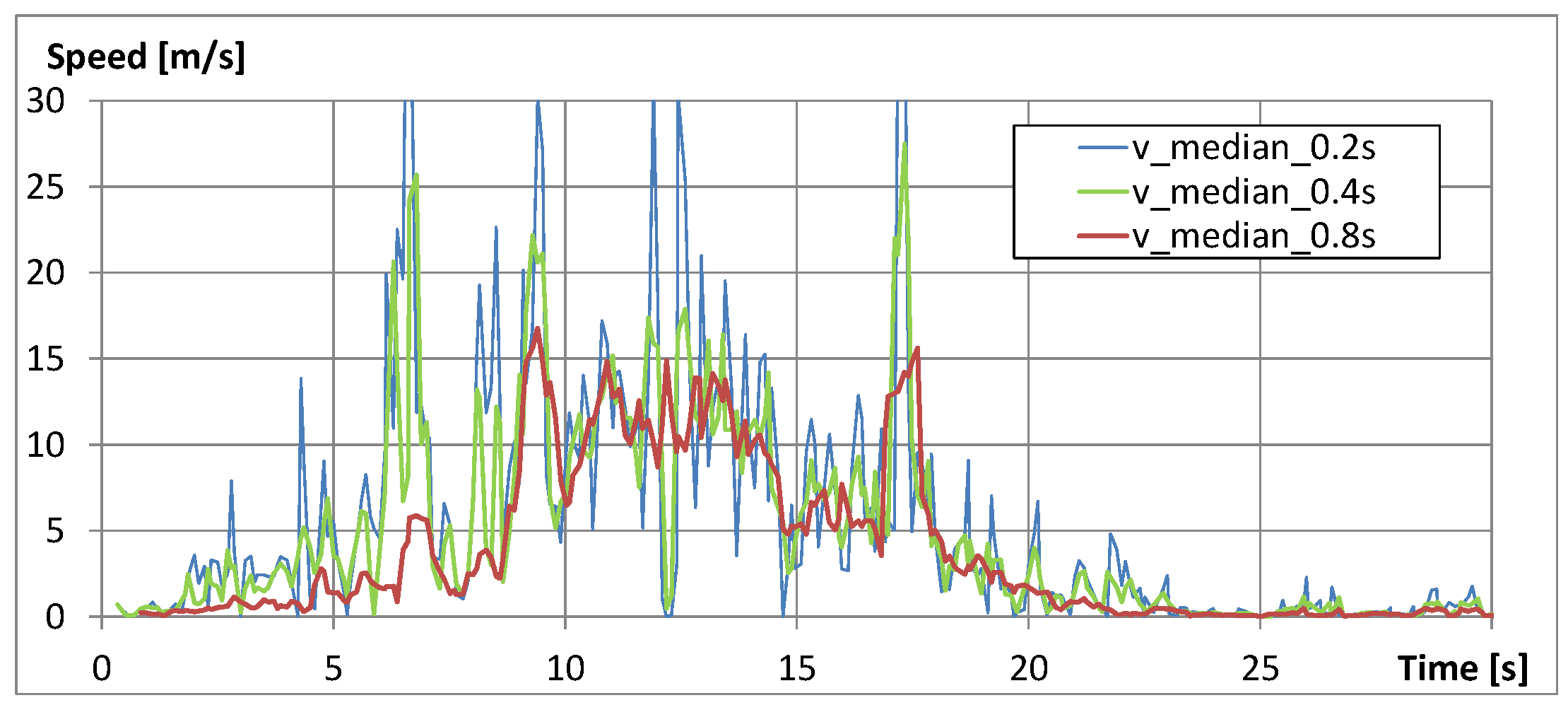
4.5. Rockfall Sensor
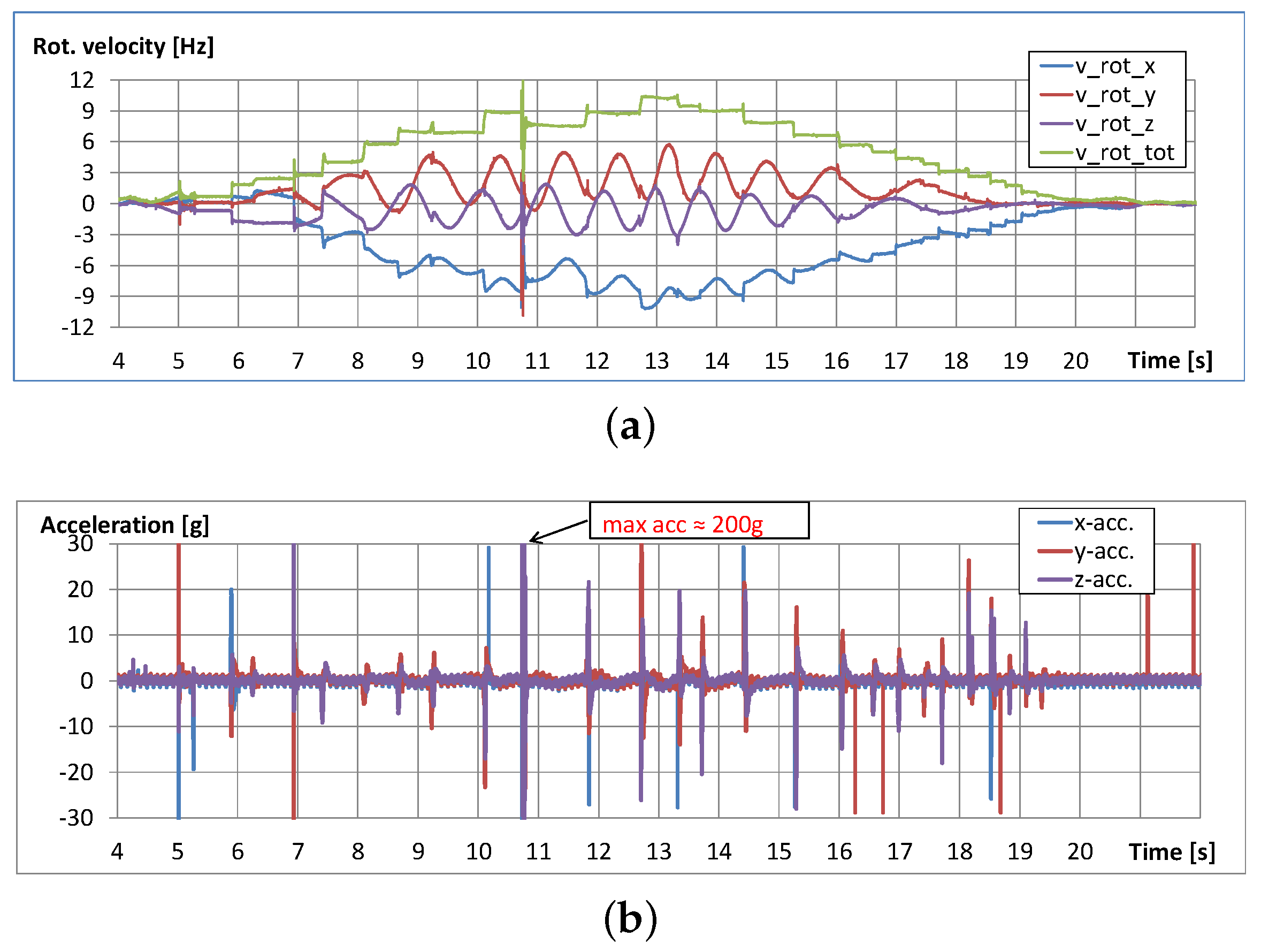
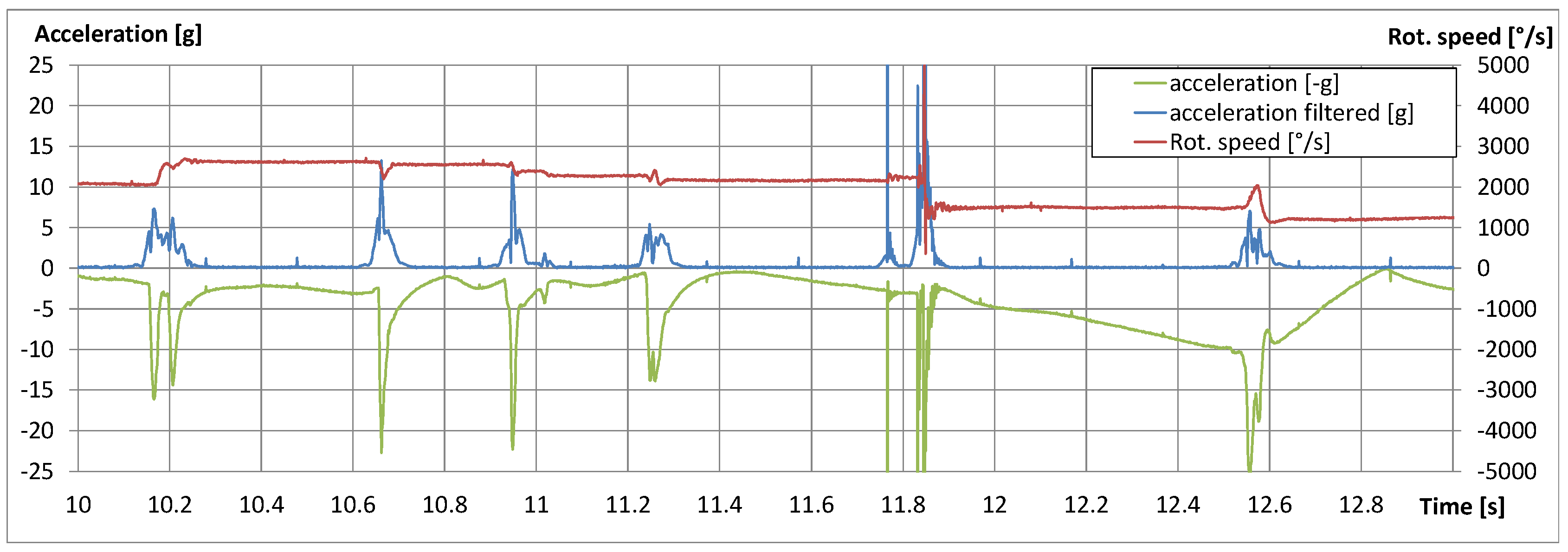
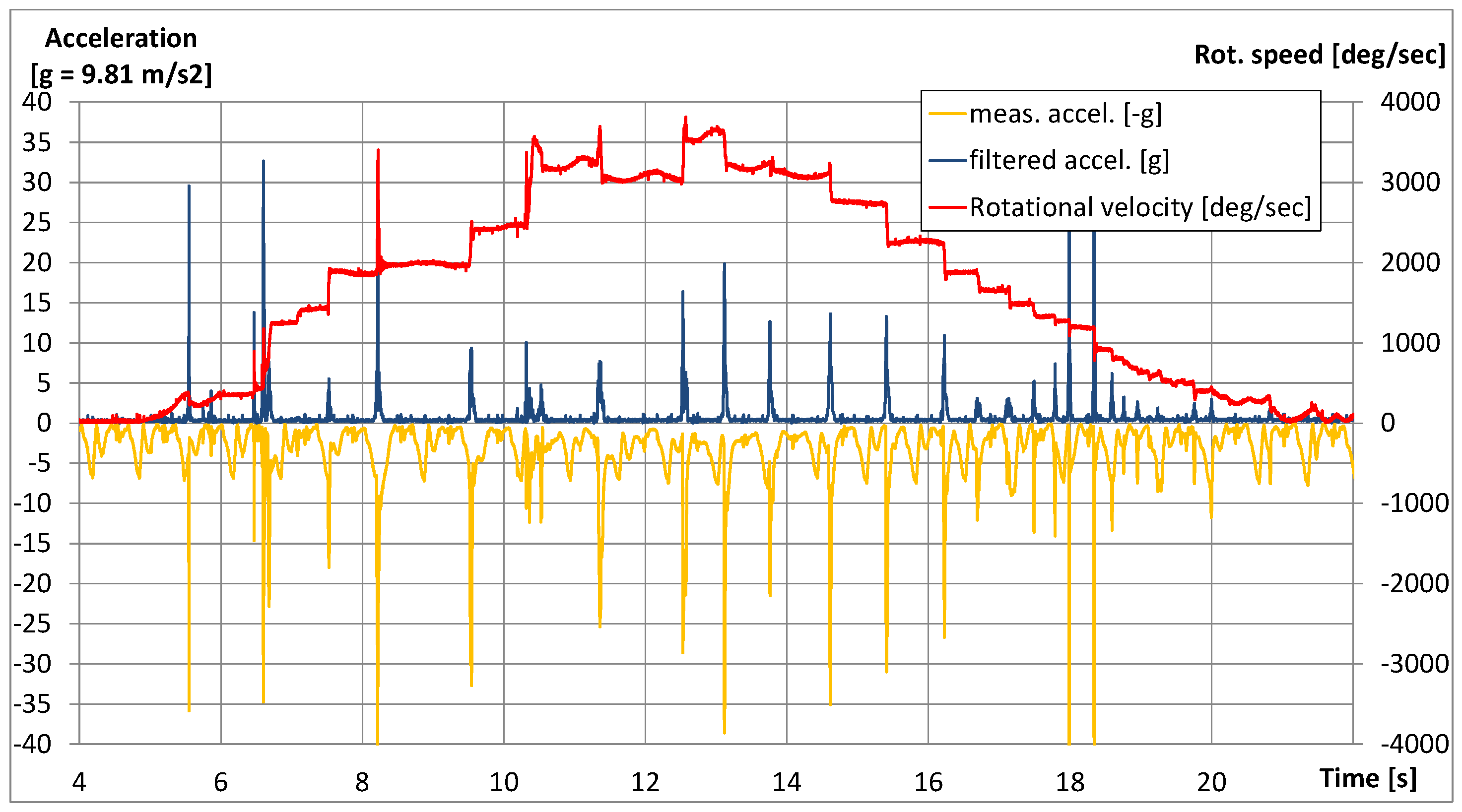
4.5.1. Rotational Speed
4.5.2. Acceleration
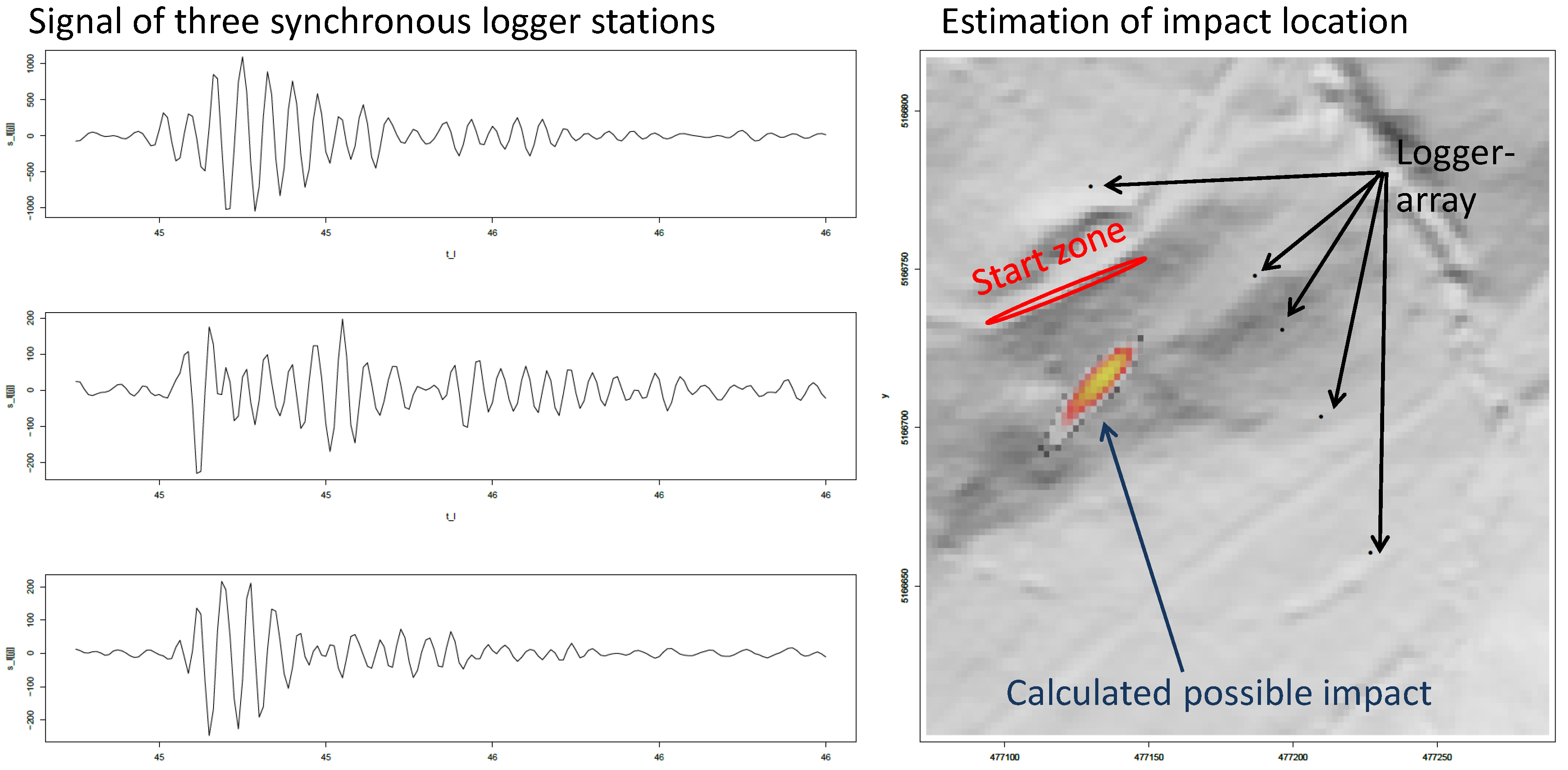
4.6. Seismic Analysis
4.7. Redundant Measurements
5. Test Evaluation
5.1. Measurement Systems
5.2. Test Setup
6. Conclusions
- having a more or less homogeneous slope from the release point to the point where rocks came to a halt;
- re-using the same blocks to obtain comparable and stochastically analysable results;
- testing different measurement systems for their suitability for future testing series.
- If the testing ground were to consist of soft soil and harder ground, impacts would have to be considered. Here the robustness of the test specimen should be evaluated for suitability for repeated usage. Ideally, its shape wouldn’t change too much as a consequence of expected flaking.
- If an LPS system were used, system settings should be adjusted to only collect raw data instead of field positions directly calculated from the system. This would facilitate consideration of the terrain’s unevenness. Further, if the expected average block speeds are known, the system’s internal speed predictor should be adjusted.
Supplementary Materials
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gerber, W. Geschwindigkeit und Energie aus der Analyse von Steinschlagspuren (velocity and kinetic energy from the analysis of rockfall trajectories). Österreichische Ing. Arch. 2015, 160, 1–12. [Google Scholar]
- Ferrari, F.; Thoeni, K.; Giacomini, A.; Lambert, C. A rapid approach to estimate the rockfall energies and distances at the base of rock cliffs. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2016. [Google Scholar] [CrossRef]
- Giani, G.P.; Giacomini, A.; Migliazza, M.; Segalini, A.; Tagliavini, S. Rock fall in situ observations, analysis and protection works. In Proceedings of the International Symposium on Landslide Risk Mitigation and Protection of Cultural and Natural Heritage, Kyoto, Japan, 15–19 January 2002; pp. 85–96. [Google Scholar]
- Giani, G.P.; Giacomini, A.; Migliazza, M.; Segalini, A. Experimental and theoretical studies to improve rock fall analysis and protection work design. Rock Mech. Rock Eng. 2004, 37, 369–389. [Google Scholar] [CrossRef]
- Dorren, L.K.A.; Berger, F.; Putters, U.S. Real-size experiments and 3-D simulation of rockfall on forested and nonforested slopes. Nat. Hazards Earth Syst. Sci. 2006, 6, 145–153. [Google Scholar] [CrossRef]
- Preh, A.; Mitchell, A.; Hungr, O.; Kolenprat, B. Stochastic analysis of rock fall dynamics on quarry slopes. Int. J. Rock Mech. Min. Sci. 2015, 80, 57–66. [Google Scholar] [CrossRef]
- Gerber, W. Auswirkungen des Felssturzes vom 11. January 2016 in Wolhusen. FAN Fachleute Naturgefahren Schweiz. FAN-Agenda 2016, 1, 13–16. [Google Scholar]
- Labiouse, V.; Descoeudres, F.; Montani, S. Experimental study of rock sheds impacted by rock blocks. Struct. Eng. Int. 1996, 6, 171–176. [Google Scholar] [CrossRef]
- Labiouse, V.; Heidenreich, B. Half-scale experimental study of rockfall impacts on sandy slopes. Nat. Hazards Earth Syst. Sci. 2009, 9, 1981–1993. [Google Scholar] [CrossRef]
- Glover, J.M.H. Rock-Shape and Its Role in Rockfall Dynamics. Ph.D. Thesis, Durham University, Durham, UK, 2015. [Google Scholar]
- Gerber, W.; Volkwein, A. Impact loads of falling rocks on granular material. In Proceedings of the 3rd Euromediterranean Symposium on Advances in Geomaterials and Structures, Djerba, Tunisia, 10–12 May 2010; Darve, F., Doghri, I., El Fatmi, R., Hassis, H., Zenzri, H., Eds.; 2010; pp. 337–342. [Google Scholar]
- Lambert, S.; Gotteland, P.; Nicot, F. Experimental study of the impact response of geocells as components of rockfall protection embankments. Nat. Hazards Earth Syst. Sci. 2009, 9, 459–467. [Google Scholar] [CrossRef]
- Volkwein, A.; Klette, J. Semi-Automatic Determination of Rockfall Trajectories. Sensors 2014, 14, 18187–18210. [Google Scholar] [CrossRef] [PubMed]
- Weber, T. Interaktion von Steinschlag mit dem Untergrund. Bachelor’s Thesis, Zurich University of Applied Sciences/ZHAW, Wadenswil, Switzerland, 2015. [Google Scholar]
- European Organization for Technical Approvals (EOTA). ETAG 027–Guideline for the European Technical Approval of Falling Rock Protection Kits; Technical Report; European Organization for Technical Approvals: Brussels, Belgium, 2012. [Google Scholar]
- Krumbein, W. Measurement and geological significance of shape and roundness of sedimentary particles. J. Sediment. Petrol. 1941, 11, 64–72. [Google Scholar] [CrossRef]
- Brügger, L. Erfassung und Auswertung von Steinschlagflugbahnen im Gelände. Bachelor’s Thesis, Zurich University of Applied Sciences/ZHAW, Wadenswil, Switzerland, 2014. [Google Scholar]
- Gerber, W.; Wartmann, C.; Glover, J. Measuring of rotation and acceleration during rockfall. In Proceedings of the Interpraevent, Lucerne, Switzerland, 30 May–2 June 2016. [Google Scholar]
- Dietze, M.; Turowski, J.M.; Cook, K.L.; Hovius, N. Spatiotemporal patterns and triggers of seismically detected Rockfalls. Earth Surf. Dynam. Discuss. 2017. [Google Scholar] [CrossRef]
- Bühler, Y.; Christen, M.; Glover, J.; Christen, M.; Bartelt, P. Significance of digital elevation model resolution for numerical rockfall simulations. In Proceedings of the 3rd International Symposium Rock Slope Stability C2ROP, Lyon, France, 15–17 November 2016; pp. 101–102. [Google Scholar]
- Bühler, Y.; Adams, M.S.; Bösch, R.; Stoffel, A. Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): Potential and limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef]
- Volkwein, A.; Glover, J.; Bourrier, F.; Gerber, W. A quality assessment of 3D video analysis for full scale rockfall experiments. In Proceedings of the EGU General Assembly 2012, Vienna, Austria, 22–27 April 2012; p. 12728. [Google Scholar]
- Gees, F. Erfassung und Auswertung von Steinschlagflugbahnen mittels Video. Bachelor’s Thesis, Zurich University of Applied Sciences/ZHAW, Wadenswil, Switzerland, 2014. [Google Scholar]
- Wikipedia, Butterworth Filter. Available online: https://en.wikipedia.org/wiki/Butterworth_filter (accessed on 27 October 2017).
- Giacomini, A.; Thoeni, K.; Lambert, C.; Booth, S.; Sloan, S.W. Experimental study on rockfall drapery systems for open pit highwalls. Int. J. Rock Mech. Min. Sci. 2012, 56, 171–181. [Google Scholar] [CrossRef]
- Christen, M. Steinschlagexperimente Am Flüelapass (GR). Available online: https://www.youtube.com/watch?v=0Zei_b7zynU (accessed on 7 November 2017).
- Mavrouli, O.C.; Abbruzzese, J.; Corominas, J.; Labiouse, V. Review and Advances in Methodologies for Rockfall Hazard and Risk Assessment. In Mountain Risks: From Prediction to Management and Governance; Advances in Natural and Technological Hazards Research; Van Asch, T., Corominas, J., Greiving, S., Malet, J.P., Sterlacchini, S., Eds.; Springer: Dordrecht, The Netherlands, 2014; Volume 34. [Google Scholar]
- De Biagi, V.; Napoli, M.L.; Barbero, M.; Peila, D. Estimation of the return period of rockfall blocks according to their size. Nat. Hazards Earth Syst. Sci. 2017, 17, 103–113. [Google Scholar] [CrossRef]
- UNI 11211–4:2012—Opere di Difesa Dalla Caduta Massi. Parte 4: Progetto Definitivo ed Esecutivo (In Italian). Available online: http://store.uni.com/catalogo/index.php/uni-11211-4-2012.html (accessed on 6 March 2017).
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection—A review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Fleris, M.; Preh, A.; Kolenprat, B. Study of rockfalls in a quarry environment: Physical and numerical experiments. In Proceedings of the 6th Interdisciplinary Workshop on Rockfall Protection (RocExs), Barcelona, Spain, 22–24 May 2017; Available online: http://congress.cimne.com/rocexs2017/frontal/Doc/Ebook.pdf (accessed on 7 November 2017).
- Niklaus, P.; Birchler, T.; Aebi, T.; Schaffner, M.; Cavigelli, L.; Caviezel, A.; Magno, M.; Benini, L. StoneNode: A low-power sensor device for induced rockfall experiments. In Proceedings of the 2017 IEEE Sensors Applications Symposium (SAS 2017), Glassboro, NJ, USA, 13–15 March 2017. [Google Scholar] [CrossRef]
- Lardon, J. Vergleich von Steinschlagsimulationen mit den entsprechenden Feldversuchen. Bachelor’s Thesis, Zurich University of Applied Sciences/ZHAW, Wadenswil, Switzerland, 2014. [Google Scholar]
- Sala, Z.; Hutchinson, D.J.; Ondercin, M. Game engine based rockfall modelling techniques applied to natural slopes. Canadian Geotechnics and Geoscience. In Proceedings of the GeoOttawa, Ottawa, ON, Canada, 1–4 October 2017. [Google Scholar]
- Sala, Z.; Hutchinson, D.J.; Ondercin, M. Application of the unity rockfall model to variable surface material conditions. Geophysical Research Abstracts. In Proceedings of the 19th EGU General Assembly, EGU2017, Vienna, Austria, 23–28 April 2017; Volume 19, p. 10745. [Google Scholar]



| Release Position | X | Y | Z |
|---|---|---|---|
| A | 2.70 | 89.84 | 80.50 |
| B | 5.85 | 91.64 | 80.19 |
| C | 10.18 | 94.21 | 80.03 |
| D | 13.17 | 95.93 | 79.81 |
| E | 16.56 | 98.01 | 79.53 |
| F | 21.82 | 101.27 | 79.09 |
| G | 26.33 | 104.04 | 78.65 |
| H | 43.28 | 114.34 | 77.16 |
| I | 51.87 | 120.82 | 76.34 |
| Offset | +696,608 | +167,635 | +1600 |
| (to be added to above coordinates) | |||
| Block Number | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Material | Gneis | Lime | Gneiss | Gneiss | Gneiss | Concrete | |
| Mass | kg | 68.7 | 78.7 | 43 | 40.3 | 19.3 | 45 |
| Dimensions | cm | 37 | 50 | 53 | 46 | 40 | 30 |
| cm | 37 | 39 | 29 | 30 | 25 | 30 | |
| cm | 32 | 30 | 20 | 20 | 18 | 30 | |
| Aspect ratio | 1.2 | 1.7 | 2.7 | 2.3 | 2.2 | 1.0 | |
| Total volume | liter | 25.9 | 30.5 | 16.2 | 14.2 | 8.3 | 19.0 |
| Length borehole | mm | 313 | 269 | 170 | 286 | 162 | 300 |
| Diameter borehole | mm | 69 | 69 | 69 | 69 | 69 | 70 |
| Volume borehole | liter | 0.70 | 0.60 | 0.38 | 0.64 | 0.36 | 0.69 |
| Netto volume | liter | 25.20 | 29.90 | 15.82 | 13.56 | 7.94 | 18.31 |
| Material density | kg/liter | 2.73 | 2.63 | 2.72 | 2.97 | 2.43 | 2.46 |
| Average density (with borehole) | kg/liter | 2.65 | 2.58 | 2.65 | 2.84 | 2.33 | 2.37 |
| Block Number | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Release position | ||||||
| A | ||||||
| B | ++++ | ++++ | oo | o+++ | ||
| +-+- | ++++ | +o-++ | ||||
| C | ++o- | +++ | + | +++ | ||
| D | o | - | o | |||
| E | + | |||||
| F | o-o | +++ | o | ooo | oo | |
| o++ | ++ | o+ | ||||
| G | o++o | +++ | oo | o++ | -o+ | |
| -++ | +++ | ++- | ++ | |||
| I | +++ | +++ | o+++ | ++++ | - - - | |
| ++ | ++ | o+- | ||||
| Comment | no live position | no live position | no live position | |||
| no rock sensor | no rock sensor |
| Horizontal Distance [m] | Vertical Distance [m] | Shadow Angle | Travel Time [sec] | Average Speed | |||
|---|---|---|---|---|---|---|---|
| [–] | [deg] | hor. [m/s] | skew [m/s] | ||||
| Minimum | 22.4 | 51.4 | 38% | 21.0 | 11.5 | 2.1 | 2.4 |
| Maximum | 128.1 | 22.0 | 98% | 44.5 | 43.2 | 5.5 | 6.1 |
| Mean | 92.8 | 48.2 | 54% | 28.3 | 23.4 | 4.2 | 4.7 |
| Median | 95.6 | 49.2 | 52% | 27.4 | 23.5 | 4.2 | 4.7 |
| Std. dev. | 20.1 | 4.7 | 11% | 4.5 | 3.3 | 0.6 | 0.6 |
| Jump | Rockfall Sensor | Video Analysis | LPS | max. Diff. | |||
|---|---|---|---|---|---|---|---|
| 1 | Rotational speed [/s] | 2758 | 2571 | 187 | = | 7% | |
| 2 | 2192 | 2250 | 58 | = | 3% | ||
| 3 | 2031 | 2000 | 31 | = | 2% | ||
| 1 | Jump duration [s] | 0.49 | 0.5 | 0.01 | = | 2% | |
| 2 | 0.7 | 0.7 | 0.0 | = | 0% | ||
| 3 | 0.72 | 0.7 | 0.02 | = | 2% | ||
| 1 | Velocity [m/s] | 10.7 | 9.6–10.4 | 1.1 | = | 10% | |
| 2 | 8.4 | 5.6–10.4 | 2.8 | = | 33% | ||
| 3 | 7.4 | 5.6–7.9 | 1.8 | = | 24% | ||
| 1–2 | Impact acceleration [m/s] | 76 | 60 | 16 | = | 21% | |
| 2–3 | 46 | 36 | 10 | = | 22% | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volkwein, A.; Brügger, L.; Gees, F.; Gerber, W.; Krummenacher, B.; Kummer, P.; Lardon, J.; Sutter, T. Repetitive Rockfall Trajectory Testing. Geosciences 2018, 8, 88. https://doi.org/10.3390/geosciences8030088
Volkwein A, Brügger L, Gees F, Gerber W, Krummenacher B, Kummer P, Lardon J, Sutter T. Repetitive Rockfall Trajectory Testing. Geosciences. 2018; 8(3):88. https://doi.org/10.3390/geosciences8030088
Chicago/Turabian StyleVolkwein, Axel, Lucas Brügger, Fabio Gees, Werner Gerber, Barbara Krummenacher, Peter Kummer, Jessica Lardon, and Tobias Sutter. 2018. "Repetitive Rockfall Trajectory Testing" Geosciences 8, no. 3: 88. https://doi.org/10.3390/geosciences8030088
APA StyleVolkwein, A., Brügger, L., Gees, F., Gerber, W., Krummenacher, B., Kummer, P., Lardon, J., & Sutter, T. (2018). Repetitive Rockfall Trajectory Testing. Geosciences, 8(3), 88. https://doi.org/10.3390/geosciences8030088




