Comparison of Geometric and Volumetric Methods to a 3D Solid Model for Measurement of Gully Erosion and Sediment Yield
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Field Setup
2.2. Erosion Estimation Methods
2.2.1. Bucket Method
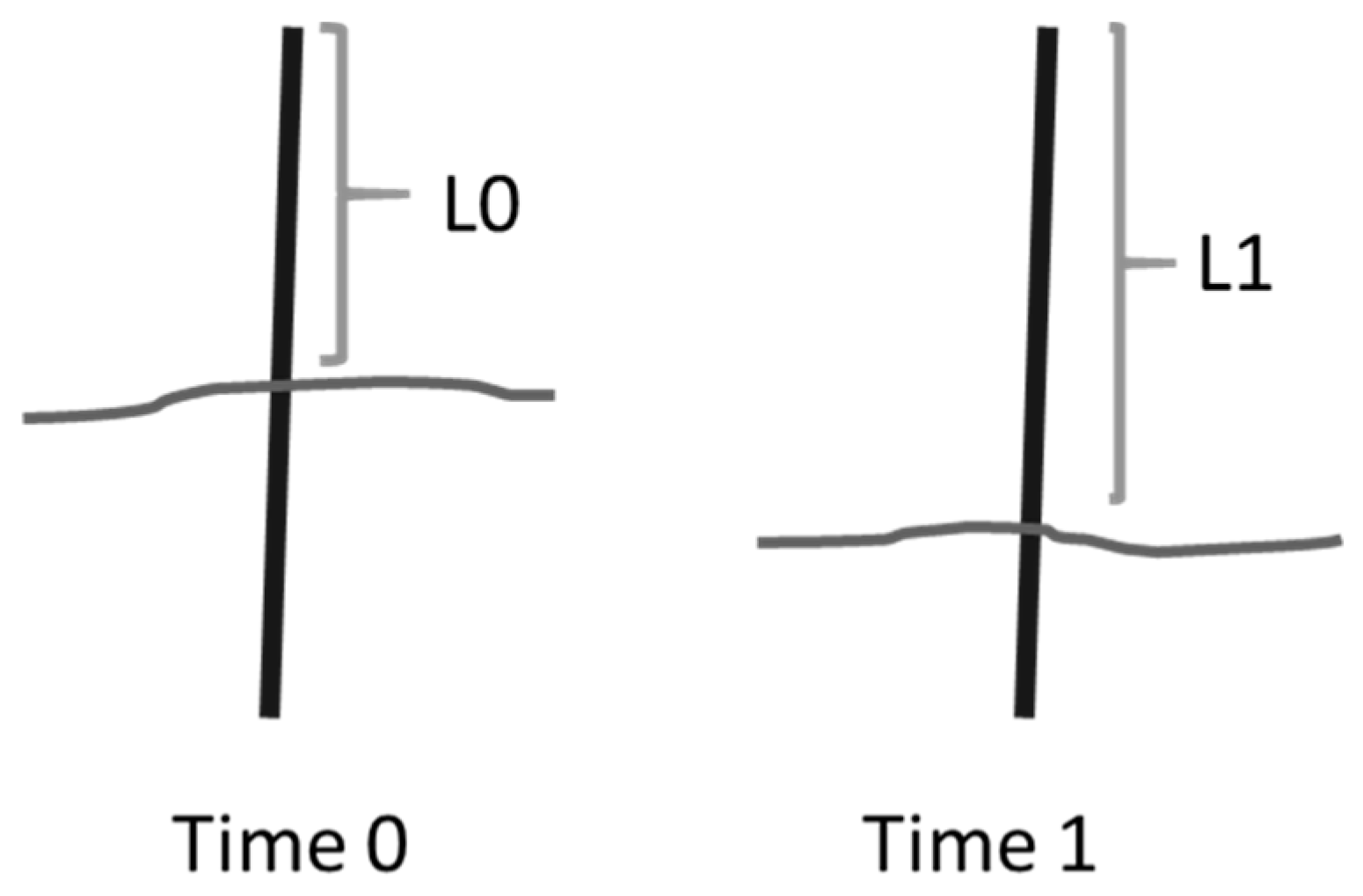
2.2.2. Erosion Pins
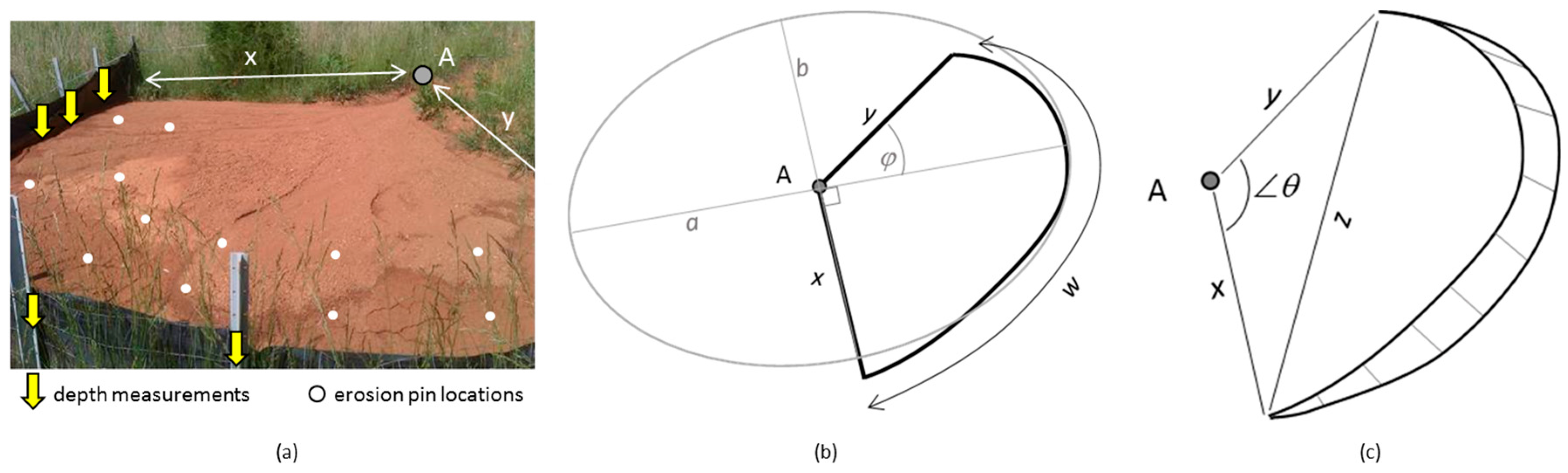
2.2.3. Geometric Methods
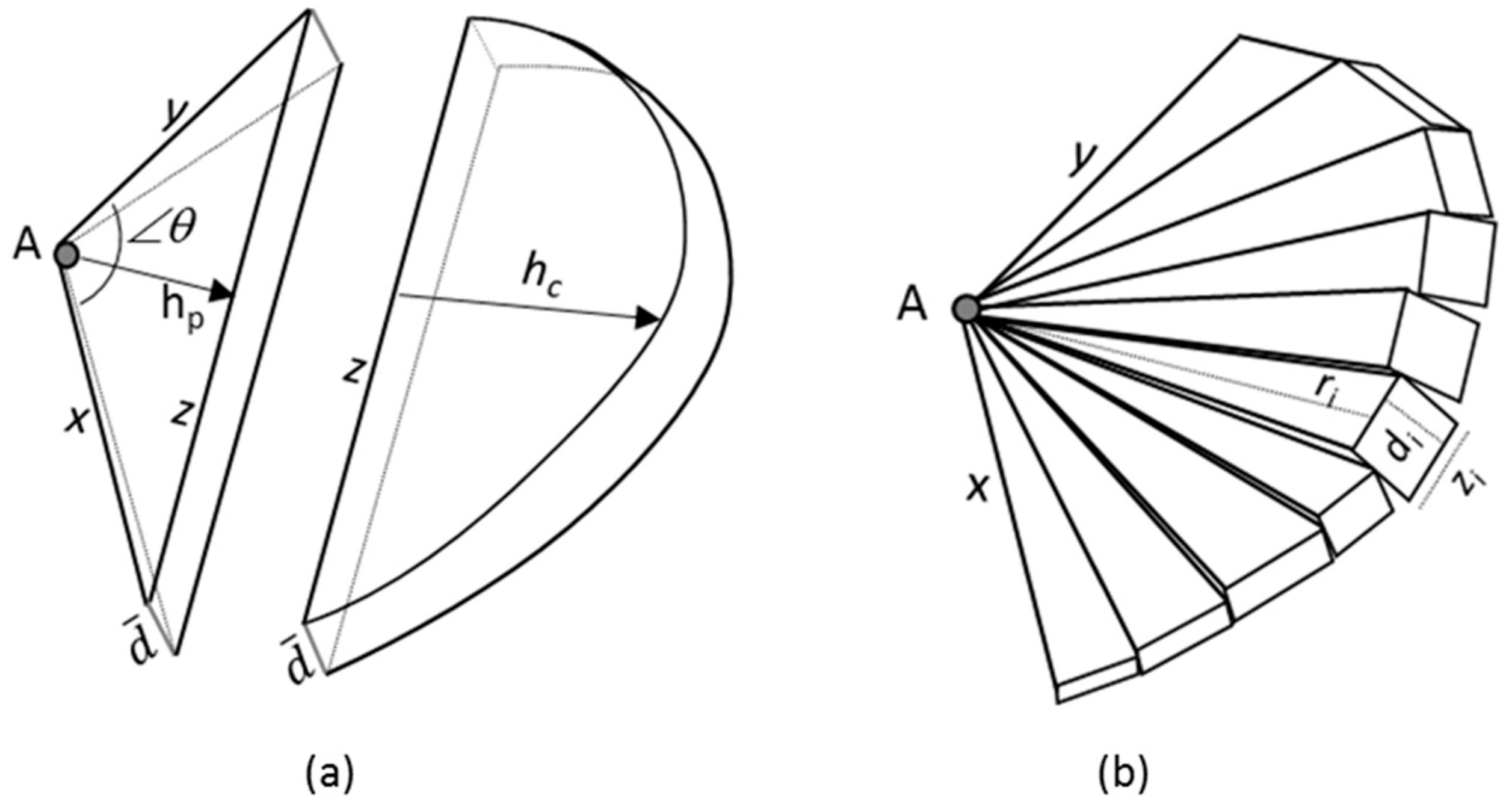
2.2.4. The 3D Solid Model
3. Results
3.1. Bucket Method
3.2. Erosion Pins
3.3. Geometric Methods
3.4. 3D Computer Model
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully erosion and environmental change: Importance and research needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Valentin, C.; Poesen, J.; Yong, L. Gully erosion: Impacts, factors and control. Catena 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Ramos-Diez, I.; Navarro-Hevia, J.; San Martin Fernandez, R.; Diaz-Gutierrez, V.; Mongil-Manso, J. Evaluating methods to quantify sediment volumes trapped behind check dams, Saldana badlands (Spain). Int. J. Sediment Res. 2017, 32, 1–11. [Google Scholar] [CrossRef]
- Castillo, C.; Gómez, J.A. A century of gully erosion research: Urgency, complexity and study approaches. Earth Sci. Rev. 2016, 160, 300–319. [Google Scholar] [CrossRef]
- Nearing, M.A.; Jetten, V.; Baffaut, C.; Cerdan, O.; Couturier, A.; Hernandez, M.; Le Bissonnais, Y.; Nichols, M.H.; Nunes, J.P.; Renschler, C.S. Modeling response of soil erosion and runoff to changes in precipitation and cover. Catena 2005, 61, 131–154. [Google Scholar] [CrossRef]
- Luffman, I.E.; Nandi, A.; Spiegel, T. Gully morphology, hillslope erosion, and precipitation characteristics in the Appalachian Valley and Ridge province, southeastern USA. Catena 2015, 133, 221–232. [Google Scholar] [CrossRef]
- Gatto, L.W.; Ferrick, M.G. Overland Erosion due to Freeze—Thaw Cycling Cold Regions Research Overland Erosion Due To Freeze—Thaw Cycling; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 2003. [Google Scholar]
- Ferrick, M.G.; Gatto, L.W. Quantifying the effect of a freeze-thaw cycle on soil erosion: Laboratory experiments. Earth Surf. Process. Landf. 2005, 30, 1305–1326. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Yang, S. The classification and assessment of freeze-thaw erosion in Tibet. J. Geogr. Sci. 2007, 17, 165–174. [Google Scholar] [CrossRef]
- Kong, B.; Yu, H. Estimation model of soil freeze-thaw erosion in Silingco watershed wetland of northern Tibet. Sci. World J. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Barnes, N.; Luffman, I.; Nandi, A. Gully erosion and freeze-thaw processes in clay-rich soils, northeast Tennessee, USA. GeoResJ 2016, 9, 67–76. [Google Scholar] [CrossRef]
- Yan, F.L.; Shi, Z.H.; Li, Z.X.; Cai, C.F. Estimating interrill soil erosion from aggregate stability of Ultisols in subtropical China. Soil Tillage Res. 2008, 100, 34–41. [Google Scholar] [CrossRef]
- Marzen, M.; Iserloh, T.; de Lima, J.L.M.P.; Ries, J.B. The effect of rain, wind-driven rain and wind on particle transport under controlled laboratory conditions. Catena 2016, 145, 47–55. [Google Scholar] [CrossRef]
- Guerra, A.J.T.; Fullen, M.A.; Jorge, M.D.C.O.; Bezerra, J.F.R.; Shokr, M.S. Slope processes, mass movement and soil erosion: A review. Pedosphere 2017, 27, 27–41. [Google Scholar] [CrossRef]
- Reusser, L.; Bierman, P.; Rood, D. Quantifying human impacts on rates of erosion and sediment transport at a landscape scale. Geology 2015, 43, 171–174. [Google Scholar] [CrossRef]
- Cain, S.A. Pollen Analysis of Some Buried Soils, Spartanburg County, South Carolina. Bull. Torrey Bot. Club 1944, 71, 11–22. [Google Scholar] [CrossRef]
- Hack, J.T. Rock Control and Tectonism—Their Importance in Shaping the Appalachian Highlands; U.S. Geological Survey: Reston, VA, USA, 1978.
- Staheli, A.C.; Ogren, D.E.; Whorton, C.H. Age of swamps in the Alcovy River drainage basin. Southeast. Geol. 1974, 16, 102–106. [Google Scholar]
- Matthews, W.H. Cenozoic erosion and erosion surfaces of eastern North America. Am. J. Sci. 1975, 275, 818–824. [Google Scholar] [CrossRef]
- Hancock, G.R.; Evans, K.G. Gully, channel and hillslope erosion—An assessment for a traditionally managed catchment. Earth Surf. Process. Landf. 2010, 35, 1468–1479. [Google Scholar] [CrossRef]
- Hudson, N. Field Measurement of Soil Erosion and Runoff; Food & Agriculture Organization: Rome, Italy, 1993; Volume 68, ISBN 9251034060. [Google Scholar]
- Keay-Bright, J.; Boardman, J. Evidence from field-based studies of rates of soil erosion on degraded land in the central Karoo, South Africa. Geomorphology 2009, 103, 455–465. [Google Scholar] [CrossRef]
- Smith, H.G.; Dragovich, D. Sediment budget analysis of slope–channel coupling and in-channel sediment storage in an upland catchment, southeastern Australia. Geomorphology 2008, 101, 643–654. [Google Scholar] [CrossRef]
- Castillo, V.M.; Mosch, W.M.; García, C.C.; Barberá, G.G.; Cano, J.A.N.; López-Bermúdez, F. Effectiveness and geomorphological impacts of check dams for soil erosion control in a semiarid Mediterranean catchment: El Carcavo (Murcia, Spain). Catena 2007, 70, 416–427. [Google Scholar] [CrossRef]
- Romero-Díaz, A.; Alonso-Sarriá, F.; Martínez-Lloris, M. Erosion rates obtained from check-dam sedimentation (SE Spain). A multi-method comparison. Catena 2007, 71, 172–178. [Google Scholar] [CrossRef]
- Díaz, V.; Mongil, J.; Navarro, J. Topographical surveying for improved assessment of sediment retention in check dams applied to a Mediterranean badlands restoration site (Central Spain). J. Soils Sediments 2014, 14, 2045–2056. [Google Scholar] [CrossRef]
- Ashida, K.; Takahashi, T.; Sawada, T. Sediment Yield and Transport on a Mountainous Small Watershed. Bull. Disaster. Prev. Res. Inst. 1976, 26, 119–144. [Google Scholar]
- Namikas, S.L. Field Evaluation of Two Traps for High-Resolution Aeolian Transport Measurements. J. Coast. Res. 2002, 18, 136–148. [Google Scholar] [CrossRef]
- Sougnez, N.; van Wesemael, B.; Vanacker, V. Low erosion rates measured for steep, sparsely vegetated catchments in southeast Spain. Catena 2011, 84, 1–11. [Google Scholar] [CrossRef]
- Ramos-Diez, I.; Navarro-Hevia, J.; Fernández, R.S.M.; Díaz-Gutiérrez, V.; Mongil-Manso, J. Geometric models for measuring sediment wedge volume in retention check dams. Water Environ. J. 2016, 30, 119–127. [Google Scholar] [CrossRef]
- Bellin, N.; Vanacker, V.; van Wesemael, B.; Solé-Benet, A.; Bakker, M.M. Natural and anthropogenic controls on soil erosion in the internal betic Cordillera (Southeast Spain). Catena 2011, 87, 190–200. [Google Scholar] [CrossRef][Green Version]
- Castillo, C.; Taguas, E.V.; Zarco-Tejada, P.; James, M.R.; Gómez, J.A. The normalized topographic method: An automated procedure for gully mapping using GIS. Earth Surf. Process. Landf. 2014, 39, 2002–2015. [Google Scholar]
- Kaiser, A.; Neugirg, F.; Rock, G.; Müller, C.; Haas, F.; Ries, J.; Schmidt, J. Small-Scale Surface Reconstruction and Volume Calculation of Soil Erosion in Complex Moroccan Gully Morphology Using Structure from Motion. Remote Sens. 2014, 6, 7050–7080. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Abellan, A.; Schindewolf, M. Time lapse structure-from-motion photogrammetry for continuous geomorphic monitoring. Earth Surf. Process. Landf. 2017, 42, 2240–2253. [Google Scholar] [CrossRef]
- Castillo, C.; Marín-Moreno, V.J.; Pérez, R.; Muñoz-Salinas, R.; Taguas, E.V. Accurate automated assessment of gully cross-section geometry using the photogrammetric interface FreeXSapp. Earth Surf. Process. Landf. 2018. [Google Scholar] [CrossRef]
- Didoné, E.J.; Minella, J.P.G.; Merten, G.H. Quantifying soil erosion and sediment yield in a catchment in southern Brazil and implications for land conservation. J. Soils Sediments 2015, 15, 2334–2346. [Google Scholar] [CrossRef]
- De Paor, D.G. Virtual Rocks. GSA Today 2016, 26, 4–22. [Google Scholar] [CrossRef]
- Bristowe, A.; Parrott, A.; Hack, J.; Pencharz, M.; Raath, M. A non-destructive investigation of the skull of the small theropod dinosaur, Ceolophysis rhodesiensis, using CT scans and rapid prototyping. Palaeontol. Afr. 2004, 40, 31–36. [Google Scholar]
- Hasiotis, S.T.; Hirmas, D.R.; Platt, B.F.; Raynolds, J. New frontiers in ichnology using MLT (Multistripe Laser Triangulation) and rapid prototyping technology for three-dimensional analysis, printing, and sharing of modern and ancient traces with other ichnophiles. In Northeastern (46th Annual) and North-Central (45th Annual) Joint Meeting of the Geological Society of America Abstracts with Programs; Geological Society of America: Pittsburgh, PA, USA, 2011; p. 81. [Google Scholar]
- Hyatt, J.A.; Rosiene, J. Preparing image maps, physical models, and analyzing topographic form using terrestrial laser scanning data collected at Dinosaur State Park, Rocky Hill, CT. In Proceedings of the Northeastern Section Geological Society of America 48th Annual Meeting; Geological Society of America: Bretton Woods, NH, USA, 2013; pp. 53–56. [Google Scholar]
- Horowitz, S.S.; Schultz, P.H. Printing space: Using 3D printing of digital terrain models in geosciences education and research. J. Geosci. Educ. 2014, 62, 138–145. [Google Scholar] [CrossRef]
- Hasiuk, F.J.; Harding, C. Touchable topography: 3D printing elevation data and structural models to overcome the issue of scale. Geol. Today 2016, 32, 16–20. [Google Scholar] [CrossRef]
- Hasiuk, F.J.; Harding, C.; Renner, A.R.; Winer, E. TouchTerrain: A simple web-tool for creating 3D-printable topographic models. Comput. Geosci. 2017, 109, 25–31. [Google Scholar] [CrossRef]
- Hasiuk, F. Making things geological: 3-D printing in the geosciences. GSA Today 2014, 24, 28–29. [Google Scholar] [CrossRef]
- Bourke, M.; Viles, H.; Nicoli, J.; Lyew-Ayee, P.; Ghent, R.; Holmund, J. Innovative applications of laser scanning and rapid prototype printing to rock breakdown experiments. Earth Surf. Process. Landf. 2008, 33, 1614–1621. [Google Scholar] [CrossRef]
- Robichaud, P.R.; Brown, R.E. Silt Fences: An Economical Technique for Measuring Hillslope Soil Erosion; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Washington, DC, USA, 2002.
- Martín-Rosales, W.; Pulido-Bosch, A.; Gisbert, J.; Vallejos, A. Sediment yield estimation and check dams in a semiarid area (Sierra de Gádor, southern Spain). IAHS-AISH Publ. 2003, 51–58. [Google Scholar]
- Robichaud, P.R.; McCool, D.K.; Pannkuk, C.D.; Brown, R.E.; Mutch, P.W. Trap Efficiency of Silt Fences Used in Hillslope Erosion Studies. In Proceedings of the International Symposium on Soil Erosion for the 21st Century, Honolulu, HI, USA, 3–5 January 2001; pp. 541–543. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Washington County Soil Survey Report; United States Department of Agriculture: Washington, DC, USA, 2011.
- Nandi, A.; Luffman, I. Erosion related changes to physicochemical properties of Ultisols distributed on calcareous sedimentary rocks. J. Sustain. Dev. 2012, 5, 52–68. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Zeitschrift 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Khan, M.F. Arc length of an elliptical curve. Int. J. Sci. Res. Publ. 2013, 3, 1–5. [Google Scholar]
- Eberly, D. The Area of Intersecting Ellipses. Available online: https://www.geometrictools.com/Documentation/AreaIntersectingEllipses.pdf (accessed on 10 January 2018).
- Weisstein, E.W. Heron’s Formula. Available online: http://mathworld.wolfram.com/HeronsFormula.html (accessed on 20 January 2018).
- Weisstein, E.W. Horizontal Cylindrical Segment. Available online: http://mathworld.wolfram.com/HorizontalCylindricalSegment.html (accessed on 10 January 2018).
- Dassault Systemes SA SolidWorks 2016. Available online: https://www.3ds.com/products-services/solidworks/ (accessed on 10 January 2018).
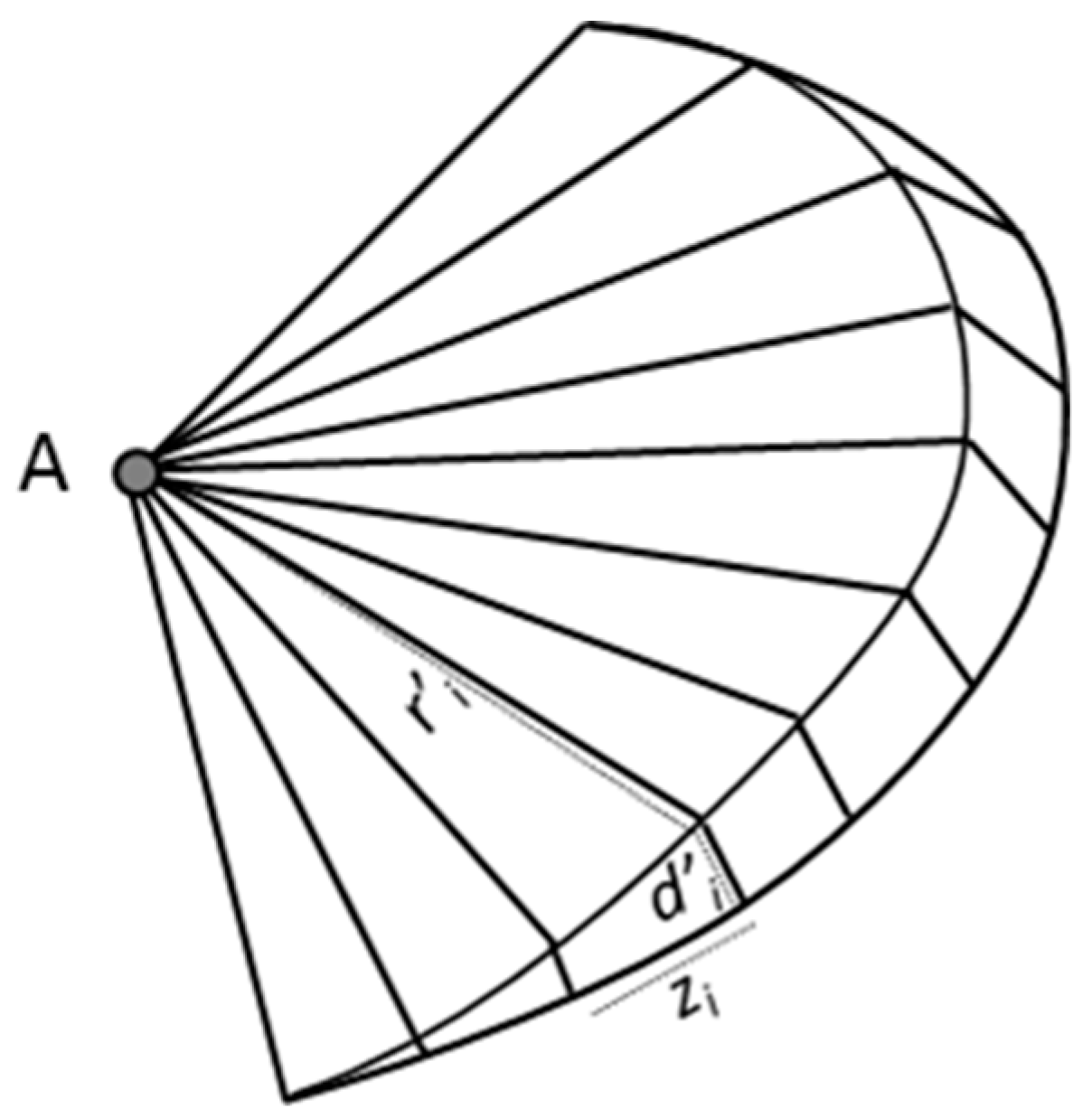
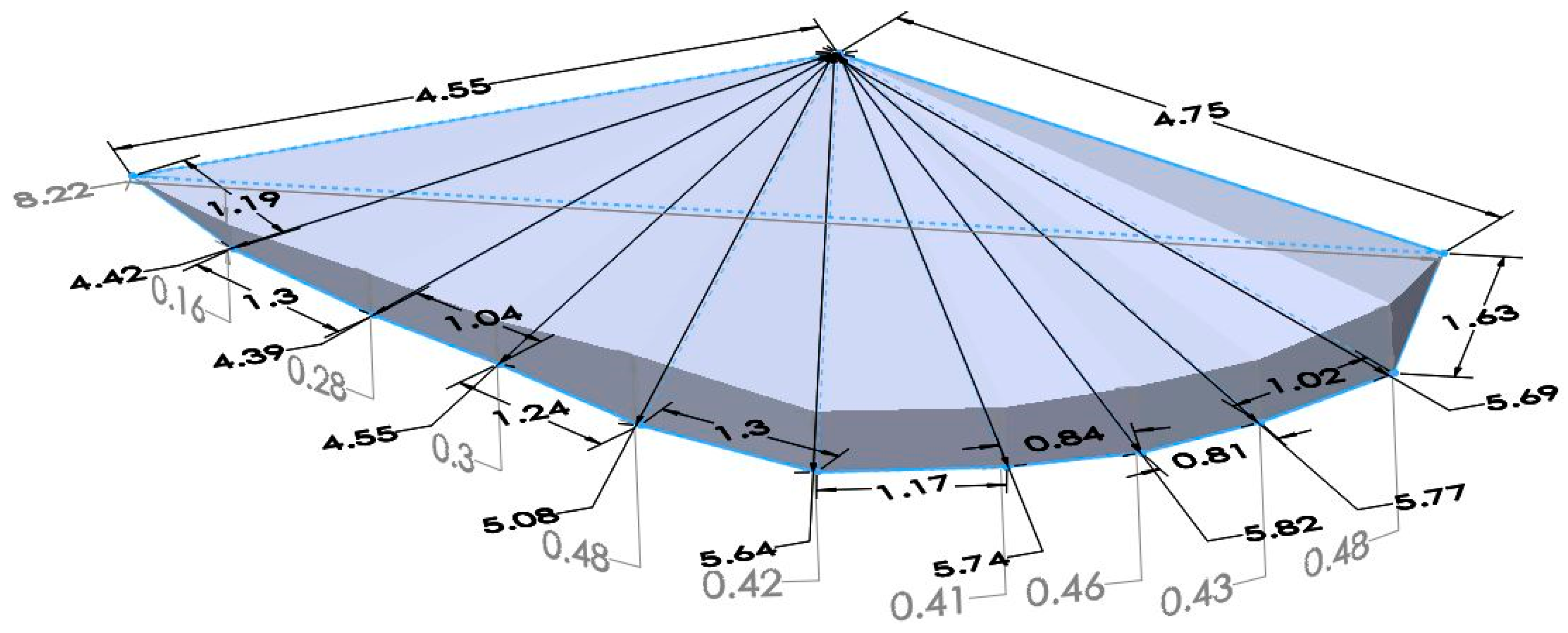
| Date | Days | Buckets (10 L) | Volume (m3) | Deposition Rate (m3/y) | Scaled for 93% Trap Efficiency (m3/y) |
|---|---|---|---|---|---|
| 16 February 2011 to 11 May 2012 | 456 | 1036 | 10.36 | 8.29 | 8.92 |
| 18 May 2012 to 17 August 2012 | 94 | 801 | 8.01 | 31.10 | 33.44 |
| 21 August 2012 to 27 February 2013 | 192 | 891 | 8.91 | 16.94 | 18.21 |
| Totals or averages | 742 | 2728 | 27.28 | 13.42 | 14.43 |
| Dates | Days | Gully | Delta | |||||
|---|---|---|---|---|---|---|---|---|
| Average Pin Change (mm) | Erosion (−) Rate (mm/y) | Sediment Yield (m3/y) | Average Pin Change (mm) | Deposition (+) Rate (mm/y) | Sediment Accummlation (m3/y) | Accummlation Adjusted for 93% Trap Efficiency (m3/y) | ||
| 25 April 2011 to 11 May 2012 | 382 | 38.6 | 36.9 | 20.1 | 207.8 | 198.6 | 6.8 | 7.4 |
| 23 May 2012 to 16 August 2012 | 85 | −10.7 | −45.9 | −25.0 | 288.9 | 1240.6 | 42.7 | 46.0 |
| 29 August 2012 to 23 February 2013 | 178 | −28.8 | −59.0 | −32.1 | 322.1 | 660.5 | 22.8 | 24.5 |
| Average | −0.3 | −22.7 | −12.3 | 272.9 | 699.9 | 24.1 | 25.9 | |
| Trapezoidal Segment i | Average Depth (m) di | Width (m) zi | Average Radius (m) ri | Volume (m3) Vi |
|---|---|---|---|---|
| 1 | 0.08 | 1.19 | 4.49 | 0.14 |
| 2 | 0.22 | 1.30 | 4.41 | 0.42 |
| 3 | 0.29 | 1.04 | 4.47 | 0.45 |
| 4 | 0.39 | 1.25 | 4.81 | 0.78 |
| 5 | 0.45 | 1.30 | 5.36 | 1.04 |
| 6 | 0.42 | 1.17 | 5.69 | 0.92 |
| 7 | 0.44 | 0.84 | 5.78 | 0.70 |
| 8 | 0.45 | 0.81 | 5.79 | 0.70 |
| 9 | 0.46 | 1.02 | 5.73 | 0.88 |
| 10 | 0.24 | 1.63 | 5.22 | 0.68 |
| Total Volume | 6.71 | |||
| Sediment yield (m3/y) | 5.45 | |||
| Scale for 93% trap efficiency (m3/y) | 5.85 | |||
| Method | Sediment Yield (m3/y) | % Yield Difference | Considerations | |
|---|---|---|---|---|
| Buckets | 14.43 | 160 | Air space in buckets, overfilling. Inability to remove all sediment in one day, additional deposition during removal may cause overestimation. | |
| Erosion Pins | Gully | 12.33 | 123 | Pins represent small part of eroding area. Eroded sediment may be redeposited in gully. |
| Delta | 25.93 | 368 | Delta pins located in area of greatest deposition and no pins installed on shallow margins of sediment wedge. | |
| Geometric | Trapezoidal prism/cylinder segment | 9.19 | 66 | Depth was averaged across wedge face. Depth at fence assumed to equal depth along chord z. Elliptical silt fence approximated with cylinder. Base and surface of wedge assumed to be planar. |
| Sum of trapezoidal pyramids | 5.85 | 5.7 | Fence assumed to be planar between fence posts, with negligible bowing between posts. Base and surface of wedge assumed to be planar. | |
| 3D model | 5.54 | - | Fades from measurable depth to zero depth in end segments. Continuous sediment surface and base. | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luffman, I.; Nandi, A.; Luffman, B. Comparison of Geometric and Volumetric Methods to a 3D Solid Model for Measurement of Gully Erosion and Sediment Yield. Geosciences 2018, 8, 86. https://doi.org/10.3390/geosciences8030086
Luffman I, Nandi A, Luffman B. Comparison of Geometric and Volumetric Methods to a 3D Solid Model for Measurement of Gully Erosion and Sediment Yield. Geosciences. 2018; 8(3):86. https://doi.org/10.3390/geosciences8030086
Chicago/Turabian StyleLuffman, Ingrid, Arpita Nandi, and Benjamin Luffman. 2018. "Comparison of Geometric and Volumetric Methods to a 3D Solid Model for Measurement of Gully Erosion and Sediment Yield" Geosciences 8, no. 3: 86. https://doi.org/10.3390/geosciences8030086
APA StyleLuffman, I., Nandi, A., & Luffman, B. (2018). Comparison of Geometric and Volumetric Methods to a 3D Solid Model for Measurement of Gully Erosion and Sediment Yield. Geosciences, 8(3), 86. https://doi.org/10.3390/geosciences8030086





