Optimum Design of Curved Surface Sliders Based on Site-Specific Seismic Input and Its Sensitivity
Abstract
:1. Introduction
2. Optimum Curved Surface Sliders for Minimum Structural Acceleration
2.1. Linear Elastic Response Spectrum Method
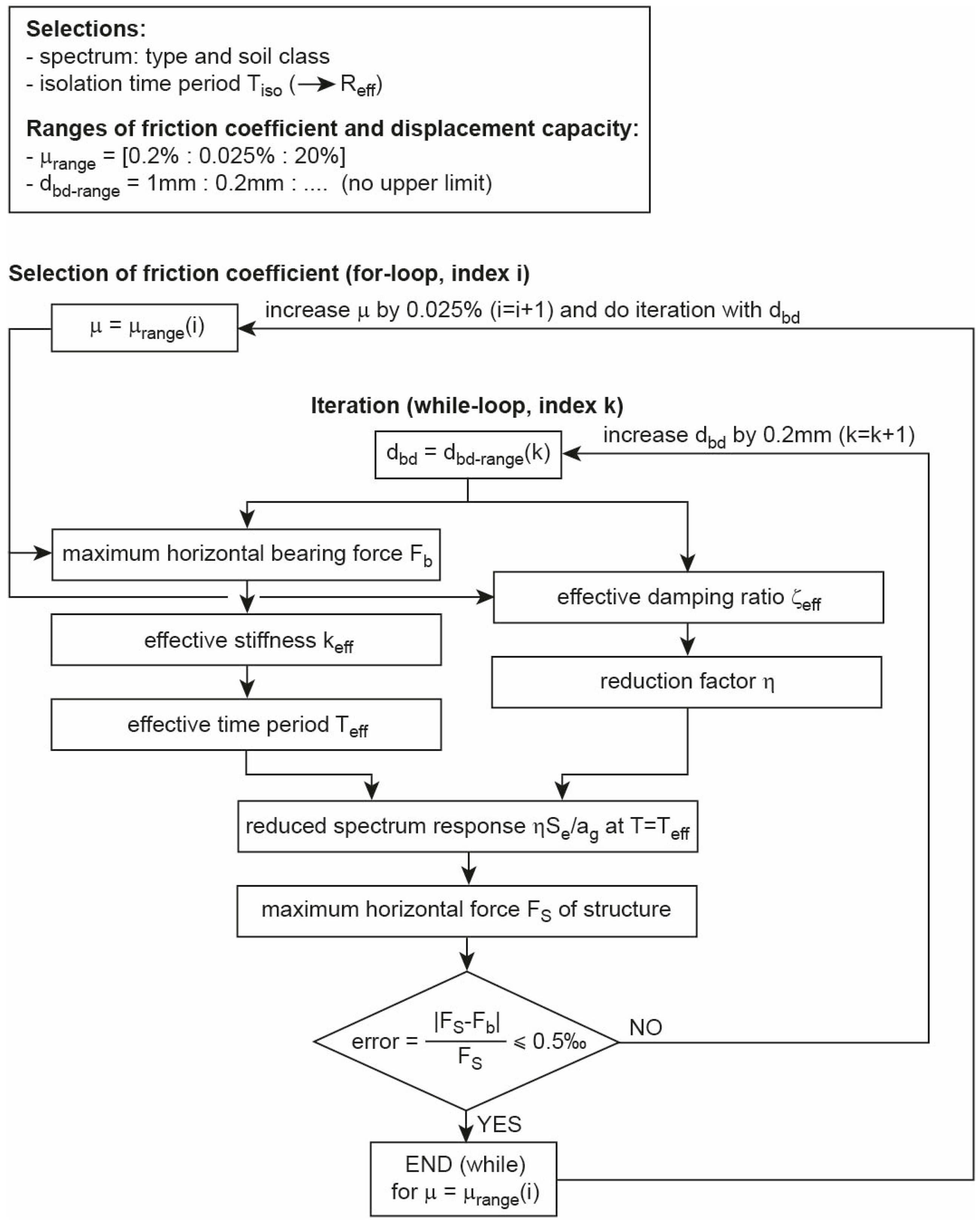
2.2. Optimum CSS Design for Minimum Structural Acceleration
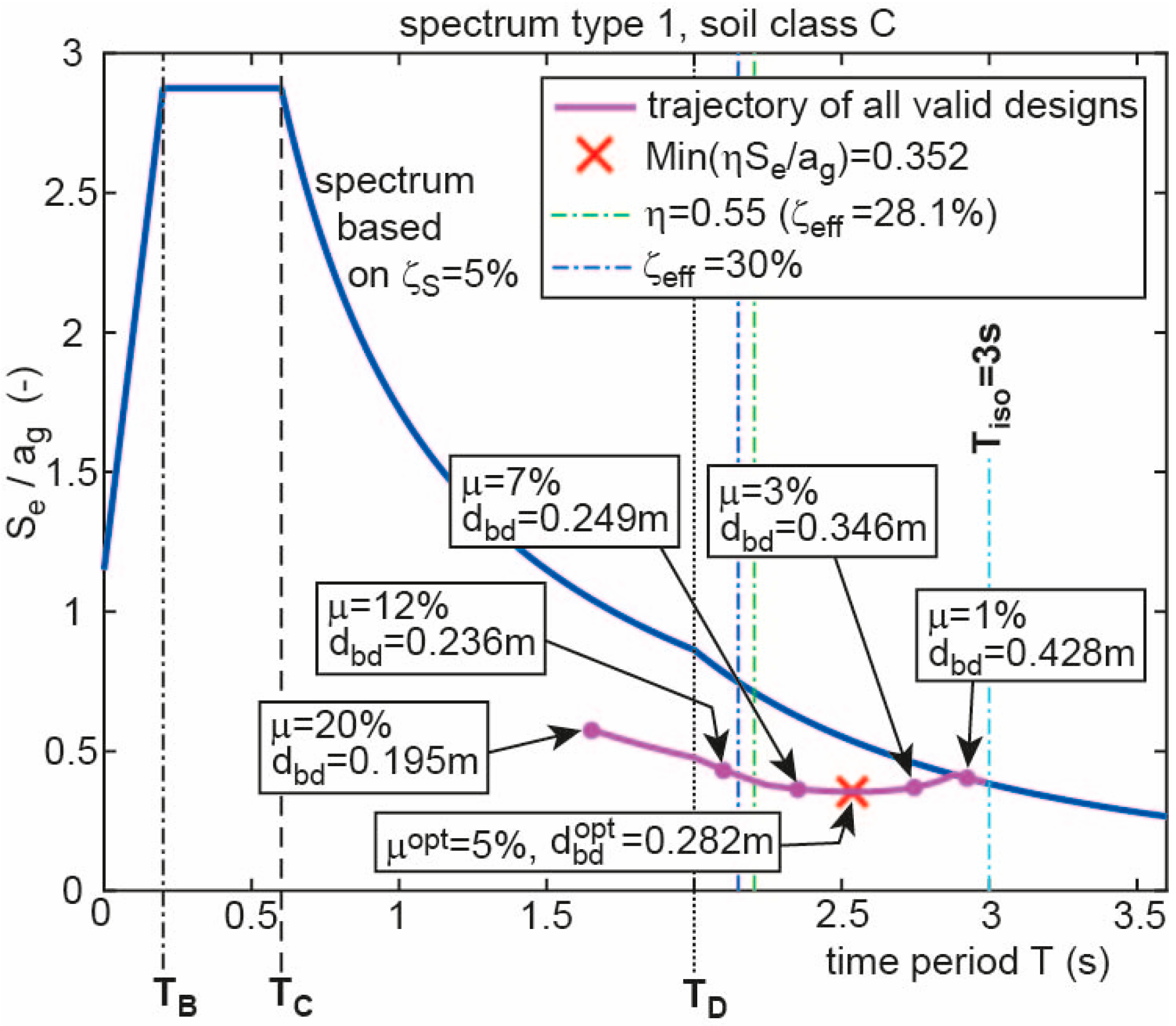
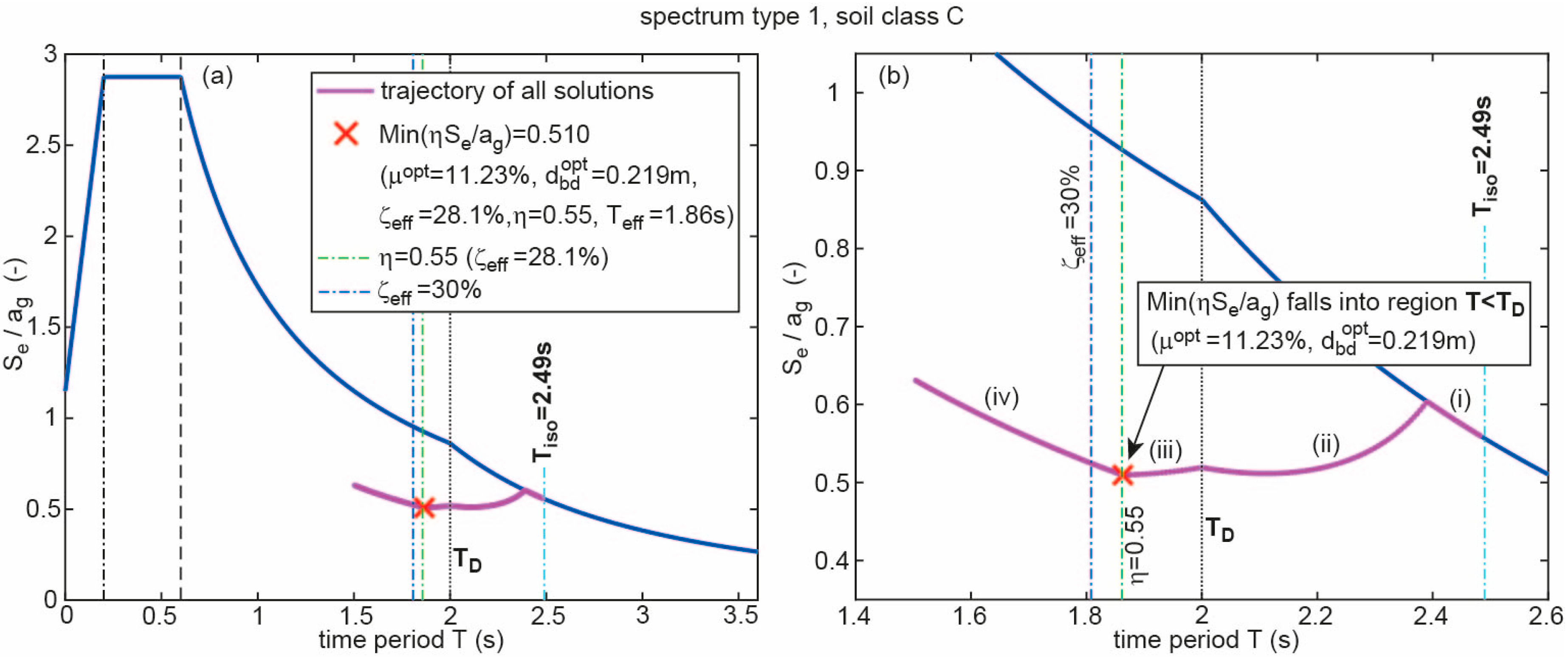
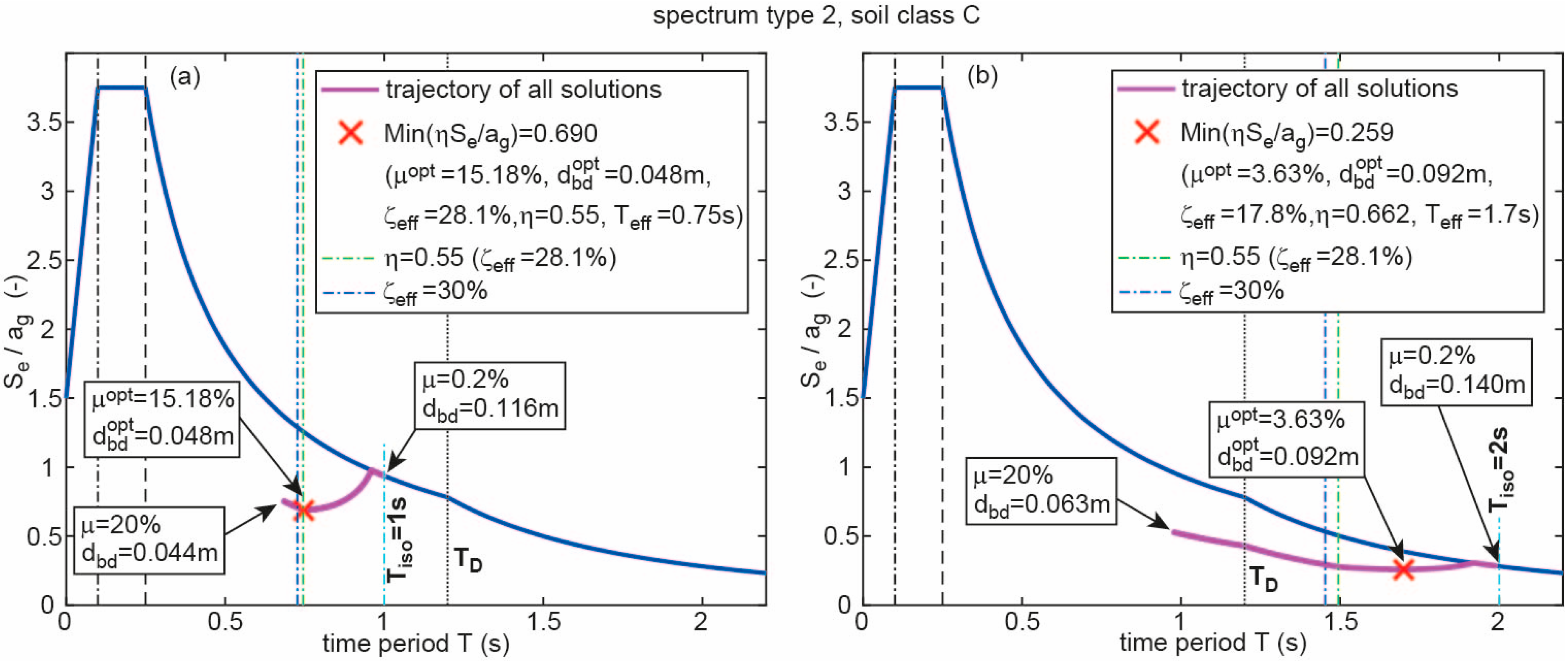
- The trajectory of the valid CSS designs starts at due to the smallest considered friction coefficient = 0.2% and then primarily propagates to the “left”, i.e., to lower values of due to the increasing values of and the acceleration response of the trajectory is reduced due to 0.55 1.
- As long as 5% the trajectory of the valid CSS designs is congruent with the non-reduced acceleration response of the spectrum because = 5% leads to = 1.
- For 5% 28.1% the trajectory of the valid CSS designs is below the non-reduced acceleration response of the spectrum because 5% 28.1% results in 0.55 < 1.
- To the “left” of the vertical dash-dotted line in green due to 28.1% and hence = 0.55 the reduction factor remains at 0.55 despite increases up to its maximum tolerated value of 30% due to the increasing ; = 30% is indicated by the blue vertical dash-dotted line.
- There exists one optimum CSS design that is valid () and minimizes the structural acceleration response which is highlighted by the red cross on the trajectory.
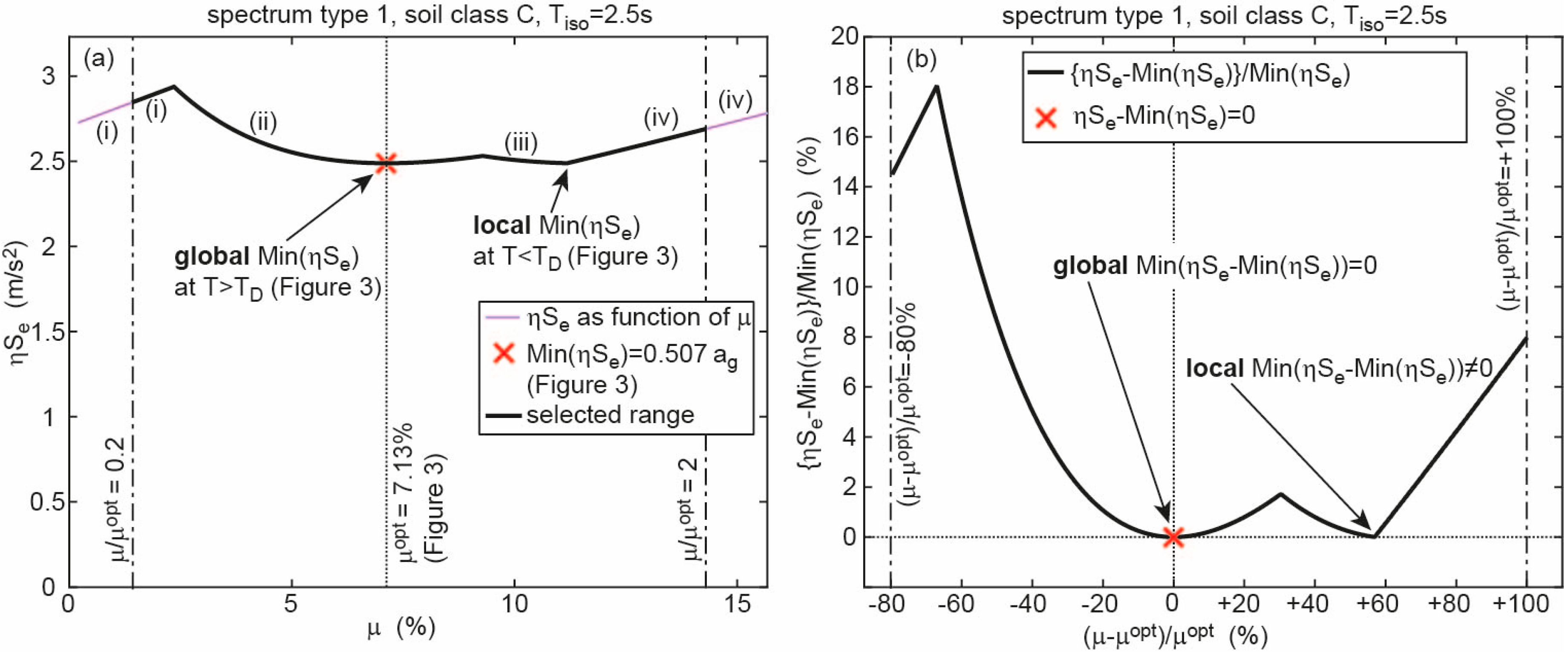
2.3. Optimization Results for Spectrum of Type 1 with Soil Class C
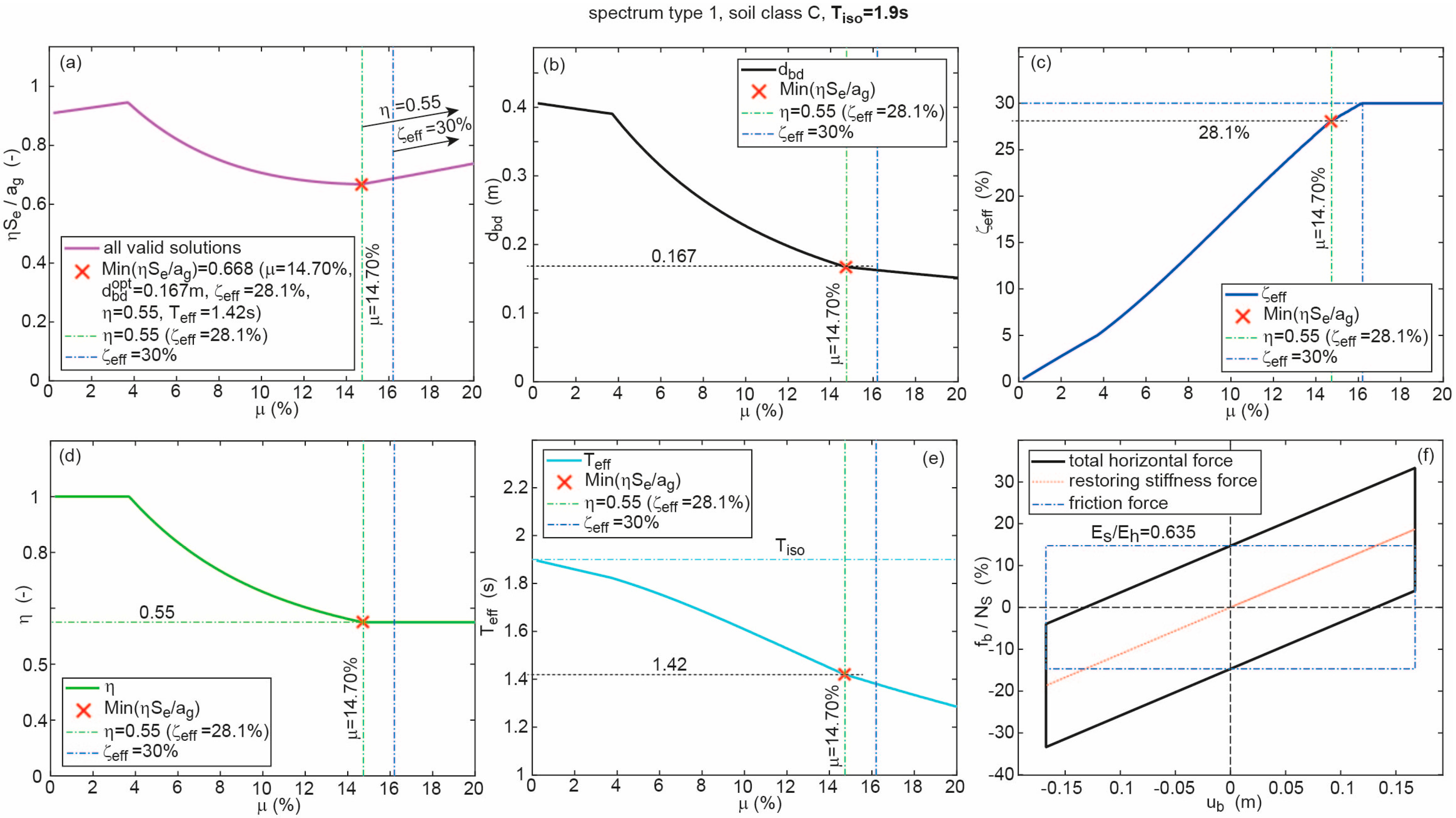
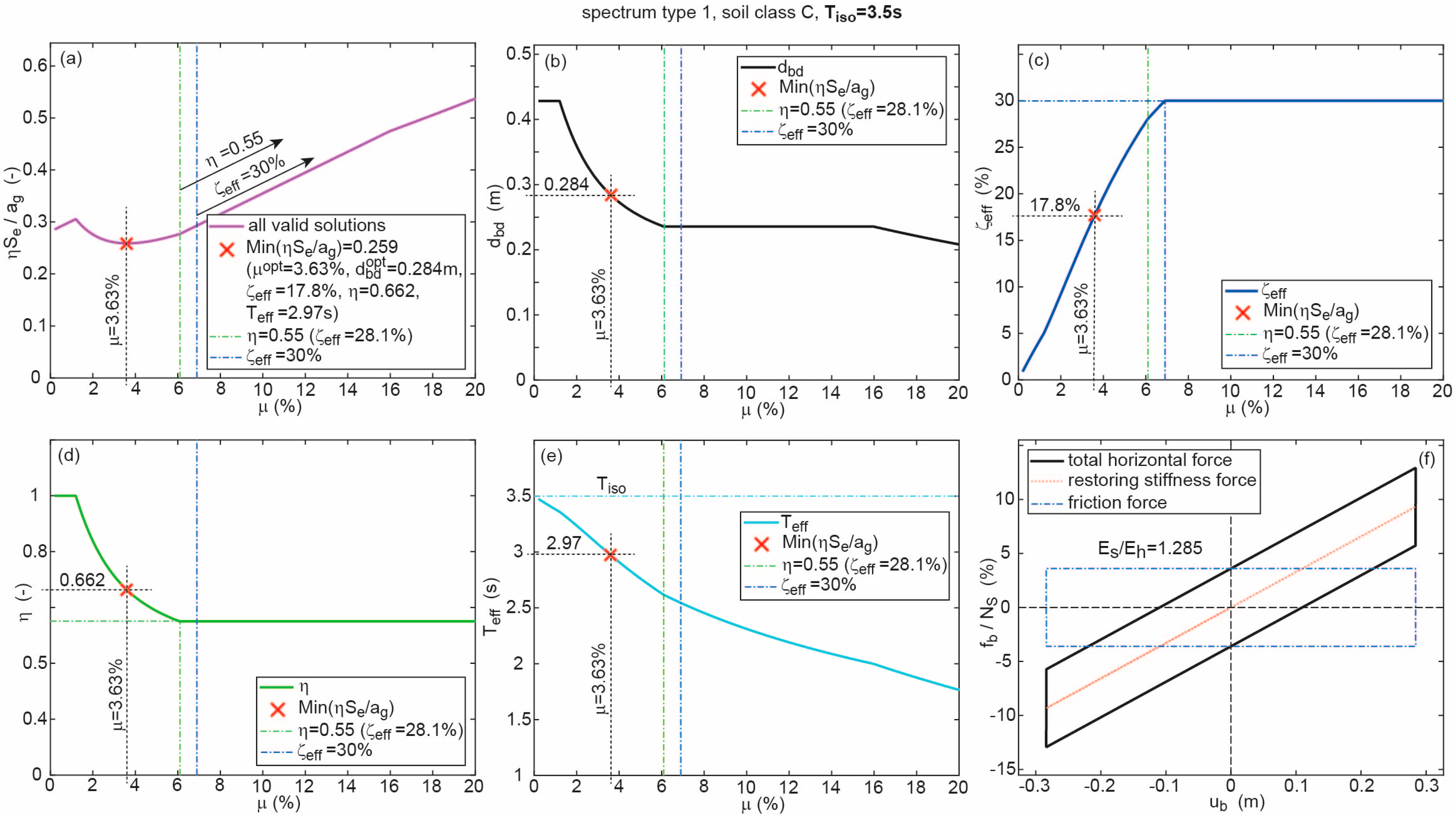
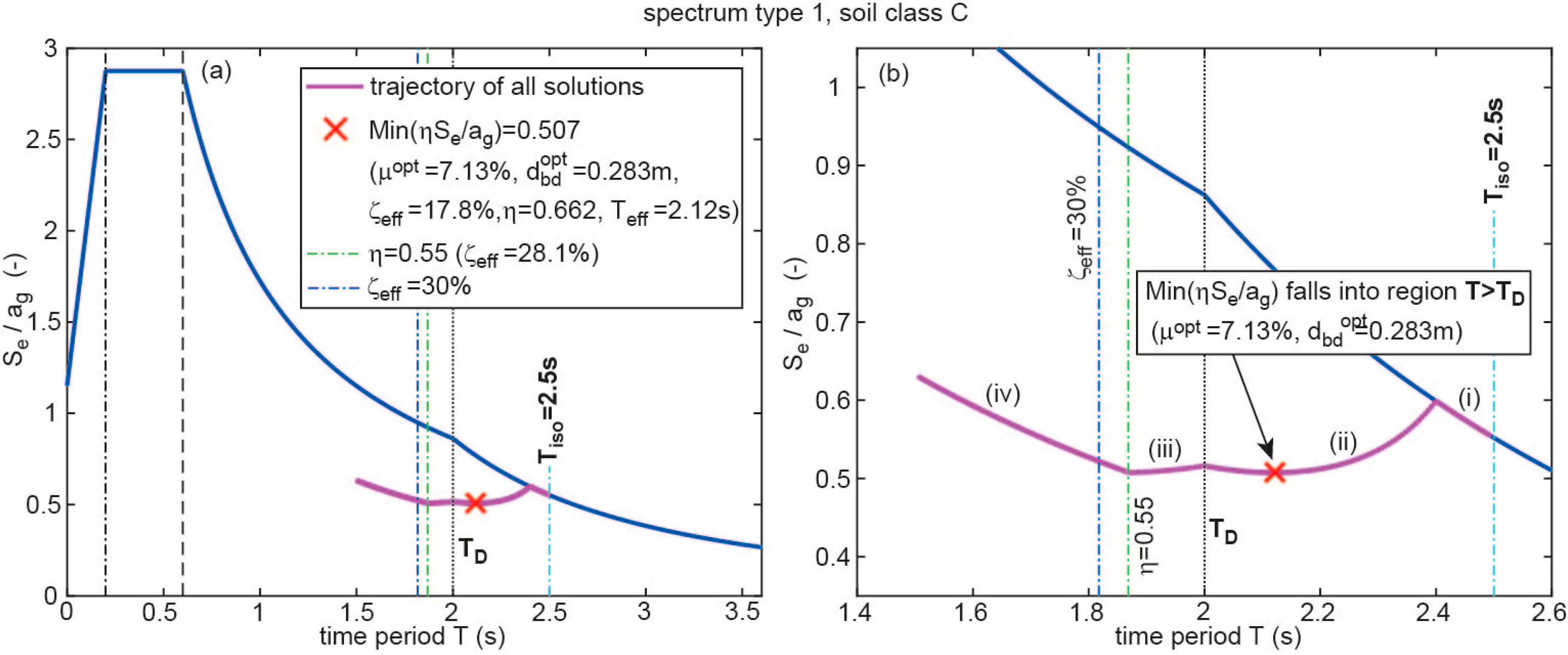
2.3.1. Optimum Solutions for Selected Isolation Time Periods
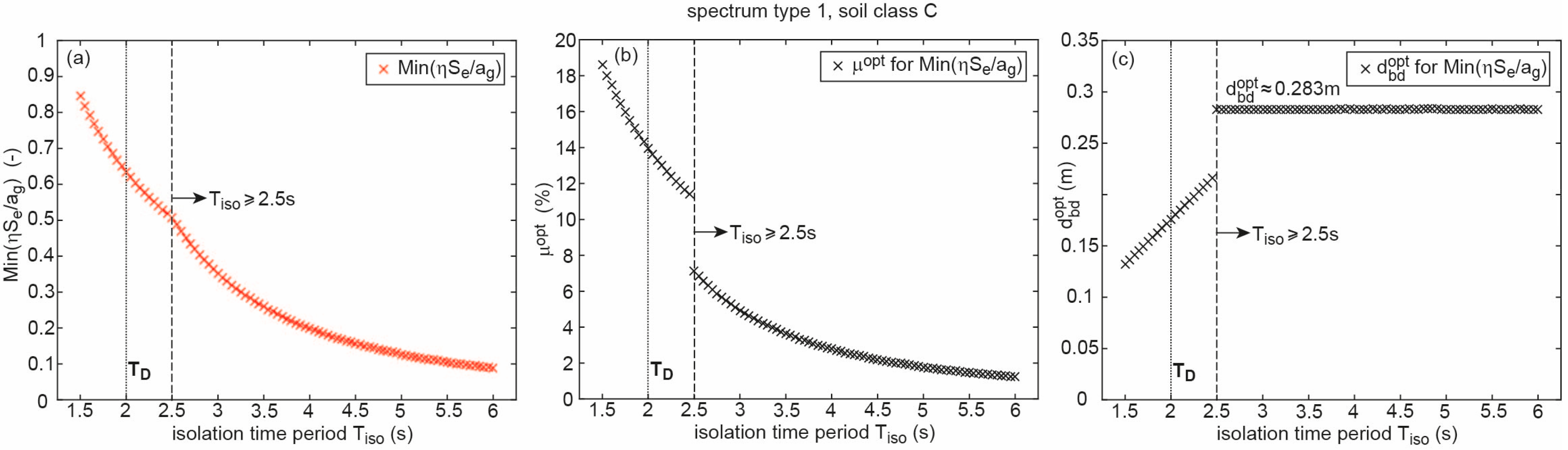
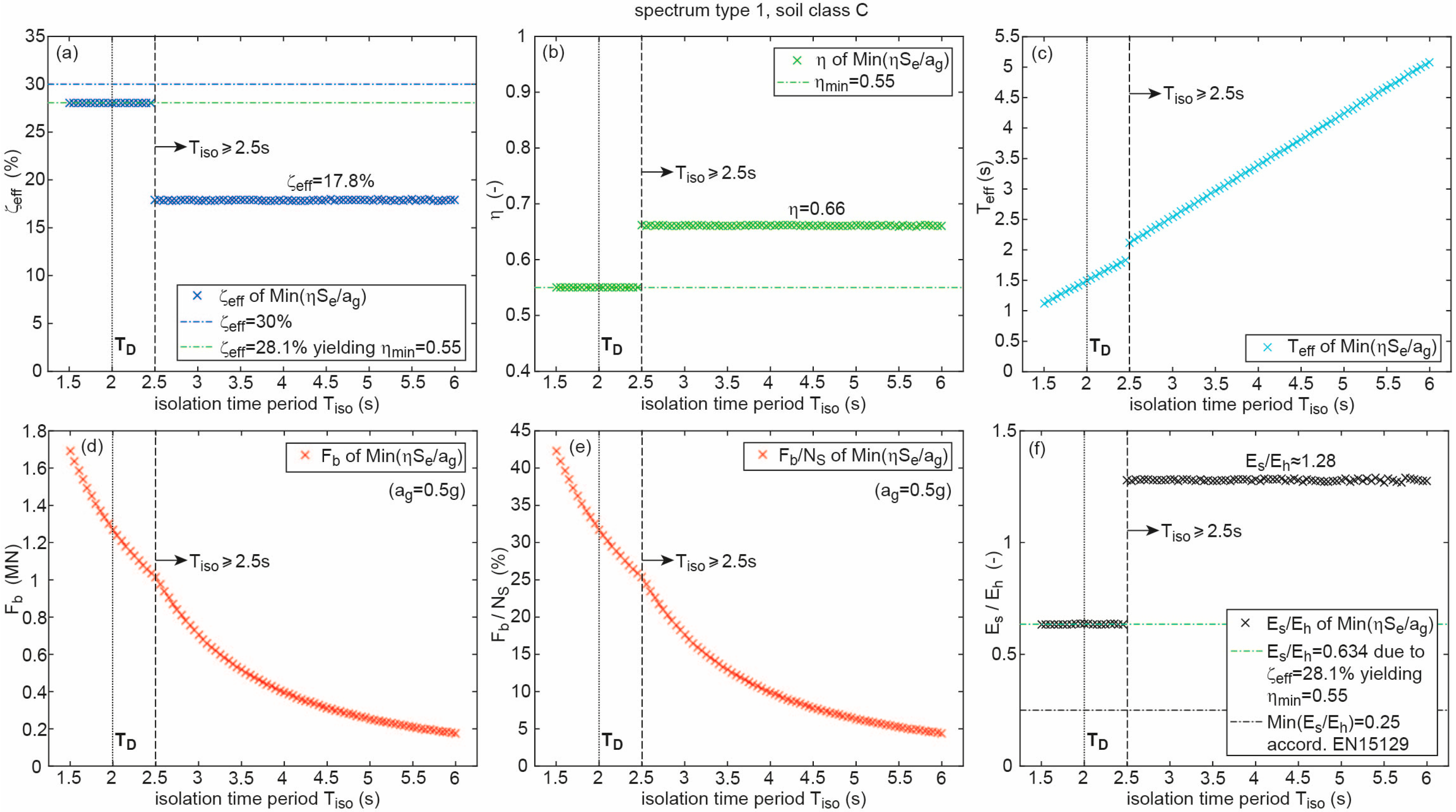
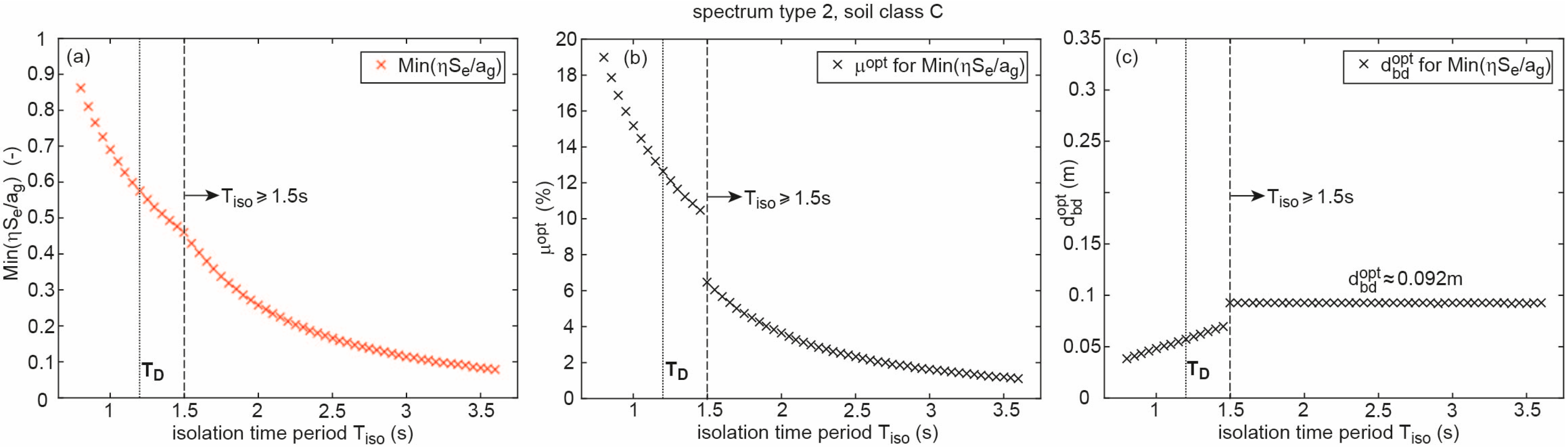
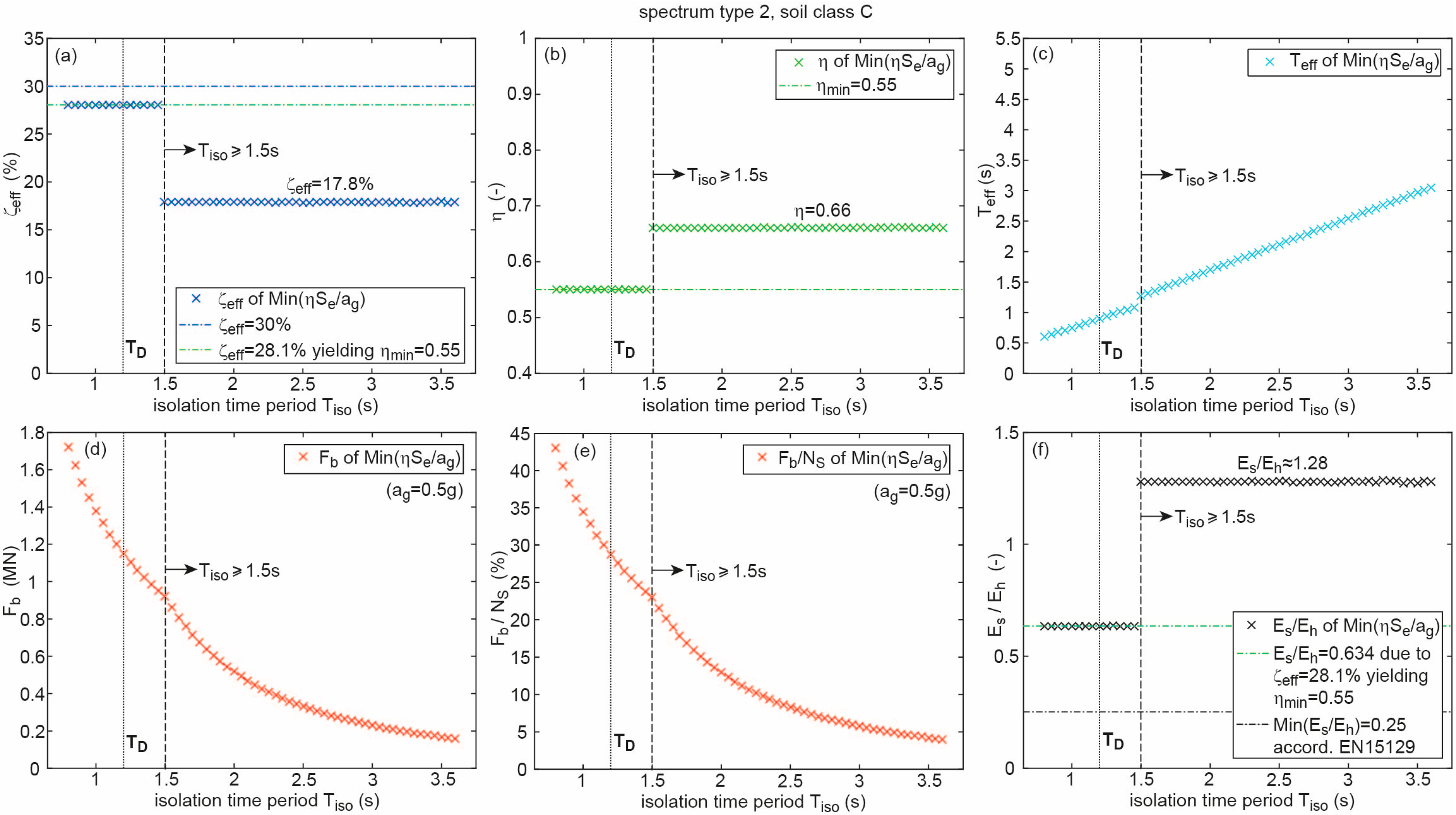
2.3.2. Optimum Solutions as Function of Isolation Time Period
- The longer is the smaller the optimum friction coefficient becomes.
- The displacement capacities of all optimum CSS design solutions whose effective time periods lie in the region are constant because at the reduction factor = 0.66 is constant and at is in proportion to whereby the according displacement is constant.; notice that = constant at only applies to the optimum CSS design solutions due to = constant in this time period range.
- The optimum CSS design in the typical isolation time period region 3.5 s < < 4.5 s is not obtained from maximum tolerated effective damping ratio = 30% but from the lower value = 17.8% evoking = 0.66.
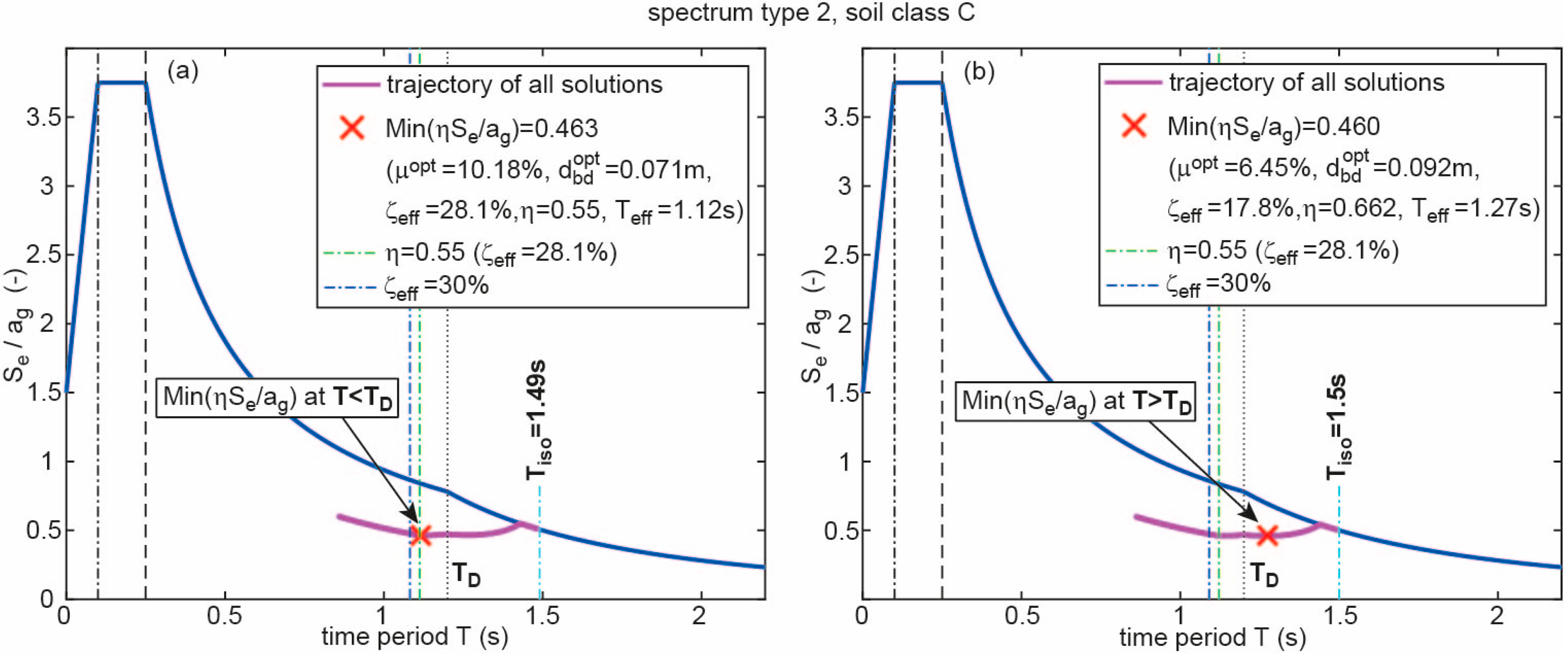
- The jump in the curves of the shown state variables at = 2.5 s is caused by the fact that the optimum CSS design lies in the region if 2.5 s, while it is located in the region if 2.5 s.
- Reasonable values for are found in the typical isolation time period region 3.5 s < < 4.5 s.
- The re-centring condition 0.25 is fulfilled for all optimum CSS designs and all considered isolation time periods .
2.4. Optimization Results for Spectrum of Type 2 with Soil Class C
3. Sensitivity of Friction Coefficient on Structural Acceleration
3.1. Sensitivity Formulation
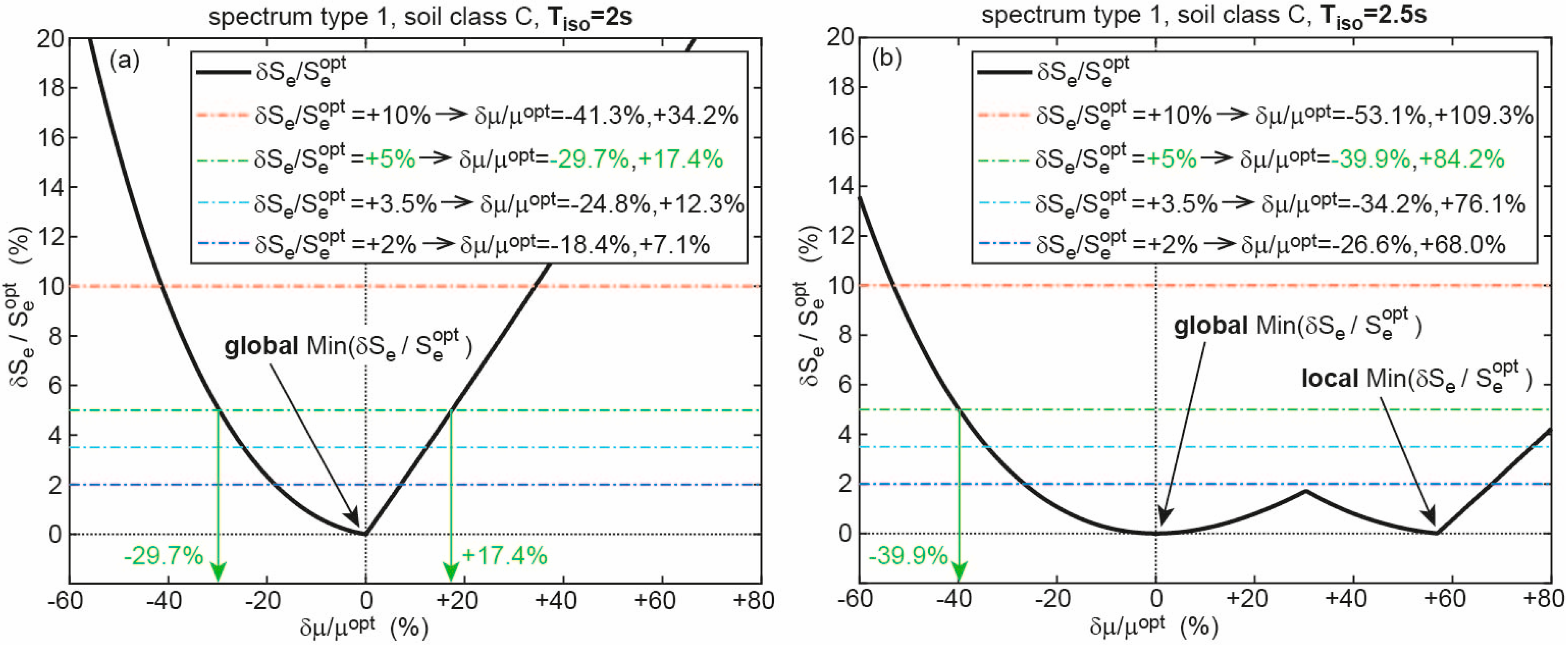
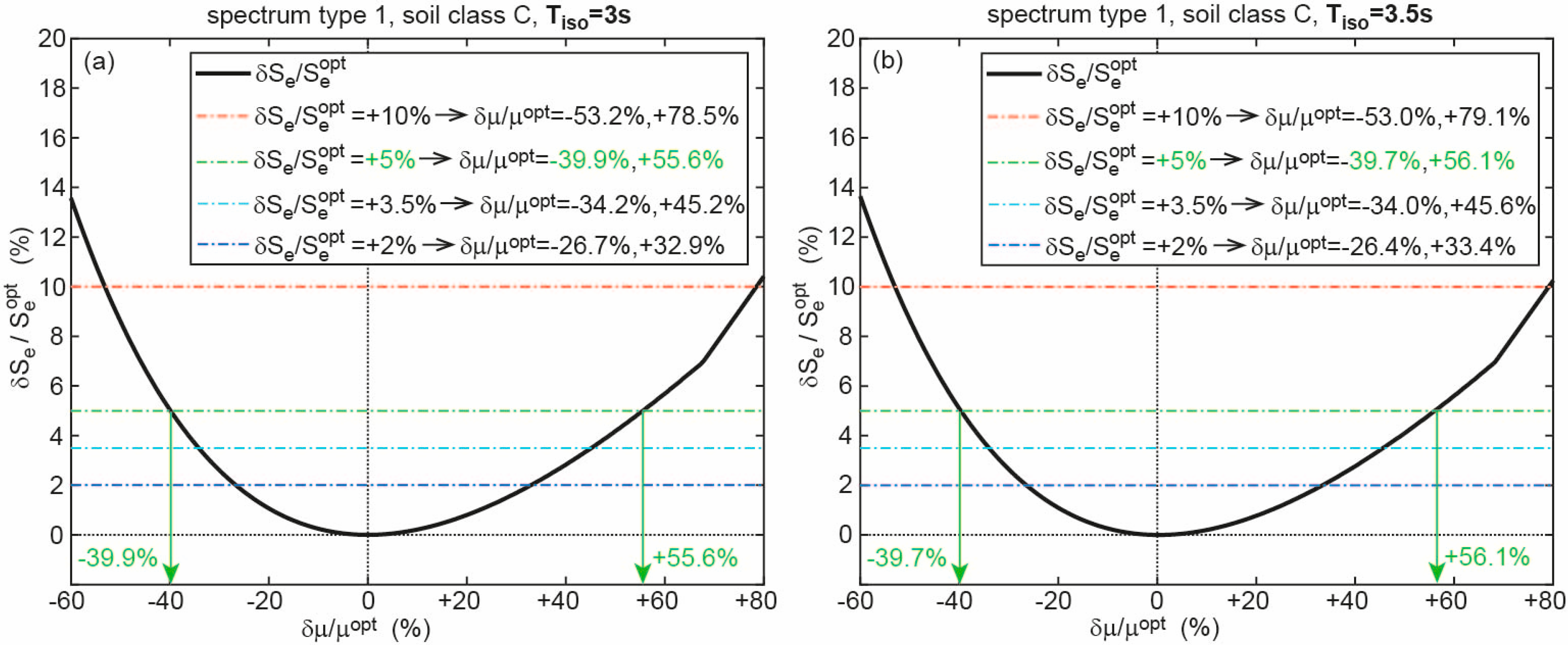
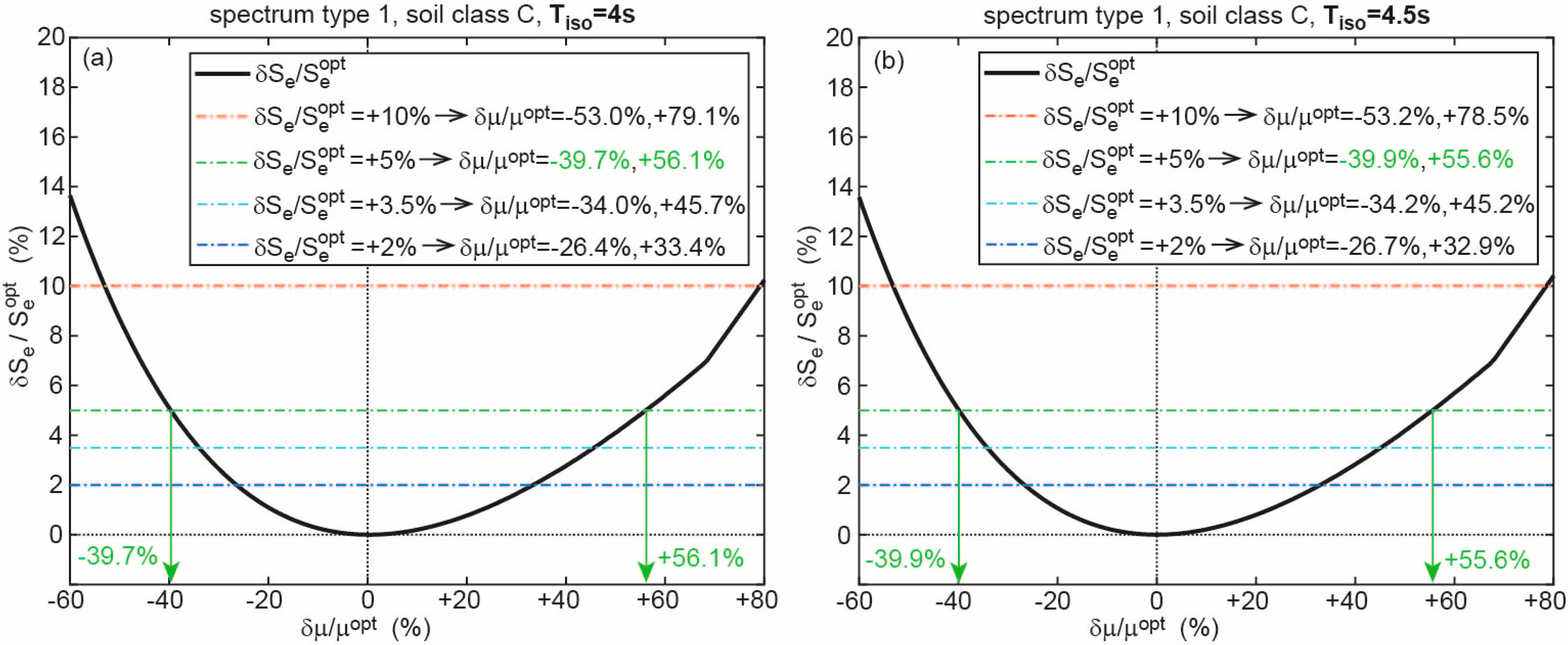
3.2. Results for Spectrum of Type 1
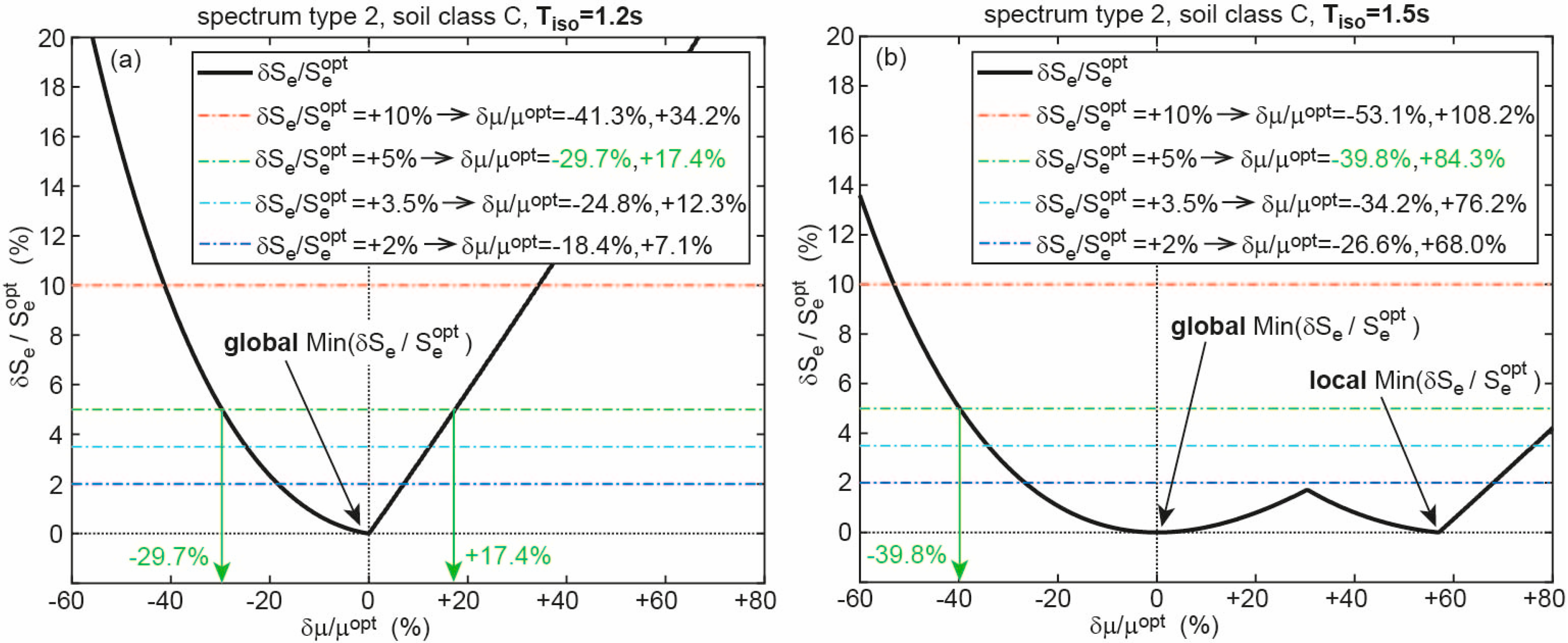
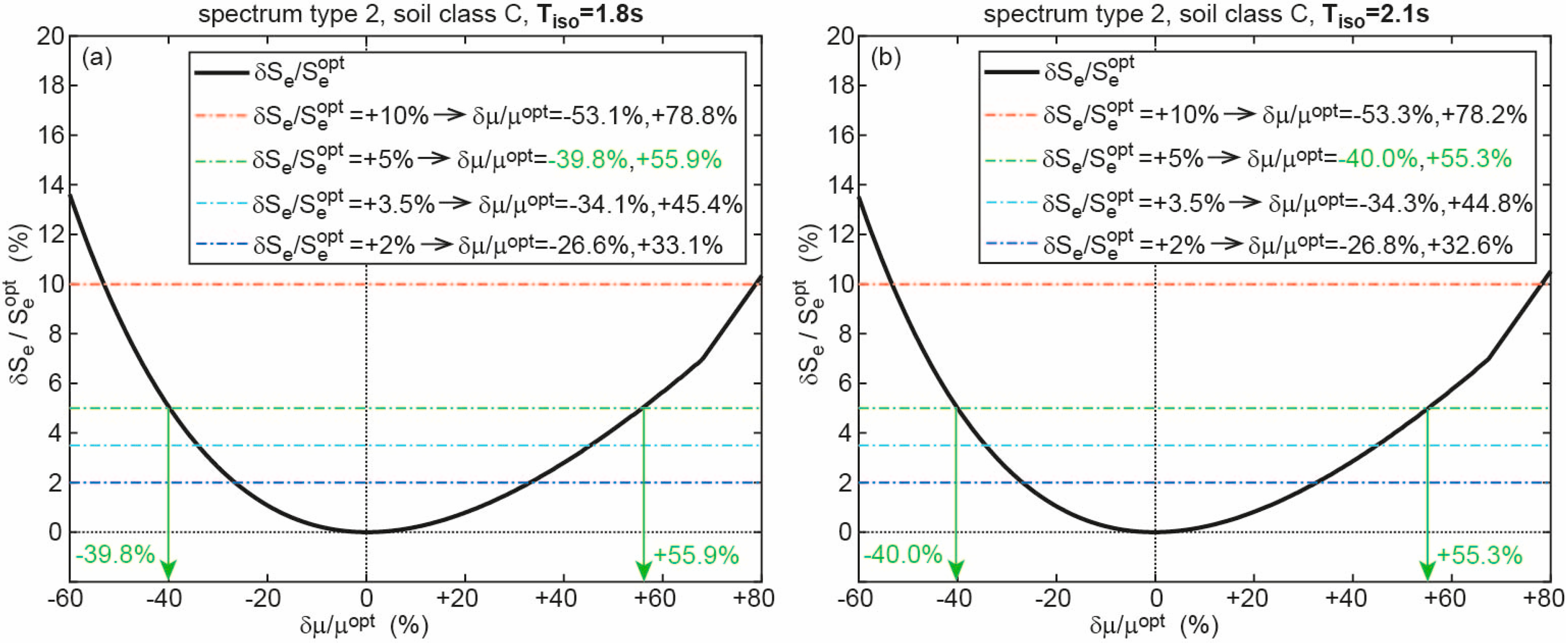
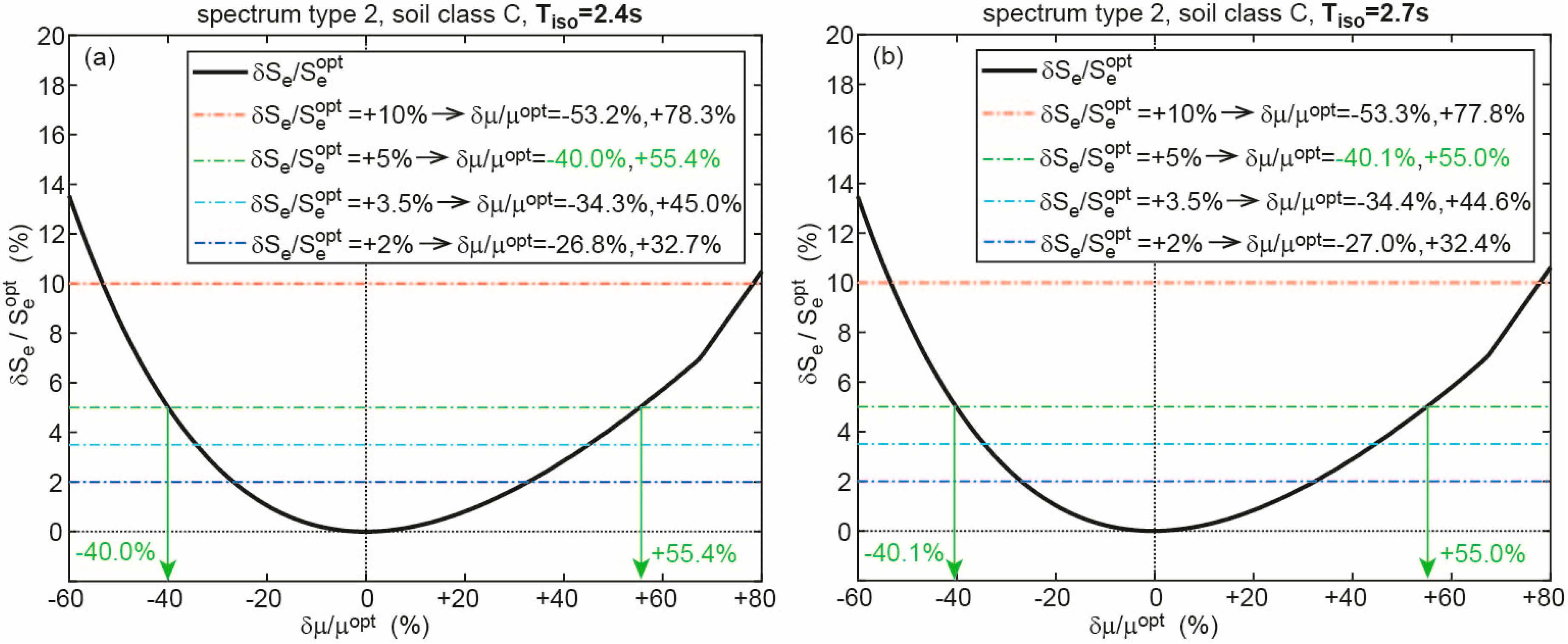
3.3. Results for Spectrum of Type 2
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yen, K.Z.Y.; Lee, Y.J. Passive Vibration Isolating System. U.S. Patent No. 6126136, 3 October 2000. [Google Scholar]
- European Committee for Standarization. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; EU: Brussels, Belgium, 2004; 321p. [Google Scholar]
- Lai, M.L.; Soong, T.T. Seismic design considerations for secondary structural systems. J. Struct. Eng. 1991, 117, 459–472. [Google Scholar] [CrossRef]
- Inaudi, J.A.; Kelly, J.M. Optimum damping in linear isolation systems. Earthq. Eng. Struct. Dyn. 1993, 22, 583–598. [Google Scholar] [CrossRef]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar] [CrossRef]
- Hall, J.F. Discussion: The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 1717–1720. [Google Scholar] [CrossRef]
- Du, Y.; Zhao, G. Analysis of effect of non-classical damping on isolated structure and optimum damping. J. Earthq. Eng. Eng. Vib. 2000, 20, 100–107. [Google Scholar]
- Jangid, R.S. Optimum friction pendulum system for near-fault motions. Eng. Struct. 2005, 27, 349–359. [Google Scholar] [CrossRef]
- Bucher, C. Probability-based optimization of friction damping devices. Struct. Saf. 2009, 31, 500–507. [Google Scholar] [CrossRef]
- Kovaleva, N.V.; Rutman, Y.L.; Davydova, G.V. Determination of optimal damping parameters for seismic isolation systems. Mag. Civ. Eng. 2013, 40, 107–115. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdaş, G.; Alhan, C. Optimization of seismic isolation systems via harmony search. Eng. Optim. 2014, 46, 1553–1569. [Google Scholar] [CrossRef]
- Kamalzare, M.; Johnson, E.A.; Wojtkiewicz, S.F. Efficient optimal design of passive structural control applied to isolator design. Smart Struct. Syst. 2015, 15, 847–862. [Google Scholar] [CrossRef]
- Mazza, F. Lateral-torsional response of base-isolated buildings with curved surface sliding system subjected to near-fault earthquakes. Mech. Syst. Signal Process. 2017, 92, 64–85. [Google Scholar] [CrossRef]
- Mazza, F.; Mazza, M. Sensitivity to modelling and design of curved surface sliding bearings in the nonlinear seismic analysis of base-isolated r.c. framed buildings. Soil Dyn. Earthq. Eng. 2017, 79, 951–970. [Google Scholar] [CrossRef]

| (s) | Soil Class | ||||
|---|---|---|---|---|---|
| 2 | A | +5% | −29.6%, +17.7% | 2% | −18.3%, +7.3% |
| B | +5% | −29.7%, +17.4% | 2% | −18.4%, +7.0% | |
| C | +5% | −29.7%, +17.4% | 2% | −18.4%, +7.1% | |
| D | +5% | −29.6%, +17.5% | 2% | −18.3%, +7.1% | |
| E | +5% | −29.6%, +17.6% | 2% | −18.3%, +7.2% | |
| 2.5 | A | +5% | −39.8%, +84.4% | 2% | −26.6%, +68.1% |
| B | +5% | −39.9%, +84.0% | 2% | −26.7%, +67.8% | |
| C | +5% | −39.9%, +84.2% | 2% | −26.6%, +68.0% | |
| D | +5% | −39.9%, +84.1% | 2% | −26.7%, +67.9% | |
| E | +5% | −39.9%, +84.2% | 2% | −26.7%, +67.9% | |
| 3 | A | +5% | −40.0%, +55.2% | 2% | −26.9%, +32.7% |
| B | +5% | −39.8%, +55.7% | 2% | −26.6%, +33.0% | |
| C | +5% | −39.9%, +55.6% | 2% | −26.7%, +32.9% | |
| D | +5% | −39.9%, +55.5% | 2% | −26.7%, +32.8% | |
| E | +5% | −40.0%, +55.4% | 2% | −26.8%, +32.8% | |
| 3.5 | A | +5% | −39.7%, +56.2% | 2% | −26.4%, +33.4% |
| B | +5% | −39.7%, +56.1% | 2% | −26.4%, +33.4% | |
| C | +5% | −39.7%, +56.1% | 2% | −26.4%, +33.4% | |
| D | +5% | −40.0%, +55.3% | 2% | −26.8%, +32.7% | |
| E | +5% | −40.1%, +55.1% | 2% | −26.9%, +32.5% | |
| 4 | A | +5% | −40.3%, +54.5% | 2% | −27.2%, +32.0% |
| B | +5% | −40.0%, +55.2% | 2% | −26.8%, +32.7% | |
| C | +5% | −39.7%, +56.1% | 2% | −26.4%, +33.4% | |
| D | +5% | −39.8%, +55.8% | 2% | −26.6%, +33.1% | |
| E | +5% | −39.9%, +55.5% | 2% | −26.7%, +32.8% | |
| 4.5 | A | +5% | −39.9%, +55.6% | 2% | −26.6%, +32.9% |
| B | +5% | −39.5%, +56.6% | 2% | −26.2%, +33.8% | |
| C | +5% | −39.9%, +55.6% | 2% | −26.7%, +32.9% | |
| D | +5% | −40.0%, +55.2% | 2% | −26.8%, +32.6% | |
| E | +5% | −39.7%, +56.0% | 2% | −26.5%, +33.3% | |
| 5 | A | +5% | −39.4%, +56.7% | 2% | −26.1%, +33.9% |
| B | +5% | −39.9%, +55.4% | 2% | −26.7%, +32.8% | |
| C | +5% | −39.7%, +56.1% | 2% | −26.4%, +33.4% | |
| D | +5% | −40.2%, +54.9% | 2% | −27.0%, +32.3% | |
| E | +5% | −39.6%, +56.2% | 2% | −26.4%, +33.4% |
| (s) | Soil Class | ||||
|---|---|---|---|---|---|
| 1.2 | A | +5% | −29.7%, +17.6% | 2% | −18.3%, +7.1% |
| B | +5% | −29.7%, +17.5% | 2% | −18.4%, +7.1% | |
| C | +5% | −29.7%, +17.4% | 2% | −18.4%, +7.1% | |
| D | +5% | −29.6%, +17.6% | 2% | −18.3%, +7.2% | |
| E | +5% | −29.7%, +17.4% | 2% | −18.4%, +7.1% | |
| 1.5 | A | +5% | −39.9%, +84.1% | 2% | −26.7%, +67.9% |
| B | +5% | −39.8%, +84.4% | 2% | −26.6%, +68.2% | |
| C | +5% | −39.8%, +84.3% | 2% | −26.6%, +68.0% | |
| D | +5% | −39.9%, +84.0% | 2% | −26.7%, +67.8% | |
| E | +5% | −39.8%, +84.3% | 2% | −26.6%, +68.1% | |
| 1.8 | A | +5% | −39.7%, +56.2% | 2% | −26.4%, +33.5% |
| B | +5% | −39.7%, +55.9% | 2% | −26.5%, +33.2% | |
| C | +5% | −39.8%, +55.9% | 2% | −26.6%, +33.1% | |
| D | +5% | −39.9%, +55.6% | 2% | −26.6%, +33.0% | |
| E | +5% | −39.8%, +55.8% | 2% | −26.6%, +33.1% | |
| 2.1 | A | +5% | −40.0%, +55.2% | 2% | −26.9%, +32.5% |
| B | +5% | −40.1%, +55.0% | 2% | −27.0%, +32.4% | |
| C | +5% | −40.0%, +55.3% | 2% | −26.8%, +32.6% | |
| D | +5% | −40.0%, +55.3% | 2% | −26.8%, +32.7% | |
| E | +5% | −39.7%, +56.2% | 2% | −26.4%, +33.4% | |
| 2.4 | A | +5% | −39.7%, +56.0% | 2% | −26.5%, +33.3% |
| B | +5% | −40.0%, +55.2% | 2% | −26.8%, +32.6% | |
| C | +5% | −40.0%, +55.4% | 2% | −26.8%, +32.7% | |
| D | +5% | −39.8%, +55.8% | 2% | −26.6%, +33.1% | |
| E | +5% | −40.1%, +55.0% | 2% | −27.0%, +32.4% | |
| 2.7 | A | +5% | −39.8%, +55.7% | 2% | −26.6%, +33.1% |
| B | +5% | −40.1%, +54.9% | 2% | −27.0%, +32.4% | |
| C | +5% | −40.1%, +55.0% | 2% | −27.0%, +32.4% | |
| D | +5% | −40.0%, +55.2% | 2% | −26.9%, +32.6% | |
| E | +5% | −39.9%, +55.6% | 2% | −26.7%, +32.9% | |
| 3 | A | +5% | −39.9%, +55.6% | 2% | −26.6%, +32.9% |
| B | +5% | −39.8%, +55.8% | 2% | −26.5%, +33.2% | |
| C | +5% | −40.3%, +54.5% | 2% | −27.2%, +32.0% | |
| D | +5% | −39.9%, +55.5% | 2% | −26.7%, +32.8% | |
| E | +5% | −40.0%, +55.3% | 2% | −26.8%, +32.7% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, F.; Meier, L.; Distl, J.; Braun, C. Optimum Design of Curved Surface Sliders Based on Site-Specific Seismic Input and Its Sensitivity. Geosciences 2018, 8, 83. https://doi.org/10.3390/geosciences8030083
Weber F, Meier L, Distl J, Braun C. Optimum Design of Curved Surface Sliders Based on Site-Specific Seismic Input and Its Sensitivity. Geosciences. 2018; 8(3):83. https://doi.org/10.3390/geosciences8030083
Chicago/Turabian StyleWeber, Felix, Leopold Meier, Johann Distl, and Christian Braun. 2018. "Optimum Design of Curved Surface Sliders Based on Site-Specific Seismic Input and Its Sensitivity" Geosciences 8, no. 3: 83. https://doi.org/10.3390/geosciences8030083
APA StyleWeber, F., Meier, L., Distl, J., & Braun, C. (2018). Optimum Design of Curved Surface Sliders Based on Site-Specific Seismic Input and Its Sensitivity. Geosciences, 8(3), 83. https://doi.org/10.3390/geosciences8030083






