Abstract
GASAKe is an empirical-hydrological model aimed at forecasting the time of occurrence of landslides. Activations can be predicted of either single landslides or sets of slope movements of the same type in a homogeneous environment. The model requires a rainfall series and a set of dates of landslide activation as input data. Calibration is performed through genetic algorithms, and allows for determining a family of optimal kernels to weight antecedent rainfall properly. As output, the mobility function highlights critical conditions of slope stability. Based on suitable calibration and validation samples of activation dates, the model represents a useful tool to be integrated in early-warning systems for geo-hydrological risk mitigation purposes. In the present paper, examples of application to three rock slides in Calabria and to cases of soil slips in Campania are discussed. Calibration and validation are discussed, based on independent datasets. Obtained results are either excellent for two of the Calabrian rock slides or just promising for the remaining case studies. The best performances of the model take advantage of an accurate knowledge of the activation history of the landslides, and a proper hydrological characterization of the sites. For such cases, GASAKe could be usefully employed within early-warning systems for geo-hydrological risk mitigation and Civil Protection purposes. Finally, a new release of the model is presently under test: its innovative features are briefly presented.
1. Introduction
Rainfall-induced landslides often cause significant economic loss and casualties in Calabria, as in most part of the Italian Peninsula [1,2]. Therefore, their prediction assumes a crucial role in geo-hydrological risk mitigation. The timing of activation of such phenomena is usually predicted by means of either empirical (e.g., [3] and references therein) or physically-based [4,5,6] approaches. To relate rainfall to time of slope instability, the extent of the landslide and the physical characteristics of both rainfall and involved materials (soil/rock) must be considered—e.g., in terms of intensity, duration, amount, and of infiltration capacity. Unfortunately, because of the high cost of field investigations, the parameters required by the physically-based approach are known only for a very limited number of case studies. Therefore, to model the triggering conditions of slope movements—either shallow or deep-seated—a threshold-based modelling approach can be employed [7,8]. Empirical thresholds can be expressed in terms of curves, delimiting the portion of Cartesian planes containing rainfall or hydrological conditions related to known activations. Examples of definition and application of empirical rainfall thresholds in Southern Italy are provided by [9,10,11,12,13]. In hydrological models, kernels (or filter functions) are commonly employed to express the influence of rainfall on runoff and groundwater dynamics: they are usually defined in terms of a simple, continuous analytical function. The base time (tb) of a given kernel expresses the temporal extent in which rainfall seems to have a significant effect on slope stability. The shape and the base time of the kernel are related to magnitude of the landslide and to hydro-geological complexity of the site under investigation. Finally, the predictive tool (named mobility function) can be obtained through the convolution integral between the kernel and the rainfall series [14,15,16].
2. Materials and Methods
GASAKe (Genetic-Algorithm-based Self Adaptive Kernel) is an empirical-hydrological model for predicting the timing of activation of slope movements of different types [17]. A linear and steady slope-stability response to rainfall and a classic threshold scheme are assumed in the model: the exceedance of the threshold determines the triggering of the landslide [18]. Though inspired by the FLaIR (Forecasting Landslides Induced by Rainfall) model [19,20] (already applied in several case studies, see [21,22,23]), it differs for several features and is suitable to handle complex cases: in fact, the model adopts a discrete kernel, instead of a continuous one, and is based on a genetic-algorithm procedure that allows for an effective, automated, self-adaptive calibration. The model can be applied either to single landslides, characterized by several historical activations, or to a set of similar slope movements in a homogeneous geomorphological context. Case studies may be of any depth, from shallow to deep-seated. The inputs of the model are: (i) the rainfall series and (ii) the set of known dates of landslide activation. Regarding rainfall data, GASAKe needs as input a single rainfall series at a given time scale (e.g., daily, hourly, sub-hourly rainfall); the series can be derived from one only rain gauge or by combining rainfall data from different gauges into a “synthetic” series (e.g., by means of geostatistical techniques). The temporal extent of the rainfall series must start before the first landslide activation date and terminate after the last date (e.g., at the beginning and at the end of hydrological years). The mobility function—i.e., the output of the model as obtained through calibration—highlights the most critical conditions for the stability of the considered case study: its values depend on both rainfall amounts and shape/base time of the kernel. Triggering conditions occur when the value of the mobility function exceeds a given threshold.
More in detail, calibration of the model is based on genetic algorithms (“GA”, in the following; [24,25]), which allow to obtain families of optimal, discretized solutions (kernels) that maximize the fitness function. At the beginning of a given optimization experiment, a family of kernels is randomly generated. The application to such kernels of a sequence of genetic operators—namely selection, crossover and mutation—constrained by prefixed probabilities, allows to generate a new population of candidate solutions (genotypes), to be tested as kernels in the successive GA iteration. A mobility function (phenotype) is then obtained by convolution between each kernel and rainfall, and its performance is evaluated by applying a suitable fitness function. Thanks to inherent proprieties of GA (cf., Fundamental Theorem [24]), better individuals (i.e., characterized by higher fitness values) can be obtained over time through iterations.
In GASAKe the evaluation of the phenotypes (and, therefore, of the related genotypes) is primarily based on the fitness values, Φ, defined on the relative position (rank, ki) of the peaks of the mobility function corresponding to the L dates of landslide activation [17]. It is:
When two (or more) mobility functions share the same value of fitness, a further distinction can be made based on the safety margin, Δzcr, defined as:
in which zj-min is the height of the lowest peak of the mobility function that corresponds to one of the activation dates, and zcr is the critical height, i.e., the height of the highest peak of the mobility function located just below zj-min. Kernels with similar Φ can therefore be distinguished, and those more useful for predictive purposes selected, being characterized by larger separations among the peaks of the mobility function either corresponding to dates of activation or not.
Over several GA iterations, the mobility function is forced toward a shape characterized by peaks coinciding with the dates of landslide occurrence. An optimal kernel leads to a mobility function having the highest peaks in correspondence to such dates; further peaks may also be present, but characterized by lower values.
The best Q kernels obtained in the calibration phase can be utilized to synthetize “average” kernels to be employed for validation, by considering further dates of landslide activation (and appropriate rainfall series). Up to date, a set of Q = 100 optimal kernels has been employed during tests and first applications of the model to several case studies in Southern Italy. Once validated, the model can finally be applied—e.g., in support of an early-warning system—to estimate the timing of future landslide activations in the same study area, by employing measured or forecasted rainfall. In Figure 1, the calibration and validation procedures are schematically shown. For the sake of brevity, a complete description of the model is not reported here; however, a more detailed overview of its main features and of the calibration/validation procedures can be found in [3].
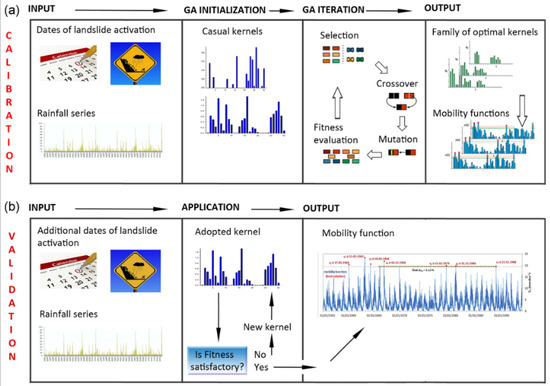
Figure 1.
Schematic sketch of: (a) the calibration and (b) the validation procedures of GASAKe.
3. Case Studies
The model was applied to different case studies in Southern Italy (Figure 2), and precisely to 3 rock slides in northern Calabria and to a set of shallow landslides (soil slip-debris flows) in Campania. Table 1 lists the average rainfall recorded near the considered case studies, while Table 2 and Table 3 list the main characteristics of the considered slope movements.
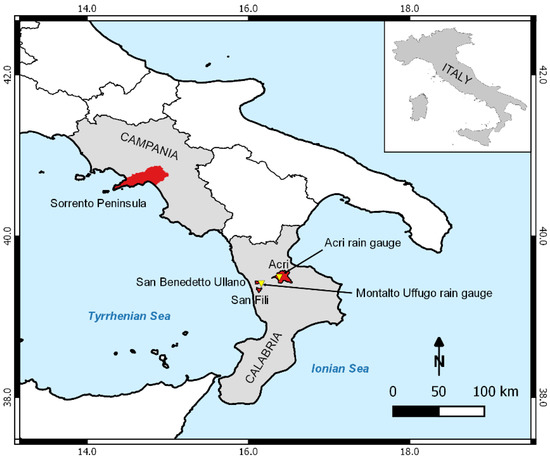
Figure 2.
Location of the case studies (marked in red) in Calabria and Campania regions (marked in grey). Yellow triangles indicate Acri and Montalto Uffugo rain gauges.

Table 1.
Average monthly and annual rainfall (MR, in mm) and number of rainy days (MRD) at rain gauges near the considered case studies. Key: (AC) Acri rain gauge (750 m a.s.l.); (MU) Montalto Uffugo rain gauge (468 m a.s.l.); (GR) Gragnano rain gauge (185 m a.s.l.).

Table 2.
Main characteristics of the Calabrian case studies. In Italics, the dates of activation used for validation. Employed data series range from the beginning of the calibration periods to the end of the validation period (cf. last column). No missing data characterize the considered rain series.

Table 3.
Main characteristics of the considered Campanian case studies. Key: (M) multiple activation; (S) single activation. In Italics, the date of activation used for validation. Employed data series range from the beginning of the calibration periods to the end of the validation period (cf. last column). The Gragnano rain gauge was employed for the Campanian cases. Missing values (about 2% of the whole set) were taken from the Castellammare and Tramonti-Chiunzi gauges.
3.1. Calabrian Case Studies
Calabria is an accretionary wedge made of a series of Jurassic to Early Cretaceous ophiolite-bearing tectonic units, plus overlying Hercynian and pre-Hercynian basement nappes [26]. Because of its geodynamic history [27,28,29,30], the lithological units that make up the Calabrian Arc are commonly characterized by pervasive fracture systems that favored the development of severe weathering processes. The combined effect of tectonic disturbance, differentiated uplift, erosive processes, and chemical-physical alteration influenced physiographic setting of the region, allowing for widespread slope movements of various types and extensions. In addition to earthquakes, meteoric events represent the main triggering factor of landslides in Calabria [31]. These latter pose serious risk conditions in much of the region [32,33,34,35,36,37,38,39]. The climate is Mediterranean (Csa, according to [40]). The Tyrrhenian sector is rainier than the Ionian one (1200–2000 mm vs. 500 mm); nevertheless, the most severe storms occur more frequently on the Ionian side of the region [41]. According to [42], heavy and frequent winter rainfall, caused by cold fronts mainly approaching from NW, and autumn rains, determined by cold air masses from NE, affect the region. In spring, rains show lower intensities than in autumn, while strong convective storms are common at the end of summer. Average yearly rainfall varies between 1000 and 2000 mm/y in mountainous and internal areas, and between 600 and 900 mm/y in coastal areas, with a mean regional value of about 1150 mm/y. Over 70% of the yearly precipitation occurs from October to March, with negligible monthly values from June to September. Concerning the effects of climate change in Calabria, a reduction of annual and winter amounts and an increase of summer rainfall has been recorded in the past decades (e.g., [43,44]).
3.1.1. The Acri—Serra di Buda Landslide
The village of Acri (Figure 3) is located on the Sila Massif, on the right flank of the Crati Graben, a tectonic depression belonging to the Calabrian-Sicilian Rift Zone [27]. The area is marked by a couple of regional, recent/active systems, made of N–S trending normal faults and of WNW–ESE trending strike-slip faults [45,46]. Along the N–S trending system, Palaeozoic metamorphic and igneous rocks (gneiss and granite, commonly weathered) of the Sila Massif, to the East, give place to Late Miocene-Quaternary sediments (mainly conglomerate, sand and clay) of the graben, to the West [47].
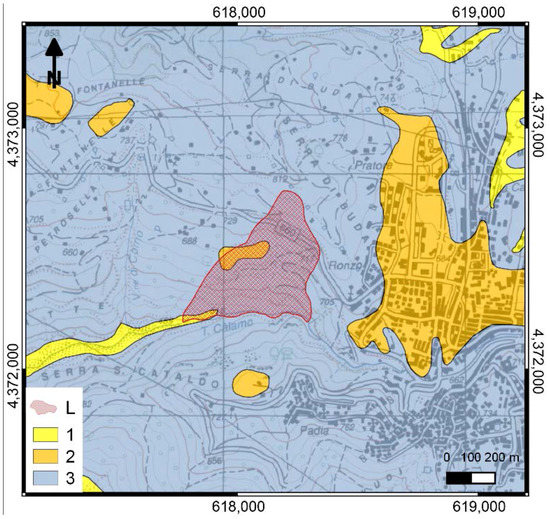
Figure 3.
Lithological sketch of the Serra di Buda landslide at Acri. Key: (1) Alluvium, colluvium and residual soil; (2) conglomerate and sandstone; (3) Igneous and medium-high grade metamorphic rock. The landslide (L) is marked by a red hatched polygon. Topographic base map after 1:25,000 IGMI sheets; lithological map after [47], Geological map of Calabria (scale 1:25,000), mod.
The translational rock slide of Serra di Buda is a portion of a Sackung [48] that threatens the surroundings of the village of Acri. The landslide involves weathered gneissic and granitic rocks. In the last 100 years, it suffered from several reactivations and the Civil Authorities had to close the state road to traffic on several occasions, thus causing serious connection problems with the main urban centers of the area (mainly located in the nearby valley). In the present study, only a subset of the known dates of activation are considered: based on hydrological analyses, [49] showed either scarce or no direct correlation between some of the historical dates of mobilization and rainfall amounts. For such dates, further analyses are needed to better evaluate the possible causes of activation [50].
3.1.2. The San Benedetto Ullano—San Rocco Landslide
The village of San Benedetto Ullano (Figure 4) is located on the left flank of the Crati Graben, at the base of the Coastal Chain. The area is marked by the San Fili-San Marco Argentano normal fault, a N–S trending active structure ca. 30 km long. Along the fault, the metamorphic rocks (mainly gneiss, schist and phyllite) of the Coastal Chain, to the West, give place to Pliocene-Quaternary sediments (conglomerate, sand and clay) and subordinate Miocene outcrops (conglomerate and evaporate rocks), to the East [47]. Note that, at the rain gauge of Montalto Uffugo (in the surroundings of San Benedetto Ullano), the highest Calabrian amounts of mean annual rainfall are recorded.
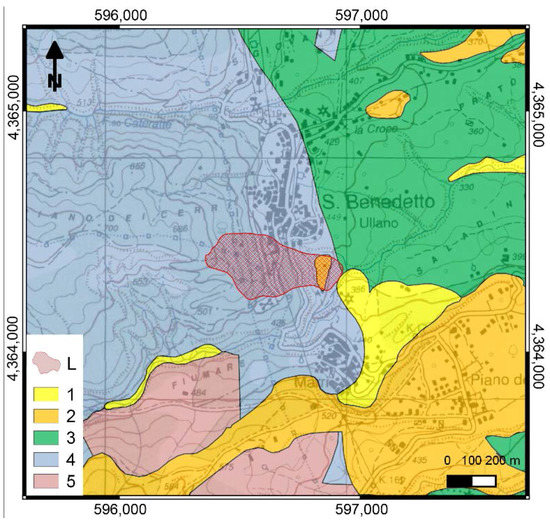
Figure 4.
Lithological sketch of the San Rocco landslide at San Benedetto Ullano. Key: (1) Alluvium, colluvium, and residual soil; (2) conglomerate and sandstone; (3) Clay and clayey flysch; (4) Igneous and medium-high grade metamorphic rock; (5) Argillite and low-grade metamorphic rock. The landslide (L) is marked by a red hatched polygon. Topographic base map after 1:25,000 IGMI sheets; lithological map after [47], Geological map of Calabria (scale 1:25,000), mod.
The San Rocco translational rock slide developed mainly in gneissic rocks at the southern margin of the village, between the historical center and the cemetery [14,51,52]. Between January 2009 and March 2013, a series of 3 major re-activations was observed, with serious damage to the provincial road; the Cemetery and several buildings at the southern margin of the village were also affected by widespread opening of fissures and fractures.
3.1.3. The San Fili—Uncino Landslide
The village of San Fili (Figure 5) is located on the left flank of the Crati graben. In the area, N–S trending normal faults mark the transition between Palaeozoic weathered metamorphic rocks of the Coastal Chain (migmatitic gneiss and biotitic schist), mantled by a late Miocene sedimentary cover of conglomerate, arenite and marly clay, to the West, and Pliocene–Quaternary sediments (sand and clay) of the graben, to the East [47]. The village lies in the intermediate sector between two faults, cut by a NE–SW trending connection fault delimiting Miocene sediments, to the North, from gneissic rocks, to the South.
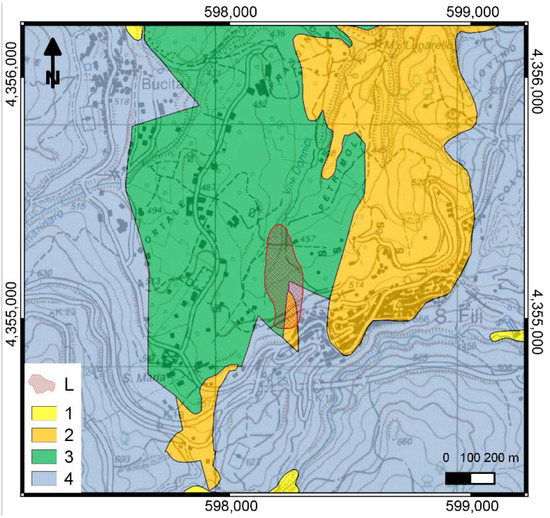
Figure 5.
Lithological sketch of the Uncino landslide at San Fili. Key: (1) Alluvium, colluvium, and residual soil; (2) conglomerate and sandstone; (3) Clay and clayey flysch; (4) Igneous and medium-high grade metamorphic rock. The landslide (L) is marked by a red hatched polygon. Topographic base map after 1:25,000 IGMI sheets; lithological map after [47], Geological map of Calabria (scale 1:25,000), mod.
The Uncino rock slide developed at the western margin of San Fili, involving Miocene sediments (clay and subordinate sandstone) overlaying Palaeozoic metamorphic rocks (gneiss and biotitic schist). In historical time, the slope movements repeatedly affected the village, damaging the railway and the local road network, as well as some buildings: the most ancient known activation dates to the beginning of the twentieth century [53]; from 1960 to 1990, the regional railroad was frequently damaged or even interrupted [54]. Cumulated antecedent rains corresponding to known activations of the Uncino landslide were analyzed by considering the records of the Montalto Uffugo rain gauge [17]. Based on trends of antecedent rains in the 30–180 days before activations, the activation dates to be used for hydrological analyses could be selected.
3.2. Campanian Ccase Studies
The Sorrento Peninsula (Figure 6) is in western Campania, Southern Italy, within the frame of the Neogene Apennine Chain [55]. In the area, Mesozoic limestone mainly crops out, covered by Miocene flysch, Pleistocene volcanic deposits (pyroclastic fall, ignimbrite), and Pleistocene detrital–alluvial deposits [56]. The carbonate bedrock constitutes a monocline, gently dipping towards WNW, mantled by sedimentary and volcanoclastic deposits, with thicknesses ranging from a few decimeters to tens of meters.
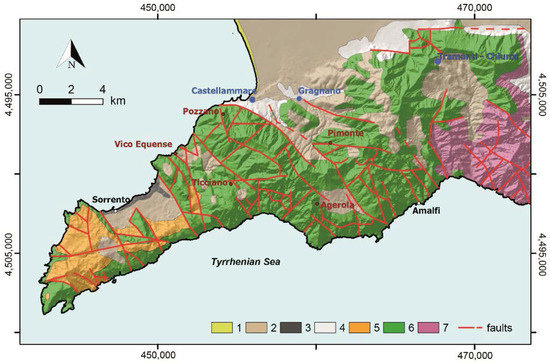
Figure 6.
Lithological sketch of the Sorrento Peninsula. Key: (1) beach deposit (Holocene); (2) pyroclastic fall deposit (late Pleistocene–Holocene); (3) Campanian ignimbrite (late Pleistocene); (4) detrital alluvial deposit (Pleistocene); (5) flysch deposit (Miocene); (6) limestone (Mesozoic); (7) dolomitic limestone (Mesozoic). Red lines mark the main faults; red circles and red labels, the sites affected by shallow landslide activations; blue circles, the rain gauges; white circles, the main localities (after [17], mod.).
Hot, dry summers and moderately cold and rainy winters characterize the study area; its climate is Mediterranean (Csa, according to [40]). Average annual rainfall varies from 900 mm, west of Sorrento, to 1500 mm at Mt. Faito; moving inland to the East, it reaches 1600 mm at Mt. Cerreto and 1700 mm at the Chiunzi pass [57]. On average, annual totals are concentrated on about 95 rainy days. During the driest 6 months (from April to September), only 30% of the annual rainfall is recorded in about 30 rainy days. During the three wettest months (November, October, and December), a similar amount is recorded in about 34 rainy days [58]. In the area, convective rainstorms commonly occur at the beginning of the rainy season (from September to October). In autumn–winter, either high intensity or long duration rainfall are usually recorded, while uniformly distributed rains generally occur in spring. Both at sea level and higher elevations, the southern slopes of the Peninsula are characterized by smaller average annual maxima of daily rainfall with respect to the northern slopes [59]. Severe storms frequently trigger shallow landslides in the volcanoclastic cover of the Peninsula. Landslide sources show a wide range of planforms (i.e., elongated, triangular, grape-like and compound), extensions (from 100 m up to 20,000 m2), and depths (from 0.5 to 4 m). Soil slips usually propagate seaward as either debris flows or avalanches, often increasing their original volume by entraining material along the tracks, and eventually causing casualties and serious damage to urbanized areas and transportation facilities [60,61,62].
In the second half of the 20th century, shallow landslides activated on several occasions nearby Castellammare di Stabia: in Table 3, the major events recorded between Vico Equense and Gragnano are listed, with details on types of events and affected sites. All such events occurred between November and March, a period characterized by a medium to low suction range and included in the rainy season (October to April), according to [63]. Rainfall responsible for landslide occurrences in the Sorrento Peninsula were extracted from the records of the nearest gauges (i.e., Gragnano, Castellammare, and Tramonti-Chiunzi; Figure 6). The trends of antecedent rains look quite different. Based on hydrological consideration, the dates of activation were selected for calibration and validation of the model.
4. Results and Discussion
For each case study, the model was optimized by considering a subset of calibration dates, and then validated against further dates of activation. The calibration and validation periods were defined based on rainfall data availability, seasonality, and quality of information on activation dates (Table 2 and Table 3). More in detail, optimal kernels were obtained in calibration by averaging the best 100 filter functions. Validation was then performed by applying such average kernels to the remaining activation dates (i.e., a temporal validation was performed). The optimal kernels and mobility functions for the considered case studies are shown in Figure 7, Figure 8, Figure 9 and Figure 10. Calibration and validation results are synthetized in Table 4.
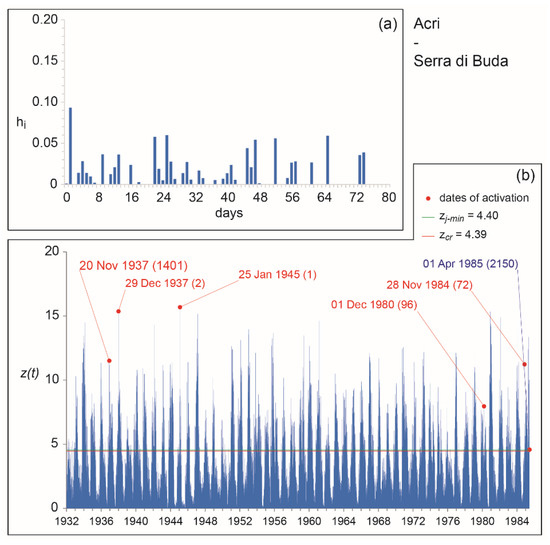
Figure 7.
Acri—Serra di Buda case study: (a) optimal kernel; (b) mobility function obtained by applying the optimal kernel to the entire set of available activation dates (cf. [50]).
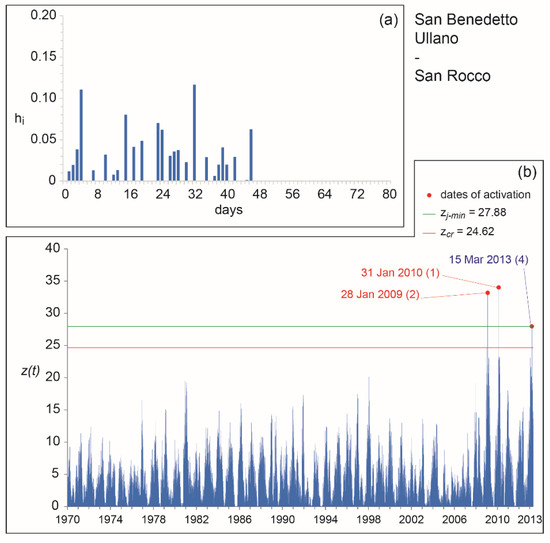
Figure 8.
San Benedetto Ullano—San Rocco case study: (a) optimal kernel; (b) mobility function obtained by applying the optimal kernel to the entire set of available activation dates (cf. [54,64]).
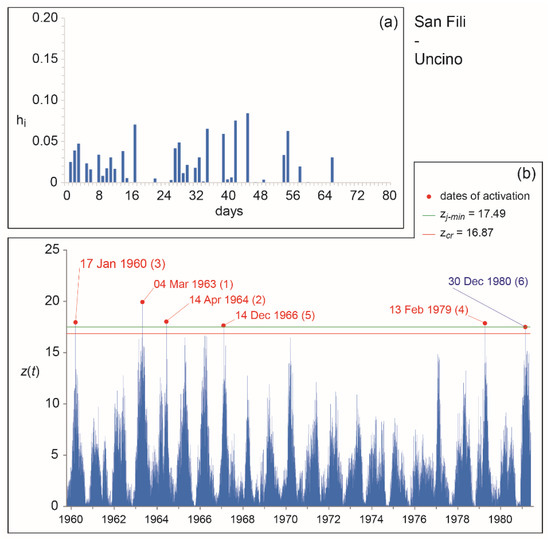
Figure 9.
San Fili—Uncino case study: (a) optimal kernel; (b) mobility function obtained by applying the optimal kernel to the entire set of available activation dates (cf. [17]).
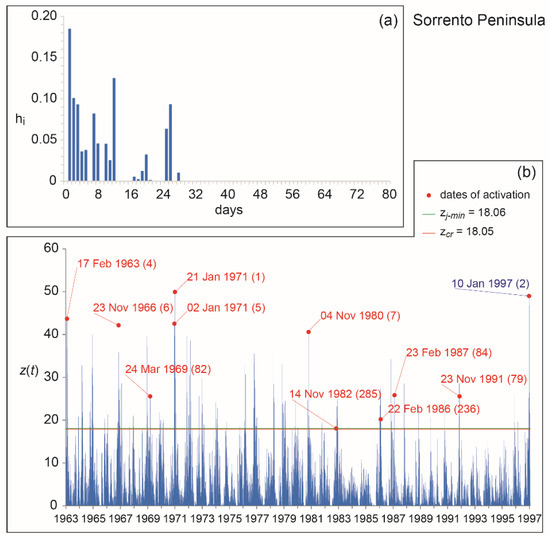
Figure 10.
Sorrento Peninsula case study: (a) optimal kernel; (b) mobility function obtained by applying the optimal kernel to the entire set of available activation dates (cf. [17]).

Table 4.
Model results for the considered case studies. For each case, the following details are listed: landslide type; number of activation dates employed for calibration and validation; base time of the optimal kernel; maximum fitness obtained in calibration and in validation.
The base times of the optimal kernels for the considered case studies are quite consistent with landslide magnitudes, being tb of the Sorrento Peninsula about a half of the Calabrian cases. Base times also reflect permeability and extent of underground water patterns of the drainage basins feeding the landslide sites. In the case of the shallow landslides of the Sorrento Peninsula, shorter base times and higher influence of most recent rainfall can be observed with respect to the Calabrian rock slides, evidencing a faster slope stability response to rainfall as potential triggering factor.
As for the case studies considered in this paper, calibration and validation results show fitness values ranging from 81% to 100 % and from 62% to 100%, respectively. The best model performances were obtained for the case studies of San Fili—Uncino and San Benedetto Ullano—San Rocco, while less satisfactorily results characterize the Sorrento Peninsula and Acri—Serra di Buda cases. It should be noticed that, for the San Rocco landslide, the fitness obtained in validation is affected by a false alarm predicted by the model just the day before the activation of the phenomenon (as known from local archives).
Generally speaking, case studies characterized by fewer activation dates are simpler to model. On the other hand, model performances are known to be hampered by quality or completeness of input data (e.g., missing dates of activation; dates related to other triggering factors; unsuitability of the rain gauge network) [65]. Furthermore, available rain gauges are usually far from the sites of interest, and located at either different elevations or aspects. Uncertainty in rainfall estimation has a strong impact on the identification of the triggering rainfall [66,67]. Still, information regarding activation dates is commonly incomplete or poorly accurate [10]. As a whole, such uncertainties may strongly affect the calibration and the validation of the models.
In this study, the best results obtained were presumably favored by:
- accurate recording of damaging events along the railway track, for the Uncino rock slide;
- accurate monitoring of landslide activations and damaging events at the margin of the village, for the San Rocco rock slide;
- good representativeness of the rainfall series recorded at the Montalto Uffugo rain gauge, for both the Uncino and the San Rocco rock slides.
As for the weakest results, they may be explained by considering the following issues:
- for the Sorrento Peninsula case study, significant heterogeneities in slope materials and differences in extent of shallow landslides reasonably affected model performances. In addition, dates of landslide activation may be missing, especially for soils slips triggered in remote areas. Rainfall events responsible for shallow landslide activations are usually short and spatially limited (e.g., convective storms), and can barely be recorded by the rain gauge network. Consequently, the representativeness of the rain series cannot be guaranteed for such type of meteoric events.
- for the Acri case study, some of the considered activations may refer to secondary portions of the rock slide. For some dates, historical archives are not, in fact, detailed enough to permit an accurate understanding of the mobilized volumes. Consequently, movements affecting only portions of the rock slide—or even other nearby landslides developed in the same Sackung—may be erroneously attributed to the investigated phenomenon.
5. Conclusions and Perspectives
In the present paper, examples of application of GASAKe have been presented, with reference to soil slips and rock slides in Southern Italy. For all cases, both calibration and validation of the model were performed using independent datasets. Obtained results sound either excellent (cf. San Fili—Uncino and San Benedetto Ullano—San Rocco cases) or just promising (Sorrento Peninsula, and Acri—Serra di Buda cases).
For the Uncino and the San Rocco landslides, the activation dates are correctly predicted by the model, evidently thanks to an accurate knowledge of the activation history of the landslide, and a proper hydrological characterization of the site. For such case, GASAKe could be applied to predict the timing of activation of future landslide activations in the same areas. Thanks to kernels obtained in calibration, the model could be usefully employed within early-warning systems for geo-hydrological risk mitigation and Civil Protection purposes, also based on predicted rainfall.
Conversely, for the Serra di Buda and the Sorrento Peninsula cases, weaker model performances appear to be influenced by an inaccurate knowledge of the activation dates and/or rainfall series—as generally occurs with hydrological models. Nevertheless, such results still sound encouraging, provided that quality and completeness of data were improved. For past activations, further investigations may allow to better define the history of landslide mobilizations in the considered areas; rainfall data recorded at the surface by the gauge network may profitably be combined with weather radar prospections (cf. e.g., [68,69]). Moreover, it would be desirable that regional geological and hydrographic services were strengthened to guarantee adequate activities of surveying and monitoring of the geo-hydrological events, by implementing and updating suitable data bases on triggered slope movements (including details such as location, type, type of involved materials, dates of activation, damage). As for the rains, the networks may be improved by adding further gauges and/or radar installations.
It is worth observing that, due to its empirical/hydrological nature, GASAKe needs a representative sample of data for calibration and validation. Such phases are both crucial for properly tuning any prediction model, particularly when it is aimed at being implemented into an early-warning system. In some of the cases analyzed in this paper, the number of available activation dates was not large enough to permit the selection of different sub-samples, thus only one date of activation (i.e., the last) was considered for all validations. Nevertheless, such type of approach can be viewed in terms of an “operative” application of the model in an operational warning system (i.e., used to predict the “next” activation, based on the known history of landslide movements in a given area).
With respect to other empirical/hydrological models, the main advantages implemented in GASAKe are: (i) the automatic calibration of the model by means of genetic algorithms; (ii) the high degrees of freedom of the kernel (in fact, a fixed mathematical function is not required). The adoption of Genetic Algorithms allows for a thorough exploration of the “solution space”, and guarantees that best solutions to any problem can be obtained (following Holland’s Fundamental Theorem [24]). Moreover, the initial shape of the kernel can be suggested from the operator or even left at random. During model iterations, the shape of the kernels evolves (as their length), thanks to genetic operators, and can reach any type of final configuration. The above features are deemed of outmost value, as they allow to limit subjectivity in the application of a model [70].
If analyzed in detail, the kernels obtained with GASAKe may appear difficult to understand in physical terms. Nevertheless, in most real cases, slope instability needs to be explained by a complex interplay of several groundwater paths. These latter commonly result in kernels with quite irregular patterns, and cannot be simulated by simplified analytical functions. According to [71], kernels characterized by complex patterns (and many parameters) are commonly needed to simulate groundwater dynamics. Being characterized by higher complexity, resulting kernels do not necessarily imply greater predictive uncertainties [72,73].
A new release of the model is presently being tested against a set of case studies of different types and extent, selected in diverse geological contexts. Among the improvements, some concern the Genetic Algorithms utilized for the optimization: in particular, a set of selection criteria (roulette, ranking, stochastic tournament, deterministic tournament) will be available shortly, also considering different combinations of ordering criteria (by including the safety margin, the base time, and the first-order momentum to the main fitness of the kernel). Obtained kernels can be post-processed and analyzed in terms of either control points or analytical functions, to allow for deeper hydro-geological ruminations. The final regression of kernels into analytical functions may allow a better understanding of complex groundwater behaviors, and hence landslide responses to antecedent rainfall. Finally, some computational improvements concern smaller requirements of storage capacity and higher execution speed, thanks to parallel optimization that allows for reducing elaborations by ca. 1/50, which will allow improvements in the model performances for an effective implementation in early-warning systems.
Acknowledgments
Authors are grateful to Alessio De Rango, Donato D’Ambrosio, William Spataro, and Rocco Rongo (Department of Mathematics and Informatics, University of Calabria, Italy) for discussions and support in the development and testing phases of the model. Authors acknowledge the Editor and three anonymous Referees for their comments and suggestions that allowed improvements to the original version of the manuscript.
Author Contributions
All the authors contributed to the design and implementation of the research, to the analysis of the results and to the preparation of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guzzetti, F. Landslides fatalities and the evaluation of landslide risk in Italy. Eng. Geol. 2000, 58, 89–107. [Google Scholar] [CrossRef]
- Iovine, G.; Gariano, S.L.; Terranova, O. Alcune riflessioni sull’esposizione al rischio da frane superficiali alla luce dei recenti eventi in Italia meridionale. Geologi Calabria 2009, 10, 4–31. (In Italian) [Google Scholar]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Greco, R.; Comegna, R.; Damiano, E.; Guida, A.; Olivares, L.; Picarelli, L. Hydrological modelling of a slope covered with shallow pyroclastic deposits from field monitoring data. Hydrol. Earth Syst. Sci. 2013, 17, 4001–4013. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Derivation and evaluation of landslide-triggering thresholds by a Monte Carlo approach. Hydrol. Earth Syst. Sci. 2014, 18, 4913–4931. [Google Scholar] [CrossRef]
- Alvioli, M.; Baum, R.L. Parallelization of the TRIGRS model for rainfall-induced landslides using the message passing interface. Environ. Modell. Softw. 2016, 81, 122–135. [Google Scholar] [CrossRef]
- Rossi, M.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Luciani, S.; Ardizzone, F.; Balducci, V.; Bianchi, C.; Cardinali, M.; Fiorucci, F.M. SANF: National warning system for rainfall-induced landslides in Italy. In Landslides and Engineered Slopes: Protecting Society through Improved Understanding; Taylor & Francis Group: London, UK, 2012; pp. 1895–1899. [Google Scholar]
- De Luca, D.; Versace, P. Diversity of rainfall thresholds for early warning of hydro-geological disasters. Adv. Geosci. 2017, 44, 53–60. [Google Scholar] [CrossRef]
- Vennari, C.; Gariano, S.L.; Antronico, L.; Brunetti, M.T.; Iovine, G.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Rainfall thresholds for shallow landslide occurrence in Calabria, southern Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 317–330. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Pisano, L.; Vennari, C.; Vessia, G.; Trabace, M.; Amoruso, G.; Loiacono, P.; Parise, M. Data collection for reconstructing empirical rainfall thresholds for shallow landslides: Challenges and improvements in the Daunia Sub-Apennine (Southern Italy). Rend. Online Soc. Geol. Ital. 2015, 35, 236–239. [Google Scholar] [CrossRef]
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Guzzetti, F. Rainfall thresholds for the possible landslide occurrence in Sicily (Southern Italy) based on the automatic reconstruction of rainfall events. Landslides 2016, 13, 165–172. [Google Scholar] [CrossRef]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F.; Calvello, M. Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Iovine, G.; Iaquinta, P.; Terranova, O. Emergency management of landslide risk during Autumn-Winter 2008/2009 in Calabria (Italy). The example of San Benedetto Ullano. In Proceedings of the 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009; pp. 2686–2693. [Google Scholar]
- Iovine, G.; Petrucci, O.; Rizzo, V.; Tansi, C. The March 7th 2005 Cavallerizzo (Cerzeto) landslide in Calabria-Southern Italy. In Proceeding of the 10th IAEG Congress: Engineering Geology for Tomorrow’s Cities, Nottingham, UK, 6–10 September 2006. [Google Scholar]
- Terranova, O.; Lollino, P.; Gariano, S.L.; Iaquinta, P.; Iovine, G. Un sistema integrato di sorveglianza per la mitigazione del rischio da frana. Geologi Calabria 2010, 11, 6–28. (In Italian) [Google Scholar]
- Terranova, O.; Gariano, S.L.; Iaquinta, P.; Iovine, G. GASAKe: Forecasting landslide activations by a genetic-algorithms-based hydrological model. Geosci. Model Dev. 2015, 8, 1955–1978. [Google Scholar] [CrossRef]
- Terranova, O.; Iaquinta, P.; Gariano, S.L.; Greco, R.; Iovine, G. CMSAKe: A hydrological model to forecasting landslide activations. In Landslide Science and Practice; Springer: Berlin, Germany, 2013; pp. 73–79. [Google Scholar]
- Sirangelo, B.; Versace, P. A real time forecasting for landslides triggered by rainfall. Meccanica 1996, 31, 1–13. [Google Scholar] [CrossRef]
- Capparelli, G.; Versace, P. FLaIR and SUSHI: Two mathematical models for early warning of landslides induced by rainfall. Landslides 2011, 8, 67–79. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Defining rainfall thresholds for early warning of rainfall-triggered landslides: The case of North-East Sicily. In Landslide Science and Practice; Springer: Berlin, Germany, 2013; pp. 257–263. [Google Scholar]
- Capparelli, G.; Giorgio, M.; Greco, R. Shallow landslides risk mitigation by early warning: The Sarno case. In Landslide Science and Practice; Springer: Berlin, Germany, 2013; pp. 767–772. [Google Scholar]
- Greco, R.; Giorgio, M.; Capparelli, G.; Versace, P. Early warning of rainfall-induced landslides based on empirical mobility function predictor. Eng. Geol. 2013, 153, 68–79. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 0262082136. [Google Scholar]
- D’Ambrosio, D.; Spataro, W.; Rongo, R.; Iovine, G. Genetic algorithms, optimization, and evolutionary modeling. In Treatise on Geomorphology. Quantitative Modeling of Geomorphology; Shroder, J., Baas, A.C.W., Eds.; Academic Press: San Diego, CA, USA, 2013; pp. 74–97. [Google Scholar]
- Amodio-Morelli, L.; Bonardi, G.; Colonna, V.; Dietrich, D.; Giunta, G.; Ippolito, F.; Liguori, V.; Lorenzoni, S.; Paglionico, A.; Perrone, V. L’arco calabro-peloritano nell’orogene appenninico-maghrebide. Mem. Soc. Geol. Ital. 1976, 17, 1–60. (In Italian) [Google Scholar]
- Monaco, C.; Tortorici, L. Active faulting in the Calabrian Arc and eastern Sicily. J. Geodyn. 2000, 29, 407–424. [Google Scholar] [CrossRef]
- Tortorici, L.; Monaco, C.; Tansi, C.; Cocina, O. Recent and active tectonics in the Calabrian Arc (southern Italy). Tectonophysics 1995, 243, 37–55. [Google Scholar] [CrossRef]
- Van Dijk, J.P.; Bello, M.; Brancaleoni, G.P.; Cantarella, G.; Costa, V.; Frixa, A.; Golfetto, F.; Merlini, S.; Riva, M.; Torricelli, S.; Toscano, C.; Zerilli, A. A regional structural model for the northern sector of the Calabrian Arc (southern Italy). Tectonophysics 2000, 324, 267–320. [Google Scholar] [CrossRef]
- Tansi, C.; Muto, F.; Critelli, S.; Iovine, G. Neogene-Quaternary strike-slip tectonics in the central Calabrian Arc (southern Italy). J. Geodyn. 2007, 43, 393–414. [Google Scholar] [CrossRef]
- Sorriso-Valvo, G.M. Mass movements and slope evolution in Calabria. Proceedings of 4th International Conference and Field Workshop on Landslides, Tokyo, Japan, 23–31 August 1985; pp. 23–30. [Google Scholar]
- Carrara, A.; Catalano, E.; Sorriso-Valvo, G.M.; Reali, C.; Merenda, L.; Rizzo, V. Landslide morphometry and typology in two zones, Calabria, Italy. Bull. Eng. Geol. Environ. 1977, 16, 8–13. [Google Scholar]
- Carrara, A.; Merenda, L.; Nicoletti, P.G.; Sorriso-Valvo, G.M. Slope instability in Calabria, Italy. In Proceedings of the Polish-Italian Seminar on Superficial Mass Movement in Mountain Regions, Szymbark, Poland, 17–19 May 1979; pp. 47–62. [Google Scholar]
- Crescenzi, E.; Grassi, D.; Iovine, G.; Merenda, L.; Miceli, F.; Sdao, F. Fenomeni di instabilità franosa nei centri abitati calabri: Esempi rappresentativi. Geol. Appl. Hydrogeo. 1996, 31, 203–226. (In Italian) [Google Scholar]
- Iovine, G.; Merenda, L. Nota illustrativa alla “Carta delle frane e della mobilizzazione diastrofica dal 1973 ad oggi nel bacino del Torrente Straface (Alto Jonio; Calabria)”. Geol. Appl. Hydrogeol. 1996, 31, 107–128. (In Italian) [Google Scholar]
- Iovine, G.; Petrucci, O. Effetti sui versanti e nel fondovalle indotti da un evento pluviale eccezionale nel bacino di una fiumara calabra (T. Pagliara). Boll. Soc. Geol. Ital. 1998, 117, 821–840. (In Italian) [Google Scholar]
- Iovine, G.; Parise, M.; Tansi, C. Slope movements and tectonics in North-Eastern Calabria (Southern Italy). In Proceedings of the 7th International Symposium on Landslides (ISL’96): Landslides Glissements de Terrain, Trondheim, 17–21 June 1996; pp. 785–790. [Google Scholar]
- Ferrari, E.; Iovine, G.; Petrucci, O. Evaluating landslide hazard through geomorphologic, hydrologic and historical analyses in north-eastern Calabria (southern Italy). In Proceedings of the EGS Plinius Conference on Mediterranean Storms, Maratea, Italia, 14–16 October 1999; pp. 425–438. [Google Scholar]
- Tansi, C.; Iovine, G.; Folino-Gallo, M. Tettonica attiva e recente; e manifestazioni gravitative profonde; lungo il bordo orientale del graben del Fiume Crati (Calabria settentrionale). Boll. Soc. Geol. Ital. 2005, 124, 563–578. (In Italian) [Google Scholar]
- Köppen, W.P. Climatologia con un Estudio de los Climas de la Tierra; Fondo de Cultura Economica: Ciudad de Mexico City, Mexico, 1948; p. 479. [Google Scholar]
- Terranova, O. Caratteristiche degli eventi pluviometrici a scala giornaliera in Calabria. In Proceeding of the XXIX Convegno di Idraulica e Costruzioni Idrauliche, Trento, Italy, 7–10 September 2004; pp. 343–350. (In Italian). [Google Scholar]
- Terranova, O.; Gariano, S.L. Rainstorms able to induce flash floods in a Mediterranean-climate region (Calabria, southern Italy). Nat. Hazard Earth Syst. Sci. 2014, 14, 2423–2434. [Google Scholar] [CrossRef]
- Ferrari, E.; Terranova, O. Non-parametric detection of trends and change point years in monthly and annual rainfalls. In Proceedings of the 1st Italian-Russian Workshop on New Trend in Hydrology, Rende (CS), Italy, 24–26 September 2002; pp. 177–188. (In Italian). [Google Scholar]
- Terranova, O.; Gariano, S.L. Regional investigation on seasonality of erosivity in the Mediterranean environment. Environ. Earth Sci. 2015, 73, 311–324. [Google Scholar] [CrossRef]
- Iovine, G.; Tansi, C.; Folino-Gallo, M. Strutture da accomodamento tettono-gravitativo nell’evoluzione tardiva dei sistemi di catena: Il caso di studio di Acri (Calabria settentrionale). Boll. Soc. Geol. Ital. 2004, 123, 39–51. (In Italian) [Google Scholar]
- Tansi, C.; Talarico, A.; Iovine, G.; Folino Gallo, M.; Falcone, G. Interpretation of radon anomalies in seismotectonic and tectonic-gravitational setting of the south-eastern Crati Graben (Northern Calabria, Italy). Tectonophysics 2005, 396, 181–193. [Google Scholar] [CrossRef]
- Carta Geologica della Calabria; CASMEZ: Ercolano, Napoli, Italia, 1967. (In Italian)
- Sorriso-Valvo, G.M. 1:250,000 Scale Map of the Large Landslides and of the Deep-Seated Gravitational Slope Deformations of Calabria; Selca: Firenze, Italia, 1996. [Google Scholar]
- Terranova, O.; Antronico, L.; Gullà, G. Landslide triggering scenarios in homogeneous geological contexts: The area surrounding Acri (Calabria, Italy). Geomorphology 2007, 87, 250–267. [Google Scholar] [CrossRef]
- Gariano, S.L.; Terranova, O.G.; Greco, R.; Iaquinta, P.; Iovine, G. Forecasting the timing of activation of rainfall-induced landslides. An application of GA-SAKe to the Acri case study (Calabria, Southern Italy). Geophys. Res. Abstr. 2013, 15, EGU2013-678. [Google Scholar]
- Iovine, G.; Lollino, P.; Gariano, S.L.; Terranova, O. Coupling limit equilibrium analyses and real-time monitoring to refine a landslide surveillance system in Calabria (southern Italy). Nat. Hazard Earth Syst. Sci. 2010, 10, 2341–2354. [Google Scholar] [CrossRef][Green Version]
- Capparelli, G.; Iaquinta, P.; Iovine, G.; Terranova, O.G.; Versace, P. Modelling the rainfall-induced mobilization of a large slope movement in northern Calabria. Nat. Hazards 2012, 61, 247–256. [Google Scholar] [CrossRef]
- Sorriso-Valvo, G.M.; Antronico, L.; Catalano, E.; Gullà, G.; Tansi, C.; Dramis, F.; Ferrucci, F.; Fantucci, R. The Temporal Stability and Activity of Landslides in Europe with Respect to Climatic Change (TESLEC); Final Report; Istituto di Ricerca per la Protezione Idrogeologica (IRPI): Turin, Italy, 1996. [Google Scholar]
- Iovine, G.; De Rango, A.; Gariano, S.L.; Terranova, O. Forecasting landslide activations by means of GA-SAKe. An example of application to three case studies in Calabria (Southern Italy). Geophys. Res. Abstr. 2016, 18, 4645. [Google Scholar]
- Ippolito, F.; D’Argenio, B.; Pescatore, T.; Scandone, P. Structural–stratigraphic units and tectonic framework of Southern Apennines. In Geology of Italy; Squyres, C., Ed.; Earth Sciences Society of the Libyan Arab Republic: Tripoli, Libya, 1975; pp. 317–328. [Google Scholar]
- Di Crescenzo, G.; Santo, A. Analisi morfologica delle frane da scorrimento-colata rapida in depositi piroclastici della Penisola Sorrentina (Campania). Geogr. Fis. Dinam. Quat. 1999, 22, 57–72. (In Italian) [Google Scholar]
- Ducci, D.; Tranfaglia, G. L’impatto dei cambiamenti climatici sulle risorse idriche sotterranee in Campania. Boll Ordine Geol. Campania 2005, 1–4, 13–21. (In Italian) [Google Scholar]
- Servizio Idrografico. Annali Idrologici: Parte I; Compartimento di Napoli, Istituto poligrafico e Zecca dello Stato: Rome, Italy, 1948–1999.
- Rossi, F.; Villani, P. Valutazione Delle Piene in Campania; CNR-GNDCI publications No. 1470; Grafica Metelliana: Cava de’ Tirreni, Italia, 1994. (In Italian) [Google Scholar]
- Mele, R.; Del Prete, S. Lo studio della franosità storica come utile strumento per la valutazione della pericolosità da frane. Un esempio nell’area di Gragnano (Campania). Boll. Soc. Geol. Ital. 1999, 118, 91–111. (In Italian) [Google Scholar]
- Calcaterra, D.; Santo, A. The January 10, 1997 Pozzano landslide, Sorrento Peninsula, Italy. Eng. Geol. 2004, 75, 181–200. [Google Scholar]
- Di Crescenzo, G.; Santo, A. Debris slides-rapid earth flows in the carbonate massifs of the Campania region (Southern Italy): Morphological and morphometric data for evaluating triggering susceptibility. Geomorphology 2005, 66, 255–276. [Google Scholar]
- Cascini, L.; Sorbino, G.; Cuomo, S.; Ferlisi, S. Seasonal effects of rainfall on the shallow pyroclastic deposits of the Campania region (southern Italy). Landslides 2014, 11, 779–792. [Google Scholar] [CrossRef]
- Terranova, O.; Greco, V.R.; Gariano, S.L.; Pascale, S.; Rago, V.; Caloiero, P.; Iovine, G. Monitoring and modelling for landslide risk mitigation and reduction. The case study of San Benedetto Ullano (Northern Calabria-Italy). Geophys. Res. Abstr. 2016, 18, 4708. [Google Scholar]
- Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Influence of uncertain identification of triggering rainfall on the assessment of landslide early warning thresholds. Nat. Hazards Earth Syst. Sci. Discuss. 2017. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Crema, S.; Marchi, L.; Marra, F.; Guzzetti, F.; Borga, M. Impact of uncertainty in rainfall estimation on the identification of rainfall thresholds for debris flow occurrence. Geomorphology 2014, 221, 286–297. [Google Scholar] [CrossRef]
- Marra, F.; Destro, E.; Nikolopoulos, E.I.; Zoccatelli, D.; Creutin, J.D.; Guzzetti, F.; Borga, M. Impact of rainfall spatial aggregation on the identification of debris flow occurrence thresholds. Hydrol. Earth Syst. Sci. 2017, 21, 4525–4532. [Google Scholar] [CrossRef]
- Gabriele, S.; Terranova, O.; Pascale, S.; Rago, V.; Chiaravalloti, F.; Sabatino, P.; Brocca, L.; Laviola, S.; Baldini, L.; Federico, S. RAMSES: A nowcasting system for mitigating geo-hydrological risk along the railway. Geophys. Res. Abstr. 2016, 18, 8462. [Google Scholar]
- Rago, V.; Chiaravalloti, F.; Chiodo, G.; Gabriele, S.; Lupiano, V.; Nicastro, R.; Pellegrino, A.D.; Procopio, A.; Siviglia, S.; Terranova, O.G.; Iovine, G. Geomorphic effects caused by heavy rainfall in southern Calabria (Italy) on 30 October–1 November 2015. J. Maps 2017, 13, 836–843. [Google Scholar] [CrossRef]
- D’Ambrosio, D.; Spataro, W.; Rongo, R.; Iovine, G. Genetic algorithms, optimization, and evolutionary modeling. In Treatise on Geomorphology, Volume 2, Quantitative Modeling of Geomorphology; Baas, A., Ed.; Academic Press: San Diego, CA, USA, 2013; pp. 74–97. [Google Scholar]
- Pinault, J.-L.; Plagnes, V.; Aquilina, L. Inverse modeling of the hydrological and the hydrochemical behavior of hydrosystems: Characterization of karst system functioning. Water Resour. Res. 2001, 37, 2191–2204. [Google Scholar] [CrossRef]
- Fienen, M.N.; Doherty, J.E.; Hunt, R.J.; Reeves, H. Using Prediction Uncertainty Analysis to Design Hydrologic Monitoring Networks: Example Applications from the Great Lakes Water Availability Pilot Project; Scientific Investigations Report 2010-5159, U.S. Geological Survey: Reston, VA, USA, 2010. [Google Scholar]
- Long, A.J. RRAWFLOW: Rainfall-response aquifer and watershed flow model (v1.15). Geosci. Model Dev. 2015, 8, 865–880. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).