A Non-Extensive Statistical Mechanics View on Easter Island Seamounts Volume Distribution
Abstract
:1. Introduction
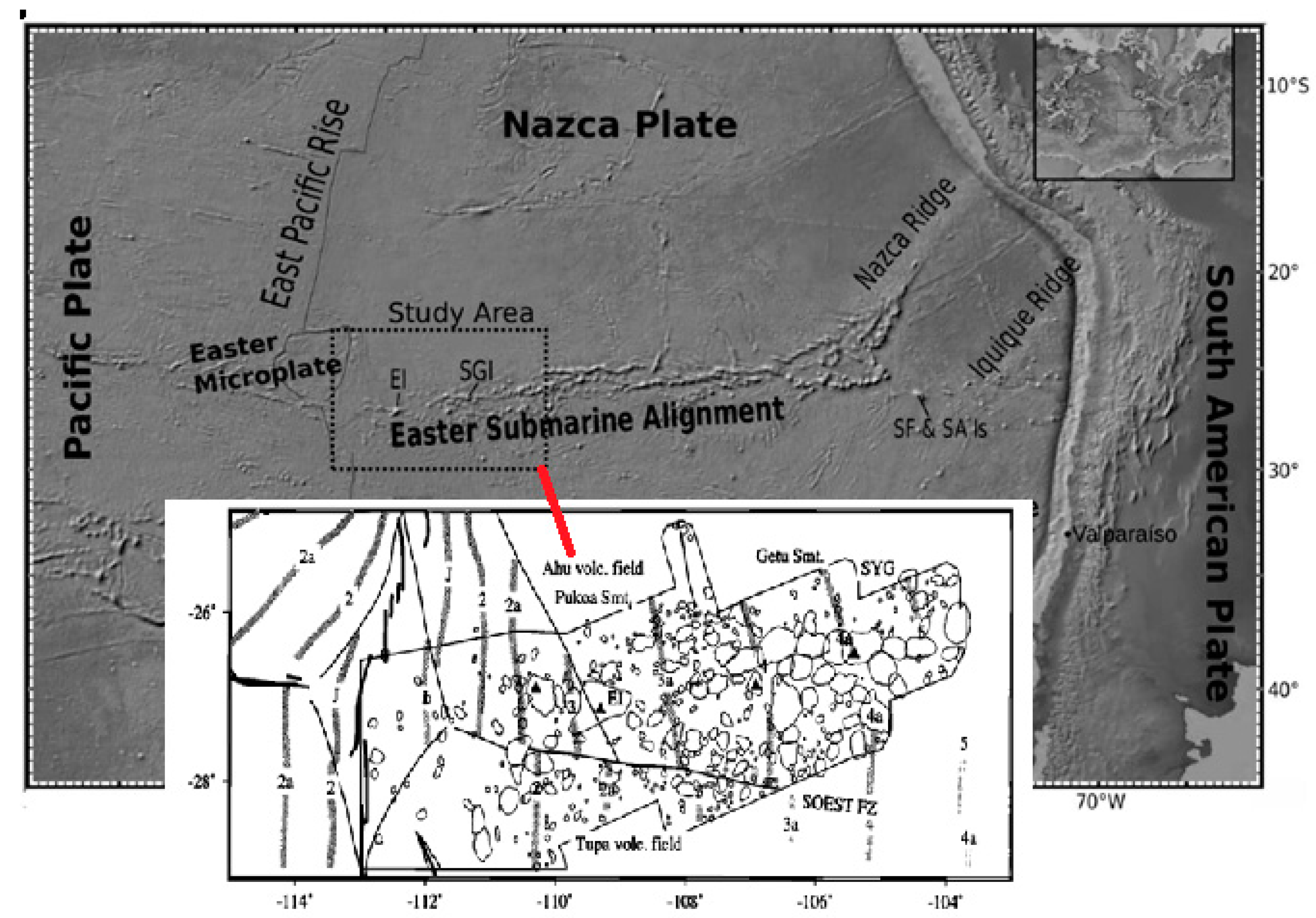
2. Regional Tectonic Setting and Bathymetric Data Used
3. Principles of Non-Extensive Statistical Physics and Estimation of Seamount Frequency-Volume Distribution
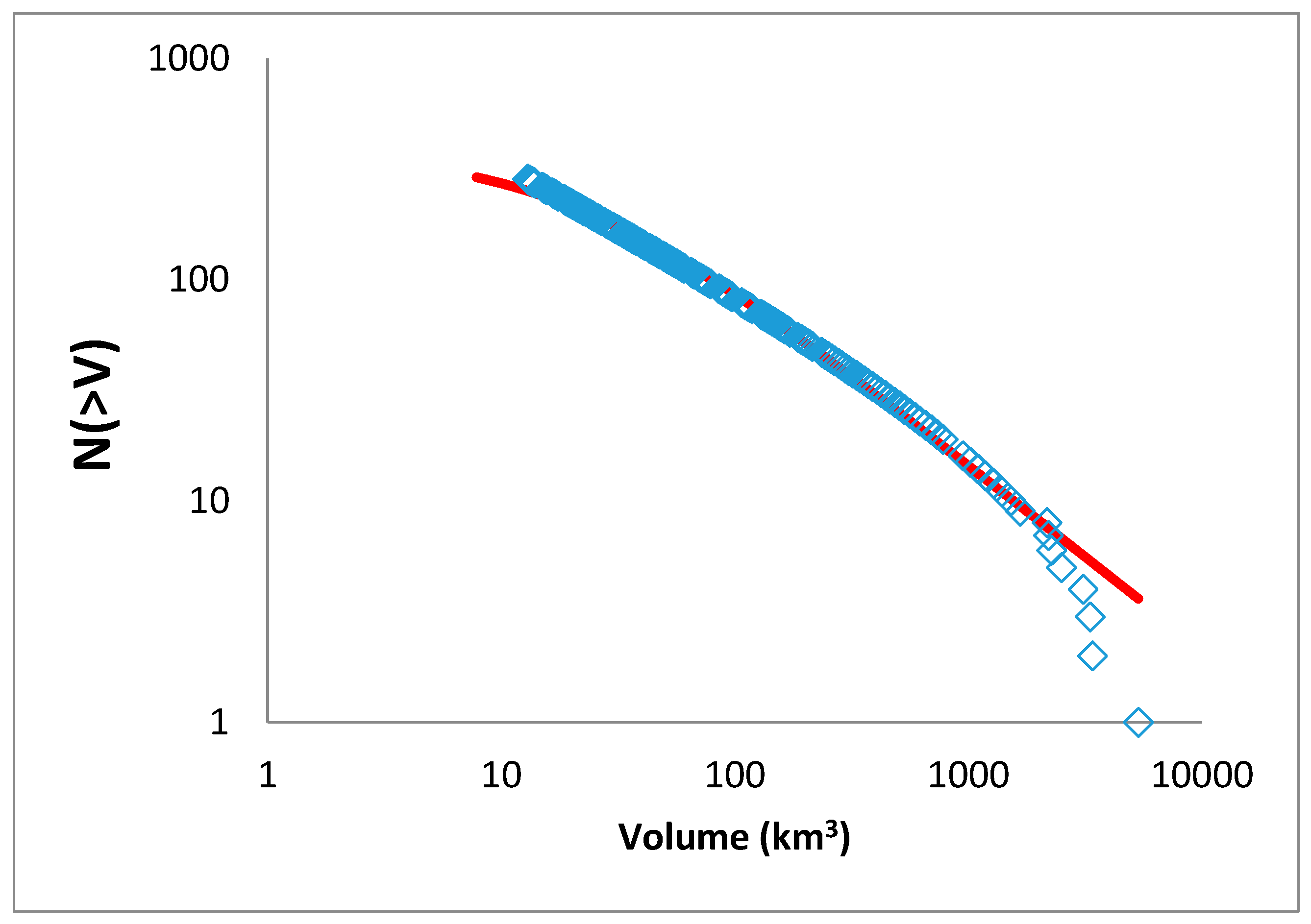
4. ESC Data Analysis and Discussion
5. Conclusions
Conflicts of Interest
References
- Menard, H. Marine Geology of the Pacific; McGraw-Hill: New York, NY, USA, 1964; p. 271. [Google Scholar]
- Holtzman, B.K. Questions on the existence, persistence, and mechanical effects of a very small melt fraction in the asthenosphere. Geochem. Geophys. Geosyst. 2016, 17, 470–484. [Google Scholar] [CrossRef]
- Vogt, P.R. Volcano height and plate thickness. Earth Planet. Sci. Lett. 1974, 23, 337–342. [Google Scholar] [CrossRef]
- Spence, D.A.; Turcotte, D.L. Magma Driven propagation of cracks. J. Geophys. Res. 1985, 90, 575–580. [Google Scholar] [CrossRef]
- Gass, I.G.; Chapman, D.S.; Pollack, H.N.; Thorpe, R.S. Geological and geophysical parameters of mid-plate volcanism. Philos. Trans. R. Soc. Lond. 1978, 288, 581–597. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. How many plumes are there? Earth Planet. Sci. Lett. 1999, 174, 113–124. [Google Scholar] [CrossRef]
- Wessel, P.; Lyons, S. Distribution of large Pacific seamounts from Geosat/ERS-l: Implications for the history of intraplate volcanism. J. Geophys. Res. 1997, 102, 22459–22475. [Google Scholar] [CrossRef]
- Batiza, R. Abundances, distribution and sizes of volcanoes in the Pacific Ocean and implications for the origin of non-hotspot volcanoes. Earth Planet. Sci. Lett. 1982, 60, 195–206. [Google Scholar] [CrossRef]
- Simons, K.; Dixon, J.; Schilling, J.G.; Kingsley, R.; Poreda, R. Volatiles in basaltic glasses from the Easter-Salas y Gómez Seamount Chain and Easter Microplate: Implications for geochemical cycling of volatile elements. Geochem. Geophys. Geosyst. 2002, 3, 1–29. [Google Scholar] [CrossRef]
- Rappaport, Y.; Naar, D.F.; Barton, C.C.; Liu, Z.J.; Hey, R.N. Morphology and distribution of seamounts surrounding Easter Island. J. Geophys. Res. 1997, 102, 24713–24728. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences: Chaos, Fractals, Selforganization and Disorder, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hergarten, S. Self-Organized Criticality in Earth Systems; Springer: New York, NY, USA, 2002. [Google Scholar]
- Turcotte, D.L.; Newman, W.I.; Gabrielov, A. A Statistical Physics Approach to Earthquakes, Geocomplexity and the Physics of Earthquakes; American Geophysical Union: Washington, DC, USA, 2000. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009; pp. 1–382. [Google Scholar]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Michas, G.; Papadakis, G. A description of seismicity based on non-extensive statistical physics: A review. In Earthquakes and Their Impact on Society; Series Title: Springer Natural Hazard; Springer: New York, NY, USA, 2015; ISBN 978-331921753-6. [Google Scholar]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. A Nonextensive Statistical Physics Analysis of the 1995 Kobe, Japan Earthquake. Pure Appl. Geophys. 2014, 172, 1923–1931. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Non-extensive statistical physics applied to heat flow and the earthquake frequency-magnitude distribution in Greece. Phys. A Stat. Mech. Its Appl. 2016, 456, 135–144. [Google Scholar] [CrossRef]
- Christopoulos, S.R.G.; Sarlis, N.V. q-exponential relaxation of the expected avalanche size in the coherent noise model. Phys. A Stat. Mech. Its Appl. 2014, 407, 216–225. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive approach to risk assessment. Nat. Hazards Earth Syst. Sci. 2009, 9, 211–216. [Google Scholar] [CrossRef]
- Vallianatos, F. On the statistical physics of rockfalls: A non-extensive view. Europhys. Lett. 2013, 101, 10007. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Phys. A Stat. Mech. Its Appl. 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field. Phys. A Stat. Mech. Its Appl. 2011, 390, 1773–1778. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions. Europhys. Lett. 2012, 97, 58002. [Google Scholar] [CrossRef]
- Vallianatos, F. Transient Electromagnetic Method in the Keritis basin (Crete, Greece): Evidence of hierarchy in a complex geological structure in view of Tsallis distribution. Ann. Geophys. 2017, 60. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. A non-extensive statistics of the fault-population at the Valles Marineris extensional province, Mars. Tectonophysics 2011, 509, 50–54. [Google Scholar] [CrossRef]
- Vallianatos, F.; Kokinou, E.; Sammonds, P. Non Extensive statistical physics approach to fault population distribution. A case study from the Southern Hellenic Arc (Central Crete). Acta Geophys. 2011, 59, 770–784. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Statistical Mechanics and scaling of fault population with increasing strain in the Corinth Rift. Earth Planet. Sci. Lett. 2015, 431, 150–163. [Google Scholar] [CrossRef]
- Searle, R.C.; Bird, R.T.; Rusby, R.I.; Naar, D.F. The development of two oceanic microplates: Easter and Juan Fernandez microplates, East Pacific Rise. J. Geol. Soc. 1993, 150, 965–976. [Google Scholar] [CrossRef]
- Martínez, F.; Hey, R.N.; Johnson, P. The East ridge system 28.5°–32° S East Pacific Rise: Implications for overlapping spreading center development. Earth Planet. Sci. Lett. 1997, 151, 13–31. [Google Scholar] [CrossRef]
- Naar, D.F.; Hey, R.N. Fast rift propagation along the East Pacific Rise near Easter Island. J. Geophys. Res. 1986, 91, 3425–3438. [Google Scholar] [CrossRef]
- Hey, R.N.; Johnson, P.D.; Martínez, F.; Korenaga, J.; Somers, M.L.; Huggett, Q.J.; LeBas, T.B.; Rusby, R.I.; Naar, D.F. Plate boundary reorganization at a large offset, rapidly propagating rift. Nature 1995, 378, 167–170. [Google Scholar] [CrossRef] [PubMed]
- Bonatti, E.; Harrison, C.G.A.; Fisher, D.E.; Honnorez, J.; Schilling, J.G.; Stipp, J.J.; Zentilli, M. Easter Volcanic Chain (southeast Pacific): A mantle hot line. J. Geophys. Res. 1977, 82, 2457–2478. [Google Scholar] [CrossRef]
- Somers, M.L.; Huggett, D.Q.J. From GLORIA to GLORI-B: New upgrades add swath bathymetry to 20 years old GLORIA reconnaissance sonar images. Sea Technol. 1993, 34, 64–68. [Google Scholar]
- Naar, D.F. Drift Expedition Leg 6 Web Site, 2002. Available online: http://www.soest.hawaii.edu/pwessel/drft06rr/ (accessed on 1 November 2017).
- Tsekouras, G.A.; Tsallis, C. Generalized entropy arising from a distribution of q indices. Phys. Rev. E 2005, 71, 046144. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran-Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Tebbens, S.F.; Burroughs, S.M.; Barton, C.C.; Naar, D.F. Statistical self-similarity of hotspot seamount volumes modeled as self-similar criticality. Geophys. Res. Lett. 2001, 28, 2711–2714. [Google Scholar] [CrossRef]
- Kendal, W.S. Self-organized criticality attributed to a central limit-like convergence effect. Phys. A Stat. Mech. Its Appl. 2015, 421, 141–150. [Google Scholar] [CrossRef]
- Pérez-López, R.; Legrand, D.; Garduño-Monroy, V.H.; Rodríguez-Pascua, M.A.; Giner-Robles, J.L. Scaling laws of the size-distribution of monogenetic volcanoes within the Michoacán-Guanajuato Volcanic Field (Mexico). J. Volcanol. Geotherm. Res. 2011, 201, 65–72. [Google Scholar] [CrossRef]
- Bebbington, M.S. Long-term forecasting of volcanic explosivity. Geophys. J. Int. 2014, 197, 1500–1515. [Google Scholar] [CrossRef]
- Cannavò, F.; Nunnari, G. On a possible unified scaling law for volcanic eruption durations. Sci. Rep. 2016, 6, 22289. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F. A Non-Extensive Statistical Mechanics View on Easter Island Seamounts Volume Distribution. Geosciences 2018, 8, 52. https://doi.org/10.3390/geosciences8020052
Vallianatos F. A Non-Extensive Statistical Mechanics View on Easter Island Seamounts Volume Distribution. Geosciences. 2018; 8(2):52. https://doi.org/10.3390/geosciences8020052
Chicago/Turabian StyleVallianatos, Filippos. 2018. "A Non-Extensive Statistical Mechanics View on Easter Island Seamounts Volume Distribution" Geosciences 8, no. 2: 52. https://doi.org/10.3390/geosciences8020052
APA StyleVallianatos, F. (2018). A Non-Extensive Statistical Mechanics View on Easter Island Seamounts Volume Distribution. Geosciences, 8(2), 52. https://doi.org/10.3390/geosciences8020052



