Abstract
In the volcanic complex processes, inherent long-range interactions exist suggesting that Non-Extensive Statistical mechanics could be used to describe fundamental properties of the system. Based on the non-extensive Tsallis entropy a frequency-volume distribution function is suggested for the Easter Island-Salas y Gomez seamounts chain. Our results demonstrate the applicability of fundamental principles of Tsallis entropy to derive the cumulative distribution of seamounts volumes. The work suggests that the processes responsible for hotspot seamount formation are complex and the cumulative frequency-volume distribution of seamounts in the Easter Island/Salas y Gomez Chain (ESC) are well-described by a q-exponential function. The analysis leads to a non-extensive index q = 1.54 in agreement with that presented in other geodynamic or laboratory scale effects.
1. Introduction
The geodynamic processes of the lithosphere can leave traces on the seafloor. Such traces in the Oceanic intraplate topography are the volcanic islands and seamounts. Seamounts constitute one of the most direct evidence of intraplate volcanism, spread out as they are located between mid-ocean ridges and continental margins. A seamount defined as an isolated elevation on the oceanic seafloor with a circular or elliptical shape with comparatively steep slopes and relatively small summit area [1]. Seamounts are produced by volcanic processes taking place near mid-ocean ridges, mostly of basaltic composition, erupt onto the seafloor and remain there as the lithosphere below them subsides and accumulates sediments with age. Its volcanism arises from reservoirs of fractional melt in the asthenosphere [2], which controls the birth and development of seamounts supplied it with heat or magma. The magma must have enough hydraulic head [3] and latent heat to penetrate the strong oceanic lithosphere without freezing during ascent [4], while the lithosphere must remain over the heat source or magma pool long enough for the volcano to developed [5].
The volume distribution of seamounts as recorded in catalogs define new constraints on the volume of asthenospheric melt available for eruption. Such constraints could help to understand melt production which may constrain the processes responsible for generating asthenospheric melt. The frequency-volume distributions of seamounts (submarine volcanoes) have been used to discern size and number of mantle plumes transporting heat to the base of the lithosphere [6] searching the possibility these distributions to provide insight into magma size distribution through the earth’s crust. Previous work on seamount size distributions used height measurements [7]. Volume is a more meaningful measure than height, as it provides a three-dimensional size measurement used in [8] for North Pacific seamounts.
In this work we focused in the Easter Island and Salas y Gómez Island chain of seamounts or volcanoes [7] called as Easter Seamounts Chain (ESC). The chain runs roughly 3000 km from the East Pacific Rise to the Chile-Peru Trench and it is the result of a long and complex interaction between the ocean lithosphere and underlying mantle, leading in a superfast spreading geoenvironment.
The Easter Seamounts Chain is formed by large seamounts, which can reach heights of more than 3000 m above the adjacent seafloor. This chain crosses the East Pacific Rise at about 27° S [9,10]. The average width of this seamount chain is about 200 km. We examine the cumulative frequency-volume distribution of 383 ESC seamounts over 200 m in height (including two volcanic islands) identified and measured in [10] using Sea Beam and GLORI-B swath bathymetry maps. The base of each seamount was located at the sharp break in slope from the surrounding seafloor and each volume used was estimated by summing the volumes above each pixel in the basal area.
Recently, the statistical properties of Earth and planetary physics processes have attracted a wide interest in the geocomplexity community [11,12]. In this context, Earth processes can be seen as the outcome of the irreversible dynamics of a long-range, interacting, disordered system [13]. The main motivation of the work is starting from complexity theory to establish a volume–frequency distribution of seamounts, using concepts of non-extensive statistical mechanics and to relate our results with that previously published using empirical power law fitting.
To describe the long-range interaction, we can consider the use of statistical physics to understand the collective properties of ESC seamounts. Non-extensive statistical physics (NESP) is the appropriate methodology to describe effects where long-range dependence effects are important. Non-extensive statistical physics (NESP), originally was introduced in [14], recently summarized in [15], while its validity in Earth Sciences is reviewed in [16,17]. NESP is based on Tsallis entropy, a generalization of the classic Boltzmann-Gibbs entropy and has the main advantage that it considers all-length scale correlations among the elements of a system, leading to a very common in Earth Sciences asymptotic power-law behavior. Non-extensivity represents one of the most intriguing characteristics of systems that have experienced long-range spatial correlations [15]. Since they are key components of Earth physics processes, Tsallis statistical mechanics is suitable to explore the distribution of seamounts in ESC. Its applicability in Earth and planetary physics has been demonstrated in a series of recent publications on seismicity [16,17,18,19,20,21], natural hazards [22,23], plate tectonics [24], geomagnetic reversals [25], rock physics [26], applied geophysics [27], and Earth’s and Mars’ fault-length distributions [28,29,30].
This study is unique because it is the first study of its kind to investigate frequency-volume distribution of volcanoes in both a hotspot and superfast seafloor spreading environment, using Tsallis entropy approach. The question whether submarine volcanoes and seamounts are described by non-extensive statistical physics, even at the phenomenological level (i.e., without specifying any underlying model), represents a challenge. This is the problem we address here. Our aim is not to develop a precise model, but rather to present a simple argument of physical plausibility.
2. Regional Tectonic Setting and Bathymetric Data Used
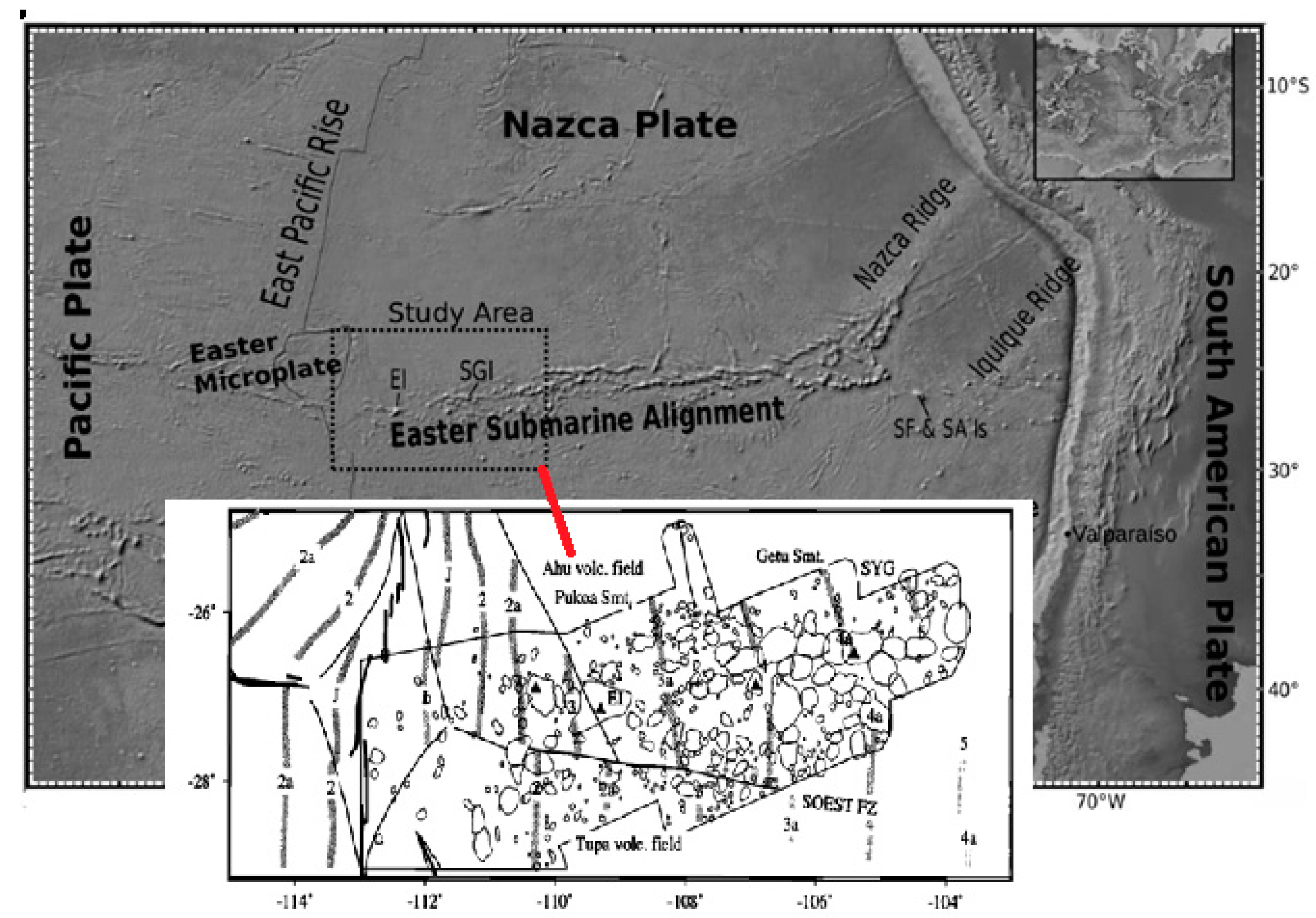
In the broader region tectonic, the Nazca, Easter and Pacific plates converge against each other. The Easter Island and Salas y Gómez Islands are located (Figure 1) on the Nazca Plate [31]. The oceanic crust in the area spreads at rate of 149 km/Myr [32]. The average spreading rate between the Pacific and Nazca plates is close to 150 km/Myr [33,34]. Therefore, this region has the highest rate of crust formation in the Pacific Basin [10].
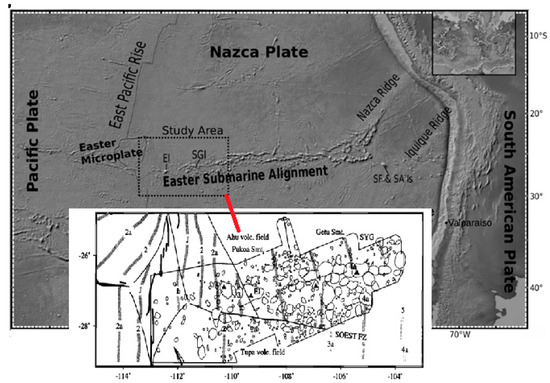
Figure 1.
Map of the topography of the southeastern Pacific created using the Global Topography database. The study area is indicated by the dotted which includes Easter Island (EI) and Salas y Gómez Island (SGI). The Easter Island/Salas y Gomez Chain (ESC) is extracted in the map (modified from [10]).
Given that volcanism found along the Easter Seamount Chain is anomalously young, a formation mechanism is assumed to exist based on the hypothesis of a “hot line” lying on double convection of the mantle and suggested that the chain was been created by the upwelling of part of the magmas brought by these convective cells transverse to the plate movement [35]. A broad chain of seamounts extends from the East Pacific Rise eastward toward South America in the southeastern Pacific in a region influenced by superfast spreading and hotspot volcanism. The seamount population is extracted using the nearly 100% coverage of GLORI-B [36] and Sea Beam 2000 bathymetry data. Analysis of the side-scan and bathymetry data, collected on the GLORIA expedition in early 1993 [37] show that seamounts in the Easter-Salasy Gomez Islands area (25°–29° S, 113°–104° W) have a variability in shape and size (height and volume) distributions [10].
The methodology employed for the determination of the dimensions and shapes of the seamounts was described in [10], where seamounts with heights greater than 200 m, considered. The reason for this criterion is that they acquired bathymetry from the GLORI-B side-scan sonar, which had good lateral coverage, but with less spatial resolution than multi beam bathymetry. A detailed presentation of ESC geotectonic setting along with data collection procedure is given in detail in [31,32,33,34,35].
3. Principles of Non-Extensive Statistical Physics and Estimation of Seamount Frequency-Volume Distribution
Here we recapitulate the principles of non-extensive statistical mechanics since this work is its first application in sub-marine volcano science community. The cornerstone of NESP is the non-additive entropy Sq [14,15], which is non-additive in the sense that it is not proportional to the number of the system’s elements, as in the Boltzmann-Gibbs entropy SBG. The Tsallis entropy Sq reads as:
where kB is Boltzmann’s constant; pi is a set of probabilities; W is the total number of microscopic configurations; and q the entropic index.
This last index is a measure of the non-additivity of the system and for the particular case q = 1, the Boltzmann-Gibbs entropy SBG is obtained; . We note that for q = 1, we obtain the well-known exponential distribution [14]. The cases q > 1 and q < 1 correspond to sub-additivity and super-additivity, respectively. Although Tsallis entropy shares a lot of common properties with the Boltzmann-Gibbs entropy, SBG is additive, whereas Sq (q ≠ 1) is non-additive [15]. According to this property, SBG exhibits only short-range correlations, and the total entropy depends on the size of the systems’ elements. Alternatively, Sq allows all-length scale correlations and seems more adequate for complex dynamical systems, especially when long-range correlations between the elements of the system are present.
In the Tsallis entropy approach, additivity is violated, as defined in classical statistical mechanics and formulated by Boltzmann-Gibbs. For a system composed of two statistically independent subsystems, A and B, the Tsallis entropy satisfies the equation [15]:
The non-additivity is indicated by the last term on the right side of equation above and represents the interaction between the two subsystems A and B. In order to estimate the probability distribution p(V) of seamounts volume V, we maximized the non-extensive entropy under the appropriate constraints, using the Lagrange-multipliers method. The first constraint used refers to the normalization condition that reads as: . Introducing the generalized expectation value (q-expectation value), Vq which is defined as: , where the escort probability is given in [15] as: , the extremization of Sq with the above constraints yields to the probability distribution of p(V) as [18,19,20,21]:
We recall that the Q-exponential function is defined as:
The normalized cumulative number of seamounts can be obtained by integrating the probability density function p(V) as:
where N(>V) is the number of seamounts with volume larger than V. In the latter expression, if we define leads to:
having a typical Q-exponential form.
The above approach is based on the existence of only one complex mechanism described by a unique q- (or Q) parameter. A self–consistent generalization of the aforementioned standard presentation of non-extensive statistical physics, was proposed, based on the idea of using not just one q entropic index but a whole distribution (spectrum) of them [38]. In the spirit of generalized non-extensive statistical mechanics, a generalization of the classical Tsallis entropy Sq, proposed in [38], given by the form , where the function is the inverse of the one, defined as the solution of with [38]. The non-negative, normalized distribution f(z) is called Q-spectral function (QSF) and represents the spectrum of q entropic indices that contribute in the entropic functional. For we lead to the non-extensive entropy defined in [15] while for we recover the BG entropy.
This approach applied in a broad selection of problems (see [15,16,17] and references there in) where crossover statistics appears (i.e., a change of Q parameter to a different one). In this frame a crossover formulation of non-extensive statistical physics introduced where two entropic indices introduced to describe a crossover to another type of behavior at large values of the investigated physical parameter, in our case the seamount volume V. In this case we should have [39]
as a formulation that presents two mechanisms (as described by the exponents R and Q) in view on Tsallis approach.
In the case where 1 ≤ R < Q the solution of (3) is given by
and hence
with where F is the hypergeometric function.
The solution of Equation (3) for βR << βQ defines three regions. The asymptotic behavior of the first region related to the very small values of the volume V and is
where .
In the second region, with the moderate values of V, the asymptotic behavior is expressed by a power law:
where , while the third region describes the range of large values by a power law given as:
Special attention deserves the crossover from anomalous (Q ≠ 1) to normal (R = 1) statistical mechanics, with increasing of the seamount volume V. In this case Equation (3) is modified as
and includes both the normal and anomalous cases in the first and second term, respectively. The analytic solution is
where C is a normalization factor, and βQ and β1 positive parameters that lead to a function p(V) that decreases monotonically with increasing V as presented in [24].
Expanding the exponential term in (6) it can be verified that in the case where the asymptotic behaviour of the probability distributions simplified as a Q-exponential
while
where Vc is the crossover point between the anomalous (Q ≠ 1) to normal (R = 1) statistical mechanics. Equation (7a) lead to the Q-exponential of Equation (2) for a cumulative distribution function .
4. ESC Data Analysis and Discussion
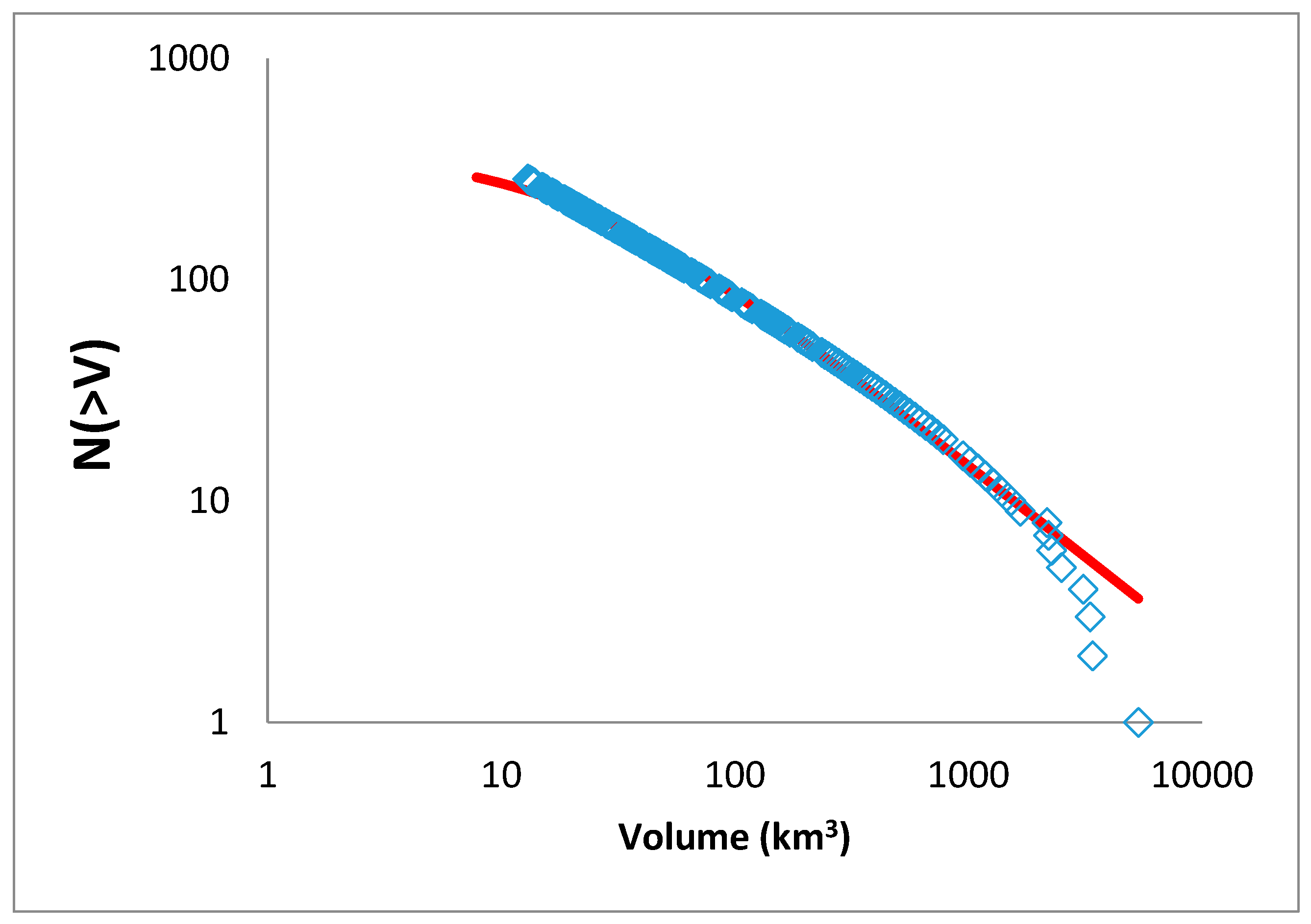
The statistical physics of seamounts and submarine volcanoes involves the evaluation of their volume–frequency distribution. Figure 2 presents the cumulative frequency-volume distribution P(>V) of Easter island seamounts as a function of V, along with the Q-exponential function that describes the data for V < Vc ≈ 1200 km3. The analysis of ESC volume-distribution (see Figure 2) leads to Q = 2.20 with an error of 0.01 which leads to q = 1.54. For V > Vc an exponential function describes the data, in agreement with the asymptotic behavior presented in Equations (7a) and (7b).
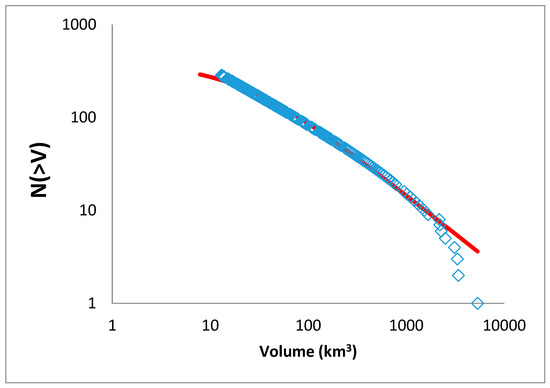
Figure 2.
The cumulative distribution function P(>V) of ESC volume data (diamond blue) as reported in [40], fitted with a Q-exponential (red line) with Q = 2.20 and a geometric factor Vq ≈ 24 km3. The Q = 2.20 leads to q = 1.54.
In the present work, we have applied the ideas of NESP on cumulative volume–frequency distributions P(>V) to the Easter island seamounts. Our data suggest that the use of NESP is proper for the description of the cumulative volume–frequency distributions P(>V) to the Easter island seamounts, using the ideas of Tsallis entropy, leading to a Q-exponential distribution with a Q = 2.20 ± 0.01. We note that this is the first time our method applied to such a field, demonstrating the capability of Tsallis Entropy in a volcanic system. Many empirical distribution functions were already proposed in the past decade, mainly based on empirical and not physically justified approaches [6,7,8,9,10]. Among them exponential and power law distributions have been suggested to statistical characterize seamounts volume distributions, based on the argument that power law results when the seamounts organized in terms of self-organized criticality (SOC) [40]. In the context of SOC, [11,12,41] the cumulative frequency volume distribution of seamounts can be well described by the power-law relation [41,42,43] in a similar way as in other parameters in volcanic systems [44]. The power-law frequency volume distribution is the only distribution that does not have a characteristic scale and can be explained in terms of scale invariance, i.e., fractal statistics [11,12,44].
In the frame of non-extensive statistical mechanics approach for seamount volumes bigger than a given one Vo we lead to a power law description of the distribution function and in such a case the cumulative distribution is with an exponent and in agreement with the power law empirically used to describe the seamount distribution [40] with β = 0.85 close to that presented in [40]. To have an estimation of Vο we select the volume where the power law approximation of P(>V) takes the value P(>V) = 1 leading to . We observe that β < 1 leading to , in agreement with previous published results on earth physics processes in a broad range of scales from laboratory up to geodynamic one [16,17]. For Vq = 24 km3 as estimated for the fitting of Q-exponential (see Figure 2) we lead to Vo = 20 km3 which is similar with the cut off used in [40].
The generic expression of frequency–magnitude distribution given in Equations (7a) and (7b) are straightforward generalization of power and exponential laws, up to now used to describe seamount data. The latter expression could explain the behavior of the distribution in a broad range of volumes possibly leading to new estimations of hazard and risk.
5. Conclusions
In the present work we demonstrate the feasibility of the non-extensive statistics applied to the volume distribution of the ESC volumes. The distribution shows power law features as other distributions on Earth sciences mentioned in [11,16,17,40,41,42,43,44] with q values in the range 1.5 < q < 2. Since Equation (7a) can fit the ESC dataset well with leading to a q = 1.54, we lead to a q-value which is a quantitative measure of the scale of the spatial interactions in ESC seamount system. A q value close to 1 indicates short-ranged spatial correlations. As q increases the physical state (in the sense of statistical physics) becomes much more complex. Note that our results are not based on an empirical guess for the seamount volume distribution but derived from the first principle of non-extensive Tsallis entropy formalism, which is completely universal and has a long range of application [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The physical meaning underlying the non-extensive entropy formalism is that the final geophysical state can be considered as a collection of heating parts which, after division, have the sum of individual entropies larger than the entropy of the initial state. The latter is straightforward from the concept of not additivity since . In addition, since we can assume that ESCconsists of many non-independent subvolumes, the non-additivity index q could be interpreting as an approximate measure of the long-range interacting subsystems.
Summarizing we can state that the use of Tsallis entropy and non-extensive statistics is a proper methodology to describe the ESC frequency-volume distribution. The obtained distribution function incorporates the characteristics of non-extensivity into the cumulative distribution of ESC volumes and explains the observed power law behavior, along with a rollover observed for very small and very large ones, describing the real data very well, indicating that the rollover is a generic property in the frequency distribution at small and large volumes and can be regarded as the manifestation of the physical foundation of non-extensive Tsallis entropy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Menard, H. Marine Geology of the Pacific; McGraw-Hill: New York, NY, USA, 1964; p. 271. [Google Scholar]
- Holtzman, B.K. Questions on the existence, persistence, and mechanical effects of a very small melt fraction in the asthenosphere. Geochem. Geophys. Geosyst. 2016, 17, 470–484. [Google Scholar] [CrossRef]
- Vogt, P.R. Volcano height and plate thickness. Earth Planet. Sci. Lett. 1974, 23, 337–342. [Google Scholar] [CrossRef]
- Spence, D.A.; Turcotte, D.L. Magma Driven propagation of cracks. J. Geophys. Res. 1985, 90, 575–580. [Google Scholar] [CrossRef]
- Gass, I.G.; Chapman, D.S.; Pollack, H.N.; Thorpe, R.S. Geological and geophysical parameters of mid-plate volcanism. Philos. Trans. R. Soc. Lond. 1978, 288, 581–597. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. How many plumes are there? Earth Planet. Sci. Lett. 1999, 174, 113–124. [Google Scholar] [CrossRef]
- Wessel, P.; Lyons, S. Distribution of large Pacific seamounts from Geosat/ERS-l: Implications for the history of intraplate volcanism. J. Geophys. Res. 1997, 102, 22459–22475. [Google Scholar] [CrossRef]
- Batiza, R. Abundances, distribution and sizes of volcanoes in the Pacific Ocean and implications for the origin of non-hotspot volcanoes. Earth Planet. Sci. Lett. 1982, 60, 195–206. [Google Scholar] [CrossRef]
- Simons, K.; Dixon, J.; Schilling, J.G.; Kingsley, R.; Poreda, R. Volatiles in basaltic glasses from the Easter-Salas y Gómez Seamount Chain and Easter Microplate: Implications for geochemical cycling of volatile elements. Geochem. Geophys. Geosyst. 2002, 3, 1–29. [Google Scholar] [CrossRef]
- Rappaport, Y.; Naar, D.F.; Barton, C.C.; Liu, Z.J.; Hey, R.N. Morphology and distribution of seamounts surrounding Easter Island. J. Geophys. Res. 1997, 102, 24713–24728. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences: Chaos, Fractals, Selforganization and Disorder, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hergarten, S. Self-Organized Criticality in Earth Systems; Springer: New York, NY, USA, 2002. [Google Scholar]
- Turcotte, D.L.; Newman, W.I.; Gabrielov, A. A Statistical Physics Approach to Earthquakes, Geocomplexity and the Physics of Earthquakes; American Geophysical Union: Washington, DC, USA, 2000. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics—Approaching a Complex World; Springer: New York, NY, USA, 2009; pp. 1–382. [Google Scholar]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Michas, G.; Papadakis, G. A description of seismicity based on non-extensive statistical physics: A review. In Earthquakes and Their Impact on Society; Series Title: Springer Natural Hazard; Springer: New York, NY, USA, 2015; ISBN 978-331921753-6. [Google Scholar]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. A Nonextensive Statistical Physics Analysis of the 1995 Kobe, Japan Earthquake. Pure Appl. Geophys. 2014, 172, 1923–1931. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Non-extensive statistical physics applied to heat flow and the earthquake frequency-magnitude distribution in Greece. Phys. A Stat. Mech. Its Appl. 2016, 456, 135–144. [Google Scholar] [CrossRef]
- Christopoulos, S.R.G.; Sarlis, N.V. q-exponential relaxation of the expected avalanche size in the coherent noise model. Phys. A Stat. Mech. Its Appl. 2014, 407, 216–225. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive approach to risk assessment. Nat. Hazards Earth Syst. Sci. 2009, 9, 211–216. [Google Scholar] [CrossRef]
- Vallianatos, F. On the statistical physics of rockfalls: A non-extensive view. Europhys. Lett. 2013, 101, 10007. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Phys. A Stat. Mech. Its Appl. 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field. Phys. A Stat. Mech. Its Appl. 2011, 390, 1773–1778. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behavior of fracture in triaxially deformed Etna basalt using acoustic emissions. Europhys. Lett. 2012, 97, 58002. [Google Scholar] [CrossRef]
- Vallianatos, F. Transient Electromagnetic Method in the Keritis basin (Crete, Greece): Evidence of hierarchy in a complex geological structure in view of Tsallis distribution. Ann. Geophys. 2017, 60. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. A non-extensive statistics of the fault-population at the Valles Marineris extensional province, Mars. Tectonophysics 2011, 509, 50–54. [Google Scholar] [CrossRef]
- Vallianatos, F.; Kokinou, E.; Sammonds, P. Non Extensive statistical physics approach to fault population distribution. A case study from the Southern Hellenic Arc (Central Crete). Acta Geophys. 2011, 59, 770–784. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Statistical Mechanics and scaling of fault population with increasing strain in the Corinth Rift. Earth Planet. Sci. Lett. 2015, 431, 150–163. [Google Scholar] [CrossRef]
- Searle, R.C.; Bird, R.T.; Rusby, R.I.; Naar, D.F. The development of two oceanic microplates: Easter and Juan Fernandez microplates, East Pacific Rise. J. Geol. Soc. 1993, 150, 965–976. [Google Scholar] [CrossRef]
- Martínez, F.; Hey, R.N.; Johnson, P. The East ridge system 28.5°–32° S East Pacific Rise: Implications for overlapping spreading center development. Earth Planet. Sci. Lett. 1997, 151, 13–31. [Google Scholar] [CrossRef]
- Naar, D.F.; Hey, R.N. Fast rift propagation along the East Pacific Rise near Easter Island. J. Geophys. Res. 1986, 91, 3425–3438. [Google Scholar] [CrossRef]
- Hey, R.N.; Johnson, P.D.; Martínez, F.; Korenaga, J.; Somers, M.L.; Huggett, Q.J.; LeBas, T.B.; Rusby, R.I.; Naar, D.F. Plate boundary reorganization at a large offset, rapidly propagating rift. Nature 1995, 378, 167–170. [Google Scholar] [CrossRef] [PubMed]
- Bonatti, E.; Harrison, C.G.A.; Fisher, D.E.; Honnorez, J.; Schilling, J.G.; Stipp, J.J.; Zentilli, M. Easter Volcanic Chain (southeast Pacific): A mantle hot line. J. Geophys. Res. 1977, 82, 2457–2478. [Google Scholar] [CrossRef]
- Somers, M.L.; Huggett, D.Q.J. From GLORIA to GLORI-B: New upgrades add swath bathymetry to 20 years old GLORIA reconnaissance sonar images. Sea Technol. 1993, 34, 64–68. [Google Scholar]
- Naar, D.F. Drift Expedition Leg 6 Web Site, 2002. Available online: http://www.soest.hawaii.edu/pwessel/drft06rr/ (accessed on 1 November 2017).
- Tsekouras, G.A.; Tsallis, C. Generalized entropy arising from a distribution of q indices. Phys. Rev. E 2005, 71, 046144. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran-Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Tebbens, S.F.; Burroughs, S.M.; Barton, C.C.; Naar, D.F. Statistical self-similarity of hotspot seamount volumes modeled as self-similar criticality. Geophys. Res. Lett. 2001, 28, 2711–2714. [Google Scholar] [CrossRef]
- Kendal, W.S. Self-organized criticality attributed to a central limit-like convergence effect. Phys. A Stat. Mech. Its Appl. 2015, 421, 141–150. [Google Scholar] [CrossRef]
- Pérez-López, R.; Legrand, D.; Garduño-Monroy, V.H.; Rodríguez-Pascua, M.A.; Giner-Robles, J.L. Scaling laws of the size-distribution of monogenetic volcanoes within the Michoacán-Guanajuato Volcanic Field (Mexico). J. Volcanol. Geotherm. Res. 2011, 201, 65–72. [Google Scholar] [CrossRef]
- Bebbington, M.S. Long-term forecasting of volcanic explosivity. Geophys. J. Int. 2014, 197, 1500–1515. [Google Scholar] [CrossRef]
- Cannavò, F.; Nunnari, G. On a possible unified scaling law for volcanic eruption durations. Sci. Rep. 2016, 6, 22289. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).