Time-Space Characterization of Wellbore-Cement Alteration by CO2-Rich Brine
Abstract
1. Introduction
2. Materials and Methods
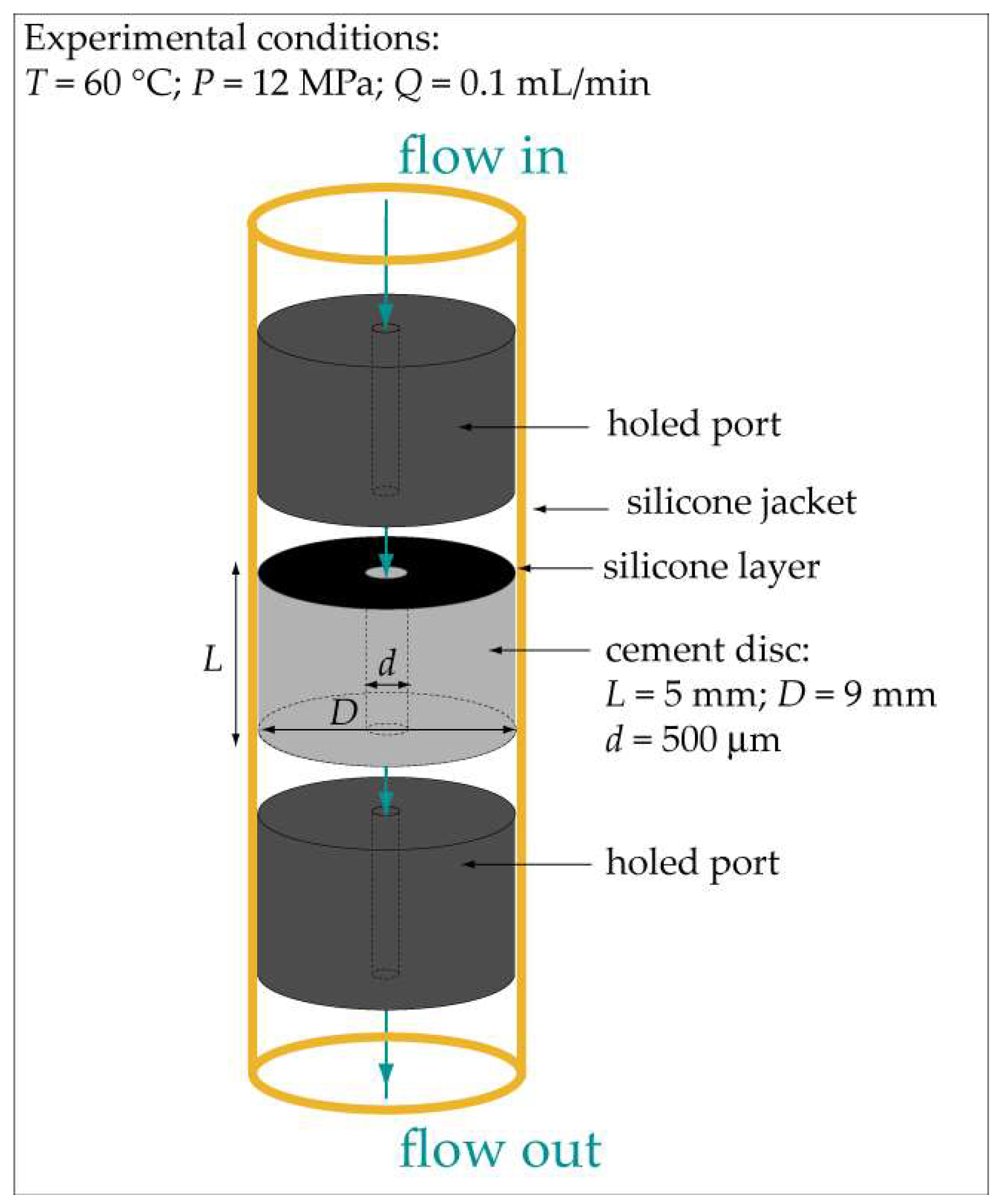
2.1. Preparation of the Cement Discs
2.2. Experimental Equipment and Procedure
3. Results
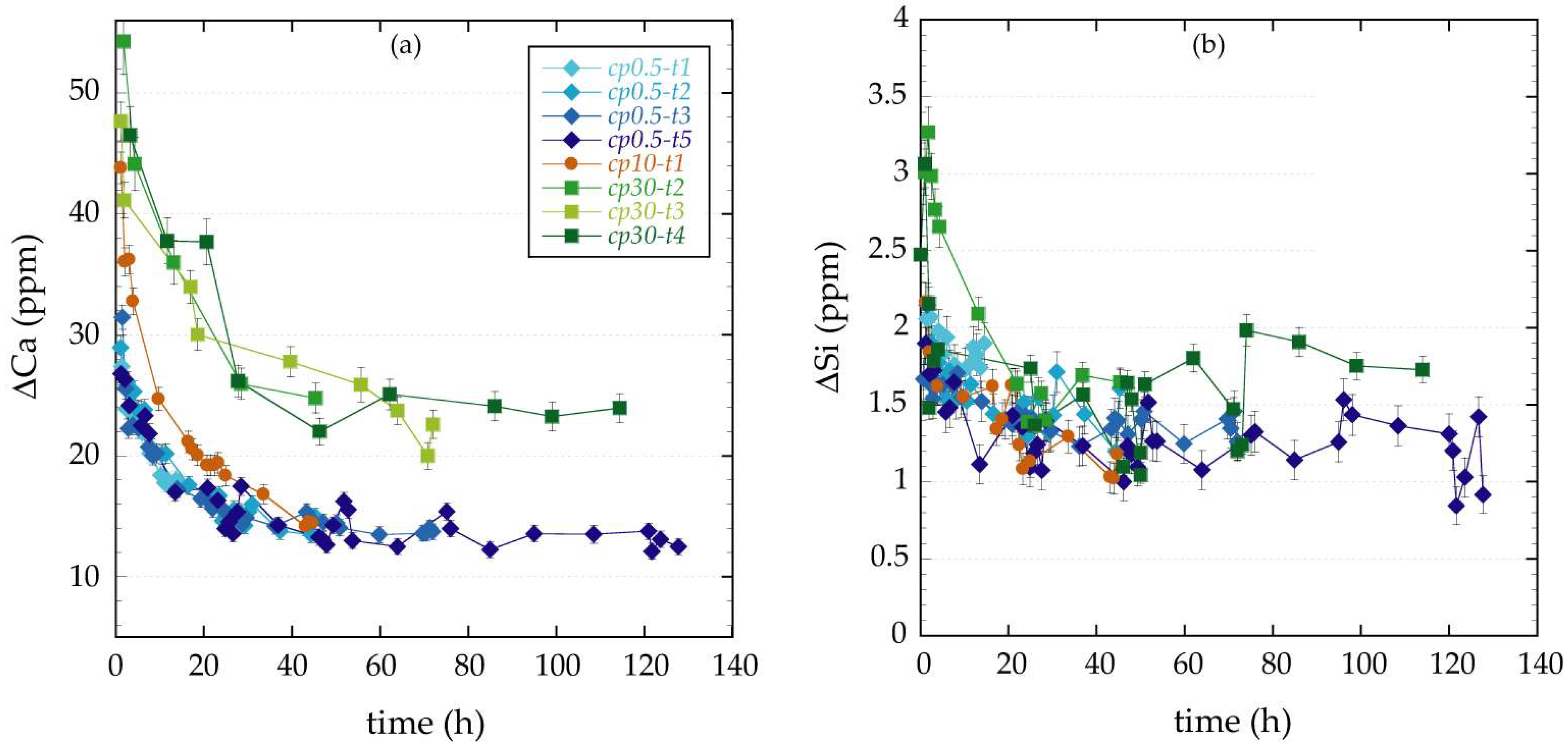
3.1. Changes in Fluid Chemistry
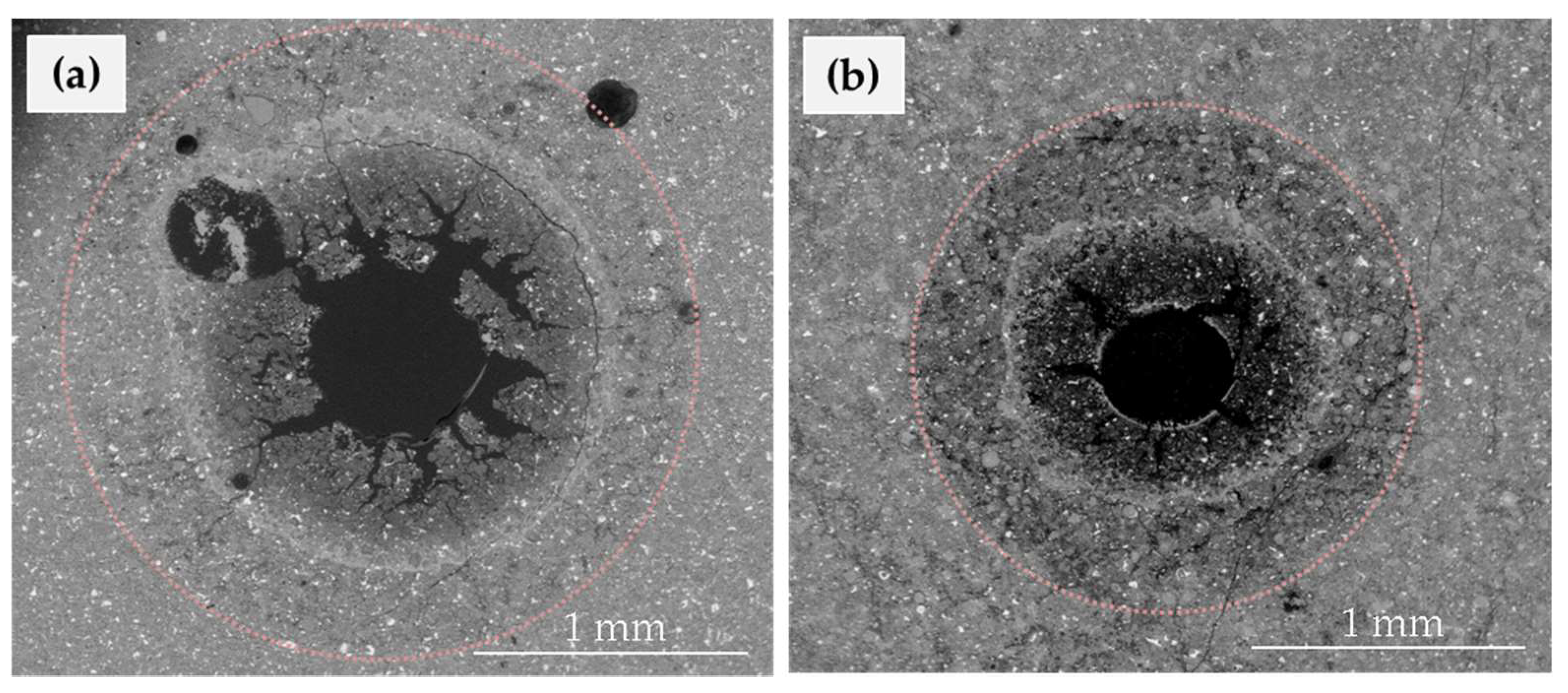
3.2. Characterization of Cement Alteration
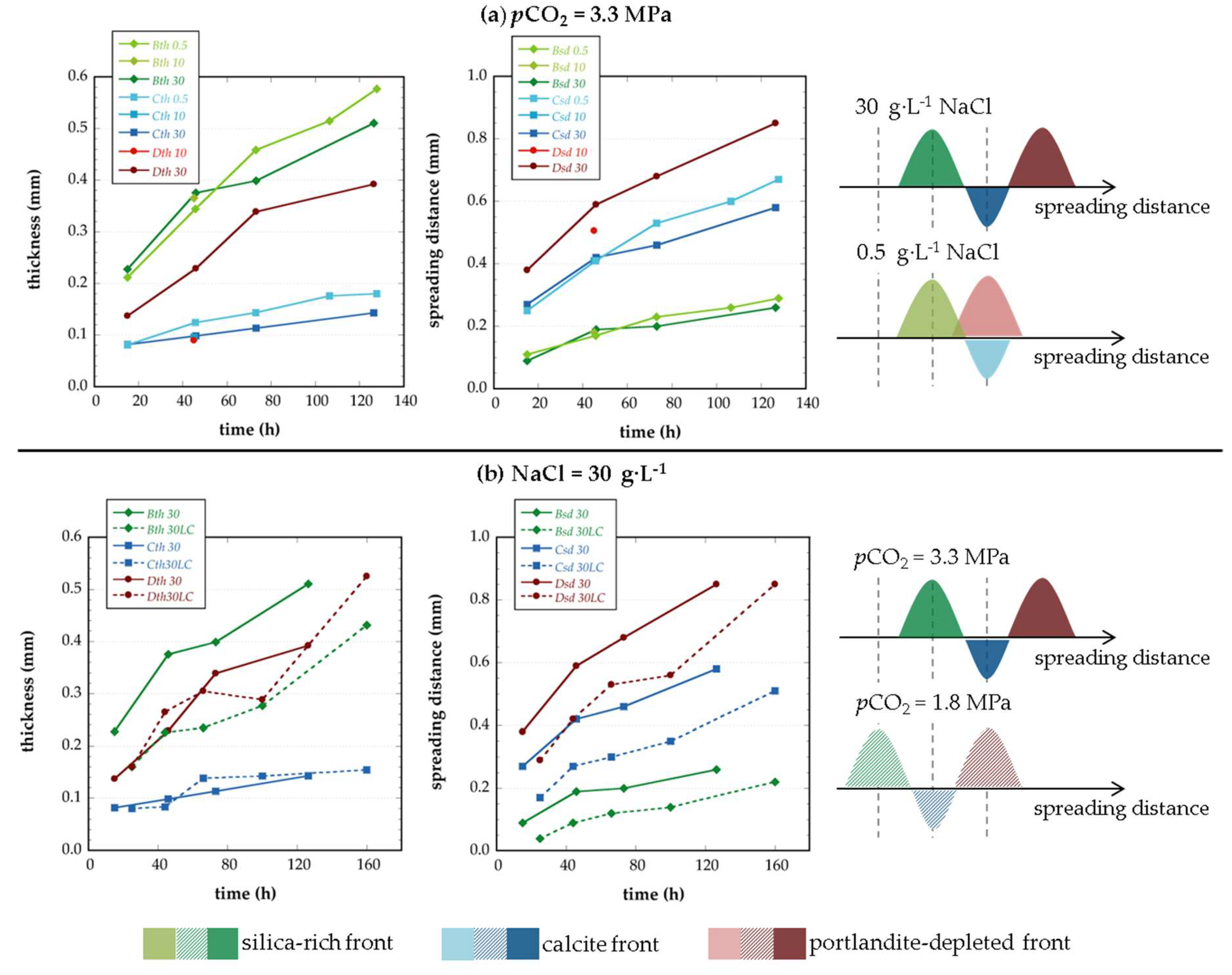
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watson, T.L.; Bachu, S. Evaluation of the potential for gas and CO2 leakage along wellbores. SPE Drill. Complet. 2009, 24, 115–126. [Google Scholar] [CrossRef]
- Ravi, K.; Bosma, M.; Gastebled, O. Safe and economic gas wells through cement design for life of the well. Soc. Pet. Eng. 2002. [Google Scholar] [CrossRef]
- Shipton, Z.K.; Evans, J.P.; Dockrill, B.; Heath, J.; Williams, A.; Kirchner, D.; Kolesar, P.T. Natural leaking CO2-charged systems as analogs for failed geologic storage reservoirs. In Carbon Dioxide Capture for Storage in Deep Geological Formations—Results from CO2 Capture Project, 1st ed.; Thomas, D., Benson, S.M., Eds.; Elsevier Science: Berkeley, CA, USA, 2005; Volume 2, pp. 699–712. ISBN 9780080457482. [Google Scholar]
- Oldenburg, C.M.; Bryant, S.L.; Nicot, J.P. Certification framework based on effective trapping for geologic carbon sequestration. Int. J. Greenh. Gas Control 2009, 3, 444–457. [Google Scholar] [CrossRef]
- Celia, M.A.; Bachu, S.; Nordbotten, J.M.; Gasda, S.E.; Dahle, H.K. Quantitative Estimation of CO2 Leakage from Geological Storage: Analytical Models, Numerical Models, and Data Needs. In Greenhouse Gas Control Technologies, 1st ed.; Wilson, M., Rubin, E.S., Keith, D.W., Gilboy, C.F., Morris, T., Thambimuthu, K., Gale, J., Eds.; Elsevier Ltd.: Oxford, UK, 2005; Volume 1, pp. 663–671. ISBN 9780080539737. [Google Scholar]
- Carroll, S.; Carey, J.W.; Dzombak, D.; Huerta, N.J.; Li, L.; Richard, T.; Um, W.; Walsh, S.D.C.; Zhang, L. review: Role of chemistry, mechanics, and transport on well integrity in CO2 storage environments. Int. J. Greenh. Gas Control 2016, 49, 149–160. [Google Scholar] [CrossRef]
- Wigand, M.; Kaszuba, J.P.; Carey, J.W.; Hollis, W.K. Geochemical effects of CO2 sequestration on fractured wellbore cement at the cement/caprock interface. Chem. Geol. 2009, 265, 122–133. [Google Scholar] [CrossRef]
- Walsh, S.D.; Du Frane, W.L.; Mason, H.E.; Carroll, S.A. Permeability of wellbore-cement fractures following degradation by carbonate brine. Rock Mech. Rock Eng. 2013, 46, 455–464. [Google Scholar] [CrossRef]
- Cheshire, M.C.; Stack, A.G.; Carey, J.W.; Anovitz, L.M.; Prisk, T.R.; Ilavsky, J. Wellbore cement porosity evolution in response to mineral alteration during CO2 flooding. Environ. Sci. Technol. 2016, 51, 692–698. [Google Scholar] [CrossRef] [PubMed]
- Crow, W.; Williams, D.B.; Carey, J.W.; Celia, M.; Gasda, S. Wellbore integrity analysis of a natural CO2 producer. Energy Proc. 2009, 1, 3561–3569. [Google Scholar] [CrossRef]
- Carey, J.W.; Svec, R.; Grigg, R.; Lichtner, P.C.; Zhang, J.; Crow, W. Wellbore integrity and CO2-rich brine flow along the casing-cement microannulus. Energy Proc. 2009, 1, 3609–3615. [Google Scholar] [CrossRef]
- Mason, H.E.; Du Frane, W.L.; Walsh, S.D.; Dai, Z.; Charnvanichborikarn, S.; Carroll, S.A. Chemical and mechanical properties of wellbore cement altered by CO2-rich brine using a multianalytical approach. Environ. Sci. Technol. 2013, 47, 1745–1752. [Google Scholar] [CrossRef] [PubMed]
- Scherer, G.W.; Kutchko, B.; Thaulow, N.; Duguid, A.; Mook, B. Characterization of cement from a well at Teapot Dome Oil Field: Implications for geological sequestration. Int. J. Greenh. Gas Control 2011, 5, 115–124. [Google Scholar] [CrossRef]
- Kutchko, B.G.; Strazisar, B.R.; Lowry, G.V.; Dzombak, D.A.; Thaulow, N. Rate of CO2 attack on hydrated class H well cement under geologic sequestration conditions. Environ. Sci. Technol. 2008, 42, 6237–6242. [Google Scholar] [CrossRef] [PubMed]
- Abdoulghafour, H.; Luquot, L.; Gouze, P. Characterization of the mechanisms controlling the permeability changes of fractured cements flowed through by CO2-rich brine. Environ. Sci. Technol. 2013, 47, 10332–10338. [Google Scholar] [CrossRef] [PubMed]
- Luquot, L.; Abdoulghafour, H.; Gouze, P. Hydro-dynamically controlled alteration of fractured Portland cements flowed by CO2-rich brine. Int. J. Greenh. Gas Control 2013, 16, 167–179. [Google Scholar] [CrossRef]
- Kutchko, B.G.; Strazisar, B.R.; Dzombak, D.A.; Lowry, G.V.; Thaulow, N. Degradation of well cement by CO2 under geologic sequestration conditions. Environ. Sci. Technol. 2007, 41, 4787–4792. [Google Scholar] [CrossRef] [PubMed]
- Rimmelé, G.; Barlet-Gouédard, V.; Porcherie, O.; Goffé, B.; Brunet, F. Heterogeneous porosity distribution in Portland cement exposed to CO2-rich fluids. Cem. Concr. Res. 2008, 38, 1038–1048. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, D.B. Experimental assessment of brine and/or CO2 leakage through well cement at reservoir conditions. Int. J. Greenh. Gas Control 2009, 3, 494–501. [Google Scholar] [CrossRef]
- Liteanu, E.; Spiers, C.J. Fracture healing and transport properties of wellbore cement in the presence of supercritical CO2. Chem. Geol. 2010, 281, 195–210. [Google Scholar] [CrossRef]
- Jobard, E.; Sterpenich, J.; Pironon, J.; Corvisier, J.; Randi, A. Experimental modelling of the caprock/cement interface behavior under CO2 storage conditions: Effect of water and supercritical CO2 from a cathodoluminescence study. Geosciences 2018, 8, 185. [Google Scholar] [CrossRef]
- Kutchko, B.G.; Strazisar, B.R.; Huerta, N.; Lowry, G.V.; Dzombak, D.A.; Thaulow, N. CO2 reaction with hydrated class H well cement under geologic sequestration conditions: Effects of flyash admixtures. Environ. Sci. Technol. 2009, 43, 3947–3952. [Google Scholar] [CrossRef]
- Abdoulghafour, H.; Gouze, P.; Luquot, L.; Leprovost, R. Characterization and modeling of the alteration of fractured class-G Protland cement during flow of CO2-rich brine. Int. J. Greenh. Gas Control 2016, 48, 155–170. [Google Scholar] [CrossRef]
- Huet, B.M.; Prevost, J.H.; Scherer, G.W. Quantitative reactive transport modeling of Portland cement in CO2-saturated water. Int. J. Greenh. Gas Control 2010, 4, 561–574. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey Techniques and Methods: Reston, VA, USA, 2013; Chapter A43.
- Noiriel, C.; Gouze, P.; Madé, B. 3D analysis of geometry and flow changes in a limestone fracture during dissolution. J. Hydrol. 2013, 486, 211–223. [Google Scholar] [CrossRef]
- Luquot, L.; Gouze, P. Experimental determination of porosity and permeability changes induced by injection of CO2 into carbonate reservoir rocks. Chem. Geol. 2009, 265, 148–159. [Google Scholar] [CrossRef]
- Trapote-Barreira, A.; Cama, J.; Soler, J.M.; Lothenbach, B. Degradation of mortar under advective flow: Column experiments and reactive transport modeling. Cem. Concr. Res. 2016, 81, 81–93. [Google Scholar] [CrossRef]
- Barrante, J.R. Applied Mathematics for Physical Chemistry; Prentice-Hall: Upper Saddle River, NJ, USA, 1974. [Google Scholar]
- Atkinson, A.; Hearne, J.A.; Knights, C.F. Aqueous chemistry and thermodynamics modelling of CaO-SiO2-H2O gels. J. Chem. Soc. Dalton Trans. 1989, 2371–2379. [Google Scholar] [CrossRef]
- Taylor, H.F.W. Cement Chemistry, 2nd ed.; Thomas Telford Services Ltd.: London, UK, 1997. [Google Scholar]
- Soler, J.M. Thermodynamic Description of the Solubility of C-S-H Gels in Hydrated Portland Cement. Literature Review; Posiva: Eurajoki, Finland, 2007. [Google Scholar]
- Bullard, J.W.; Enjolras, E.; George, W.L.; Satterfield, S.G.; Terrill, J.E. A parallel reaction transport model applied to cement hydration and microstructure development. Model. Simul. Mater. Sci. Eng. 2010, 18, 025007. [Google Scholar] [CrossRef]
- Trapote-Barreira, A.; Cama, J.; Soler, J.M. Dissolution kinetics of C-S-H gel: Flow-through experiments. Phys. Chem. Earth 2014, 70–71, 17–31. [Google Scholar] [CrossRef]
- Mason, H.E.; Walsh, S.D.C.; DuFrane, W.L.; Carroll, S.A. Determination of diffusion profiles in altered wellbore cement using X-ray computed tomography methods. Environ. Sci. Technol. 2014, 48, 7094–7100. [Google Scholar] [CrossRef]
- Zhang, Y.; Dawe, R. The kinetics of calcite precipitation from a high salinity water. Appl. Geochem. 1998, 13, 177–184. [Google Scholar] [CrossRef]
- Zuddas, P.; Mucci, A. Kinetics of calcite precipitation from seawater: II. The influence of the ionic strength. Geochim. Cosmochim. Acta 1998, 5, 757–766. [Google Scholar] [CrossRef]
- Galan, I.; Glasser, F.; Andrade, C.; Baza, D. Dissolution of portlandite. In Proceedings of the 13th International Congress on the Chemistry on Cement, Madrid, Spain, 3–8 July 2011; pp. 1–7. [Google Scholar]


| Experiment Label | Elapsed Time | Input Solution | pCO2 | Chemical Analysis | SEM Analysis |
|---|---|---|---|---|---|
| (h) | (g∙L−1 NaCl) | (MPa) | |||
| First Set of Experiments | |||||
| cp0.5-t1 | 15.0 | 0.5 | 3.3 | OK | OK |
| cp0.5-t2 | 45.7 | 0.5 | 3.3 | OK | OK |
| cp0.5-t3 | 73.0 | 0.5 | 3.3 | OK | OK |
| cp0.5-t4 | 106.4 | 0.5 | 3.3 | - | OK |
| cp0.5-t5 | 127.8 | 0.5 | 3.3 | OK | OK |
| cp10-t1 | 45.0 | 10 | 3.3 | OK | OK |
| cp30-t1 | 15.0 | 30 | 3.3 | - | OK |
| cp30-t2 | 45.9 | 30 | 3.3 | OK | OK |
| cp30-t3 | 73.1 | 30 | 3.3 | OK | OK |
| cp30-t4 | 126.4 | 30 | 3.3 | OK | OK |
| Second Set of Experiments | |||||
| cp30LC-t1 | 25.1 | 30 | 1.8 | - | OK |
| cp30LC-t2 | 44.2 | 30 | 1.8 | - | OK |
| cp30LC-t3 | 66.3 | 30 | 1.8 | - | OK |
| cp30LC-t4 | 100.5 | 30 | 1.8 | - | OK |
| cp30LC-t5 | 160.5 | 30 | 1.8 | - | OK |
| Input Solution | |||||
|---|---|---|---|---|---|
| Set of Experiments | First Set | Second Set | |||
| NaCl | g∙L−1 | 0.5 | 10 | 30 | |
| (a) T = 60 °C, P = 12 MPa | |||||
| pH | 8.02 | 7.68 | 7.64 | 7.77 | |
| I | 0.01 | 0.18 | 0.53 | 0.52 | |
| Na | ppm | 204.5 | 3977.3 | 12,226.1 | 11,604.4 |
| Cl | ppm | 326.3 | 6119.2 | 18,786.5 | 17,933.1 |
| Ca | ppm | 17.6 | 21.3 | ||
| Mg | ppm | 7.3 | - | ||
| K | ppm | 0.4 | - | ||
| Si | ppm | 3.8 | - | ||
| S(6) | ppm | 0.7 | - | ||
| N(5) | ppm | 0.7 | - | ||
| (b) T = 60 °C, P = 12 MPa + CO2 | |||||
| pH | 3.68 | 3.77 | 3.95 | 3.42 | |
| CO2 | mol∙L−1 | 0.44 | 0.23 | ||
| pCO2 | MPa | 3.31 | 1.81 | ||
| SI-CH | −16.47 | −16.61 | −16.39 | −17.34 | |
| SI-CSH | −23.42 | −23.61 | −23.21 | −39.22 | |
| Reaction Layers | ||||||
|---|---|---|---|---|---|---|
| Experiment Label | B | C | D | |||
| Silica-rich | Calcite | Portlandite-depleted | ||||
| Bth | Bsd | Cth | Csd | Dth | Dsd | |
| (mm) | ||||||
| First Set of Experiments | ||||||
| cp0.5-t1 | 0.21 | 0.11 | 0.08 | 0.25 | - | - |
| cp0.5-t2 | 0.34 | 0.17 | 0.12 | 0.41 | - | - |
| cp0.5-t3 | 0.46 | 0.23 | 0.14 | 0.53 | - | - |
| cp0.5-t4 | 0.51 | 0.26 | 0.18 | 0.60 | - | - |
| cp0.5-t5 | 0.58 | 0.29 | 0.18 | 0.67 | - | - |
| cp10-t1 | 0.37 | 0.18 | 0.10 | 0.41 | 0.09 | 0.51 |
| cp30-t1 | 0.23 | 0.09 | 0.08 | 0.27 | 0.14 | 0.38 |
| cp30-t2 | 0.38 | 0.19 | 0.10 | 0.42 | 0.23 | 0.59 |
| cp30-t3 | 0.40 | 0.20 | 0.11 | 0.46 | 0.34 | 0.68 |
| cp30-t4 | 0.51 | 0.26 | 0.14 | 0.58 | 0.39 | 0.85 |
| Second Set of Experiments | ||||||
| cp30LC-t1 | 0.16 | 0.04 | 0.08 | 0.17 | 0.16 | 0.29 |
| cp30LC-t2 | 0.23 | 0.09 | 0.08 | 0.27 | 0.26 | 0.42 |
| cp30LC-t3 | 0.23 | 0.12 | 0.14 | 0.30 | 0.31 | 0.53 |
| cp30LC-t4 | 0.28 | 0.14 | 0.14 | 0.35 | 0.29 | 0.56 |
| cp30LC-t5 | 0.43 | 0.22 | 0.15 | 0.51 | 0.53 | 0.85 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Rios, M.; Gouze, P. Time-Space Characterization of Wellbore-Cement Alteration by CO2-Rich Brine. Geosciences 2018, 8, 490. https://doi.org/10.3390/geosciences8120490
Garcia-Rios M, Gouze P. Time-Space Characterization of Wellbore-Cement Alteration by CO2-Rich Brine. Geosciences. 2018; 8(12):490. https://doi.org/10.3390/geosciences8120490
Chicago/Turabian StyleGarcia-Rios, Maria, and Philippe Gouze. 2018. "Time-Space Characterization of Wellbore-Cement Alteration by CO2-Rich Brine" Geosciences 8, no. 12: 490. https://doi.org/10.3390/geosciences8120490
APA StyleGarcia-Rios, M., & Gouze, P. (2018). Time-Space Characterization of Wellbore-Cement Alteration by CO2-Rich Brine. Geosciences, 8(12), 490. https://doi.org/10.3390/geosciences8120490




