Coastal Flood Modeling Challenges in Defended Urban Backshores
Abstract
1. Introduction
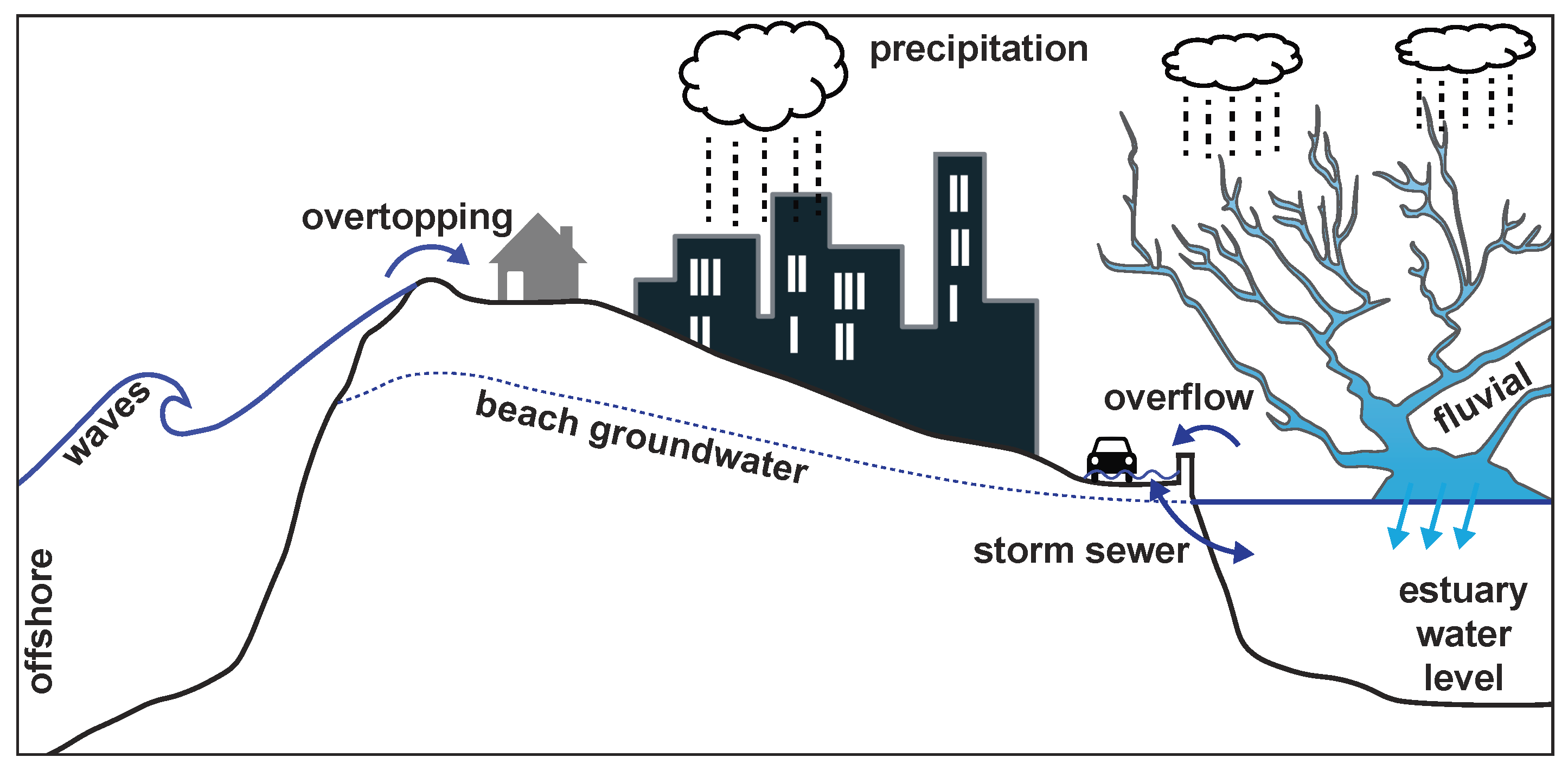
2. State of Knowledge
2.1. Overland Flow Modeling
Shallow Water Equations
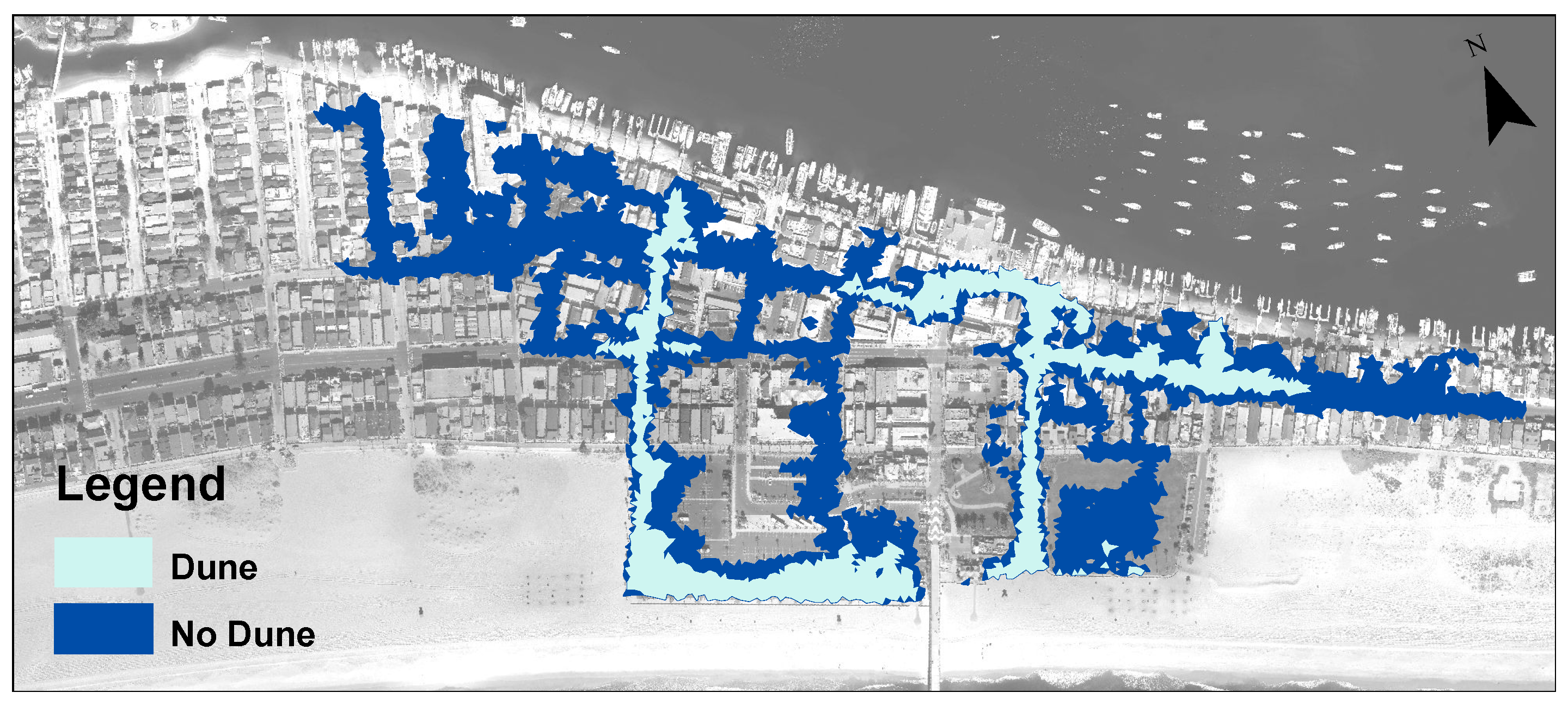
2.2. Terrain and Infrastructure
2.3. Boundary Conditions
2.3.1. Water Level
2.3.2. Hydrologic Impacts
2.3.3. Wave Overtopping
3. Wave Overtopping Models
3.1. Empirical Wave Overtopping Models
3.2. Numerical Wave Overtopping Models
3.2.1. Navier–Stokes Equations
3.2.2. Boussinesq
3.2.3. Nonlinear Shallow Water Equations
3.3. Overtopping Flood Validation
4. Flood Model Evaluation
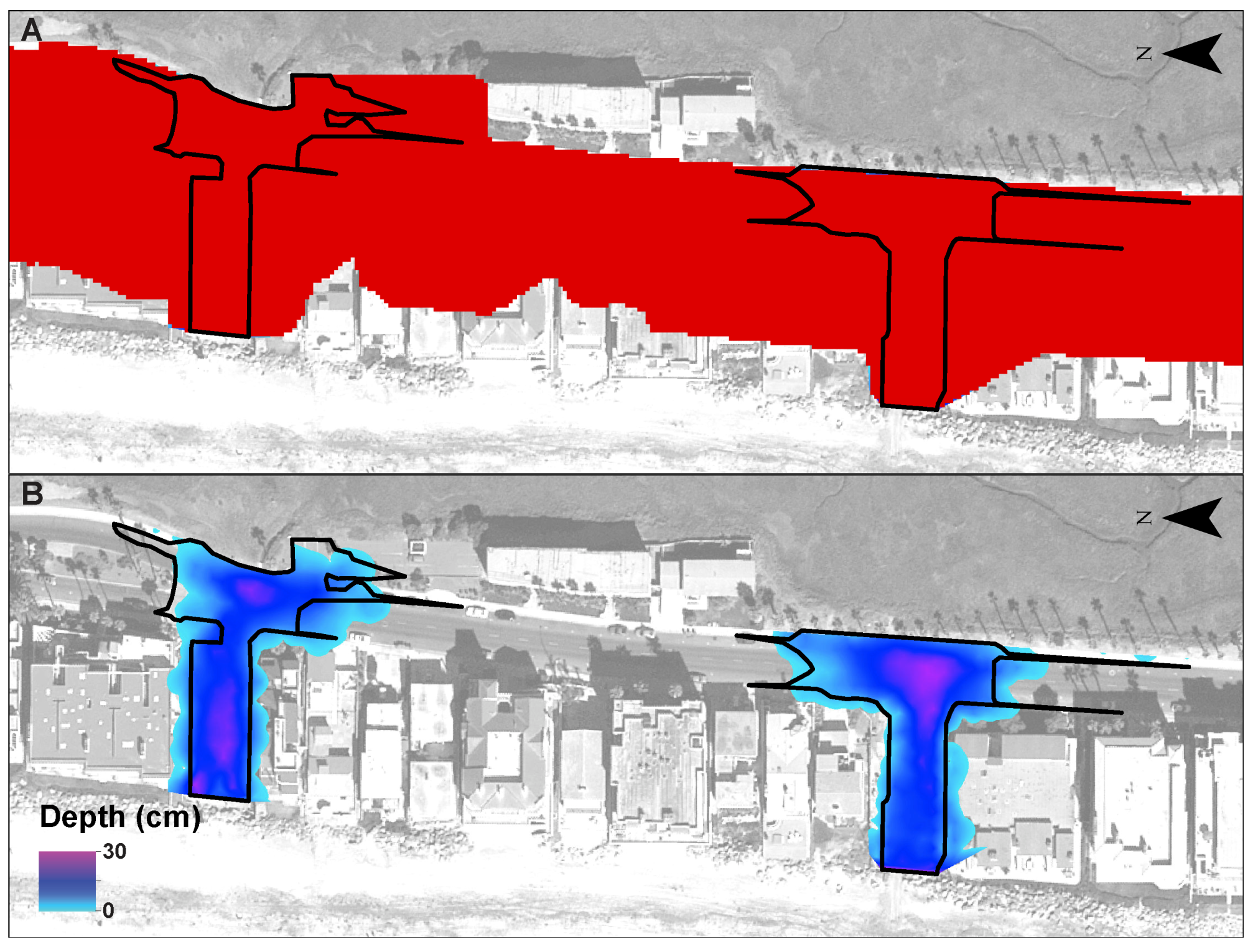
4.1. Flood Extent
4.2. Hydrodynamic Validation
5. Multi-Pathway Flooding
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| FEMA | Federal Emergency Management Agency |
| DEM | Digital Elevation Model |
| DSM | Digital Surface Model |
| DTM | Digital Terrain Model |
| RTK | Real Time Kinematic |
| TAW | Technical Advisory Committee for Water Retaining Structures |
| NLSW | NonLinear Shallow Water |
| RANS | Raynolds Averaged Navier Stokes |
| LES | Large Eddy Simulation |
| SPH | Smooth Particly Hydrodynamics |
| GLM | Generalized Lagrangian Mean |
References
- Nicholls, R.J. Planning for the impacts of sea level rise. Oceanography 2011, 24, 144–157. [Google Scholar] [CrossRef]
- Merkens, J.L.; Reimann, L.; Hinkel, J.; Vafeidis, A.T. Gridded population projections for the coastal zone under the Shared Socioeconomic Pathways. Glob. Planet. Chang. 2016, 145, 57–66. [Google Scholar] [CrossRef]
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.S.; Nunn, P.; et al. Sea level change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Chang; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1137–1216. [Google Scholar]
- Hansen, J.; Sato, M.; Hearty, P.; Ruedy, R.; Kelley, M.; Masson-Delmotte, V.; Russell, G.; Tselioudis, G.; Cao, J.; Rignot, E.; et al. Ice melt, sea level rise and superstorms: Evidence from paleoclimate data, climate modeling, and modern observations that 2∘C global warming is highly dangerous. Atmos. Chem. Phys. Dis. 2015, 16, 3761–3862. [Google Scholar] [CrossRef]
- DeConto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Carson, M.; Köhl, A.; Stammer, D.; Slangen, A.B.A.; Katsman, C.A.; van de Wal, R.S.W.; Church, J.; White, N. Coastal sea level changes, observed and projected during the 20th and 21st century. Clim. Chang. 2016, 134, 269–281. [Google Scholar] [CrossRef]
- Hunter, J. A simple technique for estimating an allowance for uncertain sea-level rise. Clim. Chang. 2012, 113, 239–252. [Google Scholar] [CrossRef]
- Sweet, W.V.; Park, J. From the extreme to the mean: Acceleration and tipping points of coastal inundation from sea level rise. Earth’s Future 2014, 2, 579–600. [Google Scholar] [CrossRef]
- Fewtrell, T.; Bates, P.D.; Horritt, M.; Hunter, N. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Process. Int. J. 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Ntelekos, A.A.; Oppenheimer, M.; Smith, J.A.; Miller, A.J. Urbanization, climate change and flood policy in the United States. Clim. Chang. 2010, 103, 597–616. [Google Scholar] [CrossRef]
- Hanson, S.; Nicholls, R.; Ranger, N.; Hallegatte, S.; Corfee-Morlot, J.; Herweijer, C.; Chateau, J. A global ranking of port cities with high exposure to climate extremes. Clim. Chang. 2011, 104, 89–111. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802. [Google Scholar] [CrossRef]
- Hinkel, J.; Lincke, D.; Vafeidis, A.T.; Perrette, M.; Nicholls, R.J.; Tol, R.S.; Marzeion, B.; Fettweis, X.; Ionescu, C.; Levermann, A. Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc. Natl. Acad. Sci. USA 2014, 111, 3292–3297. [Google Scholar] [CrossRef] [PubMed]
- Prime, T.; Brown, J.M.; Plater, A.J. Physical and economic impacts of sea-level rise and low probability flooding events on coastal communities. PLoS ONE 2015, 10, e0117030. [Google Scholar] [CrossRef] [PubMed]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093. [Google Scholar] [CrossRef]
- Divoky, D.; Battalio, R.; Dean, B.; Collins, I.; Hatheway, D.; Scheffner, N. Storm Meteorology. FEMA Coastal Flood Hazard Analysis and Mapping Guidelines, Focused Study Report; Technical Report, FEMA Tech. Rep; Federal Emergency Management Agency: Washington, DC, USA, 2005.
- Glahn, B.; Taylor, A.; Kurkowski, N.; Shaffer, W.A. The role of the SLOSH model in National Weather Service storm surge forecasting. Natl. Weather Digest 2009, 33, 3–14. [Google Scholar]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef]
- Gallien, T.; Schubert, J.; Sanders, B. Predicting tidal flooding of urbanized embayments: A modeling framework and data requirements. Coast. Eng. 2011, 58, 567–577. [Google Scholar] [CrossRef]
- Gallien, T.; Sanders, B.; Flick, R. Urban coastal flood prediction: Integrating wave overtopping, flood defenses and drainage. Coast. Eng. 2014, 91, 18–28. [Google Scholar] [CrossRef]
- Ramirez, J.A.; Lichter, M.; Coulthard, T.J.; Skinner, C. Hyper-resolution mapping of regional storm surge and tide flooding: Comparison of static and dynamic models. Nat. Hazards 2016, 82, 571–590. [Google Scholar] [CrossRef]
- Purvis, M.J.; Bates, P.D.; Hayes, C.M. A probabilistic methodology to estimate future coastal flood risk due to sea level rise. Coast. Eng. 2008, 55, 1062–1073. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Mentaschi, L.; Dottori, F.; Giardino, A.; Bouziotas, D.; Bianchi, A.; Salamon, P.; Feyen, L. Developments in large-scale coastal flood hazard mapping. Nat. Hazards Earth Syst. Sci. 2016, 16, 1841–1853. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef] [PubMed]
- Rueda, A.; Vitousek, S.; Camus, P.; Tomás, A.; Espejo, A.; Losada, I.J.; Barnard, P.L.; Erikson, L.H.; Ruggiero, P.; Reguero, B.G.; et al. A global classification of coastal flood hazard climates associated with large-scale oceanographic forcing. Sci. Rep. 2017, 7, 5038. [Google Scholar] [CrossRef] [PubMed]
- Bates, P.D.; Dawson, R.J.; Hall, J.W.; Horritt, M.S.; Nicholls, R.J.; Wicks, J.; Hassan, M.A.A.M. Simplified two-dimensional numerical modelling of coastal flooding and example applications. Coast. Eng. 2005, 52, 793–810. [Google Scholar] [CrossRef]
- Brown, J.D.; Spencer, T.; Moeller, I. Modeling storm surge flooding of an urban area with particular reference to modeling uncertainties: A case study of Canvey Island, United Kingdom. Water Resour. Res. 2007, 43, W06402. [Google Scholar] [CrossRef]
- Poulter, B.; Halpin, P.N. Raster modelling of coastal flooding from sea-level rise. Int. J. Geogr. Inf. Sci. 2008, 22, 167–182. [Google Scholar] [CrossRef]
- Dawson, R.J.; Dickson, M.E.; Nicholls, R.J.; Hall, J.W.; Walkden, M.J.; Stansby, P.K.; Mokrech, M.; Richards, J.; Zhou, J.; Milligan, J.; et al. Integrated analysis of risks of coastal flooding and cliff erosion under scenarios of long term change. Clim. Chang. 2009, 95, 249–288. [Google Scholar] [CrossRef]
- Martinelli, L.; Zanuttigh, B.; Corbau, C. Assessment of coastal flooding hazard along the Emilia Romagna littoral, IT. Coast. Eng. 2010, 57, 1042–1058. [Google Scholar] [CrossRef]
- Anselme, B.; Durand, P.; Thomas, Y.F.; Nicolae-Lerma, A. Storm extreme levels and coastal flood hazards: A parametric approach on the French coast of Languedoc (district of Leucate). C. R. Geosci. 2011, 343, 677–690. [Google Scholar] [CrossRef]
- Barnard, P.L.; van Ormondt, M.; Erikson, L.H.; Eshleman, J.; Hapke, C.; Ruggiero, P.; Adams, P.N.; Foxgrover, A.C. Development of the Coastal Storm Modeling System (CoSMoS) for predicting the impact of storms on high-energy, active-margin coasts. Nat. Hazards 2014, 74, 1095–1125. [Google Scholar] [CrossRef]
- Gallien, T. Validated coastal flood modeling at Imperial Beach, California: Comparing total water level, empirical and numerical overtopping methodologies. Coast. Eng. 2016, 111, 95–104. [Google Scholar] [CrossRef]
- O’Neill, A.C.; Erikson, L.H.; Barnard, P.L.; Limber, P.W.; Vitousek, S.; Warrick, J.A.; Foxgrover, A.C.; Lovering, J. Projected 21st Century Coastal Flooding in the Southern California Bight. Part 1: Development of the Third Generation CoSMoS Model. J. Mar. Sci. Eng. 2018, 6, 59. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Thieken, A.; Schmidtke, R. Estimation uncertainty of direct monetary flood damage to buildings. Nat. Hazards Earth Syst. Sci. 2004, 4, 153–163. [Google Scholar] [CrossRef]
- Heberger, M.; Cooley, H.; Herrera, P.; Gleick, P.H.; Moore, E. The Impacts of Sea-Level Rise on the California Coast; California Climate Change Center: Sacramento, CA, USA, 2009.
- Barredo, J.I.; Engelen, G. Land use scenario modeling for flood risk mitigation. Sustainability 2010, 2, 1327–1344. [Google Scholar] [CrossRef]
- Marcy, D.; Brooks, W.; Draganov, K.; Hadley, B.; Haynes, C.; Herold, N.; McCombs, J.; Pendleton, M.; Ryan, S.; Schmid, K.; et al. New mapping tool and techniques for visualizing sea level rise and coastal flooding impacts. In Solutions to Coastal Disasters 2011; American Society of Civil Engineers: Reston, VA, USA, 2011; pp. 474–490. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Bernatchez, P.; Fraser, C.; Lefaivre, D.; Dugas, S. Integrating anthropogenic factors, geomorphological indicators and local knowledge in the analysis of coastal flooding and erosion hazards. Ocean Coast. Manag. 2011, 54, 621–632. [Google Scholar] [CrossRef]
- Sanders, B.F. Hydrodynamic modeling of urban flood flows and disaster risk reduction. In Oxford Research Encyclopedia of Natural Hazard Science; Oxford University Press: New York, NY, USA, 2017. [Google Scholar]
- Hunter, N.M.; Horritt, M.S.; Bates, P.D.; Wilson, M.D.; Werner, M.G. An adaptive time step solution for raster-based storage cell modelling of floodplain inundation. Adv. Water Resour. 2005, 28, 975–991. [Google Scholar] [CrossRef]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flood simulations. Proc. Inst. Civ. Eng. Waste Resour. Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How much physical complexity is needed to model flood inundation? Hydrol. Process. 2012, 26, 2264–2282. [Google Scholar] [CrossRef]
- Neal, J.; Dunne, T.; Sampson, C.; Smith, A.; Bates, P. Optimisation of the two-dimensional hydraulic model LISFOOD-FP for CPU architecture. Environ. Model. Softw. 2018, 107, 148–157. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling floods in a dense urban area using 2D shallow water equations. J. Hydrol 2006, 327, 186–199. [Google Scholar] [CrossRef]
- Gallegos, H.A.; Schubert, J.E.; Sanders, B.F. Two-dimensional, high-resolution modeling of urban dam-break flooding: A case study of Baldwin Hills, California. Adv. Water Resour. 2009, 32, 1323–1335. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Arega, F.; Sanders, B.F. Dispersion model for tidal wetlands. J. Hydraul. Eng. 2004, 130, 739–754. [Google Scholar] [CrossRef]
- Cea, L.; French, J.; Vázquez-Cendón, M. Numerical modelling of tidal flows in complex estuaries including turbulence: An unstructured finite volume solver and experimental validation. Int. J. Numer. Methods Eng. 2006, 67, 1909–1932. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Gallegos, H.A. Integral formulation of shallow-water equations with anisotropic porosity for urban flood modeling. J. Hydrol. 2008, 362, 19–38. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F. Building treatments for urban flood inundation models and implications for predictive skill and modeling efficiency. Adv. Water Resour. 2012, 41, 49–64. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F.; Smith, M.J.; Wright, N.G. Unstructured mesh generation and landcover-based resistance for hydrodynamic modeling of urban flooding. Adv. Water Res. 2008, 31, 1603–1621. [Google Scholar] [CrossRef]
- Villaneueva, I.; Wright, N. Linking Riemann and storage cell methods for flood predictions. Proc. Inst. Civ. Eng. Waste Resour. Manag. 2006, 159, 27–33. [Google Scholar] [CrossRef]
- Sanders, B.F. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Res. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Bates, P.; Anderson, M.; Hervouet, J.M.; Hawkes, J. Investigating the behaviour of two-dimensional finite element models of compound channel flow. Earth Surf. Process. Landf. J. Br. Geomorphol. Group 1997, 22, 3–17. [Google Scholar] [CrossRef]
- Colby, J.D.; Dobson, J.G. Flood modeling in the coastal plains and mountains: Analysis of terrain resolution. Nat. Hazards Rev. 2010, 11, 19–28. [Google Scholar] [CrossRef]
- Gesch, D.B. Analysis of lidar elevation data for improved identification and delineation of lands vulnerable to sea-level rise. J. Coast. Res. 2009, 49–58. [Google Scholar] [CrossRef]
- Néelz, S.; Pender, G.; Villanueva, I.; Wilson, M.; Wright, N.; Bates, P.; Mason, D.; Whitlow, C. Using remotely sensed data to support flood modelling. Proc. Inst. Civ. Eng. Waste Resour. Manag. 2006, 159, 35–43. [Google Scholar] [CrossRef]
- Webster, T.L.; Forbes, D.L.; Dickie, S.; Shreenan, R. Using topographic lidar to map flood risk from storm-surge events for Charlottetown, Prince Edward Island, Canada. Can. J. Remote Sens. 2004, 30, 64–76. [Google Scholar] [CrossRef]
- Gallien, T.W.; Barnard, P.L.; van Ormondt, M.; Foxgrover, A.C.; Sanders, B.F. A parcel-scale coastal flood forecasting prototype for a Southern California urbanized embayment. J. Coast. Res. 2012, 29, 642–656. [Google Scholar] [CrossRef]
- Smith, R.A.; Bates, P.D.; Hayes, C. Evaluation of a coastal flood inundation model using hard and soft data. Environ. Modell. Softw. 2012, 30, 35–46. [Google Scholar] [CrossRef]
- LeRoy, S.L.; Pedreros, R.; André, C.; Paris, F.; Lecacheux, S.; Marche, F.; Vinchon, C. Coastal flooding of urban areas by overtopping: Dynamic modelling application to the Johanna storm (2008) in Gâvres (France). Nat. Hazards Earth Syst. Sci. 2015, 15, 2497–2510. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Coupling surface and subsurface flows in a depth averaged flood wave model. J. Hydrol. 2007, 337, 147–158. [Google Scholar] [CrossRef]
- Yamashita, K.; Suppasri, A.; Oishi, Y.; Imamura, F. Development of a Tsunami Inundation Analysis Model for Urban Areas Using a Porous Body Model. Geosciences 2018, 8, 12. [Google Scholar] [CrossRef]
- Baba, T.; Takahashi, N.; Kaneda, Y.; Inazawa, Y.; Kikkojin, M. Tsunami Inundation Modeling of the 2011 Tohoku Earthquake Using Three-Dimensional Building Data for Sendai, Miyagi Prefecture, Japan. In Tsunami Events and Lessons Learned: Environmental and Societal Significance; Kontar, Y., Santiago-Fandiño, V., Takahashi, T., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 89–98. [Google Scholar]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-time urban flood forecasting and modelling–a state of the art. J. Hydroinform. 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Rossman, L.; Huber, W. Storm Water Management Model (SWMM). User Manu. Version 2016, 5, 22. [Google Scholar]
- Fewtrell, T.J.; Duncan, A.; Sampson, C.C.; Neal, J.C.; Bates, P.D. Benchmarking urban flood models of varying complexity and scale using high resolution terrestrial LiDAR data. Phys. Chem. Earth 2011, 36, 281–291. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Res. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Harley, M.D.; Ciavola, P. Managing local coastal inundation risk using real-time forecasts and artificial dune placements. Coast. Eng. 2013, 77, 77–90. [Google Scholar] [CrossRef]
- Elsayed, S.M.; Oumeraci, H. Combined modelling of coastal barrier breaching and induced flood propagation using XBeach. Hydrology 2016, 3, 32. [Google Scholar] [CrossRef]
- Phillips, B.T.; Brown, J.M.; Bidlot, J.R.; Plater, A.J. Role of beach morphology in wave overtopping hazard assessment. J. Mar. Sci. Eng. 2017, 5, 1. [Google Scholar] [CrossRef]
- Gallien, T.; O’Reilly, W.; Flick, R.; Guza, R. Geometric properties of anthropogenic flood control berms on southern California beaches. Ocean Coast. Manag. 2015, 105, 35–47. [Google Scholar] [CrossRef]
- Wells, J.T.; McNinch, J. Beach scraping in North Carolina with special reference to its effectiveness during Hurricane Hugo. J. Coast. Res. 1991, 8, 249–261. [Google Scholar]
- Clark, R. Hurricane dennis supplemental damage assessment report: Impact of hurricane dennis on dog island and discussion of post-storm recovery responses. In Florida Department of Environmental Protection, Division of Water Resource Management, Bureau of Beaches and Coastal Systems; Florida Department of Environmental Protection: Tallahassee, FL, USA, 2005. [Google Scholar]
- Carley, J.T.; Shand, T.; Coghlan, I.; Blacka, M.; Cox, R.; Littman, A.; Fitzgibbon, B.; McLean, G.; Watson, P. Beach scraping as a coastal management option. In Proceedings of the 19th NSW Coastal Conference, Ballina, NSW, Australia, 10–12 November 2010. [Google Scholar]
- Rogers, J.; Research, C.I.; Association, I. Beach Management Manual; CIRIA Report; Construction Industry Research and Information Association: London, UK, 2010. [Google Scholar]
- Kratzmann, M.G.; Hapke, C.J. Quantifying anthropogenically driven morphologic changes on a barrier island: Fire Island National Seashore, New York. J. Coast. Res. 2010, 28, 76–88. [Google Scholar] [CrossRef]
- Coveney, S.; Fotheringham, A.S. The impact of DEM data source on prediction of flooding and erosion risk due to sea-level rise. Int. J. Geogr. Inf. Sci. 2011, 25, 1191–1211. [Google Scholar] [CrossRef]
- Kirshen, P.; Knee, K.; Ruth, M. Climate change and coastal flooding in Metro Boston: Impacts and adaptation strategies. Clim. Chang. 2008, 90, 453–473. [Google Scholar] [CrossRef]
- Yin, J.; Yin, Z.E.; Hu, X.M.; Xu, S.Y.; Wang, J.; Li, Z.H.; Zhong, H.D.; Gan, F.B. Multiple scenario analyses forecasting the confounding impacts of sea level rise and tides from storm induced coastal flooding in the city of Shanghai, China. Environ. Earth Sci. 2011, 63, 407–414. [Google Scholar] [CrossRef]
- Strauss, B.H.; Ziemlinski, R.; Weiss, J.L.; Overpeck, J.T. Tidally adjusted estimates of topographic vulnerability to sea level rise and flooding for the contiguous United States. Environ. Res. Lett. 2012, 7, 014033. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Knowles, N. Potential Inundation due to Rising Sea Levels in the San Francisco Bay Region; California Climate Change Center: Sacramento, CA, USA, 2010.
- Lyddon, C.; Brown, J.M.; Leonardi, N.; Plater, A.J. Uncertainty in estuarine extreme water level predictions due to surge-tide interaction. PLoS ONE 2018, 13, e0206200. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D.A. Dependence between sea surge, river flow and precipitation in south and west Britain. Hydrol. Earth Syst. Sci. 2004, 8, 973–992. [Google Scholar] [CrossRef]
- Chen, W.B.; Liu, W.C. Modeling flood inundation induced by river flow and storm surges over a river basin. Water 2014, 6, 3182–3199. [Google Scholar] [CrossRef]
- Orton, P.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries of the New York City region. J. Geophys. Res. Oceans 2012, 117, C09030. [Google Scholar] [CrossRef]
- Maskell, J.; Horsburgh, K.; Lewis, M.; Bates, P. Investigating River–Surge Interaction in Idealised Estuaries. J. Coast. Res. 2013, 30, 248–259. [Google Scholar] [CrossRef]
- Ward, P.J.; Couasnon, A.; Eilander, D.; Haigh, I.D.; Hendry, A.; Muis, S.; Veldkamp, T.I.; Winsemius, H.C.; Wahl, T. Dependence between high sea-level and high river discharge increases flood hazard in global deltas and estuaries. Environ. Res. Lett. 2018, 13, 084012. [Google Scholar] [CrossRef]
- Kumbier, K.; Cabral Carvalho, R.; Vafeidis, A.T.; Woodroffe, C.D. Investigating compound flooding in an estuary using hydrodynamic modelling: A case study from the Shoalhaven River, Australia. Nat. Hazards Earth Syst. Sci. 2018, 18, 463–477. [Google Scholar] [CrossRef]
- Joyce, J.; Chang, N.B.; Harji, R.; Ruppert, T.; Singhofen, P. Cascade impact of hurricane movement, storm tidal surge, sea level rise and precipitation variability on flood assessment in a coastal urban watershed. Clim. Dyn. 2018, 51, 383–409. [Google Scholar] [CrossRef]
- Olbert, A.I.; Comer, J.; Nash, S.; Hartnett, M. High-resolution multi-scale modelling of coastal flooding due to tides, storm surges and rivers inflows. A Cork City example. Coast. Eng. 2017, 121, 278–296. [Google Scholar] [CrossRef]
- Ikeuchi, H.; Hirabayashi, Y.; Yamazaki, D.; Muis, S.; Ward, P.J.; Winsemius, H.C.; Verlaan, M.; Kanae, S. Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 Cyclone Sidr in Bangladesh. J. Adv. Model. Earth Syst. 2017, 9, 1847–1862. [Google Scholar] [CrossRef]
- Saleh, F.; Ramaswamy, V.; Wang, Y.; Georgas, N.; Blumberg, A.; Pullen, J. A multi-scale ensemble-based framework for forecasting compound coastal-riverine flooding: The Hackensack-Passaic watershed and Newark Bay. Adv. Water Res. 2017, 110, 371–386. [Google Scholar] [CrossRef]
- Molinari, D.; De Bruijn, K.M.; Castillo-Rodríguez, J.T.; Aronica, G.T.; Bouwer, L.M. Validation of flood risk models: Current practice and possible improvements. Int. J. Dis. Risk 2018. [Google Scholar] [CrossRef]
- Archetti, R.; Bolognesi, A.; Casadio, A.; Maglionico, M. Development of flood probability charts for urban drainage network in coastal areas through a simplified joint assessment approach. Hydrol. Earth Syst. Sci. 2011, 15, 3115–3122. [Google Scholar] [CrossRef]
- Lian, J.; Xu, K.; Ma, C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river network: A case study of Fuzhou City, China. Hydrol. Earth Syst. Sci. 2013, 17, 679. [Google Scholar] [CrossRef]
- Cheng, H.P.; Cheng, J.R.C.; Hunter, R.M.; Lin, H.C. Demonstration of a Coupled Watershed-Nearshore Model; Technical Report; Engineer Research and Development Center: Vicksburg, MS, USA, 2010. [Google Scholar]
- Tang, H.; Kraatz, S.; Wu, X.; Cheng, W.; Qu, K.; Polly, J. Coupling of shallow water and circulation models for prediction of multiphysics coastal flows: Method, implementation, and experiment. Ocean Eng. 2013, 62, 56–67. [Google Scholar] [CrossRef]
- Thompson, C.M.; Frazier, T.G. Deterministic and probabilistic flood modeling for contemporary and future coastal and inland precipitation inundation. Appl. Geogr. 2014, 50, 1–14. [Google Scholar] [CrossRef]
- Horn, D.P. Measurements and modelling of beach groundwater flow in the swash-zone: A review. Cont. Shelf Res. 2006, 26, 622–652. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Mullaney, J.R.; Stone, J.R.; Skinner, B.J.; Ramlow, M.A. Preliminary Investigation of the Effects of Sea-Level Rise on Groundwater Levels in New Haven, Connecticut; Technical Report; US Geological Survey: Reston, VA, USA, 2012. [Google Scholar]
- Rotzoll, K.; Fletcher, C.H. Assessment of groundwater inundation as a consequence of sea-level rise. Nat. Clim. Chang. 2013, 3, 477. [Google Scholar] [CrossRef]
- Hoover, D.J.; Odigie, K.O.; Swarzenski, P.W.; Barnard, P. Sea-level rise and coastal groundwater inundation and shoaling at select sites in California, USA. J. Hydrol. Reg. Stud. 2017, 11, 234–249. [Google Scholar] [CrossRef]
- Grant, U. Influence of the Water Table on Beach Aggradation and Degradation. J. Mar. Res. 1948, 7, 655–660. [Google Scholar]
- Puleo, J.A.; Lanckriet, T.; Wang, P. Near bed cross-shore velocity profiles, bed shear stress and friction on the foreshore of a microtidal beach. Coast. Eng. 2012, 68, 6–16. [Google Scholar] [CrossRef]
- Grant, U. Effect of ground-water table on beach erosion. Geol. Soc. Am. Bull. 1946, 57, 1252. [Google Scholar]
- Turner, I.L.; Coates, B.P.; Acworth, R.I. Tides, waves and the super-elevation of groundwater at the coast. J. Coast. Res. 1997, 46–60. [Google Scholar]
- Heiss, J.W.; Puleo, J.A.; Ullman, W.J.; Michael, H.A. Coupled surface-subsurface hydrologic measurements reveal infiltration, recharge, and discharge dynamics across the swash zone of a sandy beach. Water Resour. Res. 2015, 51, 8834–8853. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Brovelli, A.; Barry, D.A.; Li, L. Wave-induced water table fluctuations, sediment transport and beach profile change: Modeling and comparison with large-scale laboratory experiments. Coast. Eng. 2011, 58, 103–118. [Google Scholar] [CrossRef]
- Pintado-Patiño, J.C.; Torres-Freyermuth, A.; Puleo, J.A.; Pokrajac, D. On the role of infiltration and exfiltration in swash zone boundary layer dynamics. J. Geophys. Res. C Oceans 2015, 120, 6329–6350. [Google Scholar] [CrossRef]
- Habel, S.; Fletcher, C.H.; Rotzoll, K.; El-Kadi, A.I. Development of a model to simulate groundwater inundation induced by sea-level rise and high tides in Honolulu, Hawaii. Water Res. 2017, 114, 122–134. [Google Scholar] [CrossRef] [PubMed]
- Arns, A.; Dangendorf, S.; Jensen, J.; Talke, S.; Bender, J.; Pattiaratchi, C. Sea-level rise induced amplification of coastal protection design heights. Sci. Rep. 2017, 7, 40171. [Google Scholar] [CrossRef] [PubMed]
- Altomare, C.; Suzuki, T.; Chen, X.; Verwaest, T.; Kortenhaus, A. Wave overtopping of sea dikes with very shallow foreshores. Coast. Eng. 2016, 116, 236–257. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Shaeri, S.; Jafari, E. Prediction of wave overtopping at vertical structures. Coast. Eng. 2016, 109, 42–52. [Google Scholar] [CrossRef]
- Formentin, S.M.; Zanuttigh, B.; van der Meer, J.W. A neural network tool for predicting wave reflection, overtopping and transmission. Coast. Eng. J. 2017, 59, 1750006. [Google Scholar] [CrossRef]
- Van der Meer, J.W. Wave run-up and overtopping. In Dikes and Revetments; Routledge: London, UK, 2017; pp. 145–160. [Google Scholar]
- Hubbard, M.E.; Dodd, N. A 2D numerical model of wave run-up and overtopping. Coast. Eng. 2002, 47, 1–26. [Google Scholar] [CrossRef]
- Hunt, J. Inland and coastal flooding: Developments in prediction and prevention. Phiosl. Trans. R. Soc. Lond. A 2005, 363, 1475–1491. [Google Scholar] [CrossRef]
- Wadey, M.P.; Nicholls, R.J.; Hutton, C. Coastal flooding in the Solent: An integrated analysis of defences and inundation. Water 2012, 4, 430–459. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 57–588. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Oceans 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Sinha, A. Generation of waves in Boussinesq models using a source function method. Coast. Eng. 1999, 36, 271–299. [Google Scholar] [CrossRef]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Williams, H.E.; Briganti, R.; Pullen, T. The role of offshore boundary conditions in the uncertainty of numerical prediction of wave overtopping using non-linear shallow water equations. Coast. Eng. 2014, 89, 30–44. [Google Scholar] [CrossRef]
- Lynett, P.J. Nearshore wave modeling with high-order Boussinesq-type equations. J. Water Port Coast. Ocean Eng. 2006, 132, 348–357. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). Coastal Wave Runup and Overtopping. In Guidance for Flood Risk Analysis and Mapping; Federal Emergency Management Agency: Washington, DC, USA, 2018. [Google Scholar]
- Laudier, N.A.; Thornton, E.B.; MacMahan, J. Measured and modeled wave overtopping on a natural beach. Coast. Eng. 2011, 58, 815–825. [Google Scholar] [CrossRef]
- Chini, N.; Stansby, P. Extreme values of coastal wave overtopping accounting for climate change and sea level rise. Coast. Eng. 2012, 65, 27–37. [Google Scholar] [CrossRef]
- Lynett, P.J.; Melby, J.A.; Kim, D.H. An application of Boussinesq modeling to hurricane wave overtopping and inundation. Ocean Eng. 2010, 37, 135–153. [Google Scholar] [CrossRef]
- Cheung, K.; Phadke, A.; Wei, Y.; Rojas, R.; Douyere, Y.M.; Martino, C.; Houston, S.; Liu, P.F.; Lynett, P.; Dodd, N.; et al. Modeling of storm-induced coastal flooding for emergency management. Ocean Eng. 2003, 30, 1353–1386. [Google Scholar] [CrossRef]
- Hu, K.; Mingham, C.G.; Causon, D.M. Numerical simulation of wave overtopping of coastal structures using the non-linear shallow water equations. Coast. Eng. 2000, 41, 433–465. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Guanche, R.; Gonzalez-Ondina, J.M. Numerical analysis of wave overtopping of rubble mound breakwaters. Coast. Eng. 2008, 55, 47–62. [Google Scholar] [CrossRef]
- Liu, P.L.F.; Lin, P.; Chang, K.A.; Sakakiyama, T. Numerical modeling of wave interaction with porous structures. J. Water Port Coast. Ocean Eng. 1999, 125, 322–330. [Google Scholar] [CrossRef]
- Okayasu, A.; Suzuki, T.; Matsubayashi, Y. Laboratory experiment and three-dimensional Large Eddy Simulation of wave overtopping on gentle slope seawalls. Coast. Eng. J. 2005, 47, 71–89. [Google Scholar] [CrossRef]
- Kikkawa, H.; Shi-igai, H.; Kono, T. Fundamental study of wave over-topping on levees. Coast. Eng. Jpn. 1968, 11, 107–115. [Google Scholar] [CrossRef]
- Ahrens, J. Prediction of Irregular Wave Overtopping; Technical Report; U.S. Army Coastal Engineering Research Center: Springfield, VA, USA, 1977.
- Owen, M. Design of Seawalls Allowing for Wave Overtopping; Report No. EX 924; Hydraulics Research Station: Wallingford, UK, 1980. [Google Scholar]
- Ahrens, J.P.; Heimbaugh, M.S.; Davidson, D.D. Irregular Wave Overtopping of Seawall/revetment Configurations, Roughans Point, Massachusetts: Experimental Model Study; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1986; Volume 86.
- Ahrens, J.P.; Heimbaugh, M.S. Seawall overtopping model. In Coastal Engineering 1988; ASCE Library: Reston, VA, USA, 1989; pp. 795–806. [Google Scholar]
- Schüttrumpf, H. Wellenüberlauf bei Seedeichen—Experimentelle und theoretische Untersuchungen. Ph.D. Thesis, Technical University Carolo-Wilhelmina, Braunschweig, Germany, 2001. [Google Scholar]
- De Waal, J.; Van der Meer, J. Wave runup and overtopping on coastal structures. In Coastal Engineering 1992; ASCE Library: Reston, VA, USA, 1993; pp. 1758–1771. [Google Scholar]
- van der Meer, J.W. Conceptual design of rubble mound breakwaters. In Advances In Coastal And Ocean Engineering: (Volume 1); World Scientific: Toh Tuck, Singapore, 1995; pp. 221–315. [Google Scholar]
- Hedges, T.; Reis, M. Random wave overtopping of simple sea walls: A new regression model. Proc. Inst. Civ. Eng. Water Marit. Energy 1998, 130, 0001–0010. [Google Scholar] [CrossRef]
- van der Meer, J. Technical Report Wave Run-Up and Wave Overtopping at Dikes; TAW report (incorporated in the EurOtop manual); Technical Advisory Committee on Food Defence: Delft, The Nederlands, 2002.
- Mase, H.; Hedges, T.; Shareef, M.; Nagahashi, S. Wave overtopping formula for gentle slopes incorporating wave runup. Proc. Coast. Eng. 2003, 50, 636–640. [Google Scholar]
- Pullen, T.; Allsop, N.; Bruce, T.; Kortenhaus, A.; Schütrumpf, H.; Van Der Meer, J. EurOtop: Wave Overtopping of Sea Defences and Related Structures: Assessment Manual. Environment Agency, UK/Expertise Netwerk Waterkeren, NL/Kuratorium fur Forschung im Kusteningenieurwesen, DE; Technical Report; Environment Agency: Bristol, UK, 2007; 178p, ISBN 978-3-8042-1064-6. [Google Scholar]
- Reis, M.T.; Hu, K.; Hedges, T.S.; Mase, H. A comparison of empirical, semiempirical, and numerical wave overtopping models. J. Coast. Res. 2008, 24, 250–262. [Google Scholar] [CrossRef]
- van der Meer, J.; Allsop, N.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Zanuttigh, B. Eurotop 2016: Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but For Worldwide Application; Environmental Agency: London, UK, 2016.
- Bertin, X.; Li, K.; Roland, A.; Zhang, Y.J.; Breilh, J.F.; Chaumillon, E. A modeling-based analysis of the flooding associated with Xynthia, central Bay of Biscay. Coast. Eng. 2014, 94, 80–89. [Google Scholar] [CrossRef]
- Tsoukala, V.K.; Chondros, M.; Kapelonis, Z.G.; Martzikos, N.; Lykou, A.; Belibassakis, K.; Makropoulos, C. An integrated wave modelling framework for extreme and rare events for climate change in coastal areas–the case of Rethymno, Crete. Oceanologia 2016, 58, 71–89. [Google Scholar] [CrossRef]
- Christensen, E.D.; Deigaard, R. Large eddy simulation of breaking waves. Coast. Eng. 2001, 42, 53–86. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Rogers, B. Numerical modeling of water waves with the SPH method. Coast. Eng. 2006, 53, 141–147. [Google Scholar] [CrossRef]
- Hsu, T.J.; Sakakiyama, T.; Liu, P.L.F. A numerical model for wave motions and turbulence flows in front of a composite breakwater. Coast. Eng. 2002, 46, 25–50. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.F. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Miyata, H. Finite-difference simulation of breaking waves. J. Comput. Phys. 1986, 65, 179–214. [Google Scholar] [CrossRef]
- Watanabe, Y.; Saeki, H. Three-dimensional large eddy simulation of breaking waves. Coast. Eng. J. 1999, 41, 281–301. [Google Scholar] [CrossRef]
- Wu, T.R. A Numerical Study of Three-Dimensional Breaking Waves and Turbulence Effects. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, August 2004. [Google Scholar]
- Garcia, N.; Lara, J.; Losada, I. 2-D numerical analysis of near-field flow at low-crested permeable breakwaters. Coast. Eng. 2004, 51, 991–1020. [Google Scholar] [CrossRef]
- Lara, J.; Garcia, N.; Losada, I. RANS modelling applied to random wave interaction with submerged permeable structures. Coast. Eng. 2006, 53, 395–417. [Google Scholar] [CrossRef]
- Lara, J.L.; Losada, I.J.; Liu, P.L.F. Breaking waves over a mild gravel slope: Experimental and numerical analysis. J. Geophys. Res. Oceans 2006, 111, C11019. [Google Scholar] [CrossRef]
- Losada, I.J.; Lara, J.L.; Christensen, E.D.; Garcia, N. Modelling of velocity and turbulence fields around and within low-crested rubble-mound breakwaters. Coast. Eng. 2005, 52, 887–913. [Google Scholar] [CrossRef]
- Soliman, A.S. Numerical Study of Irregular Wave Overtopping and Overflow. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2003. [Google Scholar]
- Reeve, D.; Soliman, A.; Lin, P. Numerical study of combined overflow and wave overtopping over a smooth impermeable seawall. Coast. Eng. 2008, 55, 155–166. [Google Scholar] [CrossRef]
- Thompson, D.A.; Karunarathna, H.; Reeve, D.E. Modelling extreme wave overtopping at Aberystwyth Promenade. Water 2017, 9, 663. [Google Scholar] [CrossRef]
- Li, T.; Troch, P.; De Rouck, J. Wave overtopping over a sea dike. J. Comput. Phy. 2004, 198, 686–726. [Google Scholar] [CrossRef]
- Gotoh, H.; Shao, S.; Memita, T. SPH-LES model for numerical investigation of wave interaction with partially immersed breakwater. Coast. Eng. J. 2004, 46, 39–63. [Google Scholar] [CrossRef]
- Shao, S.; Ji, C.; Graham, D.I.; Reeve, D.E.; James, P.W.; Chadwick, A.J. Simulation of wave overtopping by an incompressible SPH model. Coast. Eng. 2006, 53, 723–735. [Google Scholar] [CrossRef]
- Akbari, H. Simulation of wave overtopping using an improved SPH method. Coast. Eng. 2017, 126, 51–68. [Google Scholar] [CrossRef]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Abbott, M.; Petersen, H.; Skovgaard, O. On the numerical modelling of short waves in shallow water. J. Hydraul. Res. 1978, 16, 173–204. [Google Scholar] [CrossRef]
- Beji, S.; Nadaoka, K. A formal derivation and numerical modelling of the improved Boussinesq equations for varying depth. Ocean Eng. 1996, 23, 691–704. [Google Scholar] [CrossRef]
- Madsen, P.A.; Murray, R.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 1991, 15, 371–388. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 1992, 18, 183–204. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Water Port Coast. Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Chen, Q.; Kirby, J.T.; Dalrymple, R.A.; Kennedy, A.B.; Chawla, A. Boussinesq modeling of wave transformation, breaking, and runup. II: 2D. J. Water Port Coast. Ocean Eng. 2000, 126, 48–56. [Google Scholar] [CrossRef]
- Lynett, P.J.; Wu, T.R.; Liu, P.L.F. Modeling wave runup with depth-integrated equations. Coast. Eng. 2002, 46, 89–107. [Google Scholar] [CrossRef]
- Madsen, P.A.; Sørensen, O.; Schäffer, H. Surf zone dynamics simulated by a Boussinesq type model. Part I. Model description and cross-shore motion of regular waves. Coast. Eng. 1997, 32, 255–287. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Water Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef]
- Sørensen, O.R.; Schäffer, H.A.; Sørensen, L.S. Boussinesq-type modelling using an unstructured finite element technique. Coast. Eng. 2004, 50, 181–198. [Google Scholar] [CrossRef]
- Stansby, P.K. Solitary wave run up and overtopping by a semi-implicit finite-volume shallow-water Boussinesq model. J. Hydraul. Res. 2003, 41, 639–647. [Google Scholar] [CrossRef]
- Stansby, P.K.; Feng, T. Surf zone wave overtopping a trapezoidal structure: 1-D modelling and PIV comparison. Coast. Eng. 2004, 51, 483–500. [Google Scholar] [CrossRef]
- Orszaghova, J.; Borthwick, A.G.; Taylor, P.H. From the paddle to the beach—A Boussinesq shallow water numerical wave tank based on Madsen and Sørensen’s equations. J. Comput. Phys. 2012, 231, 328–344. [Google Scholar] [CrossRef]
- Sitanggang, K.; Lynett, P. Multi-scale simulation with a hybrid Boussinesq-RANS hydrodynamic model. Int. J. Numer. Meth. Fluids 2010, 62, 1013–1046. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid finite volume–finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Brocchini, M.; Dodd, N. Nonlinear shallow water equation modeling for coastal engineering. J. Water Port Coast. Ocean Eng. 2008, 134, 104–120. [Google Scholar] [CrossRef]
- Hibberd, S.; Peregrine, D. Surf and run-up on a beach: A uniform bore. J. Fluid Mech. 1979, 95, 323–345. [Google Scholar] [CrossRef]
- Kobayashi, N.; Watson, K.D. Wave reflection and runup on smooth slopes. Coast. Hydrodyn. 1987, 7, 548–563. [Google Scholar]
- Titov, V.V.; Synolakis, C.E. Modeling of breaking and nonbreaking long-wave evolution and runup using VTCS-2. J. Water Port Coast. Ocean Eng. 1995, 121, 308–316. [Google Scholar] [CrossRef]
- Kobayashi, N.; Wurjanto, A. Wave overtopping on coastal structures. J. Water Port Coast. Ocean Eng. 1989, 115, 235–251. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W. Irregular wave overtopping of revetments in surf zones. J. Water Port Coast. Ocean Eng. 1994, 120, 56–73. [Google Scholar] [CrossRef]
- Dodd, N. Numerical model of wave run-up, overtopping, and regeneration. J. Water Port Coast. Ocean Eng. 1998, 124, 73–81. [Google Scholar] [CrossRef]
- Shiach, J.B.; Mingham, C.G.; Ingram, D.M.; Bruce, T. The applicability of the shallow water equations for modelling violent wave overtopping. Coast. Eng. 2004, 51, 1–15. [Google Scholar] [CrossRef]
- Tuan, T.Q.; Oumeraci, H. A numerical model of wave overtopping on seadikes. Coast. Eng. 2010, 57, 757–772. [Google Scholar] [CrossRef]
- Witting, M.; Kaiser, R.; Schüttrumpf, H.; Niemeyer, H. Use of nonlinear shallow water wave overtopping models for seawall and dyke design: Validation and comparison studies. Proc. Coast. Struct. Breakwaters 2005, 269–289. [Google Scholar]
- Hu, K.; Meyer, D. The validity of the non-linear shallow water equations for modelling wave runup and reflection. Proc. ICE Coast. Struct. Breakwaters 2005, 5, 195–206. [Google Scholar]
- Pullen, T.; Allsop, N. Use of numerical models of wave overtopping: A summary of current understanding. In R&D Interim Guidance Note FD2410/GN1; Department for Environment, Food and Rural Affairs: London, UK, 2003; p. 7. [Google Scholar]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Smit, P.; Stelling, G.; Roelvink, J.A.; van Thiel de Vries, J.S.M.; McCall, R.T.; Dongeren, A.R.V.; Zwinkels, C.; Jacobs, R. XBeach: Non-Hydrostatic Model: Validation, Verification and Model Description; Technical Report; Delft University of Technology: Delft, The Nederlands, 2010. [Google Scholar]
- McCall, R.T.; van Thiel de Vries, J.S.M.; Plant, N.G.; van Dongeren, A.R.; Roelvink, J.A.; Thompson, D.M.; Reniers, A.J.H.M. Two-dimensional time dependent hurricane overwash and erosion modeling at Santa Rosa Island. Coast. Eng. 2010, 57, 668–683. [Google Scholar] [CrossRef]
- Splinter, K.D.; Palmsten, M.L. Modeling dune response to an East Coast Low. Mar. Geol. 2012, 329–331, 46–57. [Google Scholar] [CrossRef]
- McCall, R.; Masselink, G.; Poate, T.; Bradbury, A.; Russell, P.; Davidson, M. Predicting overwash on gravel barriers. J. Coast. Res. 2013, 65, 1473–1478. [Google Scholar] [CrossRef]
- McCall, R.; Masselink, G.; Poate, T.; Roelvink, J.; Almeida, L.; Davidson, M.; Russell, P. Modelling storm hydrodynamics on gravel beaches with XBeach-G. Coast. Eng. 2014, 91, 231–250. [Google Scholar] [CrossRef]
- Suzuki, T.; Altomare, C.; Veale, W.; Verwaest, T.; Trouw, K.; Troch, P.; Zijlema, M. Efficient and robust wave overtopping estimation for impermeable coastal structures in shallow foreshores using SWASH. Coast. Eng. 2017, 122, 108–123. [Google Scholar] [CrossRef]
- Lerma, A.N.; Bulteau, T.; Elineau, S.; Paris, F.; Durand, P.; Anselme, B.; Pedreros, R. High-resolution marine flood modelling coupling overflow and overtopping processes: Framing the hazard based on historical and statistical approaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 207–229. [Google Scholar] [CrossRef]
- Battjes, J.A.; Gerritsen, H. Coastal modelling for flood defence. Phiosl. Trans. R. Soc. Lond. A 2002, 360, 1461–1475. [Google Scholar] [CrossRef] [PubMed]
- Thomalla, F.; Brown, J.; Kelman, I.; Möller, I.; Spence, R.; Spencer, T. Towards an integrated approach for coastal flood impact assessment. In Solutions to Coastal Disasters’ 02; ASCE Library: Reston, VA, USA, 2002; pp. 142–158. [Google Scholar]
- Taylor, P.J. Quantitative Methods in Geography: An Introduction to Spatial Analysis; Houghton Mifflin Harcourt: Boston, MA, USA, 1977. [Google Scholar]
- Plant, N.G.; Stockdon, H.F. How well can wave runup be predicted? Comment on Laudier et al. (2011) and Stockdon et al. (2006). Coast. Eng. 2015, 102, 44–48. [Google Scholar] [CrossRef]
- Cooper, H.M.; Zhang, C.; Selch, D. Incorporating uncertainty of groundwater modeling in sea-level rise assessment: A case study in South Florida. Clim. Chang. 2015, 129, 281–294. [Google Scholar] [CrossRef]
- Sukop, M.C.; Rogers, M.; Guannel, G.; Infanti, J.M.; Hagemann, K. High temporal resolution modeling of the impact of rain, tides, and sea level rise on water table flooding in the Arch Creek basin, Miami-Dade County Florida USA. Sci. Total Environ. 2018, 616, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Masterson, J.P.; Garabedian, S.P. Effects of sea-level rise on ground water flow in a coastal aquifer system. Groundwater 2007, 45, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Walter, D.A.; McCobb, T.D.; Masterson, J.P.; Fienen, M.N. Potential Effects of Sea-Level Rise on the Depth to Saturated Sediments of the Sagamore and Monomoy flow lenses on Cape Cod, Massachusetts; Technical Report; US Geological Survey: Reston, VA, USA, 2016.
- Elsayed, S.M.; Oumeraci, H. Modelling and mitigation of storm-induced saltwater intrusion: Improvement of the resilience of coastal aquifers against marine floods by subsurface drainage. Environ. Model. Softw. 2018, 100, 252–277. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallien, T.W.; Kalligeris, N.; Delisle, M.-P.C.; Tang, B.-X.; Lucey, J.T.D.; Winters, M.A. Coastal Flood Modeling Challenges in Defended Urban Backshores. Geosciences 2018, 8, 450. https://doi.org/10.3390/geosciences8120450
Gallien TW, Kalligeris N, Delisle M-PC, Tang B-X, Lucey JTD, Winters MA. Coastal Flood Modeling Challenges in Defended Urban Backshores. Geosciences. 2018; 8(12):450. https://doi.org/10.3390/geosciences8120450
Chicago/Turabian StyleGallien, Timu W., Nikos Kalligeris, Marie-Pierre C. Delisle, Bo-Xiang Tang, Joseph T. D. Lucey, and Maria A. Winters. 2018. "Coastal Flood Modeling Challenges in Defended Urban Backshores" Geosciences 8, no. 12: 450. https://doi.org/10.3390/geosciences8120450
APA StyleGallien, T. W., Kalligeris, N., Delisle, M.-P. C., Tang, B.-X., Lucey, J. T. D., & Winters, M. A. (2018). Coastal Flood Modeling Challenges in Defended Urban Backshores. Geosciences, 8(12), 450. https://doi.org/10.3390/geosciences8120450




