The Hyper-Angular Cube Concept for Improving the Spatial and Acoustic Resolution of MBES Backscatter Angular Response Analysis
Abstract
1. Introduction
Study Objectives
2. Materials and Methods
2.1. The Hyper-Angular Cube Matrix
2.2. Supervised Machine Learning Algorithms
2.3. Training Set Selection
3. Results
3.1. Comparison of Angular Responses from Dense Soundings with Interpolated and Synthetic Cubes (iHAC and sHAC)
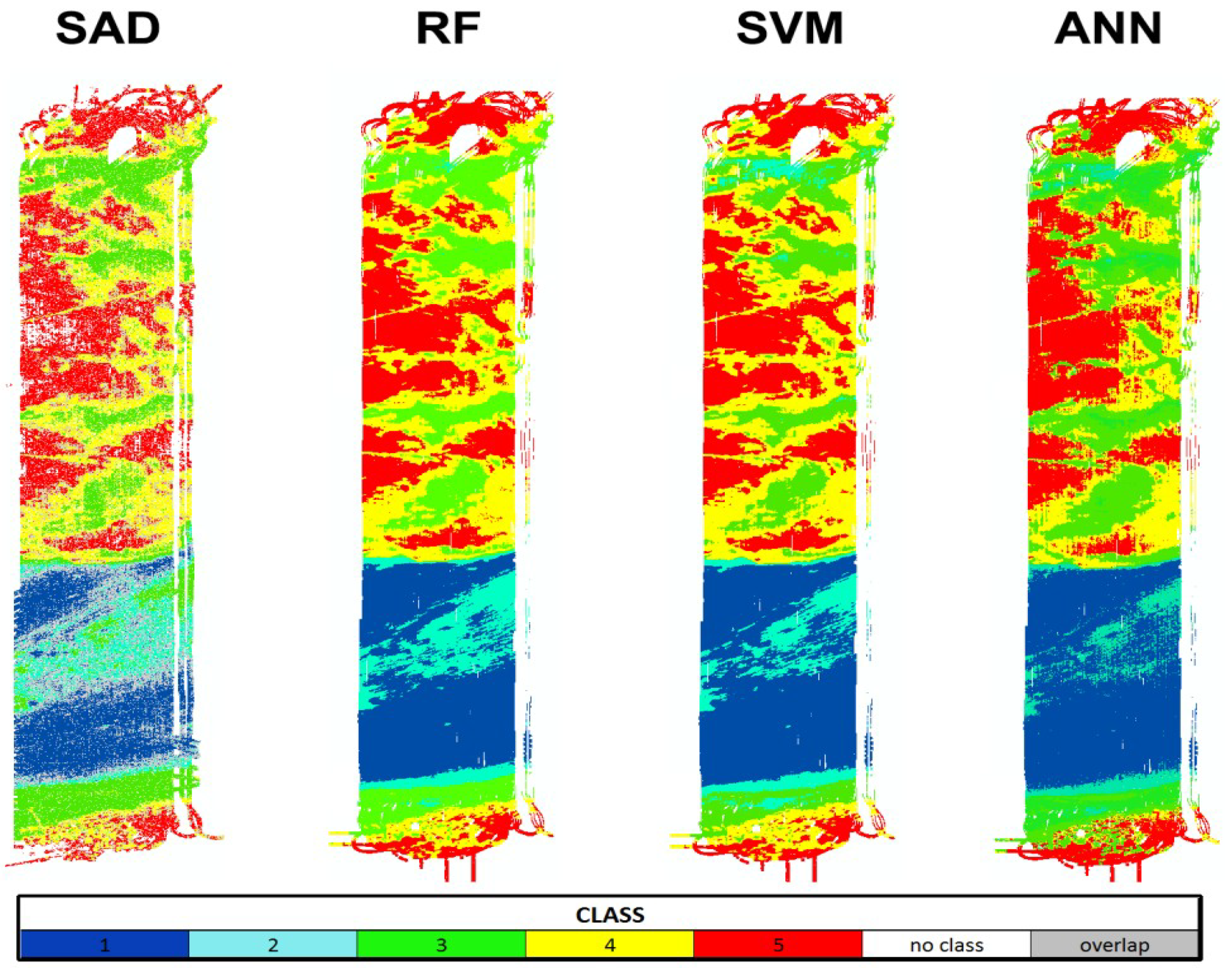
3.1.1. SAD
3.1.2. RF
3.1.3. SVM
3.1.4. ANN
3.2. Validation
4. Discussion
4.1. Effectiveness of the HAC Matrix for Improving the Spatial and Acoustic Resolution of ARA
4.2. Suitability of Machine Learning Algorithms for Advanced Seafloor Mapping Using the HAC
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hughes-Clarke, J.E. Multispectral Acoustic Backscatter from Multibeam—Improved Classification Potential, U.S. In Proceedings of the Hydrographic Conference, National Harbor, MD, USA, 16–19 March 2015. [Google Scholar]
- Augustin, J.-M.; Lamarche, G. High redundancy multibeam echosounder backscatter coverage over strong relief. In Seabed and Sediment Acoustics: Measurements and Modelling Conference; University of Bath: Bath, UK, 2015; p. 37. [Google Scholar]
- Alevizos, E.; Snellen, M.; Simons, D.G.; Siemes, K.; Greinert, J. Multi-angle backscatter classification and sub-bottom profiling for improved seafloor characterization, Special Issue “Seafloor backscatter from swath echosounders: technology and applications”. Mar. Geophys. Res. 2017, 39, 289–306. [Google Scholar] [CrossRef]
- APL-UW. High-Frequency Ocean Environmental Acoustic Models Handbook (APL-UW TR 9407); Applied Physics Laboratory, University of Washington: Seattle, WA, USA, 1994. [Google Scholar]
- Fonseca, L.; Brown, C.; Calder, B.; Mayer, L.; Rzhanov, Y. Angular range analysis of acoustic themes from Stanton Banks Ireland: A link between visual interpretation and multibeam echosounder angular signatures. Appl. Acoust. 2009, 70, 1298–1304. [Google Scholar] [CrossRef]
- Hasan, R.C.; Ierodiaconou, D.; Laurenson, L. Combining angular response classification and backscatter imagery segmentation for benthic biological habitat mapping. Estuar. Coast. Shelf Sci. 2012, 97, 1–9. [Google Scholar] [CrossRef]
- Che Hasan, R.; Ierodiaconou, D.; Laurenson, L.; Schimel, A. Integrating multibeam backscatter angular response; mosaic and bathymetry data for benthic habitat mapping. PLoS ONE 2014, 9, e97339. [Google Scholar] [CrossRef] [PubMed]
- Rzhanov, Y.; Fonseca, L.; Mayer, L. Construction of seafloor thematic maps from multibeam acoustic backscatter angular response data. Comput. Geosci. 2012, 41, 181–187. [Google Scholar] [CrossRef]
- Huang, Z.; Siwabessy, J.; Nichol, S.; Anderson, T.; Brooke, B. Predictive mapping of seabed cover types using angular response curves of multibeam backscatter data: Testing different feature analysis techniques. Cont. Shelf Res. 2013, 61–62, 12–22. [Google Scholar] [CrossRef]
- Clarke, J.H. Towards remote seafloor classification using the angular response of acoustic backscattering: A case study from multiple overlapping GLORIA data. IEEE J. Oceanic Eng. 1994, 19, 112–127. [Google Scholar] [CrossRef]
- Parnum, I.M. Benthic habitat mapping using multibeam sonar systems. Ph.D. Thesis, Curtin University, Perth, Australian, 2007. [Google Scholar]
- McGonigle, C.; Brown, C.; Quinn, R.; Grabowski, J. Evaluation of image-based multibeam sonar backscatter classification for benthic habitat discrimination and mapping at Stanton Banks UK. Estuar. Coast. Shelf Sci. 2009, 81, 423–437. [Google Scholar] [CrossRef]
- Alevizos, E. An object-based seafloor classification tool using recognition of empirical angular backscatter signatures. In Proceedings of the GEOHAB 2017, Halifax, Canada, 1–5 May 2017. [Google Scholar] [CrossRef]
- Huang, Z.; Siwabessy, J.; Nichol, S.L.; Brooke, B.P. Predictive mapping of seabed substrata using high-resolution multibeam sonar data: a case study from a shelf with complex geomorphology. Mar. Geol. 2014, 357, 37–52. [Google Scholar]
- Huang, Z.; Siwabessy, J.; Cheng, H.; Nichol, S. Using multibeam backscatter data to investigate sediment-acoustic relationships. J. Geophys. Res. Ocean. 2018, 123, 4649–4665. [Google Scholar] [CrossRef]
- Lamarche, G.; Lurton, X.; Verdier, A.-L.; Augustin, J.-M. Quantitative characterisation of seafloor substrate and bedforms using advanced processing of multibeam backscatter-Application to Cook Strait; New Zealand. Cont. Shelf Res. 2011, 31, S93–S109. [Google Scholar] [CrossRef]
- Kloser, R.J.; Penrose, J.D.; Butler, A.J. Multi-beam backscatter measurements used to infer seabed habitats. Cont. Shelf Res. 2010, 30, 1772–1782. [Google Scholar] [CrossRef]
- Parnum, I.M.; Gavrilov, A.N. High-frequency multibeam echo-sounder measurements of seafloor backscatter in shallow water: Part 1—Data acquisition and processing. Underw. Technol. 2011, 30, 3–12. [Google Scholar] [CrossRef]
- Lurton, X.; Lamarche, G. Backscatter measurements by seafloor-mapping sonars. Guidelines and Recommendations. Collect. Rep. Memb. GeoHab Backscatter Work. Gr. 2015, 5, 200. [Google Scholar]
- Beaudoin, J.; Clarke, J.E.; Van Den Ameele, E.J.; Gardner, J.V. Geometric and radiometric correction of multibeam backscatter derived from Reson 8101 systems. In Proceedings of the Canadian Hydrographic Conference 2002, Association Ottawa, ON, Canada, 28–31 May 2002. [Google Scholar]
- Schimel, A.C.; Beaudoin, J.; Parnum, I.M.; Le Bas, T.; Schmidt, V.; Keith, G.; Ierodiacono, D. Multibeam sonar backscatter data processing. Mar. Geophys. Res. 2018, 39, 121–137. [Google Scholar] [CrossRef]
- Fonseca, L.; Calder, B. Geocoder: An efficient backscatter map constructor. In Proceedings of the U.S. Hydrographic Conference 2005, San Diego, CA, USA, 29–31 March 2005. [Google Scholar]
- Gavrilov, A.N.; Siwabessy, P.J.W.; Parnum, I.M. Multibeam echo Sounder Backscatter Analysis; Centre for Marine Science and Technology: Perth, Australian, 2005. [Google Scholar]
- Benediktsson, J.A.; Sveinsson, J.R.; Arnason, K. Classification and feature extraction of AVIRIS data. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1194–1205. [Google Scholar] [CrossRef]
- Dawoud, N.N.; Samir, B.B.; Janier, J. Fast template matching method based optimized sum of absolute difference algorithm for face localization. Int. J. Comp. Appl. 2011, 18, 30–34. [Google Scholar]
- Lucieer, V.; Hill, N.A.; Barrett, N.S.; Nichol, S. Do marine substrates ‘look’ and ‘sound’ the same? Supervised classification of multibeam acoustic data using autonomous underwater vehicle images. Estuar. Coast. Shelf Sci. 2013, 117, 94–106. [Google Scholar] [CrossRef]
- Diesing, M.; Green, S.L.; Stephens, D.; Lark, R.M.; Stewart, H.A.; Dove, D. Mapping seabed sediments: Comparison of manual, geostatistical, object-based image analysis and machine learning approaches. Continent. Shelf Res. 2014, 84, 107–119. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Li, J.; Tran, M.; Siwabessy, J. Selecting optimal random forest predictive models: a case study on predicting the spatial distribution of seabed hardness. PLoS ONE 2016, 11, e0149089. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Alvarez, B.; Siwabessy, J.; Tran, M.; Huang, Z.; Przeslawski, R.; Radke, L.; Howard, F.; Nichol, S. Application of random forest, generalised linear model and their hybrid methods with geostatistical techniques to count data: Predicting sponge species richness. Environ. Model. Softw. 2017, 97, 112–129. [Google Scholar] [CrossRef]
- Roberts, J.J.; Best, B.D.; Dunn, D.C.; Treml, E.A.; Halpin, P.N. Marine Geospatial Ecology Tools: An integrated framework for ecological geoprocessing with ArcGIS, Python, R, MATLAB, and C++. Environ. Model. Softw. 2010, 25, 1197–1207. [Google Scholar] [CrossRef]
- Stephens, D.; Diesing, M. A Comparison of Supervised Classification Methods for the Prediction of Substrate Type Using Multibeam Acoustic and Legacy Grain-Size Data. PLoS ONE 2014, 9, e93950. [Google Scholar] [CrossRef] [PubMed]
- Coleman, A.M. An adaptive Landscape classification procedure using geoinformatics and artificial neural networks. MSc Thesis, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands, June 2008. [Google Scholar]
- van Leeuwen, B. Artificial neural networks and geographic information systems for inland excess water classification. Ph.D. Thesis, University of Szeged, Szeged, Hungary.
- Visser, H.; de Nijs, T. The Map Comparison Kit. Environ. Model. Softw. 2006, 21, 346–358. [Google Scholar] [CrossRef]
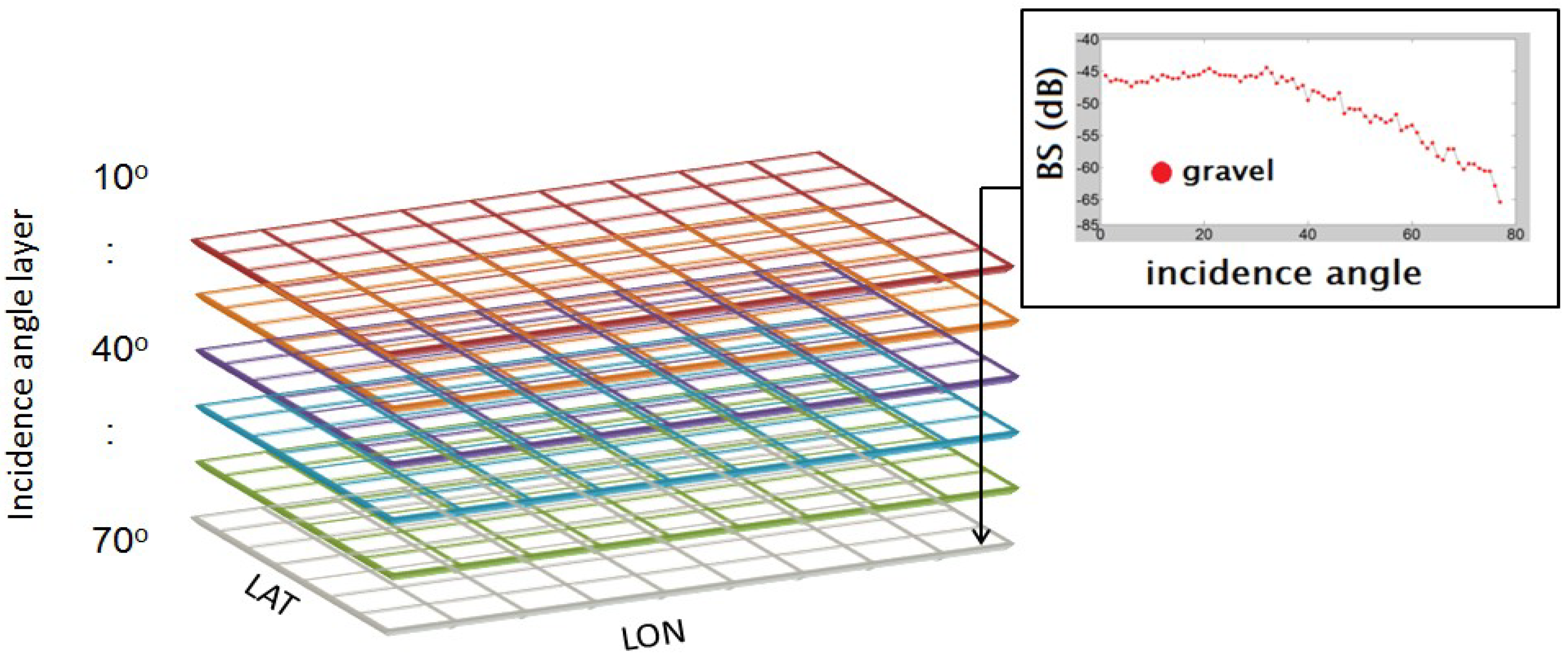
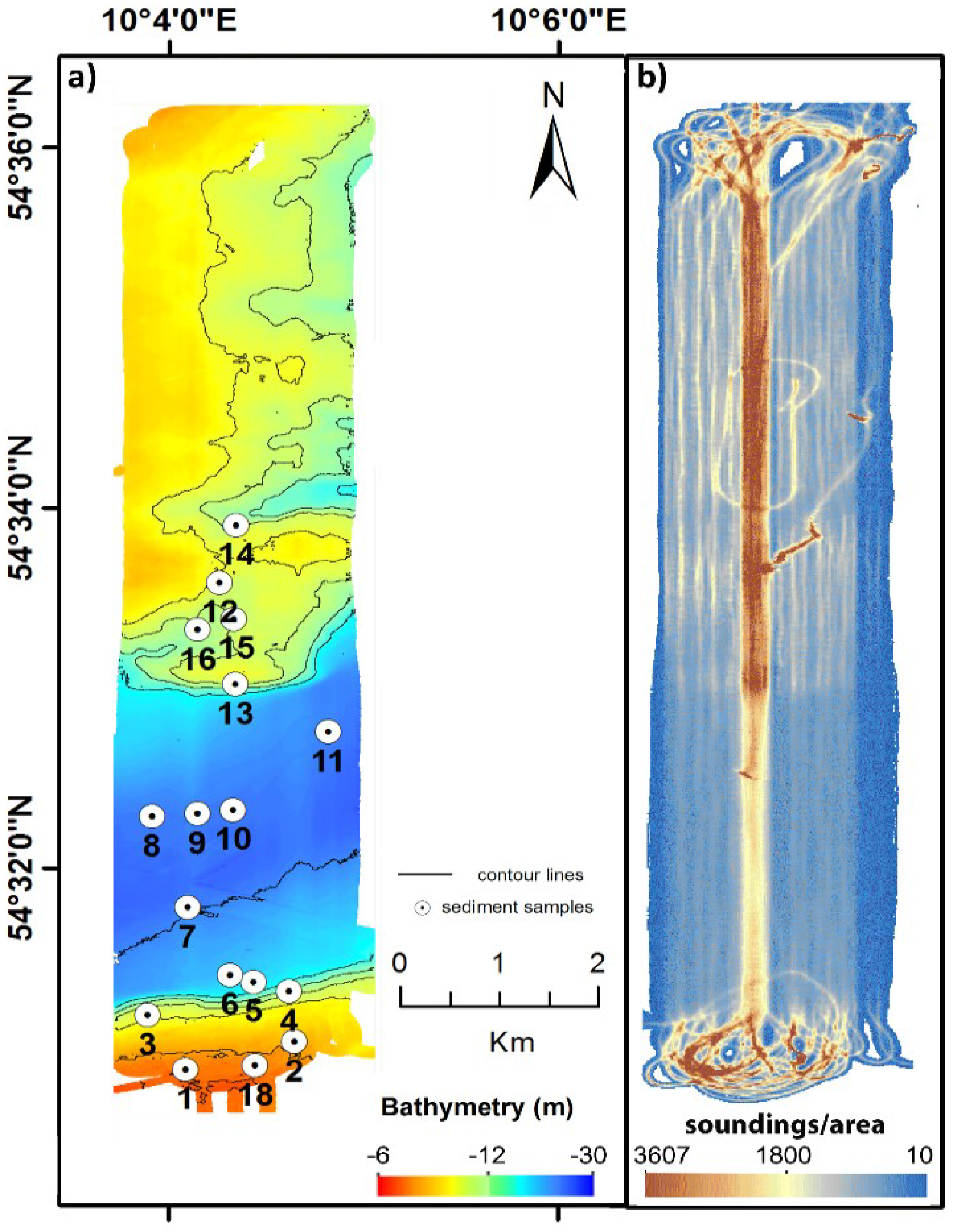
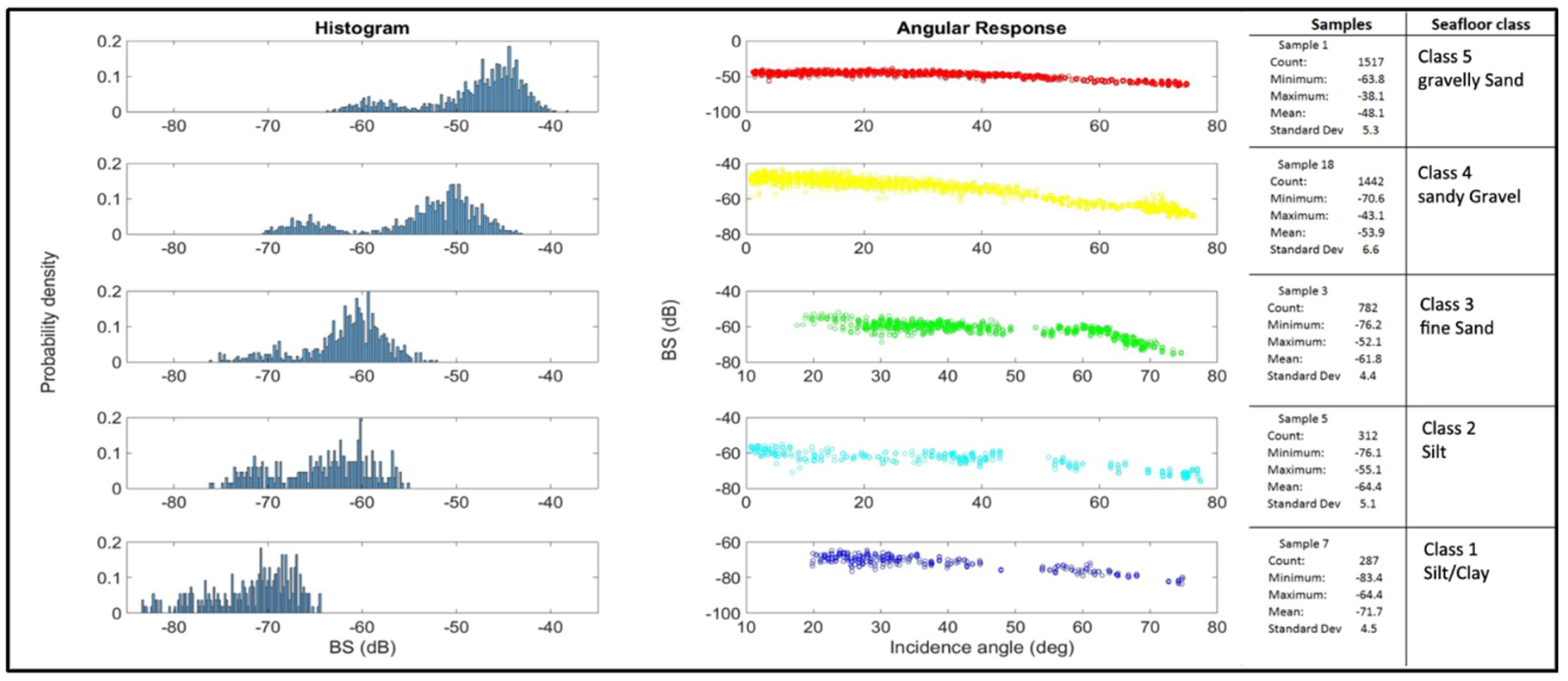
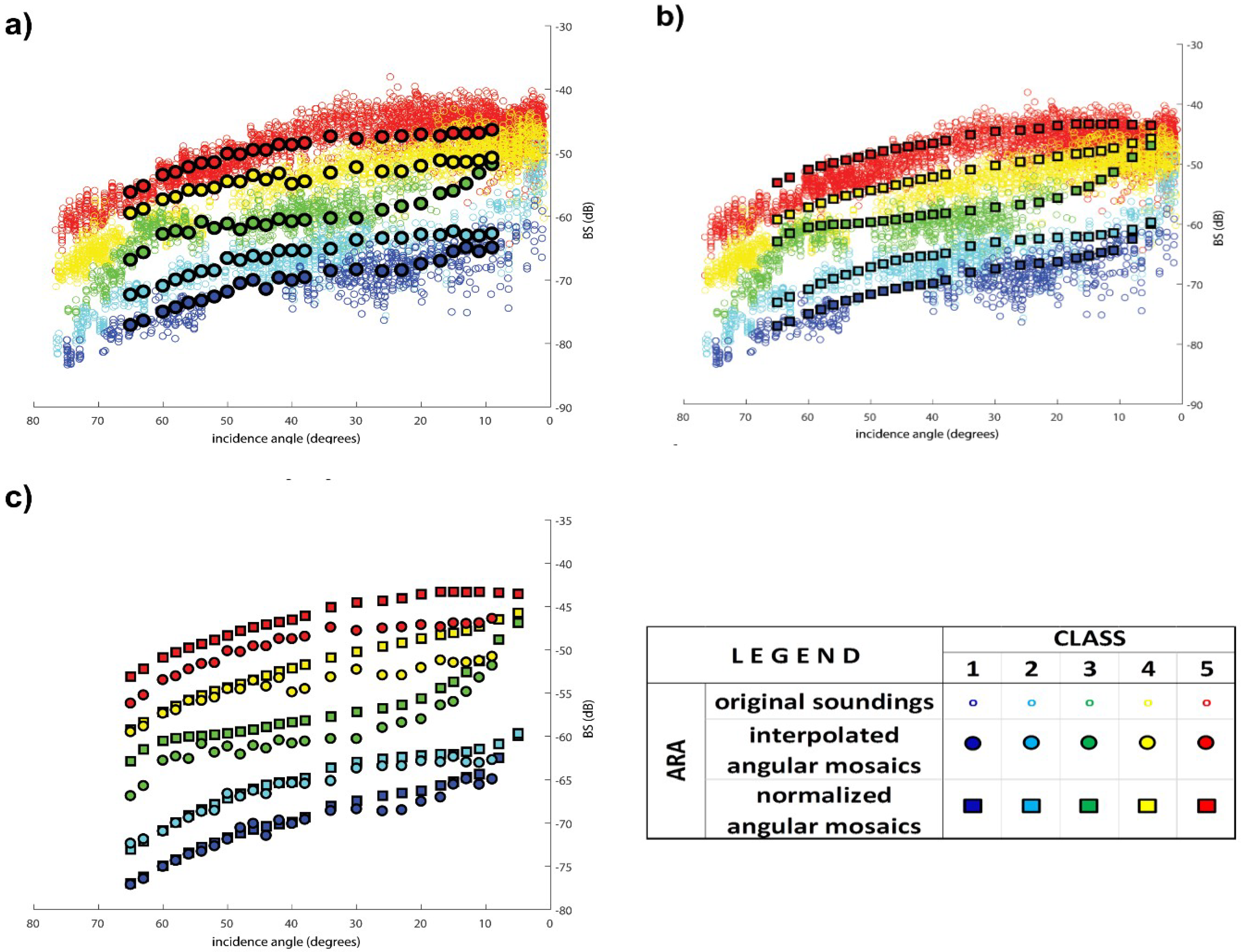
| Sample | wt.% >6.3 mm | wt.% 2–6.3 mm | wt.% 2 mm–500 µm | wt.% <500 µm | Shells/Pebbles | D50 (<500 µm) | Mode (<500 µm) | D50 All (µm) | Mode All (µm) | Bayes Class |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.59 | 20.17 | 34.12 | 31.12 | 1/1 | 240.0 | 246.0 | 2600 | 1000 | 5 |
| 2 | 2.23 | 30.89 | 21.96 | 44.91 | 1/1 | 220.0 | 246.0 | 1800 | 4000 | 5 |
| 3 | 0.00 | 0.65 | 14.49 | 84.86 | 1/0 | 170.0 | 197.0 | 210 | 180 | 3 |
| 4 | 0.00 | 0.49 | 2.56 | 96.95 | 1/0 | 151.8 | 191.5 | 200 | 180 | 3 |
| 5 | 0.00 | 0.69 | 3.28 | 96.03 | 1/0 | 41.3 | 73.0 | 100 | 90 | 2 |
| 6 | 0.00 | 0.00 | 0.00 | 100.00 | 0/0 | 23.0 | 44.3 | 50 | 40 | 2 |
| 7 | 0.00 | 0.00 | 0.00 | 100.00 | 0/0 | 23.0 | 43.5 | 50 | 40 | 1 |
| 8 | 0.00 | 0.00 | 0.00 | 100.00 | 0/0 | 26.3 | 43.0 | 50 | 40 | 1 |
| 9 | 0.00 | 3.39 | 0.74 | 95.87 | 0/0 | 20.8 | 41.0 | 40 | 40 | 3 |
| 10 | 0.00 | 0.00 | 0.72 | 99.28 | 0/0 | 21.0 | 43.8 | 40 | 40 | 2 |
| 11 | 0.00 | 0.72 | 0.24 | 99.04 | 0/0 | 20.5 | 42.0 | 50 | 40 | 2 |
| 12 | 0.00 | 0.42 | 15.36 | 84.21 | 1/1 | 197.0 | 236.0 | 320 | 250 | 4 |
| 13 | 0.00 | 0.27 | 7.89 | 91.84 | 1/0 | 157.0 | 270.0 | 290 | 250 | 3 |
| 14 | 0.00 | 0.38 | 21.87 | 77.76 | 1/1 | 192.0 | 216.0 | 280 | 180 | 3 |
| 15 | 0.00 | 0.40 | 4.08 | 95.52 | 1/0 | 206.0 | 236.0 | 220 | 130 | 3 |
| 16 | 0.00 | 0.07 | 7.94 | 92.00 | 1/1 | 236.0 | 246.0 | 460 | 350 | 3 |
| 17 | 0.00 | 8.06 | 18.38 | 73.57 | 0/1 | 84.0 | 188.0 | 210 | 180 | 4 |
| 18 | 0.00 | 1.41 | 31.15 | 67.44 | 1/0 | 282.0 | 270.0 | 270 | 350 | 4 |
| iHAC (Interpolation) | Agreement Scores with Bayesian Classification Map [3] | sHAC (Normalization) | Agreement Scores with Bayesian Classification Map [3] | ||||
|---|---|---|---|---|---|---|---|
| Supervised Classification Map | Kappa | K Loc | K Hist | Supervised Classification Map | Kappa | K Loc | K Hist |
| SAD | 0.61 | 0.70 | 0.86 | SAD | 0.53 | 0.66 | 0.83 |
| RF | 0.73 | 0.86 | 0.86 | RF | 0.61 | 0.67 | 0.81 |
| SVM | 0.68 | 0.84 | 0.81 | SVM | 0.54 | 0.66 | 0.82 |
| ANN | 0.68 | 0.77 | 0.88 | ANN | 0.55 | 0.69 | 0.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alevizos, E.; Greinert, J. The Hyper-Angular Cube Concept for Improving the Spatial and Acoustic Resolution of MBES Backscatter Angular Response Analysis. Geosciences 2018, 8, 446. https://doi.org/10.3390/geosciences8120446
Alevizos E, Greinert J. The Hyper-Angular Cube Concept for Improving the Spatial and Acoustic Resolution of MBES Backscatter Angular Response Analysis. Geosciences. 2018; 8(12):446. https://doi.org/10.3390/geosciences8120446
Chicago/Turabian StyleAlevizos, Evangelos, and Jens Greinert. 2018. "The Hyper-Angular Cube Concept for Improving the Spatial and Acoustic Resolution of MBES Backscatter Angular Response Analysis" Geosciences 8, no. 12: 446. https://doi.org/10.3390/geosciences8120446
APA StyleAlevizos, E., & Greinert, J. (2018). The Hyper-Angular Cube Concept for Improving the Spatial and Acoustic Resolution of MBES Backscatter Angular Response Analysis. Geosciences, 8(12), 446. https://doi.org/10.3390/geosciences8120446





