Efficiency of a Digital Particle Image Velocimetry (DPIV) Method for Monitoring the Surface Velocity of Hyper-Concentrated Flows
Abstract
1. Introduction
2. Materials and Methods
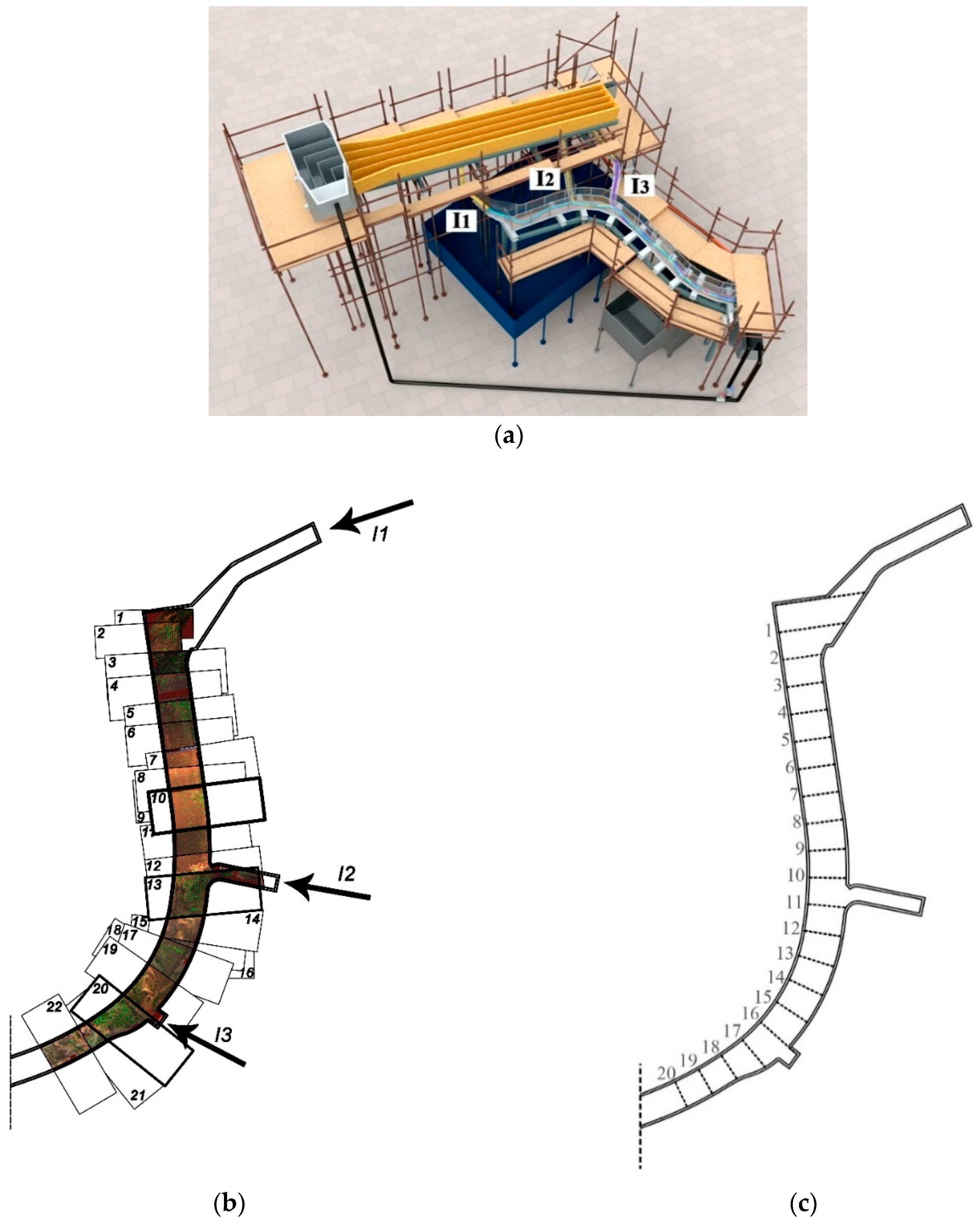
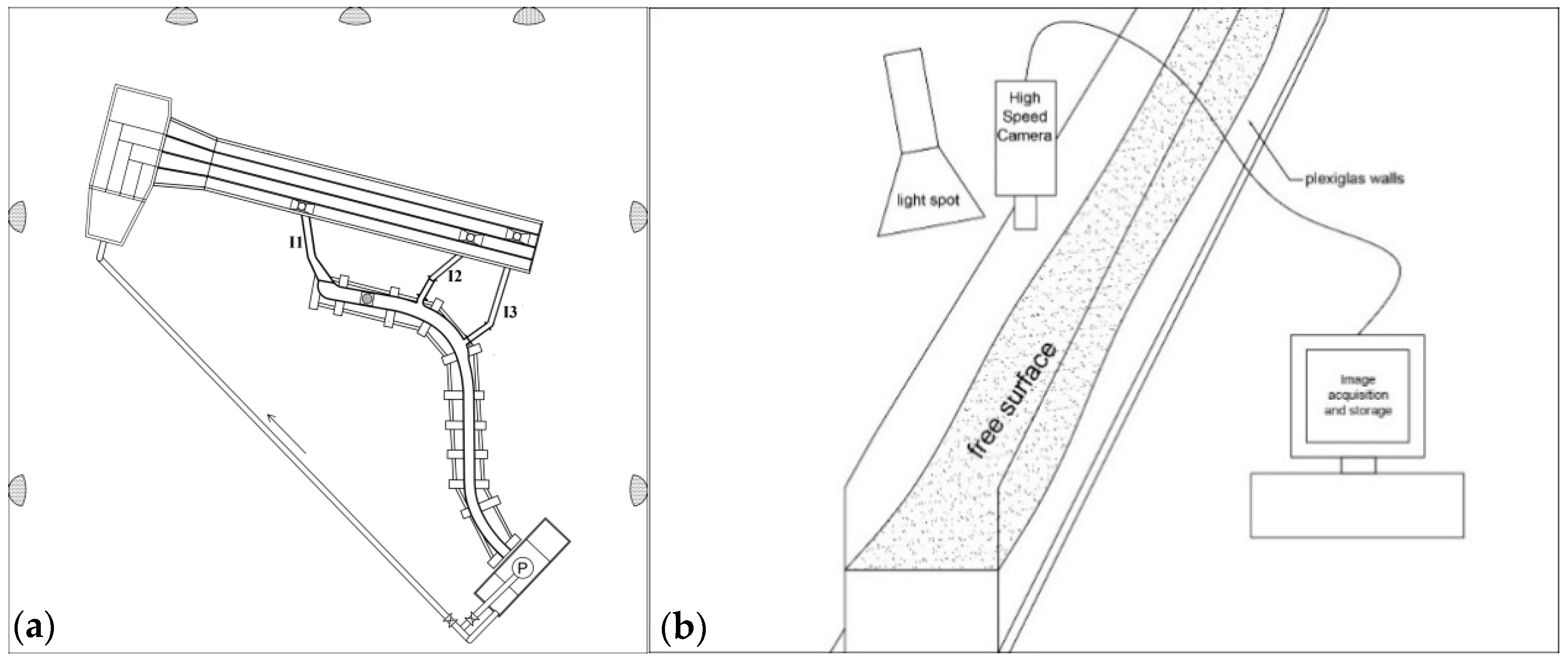
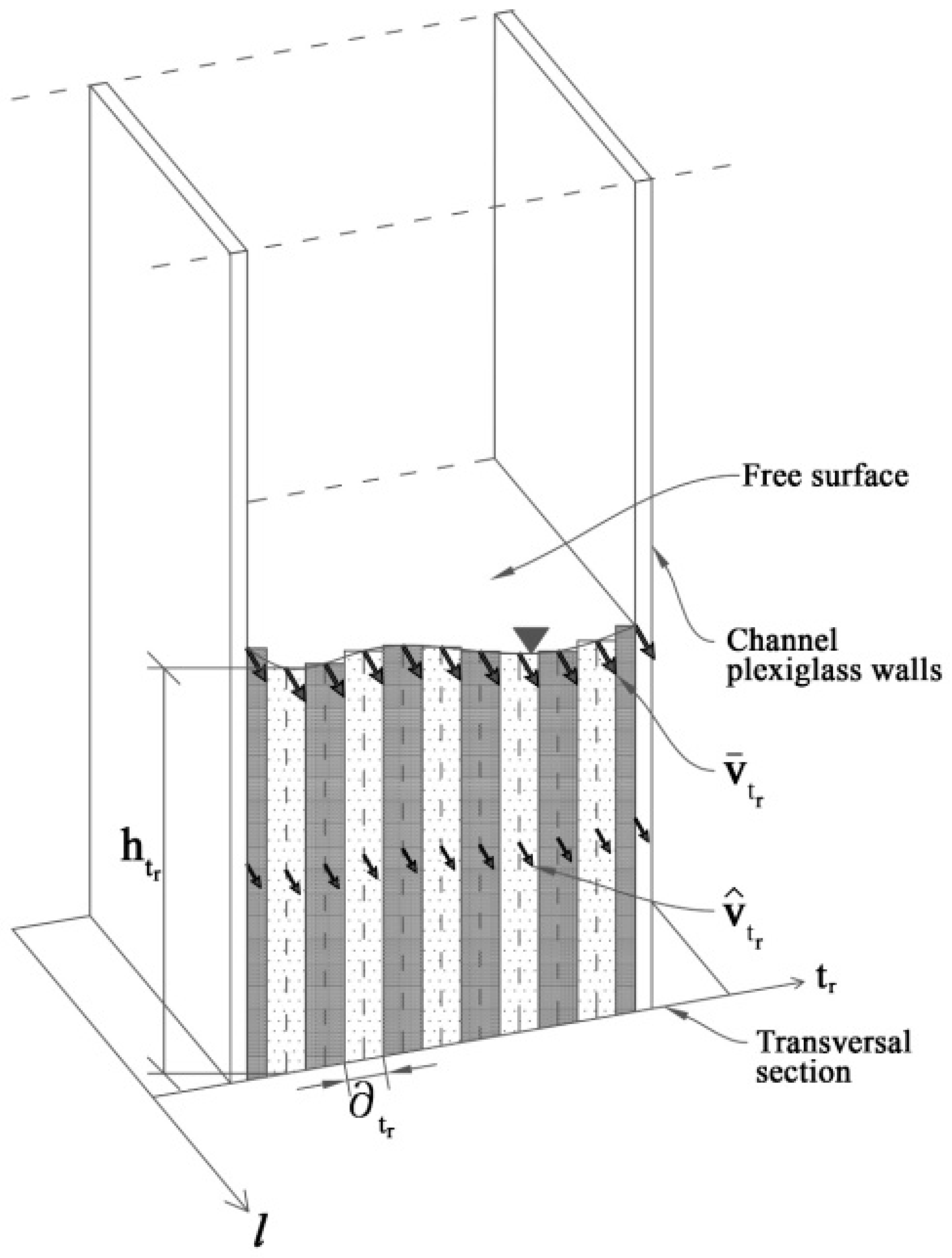
2.1. Experimental Apparatus and Conditions
2.2. Acquisition and Processing Methodology
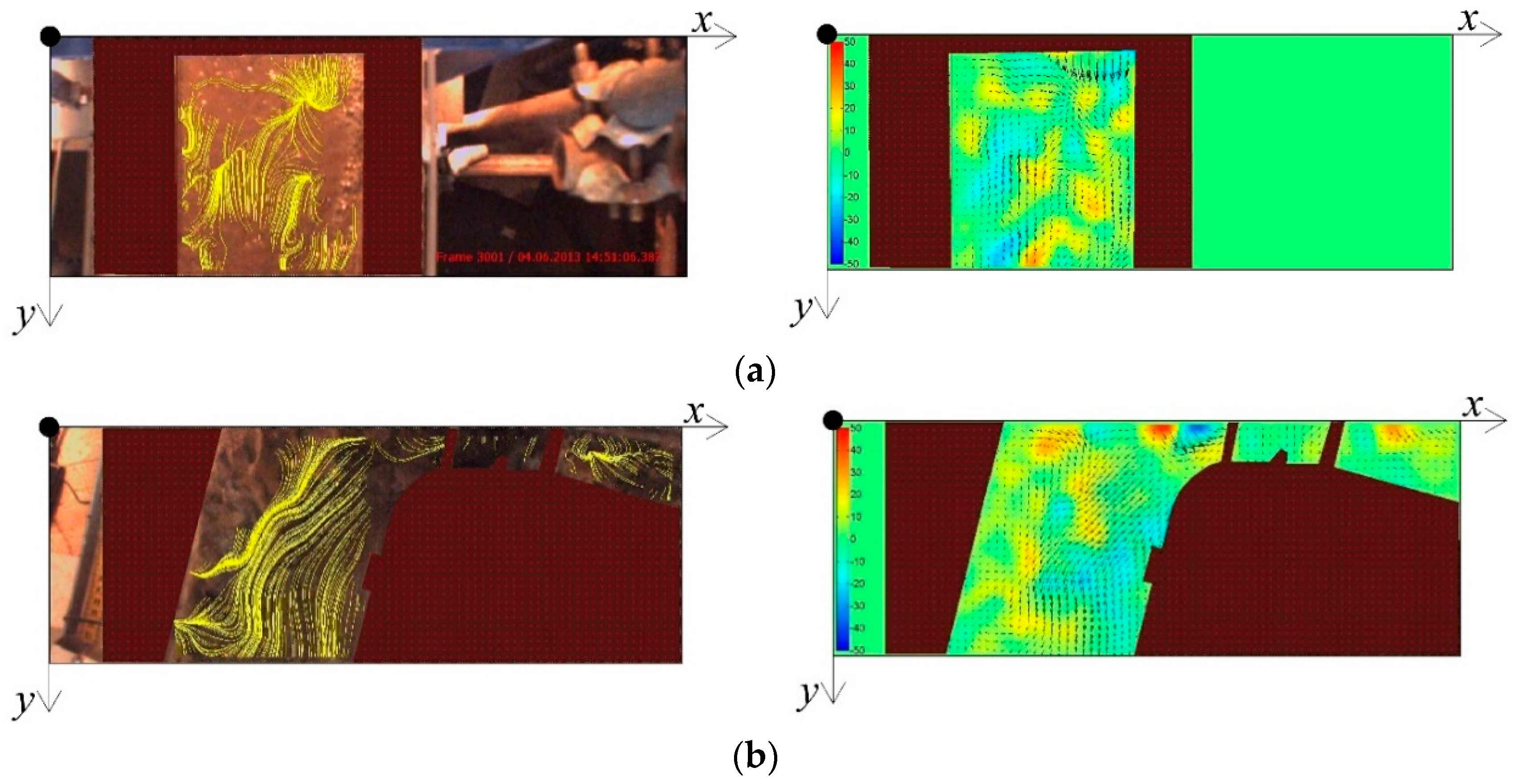
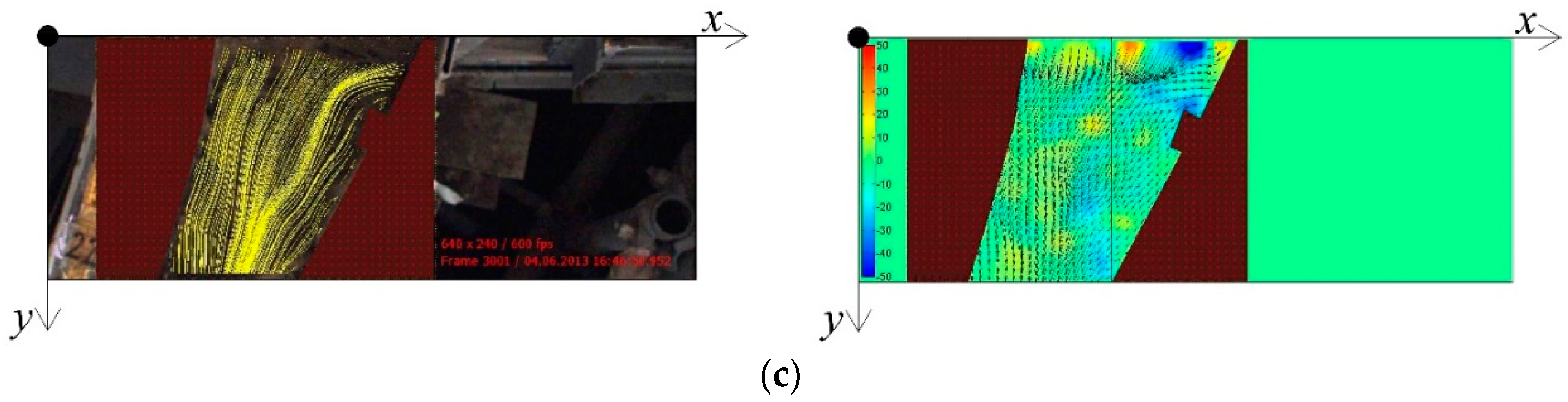
2.3. Surface Velocity Estimation by PIV Method
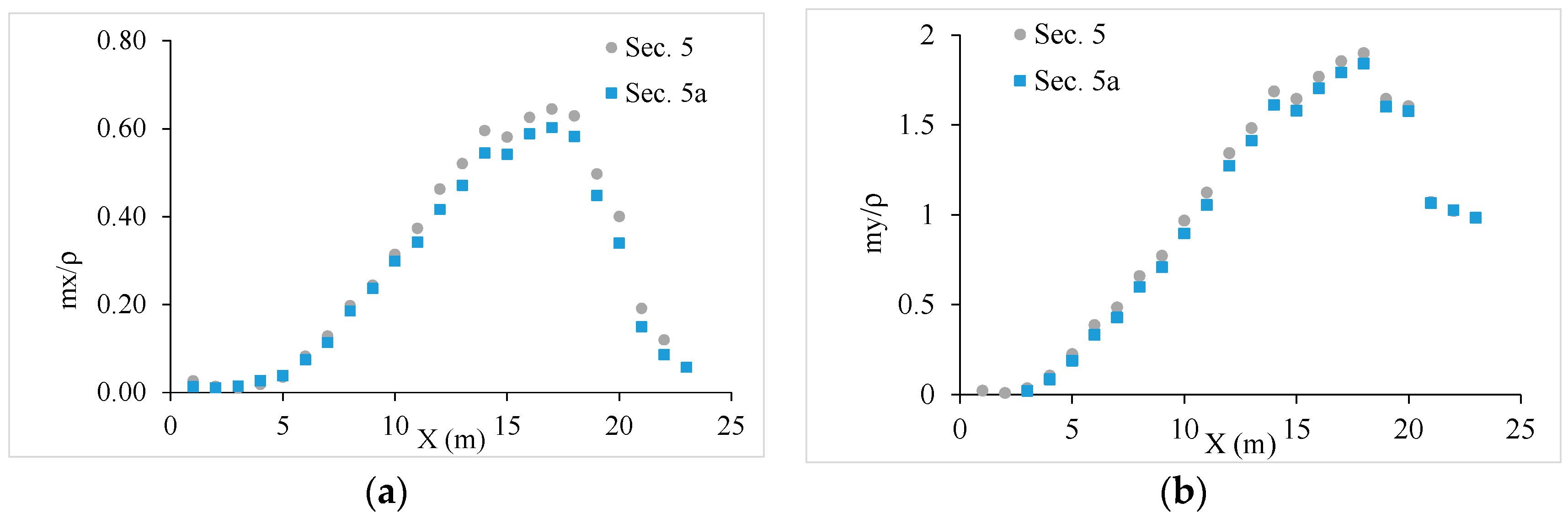
3. Results and Discussion
3.1. Estimation Error
3.2. Discharge Estimation
4. Conclusions
- -
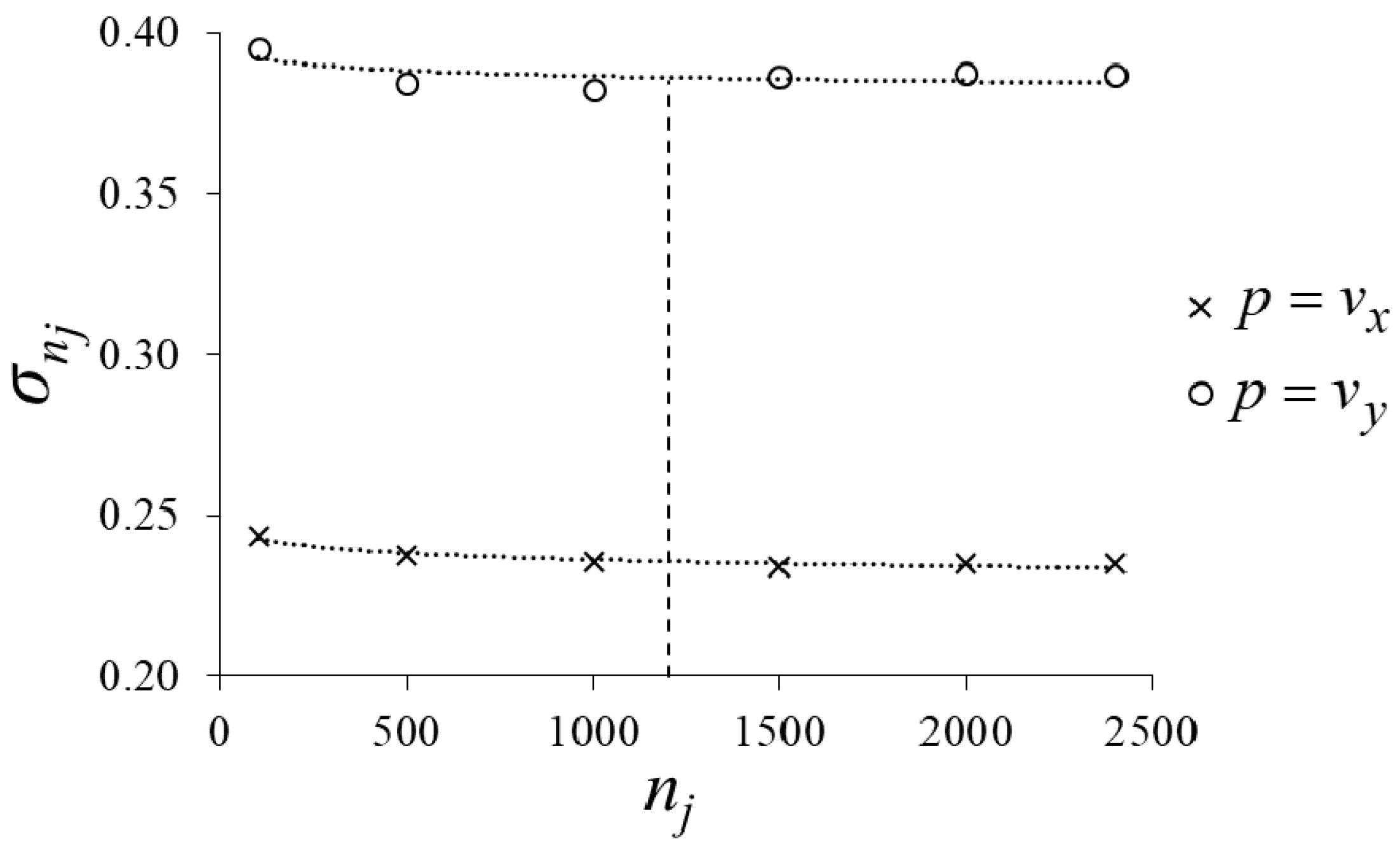
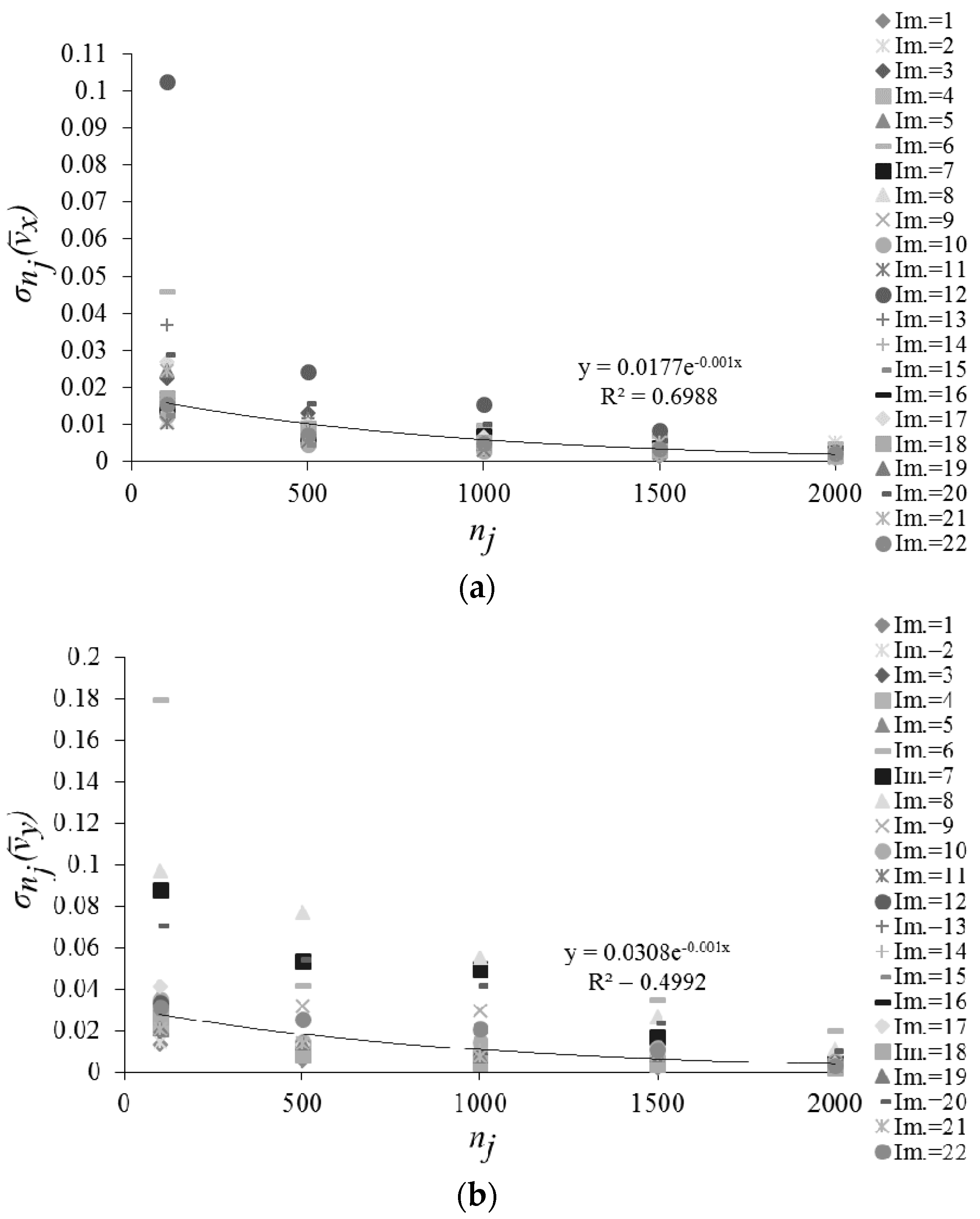
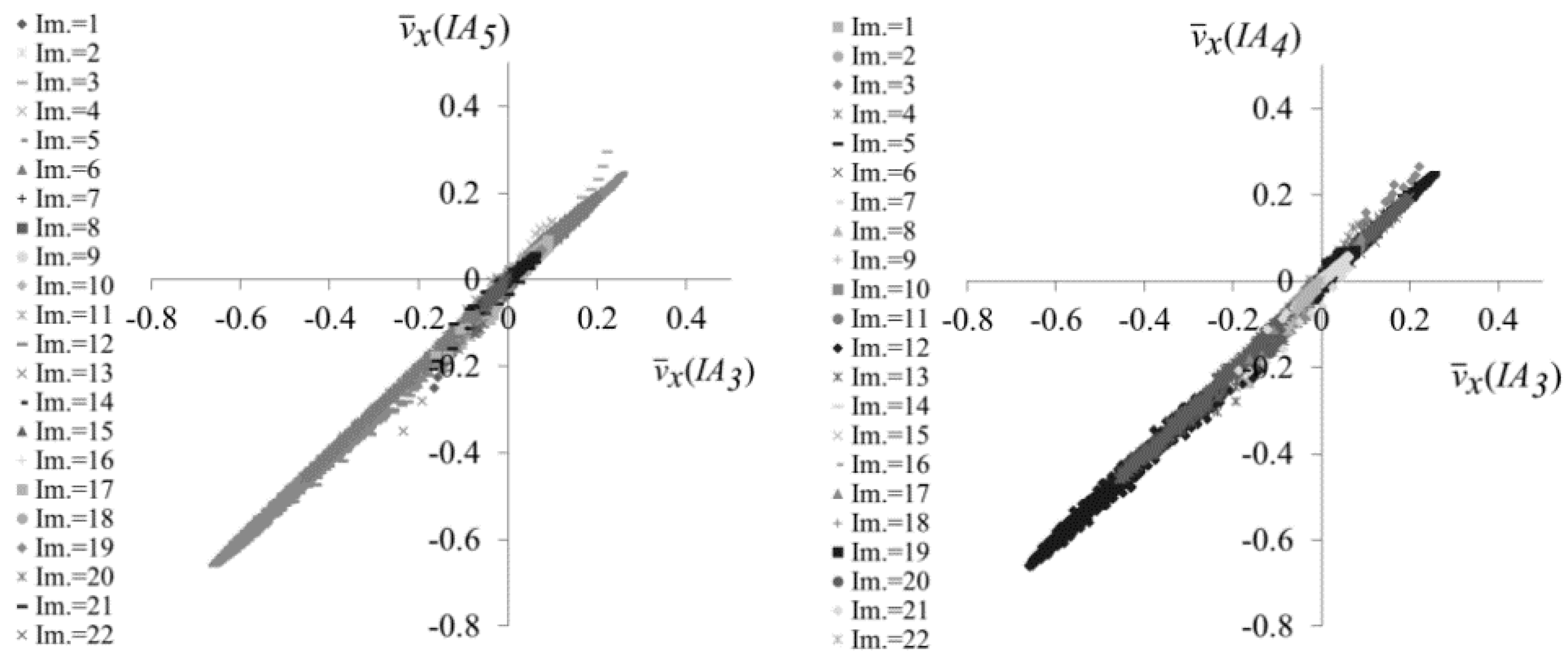
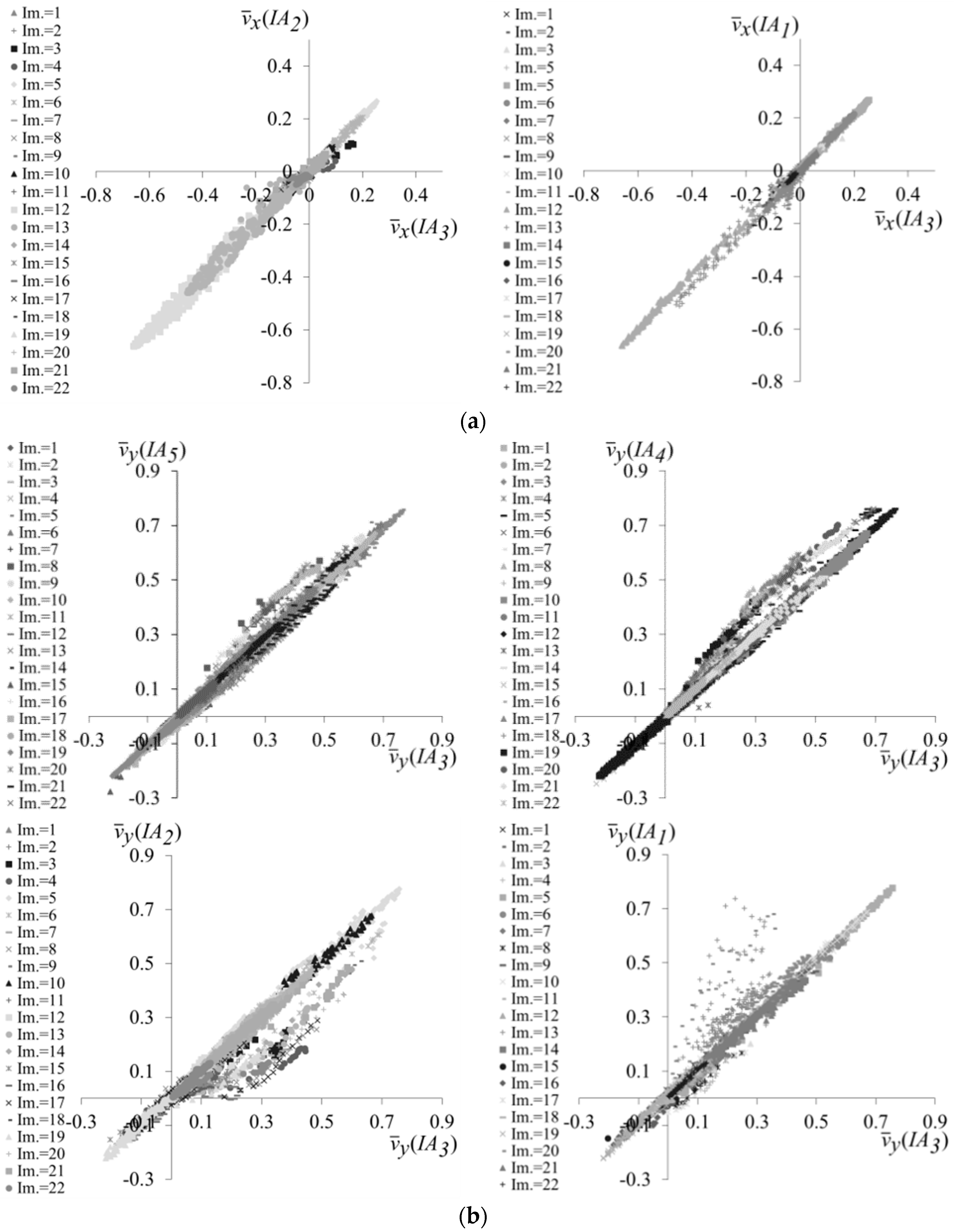
- the estimation error of the surface velocity decreases as the number of pairs of frames increases. In particular, for the examined case, the estimation error assumes a low and an almost constant value as the number of processed pairs of frames is greater than 1200 (i.e., equal to or greater than half of the available pairs of frames);
- -
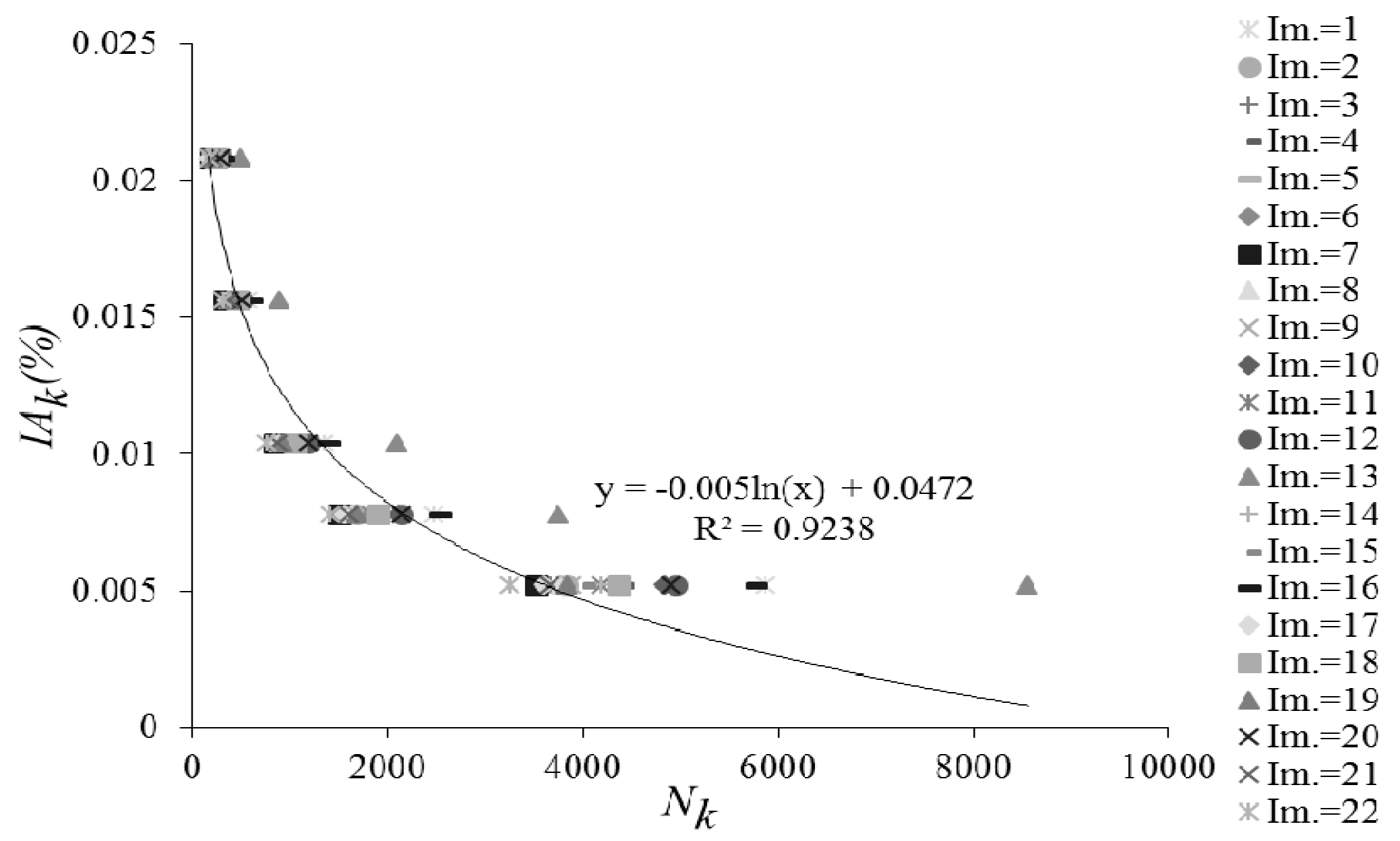
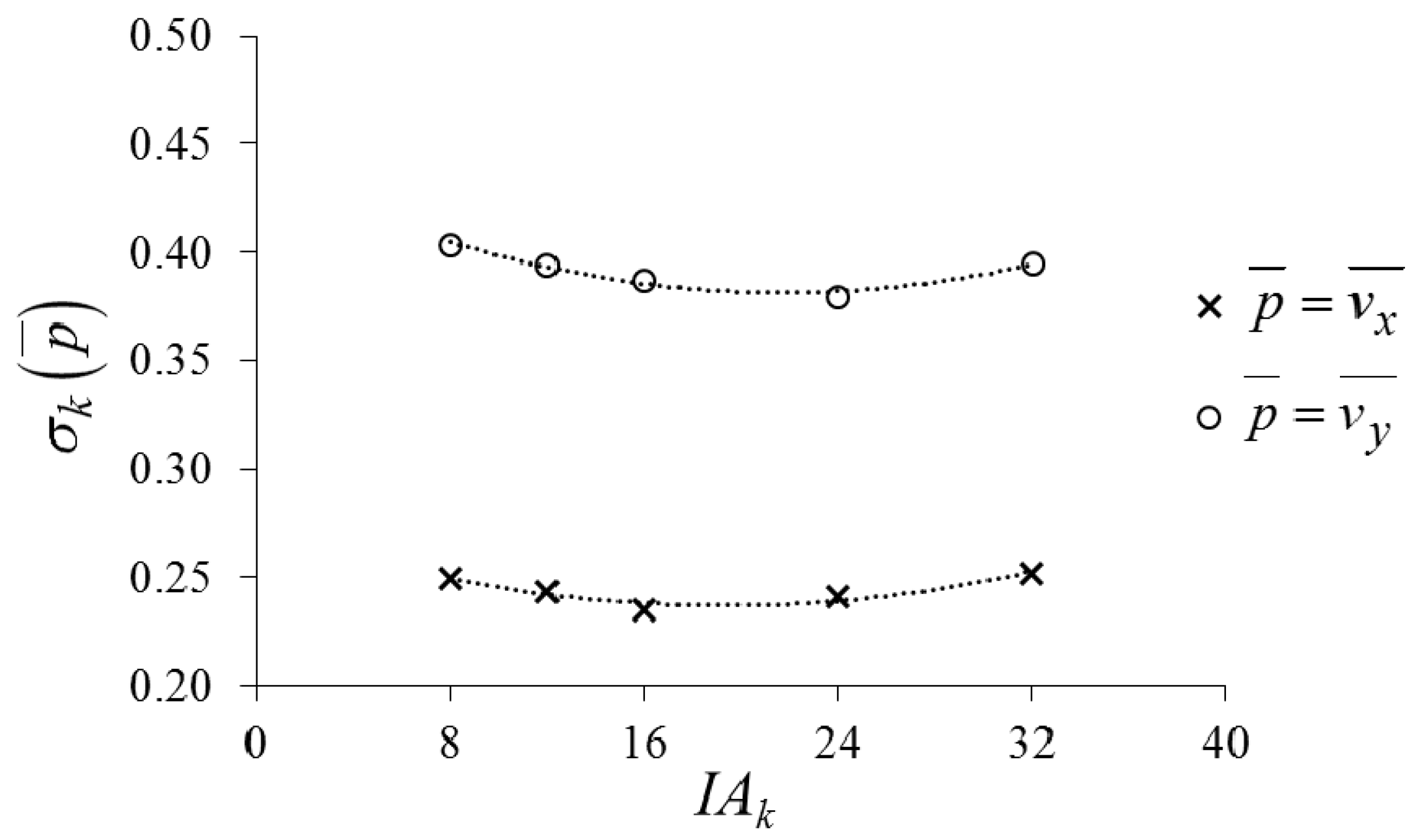
- the size of the interrogation area plays an important role in the surface velocity estimation. It has been verified that the number of nodes increases with a logarithm law as the interrogation area decreases. But, the problem is that a high extension of the data sample makes the modeling process too time-consuming. As result of the sensitivity analysis of the surface velocity to the size of the interrogation area, it has been found that a reduction of the size of the interrogation area of about one half compared to the initial size represents a good compromise between the extension of the data sample and the accurate estimation of flow velocity;
- -
- the application of the PIV method has provided detailed information of the spatial distributions of instantaneous surface velocity vectors and of free surface perturbations related to the formation of large eddies downstream of the confluences. Furthermore, by using the spatial distributions of time-averaged surface velocity obtained by applying the PIV analysis, the values of the discharge in peculiar sections along the channel have been estimated. The good agreement between the estimated values of the discharge and the measured ones has demonstrated the ability of the digital image-technique for remote monitoring of free-surface velocity and discharge measurement.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, R.A.; Pasternack, G.B. Hydrologic and topographic variability modulate channel change in mountain rivers. J. Hydrol. 2014, 510, 551–564. [Google Scholar] [CrossRef]
- Sukhodolov, A.; Sukhodolova, T. Evolution of mixing layers in turbulent flow over submersed vegetation: Field experiments and measurement study. In Proceedings of the International Congress Riverflow, Lisbon, Portugal, 6–8 September 2006. [Google Scholar]
- Rehmel, M. Application of Acoustic Doppler Velocimeters for Streamflow Measurements. J. Hydraul. Eng.-ASCE 2007, 133, 1433–1438. [Google Scholar] [CrossRef]
- Moramarco, T.; Singh, V.P. Formulation of the entropy parameter based on hydraulic and geometric characteristics of river cross sections. J. Hydrol. Eng. 2010, 15, 852–858. [Google Scholar] [CrossRef]
- Moramarco, T.; Termini, D. Entropic approach to estimate the mean flow velocity: Experimental investigation in laboratory flumes. Environ. Fluid Mech. 2015, 15, 1163–1179. [Google Scholar] [CrossRef]
- Termini, D.; Moramarco, T. Application of entropic approach to estimate the mean flow velocity and manning roughness coefficient in a high-curvature flume. Hydrol. Res. 2016, 48, 634–645. [Google Scholar] [CrossRef]
- Schabacker, J.; Bölcs, A. Investigation of Turbulent Flow by means of the PIV Method. In Proceedings of the 13th Symposium on Measuring Techniques for Transonic and Supersonic Flows in Cascades and Turbomachines, LTT-CONF-1996-001, Iowa City, IA, USA, 11–14 July 1996. [Google Scholar]
- Jodeau, M.; Hauet, A.; Paquier, A.; Le Coz, J.; Dramais, G. Application and evaluation of LS-PIV technique for the monitoring of river surface in high flow conditions. Flow Meas. Instrum. 2008, 19, 117–127. [Google Scholar] [CrossRef]
- Hauet, A.; Creutin, J.D.; Belleudy, P.; Muste, M.; Krajewski, W. Discharge measurement using Large Scale PIV under varied flow conditions—Recent results, accuracy and perspectives. In Proceedings of the International Congress Riverflow, Lisbon, Portugal, 6–8 September 2006. [Google Scholar]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef]
- Voulgaris, G.; Trowbridge, J.H. Evaluation of the acoustic doppler velocimeter (ADV) for turbulence measurements. J. Atmos. Ocean. Technol. 1998, 15, 272–289. [Google Scholar] [CrossRef]
- Pereira, F.; Gharib, M.; Dabiri, D.; Modarress, D. Defocusing DPIV: A 3-component 3-D DPIV measurement technique application to bubbly flows. Exp. Fluids 2000, 29, S78–S84. [Google Scholar] [CrossRef]
- García, C.; Cantero, M.; Niño, Y.; García, M. Turbulence Measurements with Acoustic Doppler Velocimeters. J. Hydraul. Eng.-ASCE 2005, 131, 1062–1073. [Google Scholar] [CrossRef]
- Sarno, L.; Papa, M.N.; Tai, Y.C.; Carravetta, A.; Martino, R. A reliable PIV approach for measuring velocity profiles of highly sheared granular flows. In Proceedings of the 7th International Conference on Engineering Mechanics, Structures, Engineering Geology. WSAS Conference, Salerno, Italy, 3–5 June 2014; pp. 134–141. [Google Scholar]
- Creutin, J.; Muste, M.; Bradley, A.; Kim, S.; Kruger, A. River gauging using PIV technique: A proof of concept experiment on the Iowa River. J. Hydrol. 2003, 277, 182–194. [Google Scholar] [CrossRef]
- Adrian, R.J. Twenty years of particle image velocimetry. Exp. Fluids 2005, 39, 159–169. [Google Scholar] [CrossRef]
- Medina, V.; Bateman, A. Debris flow entrainment experiments at UPC, interpretation and challenges. In Proceedings of the 7th International Conference on Engineering Mechanics, Structures, Engineering Geology, WSAS Conference, Salerno, Italy, 3–5 June 2014; pp. 38–44. [Google Scholar]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1998, 36, 397–414. [Google Scholar] [CrossRef]
- Rahimzadeh, H.; Fathi, N.; Assodeh, M.H. An Experimental Model of Flow Surface Patterns at Vertical Downward Intake with Numerical Validation. In Proceedings of the 2006 IASME/WSEAS International Conference on Water Resources. Hydraulics & Hydrology, Chalkida, Greece, 11–13 May 2006; pp. 111–118. [Google Scholar]
- Meselhe, E.; Peeva, T.; Muste, M. Large Scale Particle Image Velocimetry for Low Velocity and Shallow Water Flows. J. Hydraul. Eng.-ASCE 2004, 130, 937–940. [Google Scholar] [CrossRef]
- Lueptow, R.M.; Akonur, A.; Shinbrot, T. PIV for granular flows. Exp. Fluids 2000, 18, 183–186. [Google Scholar] [CrossRef]
- Eckart, W.; Gray, J.M.N.T.; Hutter, K. Particle Image Velocimetry (PIV) for Granular Avalanches on Inclined Planes; Hutter, K., Kirchner, N., Eds.; Springer: Berlin, Germany, 2003; pp. 195–218. [Google Scholar]
- Pudasaini, S.P.; Hsiau, S.S.; Wang, Y.; Hutter, K. Velocity measurements in dry granular avalanches using particle image velocimetry technique and comparison with theoretical predictions. Phys. Fluids 2005, 17, 093301. [Google Scholar] [CrossRef]
- Pudasaini, S.P.; Hutter, K.; Hsiau, S.S.; Tai, S.C.; Wang, Y.; Katzenbach, R. Rapid flow of dry granular materials down inclined chutes impinging on rigid walls. Phys. Fluids 2007, 19, 053302. [Google Scholar] [CrossRef]
- Sheng, L.T.; Kuo, C.Y.; Tai, Y.C.; Hsiau, S.S. Indirect measurements of streamwise solid fraction variations of granular flows accelerating down a smooth rectangular chute. Exp. Fluids 2011, 51, 1329. [Google Scholar] [CrossRef]
- Sarno, L.; Papa, M.N.; Villani, P.; Tai, Y.C. An optical method for measuring the near-wall volume fraction in granular dispersions. Granul. Matter 2016, 18, 80. [Google Scholar] [CrossRef]
- Sarno, L.; Carleo, L.; Papa, M.N.; Villani, P. Experimental Investigation on the Effects of the Fixed Boundaries in Channelized Dry Granular Flows. Rock Mech. Rock Eng. 2018, 51, 203–225. [Google Scholar] [CrossRef]
- Sarno, L.; Carravetta, A.; Tai, Y.C.; Martino, R.; Papa, M.N.; Kuo, C.Y. Measuring the velocity fields of granular flows–Employment of a multi-pass two-dimensional particle image velocimetry (2D-PIV) approach. Adv. Powder Technol. 2018. [Google Scholar] [CrossRef]
- Lauterborn, W.; Vogel, A. Modern Optical Techniques in Fluid Mechanics. Annu. Rev. Fluid. Mech. 1984, 16, 223–244. [Google Scholar] [CrossRef]
- Huang, H.; Dabiri, D.; Gharib, M. On errors of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1427–1440. [Google Scholar] [CrossRef]
- Huang, H.T.; Fiedler, H.E.; Wang, J.J. Limitation and Improvement of PIV. Exp. Fluids 1993, 15, 263–273. [Google Scholar] [CrossRef]
- Hart, D.P. Piv error correction. Exp. Fluids 2000, 29, 13–22. [Google Scholar] [CrossRef]
- Termini, D.; Di Leonardo, A. Propagation of Hyperconcentrated flows in protection channels around urban areas: Experimental investigation. In Urban and Urbanization, 1st ed.; St. Kliment Ohridski University Press: Sofia, Bulgaria, 2014; pp. 125–133. [Google Scholar]
- Termini, D.; Di Leonardo, A. Hyper-concentrated flow and surface velocity estimation: A study case. In Proceedings of the 8th International Conference on Environmental and Geological Science and Engineering. WSAS Conference, Salerno, Italy, 27–29 June 2015. [Google Scholar]
- Termini, D.; Di Leonardo, A. Digital image-based technique for monitoring surface velocity: Sensitivity analysis with processing parameters using data of a study case. In Proceedings of the Riverflow 2016, Iowa City, IA, USA, 27–29 July 2016. [Google Scholar]
- Thielicke, W.; Stamhuis, E.J. PIVlab–Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab–Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB (version: 1.43). 2014. Available online: http://dx.doi.org/10.6084/m9.figshare.1092508 (accessed on 2 August 2005).
- Thielicke, W. The Flapping Flight of Birds–Analysis and Application. [S.l.]: [S.n.]. Ph.D. Thesis, Rijksuniversiteit Groningen, Groningen, The Netherlands. Published in 2014. Available online: http://irs.ub.rug.nl/ppn/382783069 (accessed on 16 October 2018).
- Kantoush, S.A.; Schleiss, A.J.; Sumi, T.; Murasaki, M. LSPIV implementation for environmental flow in various laboratory and field cases. J. Hydro-Environ. Res. 2011, 5, 263–276. [Google Scholar] [CrossRef]
- Rowinski, P. Experimental Methods in Hydraulic Research; Springer: Berlin, Germany, 2011. [Google Scholar]
- Utami, T.; Blackwelder, R.F. A cross-correlation technique for velocity field extraction from particulate visualization. Exp. Fluids 1991, 10, 213–223. [Google Scholar] [CrossRef]
- Grossfield, A.; Zuckerman, D. Quantifying uncertainty and sampling quality in biomolecular simulations. Ann. Rep. Comput. Chem. 2009, 1, 23–48. [Google Scholar]
- Gonzales, R.; Wintz, P. Digital Image Processing; Longman Higher Education: Harlow, UK, 1997. [Google Scholar]
- Scarano, F.; Riethmuller, M.L. Iterative multigrid approach in PIV image processing with discrete window offset. Exp. Fluids 1999, 26, 514–523. [Google Scholar] [CrossRef]
- Willert, C.E.; Gharib, M. Digital particle image velocimetry. Exp. Fluids 1999, 10, 181–193. [Google Scholar] [CrossRef]
- Polatel, C. Indexing free-surface velocity: A prospect for remote discharge estimation. In Proceedings of the 31th Congress International International Association Hydraulic Engineering and Research, Seoul, Korea, 11–16 September 2005. [Google Scholar]
- Welber, M.; Le Coz, J.; Laronne, J.B.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
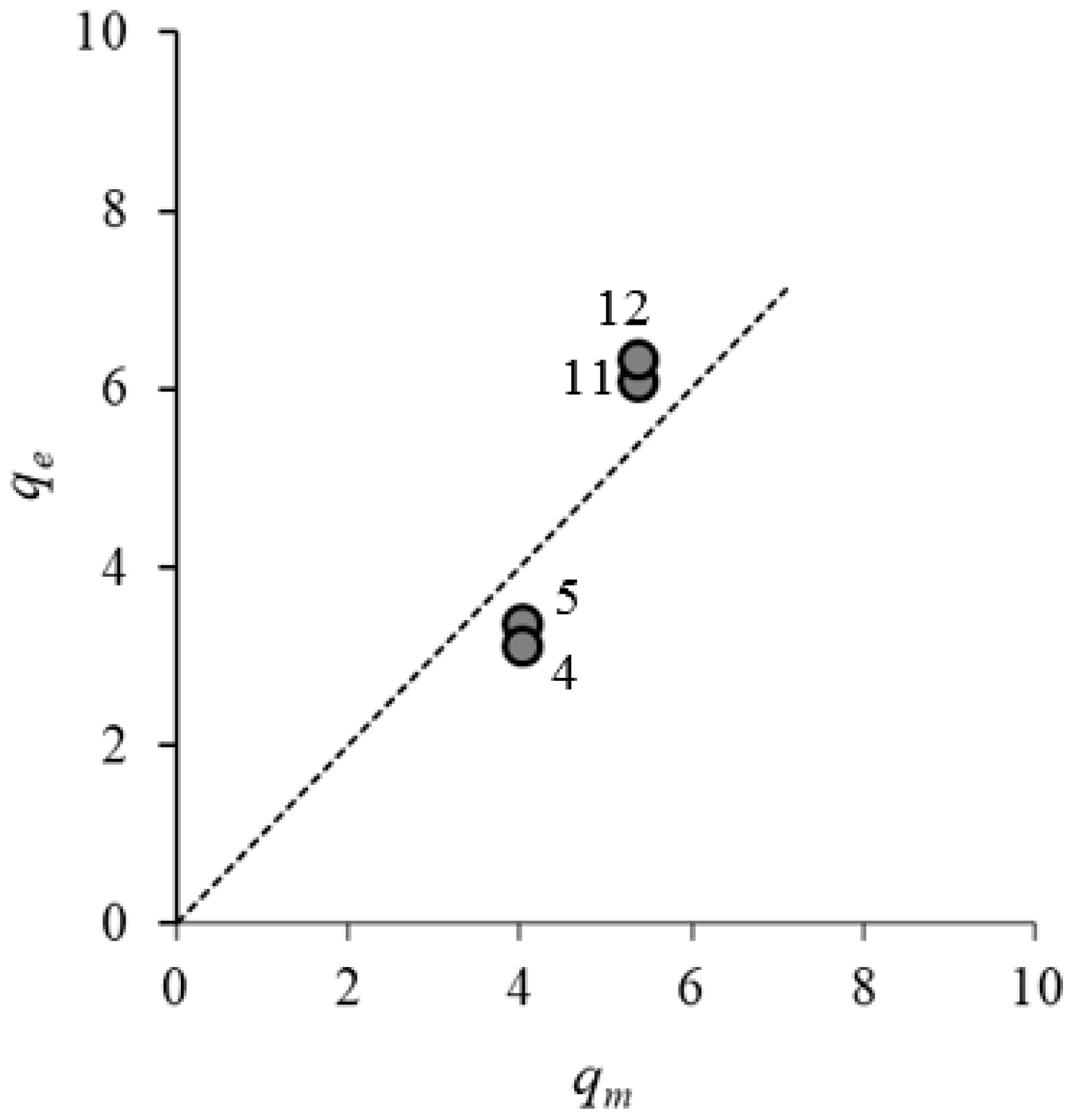
| Section | σq | qe (m3/s) |
|---|---|---|
| 4 | 0.17 | 0.0035 |
| 5 | 0.22 | 0.0033 |
| 11 | −0.13 | 0.0061 |
| 12 | −0.18 | 0.0063 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Termini, D.; Di Leonardo, A. Efficiency of a Digital Particle Image Velocimetry (DPIV) Method for Monitoring the Surface Velocity of Hyper-Concentrated Flows. Geosciences 2018, 8, 383. https://doi.org/10.3390/geosciences8100383
Termini D, Di Leonardo A. Efficiency of a Digital Particle Image Velocimetry (DPIV) Method for Monitoring the Surface Velocity of Hyper-Concentrated Flows. Geosciences. 2018; 8(10):383. https://doi.org/10.3390/geosciences8100383
Chicago/Turabian StyleTermini, Donatella, and Alice Di Leonardo. 2018. "Efficiency of a Digital Particle Image Velocimetry (DPIV) Method for Monitoring the Surface Velocity of Hyper-Concentrated Flows" Geosciences 8, no. 10: 383. https://doi.org/10.3390/geosciences8100383
APA StyleTermini, D., & Di Leonardo, A. (2018). Efficiency of a Digital Particle Image Velocimetry (DPIV) Method for Monitoring the Surface Velocity of Hyper-Concentrated Flows. Geosciences, 8(10), 383. https://doi.org/10.3390/geosciences8100383






