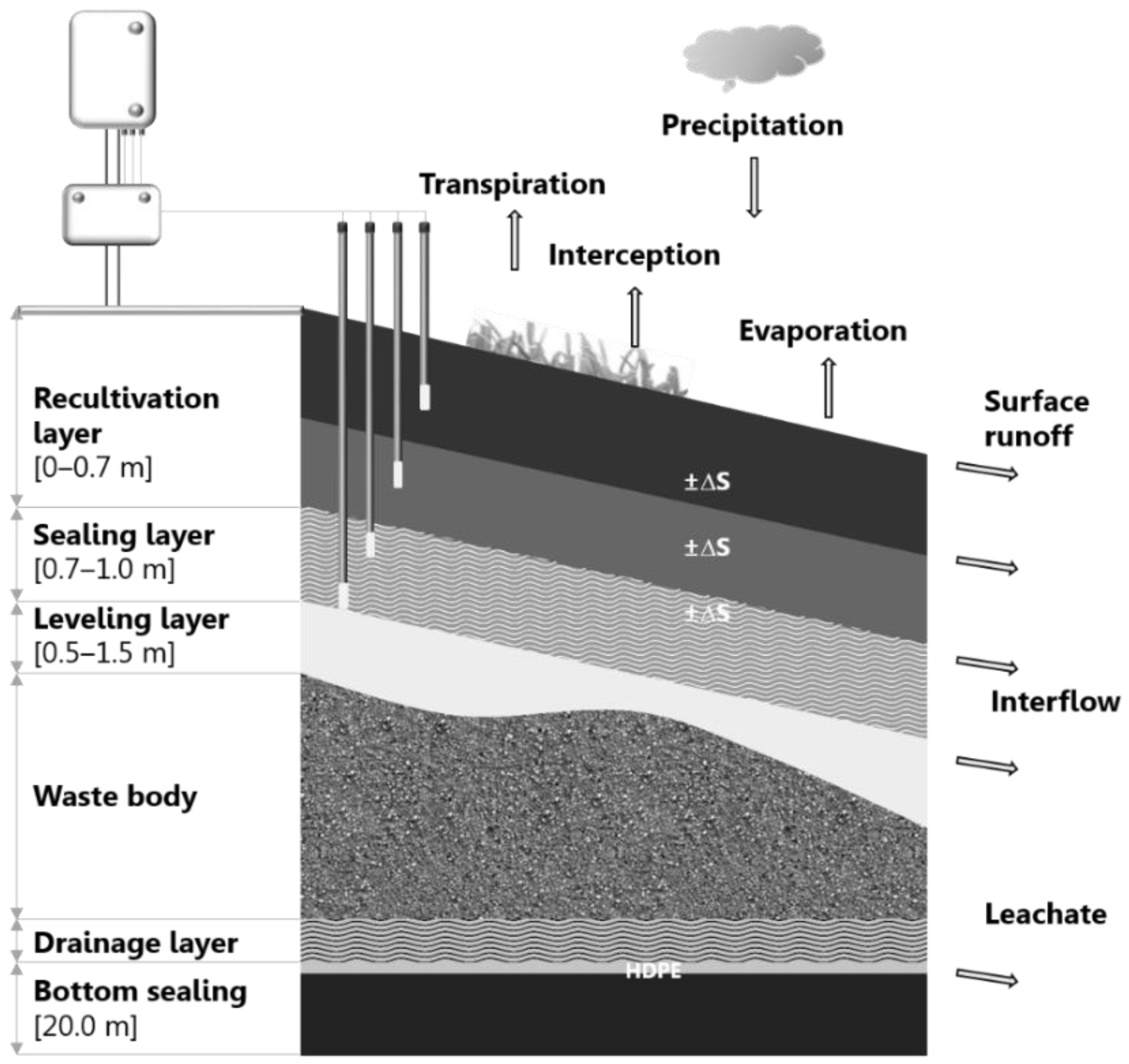
2.1. Study Site
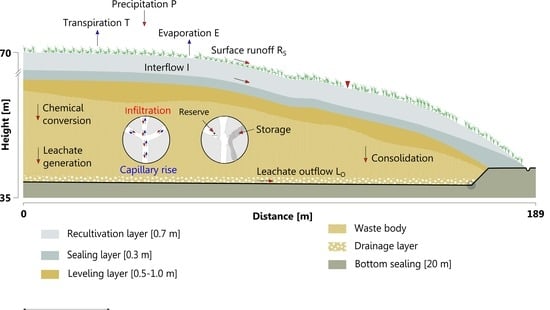
The Rastorf landfill in Schleswig-Holstein (Northern Germany) is divided into three areas: I (21,275 m
2), II (29,961 m
2), and III (22,208 m
2), and consists of a bottom layer of hardly permeable clay up to 20 m thick (
Figure 1).
A high-density polyethylene layer of 2.5 mm thickness and an added drainage system above the clayey bottom layer collects the leachate before treatment by reverse osmosis.
The 1.0 m thick mineral capping system consists of a recultivation layer and a sealing layer. The recultivation layer consists of a 0.4 m humic top soil and a 0.3 m sandy loam substrate with minor organic carbon content in its function as combined evapotranspiration and lateral drainage layer above the sealing layer. The 0.3 m thick sealing layer serves as root barrier and provides a downslope lateral drainage (interflow) below the recultivation layer.
The landfill surface is covered with different types of grass: Perennial ryegrass (Lolium perenne), meadow fescue (Festuca pratensis), red fescue (Festuca rubra), sheep fescue (Festuca ovina), and orchard grass (Dactylis glomerata) with a surface distribution of 90%–95%, while the rest is distributed among white clover (Trifolium repens) and red clover (Trifolium pratense). In relation to grassland management, two cuts per year are essential.
2.3. Observation of the Water Balance Components of the Rastorf Landfill
In order to calculate the water balance for each area (I, II, III) a weather station (UGT, Freising, Germany) located close to the landfill (54°28′11″ N, 10°32′18″ E) recorded actual meteorological data, such as precipitation, air temperature, wind speed, wind direction, air pressure, and relative humidity, on daily basis. Global solar radiation was calculated on the basis of the following literature [
18,
19,
20]. In addition, wind speed was measured at 10 m height and a logarithmic approximation was used to calculate wind speed for 2 m height [
21]. Leaf area index (LAI) was calculated on the basis of the quarterly measured average vegetation height (z) in meters (m) in 8–10 repetitive transects (1 m
2) per area with a folding ruler as follows [
19]:
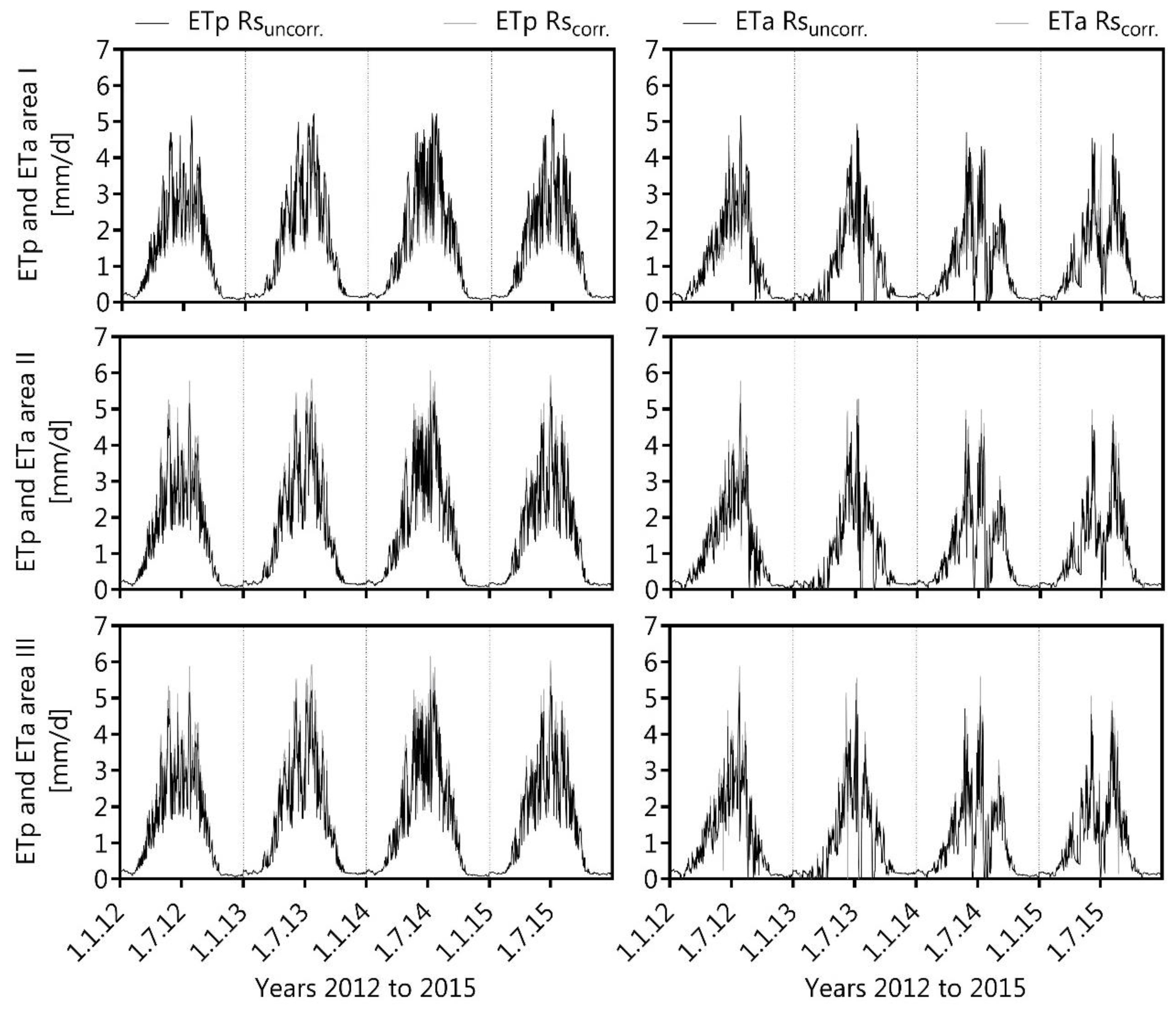
Actual evapotranspiration was estimated as a residual value using the water-balance equation; interception height was calculated according to the literature [
22] with an LAI of 2 m
2/m
2 in the winter period and 4 m
2/m
2 in the summer period, respectively.
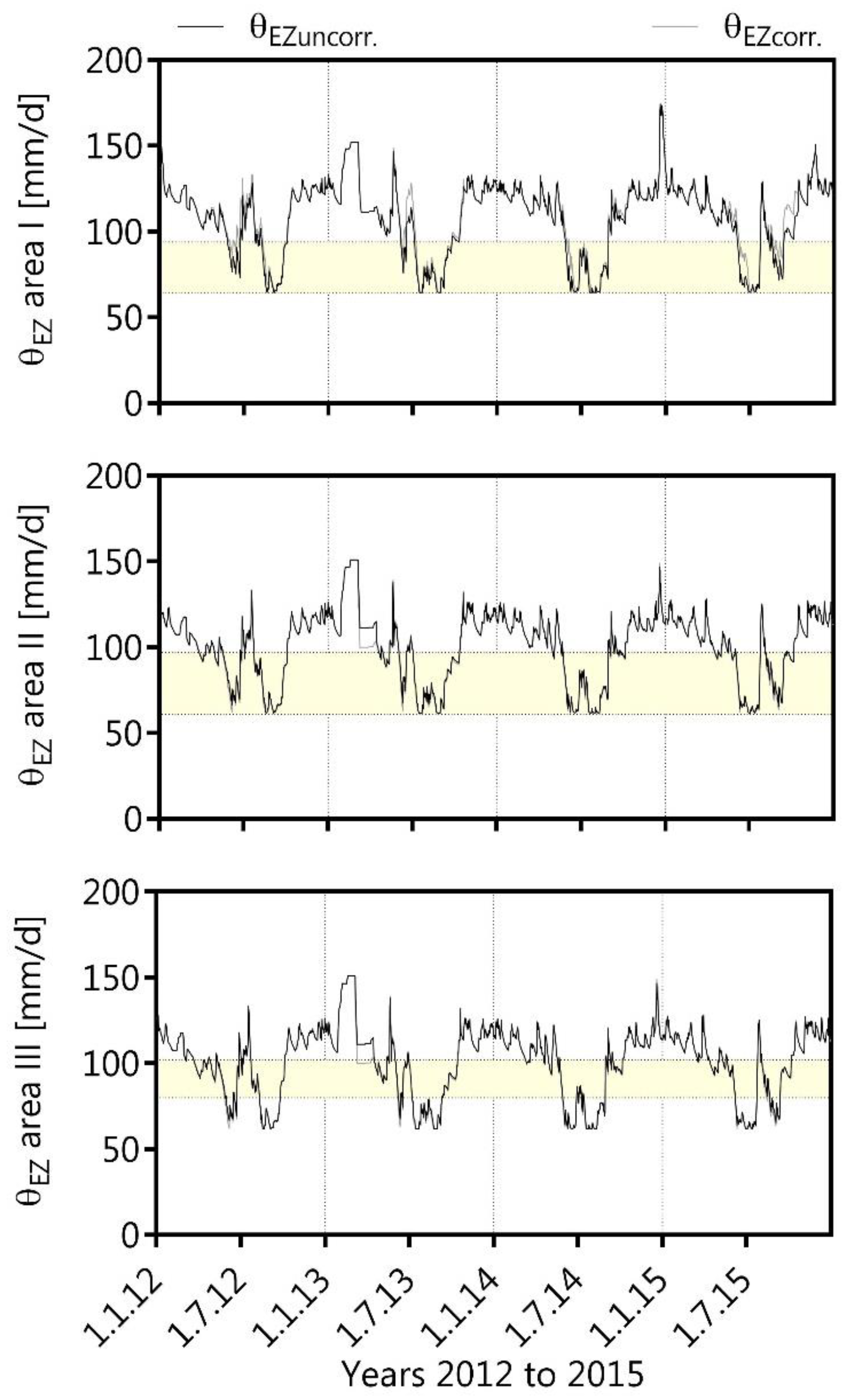
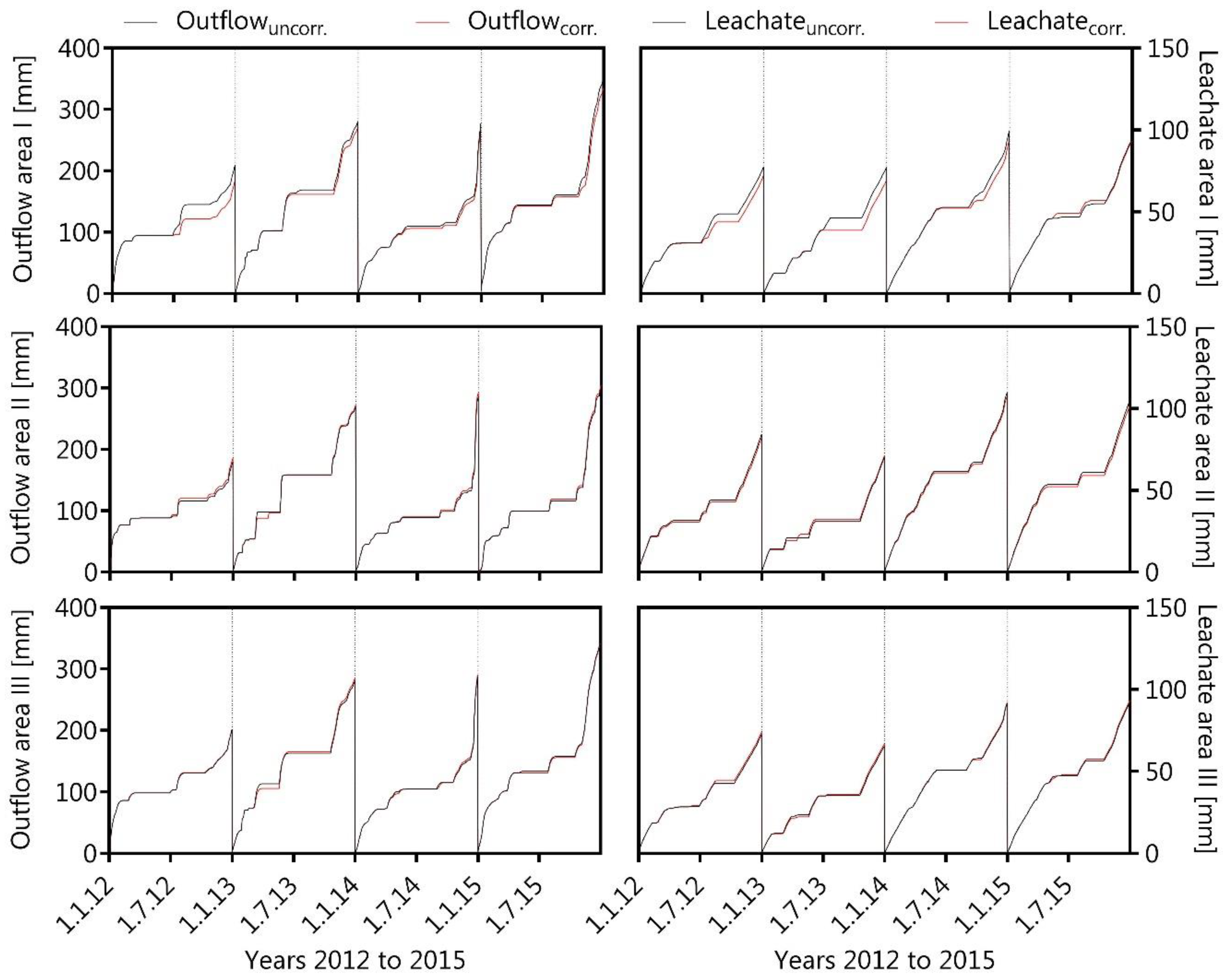
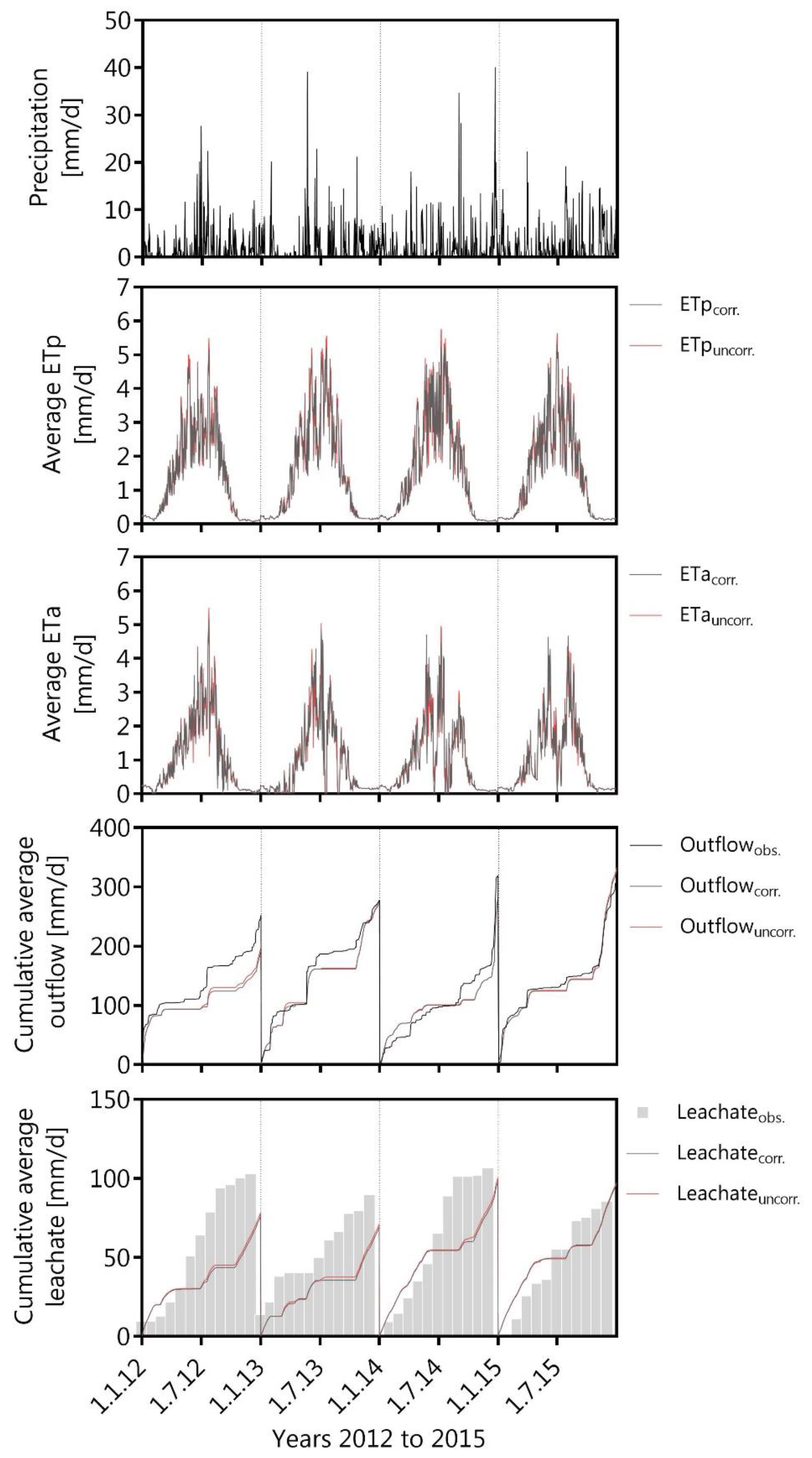
The surface runoff and the interflow were captured in 6 areas through (a) v-notch weirs with electric contact gauges that recorded water levels in the shafts and data loggers that calculate flow rates between 0.04 dm3/ and 315 dm3/s, and (b) tipping counters with a maximum flow capacity of 60 dm3 per 10 min, respectively. The leachate rate as water percolation through the waste body was estimated on a monthly basis using data from the landfill leachate-treatment (reverse osmosis) facility. In addition, changes in soil-moisture contents at the beginning of each year were continuously estimated by the Theta Probe ML2x frequency domain that recorded the water content in 0.2, 0.5, 0.8, and 1.0 m depth with a standard data logger DL 200 (Umwelt-Geräte-Technik GmbH, Müncheberg, Germany).
2.4. HELP Model
The HELP model is a quasi-two-dimensional hydrologic model that combines one-dimensional soil physical and hydrological processes in (a) vertical direction (saturated and unsaturated vertical flow) and (b) lateral direction (i.e., lateral drainage) according to the literature [
10]. Thus, the model requires landfill design and weather data as well as material properties such as porosity (TP), field capacity (FC), wilting point (WP), and Ks values as input parameters, regularly [
23]. In addition, the evaporative zone is typically equal to root depth, estimated with field-tracer experiments (Brilliant Blue tracer) and also calculated on the basis of FC, PWP, and actual water content for autumn in a dry year (i.e., 2008) following reference [
24] that equals the maximum soil depth from which water can be removed through evapotranspiration [
3,
25]. With respect to the landfill design data, the upper part of the recultivation layer (0–0.4 m) was classified as the vertical percolation layer, the bottom part (0.4–0.7 m) was conducted as the lateral drainage layer to consider lateral saturated hydraulic conductivity, and the water flow between areas I, II, and III is restricted by the drainage system (constrained condition). The sealing layer was classified as the barrier soil liner.
Water balance calculations are based on analytical and empirical equations, of which a detailed description is given by the following equation [
23,
25],
where L = leachate rate, P = precipitation, ETa = actual evapotranspiration (including interception), R = runoff, D = lateral drainage, ∆S = change in soil moisture content in mm per year, and m
3 and the time, t, is calculated in daily steps, subscript i, from 1 January 2012 until 31 December 2015 (1460 days).
The potential evapotranspiration consists of (a) evaporation of the surface water (primarily evaporation of intercepted water, plus the evaporation of snow), (b) soil evaporation, and (c) plant transpiration computed by a simplified approach [
26],
where E
oi = potential evapotranspiration on day i (mm), PENR
i = radiative component on day i (langleys), where 1 langley = 41,840 J/m
2, PENA
i = aerodynamic component on day i (langleys), L
v = latent heat for vaporization (for evaporating water) or latent heat of fusion (for evaporating snow) in langleys per mm of water, T
d = dew-point and T
s = snow temperature (°C).
The ETa was mainly calculated according to procedure described by reference [
27] using a model of vegetation growth and decay [
28]. Thus, the vegetative growth and decay submodel included in HELP was taken from the simulation model for water resources in rural basins (SWRRB) [
28], whose developers adopted it in a simplified form from the EPIC model [
29]. Therefore, FC (US: −33 kPa) is the lowest soil water content to allow unsaturated vertical flow (drainage) within the evaporative zone [
30]. The interception-storage and interception-height capacity were calculated by the approach of reference [
22], modified and adapted to German standards [
31]. Vertical percolation (drainage) is modeled according to Darcy (1856) [
32] using the equation for unsaturated hydraulic conductivity K(h) in cm/s, which again is based on the approach of reference [
33]. Saturated lateral drainage is modeled after a steady-state solution of the Boussinesq equation in combination with the Dupuit–Forchheimer assumptions [
34], which consider the Ks value of the drainage layer. The K(h) values for each soil layer were calculated based on measurements of changes in the water content and matric potential over depth and time as follows,
where θ = actual volumetric water content (m
3/m
3), θ
r = residual volumetric water content (m
3/m
3), Φ = total porosity (m
3/m
3), λ = pore-size distribution index (-), and WP = wilting point (m
3/m
3).
The HELP model allows only downward flow in barrier soil liners, while the leachate rate (percolation through the layer) depends upon the depth of the water-saturated soil (head) above the base of the layer, the liner thickness, and the Ks value of the barrier soil. Leachate occurs under those conditions whenever the moisture content of the layer above the liner is greater than the field capacity of the layer [
23,
25].
The rainfall–runoff process is modeled using the SCS curve-number method with values above 0 up to 100 [
35]. Therefore, the curve number (CN) is an empirical parameter to predict runoff or infiltration from rainfall excess. CN values for areas I, II, and III were obtained under the terms of the surface slope, the slope length, and the vegetation cover, and also modified according to the previous sensitivity analysis [
36],
where R = runoff (m
3), P = precipitation (m
3), S = potential maximum soil-moisture retention when the runoff begins (m
3), I
a = initial water abstractions (sum of interception + evapotranspiration + infiltration + depression storage) in m
3, and CN = curve number.
The lateral drainage layer required information about maximum drainage length as length of the horizontal projection of a representative flow path and the drain slope for areas I, II, and III. Therefore, the lateral drainage equation written in dimensionless form as [
23],
where x* = x/L (dimensionsless horizontal distance), y* = y/L (dimensionsless depth of saturation above liner), q
D* = q
D/K
D (dimensionsless lateral drainage rate) with K
D = saturated hydraulic conductivity of the drain layer (cm/s), and α = inclination angle of the liner surface.
2.6. Model Calibration and Sensitivity Analysis
Calibration is the adaption of the model to reality; thus, various procedures are possible for calibration. In this study, the calibration procedure for the period from 2008 to 2011 is shown for Area I. Therefore, a so-called ‘zero alternative’ (
za) was used, where all input variables were set to values determined in the laboratory. The ‘zero-alternative’ is not actually a calibration in the strict sense, but a simulation with observed values to check the quality of observed input quantities for the estimation of output quantities [
37]. For calibration in the strict sense, input data were stepwise changed to minimize the deviation between the observed and modeled (a) outflow and (b) leachate data, also well described for the Rastorf landfill with the so-called ‘calibration alternative’ (
ca) in the literature [
38]. Analogous to the validation study for the HELP model [
37], calibration data should be changed until the modeled output quantities are reproduced to within 0.1 mm of the observed data. The last step included the validation of the model for the period from 2012 to 2015, because the validity of the input and output data for the comparison of observed and modeled data is of major importance [
31,
39].
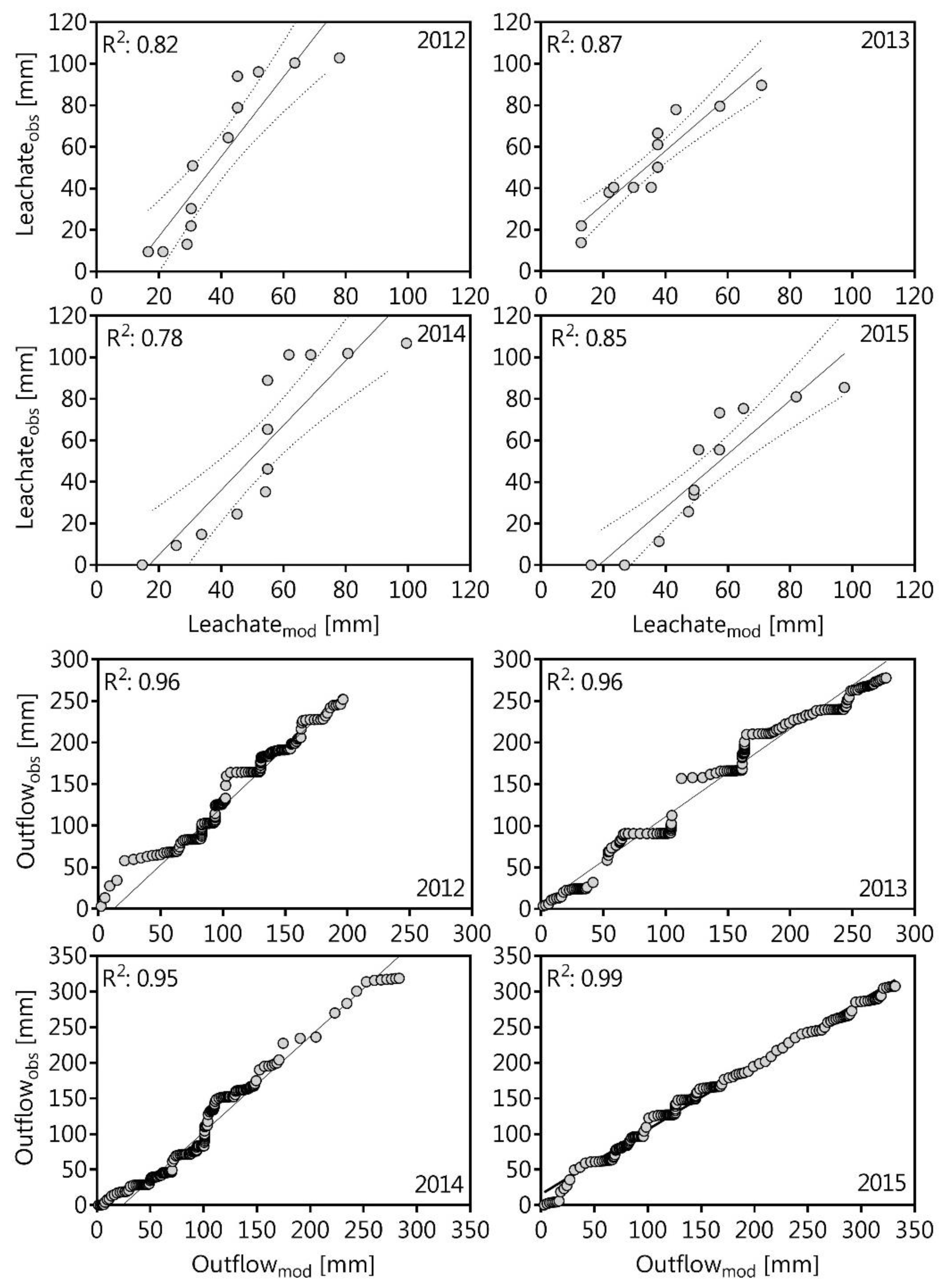
In this study, evaporative zone depth and slope gradient were used as parameters for sensitivity analysis, while soil physical properties did not change over time. Statistical quality criteria were used to represent the deviations between the modeled (x
mod) and the observed (x
obs) water balance parameters [
40]. Therefore, the higher the arithmetic mean, the higher the root mean square error (RMSE):
The RMSE observations’ standard deviation ratio (RSR) was calculated as the ratio of the RMSE and standard deviation of the observed data [
41]:
The model quality can be obtained by the Nash–Sutcliffe efficiency index as the sum of the absolute squared differences between modeled and observed data as follows [
39,
42]:
In addition to a perfect linear relationship (NSE = 1), an NSE value < 0 indicates that the averaged observed data provide a better prediction of the problem than the modeled data [
39].
The coefficient of determination (R
2) is an index of goodness of fit and is determined from the covariance of the modeled and observed data and their individual variances [
41]: