Abstract
This study assessed the uncertainty in flood impact assessment (FIA) that may be introduced by errors in moderate resolution regional and moderate resolution global Digital Elevation Models (DEM). One arc-second National Elevation Dataset (NED) and one arc-second Shuttle Radar Topography Mission (SRTM) DEMs were selected to represent moderate resolution regional and global DEMs. The relative performance for scenarios based on each of the DEMs was compared to a “control” terrain (combination of surveyed river bathymetry and a 1/3 arc-second LiDAR for floodplains)-based scenario. Furthermore, a conveyance-based DEM correction technique was applied to the DEMs for investigating the suitability of the technique on selected DEMs, and determining subsequent improvement in the FIA. The May 2010 flood on the Cumberland River near Nashville, TN, was selected as the case study. It was found that the hydraulic properties necessary to implement the selected DEM correction technique could be more readily estimated from NED compared to SRTM. However, this study also prescribed alternate methods to extract necessary hydraulic properties if the DEM quality was compromised. NED-based hydrodynamic modeling resulted in a high overestimation of the simulated flood stage, but the SRTM-based model was unable to produce any reasonable result prior to DEM correction. Nevertheless, after DEM correction, both models became stable and produced less error. Error in simulated flood consequence (i.e., total structures affected and total loss in dollars) also dropped accordingly, following the DEM correction. Therefore, application of this conveyance-based correction technique is reasonably effective on both moderate-resolution regional and global DEMs. The effectiveness of the technique on moderate resolution global DEM underscores the potential for users of remote and data-poor areas.
1. Introduction
Floods account for 43% of all natural disasters [1] that cause death, adverse health effects, property damage, and socio-economic imbalance [2,3,4]. By 2001, flooding became seven times more frequent around the world compared to 1975. From 1975 to 2001, the number of people at risk and fatalities due to floods increased by nine times [5]. The increasing trend of flood disasters continued into the 21st century as well. Between 1995 and 2015, floods affected 2.3 billion people globally and killed 157,000 [1]. Increasing flood frequency, along with unplanned urbanization, population growth, and resource limitation is making flood risk management more challenging [6,7]. However, two-thirds of flood-related economic losses remain unreported [8]. This data gap is more prevalent in developing countries than in developed ones. Therefore, it is a global concern because sustainable flood risk management (FRM) attempts to combine the knowledge from past events and the existing situation to better prepare for the future. Flood impact assessment (FIA) is an important component of FRM that estimates the direct and indirect consequences of a flood event. Necessary flood parameters (i.e., depth, extent, velocity, duration) for consequence assessment are commonly derived from hydrodynamic modeling.
The accuracy of both hydrodynamic modeling and FIA are subject to accuracy and availability of data (i.e., hydrologic, terrain, land use, infrastructure). For instance, Bhuyian and [9] showed that flood consequence estimates could be affected by the elevation error (hereafter called as “error”) and spatial resolution of the Digital Elevation Model (DEM). Root mean square error (RMSE) for some of the commonly used DEMs such as National Elevation Dataset (NED), Shuttle Radar Topography Mission (SRTM), and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) version 2 are 1.84, 4.01, and 8.68 m respectively at one-arc second spatial resolution [10]. Global DEMs (i.e., SRTM and ASTER) often have a higher error but are suitable for remote areas for their wider coverage. However, SRTM is a better choice for flood modeling in such areas, considering the low RMSE and recently (the year 2015) published one-arc second products for areas outside of the USA. Therefore, being able to reduce errors in SRTM DEM would help to improve FIA in remote and data-poor areas.
The primary sources of error in a spaceborne DEM (i.e., SRTM) are speckle noise, stripe noise, absolute bias, and tree height bias, in addition to the inability of mapping river bathymetry [11,12,13,14]. The first four error sources primarily affect hydraulic connectivity within the floodplain, and inaccurate river bathymetry affects the river conveyance. Spaceborne, regional and local DEMs all suffer from the limited representation of river bathymetry. This is often supplemented by overlaying surveyed river cross sections on a reach scale. However, this approach is unfeasible on a regional to global scale [13]. There have been multiple methods in practice to correct DEM for better representation of river conveyance in the absence of surveyed cross sections. The existing methods are either based on a prismatic channel assumption or limited to only water surface elevation (WSE) prediction [14,15,16,17]. However, river planform (i.e., channel alignment, width, curvature, etc.) itself is dynamic [18], which may dictate the flow parameters (i.e., stage, flow, inundation, velocity) and, hence, influence flood consequences. Considering the existing approaches, [19] proposed a conveyance-based DEM correction technique combining river planform, geometry, and historical stage-discharge relation to generating modified bathymetry along defined cross-sections. This technique incorporates channel conveyance along with the location of thalweg in parabolic shaped cross-sections. They were able to implement the DEM correction technique on a 1/3 arc-second NED DEM to perform hydrodynamic simulations of historic flood events. However, extra effort may be required if DEM correction is intended on a global DEM such as SRTM, because of high error (channels and floodplains) and moderate resolutions of global DEMs. Moderate-resolution DEMs are often preferred for ease of data handling or lack of fine resolution data for FIA. Therefore, it is important to estimate the extent to which conveyance-based DEM correction technique can perform using moderate resolution regional or global DEM.
Another motivation for exploring errors in global DEMs is to aid the future satellite remote sensing missions expected to map indirectly floodplain elevations on a global scale. One such mission is the proposed Surface Water Ocean Topography (SWOT) mission [20]. SWOT aims to provide an understanding of the behavior of river water elevation that is 100 m wide against the backdrop of human impacts on the water cycle (i.e., global warming, river regulation, etc.). Although SWOT’s signal-to-noise ratio for land topography is expected to be poor, it is expected that many years of repeatedly using SWOT to make elevation observations of water inundation extent in dynamic rivers can help create a globally consistent “floodplain DEM.” This can be used to aid the community’s existing efforts on flood inundation already being done through satellite imagery [21,22]. Thus looking for possible solutions via linking remotely sensed river water elevation (i.e., SWOT) with existing DEM correction techniques would help reducing dependence on in-situ stage measurements.
The research questions presented in this study were (i) what are the limitations of implementing a conveyance-based DEM correction on a moderate resolution (one-arc second) regional (i.e., NED) or global DEM (i.e., SRTM)? (ii) What is the corresponding impact in FIA after applying a conveyance-based DEM correction technique to the aforementioned DEMs? These questions were addressed through the following objectives:
- To implement a conveyance-based DEM correction technique [19] on moderate resolution NED and SRTM DEMs.
- To estimate the impact on FIA after applying the conveyance-based DEM correction technique on selected NED and SRTM DEMs.
2. Methodology
The scope of this study was limited to correcting one moderate resolution regional DEM and one moderate resolution global DEM dataset for FIA of the 2010 Nashville flood. The uncorrected DEMs are hereafter called “base” DEMs. This study applied the DEM correction technique by [4] on the base DEMs to quantify the relative improvement in FIA. DEMs are called “modified” DEMs after applying the aforementioned DEM correction. The base and modified DEM datasets are collectively called “test” terrain datasets. A “control” terrain dataset was produced from the best available terrain dataset at disposal. Models based on control and test terrain datasets are hereafter named “control scenario” and “test scenarios.” The relative accuracies of FIAs derived from test scenarios were compared to the control scenario. A summary of the methodology is presented in the next sub-sections along with a flowchart (Figure 1).
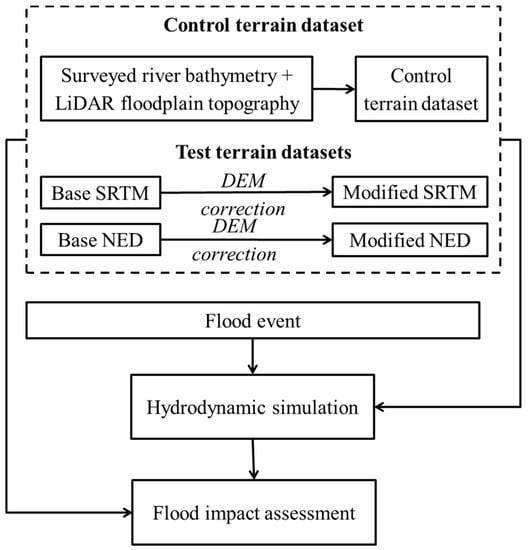
Figure 1.
Methodology flowchart.
2.1. Control and Test Terrain Datasets
First, the control terrain dataset was produced by merging field-surveyed river bathymetry and LiDAR floodplain topography. Second, base DEMs for the study area were collected from the U.S. Geological Survey (USGS) Earth Explorer. Third, the DEM correction technique as described by [19] was employed to correct the base DEMs. This correction technique works on predefined cross-section alignments and requires prior knowledge of the longitudinal slope, stage-discharge relation and flow roughness of the study reach. Four major steps of implementing this DEM correction technique are briefly described below.
2.1.1. Raster Processing
The river centerline and bank lines were traced over a Landsat satellite image. The cross-section alignments for DEM correction were kept same as the surveyed ones. The point with the steepest gradient (slope) on each side of the bank was considered as high bank points (hbp) for respective sides.
2.1.2. Hydrologic Processing
The flow corresponding to the DEM elevation at a nearby stream gage is called the “reference flow.” Reference flows corresponding to each DEM source were estimated from a stage-discharge plot of the nearby stream gage.
2.1.3. Three-Point Cross-Section Generation
The longitudinal slope of the river was estimated for each DEM source (NED and SRTM) and was calculated via linear correlation of center point elevations (from base DEMs) with respect to their chainage. A reasonable Manning’s roughness factor for the entire study reach was selected as an input for the DEM correction technique. Thalweg locations were estimated by channel width and side slope. Thalweg elevation for each cross-section was calculated via solving Manning’s equation utilizing the reference flow, longitudinal slope, and the Manning’s roughness factor.
2.1.4. Raster Modification
Modified elevation for points along the cross-sections were calculated assuming parabolic cross-sections. The point elevations were then interpolated to produce bathymetry corrected (along with the predefined river cross-sections) raster. The values of base DEM along the river were then replaced by the values from the corrected raster to produce modified DEM.
2.2. Flood Event
A historic flood event was selected for which inundation extent was readily available.
2.3. Hydrodynamic Simulation
To perform the comparative FIA, a one-dimensional hydrodynamic model was set up using the Hydrologic Engineering Center’s River Analysis System (HEC-RAS). Input hydrologic data for the hydrodynamic model was collected at available stream gages within the study area. The hydrodynamic model was calibrated for the control scenario. Manning’s roughness factor was selected as the calibration parameter while keeping the downstream flowing at a normal depth. The simulated flood extent was also compared to an observed flood inundation map to validate the performance of the control scenario. The calibrated hydrodynamic model parameters (i.e., Manning’s roughness factor) were used to simulate the test scenarios. Corresponding flood parameters (i.e., stage, flow, inundation extent) were used for FIA.
2.4. Flood Impact Assessment
The Hydrologic Engineering Center’s Flood Impact Assessment (HEC-FIA) was selected to estimate flood consequences for the study event. The ease of coupling HEC-RAS model outputs with HEC-FIA played a key role in selecting these platforms for this research. For each scenario, the geospatial information (river alignment, impact area) and simulation period were kept the same as the corresponding hydrodynamic simulation. The warning times for each scenario were also assigned, corresponding to the flood stage at a flood-warning gage within the study reach. Simulated flood parameters (maximum inundation extent, maximum depth and arrival time) for individual scenarios were furnished as the primary input for FIA. Local inventories such as infrastructures, administrative areas, and agricultural use were generated from the Hazus-MH 2.1 database. Flood consequences estimated via a control scenario were used as the baseline for comparison with test scenario-derived estimates. It was assumed that the control terrain data would best agree with the field condition because that was derived from the best available data (i.e., field-surveyed data and LiDAR).
3. Case Study and Data
3.1. Study Area
The study area was a 62 km stretch of the Cumberland River downstream of the Old Hickory Dam (OHD) to Cockril Bend near Nashville. The main stretch of the river carries releases from J. Percy Priest Dam and OHD. It also carries flows from nearby creeks such as Mill Creek, White Creek, Browns Creek, Dry Creek, and Mansker Creek. Figure 2 shows the study area along with available stream gage locations and major water bodies.
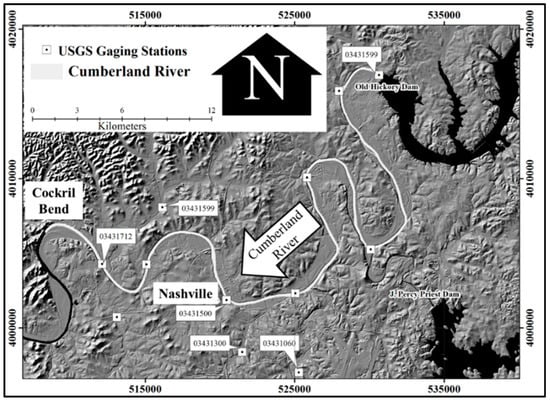
Figure 2.
Study area of the Cumberland River (shown in gray) along with nearby water bodies and U.S. Geological Survey (USGS) stream gages (shown in white boxes).
3.2. Study Period
The 2010 Nashville flood was one of the largest floods in the study area that were caused by heavy rainfall. It peaked on 3 May 2010, at Nashville where the recorded peak discharge (5600 m3/s) was close to a 200-year return period flood. It exceeded the National Weather Services (NWS) flood stage (122.22 m) near Nashville on 2 May 2010, and stayed for more than four days. Therefore, the study period from 29 April to 7 May 2010, was selected such that the entire flood could be included in the simulation.
3.3. Terrain Datasets
One-arc second global regional and one-second global DEM were selected for this research. NED was selected as a representative of regional DEMs because it provides the best quality terrain data for the USA at various spatial resolutions. As already mentioned, SRTM was selected because of its global coverage and better accuracy relative to other global DEMs. One arc-second spatial resolution was selected because (i) one arc-second is the finest spatial resolution available for SRTM and (ii) one arc-second DEMs can produce considerably more accurate FIA with reasonable computational efficiency [9]. Figure 3 shows cross-sections derived from test terrain datasets before DEM correction (base NED and base SRTM) compared to control (or surveyed). It can be noted that both DEMs significantly misrepresent the channel conveyance and bankline features (i.e., levee). A short summary of control and test terrain datasets is given below.
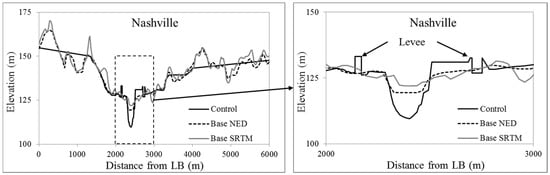
Figure 3.
Comparison of a cross-section derived from control and test (base) terrain datasets near Nashville. The right figure shows the zoomed in picture of the dotted box in the left figure.
3.3.1. Control Terrain Dataset
These consisted of 68 surveyed cross-sections for bathymetric data (provided by U.S. Army Corps, Nashville District) and 1/3 arc-second LiDAR DEM for floodplain data. The surveyed cross-sections and LiDAR were merged to set up the control scenario (model based on control terrain dataset).
3.3.2. Test Terrain Datasets
(a) Base DEMs: Consisted of the same number and alignments of cross-sections as the control terrain dataset. One arc-second NED and void-filled SRTM (V2) were used as sources of elevation data for both channel and floodplains for setting up scenarios based on respective base DEMs. The void-filled SRTM (V2) is hereafter called as SRTM.
(b) Modified DEMs: The base DEMs were modified (via [19]) along the defined cross-sections to improve channel conveyance and produce the corresponding modified DEMs (NED or SRTM). The DEM modification technique would only correct the channel but leave the floodplain elevations the same as the base DEM. The modified NED and modified SRTM DEMs were used as sources of elevation data for setting up scenarios based on respective DEMs.
4. Results
4.1. Control and Test Terrain Datasets
As already mentioned, the control terrain dataset was produced via data provided by the U.S. Army Corps, Nashville District, and LiDAR DEM. The base (or uncorrected) test terrain datasets were collected from USGS Earth Explorer. The base DEMs (NED and SRTM) were modified according to the technique described by [19]. The average channel width for the study reach was 180 m. Hence, the swath of the floodplain to be included was 90 m (half the length average channel width) on each bank along with the available channel width in DEM. Stage and flow data from October 2011 to July 2014 at the USGS stream gage at Nashville were used to produce a stage-discharge correlation. The flow corresponding to the DEM elevation near the Nashville stream gage was used to determine reference flow for each DEM source (NED and SRTM). In this study, the reference flow was 1360 m3/s and 2408 m3/s for NED and SRTM, respectively. Manning’s roughness factor of 0.03 was employed in estimating the thalweg depth for both DEM sources.
One of the challenges employing the selected DEM correction technique was to estimate the channel slope accurately. Channel slopes were calculated from respective DEMs according to the method described by [23]. The slope estimations were performed on 68 predefined HEC-RAS cross-section locations. The spacing of consecutive cross-sections ranged from 14 m to 4288 m (880 m on average). For simplicity, the river reach was considered having only one linear downward slope. Longitudinal slopes and differential channel slopes (slope between two consecutive cross-sections) were calculated to determine the representative channel slope from each DEM. Table 1 lists the summary of differential slopes and longitudinal slopes calculated from DEMs of both sources. It shows that the differential slope and the longitudinal slopes derived from NED were consistent for almost the entire reach, but for SRTM they varied significantly. Therefore, for NED, the entire reach was considered as representative reach for determining the longitudinal channel slope. To offset the inconsistency in SRTM, the study reach was split into two segments to find a representative longitudinal slope. It was noticed that the standard deviation in differential slopes derived from SRTM DEM was lowest at downstream 22.5 km reach (DS stretch). An additional analysis on a differential slope on more than 6000 points along the river (about 61 km long) also yielded a similar result. It showed that the standard deviation (of differential slope in SRTM) of US stretch was four times compared to that of DS stretch, indicating abrupt undulation in the DEM elevation over the river in US stretch. Therefore, for SRTM, the longitudinal channel slope calculated from the DS stretch was used as the representative of the entire reach. Thus, the estimated channel slope from NED and SRTM were 0.000070 m/m and 0.000077 m/m, respectively.

Table 1.
Summary of differential slopes (slope between two consecutive cross-sections) and longitudinal slopes calculated from the National Elevation Dataset (NED) and the Shuttle Radar Topography Mission (SRTM).
The selected DEM correction technique prescribed generic Topo to Raster tool in ARC-GIS using floodplain contours and a modified river bathymetry to replace the DEM elevation over the river with spatially interpolated modified bathymetry. However, it was observed that larger cell size (one-arc second) for DEMs in this research was not adequate to produce an accurate modified elevation in the interpolated (modified) raster according to the selected DEM correction technique. Therefore, to avoid the local effect of uncorrected elevation points (between the defined cross-sections and over banks), modified elevation points were calculated at points spaced at a distance (~3 m) smaller than the DEM spatial resolution. The Inverse Distance Weighted (IDW) interpolation method was then employed using only the modified bathymetry along the channel. The IDW-generated channel elevation was subsequently merged with floodplain contour (derived from the respective DEM) to produce a topographic raster. Then, the existing elevation along the river in base DEM was replaced by the modified elevation from the topographic raster. The updated DEM is hereafter called the “modified DEM”. Comparison of cross-sections at Nashville and longitudinal channel profiles derived from control and test (base and modified) datasets are shown in Figure 4a,b, respectively.
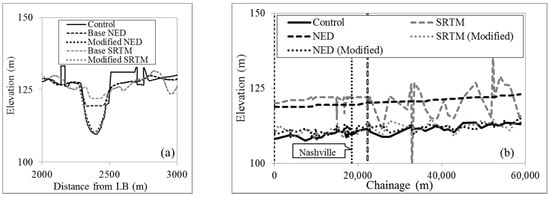
Figure 4.
Comparison of (a) cross-sections at Nashville; (b) longitudinal channel profiles derived from control and test datasets.
4.2. The 2010 Nashville Flood
The 2010 flood was the largest in the study area since 1937. Floodwaters spread over large extents on both banks of the Cumberland River, including the city of Nashville. Delineation of flood extent from a Google Earth image captured during the flood (4 May 2010) showed that the flooded extent was about 42 square km within the study area. To simulate this event, flow and stage data were acquired from available USGS stream gages and a relevant report [24]. However, the simulation did not consider any runoff (except otherwise recorded in the available gages) from the watershed that directly contributed to the river flow, because building a detailed hydrologic model was beyond the scope of this research.
4.3. Hydrodynamic Simulation
A bulk amount of model input was collected from an existing one-dimensional HEC-RAS model (developed by the U.S. Army Corps, Nashville District) covering the study area. The model used in this research consisted of 68 cross-sections, but no structure across the channel was considered except for the levee on the left bank near the city of Nashville. The initial model was built using the control terrain dataset. Flow downstream of OHD was used as an upstream boundary condition. Release from J. Percy Priest Dam and inflows from other significant tributaries were incorporated as lateral flows into the model.
The control scenario was used to calibrate the hydrodynamic model and estimate errors in the test scenarios. Manning’s roughness factor was selected as the calibration parameter with the downstream boundary being at normal flow depth at the slope of 0.00003 m/m. Calibration was performed via comparison of simulated and observed water surface elevation (WSE) at Nashville. Initial Manning’s roughness factor of 0.03 for channel and 0.04 for floodplains were used for calibration. However, the best calibration performance was achieved via scaling the initial roughness factors with discharge. In the given model setting, it was needed because the flood stage rose very rapidly (about 10 m within 48 h). The calibration effort resulted in root mean square error (RMSE) and mean error of 0.5 m and 0.1 m, respectively. Scaling factors that were employed to scale the initial Manning’s roughness factors (0.03 for channel and 0.04 for floodplain) with discharge are shown in Figure 5a, and the calibration plots for WSE and discharge near Nashville are shown in Figure 5b.
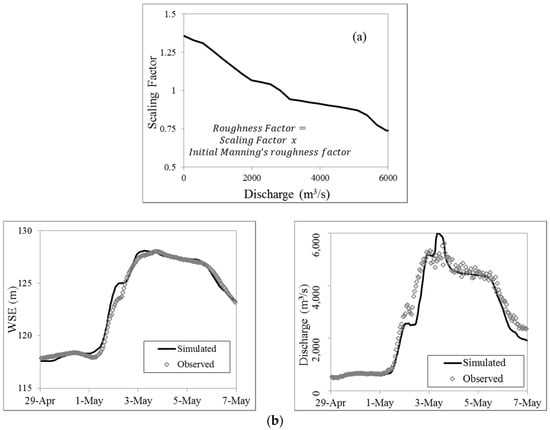
Figure 5.
(a) Factors to scale the initial Manning’s roughness factors; (b) Calibration plots for WSE and discharge near Nashville.
Calibrated model parameters were used in test scenarios to simulate the same event. The observed and simulated WSE hydrograph near Nashville for the control scenario and test scenarios are shown in Figure 6a. It was observed that the base NED-derived scenario was able to mimic the rising and recession limbs of the flood hydrograph with a high bias (more than 2 m). However, the base SRTM-derived scenario could not follow the pattern at all. The inconsistency in the shape of the simulated hydrograph indicated that the base SRTM-derived simulation actually became unstable and produced unreasonable results. The error in channel slope in the upper reach (please refer to Table 1) could be a factor causing this error. This is because gravity and hydraulic connectivity move the water downwards both in the model and in reality [13]. Additionally, the base SRTM-derived simulation was not possible in the pre-flood window (prior to 1 May). In the pre-flood window, the flow was small enough to remain within the main channel, thus abrupt changes in the riverbed elevation (in base SRTM) led to instability of the simulation. Hence, the results of the hydrodynamic simulation based on base (uncorrected) SRTM DEM should be scrutinized prior to implementing a decision-making approach.
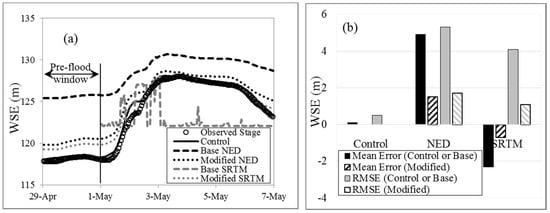
Figure 6.
(a) Hydrograph for observed and simulated stage at Nashville location; (b) performance of the simulated water surface elevation (WSE).
The given flood event was also simulated using the modified NED and modified SRTM-derived test scenarios. The simulated results showed improvement in terms of reducing bias (in the NED-derived test scenario) and inconsistency in hydrograph shape (in the SRTM-derived test scenario) upon DEM modification. However, the higher error was prevalent at the pre-flood window and rising limb of the flood hydrograph. The use of normal depth (0.003 m/m slope) as the downstream boundary may have introduced this error. This boundary condition was used due to lack of available downstream data. The performance summary of the simulations are shown in Figure 6b.
Simulated flood stages (control and test scenarios) were used for inundation mapping and estimating flood depths using corresponding DEMs. The simulated flood extents were compared with the flood extent delineated from the Google Earth image of 4 May 2010 (hereafter referred to as observed flood extent). The inundated extent derived from the control scenario had less than 1% error with respect to the observed flood extent, which validated the assumption of the calibration scenario being reasonable in representing the actual field condition. However, the test scenarios showed errors at various degrees. The error in inundation extent from the base SRTM-based scenario was three times the one based on base NED. DEM modification significantly reduced the errors for both NED- and SRTM-based scenarios. However, the modified SRTM-derived model resulted in an underestimation of the total inundated area, even though the spatial extent over the floodplains was greater than that of the observed. Simulated inundation maps for control and test scenarios are shown in Figure 7a,b, respectively.
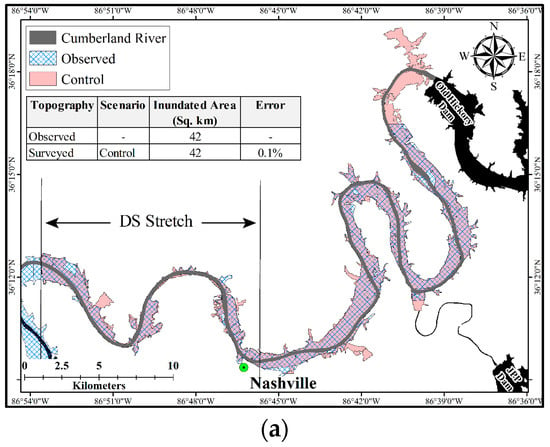
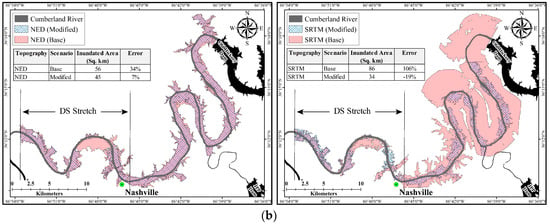
Figure 7.
(a) Comparison of observed and simulated inundation extent for control scenario; (b) Comparison of observed and simulated inundation extent for test scenarios [NED (left), SRTM (right)].
4.4. Flood Impact Assessment
Flood consequences were estimated for the control and test scenarios via HEC-FIA with river alignment and impact area (i.e., county) fixed. For individual scenarios, corresponding flood depths, flood extents, flood arrival times, and impacted census boundaries were determined. The HAZUS MH 2.1 database provided information about structural occupancy and depth-damage functions. It was found that simulation of a single flood event might end up in different consequence estimates simply because of error over waterways (i.e., river) in terrain data. The estimated monetary loss was 0.65 billion United States dollars (USD) in the control scenario, but the same consequence ranged from 0.7 to 4.2 billion USD when it was estimated via the test scenarios. Similarly, the number of affected structures was 3300 in the control scenario, while it ranged from 2400 to 19,500 in test scenarios.
5. Discussion
A conveyance-based DEM correction technique was applied on one arc-second NED and SRTM DEMs. The absence of adequate conveyance in base DEMs signifies that they are only useful in simulating flows for a very narrow window in a hydrologic year irrespective of the DEM quality. This is because in most of the days in a hydrologic year, the actual river WSE remains below the elevation present in an uncorrected (base) DEM. Therefore, the simulated stages (using uncorrected DEM as terrain) would have high error for instances when the flow remains mostly within the channel. Thus, the uncorrected DEM based models would be only applicable for narrow spans in a hydrologic year (very high flow instances).
DEM errors not only affect the channel conveyance (in DEM) but also affect other hydraulic properties (i.e., longitudinal slope, bank features). As shown in Figure 1, the DEMs failed to show the presence of levees accurately. It could be because of the coarseness of the spatial resolution of DEM, or inadequate data acquisition mechanism or timing of DEM production. DEM only represents the terrain, as it was at the time of data acquisition; hence any change on the ground surface made afterward would be absent in a DEM. Additionally, river longitudinal channel slope is often calculated from DEM elevations along the river [25,26]. It was observed that longitudinal channel slope (over entire study reach) calculated from base NED was more reliable than that of base SRTM. This affected implementation of the DEM correction technique on SRTM because longitudinal channel slope is a primary input in the selected DEM correction technique. The accuracy of SRTM DEMs immediately upstream and downstream of a dam within the entire length (about 1110 km from headwaters to the Ohio River confluence) of the Cumberland River was found to be limited. Non-void filled SRTM (V1) also exhibited similar pattern. Figure 8 shows the SRTM elevations and average WSE on streamflow gages for (a) the entire river length (1110 km) of the Cumberland River, and (b) a stretch from OHD to the Cheatham Navigation Lock (CNL). Abrupt elevation changes similar to the U.S. stretch (refer to Figure 4b) were also observed downstream of Cordell Hull and Wolf Creek Dams. This indicates the phenomena in U.S. stretch could be due to its location relative to OHD. Moreover, reservoirs also affected the accuracy of SRTM in reaches upstream of a dam. Therefore, the representative segment was selected such that it had least structural influence but long enough to exhibit the downward slope. For the SRTM-derived channel slope in this study, a 22.5 km stretch (D.S. stretch) was considered adequate because the distance from OHD to CNL was 107 km where structural presence had a significant influence on a more than 60 km river length. However, channel slope could also be estimated from streamflow gages, but in a data-poor area, that scope could be limited, leaving global DEM (i.e., SRTM) as the only viable option. Nevertheless, the agreement of the estimated channel slope from SRTM DEM and surveyed (control) bathymetric data (0.000077 and 0.000083) showed that longitudinal channel slope could be calculated via a representative segment.
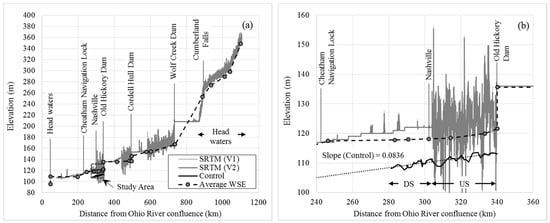
Figure 8.
SRTM elevations and average WSE for (a) entire river length (1110 km) of the Cumberland River and (b) stretch from Old Hickory Dam (OHD) to Cheatham Navigation Lock (CNL).
Interpolation of corrected bathymetric elevation along predefined cross-sections at intervals equal to the DEM spatial resolutions (as prescribed in [19] for 1/3 arc-second NED) seemed inadequate for one arc-second DEMs. Estimating modified channel bathymetry via interpolating corrected bed elevation at intervals (~3 m) smaller than the DEM spatial resolution (one-arc second or ~30 m) was useful in the given river reach (average width 180m). It was also challenging to find the exact transition points from floodplains to channel (referred to as “high bank points” or “hbp”) using one arc-second DEMs. The assistance of corresponding satellite images may help in more accurately finding the hbp if the ratio of average river width to DEM cell size (spatial resolution) is small. Nevertheless, implementation of the DEM correction technique with additional measures (i.e., estimating longitudinal channel slope from the representative segment, updating the interpolation method) successfully reduced the errors in base DEM elevations over the channel. After correcting the DEM, the RMSE in thalweg elevations (in 68 cross-sections) dropped to 1.59 m for NED, and 1.67 m for SRTM from 9.66 m to 11.46 m respectively. The resulting error in thalweg elevation was also lower than the RMSE of NED and SRTM (1.84 m and 4.01 m), estimated over multiple land cover types [10]. Additionally, the longitudinal channel slope in SRTM DEM increased from 0.000012 m/m to 0.0007 m/m where the longitudinal channel slope in control terrain dataset was 0.0008 m/m. On the contrary, the longitudinal slope in NED DEM has slightly decreased from 0.0007 m/m to 0.0006 m/m. This may have happened because the base NED-derived longitudinal profile demonstrated a step-like drop instead of decreasing gradually. The change was very small along the river length, except for sudden drops of about 0.5 m at each 10 to 15 km. This phenomenon in the base NED DEM would affect the accuracy of simulating low stages in a flood event. Nevertheless, the longitudinal slopes from both modified DEM types were close to their respective representative slopes and the one derived from the control dataset, indicating the sub-reach longitudinal channel slope can be effectively used in the discussed DEM correction technique.
The performance of the simulated WSE from control and test scenarios with respect to observed data (Figure 6b) shows that the mean errors (in simulated WSE) were 4.9 m and −2.3 m for base NED and base SRTM DEM-based test scenarios that dropped to 1.5 m and −0.7 m respectively, upon DEM correction. Similarly, the RMSE in simulated WSE dropped to 1.7 m and 1.1 m from 5.3 m and 4.1 m respectively. This shows that the DEM correction was able to cut the errors in simulated WSE up to 65%.
The errors in simulated WSE were reflected in the corresponding simulated flood extents, as shown in Figure 7b. High biases in the simulated WSE from the base NED-derived scenario produced an inundation extent 33% larger than the observed one. However, the simulated inundation extent from the base SRTM-derived scenario was scattered and resulted in a very large inundation extent. It was also noticeable that the error was high above the DS stretch where simulated flood extents spread over wide swaths of the floodplain. Inconsistencies in longitudinal channel slope along with lack of channel conveyance may have attributed to this localized error. Nevertheless, DEM correction was able to reduce the error in simulating flood extent. The simulated inundation extent from the modified NED derived test scenario resulted in an overestimation by 7%, and the modified SRTM-derived test scenario underestimated by 19%. Figure 9a shows a bar plot inundation extent from different scenarios, and Figure 9b plots the inundation extents with respect to their peak WSE above the NWS flood stage at Nashville (122.22 m). The dotted line in Figure 9b shows a correlation of flood extents with peak flood stages, excluding the base-SRTM derived scenario. The SRTM-based scenario fits into the pattern (with control, observed and NED) only after DEM modification. It indicates that for a particular area if a hydrodynamic simulation is stable, then the resulting stage-inundation extent should fit in a specific pattern data irrespective of the DEM source. However, this study only included one arc-second DEMs; therefore, the sensitivity of the correlation to change in spatial resolution of DEM was not investigated.
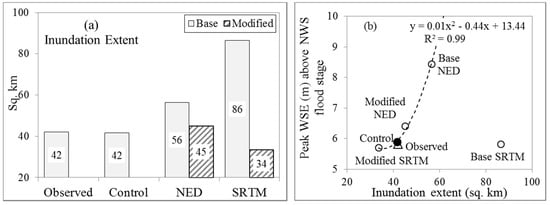
Figure 9.
(a) Bar plot inundation extents from different scenarios; (b) inundation extents versus peak WSE above the National Weather Services (NWS) flood stage at Nashville (122.22 m).
The flood extents derived from HEC-RAS one-dimensional modeling was considered adequate for this study because the comparative FIA (for four test scenarios) was done on similar model (hydrodynamic and FIA) setups. The accuracy of inundation extent obtained from control scenario (Figure 7a) also acted as a benchmark for subsequent FIAs (in test scenarios). HEC-FIA only considers the maximum inundation extent and maximum flood depth; thus, detailed assessment of spatial distribution of flow and velocity (as in a two-dimensional model) was out of scope for this research. Additionally, a one-dimensional model is often preferred when data and computation capacity are limited [27,28].
The errors and uncertainties in hydrodynamic simulations were carried over to the consequence simulations (FIA) accordingly. Figure 10 shows a number of structures affected, and total monetary loss estimated from control and test scenarios. It is interesting to find that both of these loss indexes fit very well with the corresponding inundation extent even though the base SRTM-based scenario was unstable. This finding is similar to the findings of [9]. However, the instability of the base SRTM-based model indicates that the flood consequence estimates are not entirely dependent upon the accuracy of the hydrodynamic simulation, but rather, it is dependent upon the accuracy of inundation extent and its occupancy. Nevertheless, the DEM correction successfully reduced the error in estimated flood consequences in both NED and SRTM-based scenarios. Underestimation in peak stage (refer to Figure 9b) by the modified SRTM-based scenario resulted in an underestimation of inundation extent and consequences. This could be partially caused by the errors in floodplain elevation (in DEM) that produced scattered inundation extents in addition to the lack of hydraulic properties (i.e., conveyance, slope).
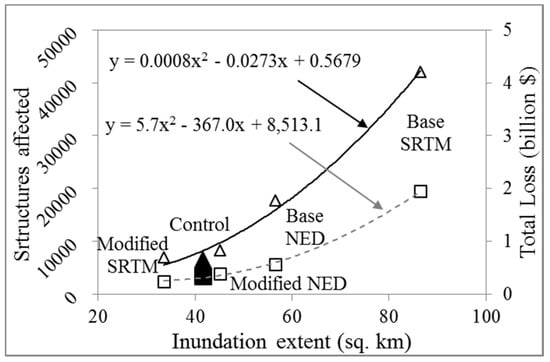
Figure 10.
Simulated flood consequences versus inundation extent.
6. Conclusions
The first objective of this research was to implement a conveyance-based DEM correction technique [19] on moderate resolution NED and SRTM DEMs. One arc-second spatial resolution was selected for both DEM sources because of data availability, convenience in data handling, and optimum simulation accuracy. The intention was to investigate challenges to implement a conveyance-based DEM correction technique on moderate resolution regional and global DEMs. The DEM correction technique by [19] showed promising results in incorporating channel conveyance into DEM-derived cross-sections for both NED and SRTM DEMs. This technique depends on some hydraulic properties (i.e., overbank elevations, side slopes, longitudinal channel slope) to characterize river cross-section shape and predict the depth of the channel thalweg that is often difficult to extract from global DEMs such as SRTM DEM. Therefore, the efficacy of the DEM correction depends upon the accuracy of DEM itself. This research has demonstrated that representative hydraulic properties (i.e., longitudinal channel slope) from a smaller segment may be used to implement DEM correction over the entire reach if the quality of DEM is compromised. Additionally, the DEM correction technique used a second-order polynomial equation to generate elevation for locations between thalweg and high-bank points. Due to a limitation in interpolation methods, coupled with the coarser spatial resolution of DEM (one-arc second), the entire conveyance was not possible to be captured, which may eventually have introduced error in the modified DEM-based scenarios. Therefore, estimating modified bathymetric elevation at a spacing smaller than the DEM spatial resolution proved helpful for the selected DEMs. The above-mentioned extensions (i.e., longitudinal slope estimation and spatial interpolation) to the selected DEM correction technique were especially helpful in correcting the SRTM DEM, highlighting the extra effort needed for correcting global DEMs. Nevertheless, the estimated river elevations via the technique in both one arc-second NED and SRTM DEM were comparable (Figure 8).
The second objective of the research was to estimate the impact on FIA after applying the conveyance-based DEM correction technique on selected NED and SRTM DEMs. NED was found to better represent the terrain compared to SRTM, and hence produced less error in FIA. It was found that NED DEM had errors mostly along channels, but SRTM DEM had errors both along the channel and over floodplains. Therefore, simulated WSE amplified at variable degrees as they were used for inundation mapping and subsequent FIA. Flood loss is calculated as a function of flood depth and flood wave [29,30]. Therefore, having a DEM that not only aids in estimating WSE properly, but also produces accurate depths on floodplains is necessary for FIA. However, it was found that DEM correction could improve the FIA by both stabilizing model performance and reducing errors. For a set of stable simulations, the consequences have been found to follow a specific pattern similar to the flood loss curve defined by [19]. It indicates that a hydraulic-based DEM correction technique can be applied on SRTM (in the case of data scarcity) to produce reasonable flood consequence estimates. However, it should be noted that the conveyance correction of DEMs over the channel does not improve the floodplain errors. Additionally, reducing reliance on the DEM-derived hydraulic property or field data is necessary for correcting DEMs over data-limited areas. Hence, an extended study on improving channel conveyance with minimum use of DEM-derived or field-surveyed input can be a potential future field of research.
Finally, the data gap not only pertains to limited access to ground surveyed data, but also includes the unavailability of up-to-date data. Many of the global DEMs are ageing, and may soon become irrelevant in featuring actual ground conditions. Hence, a hydrologically well-gauged area may become data-poor in terms of limited bathymetric data and floodplain terrain data due to rapid urbanization, modification of water routes, change in river planform, aggradation-degradation of riverbed levels etc. However, undertaking extensive field survey on a regular basis is often unfeasible. Therefore, a combination of conveyance-based (for rivers and streams) DEM correction with floodplain-based DEM corrections would be especially helpful for FIA in remote, data-poor and rapidly growing areas. Additionally, strong correlation of flood damage with inundated area indicates FIA can also be made via remotely sensed flood extent if flood extent versus damage correlations (flood loss curve) are established for a given area.
7. Future Research
DEM is a raster image that represents the terrain only for the instance of data acquisition. However, river morphology is not static. Therefore, the dynamics of riverine morphology should be considered while a DEM is used for river FIA. A possible track of future research can include adopting a DEM with the temporal variability of riverine morphology and floodplain dynamics. Studies have shown that combining time-series images with remote sensing data (i.e., elevation, land use, vegetation, etc.) may be helpful for analyzing river planform, bathymetry of water body (i.e., lake, stream) and floodplain characteristics [12,31,32,33,34]. Upcoming remote sensing missions such as SWOT can be immensely helpful in this regard, since it will provide seasonal water surface musk at a global scale [22]. A data-driven algorithm that can compile data from multiple sources (i.e., SWOT, Landsat, etc.) to observe seasonal variation for a long period would be helpful in producing a better representation of river bathymetry and floodplain elevation. Additionally, it would reduce the reliance on field data (i.e., stage-discharge relation, channel roughness, channel shape, etc.) for implementing conveyance-based DEM correction techniques.
Acknowledgments
The authors acknowledge Civil and Environmental Engineering and the Center for the Management, Utilization, and Protection of Water Resources at Tennessee Technological University for financial support. They also thank the U.S. Army Corps of Engineers, Nashville District, for providing data and models.
Author Contributions
M.N.M.B. and A.K. conceived and designed the experiments; M.N.M.B. performed the experiments and analyzed the data; M.N.M.B., A.K. and F.H. contributed towards writing the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wahlstrom, M.; Guha-Sapir, D. The Human Cost of Weather-Related Disasters 1995–2015; United Nations International Strategy for Disaster Reduction (UNISDR): Geneva, Switzerland, 2015. [Google Scholar]
- Montgomery, M.C.; Chakraborty, J. Assessing the environmental justice consequences of flood risk: A case study in Miami, Florida. Environ. Res. Lett. 2015, 10, 095010. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Fact Sheet, 2006. Flood Hazards—A National Threat; U.S. Department of the Interior: Washington, DC, USA; U.S. Geological Survey: Reston, VA, USA, 2006.
- Walker, G. Environmental Justice: Concepts, Evidence, and Politics; Routledge: New York, NY, USA, 2012. [Google Scholar]
- Jonkman, S.N. Global perspectives of loss of human life caused by floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; A special report of working groups I and II of the intergovernmental panel on climate change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Thaler, T.; Hartmann, T. Justice and flood risk management: Reflecting on different approaches to distribute and allocate flood risk management in Europe. Nat. Hazards 2016, 83, 129–147. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Risk Reduction (UNISDR). The Human Cost of Natural Disasters: A Global Perspective; UNISDR: Geneva, Switzerland, 2015. [Google Scholar]
- Bhuyian, M.N.M.; Kalyanapu, A. Accounting digital elevation uncertainty for flood consequence assessment. J. Flood Risk Manag. 2017. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Zhang, Z.; Meyer, D.; Danielson, J. Validation of the ASTER Global Digital Elevation Model Version 2 over the Conterminous United States. In Proceedings of the International Acrchives of the Photogrammetry; Remote Sensing and Spatial Information Sciences: Prague, Czech Republic, 2012; Volume XXXIX-B4, pp. 281–286. [Google Scholar]
- Kalyanapu, A.; Hossain, A.K.M.A.; Kim, J.; Yigzaw, W.; Hossain, F.; Shum, C.K. Investigating the downstream flood hazards on American River due to changes in probable maximum flood due to effects of artificial reservoir size and land use/land cover patterns. Earth Interact. 2013, 17, 1–24. [Google Scholar] [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.D.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal, J.C.; Trigg, M.A. Perspectives on Open Access High Resolution Digital Elevation Models to Produce Global Flood Hazard Layers. Front. Earth Sci. 2016, 3, 85. [Google Scholar] [CrossRef]
- Gichamo, T.Z.; Popescu, I.; Jonoski, A.; Solomatine, D. River cross-section extraction from the ASTER Global DEM for flood modeling. Environ. Model. Softw. 2012, 31, 37–46. [Google Scholar] [CrossRef]
- Merwade, V.; Maidment, D.R. A GIS Framework for Describing River Channel Bathymetry; University of Texas at Austin, Center for Research in Water Resources, J.J. Pickle Research Campus: Austin, TX, USA, 2004. [Google Scholar]
- Price, R. An optimized routing model for flood forecasting. Water Resour. Res. 2009, 45, W02426. [Google Scholar] [CrossRef]
- Yamazaki, D.; Baugh, C.A.; Bates, P.D.; Kanae, S.; Alsdorf, D.E.; Oki, T. Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling. J. Hydrol. 2012, 436–437, 81–91. [Google Scholar] [CrossRef]
- Gilvear, D.; Winterbottom, S.; Sichingabula, H. Character of channel planform change and meander development: Luangwa River, Zambia. Earth Surf. Process. Landf. 2000, 25, 421–436. [Google Scholar] [CrossRef]
- Bhuyian, M.N.M.; Kalyanapu, A.J.; Nardi, F. An approach for Digital Elevation Models (DEM) correction by improving channel conveyance. J. Hydrol. Eng. 2014. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and its capabilities for land hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Patterns of river width and surface area revealed by the satellite-derived North American River Width data set. Geophys. Res. Lett. 2015, 42, 395–402. [Google Scholar] [CrossRef]
- Prigent, C.; Lettenmaier, D.P.; Aires, F.; Papa, F. Toward a high-resolution monitoring of continental surface water extent and dynamics, at global scale: From GIEMS (Global Inundation Extent from Multi-Satellites) to SWOT (Surface Water Ocean Topography). Surv. Geophys. 2016, 37, 339–355. [Google Scholar] [CrossRef]
- Maswood, M.; Hossain, F. Advancing river modelling in ungauged basins using satellite remote sensing: The case of the Ganges-Brahmaputra-Meghna basin. Int. J. River Basin Manag. 2015. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers (USACE). Cumberland River Basin May 2010 Flood Event; USACE: Washington, DC, USA, 2010.
- Kiel, B.; Alsdorf, D.; LeFavour, G. Capability of SRTM C-and X-band DEM data to measure water elevations in Ohio and the Amazon. Photogramm. Eng. Remote Sens. 2006, 72, 313–320. [Google Scholar] [CrossRef]
- Lea, D.M.; Legleiter, C.J. Refining measurements of lateral channel movement from image time series by quantifying spatial variations in registration error. J. Geomorphol. 2016, 252, 66–79. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Scawthorn, C.; Blais, N.; Seligson, H.; Tate, E.; Mifflin, E.; Thomas, W.; Murphy, J.; Jones, C. HAZUS-MH flood loss estimation methodology. I: Overview and flood hazard characterization. J. Nat. Hazards Rev. Am. Soc. Civ. Eng. 2006. [Google Scholar] [CrossRef]
- Albano, R.; Sole, A.; Sdao, F.; Giosa, L.; Cantisani, A.; Pascale, S. A systemic approach to evaluate the flood vulnerability for an urban study case in Southern Italy. J. Water Resour. Prot. 2014, 6, 351–362. [Google Scholar] [CrossRef]
- Harrison, L.R.; Legleiter, C.J.; Wydzga, A.; Dunne, T. Channel dynamics and habitat development in a meandering, gravel-bed river. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Ko, B.C.; Kim, H.H.; Nam, J.Y. Classification of potential water bodies using Landsat 8 OLI and a combination of two boosted random forest classifiers. Sensors 2015, 15, 13763–13777. [Google Scholar] [CrossRef] [PubMed]
- LeFavour, G.; Alsdorf, D. Water slope and discharge in the Amazon River estimated using the shuttle radar topography mission digital elevation model. Geophys. Res. Lett. 2005, 32, L17404. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).