Landscape Pattern Detection in Archaeological Remote Sensing

Abstract

Automated detection of landscape patterns on Remote Sensing imagery has seen virtually little or no development in the archaeological domain, notwithstanding the fact that large portion of cultural landscapes worldwide are characterized by land engineering applications. The current extraordinary availability of remotely sensed images makes it now urgent to envision and develop automatic methods that can simplify their inspection and the extraction of relevant information from them, as the quantity of information is no longer manageable by traditional “human” visual interpretation. This paper expands on the development of automatic methods for the detection of target landscape features—represented by field system patterns—in very high spatial resolution images, within the framework of an archaeological project focused on the landscape engineering embedded in Roman cadasters. The targets of interest consist of a variety of similarly oriented objects of diverse nature (such as roads, drainage channels, etc.) concurring to demark the current landscape organization, which reflects the one imposed by Romans over two millennia ago. The proposed workflow exploits the textural and shape properties of real-world elements forming the field patterns using multiscale analysis of dominant oriented response filters. Trials showed that this approach provides accurate localization of target linear objects and alignments signaled by a wide range of physical entities with very different characteristics.

1. Introduction

Present-day landscapes have been shaped by centuries of human action. Since their settlement, ancient communities have planned, modified, and engineered the space around them: land surveying and field system deployments were some of the first forms of large-scale “landscape engineering” performed by complex societies in antiquity. Centuriation, the iconic Roman system of land subdivision into large square plots assigned to settlers, represents one of the most advanced efforts of landscape engineering of the ancient world. Its effects can be discerned even today, with this regular territorial design model continuing to have a significant influence on present-day agrarian organization in many locations across the Mediterranean basin and surrounding regions.

Remote sensing represents one of the most effective methods for the study of landscape design and patterning and has been amply and successfully applied at any latitude to land systems prospecting. While investigation methods and technologies have been, respectively, refining and progressing over time—especially after the advent of satellite imagery on the archaeological research scene—the photo-interpretation phase, in which the nature of the objects identified on imagery are determined, have continued to be based on a visual approach and manual (digital) mapping. The current unprecedented availability of Remote Sensing data should provide considerable ground for the development of alternative and more effective procedures, and should have favored a growing interest for computerized methods that can streamline and improve detection of landscape design components on from-above imagery. Instead, automated detection of landscape patterns has seen little or no progress, nor much application, in the archaeological domain in the last decade. The current remotely sensed data “deluge” makes it urgent to envision and develop computer-driven methods that can simplify the inspection of datasets and the extraction of relevant information from them, determining a shift from traditional “human” means of detection and interpretation to automated ones.

This paper expands on the development of methods for the detection of target landscape features—constituted by field system patterns—in very high spatial resolution images, and the verification of their spatial arrangement within the framework of “Visualizing Engineered Landscapes (VEiL)”, a landscape archaeology project based in Italy and focused on the centuriated landscape surrounding the Roman city of Aquileia. The targets of interest consist of a variety of similarly oriented objects (such as roads, drainage channels, etc.), disposed in parallel and orthogonal fashion concurring to demark the current Aquileian landscape organization, which reflects the one imposed by Romans from the 2nd century BC onward. The aim here is to define a workflow enabling a systematic detection of symmetrically deployed elements of the land division that concur to engineer the landscape, reducing biases derived from the subjective visual analysis of human observers. The presented approach enables the detection of similarly oriented features that are compatible with the local centurial system and automatically extracts candidate modules of the centuriation by analyzing the periodic alignment of peaks in the distribution of the oriented features. The novelty of this approach resides in that it performs computerized processes of identification directly on raster imagery (rather than e.g., on digital vector cartography) of linear elements of the landscape that align with the orientation of the local cadaster and uses them to generate all the possible centuriation module scenarios to identify the most plausible one, thus automating a process normally performed via painstaking manual calculation.

1.1. Automation in Archaeological Remote Sensing: Current State of the Research Field

Until the systematic introduction of aerial photo inspection in cadaster studies during the last third of last century, the identification of centurial systems had been largely tackled from a theoretical and speculative point of view, referring to ancient sources and epigraphic documents, or by attempting to align possible agrarian divisions with modern topographic maps, with little or no attention to the actual morphologic situation. Only the advent of airborne photography, coupled with an improved map production capacity, determined a first decisive shift in approaching centuriation scholarship [1] and laid the foundation for a new and more empirical approach to centurial grid identification proposed by the so-called Besançon Group (University of Franche-Comté, France) [2,3]. A partial dismissal of such approach in its first formulation in the last decade of last century did not stop a new generation of scholars to investigate ancient land divisions using a diachronic trans-disciplinary landscape archaeology approach based on a similar concept of archaeo-morphological analysis. Their work [4] further promoted the inclusion of geospatial datasets (including remote sensing data) and GIS analysis within the discipline. Airborne datasets continue to be fundamental in the identification of fossilized and limitedly altered centuriations in areas where post-depositional processes and phenomena have not been particularly dynamic [5,6]. Aerial images have only occasionally been substituted with satellite ones, which had the great advantage of covering broader areas; however, their use has been quite limited and confined to manual mapping of visually identified elements [7,8,9]. Very recently, a number of projects are successfully trialing the use of Lidar data in order to highlight grid boundaries in landscapes that have been essentially abandoned after the Roman period, with little or no occupation afterwards, and manually map them [10].

The present acceleration in the use of Remote Sensing imagery in a variety of disciplines is producing parallel rapid advancements in the application of automated approaches for detection and monitoring of phenomena and conditions (e.g., traffic management, ground conditions evaluation, ground change assessment, air pollution forecasting, etc.); nevertheless, such advancements do not appear to have invested much in the study of land design, historical and contemporary. More broadly, the whole field of automation in the domain of cultural landscapes studies is still moving the first, uncertain steps, despite several decades of development of Remote Sensing methods applied to archaeological scholarship, on one side, and while increasingly automated procedures for specific object detection are flourishing in an array of fields, on the other [11]. The reasons for lack of trust in automated methods in heritage recognition often come down to uneasiness amongst archaeological scholarship of losing control of the interpretation process [12]. Examples of implementation of automated approaches to archaeological aero-photointerpretation for determined objects are thus still scarce [13] and they broadly fall into an even smaller number of classes: template matching-based methods [14], custom algorithms [15], (GE)OBIA-based methods [16], and machine learning-based methods [15], all involving previous knowledge of the shape and characteristics of the searched object. Recent developments in Machine Learning and the appearance on the scientific scene of Convolutional Neural Networks (CNN) approaches [17,18], which gained credit for dramatically improving previous recognition performances, are generating enthusiasm for the possibilities of these high-end methods for the (semi)automatic detection of archaeological surface or sub-surface objects. Despite its potential, however, CNN has so far seen extremely limited development in the archaeological/cultural heritage field and only in applications where the shape of objects to detect (although variegated) were known and pertained to only one typology [15,19]. All these trials have in any case concentrated their attention on separated, single “entities” appearing with varying frequency within a landscape and not on systems of “related entities”.

Notwithstanding limited instances, a rising awareness of the necessity of turning to automated processes to study landscape arrangement constituents as a whole is now favoring the adoption of new approaches within the discipline. VEiL project seeks to contribute to the scholarship of engineered landscapes by trialing approaches that can support the automation of tedious, time consuming tasks in landscape features extraction. This is particularly relevant for projects like this, addressing the study of patterning of diverse elements, of their repetitiveness, and of the relationships between physically connected or separated landscape components that reflect the past territorial arrangement and configuration.

1.2. The Archaeological Context of the Project

The Aquileian hinterland (Figure 1) was one of the broadest rural areas in Roman Italy to be centuriated before the first part of the 2nd century BC [20]. Aquileia is an exception in the European panorama as it was scarcely touched by 20th century urbanization, and archaeological prospections can be carried out from the immediate edge of the urban perimeter into a large surrounding area, which retains a relatively intact Roman peripheral landscape around a city of relevant size in antiquity. While patches of the Aquileian landscape still preserve the imprint of the distinctive spatial signature imposed by the Romans, with its typical repetitive patterns filtering through the noise of more modern systems [21], in other areas the centuriation elements are no longer easily identifiable or irrefutably attributable to Roman intervention.

Most of the studies undertaken have ignored the archaeological and topographical reality of the area: existing theories have drawn a variety of diverging conclusions [21] almost exclusively from modern topographic maps with noticeable “mechanicism” in reconstructions of the centurial grid obtained by juxtaposing theoretical gridirons on topographical maps. Within this volatile grid, the internal partition elements of centuriation are still mostly unknown.

A further difficulty is represented by the fact that in the Aquileian territory the Roman surveyors deployed in various moments multiple centuriations with different orientations, the chronological sequence of which is still not ultimately clarified [22], although the one that is currently more clearly and broadly preserved on the landscape pertains to the supposedly latest land division phase. This, the so-called Classic Aquileian Centuriation, is characterized by a clear and consistent orientation at about 22° W from (grid) North: initially deployed in the immediate vicinities of the newly founded Roman colony, it was expanded likely until mid of the 1st century BC [22], using a centurial module of 20 × 20 actus, which was commonly used in contemporary land assignments in other areas of ancient Italy.

The study of the Roman cadaster in Aquileia is further complicated by the fact that the same areas have undergone later transformations in order to reclaim capacities for agricultural exploitation. Such reclamations are frequently characterized by regular plans that overlay the Roman module. It is therefore necessary to identify and expunge such posterior works in order to pinpoint the original Roman intervention. In many cases, however, these post-antiquity works have served to preserve some elements of the Roman land structuring.

1.3. Aims of the Project

Within this context, the VEiL project was envisioned and developed. The overall scope of this project is to unlock the rationale underpinning the processes of landscape engineering used by the Roman surveyors: pivotal for this is to identify and document the land system components characterized by long-term endurance in the landscape or their voids generated over the course of subsequent landscape transformations. The foundation of the research agenda is embodied by the ultimate identification of the “Classic” Aquileian cadaster module through the detection of its main axes, shape, size and extension as preserved by a variety of features characterizing the current landscape. This entails primarily the identification of the elements forming the grid, both the more evident centurial boundaries and the internal subdivisions aligning in a parallel or orthogonal fashion to the grid system. Accordingly, this project includes the reconnaissance on Remote Sensing imagery of more evident as well as subtle potential land division elements using a systematic combination of linear feature automated detection procedures based on signal processing and pattern recognition, as well as spatial analysis, field mapping and ground verification activities.

The workflow adopted to detect the grid components on imagery exploits the textural and shape properties of real-world elements forming the field patterns using multiscale analysis of dominant oriented response filters. Trials show that the proposed approach provides accurate localization of target linear objects and alignments signaled by a wide range of physical entities with very different characteristics. The spatial distribution of the extracted features can then be analyzed in order to determine candidates for starting point and module of the centuriation system.

2. Materials and Methods

When seeking to recognize historical components of current landscapes on remotely sensed imagery, the chances of identification can vary sensibly due to the nature of the elements that make up the past territorial organization and their preservation. One of the major issues faced by archaeologists when tackling the recognition of centurial systems in any sort of teledetected imagery is the identification of the land division boundaries as, in the past, they might have been formed by a variety of different natural or artificial elements, such as roads, fences/hedges, ditches, drainage and irrigation channels, tree lines and other landmarks [23,24] and they might be preserved in the modern-day territory by a likewise wide variety of artificial or natural markers. The issue is particularly intense in areas where later urban transformation has altered information embedded in the landscape and spatial signatures are obscured by the noise of more modern systems. This requires the use of the broadest possible range of geospatial data (including imagery) in order to ensure that their availability make up for shortcomings and voids rooted in each dataset and that all the landscapes elements relevant to centurial grid identification can be highlighted and properly considered.

2.1. Project Data Sources

Accordingly, the project has acquired a broad array of geospatial data ranging from base and thematic maps to remote sensing imagery, historic cartography and legacy data, all providing the necessary context to validate or expunge detected linear features.

Accurate base cartography is provided as freely accessible datasets made available by the Cartographic Division of the Regional Government of Friuli Venezia Giulia [25], the administrative Region within which Aquileia is located. The project has acquired shapefile datasets (RDN2008/TM33) at both 1:5000 and 1:25,000 scale as well as terrain height points and Lidar based DTMs (respectively 10 m and 1 m resolution) generated using airborne data collected in the past decade; in addition, previous digital and printed topographic maps (these last scanned and georeferenced by the project) have been acquired to avail a detailed sequence of modifications to the landscape as recorded in topo-maps of the last 40 years.

Much of the information relative to the landscape morphological arrangement needed for the goals of the project already appears in these basemaps. However, they are generally obtained via aero-photogrammetry: given the inherent subjectivity embedded in the image-interpretation process, the mapping of topographic elements ends up biased by the selection of the relevant mappable features made by the photogrammetric operators. As a consequence, only landscape elements deemed relevant to the mapping exercise are recorded. Thus produced, topographic maps do not, and often cannot, include information that is highly relevant to centurial grid detection, for example, cropmarks and soilmarks (visible on imagery) that can be referred to centuriation or ancient settlements; or features like tree lines made up by plants that in many cases were cyclically replanted over previous vegetation boundary markers used for many centuries to separate properties; or minor pathways and tracks that might preserve ancient ones. This makes using Remote Sensing imagery crucial in order to enable systematic recording of all the potential components of the centurial grid, irrespectively of how they have been preserved.

To prevent loss of information, the VEiL project has collated a vast remote sensing dataset, including imagery captured by various sources and sensors: these comprise (i) Black/White historical photographs; (ii) multispectral and hyperspectral imagery; (iii) RGB high-resolution aerial orthorectified images of different periods; (iv) Lidar data. For the specific goals of the work here described; data (i) to (iii) have been employed.

Historical aerial photographs (recorded starting in 1938), with a ground resolution varying from 1.5 to 3–4 m according to shooting period, represent a valuable source of information in that they provide information still embedded in the landscape in the second part of last century, but often no more visible on the ground nowadays due to later transformations (Figure 2). Soil and crop marks potentially related to the centurial grid are very visible in this type of imagery as well as are land boundaries and landscape arrangements superseded by more recent land reorganizations.

The hyperspectral data available to the project were acquired using MIVIS (Multispectral Infrared and Visible Imaging Spectrometer), a simultaneous spectral system that operates in the range of wavelengths from visible to Thermal infrared regions of the electromagnetic spectrum, with a surface spatial resolution of about 3 m × 3 m and an elevated number of channels (102) enabling a high spectral resolution (Figure 3). The images have been captured on two subsequent days during October 1998 in two acquisitions: a daytime shot (about 12 PM) and a so-called “night shot” (about 9–10 AM) that provided thermal values similar to the nocturnal ones.

The spectral characteristics of MIVIS data enables their use for monitoring vegetation health status using vegetation indexes and, therefore, provide the ability to identify alterations in the subsoil potentially related to archaeological deposits, which are reflected in the growth and biophysic parameters of the vegetation developing on top of them. Spectral characteristics can also be exploited by using soil indexes to increase the optical distinction between the wetness or the dryness of a portion of the ground, thus enabling the recognition of voids or artefacts lying immediately under the surface soil. Within the area covered by the acquisition (about 88 km² in extent, distributed in a polygon extending around 6.75 km in width and 12.56 km in length) over 600 multi-shaped and multi-oriented marks of potential anthropogenic origin (several of which oriented with the city plan) have been mapped using routine processing (vegetation indexes—Normalized Difference Vegetation Index (NDVI), Difference Vegetation Index (DVI), Modified Soil-adjusted Vegetation Index (MSAVI2), Generalized Difference Vegetation Index (GDVI), Green Normalized Difference Vegetation Index (GNDVI), etc. soil indexes—Principal Component Analysis PCA and Selective Principal component analysis or SPCA, Tasseled Cap) and visual detection combined with manual mapping. Besides, the MIVIS imagery displays abundance of modern landscape features aligning with the Aquileian Roman grid that, for their characteristics, can be automatically extracted with the workflow presented below (Section 2.2): the coarseness of these data enables more accurate feature extraction as the algorithm is not misled by the abundance of fine details as in the case of RGB Orthophotos. The images, however, are affected often by strong geometric distortions that alter the straightness of linear elements of the landscape, distortions that are hard to compensate for without forcing rectification procedures that dramatically alter the original aspects of the features, thus potentially misrepresenting the real geometry of landscape elements.

RGB Ortho-Imagery includes coverages from 2000, 2003, 2007 and 2011 with respectively 100, 80, 70, 50 cm ground resolution, and forms the Remote Sensing dataset with the highest spatial resolution available in this project (Figure 4). This represents the most useful set of imagery for the present work as a coverage for the whole region is available for multiple years and for the increased ground resolution of the data.

A custom-designed workflow has been applied on these photographic datasets in order to automatically detect similarly angled or orthogonal landscape elements having an orientation congruent with the Aquileian cadaster. As, clearly, not all correctly oriented features of the landscape have a correlation with the centurial grid, and orientation is not the only characteristic that linear features have to have in order to be considered parts of a cadaster, the extracted linear features have been filtered to remove those that do not carry a strong weight, i.e., those that are unlikely to be ancient, for example the majority of the minor drainage channels that follow the 22° W from N or 22° S from W (=248°) directions (respectively aligned with the major axes of the Centuriation, the Cardo Maximus and Decumanus Maximus) and that are likely to be simply later additions, kept parallel to a landscape dominated by Roman arrangements designed to be the most appropriate to ensure efficient water drainage. After they have been filtered, the frequency of the remaining elements oriented to the Roman grid is estimated from the images in order to compute the module with highest probability.

The goal of this and similar approaches is to examine a large set of hypotheses, to quickly exclude those with little promise and to provide reasonable candidates for further investigation based on more traditional archaeological approaches. Indeed, the automatic extraction of features can in no way provide direct confirmation or guarantee of identification, but can be used to reduce the amount of fieldwork and other investigation required to confirm elements of current landscape as ancient land division. To this effect, the proposed approach was based on hypotheses with no more than a simple range of acceptable values for the cadaster modules and a few well documented assumptions like the orientation of cardo and decumanus. Rather than being hypothesis-driven, the approach was oriented to evaluate what could be extracted, resulting in multiple hypotheses of which we deemed one more plausible than the others. It remains as a given that all of them need to be verified on the basis of a variety of other criteria and validation procedures, including fieldwork activities, legacy data re-evaluation and spatial analysis. However, thus reduced, verification can be performed on a very limited number of hypotheses vs a continuum.

2.2. Method

The workflow of feature extraction and detection implemented in © Matlab (R2016b, MathWorks Natick, MA, USA) seeks to estimate location and periodicity of dominant linear features on georeferenced images. In order to do that, the system needs to extract dominant lines aligned along the 22° W from N and 22° S from W (=68° E from N) directions, accumulate the georeferenced linear features from all images and fit the correct location and size of the centuriation on the dominant responses. For this reason, the workflow involves three processes: (i) filtering; (ii) thresholding and linear feature extraction; (iii) feature accumulation and periodicity estimation.

2.2.1. Filtering

The filtering process aims to estimate the presence of linear features by looking at the response of edge detection linear filters at various locations, orientations, and scales. To this end we independently convolved each image with a bank of Gabor filters at various orientations and scales.

Gabor filters [26] are directional wavelet filters that can detect the presence of specific frequencies at a given orientation, localized around a given location. This ability to detect directional high frequency locally periodic patterns made them the tool of choice in several image processing and applications such as character recognition [27] and fingerprint recognition [28]. These characteristics make them also perfectly suited for the present task, where drainage ditches in fields and other current land division components result in repetitive aligned linear features.

The spatial response of the filter is defined as follows:

$$g\left(x,y;\theta ,\lambda ,\sigma ,\gamma ,\psi \right)=exp\left(-\frac{x^{\prime }{}^2+{\gamma }^2{y}^{\prime }{}^2}{2{\sigma }^2}\right)exp\left(i\left(2\pi \frac{x^{\prime }}{\lambda }+\psi \right)\right)$$

(1)

where

$$\begin{array}{ccc}{x}^{\prime }& =& xcos\theta ysin\theta \\ y^{\prime }& =& -xsin\theta +ycos\theta \end{array}$$

and θ is the filter’s orientation, λ is its frequency, σ the scale of the filter, γ its aspect ratio, i.e., scale ratio along the direction versus orthogonal to the direction, and, finally, ψ is a phase offset, which will result in a phase shift in the complex response and is irrelevant for our analysis since we are interested in the absolute value of the response.

The bank of filters includes filters computed at various scales and orientations: the scales of the filters were 5, 10, 20, and 30 m, which include the fundamental scales of the sought after linear features, i.e., roads, canals, drain-lines, crop-marks, etc. The orientations were selected in a relatively narrow band around the known centuriation axes, i.e., 12°, 17°, 22°, 27°, and 32° W from North for the lines aligned with the cardo, and 12°, 17°, 22°, 27°, and 32° S from West for the ones aligned to the decumanus.

The spatial frequency was linked to the scale such that period length was equal to the scale, i.e., σ/λ = 1; while the aspect ratio was set to 1/3 so that the filter was fairly elongated in order to (i) increase directional accuracy; (ii) limit general high feature response; and (iii) concentrate on sizable aligned edges. Finally, the phase offset ψ was ignored (set to 0) as it does not have an effect on the absolute response value.

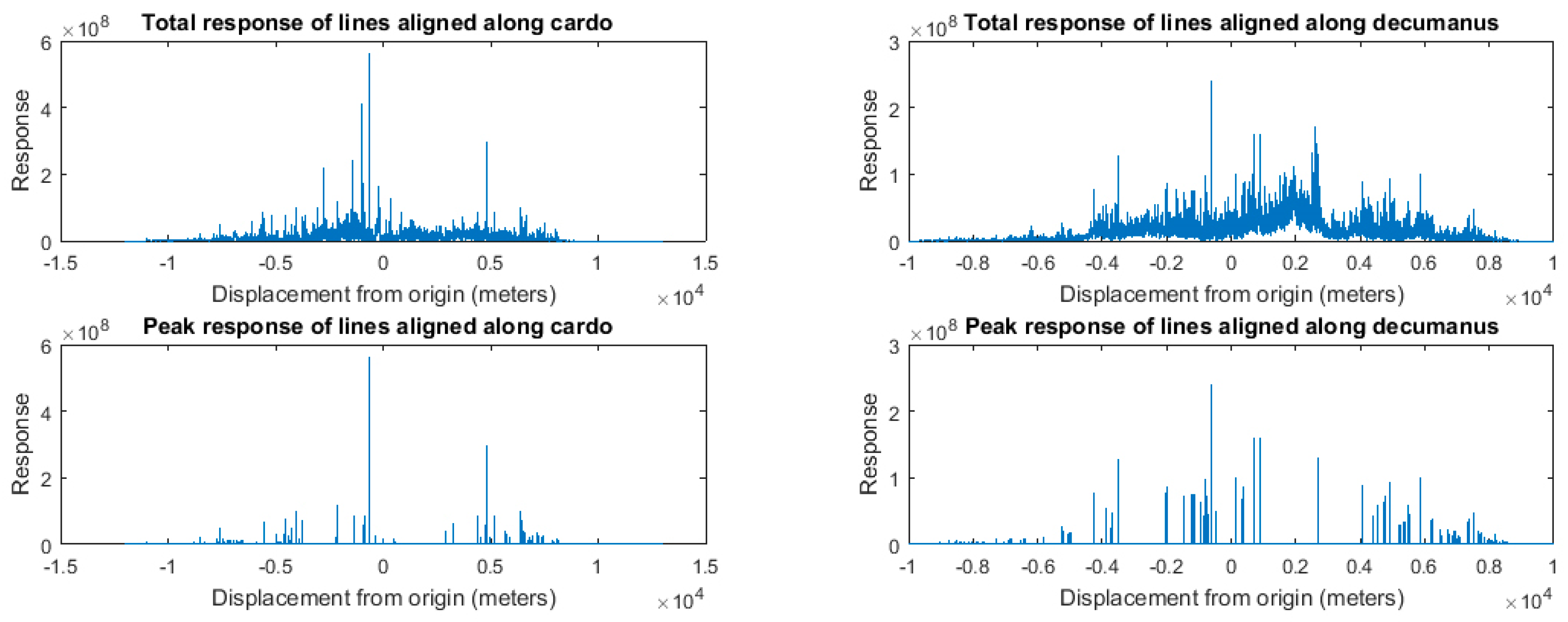
Given this filter bank each image was convolved with 40 filters resulting in 120 responses for RGB images (40 per channel). These responses were divided into two groups of 60 responses each: one for the filters with orientations around the cardo direction (22° W from N) and one for orientations around the decumanus direction (22° S from W). Then, we non-linearly accumulated the response across channels and scales. Here we accumulated by summing the square norm of the response at each location and direction (Figure 5). The goal of the non-linear accumulation is to perform a soft-max, i.e., obtain a continuous response that enhances the maximum values across channels and scales. The end result is 5 responses per dominant direction providing response in the location-orientation space.

2.2.2. Thresholding and Linear Feature Extraction

In order to extract linear feature candidates, we performed selective thresholding in the location-direction space. For each directional group, we retained locations (pixels), if the current location was a local maximum at the central direction (22° W from N for the cardo oriented group, 22° S from W for the decumanus oriented group) and its accumulated response was above an adaptive threshold. In particular, location (x,y) was retained if:

• location maximality
  resp(x,y;θ) ≥ resp(x + k dx, y + k dy; θ)
  with

  $$\begin{array}{ccc}k& =& -1,-2,1,2\\ dx& =& -sin\theta \\ dy& =& cos\theta \end{array}$$

  and θ being the group’s dominant direction (22° or 112° W from N)
• directional maximality
  resp(x,y;θ) ≥ resp(x, y; θ + dθ)
  with dθ = −10°, −5°, 5°, 10°
• adaptive thresholding

  $$resp\left(x,y,\theta \right)\ge c\underset{x,y,\theta }{max}\left(resp\left(x,y,\theta \right)\right)$$

  with the threshold parameter c being set to 0.1 in our experiments.

The result was two sets of pixel locations for each image corresponding to strong edge responses along either the cardo direction (22° W of N) or decumanus direction (22° S from W). Note that cardo and decumanus sets are independent and a pixel can appear in both sets (Figure 6).

2.2.3. Feature Accumulation and Periodicity Estimation

Given pixel-wise feature locations in each georeferenced image, we computed the geolocation of each point feature and accumulate those throughout all image sets, obtaining a set of georeferenced feature locations and their responses. In order to find the center and periodicity of such responses, first each linear response was down-projected and accumulated along the direction orthogonal to the group’s direction, i.e., cardo’s direction responses were accumulated along a line in the 22° S from W direction, while decumanus lines were accumulated along a linear space of orientation 22° N from W, thus resulting in two response histograms along the two orthogonal directions.

For ease of computation, the origin of this projected system was set at the intersection of the via Julia Augusta (State Route 352) and the virtual extension of the Anfora Canal (which flows toward SW, W of Aquileia) toward E, which is considered to be the most likely point of intersection of the cardo Maximus and decumanus Maximus [20].

These response histograms (Figure 7) take into account the locations of all coherently aligned responses, andare strongly influenced by the geometry of the spatial coverage, exhibiting a systematic size bias of the baseline responses visible in the histogram. However, we were not interested in the baseline responses, but rather in the peaks of the distribution, which correspond to directions with higher-than-usual aligned response. For this reason, we eliminated the baseline response by computing a centered average of the response over 50 m (smoothing with a centered average filter of size 50 m) and maintaining only the responses that were greater than 2.5 times the smoothed response.

The use of peaks provides the added advantage of making the approach more robust with respect to missing signals. Indeed, gaps due to missing alignments would simply result in fewer votes and, thus, smaller peaks, which are, however, still likely to be of much larger magnitude than the average response as a result of limited and localized lack of signal, and thus identifiable.

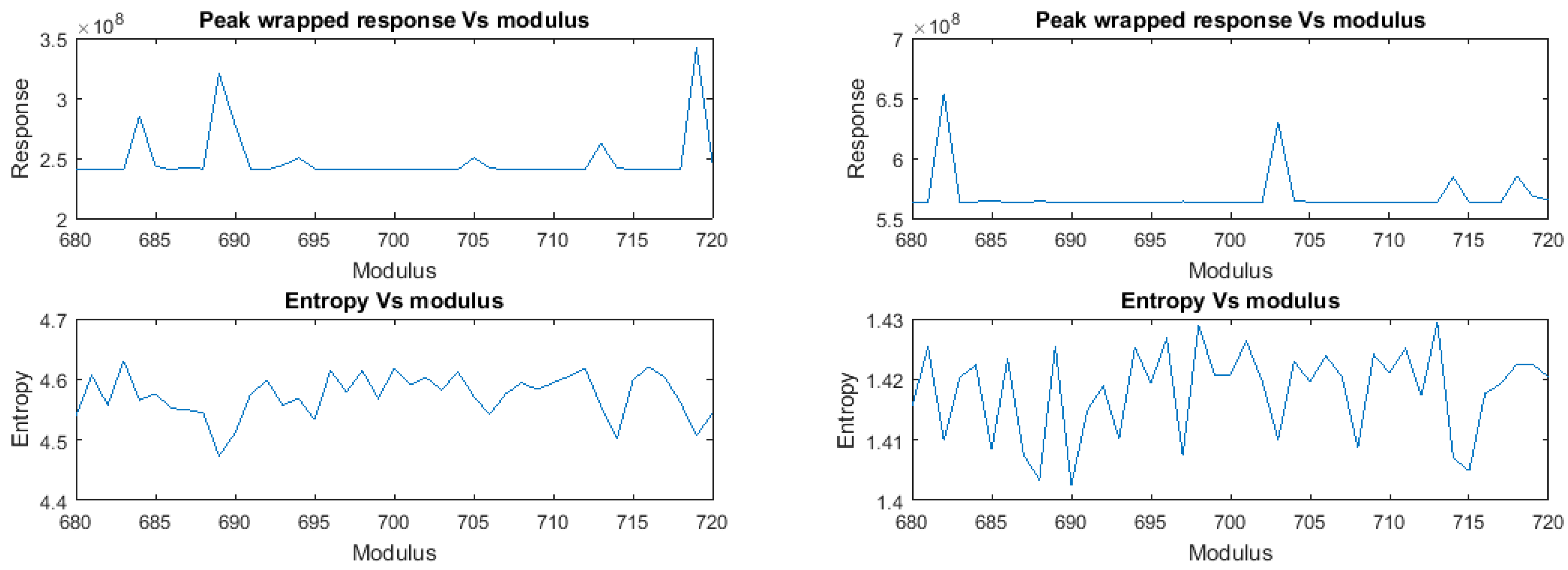
With the histograms of peak responses in hand, we sought to estimate the center location and periodicity of repeated aligned linear features, with the hope that these would correspond to location and module of centuriation patterns. To this end we tested centurial modules ranging from 600 m to 750 m in a 1 m increment. We operated on the two main orientations independently, and for each tested module we accumulated the response cyclically, wrapping around the accumulation with a period equal to the module.

$$wrappedHistogram\left(t\right)={\displaystyle \sum }_{n=-\infty }^{\infty }Histogram\left(t+nmodulus\right)$$

(2)

with t = 0...module − 1.

For each module, we retained peak value, peak location and entropy of the wrapped histogram. The Entropy is a measure of disorder or lack of information in a distribution and has maximal values when the distribution is concentrated in a few states

$$Entropy=-{\displaystyle \sum }_{i}p\left(i\right)\log \left(p\left(i\right)\right)$$

where $p\left(i\right)=\frac{wrappedHistogram\left(i\right)}{{\sum }_{j}wrappedHistogram\left(j\right)}$.

The expectation was that the correct module would exhibit better modular alignment of (peak) directional responses, resulting in a wrapped histogram with a stronger and better localized peak in correspondence to the modular location of the center of the centuriation pattern and relatively little response elsewhere. Hence, the correct module would be characterized by a maximal value in the peak value and a minimal value in the entropy associated with the corresponding wrapped histogram. Once this optimal module was detected, the location offset along the orthogonal direction could be extracted from the peak location at that module value.

Note that, due to aliasing phenomena, we would have expected similar peaks to appear at any multiple of the correct modulus. However, the limits in the search range hided such effects. Indeed, to observe them we would require the maximum value of the range to be at least twice as big as the smallest modulus, while our range went from 680 to 720 m.

3. Results

Figure 8 shows the accumulated peak responses and entropies as a function of the chosen modulus. The plots on the left are for the cardo direction, while those on the right are for the decumanus. The range of moduli taken into consideration is between 680 and 720 m.

The plot shows that there are a few peaks in the response in both directions. In particular, the cardo presents the strongest peak at 719 m, while the decumanus presents a maximum at 683 m. In both cases, the peaks correspond to minima in entropy, so, taken in isolation, they would seem to be good candidates. However, when taking into consideration both directions, these measures are not consistently good candidates for a centurial module. In fact, the closest peak in the orthogonal directions (684 m in the cardo direction and 718 in the decumanus direction) do not correspond to local minima in the entropy, suggesting that these peaks are not the result of a square grid, but rather something else, presumably Moiré patterns due to periodicity on the orthogonal direction, probably due to modern landscape linear components. Moreover, these values (718–719 m, 683–684 m) are not consistent with a centurial module and therefore can be disregarded.

The only peak presents in both direction that is consistently a local minimum for the entropy is the peak around 704 m (705 m in the cardo direction and 703 m in the decumanus direction).

4. Discussion

The presented periodicity of the feature accumulation suggests a value of 704–705 m for the grid module, which cannot exclude a 706 m result due to the resolution, a value that is fully compatible with a centurial cell. The result is quite relevant as other metrological analyses recently undertaken [29] have highlighted that the 20 × 20 actus module of Aquileia measured likely 704–705 m × 704–705 m rather than conventional 710 m. The trend is known in other early centuriations deployed in Central Italy in the initial period of the Roman colonial expansion and centuriation deployment [30] and the phenomenon connected to the variations in size of the Roman foot (pes). This represents a primary outcome of the current work, as previous scholarship related to the Aquileian cadaster has derived hypothetical grid models (of varying number of actus) based on the assumption that the centurial module would have been generated as a multiple of an actus with a standard size of 35.51 m; the outcomes of this trial show instead it could be comprised between 35.25 m and 35.3 m, thus determining a notable variation of the grid size on the long distances. A slightly smaller than “standard” centuria would also explain current unaccounted for metrological errors and mismatches verifiable on the long distance (from the centurial umbilicus of Aquileia) projecting a virtual grid with a standard module of 710 m: many already recognized and validated limites, like the ones of Sedegliano for example [21], would not be aligned to the grid-lines in this case. Redefining the measures of the “Classic” Aquileian centurion’s module has implications also in the definition of its relationship with the other centuriations that have been detected in the Friulian plain [21], establishing a relationship of antecedence with those characterized by a longer (and likely later) module, thus challenging current theories [21,22] that indicate the “Classical” centuriation as succeeding other deployments.

A generated grid of 706 m × 706 m, overlaid over the remote sensing imagery (Figure 9) and aligned along the via Julia Augusta and the Anfora Canal with origin at their intersection, shows the overlap of some of the major elements of the cadaster with the grid-lines. Several centuriation constituents line up rather accurately with the proposed virtual grid, especially in the area W of Aquileia and the main cardo. An interesting feature is that several major roads that connect to the city are aligned to the cadaster oblique to the square grid with varying, but regular ratios, like the sector of the via Gemina (exiting Aquileia at NE, linking it to ancient Emona, present Ljubljana) nearer to the city fits the grid with a ratio of 1:1.

Notwithstanding these positive empirical outcomes, the workflow is still showing some flaws that are being investigated, like the presence of very strong peaks in the wrapped histogram referring to repetitiveness of elements at distances that do not have meaning within the “space dimension” of a Roman cadaster, and that are likely generated by later landscape elements aligned with the Roman system of which they mimicked orientation and configuration. In future work, it will be likely necessary that the linear objects, once extracted, undergo through individual optical analysis to determine their congruence to the centurial grid based on a number of other variables and information (especially of archaeological nature) that can validate their historicity, rather than simply filtering them out based on a number of physical parameters. This will reduce the number of features that add complexity to the calculation.

5. Conclusions

In studying ancient regularly designed landscapes characterized by repetitive patterns, where highlighting the components of the system in order to determine repetitiveness is crucial to the goal of the research, the use of automated detection and extraction of cadaster element methods enables not only to reduce manual mapping time, but also to improve the quality and number of correct identifications. The provisional results of this work bring attention to the need of customizable tools and workflow that can streamline processes that would otherwise be alienating and time consuming. Moreover, when mapping visually identified features is undertaken via manual tracing, the possibility of introducing unwanted errors is very likely, as even a misalignment equal to 1° of orientation can generate relevant errors on long distance. Automation of processes appear therefore a desirable solution.

Clearly, as in any sort of automation, the proposed workflow has to be customized based on the goal and research questions of the project, and the design of a process aiming to extract specific objects has to start from the landscape characteristics (including the morphology) and the nature, forms, model and patterning of the system components. This experience shows that land division elements, once extracted, are likely to demand visual analysis on a one to one basis to determine their congruence to the field system based on a number of variables and criteria before bringing them into more complex statistical analysis. This process will likely be automated in a near future using approaches from Artificial intelligence and Machine Learning, but the application of these methods to the archaeological domain, as we have seen, is still in its infancy. Thus, at the moment, such vetting process will still have to be based on a combination of automated filtering and visual assessment. The results of this automated workflow are in any case just the first step of a much more complex process were theoretic models have to be substantiated and validated by spatial analysis, field mapping and ground verification activities and corroborated by archaeological information and investigation.