Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Gauged Basin Information
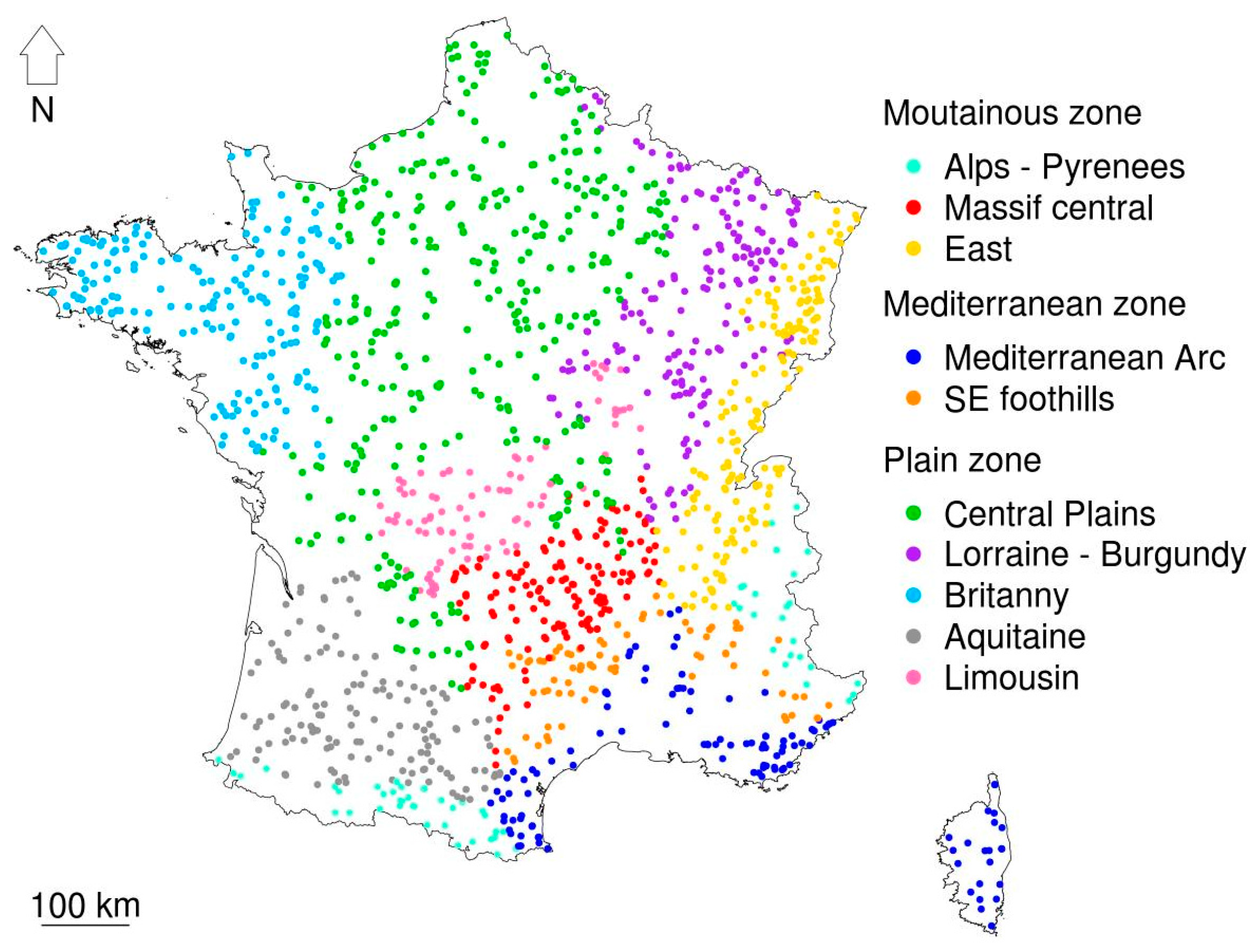
2.1.2. Regional (ised) Information
- Plains zone: Central Plains, Lorraine-Burgundy, Brittany, Aquitaine, Limousin
- Mountainous zone: Alps-Pyrenees, Massif Central, East
- Mediterranean zone: Mediterranean Arc, South-East foothills.
2.2. FFA Methods
2.2.1. At-Site Statistical Distribution
2.2.2. Local-Regional Statistical Distribution
- The GEV distribution was fitted at each site using only local data with a Bayesian procedure (with a flat prior for both the location and scale parameters and a normal prior with a 0.25 mean and standard deviation for the shape parameter).
- Each GEV parameter was related to catchment descriptors by a linear regression (independently in each of the ten regions).
- A new GEV distribution was fitted using a Bayesian approach, using informative priors based on the results of the regression. This FFA method is denoted GEV_LR throughout the article.
2.2.3. Regional Distribution
2.2.4. Process-Based Method
- A fully regionalised at-site stochastic rainfall generator is used to simulate long series of rainfall events at any point in France (kilometric resolution) at an hourly time-step. The development, calibration, regionalisation and validation of this generator have been the object of numerous studies [47,76,77,78] and are not within the scope of this paper. This generator is included in national guidance for rainfall prediction in France [79].
- A conceptual, hourly and event-based rainfall-runoff model with two reservoirs transforms at-site rainfall events into at-site flood events at the kilometric resolution. This model is a simple GR-type model [80,81] with a single parameter to calibrate. It is composed of a production reservoir whose capacity is related to hydrogeology, a routing reservoir with a uniform capacity and a 2-h unit hydrograph [46]. During a rainfall event, the production reservoir retains water and progressively saturates. This progressive saturation of the model simulates a non-linear rainfall-runoff transformation which can be related to the progressive saturation of the catchment. For more extreme events, saturation becomes complete and all the exceeding water participates in runoff. In this case, the runoff is controlled by the rainfall information. The only calibrated parameter of this model is the initial filling of this production reservoir. At-site flood quantiles are extracted directly from the empirical distribution of flood events.
- The at-site flood quantiles are aggregated to catchment outlets using an areal reduction function solely depending on the drainage area and the simulation time-step [46]. The calibration of the model aims to determine which specific flows (associated with a certain value of the parameter) should be aggregated to minimise the error between the 2-, 5- and 10-year return period SHYREG-simulated quantiles and GEV quantiles for flood peaks and daily flows. The optimal value of the parameter is then attributed to the whole catchment.
2.3. Regionalisation Schemes
- Donor catchments: sites where all data were assumed to be available; they could be used to calibrate both the FFA and the regionalisation method.
- Target catchments: sites where the flood quantiles were to be estimated; the discharge data could only be used to perform validation.
2.3.1. Spatial Proximity
2.3.2. Similarity Pooling
2.3.3. Regression-Based Method
2.4. Evaluation Criterion
- The R2 criterion evaluated the goodness-of-fit between two estimations in many sites of the same value.
- The FF score evaluates the reliability of the method by analyzing the probability associated by the method to the maximum observed flow.
- The SPAN score evaluates the stability of the method regarding calibration data.
2.4.1. Reproduction of Quantiles
- To assess the accuracy of quantiles associated with low return periods, we assumed that the locally estimated GEV_LR approach is accurate in the observation field (T ≤ 10 years) and is used as a reference to evaluate quantile estimates from other approaches (used in Table 3).
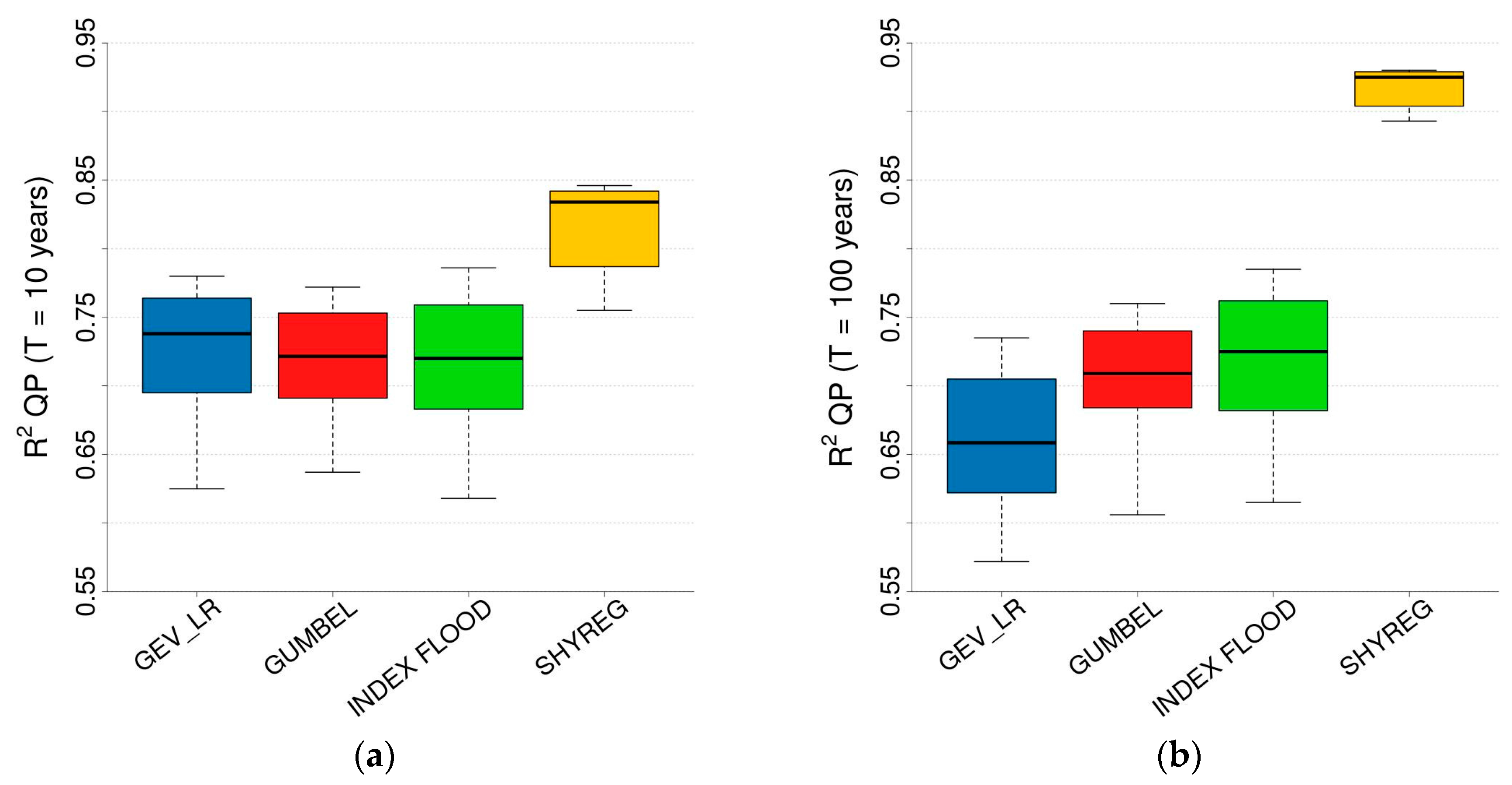
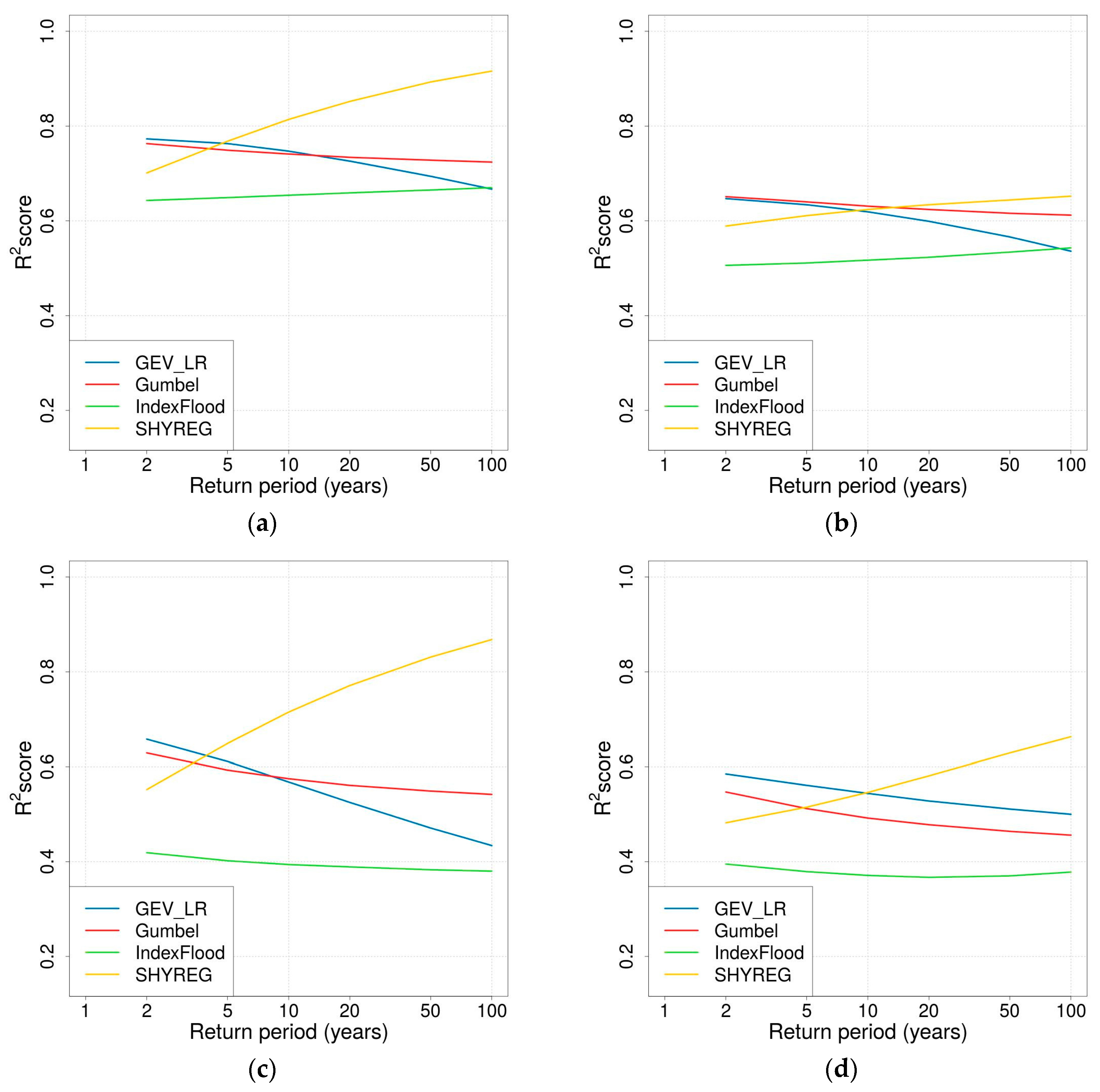
- To assess how well the regionalisation is able to reproduce the quantile estimated locally, the reference quantile of a given FFA is the local quantiles of this FFA. In this case the value of R2 does not inform on the accuracy of the regional approach because the quantile evaluated locally can be inaccurate. It can be seen as an evaluation of the stability regarding regionalisation (used in Section 3.2 and Section 3.3.2).
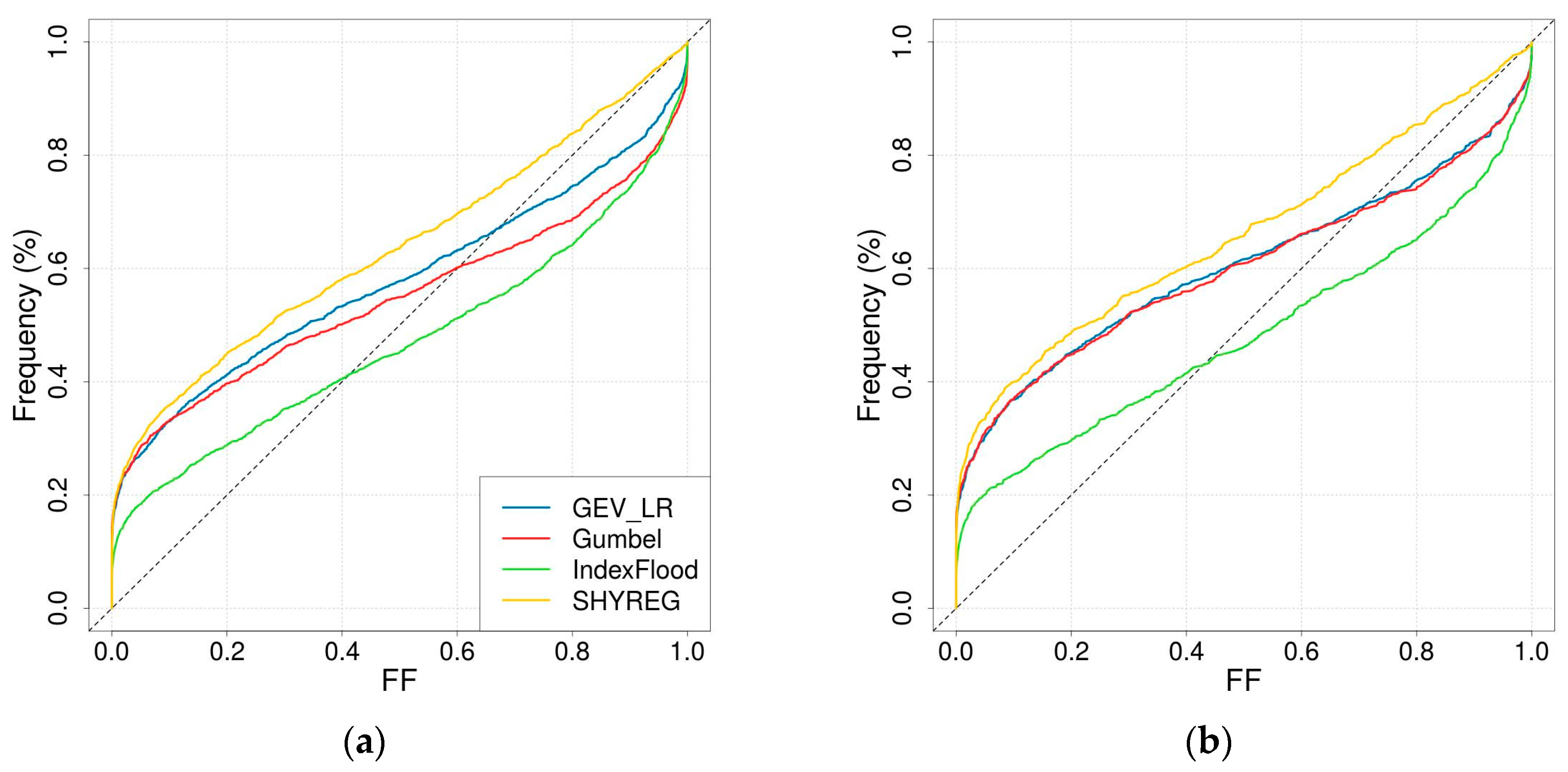
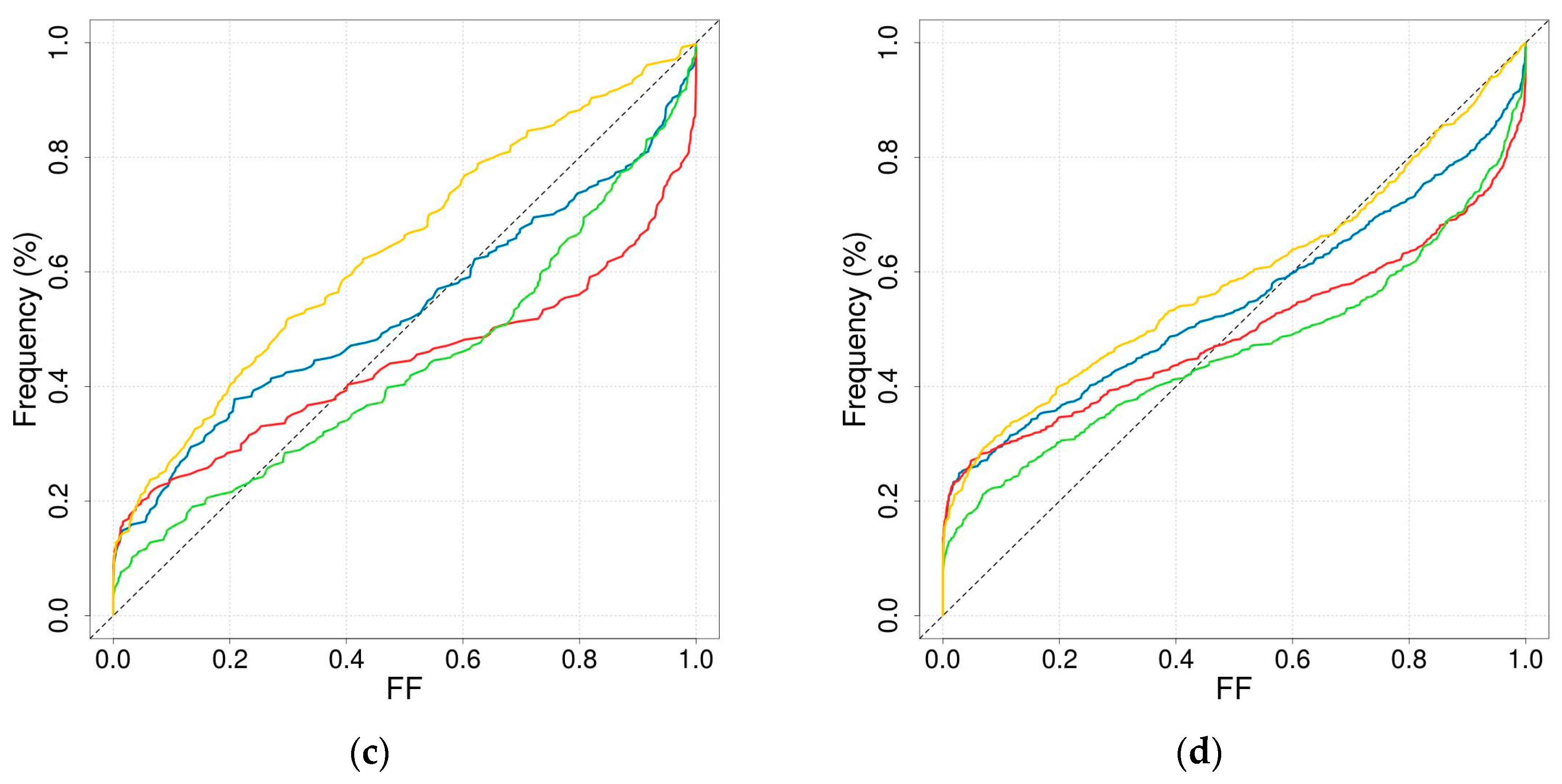
2.4.2. Reliability of Rare Quantiles
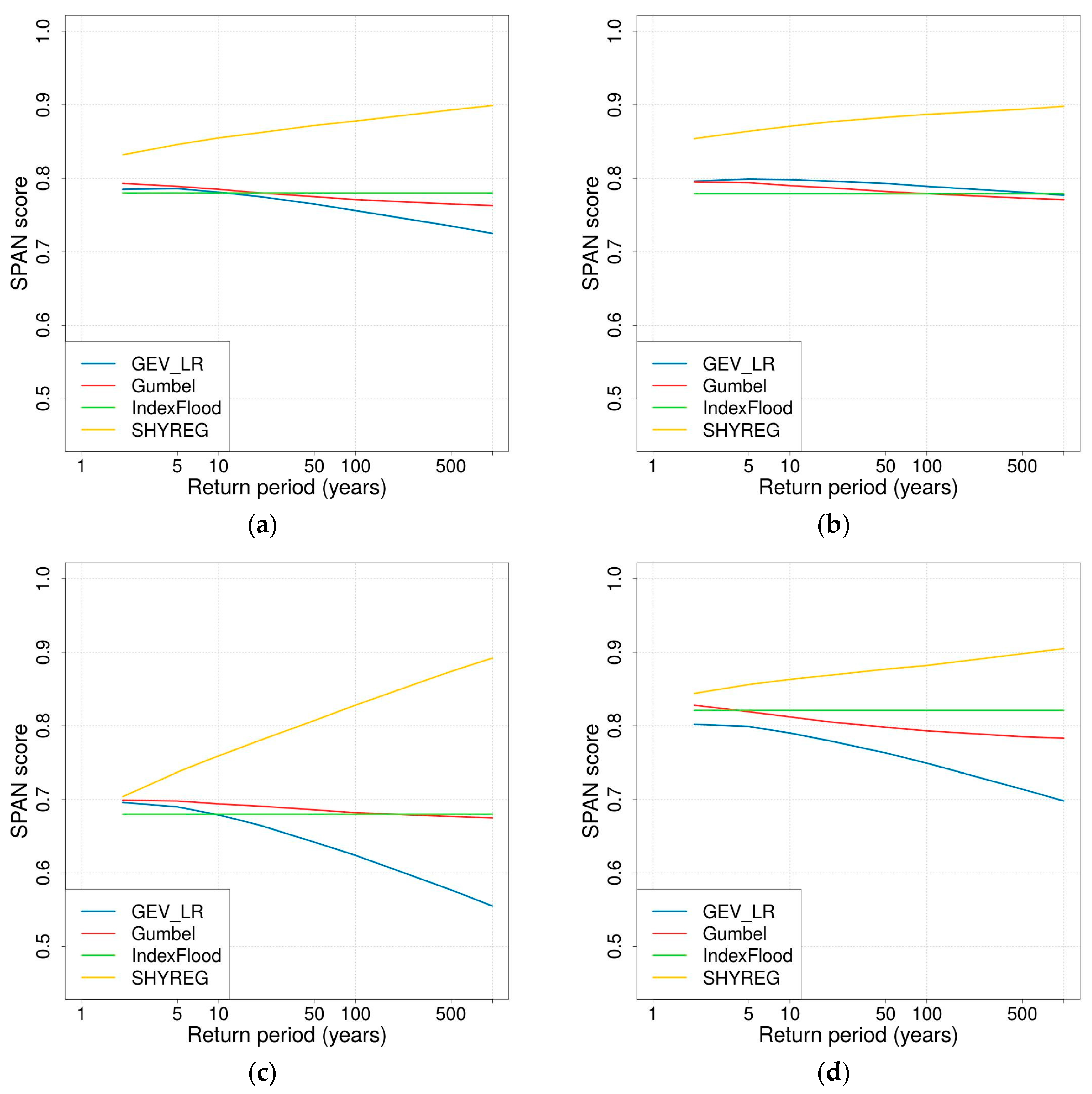
2.4.3. Stability
3. Results
3.1. At-Site FFA
3.2. Reproduction of At-Site Quantiles
3.3. Comparison of Regionalised FFAs
3.3.1. Reliability of Rare Quantiles
3.3.2. Reproduction of At-Site Estimated Quantiles
3.3.3. Stability
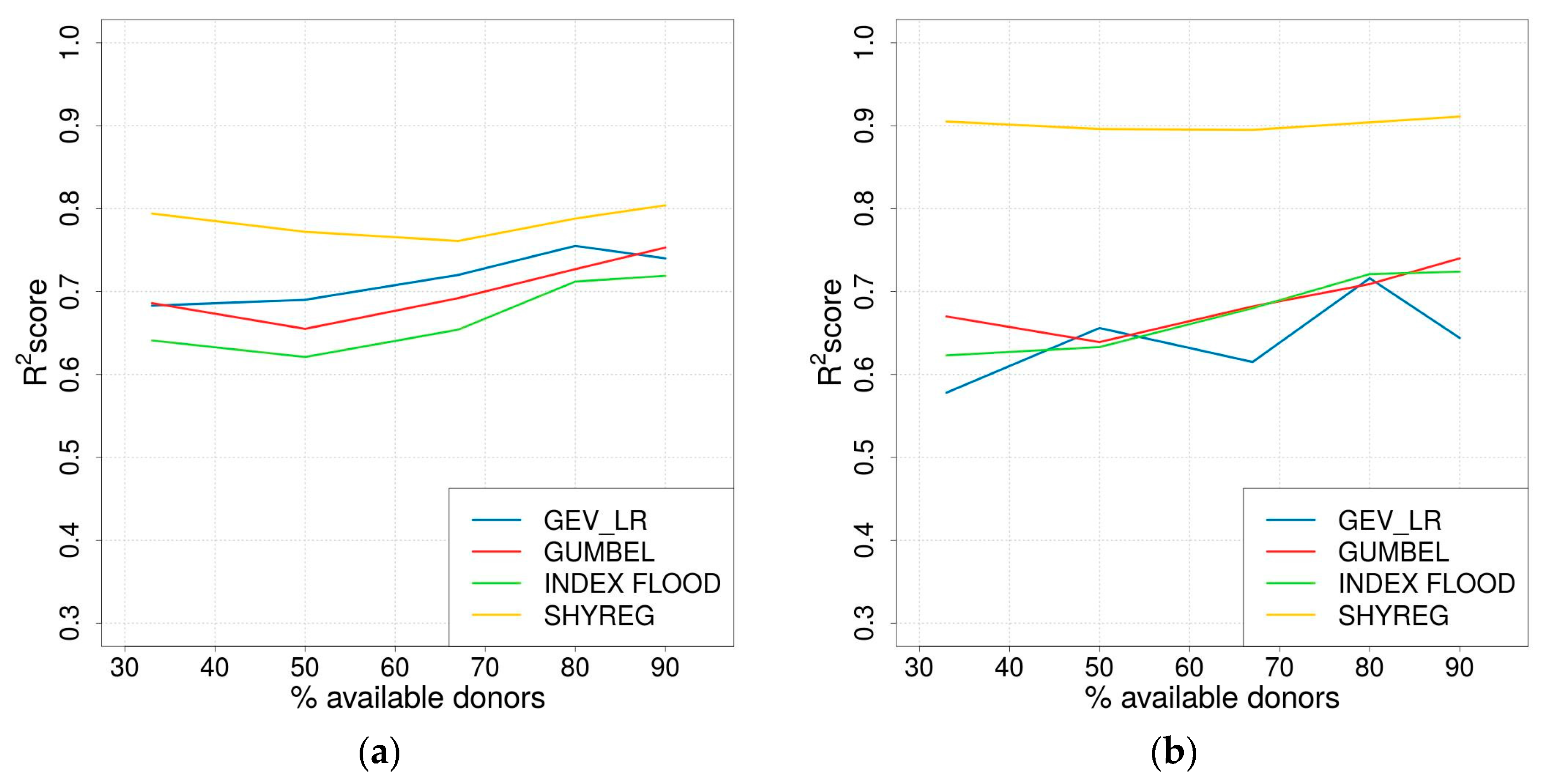
3.4. Impact of the Number of Available Donors
4. Discussion
- In the SHYREG simulation, the only parameter calibrated against discharge data is the initial filling of the production reservoir. This parameter was not very well estimated by regionalisation. The reservoir can become saturated for extreme floods; consequently, the most extreme events simulated by SHYREG does not strongly depend on the calibrated parameter. This means that in the SHYREG simulation the calibration is used to position the start of the frequency curve (i.e., low return periods), whereas the asymptotic behaviour is based almost completely on the rainfall simulation. Consequently, the upper tail of the simulated distribution is only slightly affected by regionalisation errors (contrary to the lower tail). This point explains why the stability of the regionalised SHYREG quantiles appears to increase as the return period increases (very stable extreme quantile and variable frequent quantiles), and why these extreme regionalised quantiles are very similar to the calibrated quantiles. In addition, thanks to an extensive work on rainfall analysis [47,76,92,93], SHYREG benefits from an accurate rainfall information [78] even in ungauged sites. It is not the case for other approaches, and it makes it less dependent its regionalised parameter.
- The asymptotic behaviour of a GEV distribution is highly controlled by the shape parameter. Not only is this parameter challenging to estimate using at-site data because it is very sensitive to sampling, but it is also more difficult to regionalise than the other two (the second issue can probably be related to the first one). This means that the upper tail of the flood distribution suffers significantly from regionalisation errors. This is the reason why the stability of GEV_LR-estimated quantiles appears to decrease when considering longer return periods.
- In the GUMBEL approach, a null shape parameter is imposed. Consequently, the shape of the flood distribution, and especially its skewness, remains quite stable even during the regionalisation process. Nevertheless, the GUMBEL distribution is not flexible enough to describe the dynamics of the most responsive catchments (i.e., Mediterranean catchments), which can explain why it has a tendency to underestimate extreme quantiles over the Mediterranean zone.
- The INDEX FLOOD approach is supposed to overcome the issues of stability (exhibited by the GEV_LR implementation) and flexibility (exhibited by the GUMBEL case) by considering regional distribution and local scaling indexes. Its stability does not depend on the return period considered. The comparison of the growth curves between the regions actually shows heavier upper tails for the Mediterranean and mountainous regions than for the plains. Nevertheless, in the end this approach underwent more losses during the regionalisation stages, leading to quite poor performance. This approach may have suffered from a lack of development already visible at the calibration stage. A more in-depth analysis of the definition of the regions and at-site performance would probably be necessary to enhance the performance of this method.
- Consistency between quantiles in terms of return period to estimate the entire flood frequency curve for a return period up to 1000 years;
- Consistency between quantiles in terms of time-steps to estimate maximum flow quantiles of different durations;
- Spatial consistency when several target catchments are considered, even if the spatial coherence of the estimated quantiles between the different sites was not analysed here.
5. Conclusions
- The regionalisation process is the source of substantial loss of performance in FFA. Consequently, stability regarding at-site calibration data is a very valuable advantage for regionalisation. For this reason, the process-based methods, such as SHYREG, appear to be a safe solution method for flood estimation in ungauged basins.
- Methods that do not take into account the dependency between quantiles (between the different return periods and/or time-steps) can lead to incoherent flood frequency estimation. Therefore, when interested in multiple quantile estimations one should explicitly consider these dependencies or employ an approach that does: for example, parameter regionalisation rather than quantile regionalisation.
- The results can vary greatly depending on the study area. When studying a large and variable area, discrimination by region is necessary to analyse the results. In France, the Mediterranean region should at least be considered separately.
- In the present case, for a long return period, the low dependence between the regionalised SHYREG extreme quantiles and calibration discharge data provide quantile estimates relatively close to that obtained in a gauged configuration, i.e., quantiles that can be and have already been validated [18,45].
- Due to its low dependence on calibration, the SHYREG method appeared to be less affected by decreasing the number of available gauging stations. Nevertheless, the SHYREG quantiles largely rely on previous rainfall simulations [47,76,78]; consequently, an application to other areas would still require the availability of rainfall data sets.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ministère de la Transition Écologique et Solidaire. Prévention des Inondations. Available online: http://www.developpement-durable.gouv.fr/prevention-des-inondations (accessed on 18 May 2017).
- Castellarin, A.; Kohnová, S.; Gaál, L.; Fleig, A.; Salinas, J.L.; Toumazis, A.; Kjeldsen, T.R.; Macdonald, N. Review of Applied-Statistical Methods for Flood-Frequency Analysis in Europe: WG2 of Cost Action ES0901; Castellarin, A., Kohnová, S., Gaál, L., Fleig, A., Salinas, J.L., Toumazis, A., Kjeldsen, T.R., Macdonald, N., Eds.; The Centre for Ecology & Hydrology: Lancashire, UK, 2012. [Google Scholar]
- Willems, P.; Blazkova, S.; Beven, K.J.; Arnaud, P.; Paquet, E.; Loukas, A.; Vasiliades, L.; Efstratiadis, A.; Lawrence, D.; Szolgay, J.; et al. Rewiew of European Simulation Methods for Flood-Frequency-Estimation. WG3: Flood Frequency Analysis Using Rainfall-Runoff Methods; Willems, P., Blazkova, S., Beven, K.J., Arnaud, P., Paquet, E., Loukas, A., Vasiliades, L., Efstratiadis, A., Lawrence, D., Szolgay, J., Eds.; Report of Cost Action, ES0901; The Centre for Ecology & Hydrology: Lancashire, UK, 2012. [Google Scholar]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Prescott, P.; Walden, A.T. Maximum likelihood estimation of the parameters of the generalized extreme-value distribution. Biometrika 1980, 67, 723–724. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Kuczera, G. Comprehensive at-site flood frequency analysis using monte carlo bayesian inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]
- Renard, B.; Kochanek, K.; Lang, M.; Garavaglia, F.; Paquet, E.; Neppel, L.; Najib, K.; Carreau, J.; Arnaud, P.; Aubert, Y.; et al. Data-based comparison of frequency analysis methods: A general framework. Water Resour. Res. 2013, 49, 825–843. [Google Scholar] [CrossRef]
- Ribatet, M.; Sauquet, E.; Grésillon, J.M.; Ouarda, T.B.M.J. A regional bayesian pot model for flood frequency analysis. Stoch. Environ. Res. Risk Assess. 2007, 21, 327–339. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Stedinger, J.R. Estimating a regional flood frequency distribution. Water Resour. Res. 1983, 19, 503–510. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Manual of Hydrology: Part 3; 1543A; United States Government Publishing Office: Washington, WA, USA, 1960.
- Renard, B. A bayesian hierarchical approach to regional frequency analysis. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Li, J.; Thyer, M.; Lambert, M.; Kuczera, G.; Metcalfe, A. An efficient causative event-based approach for deriving the annual flood frequency distribution. J. Hydrol. 2014, 510, 412–423. [Google Scholar] [CrossRef]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Arnaud, P.; Cantet, P.; Aubert, Y. Relevance of an at-site flood frequency analysis method for extreme events based on stochastic simulation of hourly rainfall. Hydrol. Sci. J. 2016, 61, 36–49. [Google Scholar] [CrossRef]
- Paquet, E.; Garavaglia, F.; Garçon, R.; Gailhard, J. The schadex method: A semi-continuous rainfall-runoff simulation for extreme flood estimation. J. Hydrol. 2013, 495, 23–37. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Tasker, G.D. Regional hydrologic analysis: 1. Ordinary, weighted, and generalized least squares compared. Water Resour. Res. 1985, 21, 1421–1432. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mesa, O.J.; Dawdy, D.R. Multiscaling theory of flood peaks: Regional quantile analysis. Water Resour. Res. 1994, 30, 3405–3421. [Google Scholar] [CrossRef]
- Skøien, J.O.; Merz, R.; Blöschl, G. Top-kriging—Geostatistics on stream networks. Hydrol. Earth Syst. Sci. 2006, 10, 277–287. [Google Scholar] [CrossRef]
- Micevski, T.; Hackelbusch, A.; Haddad, K.; Kuczera, G.; Rahman, A. Regionalisation of the parameters of the log-Pearson 3 distribution: A case study for New South Wales, Australia. Hydrol. Process. 2015, 29, 250–260. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A.; Stedinger, J.R. Regional flood frequency analysis using bayesian generalized least squares: A comparison between quantile and parameter regression techniques. Hydrol. Process. 2012, 26, 1008–1021. [Google Scholar] [CrossRef]
- Ahn, K.H.; Palmer, R. Regional flood frequency analysis using spatial proximity and basin characteristics: Quantile regression vs. Parameter regression technique. J. Hydrol. 2016, 540, 515–526. [Google Scholar] [CrossRef]
- Organde, D.; Arnaud, P.; Fine, J.A.; Fouchier, C.; Folton, N.; Lavabre, J. Regionalization of a flood frequency estimation method over Metropolitan France: The shyreg method. Revue des Sciences de l'Eau 2013, 26, 65–78. [Google Scholar] [CrossRef]
- Basu, B.; Srinivas, V.V. Evaluation of the index-flood approach related regional frequency analysis procedures. J. Hydrol. Eng. 2016, 21. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K. Regional flood frequency analysis and prediction in ungauged basins including estimation of major uncertainties for mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Sefton, C.E.M.; Howarth, S.M. Relationships between dynamic response characteristics and physical descriptors of catchments in England and Wales. J. Hydrol. 1998, 211, 1–16. [Google Scholar] [CrossRef]
- Seibert, J. Regionalisation of parameters for a conceptual rainfall-runoff model. Agric. For. Meteorol. 1999, 98, 279–293. [Google Scholar] [CrossRef]
- Burn, D.H. Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Burn, D.H. An appraisal of the “region of influence” approach to flood frequency analysis. Hydrol. Sci. J. 1990, 35, 149–165. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Elias, A. Monthly water balance of ungauged catchments obtained by geographical regionalization. J. Hydrol. 1995, 170, 277–291. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, W03413. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Flood frequency regionalisation—Spatial proximity vs. Catchment attributes. J. Hydrol. 2005, 302, 283–306. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Jones, D.A.; Bayliss, A.C. Improving the Floof Estimation Handbook (FEH) Statistical Procedures for Flood Frequency Estimation; SCHO0608BOFF-E; Environment Agency: Bristol, UK, 2008.
- Robson, A.J.; Reed, D.W. Floord Estimation Handbook Vol. 3: Statistical Procedures for Flood Frequency Estimation; Institute of Hydrology: Wallingford, UK, 1999; p. 338. [Google Scholar]
- Mateo Lázaro, J.; Sánchez Navarro, J.Á.; García Gil, A.; Edo Romero, V. Flood frequency analysis (FFA) in spanish catchments. J. Hydrol. 2016, 538, 598–608. [Google Scholar] [CrossRef]
- United States Geological Survey (USGS). Guidelines for Determining Flood Flow Frequency: Bulletin 17B of the Hydrology Subcomittee; United States Geological Survey: Reston, VA, USA, 1982.
- Jennings, M.E.; Thomas, W.O.; Riggs, H.C. Nationwide Summary of U.S. Geological Survey Regional Regression Equations for Estimating Magnitude and Frequency of Floods for Ungaged Sites; United States Geological Survey: Reston, VA, USA, 1993.
- Ball, J.; Weinmann, E.; Kuczera, G. Peak flow estimation. In Australian Rainfall and Runoff: A Guide to Flood Estimation; Ball, J., Babister, M., Nathan, R.J., Weeks, W., Weinmann, E., Retallick, M., Testoni, I., Eds.; Commonwealth of Australia: Canberra, Australia, 2016; Volume 3. [Google Scholar]
- Ball, J.; Weinmann, E. Flood hydrograph estimation. In Australian Rainfall and Runoff: A Guide to Flood Estimation; Ball, J., Babister, M., Nathan, R.J., Weeks, W., Weinmann, E., Retallick, M., Testoni, I., Eds.; Commonwealth of Australia: Canberra, Australia, 2016; Volume 5. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modeling: The Primer; John Wiley & Sons Ltd.: Chichester, UK, 2001. [Google Scholar]
- Kochanek, K.; Renard, B.; Arnaud, P.; Aubert, Y.; Lang, M.; Cipriani, T.; Sauquet, E. A data-based comparison of flood frequency analysis methods used in France. Nat. Hazards Earth Syst. Sci. 2014, 14, 295–308. [Google Scholar] [CrossRef]
- Aubert, Y.; Arnaud, P.; Ribstein, P.; Fine, J.A. The SHYREG flow method-application to 1605 basins in Metropolitan France. Hydrol. Sci. J. 2014, 59, 993–1005. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J. Coupled rainfall model and discharge model for flood frequency estimation. Water Resour. Res. 2002, 38, 11-1–11-11. [Google Scholar] [CrossRef]
- Ministère de l’Écologie du Développement Durable et de l’Energie. Banque hydro. Ministère de l’Ecologie du Dévelopement Durable et de l’Energie, SCHAPI. Available online: http://www.hydro.eaufrance.fr/ (accessed on 18 September 2017).
- McDonald, J.H. Handbook of Biological Statistics; Sparky House Publishing: Baltimore, MD, USA, 2009; Volume 2. [Google Scholar]
- Vidal, J.P.; Martin, E.; Franchistéguy, L.; Baillon, M.; Soubeyroux, J.M. A 50-year high-resolution atmospheric reanalysis over France with the safran system. Int. J. Climatol. 2010, 30, 1627–1644. [Google Scholar] [CrossRef]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1958; 259p.
- Aubert, Y. Estimation des Valeurs Extrêmes de Débit par la Méthode Shyreg: Réflexions sur L’équifinalité dans la Modélisation de la Transformation Pluie en Débit. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2012. [Google Scholar]
- Sol, B.; Desouches, C. Spatialisation à Résolution Kilométrique sur la France de Paramètres liés aux Précipitations; Rapport d’étude Météo-France; Convention Météo-France DPPR n 03/1735; Météo-France: Toulouse, France, 2015; 41p. [Google Scholar]
- IGN; ONEMA. BD Carthage. Available online: http://professionnels.ign.fr/bdcarthage (accessed on 18 September 2017).
- European Union Agency. European Digital Elevation Model (EU-DEM), 1st ed.; Copernicus, 2016; Available online: http://land.copernicus.eu/pan-european/satellite-derived-products/eu-dembdcarthage (accessed on 18 September 2017).
- Margat, J. Carte Hydrogéologique de la France: Systèmes Aquifères; BRGM: Orléans, France, 1978. [Google Scholar]
- Finke, P.; Hartwich, R.; Dudal, R.; Ibanez, J.; Jamagne, M.; King, D.; Montanarella, L.; Yassoglou, N. Geo-Referenced Soil Database for Europe. In Manual of Procedures, version 1.0; European Commission, 1998; Available online: https://www.researchgate.net/publication/254560058_Georeferenced_Soil_Database_for_Europe_Manual_of_Procedures_Version_10 (accessed on 18 September 2017).
- European Union SOeS. Corine Land Cover (CLC) 2012; Service de l’Observation et des statistiques (SOeS) du Commissariat Général au Développement Durable du MEDDE, 2012; Available online: http://www.statistiques.developpement-durable.gouv.fr/donnees-ligne/li/1825.html (accessed on 18 September 2017).
- Wasson, J.G.; Chandesris, A.; Pella, H.; Blanc, L. Les Hydro-Écorégions de France Métropolitaine. Approche Régionale de la Typologie des Eaux Courantes et Éléments Pour la Définition des Peuplements de Référence D'invertébrés; Ministère de l’Écologie et du Développement Durable, Cemagref BEA/LHQ, 2002; p. 190. Available online: http://www.irstea.fr/la-recherche/unites-de-recherche/maly/pole-onema-irstea/regionalisation-et-typologie/les-hydro (accessed on 18 September 2017).
- Cipriani, T.; Toilliez, T.; Sauquet, E. Estimating 10 year return period peak flows and flood durations at ungauged locations in France. Houille Blanche 2012, 4–5, 5–13. [Google Scholar] [CrossRef]
- Garcia, F. Amélioration d’une Modélisation Hydrologique Régionalisée Pour Estimer les Statistiques D’étiage. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2016. [Google Scholar]
- Hijmans, R.J.; Van Etten, J. Raster: Geographic Data Analysis and Modeling, R Package Version 2.5-8; 2014. Available online: https://CRAN.R-project.org/package=raster (accessed on 18 September 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Lê, S.; Josse, J.; Husson, F. Factominer: An R package for multivariate analysis. J. Stat. Softw. 2008, 25. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: Heidelberg, Germany, 2001. [Google Scholar]
- Geyer, C.; Johnson, L. Mcmc: Markov Chain Monte Carlo, R Package Version 0.9-4; Available online: https://CRAN.R-project.org/package=mcmc (accessed on 18 September 2017).
- Stephenson, A.G. Evd: Extreme value distributions. R News 2002, 2, 31–32. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Lu, L.H. Appraisal of regional and index flood quantile estimators. Stoch. Hydrol. Hydraul. 1995, 9, 49–75. [Google Scholar] [CrossRef]
- Gaume, E.; Gaál, L.; Viglione, A.; Szolgay, J.; Kohnová, S.; Blöschl, G. Bayesian mcmc approach to regional flood frequency analyses involving extraordinary flood events at ungauged sites. J. Hydrol. 2010, 394, 101–117. [Google Scholar] [CrossRef]
- Kjeldsen, T.R. Flood Estimation Handbook Supplementary Report No. 1: The Revitalised FSR/FEH Rainfall-Runioff Method; Centre for Ecology & Hydrology: Wallingford, UK, 2007. [Google Scholar]
- Oudin, L.; Kay, A.; Andráassian, V.; Perrin, C. Are seemingly physically similar catchments truly hydrologically similar? Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Cernesson, F. Modèle Simple de Prédetermination des Crues de Fréquences Courantes à Rares sur Petits Bassins Versants Méditéranéens. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 1993. [Google Scholar]
- Arnaud, P. Modèle de Prédétermination de Crues Basé sur la Simulation. Extension de sa Zone de Validité, Paramétrisation du Modèle Horaire par L’information Journalière et Couplage des Deux pas de Temps. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 1997. [Google Scholar]
- Cantet, P. Impacts du Changement Climatique sur les Pluies Extrêmes par L’utilisation d’un Générateur Stochastique de Pluies. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 2009. [Google Scholar]
- Cantet, P.; Arnaud, P. Gains from modelling dependence of rainfall variables into a stochastic model: Application of the copula approach at several sites. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 11227–11266. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J.; Sol, B.; Desouches, C. Cartographie de l’aléa pluviographique de la France. La Houille Blanche 2006, 5, 102–111. [Google Scholar] [CrossRef]
- Carreau, J.; Neppel, L.; Arnaud, P.; Cantet, P. Extreme rainfall analysis at ungauged sites in the south of France: Comparison of three approaches. J. Soc. Fr. Stat. 2013, 154, 119–138. [Google Scholar]
- Arnaud, P.; Lavabre, J. Estimation de L’aléa Pluvial en France Métropolitaine; QUAE; Update Sciences & Technologies: Paris, France, 2010; 158p. [Google Scholar]
- IRSTEA. Catchment Hydrology Research Group. Available online: https://webgr.irstea.fr/ (accessed on 18 September 2017).
- Coron, L.; Perrin, C.; Delaigue, O.; Andréassian, V.; Thirel, G. airGR: A suite of lumped hydrological models in an R-package. Environ. Model. Softw. 2017, in press. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef]
- Kokkonen, T.S.; Jakeman, A.J.; Young, P.C.; Koivusalo, H.J. Predicting daily flows in ungauged catchments: Model regionalization from catchment descriptors at the coweeta hydrologic laboratory, North Carolina. Hydrol. Process. 2003, 17, 2219–2238. [Google Scholar] [CrossRef]
- McIntyre, N.; Lee, H.; Wheater, H.; Young, A.; Wagener, T. Ensemble predictions of runoff in ungauged catchments. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S. Relative merits of different methods for runoff predictions in ungauged catchments. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef]
- Thomas, D.M.; Benson, M.A. Generalization of Streamflow Characteristics from Drainage-Basin Characteristics; United States Government Printing Office: Washington, DC, USA, 1975.
- Tasker, G.D.; Hodge, S.A.; Barks, C.S. Region of influence regression for estimating the 50-year flood at ungaged sites. J. Am. Water Resour. Assoc. 1996, 32, 163–170. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M.; Wagener, T.; Viglione, A.; Savenije, H. Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales; Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., Savenije, H., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 1–465. [Google Scholar]
- Arnaud, P. L’aléa Hydrométéorologique: Estimation Régionale par Simulation Stochastique des Processus; HDR; Aix Marseille Université: Aix en Provence, France, 2015. [Google Scholar]
- Arnaud, P.; Lavabre, J. Using a stochastic model for generating hourly hyetographs to study extreme rainfalls. Hydrol. Sci. J. 1999, 44, 433–446. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J.; Sol, B.; Desouches, C. Regionalization of an hourly rainfall generating model over Metropolitan France for flood hazard estimation. Hydrol. Sci. J. 2008, 53, 34–47. [Google Scholar] [CrossRef]
- Requena, A.I.; Chebana, F.; Mediero, L. A complete procedure for multivariate index-flood model application. J. Hydrol. 2016, 535, 559–580. [Google Scholar] [CrossRef]
| Characteristics | Min | 1st Quartile | Median | 3rd Quartile | Max |
|---|---|---|---|---|---|
| Observation periods (years) | 10 | 24 | 37 | 44 | 116 |
| Area (km2) | 1.5 | 86 | 198 | 599 | 10010 |
| Annual precipitation (mm) | 355 | 791 | 895 | 1055 | 1862 |
| Median resized peak flood (m3·s−1·km−1.6) | 0.73 | 10.5 | 17.8 | 28.3 | 241 |
| Type | Source | Variable | Name |
|---|---|---|---|
| Climate | SAFRAN [50] Budyko formula [51] | Aridity index | Arid |
| SAFRAN [50] | Annual mean evapotranspiration | ETP | |
| Annual mean solid precipitation | Snow | ||
| Annual mean liquid precipitation | Rain | ||
| Annual mean temperature | T | ||
| SAFRAN [50] and Aubert [52] | Annual mean soil moisture | SAJ | |
| Mean soil moisture prior to a rainy event (>20 mm) | SAJ20 | ||
| SHYREG rainfall maps [53] | Mean duration of rainfall events | DT | |
| Mean number of rainfall events per season | NE | ||
| Mean intensity of rainfall events | PJ | ||
| Morphology | From Carthage database [54] | River network density | DDr |
| Topography | Copernicus [55] | Mean elevation | Alt |
| Mean slope | Slope | ||
| Hydrogeology | Aubert [52] from Margat [56] | Capacity of the SHYREG production reservoir | AHg |
| ESDB [57] | Presence of sand bedding | HGsand | |
| Presence of rock bedding | HGrock | ||
| Low infiltration capacity class | LOWcapa | ||
| Medium infiltration capacity class | MEDcapa | ||
| High infiltration capacity class | HIGHcapa | ||
| Land use | Corine Land Cover [58] | Forest cover | Forest |
| Arable cover | Arable | ||
| Grassland cover | Grassland | ||
| Catchments | Banque Hydro [48] | Catchment area | Area |
| Catchment eastening | X | ||
| Catchment northening | Y | ||
| Regions | Hydro-Eco-Regions [59] | Hydro-Eco-Regions | / |
| Criterion | Zone | GEV_LR | GUMBEL | INDEX FLOOD | SHYREG |
|---|---|---|---|---|---|
| R2 (T = 10 years) | France | / | 0.99 | 0.94 | 0.97 |
| FF | France | 0.83 | 0.93 | 0.64 | 0.65 |
| FF | Mountainous | 0.87 | 0.88 | 0.71 | 0.75 |
| FF | Mediterranean | 0.86 | 0.78 | 0.61 | 0.71 |
| FF | Plains | 0.79 | 0.81 | 0.61 | 0.59 |
| Region | GEV_LR | Gumbel | Index Flood | SHYREG | |||
|---|---|---|---|---|---|---|---|
| Location | Scale | Shape | Location | Scale | Index | S0/A | |
| Alps-Pyrennees | Rain, grassland, PJ | T, PJ | DT | Rain | T | Rain | AHg, Grassland, rain |
| Massif Central | NE, forest | NE, PJ, forest | X | NE, forest | PJ, forest | NE, PJ, forest | Forest |
| East | NE, rain | PJ, Rain | PJ | NE | PJ | NE, Rain | MEDcapa |
| Mediterranean Arc | DT | DT, PJ, Alt | PJ, rain | DT, PJ, Alt, Snow | PJ, AHg, MEDcapa | DT, PJ, Alt, AHg | MEDcapa, AHg |
| SE foothills | PJ, area, Y | PJ, DDr, area | Forest, T | PJ | PJ | PJ, DDr, area | Area, Y |
| Centrals Plains | DDr, NE | DDr, NE | Grassland | DDr, NE | DDr, NE | DDr, NE | DDr |
| Lorraine Burgundy | DDr, arid | DDr | DDr, arid | DDr, Snow | DDr, arid, grassland | DDr, grassland | |
| Britanny | NE, Y | Y | PJ, Y, HGrock | Y, PJ, HGrock | PJ, Y, HGrock | Arid, Y | |
| Aquitaine | Alt, NE | HGsand, NE | Alt, NE, HGsand | HGsand, NE, area | Alt, area, NE | HGsand, area, Alt | |
| Limousin | DT, AHg | T | DT, AHg | Snow, arid | DT, AHg | PJ, Alt | |
| Spatial interpolation | Yes | Yes | No | Yes | Yes | Yes | No |
| R2 on parameter over target catchments | 0.76 | 0.72 | 0.36 | 0.77 | 0.70 | 0.75 | 0.39 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odry, J.; Arnaud, P. Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France. Geosciences 2017, 7, 88. https://doi.org/10.3390/geosciences7030088
Odry J, Arnaud P. Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France. Geosciences. 2017; 7(3):88. https://doi.org/10.3390/geosciences7030088
Chicago/Turabian StyleOdry, Jean, and Patrick Arnaud. 2017. "Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France" Geosciences 7, no. 3: 88. https://doi.org/10.3390/geosciences7030088
APA StyleOdry, J., & Arnaud, P. (2017). Comparison of Flood Frequency Analysis Methods for Ungauged Catchments in France. Geosciences, 7(3), 88. https://doi.org/10.3390/geosciences7030088





