Laser Ultrasound Observations of Mechanical Property Variations in Ice Cores
Abstract
:1. Introduction
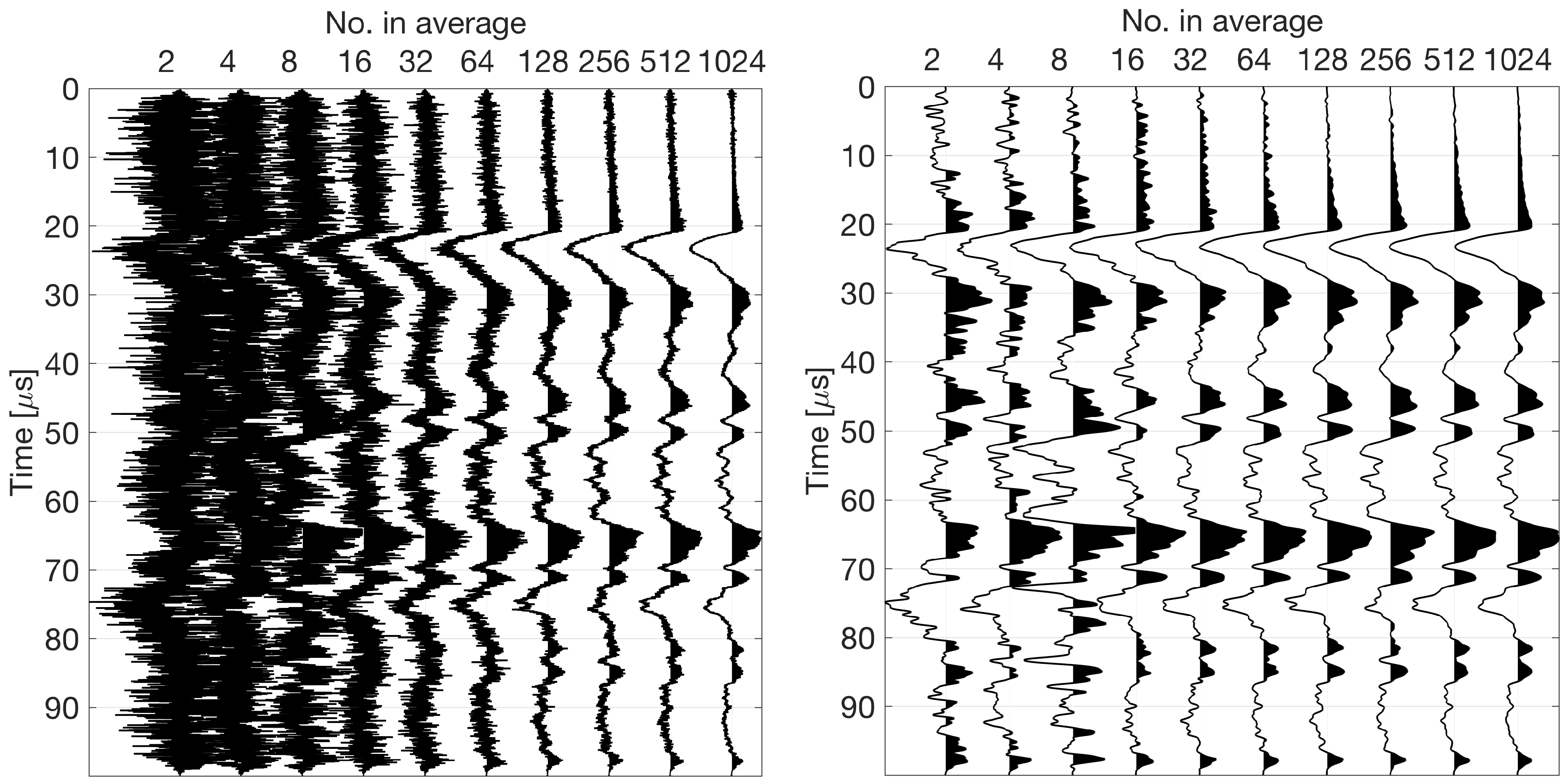
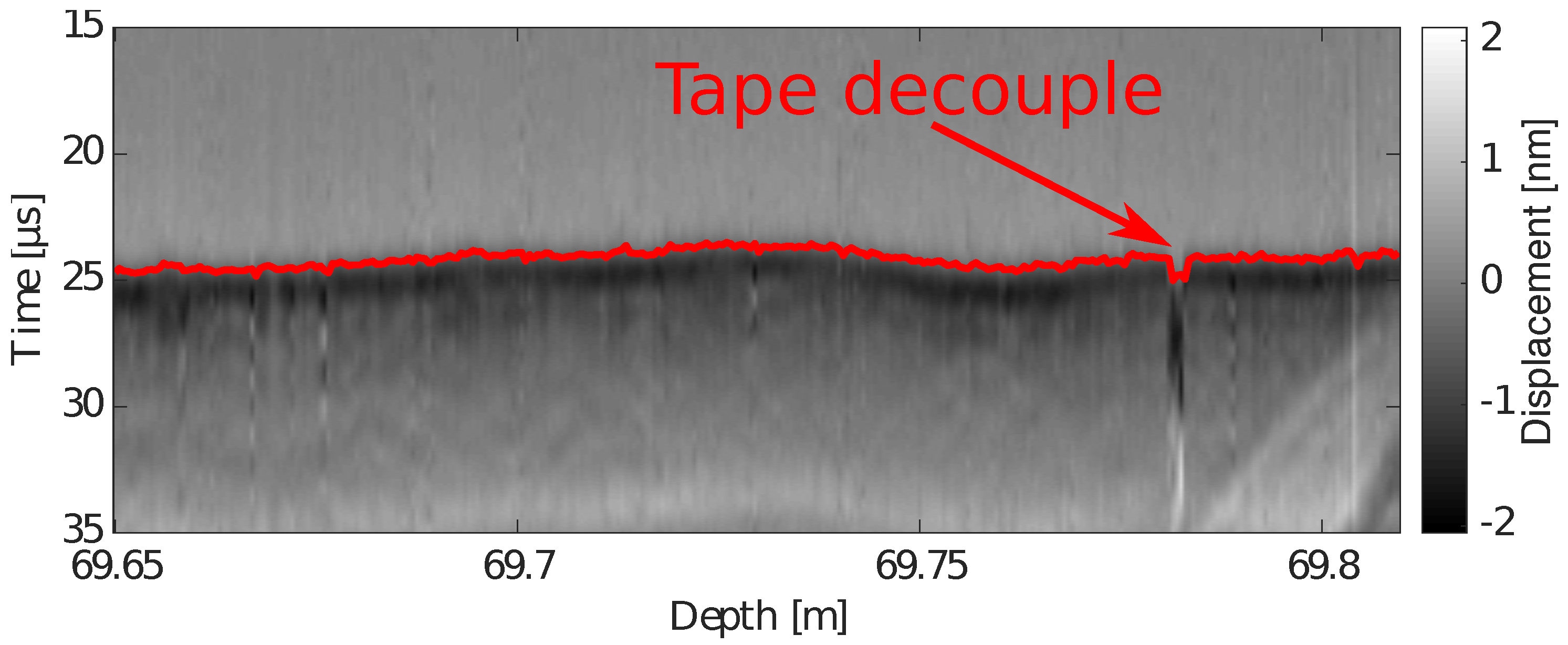
2. Laser Ultrasound Method
3. Results
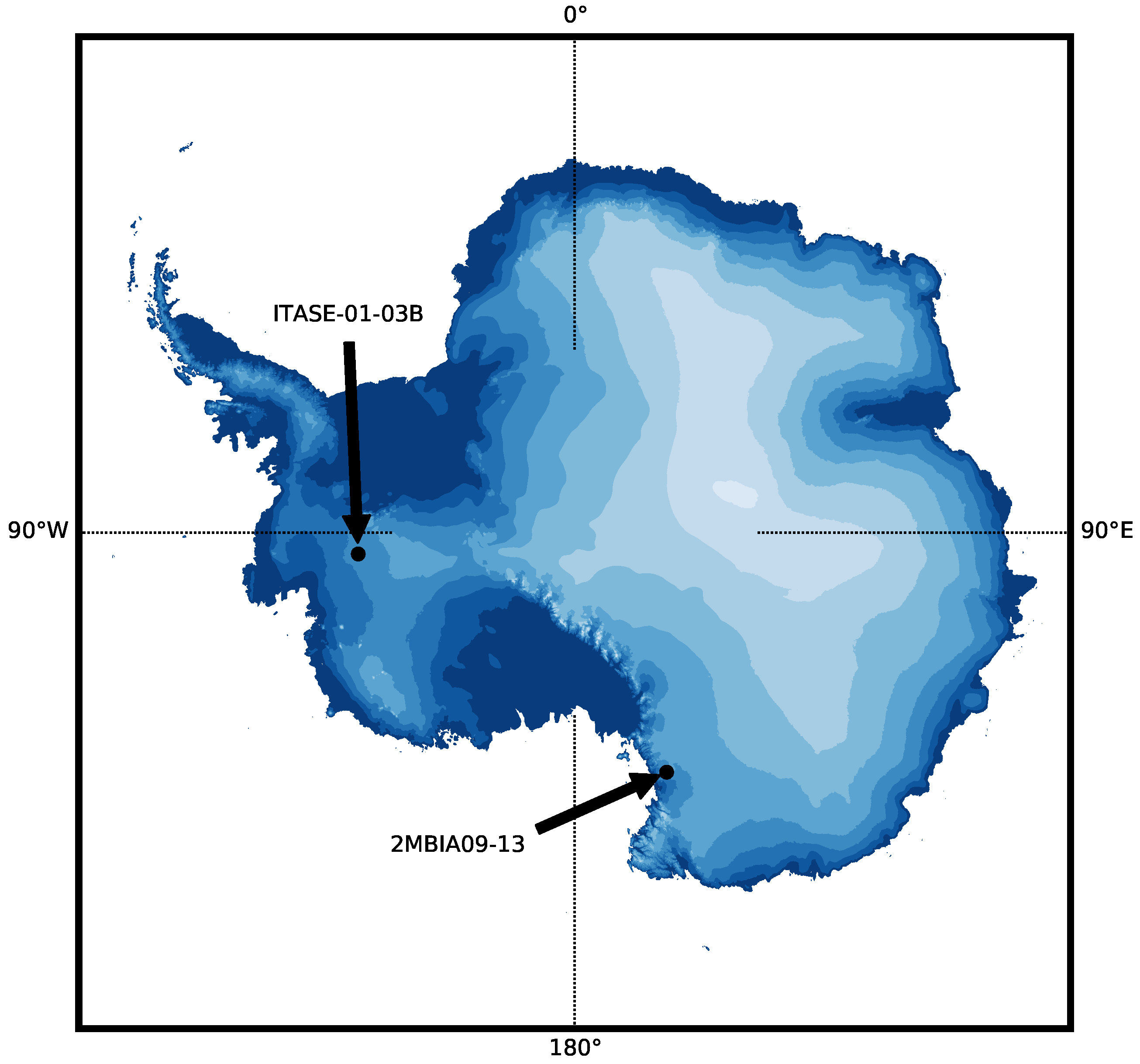
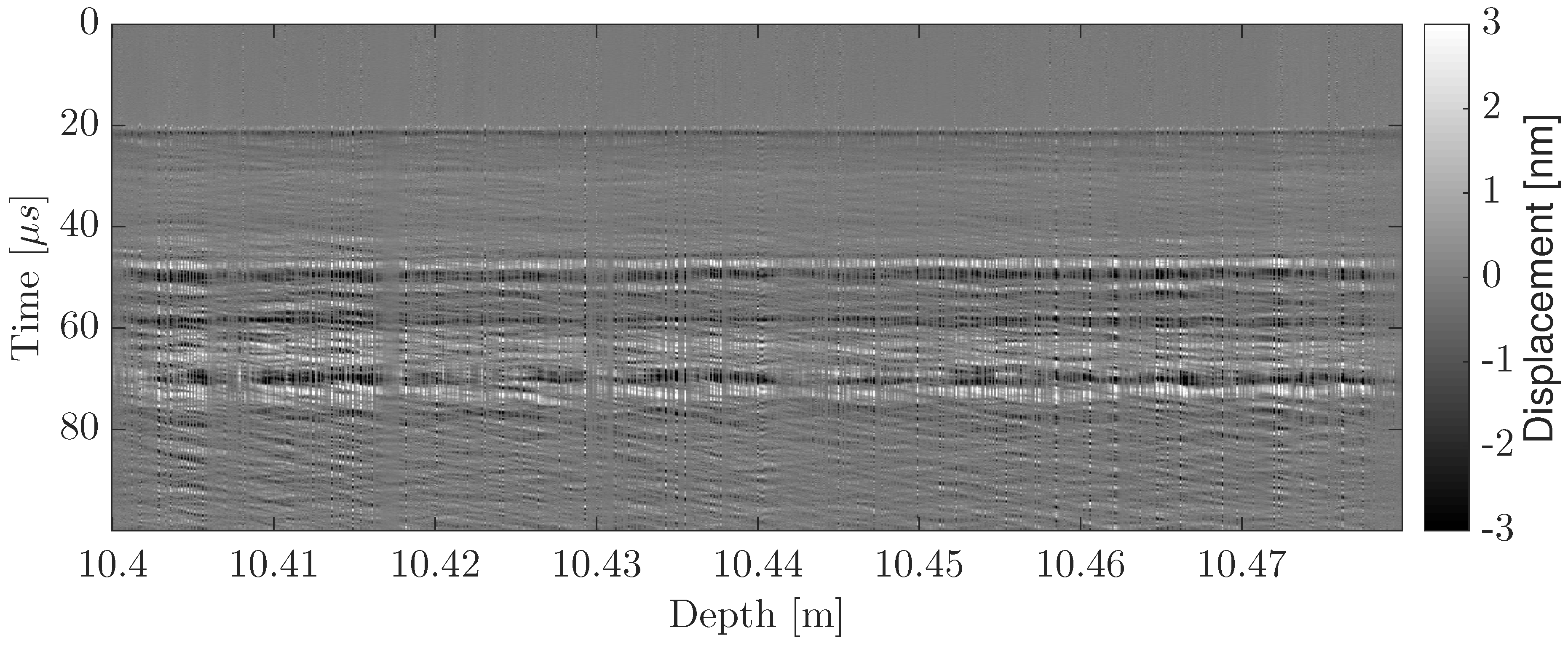
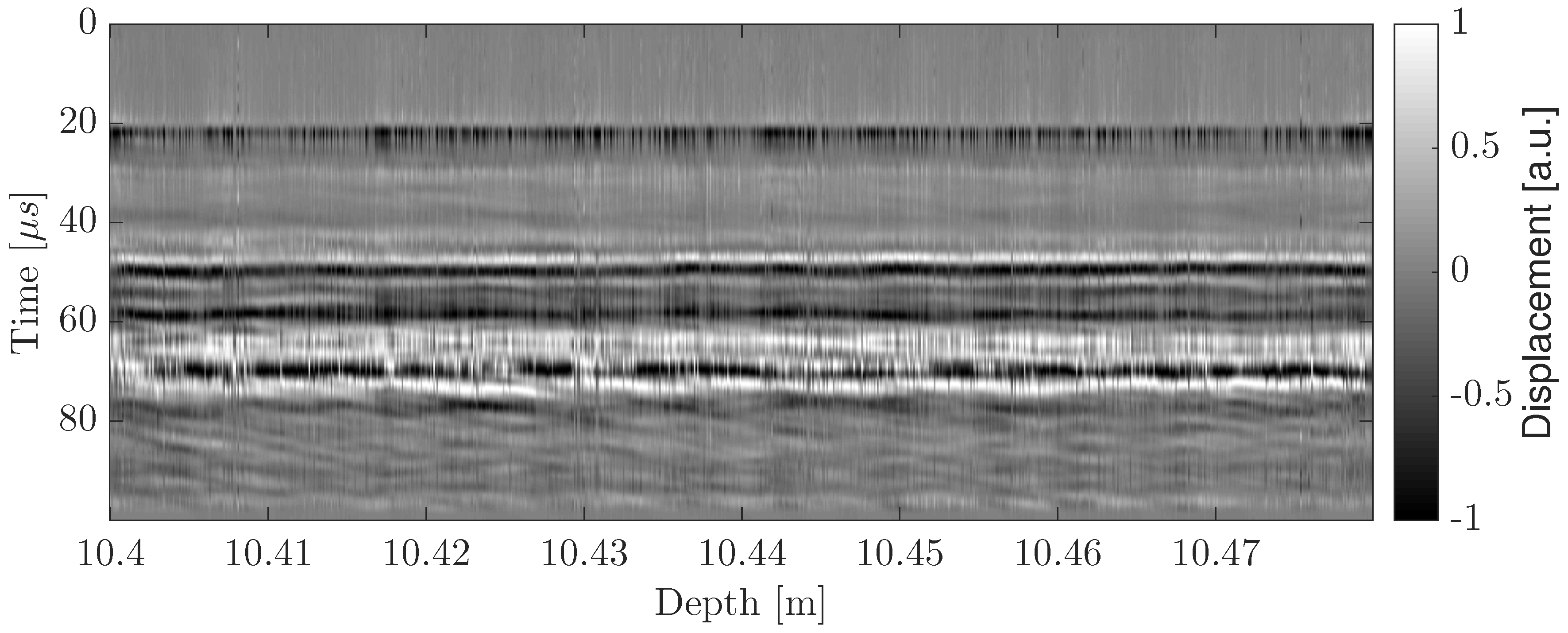
3.1. ITASE-01-3B Firn Core
3.2. 2MBIA09-13
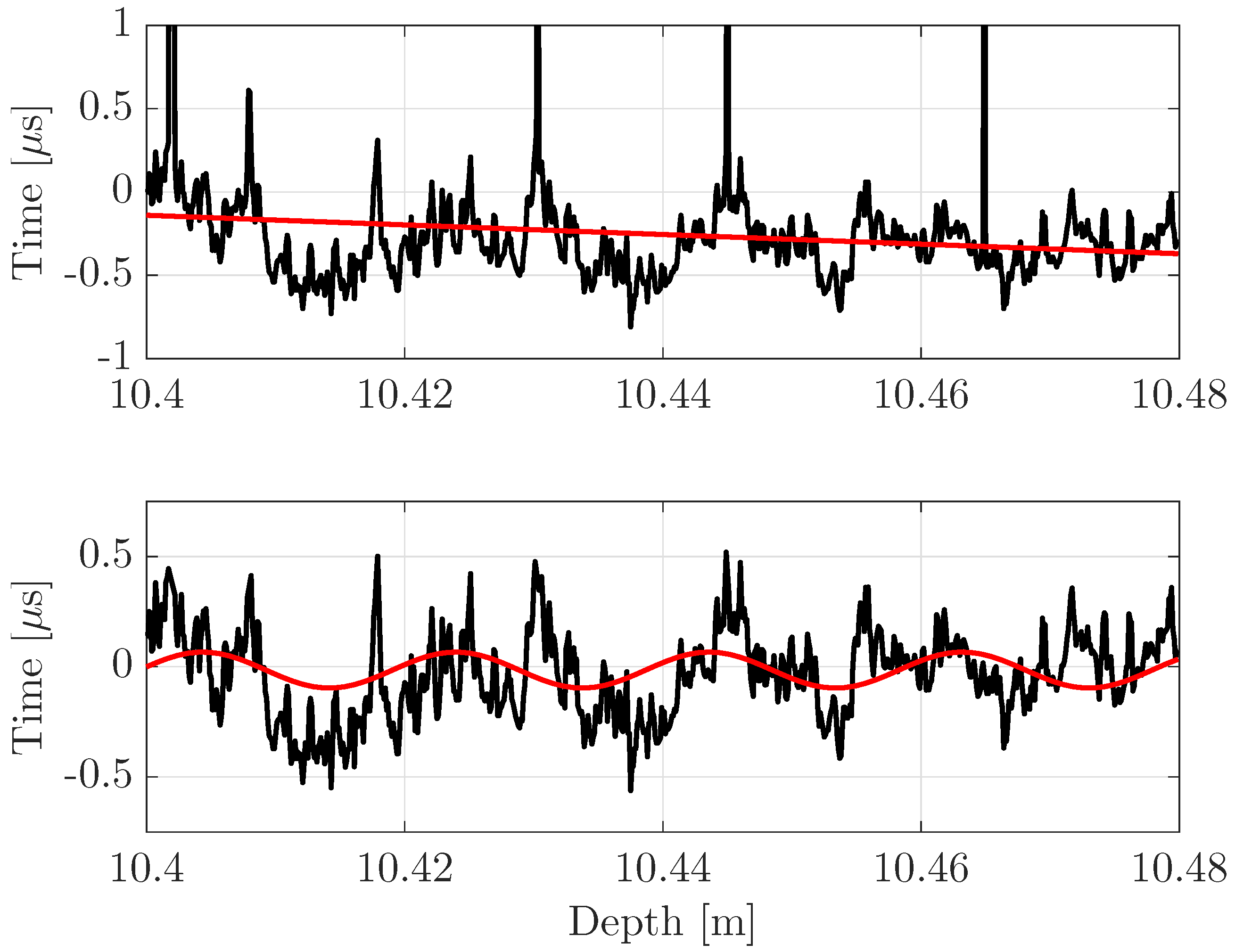
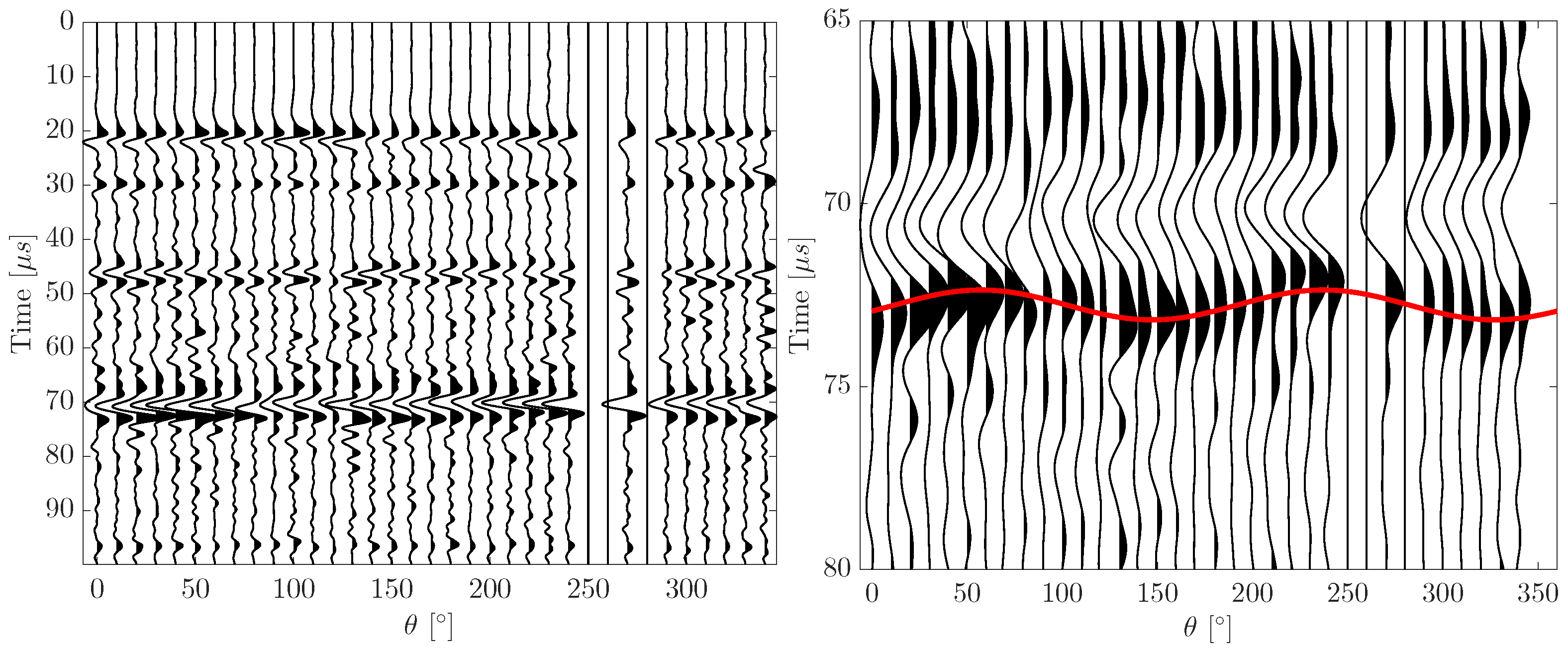
4. Discussion
4.1. Elastic Moduli and Ultrasonic Velocities
4.2. Elastic Moduli and Density Variations
4.3. Velocity Anisotropy and Preferred Crystal Orientation Fabrics
4.4. Anelasticity
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LLS | Laser-Light Scattering |
| ECM | Electrical Conductivity Measurement |
| LDV | Laser Doppler Vibrometer |
| PCI | Peripheral Component Interconnect |
| BNC | Bayonet Neill–Concelman |
| STA | Short-Time Average |
| LTA | Long-Time Average |
| MER | Modified Energy Ratio |
References
- EPICA Community Members. Eight glacial cycles from an Antarctic ice core. Nature 2004, 429, 623–628. [Google Scholar]
- McConnell, J.R.; Lamorey, G.W.; Lambert, S.W.; Taylor, K.C. Continuous Ice-Core Chemical Analyses Using Inductively Coupled Plasma Mass Spectrometry. Environ. Sci. Technol. 2002, 36, 7–11. [Google Scholar] [CrossRef] [PubMed]
- Winstrup, M.; Svensson, A.M.; Rasmussen, S.O.; Winther, O.; Steig, E.J.; Axelrod, A.E. An automated approach for annual layer counting in ice cores. Clim. Past 2012, 8, 1881–1895. [Google Scholar] [CrossRef]
- Rasmussen, S.O.; Andersen, K.K.; Svensson, A.M.; Steffensen, J.P.; Vinther, B.M.; Clausen, H.B.; Siggaard-Andersen, M.L.; Johnsen, S.J.; Larsen, L.B.; Dahl-Jensen, D.; et al. A new Greenland ice core chronology for the last glacial termination. J. Geophys. Res. Atmos. 2006, 111, 1–16. [Google Scholar] [CrossRef]
- Sigl, M.; McConnell, J.R.; Layman, L.; Maselli, O.; McGwire, K.; Pasteris, D.; Dahl-Jensen, D.; Steffensen, J.P.; Vinther, B.; Edwards, R.; et al. A new bipolar ice core record of volcanism from WAIS Divide and NEEM and implications for climate forcing of the last 2000 years. J. Geophys. Res. Atmos. 2013, 118, 1151–1169. [Google Scholar] [CrossRef]
- Hammer, C.U. Acidity of polar ice cores in relation to absolute dating, past volcanism, and radio echoes. J. Glaciol. 1980, 25, 359–372. [Google Scholar] [CrossRef]
- Hammer, C.U. Initial direct current in the buildup of space charges and the acidity of ice cores. J. Phys. Chem. 1983, 87, 4099–4103. [Google Scholar] [CrossRef]
- Taylor, K.C.; Hammer, C.U.; Alley, R.B.; Clausen, H.B.; Dahl-Jensen, D.; Gow, A.J.; Gundestrup, N.S.; Kipfstuhl, J.; Moore, J.C.; Waddington, E.D. Electrical conductivity measurements from the GISP2 and GRIP Greenland ice cores. Nature 1993, 366, 549–552. [Google Scholar] [CrossRef]
- Moore, J.; Paren, J.; Oerter, H. Sea salt dependent electrical conduction in polar ice. J. Geophys. Res. 1992, 97, 19803–19812. [Google Scholar] [CrossRef]
- Wilhelms, F.; Kipfstuhl, J.; Miller, H.; Heinloth, K.; Firestone, J. Precise dielectric profiling of ice cores: A new device with improved guarding and its theory. J. Glaciol. 1998, 44, 171–174. [Google Scholar] [CrossRef]
- Wilhelms, F. Explaining the dielectric properties of firn as a density-and-conductivity mixed permittivity (DECOMP). Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Weißbach, S.; Wegner, A.; Opel, T.; Oerter, H.; Vinther, B.M.; Kipfstuhl, S. Spatial and temporal oxygen isotope variability in northern Greenland—Implications for a new climate record over the past millennium. Clim. Past 2016, 12, 171–188. [Google Scholar] [CrossRef]
- Andersen, K.K.; Svensson, A.; Johnsen, S.J.; Rasmussen, S.O.; Bigler, M.; Röthlisberger, R.; Ruth, U.; Siggaard-Andersen, M.L.; Peder Steffensen, J.; Dahl-Jensen, D.; et al. The Greenland Ice Core Chronology 2005, 15–42 ka. Part 1: Constructing the time scale. Quat. Sci. Rev. 2006, 25, 3246–3257. [Google Scholar] [CrossRef]
- Dixon, D.; Mayewski, P.A.; Kaspari, S.; Sneed, S.; Handley, M. A 200 year sub-annual record of sulfate in West Antarctica, from 16 ice cores. Ann. Glaciol. 2004, 39, 545–556. [Google Scholar] [CrossRef]
- Della Lunga, D.; Muller, W.; Rasmussen, S.O.; Svensson, A. Location of cation impurities in NGRIP deep ice revealed by cryo-cell UV-laser-ablation ICPMS. J. Glaciol. 2014, 60, 970–988. [Google Scholar] [CrossRef]
- Sneed, S.B.; Mayewski, P.A.; Sayre, W.G.; Handley, M.J.; Kurbatov, A.V.; Taylor, K.C.; Bohleber, P.; Wagenbach, D.; Erhardt, T.; Spaulding, N.E. Instruments and Methods New LA-ICP-MS cryocell and calibration technique for sub-millimeter analysis of ice cores. J. Glaciol. 2015, 61, 233–242. [Google Scholar] [CrossRef]
- Alley, R.B.; Shuman, C.A.; Meese, D.A.; Gow, A.J.; Taylor, K.C.; Cuffey, K.M.; Fitzpatrick, J.J.; Grootes, P.M.; Zielinski, G.A.; Ram, M.; et al. Visual-stratigraphic dating of the GISP2 ice core: Basis, reproducibility, and application. J. Geophys. Res. Oceans 1997, 102, 26367–26381. [Google Scholar] [CrossRef]
- Svensson, A.; Nielsen, S.W.; Kipfstuhl, S.; Johnsen, S.J.; Steffensen, J.P.; Bigler, M.; Ruth, U.; Röthlisberger, R. Visual stratigraphy of the North Greenland Ice Core Project (NorthGRIP) ice core during the last glacial period. J. Geophys. Res. D Atmos. 2005, 110, 1–11. [Google Scholar] [CrossRef]
- Takata, M.; Iizuka, Y.; Hondoh, T.; Fujita, S.; Fujii, Y.; Shoji, H. Stratigraphic analysis of Dome Fuji Antarctic ice core using an optical scanner. Ann. Glaciol. 2004, 39, 467–472. [Google Scholar] [CrossRef]
- Ram, M.; Illing, M. Polar ice stratigraphy frotn laser-light scattering: Scattering frotn meltwater. J. Glaciol. 1994, 40, 504–508. [Google Scholar] [CrossRef]
- Bramall, N.E.; Bay, R.C.; Woschnagg, K.; Rohde, R.A.; Price, P.B. A deep high-resolution optical log of dust, ash, and stratigraphy in South Pole glacial ice. Geophys. Res. Lett. 2005, 32, L21815. [Google Scholar] [CrossRef]
- Ackermann, M.; Ahrens, J.; Bai, X.; Bartelt, M.; Barwick, S.W.; Bay, R.C.; Becka, T.; Becker, J.K.; Becker, K.H.; Berghaus, P.; et al. Optical properties of deep glacial ice at the South Pole. J. Geophys. Res. Atmos. 2006, 111, 1–26. [Google Scholar] [CrossRef]
- Meese, D.A.; Gow, A.J.; Alley, R.B.; Zielinski, G.A.; Grootes, P.M.; Ram, M.; Taylor, K.C.; Mayewski, P.A.; Bolzan, J.F. The Greenland Ice Sheet Project 2 depth-age scale. J. Geophys. Res. Oceans 1997, 102, 411–423. [Google Scholar] [CrossRef]
- Donarummo, J. Possible deposit of soil dust from the 1930’s U.S. dust bowl identified in Greenland ice. Geophys. Res. Lett. 2003, 30, 18–21. [Google Scholar] [CrossRef]
- McGwire, K.C.; Hargreaves, G.M.; Alley, R.B.; Popp, T.J.; Reusch, D.B.; Spencer, M.K.; Taylor, K.C. An integrated system for optical imaging of ice cores. Cold Reg. Sci. Technol. 2008, 53, 216–228. [Google Scholar] [CrossRef]
- Taylor, K.C.; Alley, R.B.; Meese, D.A.; Spencer, M.K.; Brook, E.J.; Dunbar, N.W.; Finkel, R.C.; Gow, A.J.; Kurbatov, A.V.; Lamorey, G.W.; et al. Dating the Siple Dome (Antarctica) ice core by manual and computer interpretation of annual layering. J. Glaciol. 2004, 50, 453–461. [Google Scholar] [CrossRef]
- Svensson, A.; Andersen, K.K.; Bigler, M.; Clausen, H.B.; Dahl-Jensen, D.; Davies, S.M.; Johnsen, S.J.; Muscheler, R.; Parrenin, F.; Rasmussen, S.O.; et al. A 60,000 year Greenland stratigraphic ice core chronology. Clim. Past 2008, 4, 47–57. [Google Scholar] [CrossRef]
- Scruby, C.; Drain, L. Laser Ultrasonics Techniques and Applications; CRC Press: Boca Raton, FL, USA, 1990; p. 462. [Google Scholar]
- Scales, J.; Malcolm, A. Laser characterization of ultrasonic wave propagation in random media. Phys. Rev. E 2003, 67, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Nishizawa, O.; Satoh, T.; Lei, X.; Kuwahara, Y. Laboratory studies of seismic wave propagation in inhomogeneous media using a laser Doppler vibrometer. Bull. Seismol. Soc. Am. 1997, 87, 809–823. [Google Scholar]
- Scales, J.A.; Van Wijk, K. Multiple scattering attenuation and anisotropy of ultrasonic surface waves. Appl. Phys. Lett. 1999, 74, 3899–3901. [Google Scholar] [CrossRef]
- Blum, T.E.; Adam, L.; Van Wijk, K. Noncontacting benchtop measurements of the elastic properties of shales. Geophysics 2013, 78, C25–C31. [Google Scholar] [CrossRef]
- Van Wijk, K.; Scales, J.A.; Mikesell, T.D.; Peacock, J.R. Toward noncontacting seismology. Geophys. Res. Lett. 2005, 32, L01308. [Google Scholar] [CrossRef]
- Mayewski, P.; Frezzotti, M.; Bertler, N.A.; van Ommen, T.; Hamilton, G.; Jacka, T.H.; Welch, B.; Frey, M.; Dahe, Q.; Jiawen, R.; et al. The International Trans-Antarctic Scientific Expedition (ITASE): An Overview. Ann. Glaciol. 2005, 41, 180–185. [Google Scholar] [CrossRef]
- Mayewski, P.A.; Dixon, D.A. US ITASE-01-3 Data Set. 2001. Available online: http://cci.icecoredata.org/data/ITASE/US{_}ITASE-01-3{_}2013.csv (accessed on 12 June 2017).
- Allen, R.V. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar]
- Earle, P.S.; Shearer, P.M. Characterization of global seismograms using an automatic-picking algorithm. Bull. Seismol. Soc. Am. 1994, 84, 366–376. [Google Scholar]
- Akram, J.; Eaton, D.W. A review and appraisal of arrival-time picking methods for downhole microseismic data. Geophysics 2016, 81, KS67–KS87. [Google Scholar] [CrossRef]
- Wong, J.; Han, L.; Stewart, R.; Bentley, L.; Bancroft, J. Geophysical Well Logs from a Shallow Test Well and Automatic Determination of Formation Velocities from Full-Waveform Sonic Logs. CSEG Rec. 2009, 34, 21–30. [Google Scholar]
- Mikesell, T.D.; van Wijk, K.; Ruigrok, E.; Lamb, A.; Blum, T.E. A modified delay-time method for statics estimation with the virtual refraction. Geophysics 2012, 77, A29–A33. [Google Scholar] [CrossRef]
- Gaci, S. The Use of Wavelet-Based Denoising Techniques to Enhance the First-Arrival Picking on Seismic Traces. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4558–4563. [Google Scholar] [CrossRef]
- Han, L.; Wong, J.; Bancroft, J.C. Time Picking and Random Noise Reduction on Microseismic Data; Technical Report; CREWES: Calgary, AB, Canada, 2009. [Google Scholar]
- Svensson, A.; Baadsager, P.; Persson, A.; Hvidberg, C.S.; Siggaard-Andersen, M.L. Seasonal variability in ice crystal properties at NorthGRIP: A case study around 301 m depth. Ann. Glaciol. 2003, 37, 119–122. [Google Scholar] [CrossRef]
- Freitag, J.; Kipfstuhl, S.; Laepple, T. Core-scale radioscopic imaging: A new method reveals density-calcium link in Antarctic firn. J. Glaciol. 2013, 59, 1009–1014. [Google Scholar] [CrossRef]
- Spaulding, N.E.; Higgins, J.A.; Kurbatov, A.V.; Bender, M.L.; Arcone, S.A.; Campbell, S.; Dunbar, N.W.; Chimiak, L.M.; Introne, D.S.; Mayewski, P.A. Climate archives from 90 to 250 ka in horizontal and vertical ice cores from the allan hills blue ice area, Antarctica. Quat. Res. 2013, 80, 562–574. [Google Scholar] [CrossRef]
- Spaulding, N.E.; Spikes, V.B.; Hamilton, G.H.; Mayewski, P.A.; Dunbar, N.W.; Harvey, R.P.; Schutt, J.; Kurbatov, A.V. Allan Hills Stable Water Isotopes, Version 1. 2012. Available online: http://cci.icecoredata.org/data/AllanHills{_}SurfaceTransect.xlsx (accessed on 13 June 2017).
- Thompson, R. A Note on Restricted Maximum Likelihood Estimation with an Alternative Outlier Model. R. Stat. Soc. 1985, 47, 53–55. [Google Scholar]
- Gow, A.J.; Meese, D.A.; Alley, R.B.; Fitzpatrick, J.J.; Anandakrishnan, S.; Woods, G.A.; Elder, B.C. Physical and structural properties of the Greenland Ice Sheet Project 2 ice core: A review. J. Geophys. Res. 1997, 102, 26559. [Google Scholar] [CrossRef]
- Tsvankin, I. Seismic Signatures and Analysis of Reflection Data in Anisotropic Media; PergamonPress: Oxford, UK, 2001; p. 456. [Google Scholar]
- Faria, S.H.; Weikusat, I.; Azuma, N. The microstructure of polar ice. Part I: Highlights from ice core research. J. Struct. Geol. 2014, 61, 2–20. [Google Scholar] [CrossRef]
- Stein, S.; Wysession, M. An Introduction to Seismology, Earthquakes, and Earth Structure; Blackwell Publishing: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hitchman, S.; van Wijk, K.; Davidson, Z. Monitoring attenuation and the elastic properties of an apple with laser ultrasound. Postharvest Biol. Technol. 2016, 121, 71–77. [Google Scholar] [CrossRef]
- Benson, C.S. Stratigraphic Studies in the Snow and Firn of the Greenland Ice Sheet. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1960. [Google Scholar]
- Alley, R.B.; Saltzman, E.S.; Cuffey, K.M.; Fitzpatrick, J.J. Summertime formation of depth hoar in central Greenland. Geophys. Res. Lett. 1990, 17, 2393–2396. [Google Scholar] [CrossRef]
- Gerland, S.; Oerter, H.; Kipfstuhl, J.; Wilhelms, F.; Miller, H.; Miners, W.D. Density log of a 181 m long ice core from Berkner Island, Antarctica. Ann. Glaciol. 1999, 29, 215–219. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. Physics of Glaciers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2010; p. 496. [Google Scholar]
- Shoji, H.; Langway, C., Jr. Physical property reference horizons. In The Environmental Record in Glaciers and Ice Sheets; John Wiley & Sons Limited: Hoboken, NJ, USA, 1989; pp. 161–175. [Google Scholar]
- Wilhelms, F. Leitfähigkeits- und Dichtemessung an Eisbohrkernen, Ber. Polarforsch; Technical Report 96; Alfred-Wegener-Inst. für Polar- und Meeresforschung: Bremerhaven, Germany, 1996. [Google Scholar]
- Hooke, R.L. Principles of Glacier Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- McClung, D.; Schaerer, P.A. The Avalanche Handbook; The Mountaineers Books: Seattle, WA, USA, 2006. [Google Scholar]
- Diez, A.; Eisen, O.; Weikusat, I.; Eichler, J.; Hofstede, C.; Bohleber, P.; Bohlen, T.; Polom, U. Influence of ice crystal anisotropy on seismic velocity analysis. Ann. Glaciol. 2014, 55, 97–106. [Google Scholar] [CrossRef]
- Gammon, P.H.; Kiefte, H.; Clouter, M.J.; Denner, W.W. Elastic constants of artificial and natural ice samples by Brillouin spectroscopy. J. Glaciol. 1983, 29, 433–460. [Google Scholar] [CrossRef]
- Bennet, H.F. An Investigation Into Velocity Anisotropy through Measurements of Ultrasonic Wave Velocities in Snow and Ice Cores From Greenland and Antarctica. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 1968. [Google Scholar]
- Bentley, C.R. Seismic-wave velocities in anisotropic ice: A comparison of measured and calculated values in and around the deep drill hole at Byrd Station, Antarctica. J. Geophys. Res. 1972, 77, 4406–4420. [Google Scholar] [CrossRef]
- Gow, A.J.; Williamson, T. Rheological implications of the internal structure and crystal fabrics of the West Antarctic ice sheet as revealed by deep core drilling at Byrd Station. Geol. Soc. Am. Bull. 1976, 87, 1665–1677. [Google Scholar] [CrossRef]
- Horgan, H.J.; Anandakrishnan, S.; Alley, R.B.; Peters, L.E.; Tsoflias, G.P.; Voigt, D.E.; Winbery, J.P. Complex fabric development revealed by englacial seismic reflectivity: Jakobshavn Isbræ, Greenland. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Horgan, H.J.; Anandakrishnan, S.; Alley, R.B.; Burkett, P.G.; Peters, L.E. Englacial seismic reflectivity: Imaging crystal-orientation fabric in West Antarctica. J. Glaciol. 2011, 57, 639–650. [Google Scholar] [CrossRef]
- Gusmeroli, A.; Pettit, E.C.; Kennedy, J.H.; Ritz, C. The crystal fabric of ice from full-waveform borehole sonic logging. J. Geophys. Res. Earth Surf. 2012, 117, 1–13. [Google Scholar] [CrossRef]
- Kohnen, H.; Gow, A.J. Ultrasonic velocity investigations of crystal anisotropy in deep ice cores from Antarctica. J. Geophys. Res. 1979, 84, 4865–4874. [Google Scholar] [CrossRef]
- Bendel, V.; Ueltzho, Ã.K.J.; Freitag, J.; Kipfstuhl, S.; Kuhs, W.F.; Garbe, C.S.; Faria, S.H. High-resolution variations in size, number and arrangement of air bubbles in the EPICA DML (Antarctica) ice core. J. Gla 2013, 59, 972–980. [Google Scholar] [CrossRef]
- Lhomme, N.; Clarke, G.K.; Marshall, S.J. Tracer transport in the Greenland Ice Sheet: constraints on ice cores and glacial history. Quat. Sci. Rev. 2005, 24, 173–194. [Google Scholar] [CrossRef]
- Gow, A.J.; Meese, D. Physical properties, crystalline textures and c-axis fabrics of the Siple Dome (Antarctica) ice core. J. Glaciol. 2007, 53, 573–584. [Google Scholar] [CrossRef]
- Faria, S.H.; Freitag, J.; Kipfstuhl, S. Polar ice structure and the integrity of ice-core paleoclimate records. Quat. Sci. Rev. 2010, 29, 338–351. [Google Scholar] [CrossRef]
- Vaughan, M.J.; van Wijk, K.; Prior, D.J.; Bowman, M.H. Monitoring the temperature dependent elastic and anelastic properties in isotropic polycrystalline ice using resonant ultrasound spectroscopy. Cryosphere 2016, 10, 2821–2829. [Google Scholar] [CrossRef]
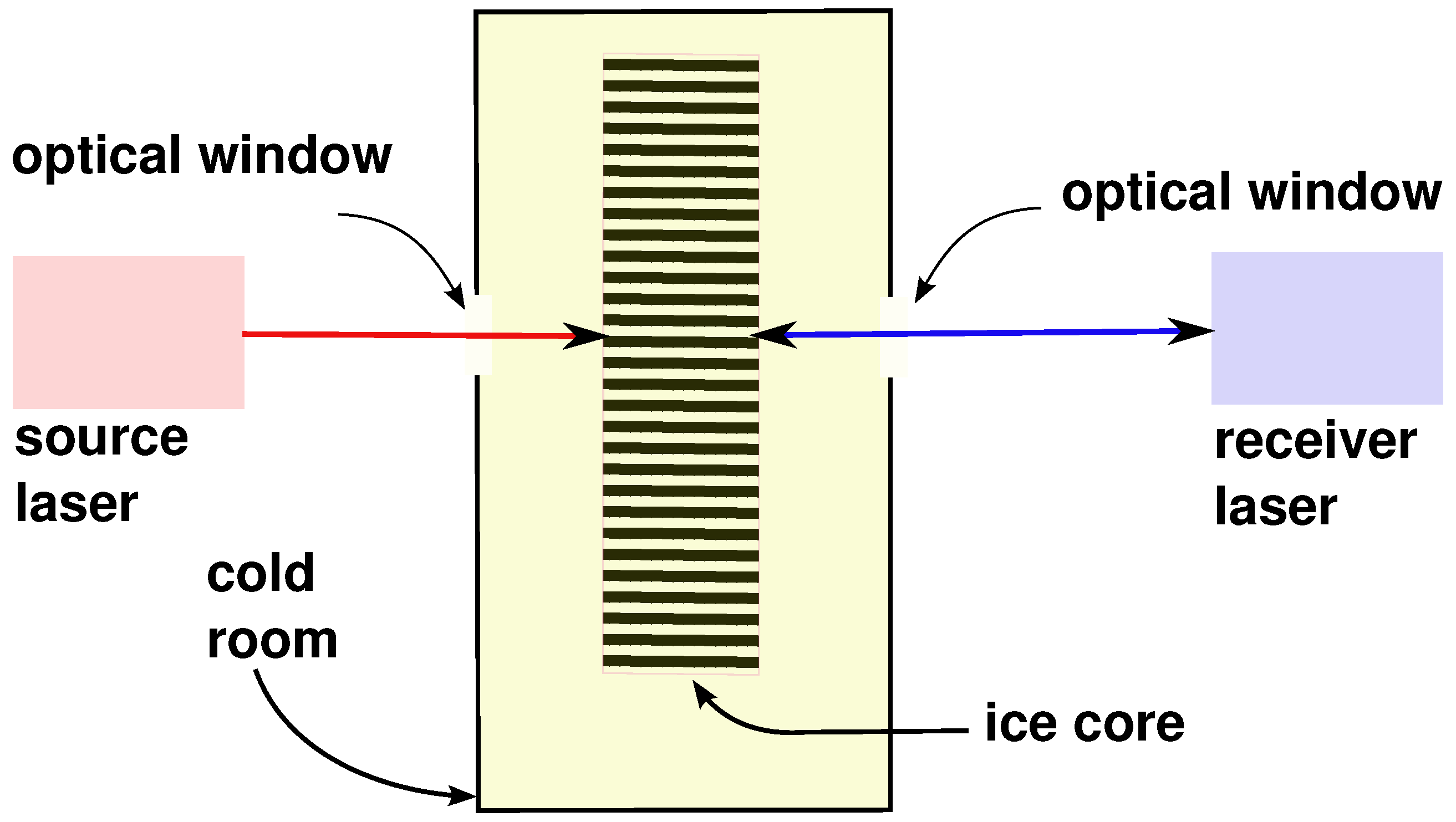



| Component | Property | Value |
|---|---|---|
| Cold room | temperature | −20 ± 0.1 C |
| Vu-Port (sapphire) window | thickness | 2.5 cm |
| Source laser | laser | Nd:YAG (yttrium aluminum garnet) |
| Source laser | wavelength | 1064 nm |
| Source laser | pulse duration | 10 ns |
| Source laser | pulse energy | 0.3 J |
| Receiver laser | laser | HeNe |
| Receiver laser | wavelength | 633 nm |
| PCI oscilloscope card | precision | 16-bit |
| PCI oscilloscope card | sample rate | samples per second |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikesell, T.D.; Van Wijk, K.; Otheim, L.T.; Marshall, H.-P.; Kurbatov, A. Laser Ultrasound Observations of Mechanical Property Variations in Ice Cores. Geosciences 2017, 7, 47. https://doi.org/10.3390/geosciences7030047
Mikesell TD, Van Wijk K, Otheim LT, Marshall H-P, Kurbatov A. Laser Ultrasound Observations of Mechanical Property Variations in Ice Cores. Geosciences. 2017; 7(3):47. https://doi.org/10.3390/geosciences7030047
Chicago/Turabian StyleMikesell, Thomas Dylan, Kasper Van Wijk, Larry Thomas Otheim, Hans-Peter Marshall, and Andrei Kurbatov. 2017. "Laser Ultrasound Observations of Mechanical Property Variations in Ice Cores" Geosciences 7, no. 3: 47. https://doi.org/10.3390/geosciences7030047
APA StyleMikesell, T. D., Van Wijk, K., Otheim, L. T., Marshall, H.-P., & Kurbatov, A. (2017). Laser Ultrasound Observations of Mechanical Property Variations in Ice Cores. Geosciences, 7(3), 47. https://doi.org/10.3390/geosciences7030047





