Investigation on Coupled Fluid-Flow and Stress in Dual Model Rock Mass with Time-Dependent Effect and Its Simulation
Abstract
:1. Introduction
2. Governing Equations
- (1)
- Rock mass is a dual-porosity, dual-permeability homogeneous isotropic continuum.
- (2)
- Strains are infinitesimal.
- (3)
- Rock material has the time-dependent mechanical behavior.
- (4)
- Darcy’s law is used to describe fluid flow in porous medium, and cubic law is used to describe the flow in fractures.
- (5)
- The density of fluid in rock mass is constant.
- (6)
- Isothermal condition is used.
2.1. Rock Mass Deformation
2.2. Fluid Flow Governing Equation
2.3. Boundary Conditions
3. Numerical Simulation
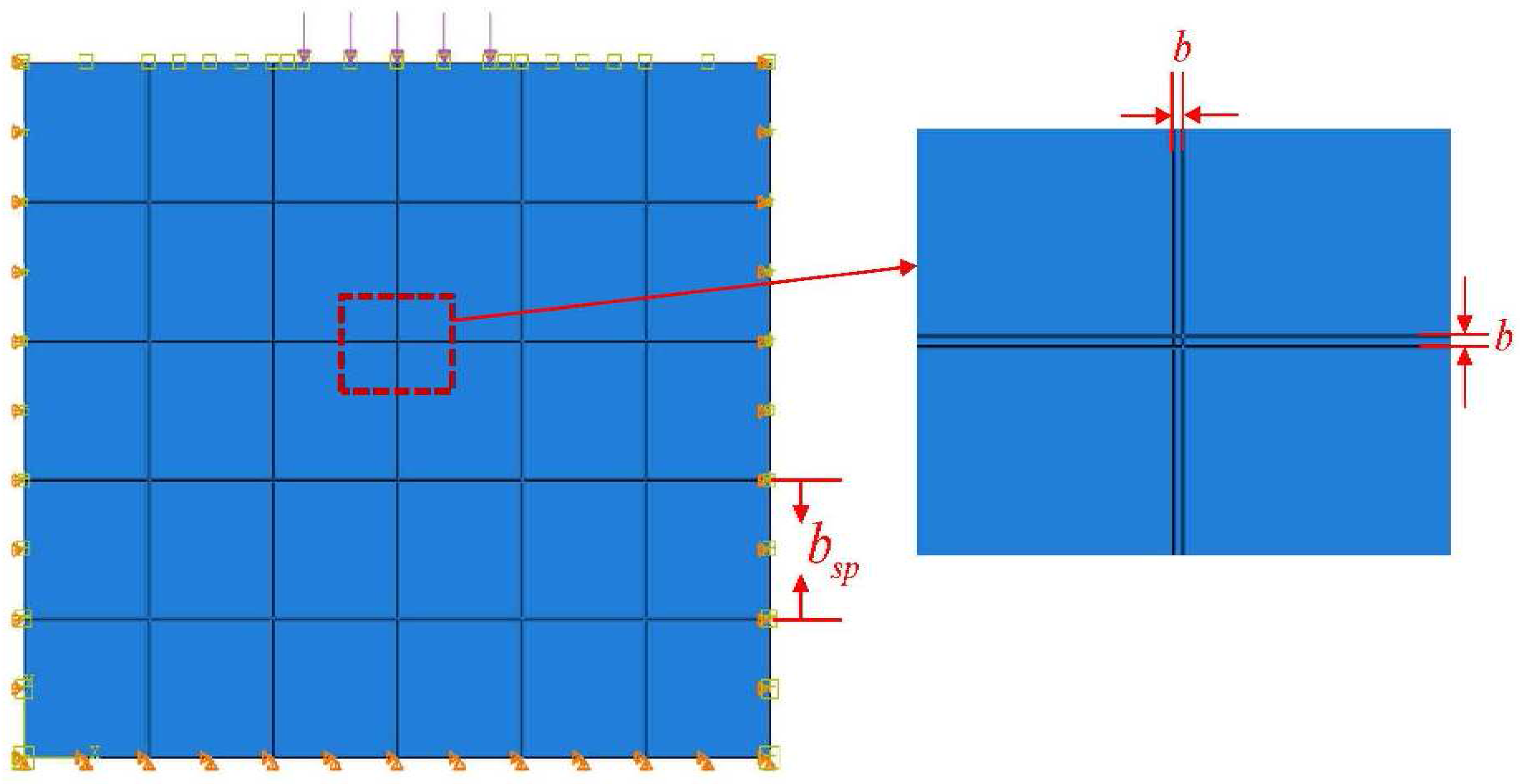
3.1. Model Description and Input Parameters
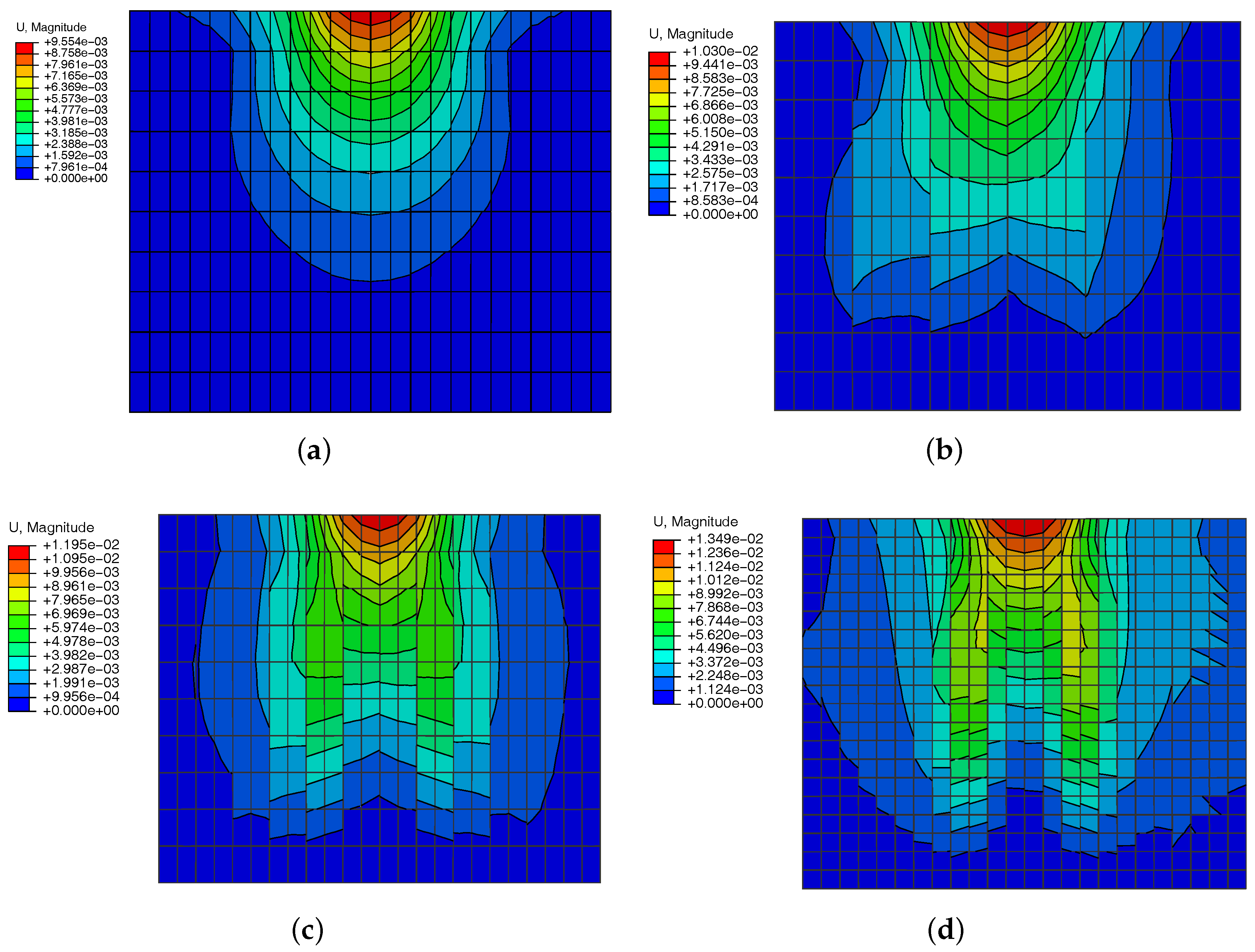
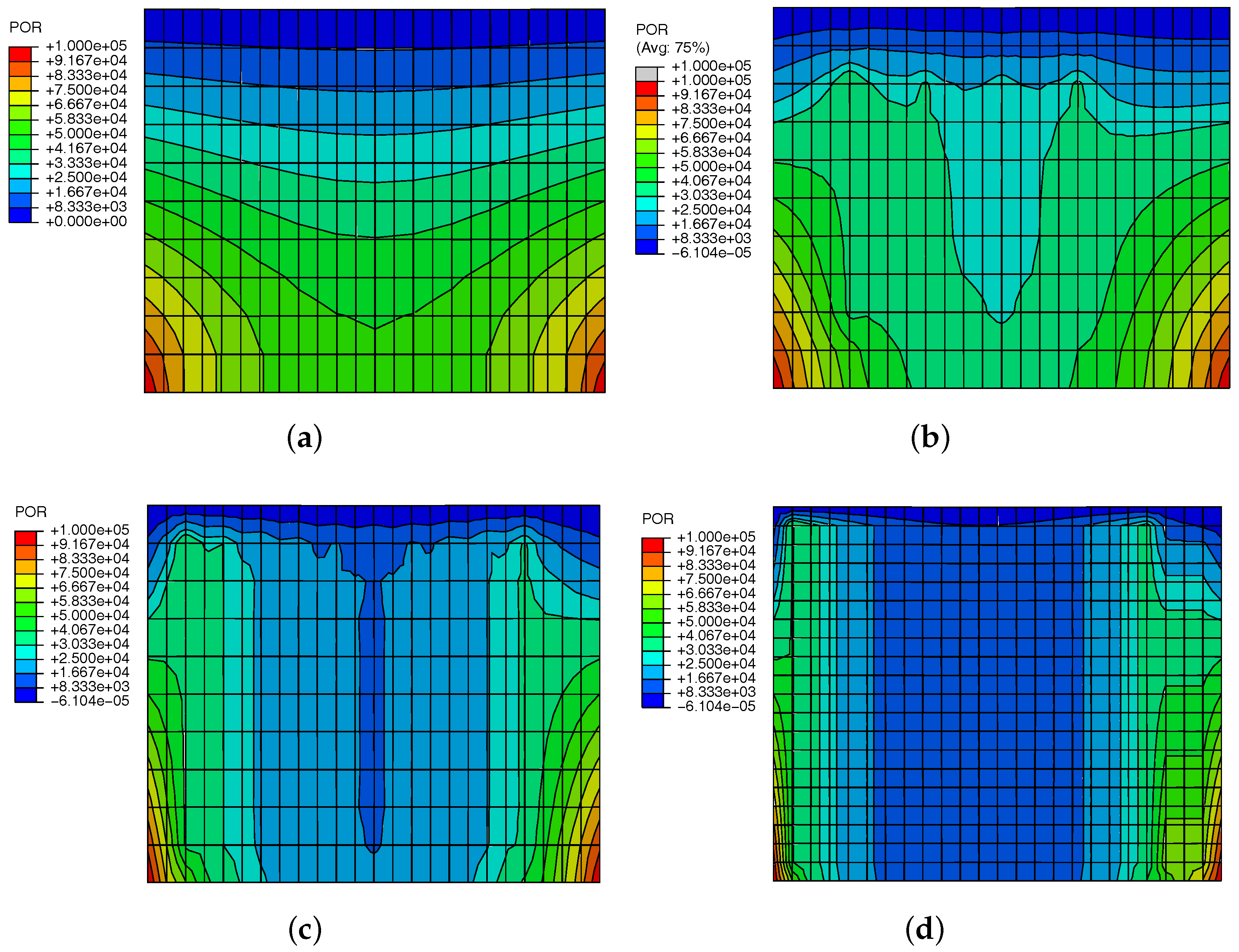
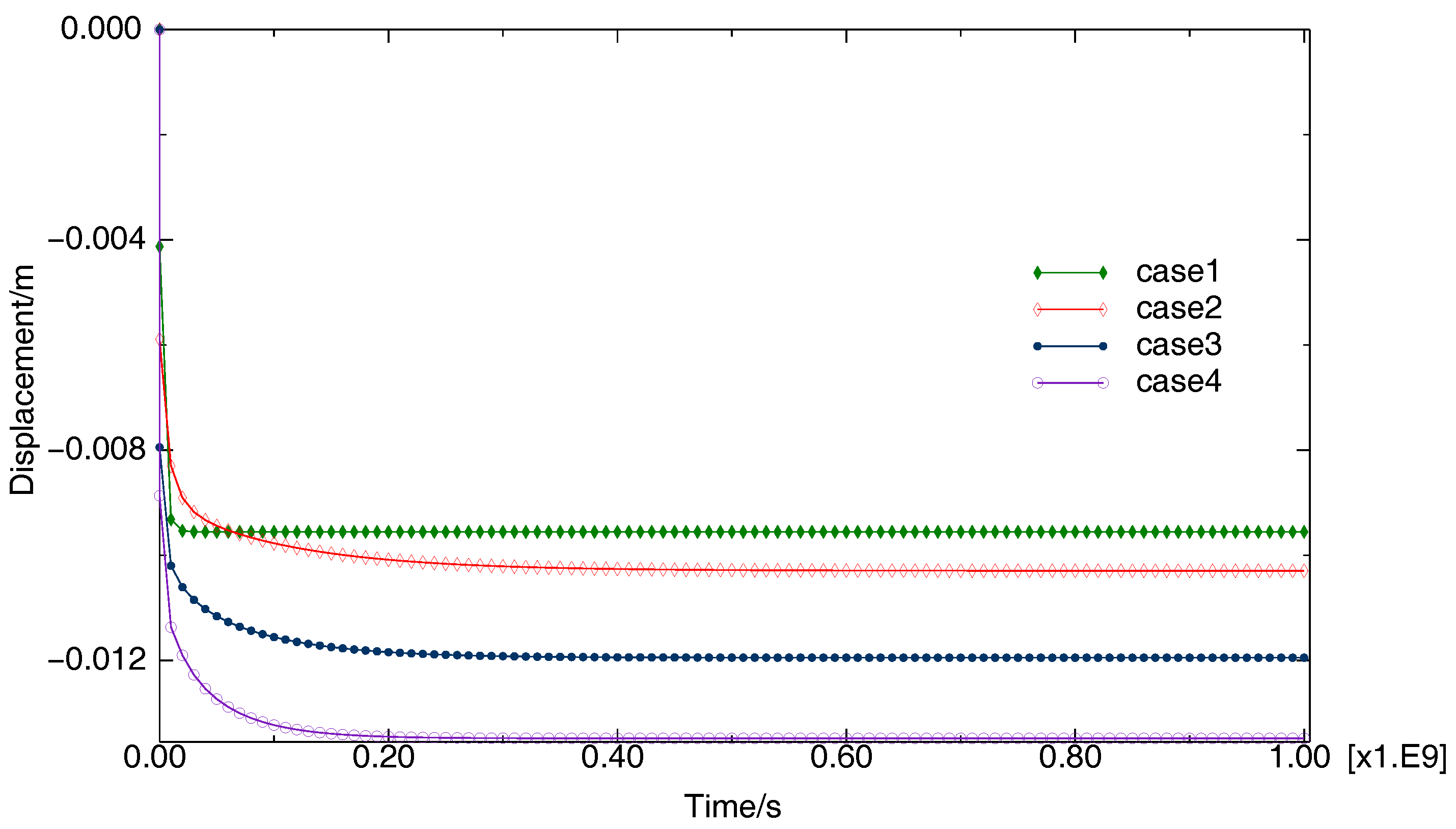
3.2. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elsworth, D.; Bai, M. Flow-Deformation Response of Dual-Porosity Media. J. Geotech. Eng. 1992, 118, 107–124. [Google Scholar] [CrossRef]
- Bai, M.; Elsworth, D. Modeling of subsidence and stress-dependent hydraulic conductivity for intact and fractured porous media. Rock Mech. Rock Eng. 1994, 27, 209–234. [Google Scholar] [CrossRef]
- Liu, J.; Elsworth, D. Three-dimensional effects of hydraulic conductivity enhancement and desaturation around mined panels. Int. J. Rock Mech. Min. Sci. 1997, 34, 1139–1152. [Google Scholar] [CrossRef]
- Bai, M.; Roegiers, J.C.; Elsworth, D. Poromechanical response of fractured-porous rock masses. J. Pet. Sci. Eng. 1995, 13, 155–168. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Elsworth, D.; Chen, Z.; Connell, L.; Pan, Z. Dual poroelastic response of a coal seam to CO2 injection. Int. J. Greenh. Gas Control 2010, 4, 668–678. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, D. Coupled fluid-flow and geomechanics for triple-porosity/dual-permeability modeling of coalbed methane recovery. Int. J. Rock Mech. Min. Sci. 2010, 47, 1242–1253. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, D. A Fully Coupled Multiphase Multicomponent Flow and Geomechanics Model for Enhanced Coalbed-Methane Recovery and CO2 Storage. SPE J. 2013, 18, 448–467. [Google Scholar] [CrossRef]
- Masoudian, M.S.; Airey, D.W.; El-Zein, A. The role of coal seam properties on coupled processes during CO2 sequestration: A parametric study. Greenh. Gases Sci. Technol. 2016, 6, 492–518. [Google Scholar] [CrossRef]
- Masoudian, M.S. Multiphysics of carbon dioxide sequestration in coalbeds: A review with a focus on geomechanical characteristics of coal. J. Rock Mech. Geotech. Eng. 2016, 8, 93–112. [Google Scholar] [CrossRef]
- Masoudian, M.; Airey, D.W.; El-Zein, A. A chemo-poro-mechanical model for sequestration of carbon dioxide in coalbeds. Géotechnique 2013, 63, 235–243. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Elsworth, D.; Qu, H.; Chen, D. Interactions of multiple processes during CBM extraction: A critical review. Int. J. Coal Geol. 2011, 87, 175–189. [Google Scholar] [CrossRef]
- Masoudian, M.S.; El-Zein, A.; Airey, D.W. Modelling stress and strain in coal seams during CO2 injection incorporating the rock-fluid interactions. Comput. Geotech. 2016, 76, 51–60. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Wilson, R.K.; Aifantis, E.C. On the theory of consolidation with double porosity. Int. J. Eng. Sci. 1982, 20, 1009–1035. [Google Scholar] [CrossRef]
- Beskos, D.E.; Aifantis, E.C. On the theory of consolidation with double porosity—II. Int. J. Eng. Sci. 1986, 24, 1697–1716. [Google Scholar] [CrossRef]
- Bai, M.; Elsworth, D.; Roegiers, J.C. Multiporosity/multipermeability approach to the simulation of naturally fractured reservoirs. Water Resour. Res. 1993, 29, 1621–1634. [Google Scholar] [CrossRef]
- Berryman, J.G.; Wang, H.F. The elastic coefficients of double-porosity models for fluid transport in jointed rock. J. Geophys. Res. Atmos. 1995, 100, 24611–24627. [Google Scholar] [CrossRef]
- Chen, H.Y.; Teufel, L.W. Coupling Fluid-Flow and Geomechanics in Dual-Porosity Modeling of Naturally Fractured Reservoirs. In Proceedings of the SPE Annual technical conference and exhibition, San Antonio, TX, USA, 5–8 October 1997; pp. 419–433. [Google Scholar] [CrossRef]
- Valliappan, S.; Khalili-Naghadeh, N. Flow through fissured porous media with deformable matrix. Int. J. Numer. Methods Eng. 1990, 29, 1079–1094. [Google Scholar] [CrossRef]
- Bagheri, M.A.; Settari, A. Modeling of Geomechanics in Naturally Fractured Reservoirs. SPE Reser. Eval. Eng. 2013, 11, 108–118. [Google Scholar]
- Zhang, Y.J.; Zhang, W.Q. Coupled hydro-mechanical model and FEM analyses for dual-porosity media. Chin. J. Geotech. Eng. 2010, 32, 325–329. [Google Scholar]
- Rutqvist, J.; Leung, C.; Hoch, A.; Wang, Y.; Wang, Z. Linked multicontinuum and crack tensor approach for modeling of coupled geomechanics, fluid flow and transport in fractured rock. J. Rock Mech. Geotech. Eng. 2013, 5, 18–31. [Google Scholar] [CrossRef]
- Gan, Q.; Elsworth, D. A continuum model for coupled stress and fluid flow in discrete fracture networks. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 43–61. [Google Scholar] [CrossRef]
- Hu, M.; Rutqvist, J.; Wang, Y. A numerical manifold method model for analyzing fully coupled hydro-mechanical processes in porous rock masses with discrete fractures. Adv. Water Resour. 2017, 102, 111–126. [Google Scholar] [CrossRef]
- Yurtdas, I. Influence of chemical degradation on mechanical behavior of a petroleum cement paste. Cement Concr. Res. 2011, 41, 412–421. [Google Scholar] [CrossRef]
- Yang, S.Q.; Cheng, L. Non-stationary and nonlinear visco-elastic shear creep model for shale. Int. J. Rock Mech. Min. Sci. 2011, 48, 1011–1020. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Q.; Li, S.; Wang, S. Estimation of in situ viscoelastic parameters of a weak rock layer by time-dependent plate-loading tests. Int. J. Rock Mech. Min. Sci. 2014, 66, 169–176. [Google Scholar] [CrossRef]
- Sun, J.; Hu, Y.Y. Time-dependent effects on the tensile strength of saturated granite at Three Gorges Project in China. Int. J. Rock Mech. Min. Sci. 1997, 34, 306.e1–306.e13. [Google Scholar] [CrossRef]
- Martìn, L.B.; Rutqvist, J.; Birkholzer, J.; Battistelli, A. Long-term modeling of coupled processes in a generic salt repository for heat-generating nuclear waste: Preliminary analysis of the impacts of halite dissolution and precipitation. In Proceedings of the Us Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Hou, Z. Mechanical and hydraulic behavior of rock salt in the excavation disturbed zone around underground facilities. Int. J. Rock Mech. Min. Sci. 2003, 40, 725–738. [Google Scholar] [CrossRef]
- Ma, X.; Zoback, M.D. Laboratory experiments simulating poroelastic stress changes associated with depletion and injection in low-porosity sedimentary rocks. J. Geophys. Res. Solid Earth 2017, 122, 2478–2503. [Google Scholar] [CrossRef]
- Weng, M.C.; Tsai, L.S.; Liao, C.Y.; Jeng, F.S. Numerical modeling of tunnel excavation in weak sandstone using a time-dependent anisotropic degradation model. Tunn. Undergr. Space Technol. 2010, 25, 397–406. [Google Scholar] [CrossRef]
- Yang, S.Q.; Jing, H.W.; Cheng, L. Influences of pore pressure on short-term and creep mechanical behavior of red sandstone. Eng. Geol. 2014, 179, 10–23. [Google Scholar] [CrossRef]
- Liu, Y. Experimental research on creep properties of limestone under fluid–solid coupling. Environ. Earth Sci. 2015, 73, 7011–7018. [Google Scholar] [CrossRef]
- Semenov, A.S.; Melnikov, B. Interactive Rheological Modeling in Elasto-visco-plastic Finite Element Analysis. Procedia 2016, 165, 1748–1756. [Google Scholar] [CrossRef]
- Masad, E.; Dessouky, S.; Little, D. Development of an Elastoviscoplastic Microstructural-Based Continuum Model to Predict Permanent Deformation in Hot Mix Asphalt. Int. J. Geomech. 2007, 7, 119–130. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Cormeau, I.C. Visco-plasticity-plasticity and creep in elastic solids-a unified numerical solution approach. Int. J. Num. Methods Eng. 1974, 8, 821–845. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Lim, K.T.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Pet. Sci. Eng. 1995, 13, 169–178. [Google Scholar] [CrossRef]
- Ranjbar, E.; Hassanzadeh, H. Matrix-fracture transfer shape factor for modeling flow of a compressible fluid in dual-porosity media. Adv. Water Resour. 2011, 34, 627–639. [Google Scholar] [CrossRef]
- Masoudian, M.S. Chemo-Hydro-Mechanical Aspects of CO2 Sequestration in Deep Coal Seams. Ph.D. Thesis, University of Sydney, Sydney, Australia, 2013. [Google Scholar]
- Simulia, D.S.; Fallis, A.; Techniques, D. Abaqus 6.10 Online Documentation; Abaqus Web; University of Calgary: Calgary, Canada, 2010. [Google Scholar]

| Parameters | Values |
|---|---|
| Youngs modulus of matrix, E (Pa) | |
| Possions ratio of matrix, | 0.2 |
| Youngs modulus of fracture, E (Pa) | |
| Possions ratio of fracture, | 0.15 |
| Concentrated force, P (Pa) | |
| Permeability of matrix, (m/s) | |
| Permeability of fracture, (m/s) | |
| Porosity of matrix | 0.1 |
| Porosity of fracture | 0.05 |
| Normal stiffness of fracture, (Pa/m) | |
| Tangential stiffness of fracture, (Pa/m) | |
| Leakage coefficient, (m/(Pa·s)) | 0.3 |
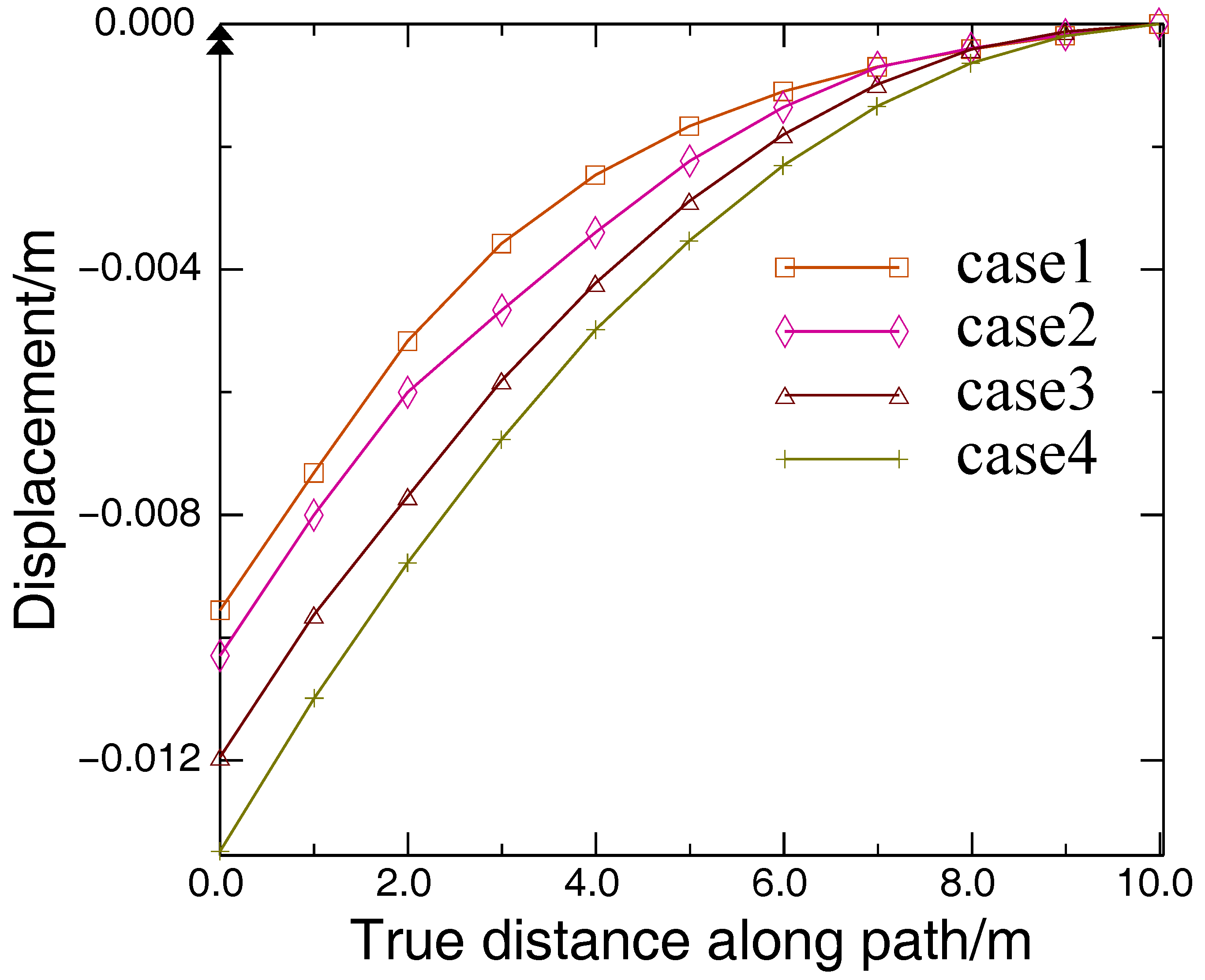
| Parameters | Values |
|---|---|
| Case 1 | |
| Fracture spacing ignoring | |
| the cracking effect in fracture, (m) | 1 |
| Case 2 | |
| Fracture spacing considering | |
| the cracking effect in fracture, (m) | 2 |
| Case 3 | |
| Fracture spacing considering | |
| the cracking effect in fracture, (m) | 1 |
| Case 4 | |
| Fracture spacing considering | |
| the cracking effect in fracture, (m) | 0.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Zhang, Q.; Li, S.; Zhao, H. Investigation on Coupled Fluid-Flow and Stress in Dual Model Rock Mass with Time-Dependent Effect and Its Simulation. Geosciences 2017, 7, 45. https://doi.org/10.3390/geosciences7030045
Zhao M, Zhang Q, Li S, Zhao H. Investigation on Coupled Fluid-Flow and Stress in Dual Model Rock Mass with Time-Dependent Effect and Its Simulation. Geosciences. 2017; 7(3):45. https://doi.org/10.3390/geosciences7030045
Chicago/Turabian StyleZhao, Moli, Qiangyong Zhang, Shucai Li, and Huan Zhao. 2017. "Investigation on Coupled Fluid-Flow and Stress in Dual Model Rock Mass with Time-Dependent Effect and Its Simulation" Geosciences 7, no. 3: 45. https://doi.org/10.3390/geosciences7030045
APA StyleZhao, M., Zhang, Q., Li, S., & Zhao, H. (2017). Investigation on Coupled Fluid-Flow and Stress in Dual Model Rock Mass with Time-Dependent Effect and Its Simulation. Geosciences, 7(3), 45. https://doi.org/10.3390/geosciences7030045





