Abstract
In this paper, an integration landslide susceptibility model by combining expert-based and bivariate statistical analysis (Landslide Susceptibility Index—LSI) approaches is presented. Factors related with the occurrence of landslides—such as elevation, slope angle, slope aspect, lithology, land cover, Mean Annual Precipitation (MAP) and Peak Ground Acceleration (PGA)—were analyzed within a GIS environment. This integrated model produced a landslide susceptibility map which categorized the study area according to the probability level of landslide occurrence. The accuracy of the final map was evaluated by Receiver Operating Characteristics (ROC) analysis depending on an independent (validation) dataset of landslide events. The prediction ability was found to be 76% revealing that the integration of statistical analysis with human expertise can provide an acceptable landslide susceptibility assessment at regional scale.
1. Introduction
Natural hazards have been studied continuously, and systematically, and during the last three decades, their frequency seems to be on the rise [1]. The need for reliable hazard maps is uncontested, in order to mitigate their effects in both natural and manmade environments. From 1900 to 2014, nearly 6% of global natural hazards were associated with landslides [2]. Mountainous or rural environments are subject to landslides as a major natural hazard which causes substantial economic, human, and environmental losses throughout the world each year [3].
Landslide Susceptibility (LS) is defined as the likelihood of a landslide occurring in an area on the basis of local terrain conditions [4]. LS zonation refers to the division of the land in homogeneous areas or domains according to the degree of actual or potential hazard [5]. In the last years, LS mapping has become a valuable tool for assessing disaster phenomena. The cartographic products of LS modeling can be used for developing mitigation plans and selecting the more suitable locations for construction.
Given the powerful abilities of Geographic Information Systems (GIS) technology to deal with a large amount of spatial data, LS is analyzed through effective spatial analysis tools. Many GIS-based approaches have been developed for LS assessment. In general, they are divided into two groups: qualitative and quantitative methods. The most important difference between these two types of methods is their degree of objectivity. The qualitative methods, used extensively during the 1970s and 1980s, depend on the knowledge and previous experience of the experts, resulting in a high degree of subjectivity. They include the geomorphological analysis [6,7] and the use of index or parameter maps. The use of index or parameter maps is subdivided into two methods: the combination or overlay of index maps [8,9] and the logical analytical models [10,11]. Some qualitative approaches, however, incorporate the idea of ranking and weighting the parameters involved, and may be semi-quantitative in nature [12]. Examples of this kind of approach are the Analytical Hierarchy Process (AHP) [13,14], the Weighted Linear Combination (WLC) [15], and their combination [16].
The quantitative methods are based on numerical expressions of the relationship between controlling factors and landslide occurrence. They include statistical analysis, geotechnical engineering approaches [17,18], and soft computing techniques such as Artificial Neural Network (ANN) [19,20,21,22], neuro-fuzzy [23,24], support vector machine [16,23] and decision tree [23,25] methods. In statistical analysis methods, the combination of parameters that have led to landslides in the past are determined statistically, and quantitative predictions are made for areas not affected by landslides but where similar background conditions exist [26]. Several researchers have applied these methods, which involve either bivariate [27,28,29,30] or multivariate analysis [16,31,32,33]. In bivariate analysis, each individual landslide-influencing factor is combined with a landslide inventory map, and weight values based on landslide densities are calculated for its corresponding categories. A well-known and widely used bivariate analysis method for LS zonation is the Landslide Susceptibility Index (LSI) [14,22,34,35]. It is increasingly recognized that in both qualitative and quantitative models, the results are prone to the inherent uncertainties related to various analysis parameters such as the errors and variability in model choice, weighting factors, data used, and human judgment [15].
In recent years, another soft computing technique, known as fuzzy logic, has been applied to map LS. Considering the determination of weightings (fuzzy membership values), this technique is either expert-based (semi-quantitative) approach or data-driven (quantitative) approach or a combination of both [36]. In expert-based approaches [37,38], the weightings are assigned based on the field knowledge of the experts, whereas in data-driven approaches [39,40] the weightings are determined according to correlations between landslide locations and landslide-conditioning factors. Such an expert-based approach, referred as Trapezoidal Fuzzy Number Weighting (TFNW) [12,41,42], was used in this study.
In Greece, previous studies concerning LS assessment have been implemented on moderate scale (1:25,000–1:500,000) using semi-quantitative methods such as AHP, WLC and TFNW [12,43,44,45], statistical analysis [22,35,46,47], ANN [22,48] and integration methods [49], and on national scale (<1:1,000,000) using statistical analysis [50,51], ANNs [50] and fuzzy logic [52].
The main aim of this paper was to improve our previous research works [12,35], integrating two different and already tested LS assessment methods: LSI and TFNW. Thus, a GIS-based integration method was developed and presented at regional scale (1:500,000) for Peloponnese peninsula, Greece. Furthermore, a validation analysis was implemented to estimate the prediction ability of the proposed method.
2. Study Area
Peloponnese was selected as the study area for the proposed method. It is one of the nine geographical departments of Greece and is located in its southern part (Figure 1). Peloponnese constitutes the largest peninsula of the country with an extent of 21,439 km2. It is divided into seven administrative prefectures: Achaia, Argolida, Arkadia, Ilia, Korinthia, Lakonia and Messinia (Figure 1), with a population of 1,086,935 inhabitants [53]. Peloponnese has a typical Mediterranean climate with a hot and relatively dry summer, and a wet season during autumn, winter and spring [54]. The climate as well as the geotectonic status, the lithology and the seismicity have mainly formed the geomorphology of the study area. In general, its geomorphology can be characterized as complex, with a mountainous interior, many coastal cliffs in the south, and basins, coastal beaches, lakes and inland basins on the west and southeast coasts.

Figure 1.
The location of the study area (Peloponnese peninsula) and the landslide inventory.
Peloponnese is a region highly vulnerable to the occurrence of severe natural disasters such as earthquakes, floods and forest fires. However, due to its complex geomorphology, all causal and triggering factors of landslide occurrence present a high spatial variability. Considering the morphological and geological conditions of Peloponnese, it is evident that slope stability is one of the most severe and frequent hazards for public safety as well as land-use planning and management of the area.
3. Materials and Methods
In order to accomplish the LS analyses in the study area, a spatial database was designed and developed, and spatial analysis tools were implemented within GIS environment with the use of an ArcGIS (version 9.3) software package. This database comprises two main parts: (a) the landslide inventory dataset and (b) the datasets for the landslide-influencing factors.
3.1. Landslide Inventory
In the present study, two main landslide inventories were used: (a) an inventory maintained by Institute of Geology and Mineral Exploration (IGME) covering a time period from 1910 to 1995 [55] and (b) an inventory, developed on the basis of fieldwork and aerial photography [56] interpretation, which contains landslide events occurring from 1995 to 2003. The final landslide dataset consists of 282 landslides (217 and 65 landslides from the first and second inventory, respectively) presented as point features in the centroid of each pixel (Figure 1). This dataset was randomly split into two separate groups: a training dataset and a validation dataset. The training dataset (75% of the landslide inventory) was used for the implementation of the model, whereas the validation dataset (25% of the landslide inventory) was used during the verification of the results produced from the model (see among others [57,58,59]). Our intention was to keep the same sampling strategy (i.e., the same percentages for training and validation datasets) for both the integration model and the single models [12,35] combined for its creation in order to increase their comparability.
The landslides under investigation have more or less the same characteristics: lateral based and downslope movement of soils or rocks. In line with [60], in this study, the term landslide is used for translational and rotational earth slides, which were recorded in landslide inventories. These events vary consistently in volume, from some thousands of m3 to several million m3 [51], and depicting small to extremely large magnitude according to [61] classification. Subaqueous and liquefaction events are not examined.
3.2. Landslide-Influencing Factors
Although there are no standard guidelines for selecting the landslide-influencing factors, the nature of the study area, the scale of the analysis, the data availability and the general literature guidelines were taken into account [26,62,63,64,65]. In this study, land cover, lithology, elevation, slope angle, slope aspect, MAP and PGA have been selected as the landslide-influencing factors.
Slope stability is highly influenced by land cover. The land cover layer was classified by following the level-1 classification scheme of the CORINE Coordinate of Information on the Environment) program data [66]. Agricultural, forest and semi-natural areas cover the main part of Peloponnese, whereas urban is the dominant land cover in the coastal zone of the peninsula.
Lithology plays a key role in landslide activity since different lithologic units have different slope stability performances [67]. The lithological layer of the study area was created from the Geological Map of Greece [68]. The main lithological formations are carbonate rocks (44%): limestones, dolomites and marbles, and Neogene sediments (22%): usually marls, sandstones and mudstones. The central and western part of Peloponese belongs to the External Hellenides, which is characterized by Mesozoic–early Cenozoic sedimentary units (mainly carbonate rocks, schists-cherts and flysch) [69]. The most critical landslide-prone formations are flysch and neogene sediments, while schists and cherts significantly contribute in landslide phenomena [51].
Among all parameters for LS zonation, elevation, slope angle and slope aspect have been recognized as the most important [70,71,72]. The elevation dataset is useful to classify the local relief and locate points of maximum and minimum heights within terrains. Furthermore, it is well supported in the literature [43,46] that slope gradients have a large impact on landsliding in Peloponnese. In the study area, the slopes vary from gentle to very steep. Most of the landslides occur on gentle natural slopes where the translational type predominates. The aspect parameter is also related to differential weathering, exposure to sunlight and drying winds and soil moisture [62]. The Digital Elevation Model (DEM) was the key to generating the topographic factors related to the landslide activity of the area under investigation. We used the DEM from SRTM (Shuttle Radar Topography Mission) database. Elevation (0–2367 m), slope angle (0°–54°) and slope aspect were extracted from this DEM.
Previous studies emphasized the need of incorporating “dynamic” factors (MAP, PGA) with other “static” factors for LS zonation mapping in areas, whereas these factors are playing an important role not only in the reactivation of old landslides but in the development of new ones [73,74]. It is, therefore, imperative to incorporate these parameters, while carrying out LS analysis in seismically active and frequently rainfall-influenced regions. The precipitation data (339–1655 mm) used in this study refers to the mean annual precipitation during the period from 1950 to 1974 (source: Public Power Company, Athens, Greece). MAP is the average of the available long-term records [75]. The study area belongs to a seismically active zone with tectonism expressed through faults, thrust zones and folds. The seismic factor (0.05–3.95 m/s2) was produced from the map of expected peak ground acceleration with a 475-year return period (10% probability of exceedance in 50 years). This map, from which the corresponding layer was derived, was launched in 1992 from the Technical Chamber of Greece. PGA is the absolute maximum amplitude of recorded ground acceleration [76]. Heavy rainfall and earthquakes have triggered several landslide events, mainly in northern and western areas of the peninsula [43,77,78]. Rainfall triggered landslides usually are rapid short moving events, while slow short-moving type also occur including extensive instability zones [79]. On the other hand, seismic triggered landslides occur in the vicinity of active faults, and usually related to other secondary seismic events, like soil liquefaction, subsidence of the coastal strip, and rock falls [80,81].
Most of the final layers were in raster format (grid), while others were converted from vector (point, line or polygon) to raster format (with cell size 250 m × 250 m for land cover, lithology, MAP and PGA factors, and 90 m × 90 m for elevation, slope angle and slope aspect factors).
3.3. Methodology
A GIS-based integration approach was developed to create a LS map using two different methods: LSI and TFNW. Such integration can adjust the parameters included in this study by means of the precise LS assessment and effectively reduce the subjectivity and uncertainty resulting from the use of single method. The LSI method was proposed by [82] and is based on the relationship between the spatial distribution of landslides and each conditioning factor [62]. Here, in order to quantify the impact of various categories for the standardization of each factor, we used the TFNW. The details of this approach have been described by [41]. The main steps of this methodology are presented below:
- (a)
- Categorization of all landslide-influencing factors. In this step, the ‘‘Natural Breaks (Jenks)’’ categorization (five categories) was implemented for the “dynamic” factors (MAP and PGA), whereas for the other two factors with continuous values (elevation and slope angle) the categorization was executed in a manual way based on their presented values. ‘‘Natural Breaks (Jenks)’’ method is a data classification method that minimizes variance within groups of data and maximizes variance between groups of data [83]. For land cover, lithology, and aspect, all the categories of the nominal scale were preserved.
- (b)
- Calculation of LSI for all factor categories (Table 1) based on Equation (1) [26]:with Ni, j the number of landslides in category j of the factor i, Ai,j the area of this category, NT the total number of landslides and AT the total area under investigation. Thus, the calculation of the landslide density in each category and of the area for each category was implemented using GIS-based overlay functions.
 Table 1. Categories, landslide densities, susceptibilities (LSI), fuzzy values and weights for landslide related factors.
Table 1. Categories, landslide densities, susceptibilities (LSI), fuzzy values and weights for landslide related factors. - (c)
- The maximum value, the range and the standard deviation of LSI values for all factors were calculated in order to interpret the importance of each factor. The range is the difference between the maximum and minimum LSI values. The standard deviation measures the spread of the LSI values about the mean value.
- (d)
- Definition of linguistic variables and fuzzy numbers for LS categories in order to incorporate uncertainty in the analysis. All fuzzy numbers were expressed as (ak, bk, ck, dk). The definition of these fuzzy numbers is presented in [12].
- (e)
- Three independent experts, with scientific background in the fields of geosciences and engineering geology, and with experience and scientific knowledge of the study area, were invited to assign a linguistic importance weighting for every category of each factor. From these linguistic judgments we obtained the corresponding fuzzy numbers. Such judgments are inevitably subjective, but, by proposing several possible scenarios, followed by the systematic testing and elimination of options, as a result of additional investigation and discussion, it is possible to develop reliable estimates. Experimental evidence suggests that group judgments appear to be more accurate than judgments of a typical group member [84]. In this case, we considered a homogeneous group of experts with equal degree of importance for each one. Accordingly, the overall expert-based judgment is the mean value of the three judgment values. The sum of these numbers is still a fuzzy number. Thus, we proceeded to the computation of the aggregated fuzzy weights of individual categories (Table 1).
- (f)
- A fourth “statistical expert” judgment was added in the above list on the basis of the statistical analysis (Table 1). This statistical interpretation was based on the LSI values for each category according to the following rules:
- In a category with LSI value between –0.15 and 0.15, a “Moderate” susceptibility was assigned.
- Categories with negative (<–0.15) LSI values were defined as zones of “Very Low” or “Low” susceptibility according to their ascending order.
- Categories with positive (>0.15) LSI values were defined as zones of “Very High” or “High” susceptibility according to their descending order.
Accordingly, the range of LSI values was interpreted for each factor according to the following rules:
- In a factor with range between 1.00 and 1.50, a “Moderate” susceptibility was assigned.
- Factors with range <1 were characterized with “Very Low” or “Low” susceptibility according to their ascending order.
- Factors with range >1.50 were characterized with “Very High” or “High” susceptibility according to their descending order.
It is worth mentioning that in our case, we assigned an equal degree of importance between the “statistical expert” and the group of experts.
- (g)
- After the defuzzification of the fuzzy weights of individual LS categories, we proceed to the computation of the normalized weights and the construction of the weight vector (Table 1). More details of this step could be found in [12].
By implementing the same procedure described previously, we used expert-based and statistical-based linguistic variables to calculate the weight of importance for each conditioning factor (Table 2).
- (h)
- The last step is the aggregation of relative values, and the generation of the final LS map (Figure 2). This step was implemented by using the WLC method [85]. We classified the final LS map into five discrete categories: “Very Low”, “Low”, “Moderate”, “High” and “Very High” landslide susceptibility according to the standard deviation classification method. This method uses the mean value to generate class breaks by adding or subtracting one standard deviation at a time [70]. Moreover, in order to maintain five categories, we embedded low and high outliers into “Very Low” and “Very High” susceptibility categories, respectively.
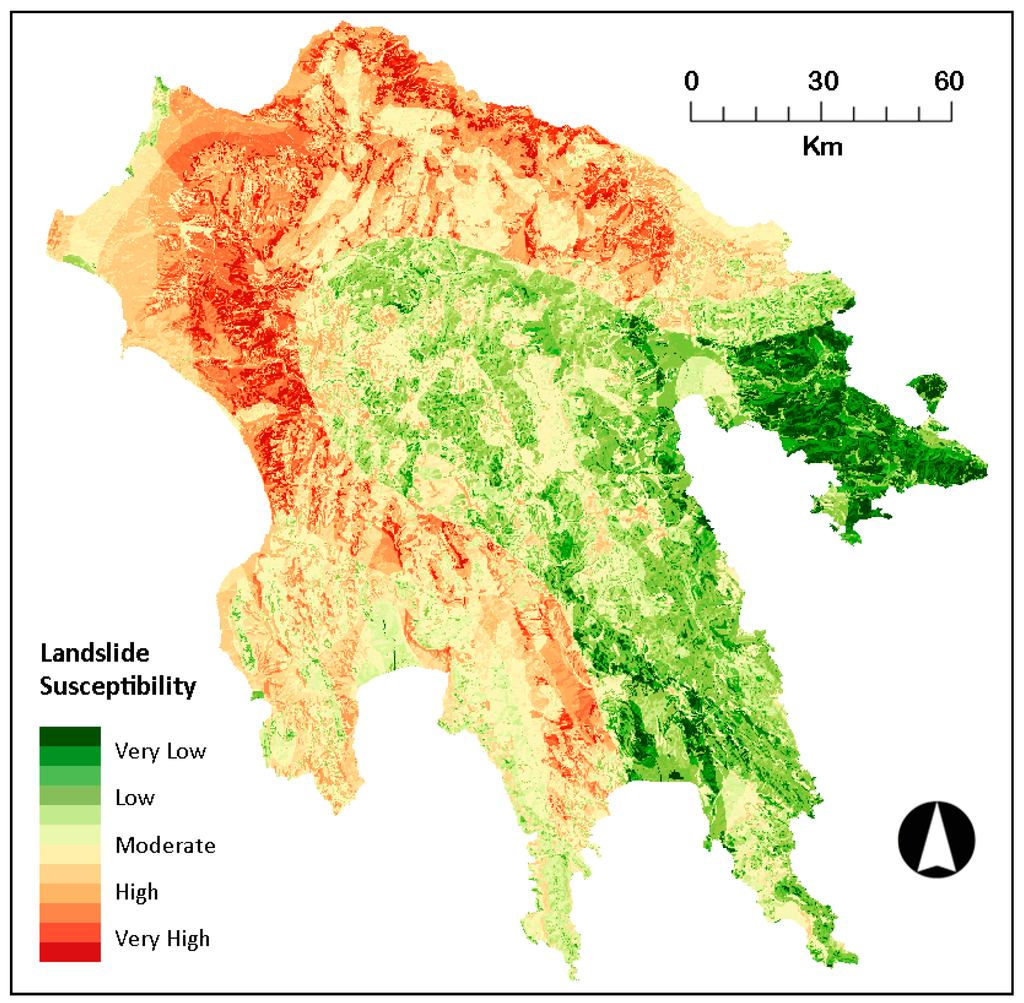 Figure 2. The landslide susceptibility map produced from the integration LSI/TFNW model.
Figure 2. The landslide susceptibility map produced from the integration LSI/TFNW model.

Table 2.
Weight values for each factor according to the integration LSI/TFNW method.
4. Results—Validation
As mentioned previously, we developed an integration LS model according to the LSI/TFNW approach. This approach allowed for the assessment of landslide susceptibility by integrating expert-based and statistical modelling methods.
The results from the LSI/TFNW model are presented in Table 1 and Table 2. The most important causal factors were found to be MAP, slope angle and lithology with weight values 0.20, 0.18 and 0.17, respectively. Elevation was the weakest factor in the scale of importance (weight value = 0.08).
The output LS map (Figure 2) from the integration model shows that 26% and 7% of the study area were classified as “High” and “Very High” susceptibility zones, respectively. The same map also shows that the zones of “High” and “Very High” susceptibility are mainly located around the northern (coastal) and western part of Peloponnese, with pockets of “High” susceptibility in the rest part of the peninsula.
The overlay of the final LS map with the landslide training dataset indicated that 28%, 42% and 24% (total: 94%) of the landslide events fall within “Very High”, “High” and “Moderate” LS zones (in total 66% of the study area), respectively. It is notable that according to the used model only 6% of the dataset falls in “Low” susceptibility zone, with no landslides into the “Very Low” susceptibly zone.
We have also proceeded with a standard validation analysis using data from landslide events, not included in the initial spatial database (validation dataset), in order to estimate the overall performance of the model in the study area. Validation is essential to know the predictive value of the model [86]. For the validation of the output, the Receiver Operating Characteristics (ROC) curve was drawn, and the Area Under Curve (AUC) value was calculated for the proposed model. ROC analysis is considered as a powerful method for the validation of LS models [87,88]. In practice, the AUC performs very well and is often used when a general measure of predictiveness is desired [89]. The AUC values range from 0.5 to 1.0. The ideal model yields a value close to 1.0 (perfect fit), whereas a value close to 0.5 indicates an inaccurate model (random fit).
Figure 3 shows the ROC curve of LSI/TFNW model for the validation dataset. The AUC value of 0.76 indicates a reasonable prediction ability of the model.
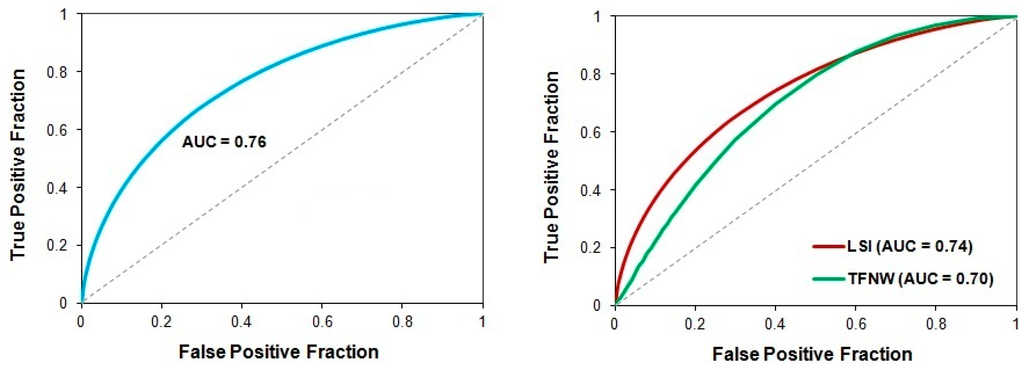
Figure 3.
ROC curves for the integration LSI/TFNW model and the combined single models, LSI and TFNW.
Previous studies [12,35] in the same area with the use of the single methods combined in this integration model (TFNW and LSI, respectively), produced slightly worse results (Figure 3). The AUC values for these models were 0.70 and 0.74, respectively, based on the standard deviation classification method for their final LS maps.
Specifically, comparing the final map of the proposed integrated method with the landslide susceptibility map produced from TFNW model [12], it is shown that in both maps 14% (3039 km2), 9% (2001 km2) and 1% (301 km2) of the study area are defined as zones of “Moderate”, “High” and “Very High” susceptibility, respectively. On the other hand, the differences between the LS maps for these three susceptibility zones are presented to cover 32% (6773 km2) of the study area. The differences for the remaining susceptibility zones (“Very Low” and “Low”) cover a restricted part of the study area (7% or 1377 km2).
In addition, comparing the final LS map of this study with this one created from LSI model [35], it is derived that in both maps 21% (4427 km2), 18% (3829 km2) and 4% (881 km2) of the study area belong to “Moderate”, “High” and “Very High”, respectively, susceptibility zones. On the contrary, the coverage of differences between the final maps for these three susceptibility zones is found to be 16% (3291 km2) of the study area. Finally, the coverage of differences for the remaining susceptibility zones is more or less similar with the relative coverage of the aforementioned comparison between integration and TFNW models.
5. Discussion
The idea of implementing an integration method for LS zonation is not new. Recent examples are the efforts of [90,91,92]. In the first study, AHP and fuzzy sets were combined to determine LS levels for areas of the Metro Vancouver region, British Columbia, Canada. The parameters were standardized to a common measurement scale using fuzzy set membership functions and the weight value for each parameter was calculated using AHP. In the second study, the authors produced a LS zonation map in the Chehelchay Basin (northeastern Iran). They applied Geographically-Weighted Principal Component Analysis (GWPCA) to calculate LS using a fuzzy gamma operator. Finally, the third study focused on the methodology of the urgent LS assessment right after the 2013 Lushan earthquake (southwest of Sichuan Province, China). An assessment approach was developed integrating bivariate statistical analysis (LSI) and AHP methods for the assignment of factor class weights and factor weights, respectively.
This study combined an expert-based semi-quantitative approach (TFNW) with a data-driven statistical method (LSI) to prepare a LS map at a regional scale on the Peloponnese peninsula, Greece. The main motivation is to create an integration model that preserves and integrates the advantages of the combined models at the specific scale of analysis. To achieve this objective, seven conditioning factors (elevation, slope angle, slope aspect, lithology, land cover, MAP and PGA) were taken into consideration.
The LSI model is a data-driven bivariate statistical approach. The bivariate statistical technique is one of the most preferable models at this scale [93]. In this LS modeling, all the problems of landslide inventory maps will automatically be inherited to the final susceptibility maps [94]. In general, a reliable, accurate and complete landslide inventory map will provide high-quality statistical models [95]. In many countries—including Greece—this kind of extended landslide inventory is not available.
On the other hand, for the expert-based fuzzy weighting model, the landslide inventory map is not needed. This kind of analysis is purely subjective. To some extent, opinions may change for every individual expert and thus may be subjected to cognitive limitations with uncertainty and subjectivity. However, methods that depend on expert opinions are often useful for regional assessments [96]. A significant part of the semi-quantitative LS research follows a similar strategy as the proposed one by inviting a limited number of experts (see among others [42,97]). The main issue is not to invite as many scientists as possible but to invite experts with detailed knowledge of the landslide events in the area under investigation and to ensure an overall consensus of their evaluation about the importance of the factors involved.
Recently, ROC analysis has been widely used in the international literature to evaluate the prediction capability of the LS mapping methods. In this study, the empiric ROC area for the integration model was estimated to be 0.76 for the validation dataset. Thus, there is 76% agreement between prepared LS map and landslide locations of the validation dataset, which is a reasonable result, taking into consideration the scale of analysis. Moreover, this model proved to be slightly more effective for the overall LS assessment of the study area as it recorded the highest percentage in our validation test in comparison with LSI and TFNW methods (74% and 70%, respectively). Therefore, the reliability of the proposed integration model is directly related to the reliability of both data-driven and expert-based methods combined. In other words, it seems that a combination of two quite satisfactory methods according to the proposed integration model generates even better results. However, this preliminary finding needs more research to be confirmed through the implementation of the proposed model in more studies areas with various geographical and geotectonic settings.
The implementation of the integration model in the study area revealed that there are different zones within Peloponnese which seem to configure various landslide susceptibility clusters. The “High” susceptibility areas are concentrated in the western Peloponnese with few scattered pockets in the remaining parts of the peninsula. Additionally, a linear concentration of “High” susceptibility values is located in the northern coastal zone of the study area. According to the final LS map, the “Very High” susceptibility zone covers a significant part of the study area (7% of the total area).
The comparison of the proposed method with the expert-based and the statistical methods showed that the integrated method illustrates more emphatically the zones of “High” or “Low” susceptibility in both of the individual methods. Accordingly, the main part the areas of “High” and “Very High” susceptibility in the hybrid map (classes “4” and “5”), is within the class “5” (“Very high” susceptibility) in the statistical and the expert-based LS maps (99% and 67%, respectively). Concerning the spatial distribution of the areas with high LS values in the integrated method, despite the preservation of the general spatial pattern (high LS values in the northern and the western part of Peloponnese) it has to be noticed that there are some pockets of high LS in areas with limited existence of previous landslides. This fact is due to the expert-based classification and it may be useful to identify high LS zones in areas with lack of landslide events.
The most important factors for the zonation of LS in the study area are MAP, slope angle and lithology. It seems that the incorporation of “dynamic” factors (MAP, PGA) in this regional analysis was more or less beneficial to the LS assessment. Among the categories of these two factors, the categories with high levels of annual precipitation (885–1079 mm) and seismic acceleration (2.54–3.11 m/s2) have the highest LSI values combining the highest landslide density and coverage area. In contrast with aforementioned categories of MAP and PGA factors, the category with 11°–15° slope angle presents the highest LSI value combining a lower landslide density and coverage area than the categories with low levels of slope angle (<10°).
Some limitations and assumptions of the proposed method have to be pointed out. First of all, as the analysis is based on medium-scale datasets, the results are unsuitable for detailed site-oriented specific analysis. At large scales, more exhaustive datasets and detailed geotechnical information are required. A second limitation is related to the landslide inventory dataset. At regional scale, this dataset does not include the total amount of the landslide events within the area under investigation. In this paper, we considered equal importance between the statistical and expert-based models for the construction of the integration model. Although this is a reasonable starting point, alternative importance ratios should be further tested. Finally, another limitation of this study is that the proposed method does not take into account the mutual relationships between causal factors. Future work will focus on this issue by combining expert-based with multivariate statistical models. Furthermore, it should be mentioned that, according to our analysis, the output LS map presents only the predicted spatial distribution of landslides. It does not present the temporal probability of landsliding.
Therefore, the results from this paper should be used in the first stage of hazard mapping, which is crucial in an essential part of quantitative risk analysis [98,99]. Despite its limitations, the proposed method can produce reliable landslide susceptibility maps at regional scale. This is very useful information for local authorities and decision makers in order to choose suitable locations for future land-use planning and implementation of developments, and target their mitigation strategies.
6. Conclusions
Statistical analysis and expert-based methods are often used to evaluate LS zonation. Considering that these general approaches have their pros and cons when applied at regional scale, we investigate the performance of an integration model. The results obtained show that it is possible to produce satisfactory LS maps with the proposed hybrid model. It seems that the overall assessment provided by the experts efficiently incorporates the knowledge of the study area and of the factors involved in the LS zonation. Thus, to some extent, the expertise of specialists can contribute to the enhancement of the standard statistical method especially in moderate and small scale analyses in areas with incomplete landslide event archives.
Further research may include the validation of the proposed model in other areas characterized by different geomorphological characteristics, and its comparison with other advanced LS models (such as logistic regression and ANN models) at regional scale.
Acknowledgments
Authors thank the three experts for their contribution in this paper. Also, authors are grateful to the anonymous reviewers for their useful comments and constructive manuscript reviewing.
Author Contributions
Christos Chalkias conceived of the study, designed the analysis, and participated in its implementation. Christos Polykretis participated in the spatial database creation and the implementation of statistical analysis, and drafted the manuscript. Maria Ferentinou and Efthimios Karymbalis participated in the design and implementation of the study and in the preparation of the validation dataset. Christos Chalkias, Christos Polykretis, Maria Ferentinou and Efthimios Karymbalis participated in the finalization of the manuscript. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, K.; Petley, D.N. Environmental Hazards: Assessing risk and reducing disaster, 5th ed.; Routledge: Abingdon, UK, 2009. [Google Scholar]
- Centre for Research on the Epidemiology of Disasters (CRED). EM-DAT: International Disaster Database; Université Catholique de Louvain: Brussels, Belgium, 2014. [Google Scholar]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Brabb, E.E. Innovative approaches to landslide hazard mapping. In Proceedings of the 4th International Symposium on Landslides, Toronto, ON, Canada, 16–21 September 1984; Volume 1, pp. 307–324.
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice; UNESCO: Paris, France, 1984; Volume 3. [Google Scholar]
- Santangelo, M.; Cardinali, M.; Rossi, M.; Mondini, A.C.; Guzzetti, F. Remote landslide mapping using a laser rangefinder binocular and GPS. Nat. Hazards Earth Syst. Sci. 2010, 10, 2539–2546. [Google Scholar] [CrossRef]
- Listo, F.L.R.; Vieira, B.C. Mapping of risk and susceptibility of shallow-landslide in the city of Sao Paulo, Brazil. Geomorphology 2012, 169–170, 30–44. [Google Scholar] [CrossRef]
- Castellanos Abella, E.A.; van Westen, C.J. Qualitative landslide susceptibility assessment bymulticriteria analysis: A case study from San Antonio del Sur, Guantánamo, Cuba. Geomorphology 2008, 94, 453–466. [Google Scholar] [CrossRef]
- Avtar, R.; Singh, C.K.; Singh, G.; Verma, R.L.; Mukherjee, S.; Sawada, H. Landslide susceptibility zonation study using remote sensing and GIS technology in the Ken-Betwa River Link area, India. Bull. Eng. Geol. Environ. 2011, 70, 595–606. [Google Scholar] [CrossRef]
- Intarawichian, N; Dasananda, S. Analytical hierarchy process for landslide susceptibility mapping in lower Mae Chaem watershed, northern Thailand. Suranaree J. Sci. Technol. 2010, 17, 277–292. [Google Scholar]
- Demir, G.; Aytekin, M.; Akgün, A.; Ikizler, S.B.; Tatar, O. A comparison of landslide susceptibility mapping of the eastern part of the North Anatolian Fault Zone (Turkey) by likelihood-frequency ratio and analytic hierarchy process methods. Nat. Hazards 2013, 65, 1481–1506. [Google Scholar] [CrossRef]
- Chalkias, C.; Ferentinou, M.; Polykretis, C. GIS supported landslide susceptibility modeling at regional scale: An expert-based fuzzy weighting method. ISPRS Int. J. Geo-Inf. 2014, 3, 523–539. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Application of the Analytical Hierarchy Process (AHP) for landslide susceptibility mapping: A case study from the Tinau watershed, west Nepal. Comput. Geosci. 2013, 52, 398–408. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Moradi, H.R.; Fatemi Aghda, S.M. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. An uncertainty and sensitivity analysis approach for GIS-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 610–638. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Michel, G.P.; Kobiyama, M.; Goerl, R.F. Comparative analysis of SHALSTAB and SINMAP for landslide susceptibility mapping in the Cunha River basin, southern Brazil. J. Soils Sediments 2014, 14, 1266–1277. [Google Scholar] [CrossRef]
- Dahal, R.K.; Bhandary, N.P.; Hasegawa, S.; Yatabe, R. Topo-stress based probabilistic model for shallow landslide susceptibility zonation in the Nepal Himalaya. Environ. Earth Sci. 2014, 71, 3879–3892. [Google Scholar] [CrossRef]
- Wu, X.; Niu, R.; Ren, F.; Peng, L. Landslide susceptibility mapping using rough sets and backpropagation neural networks in the Three Gorges, China. Environ. Earth Sci. 2013, 70, 1307–1318. [Google Scholar] [CrossRef]
- Bi, R.; Schleier, M.; Rohn, J.; Ehret, D.; Xiang, W. Landslide susceptibility analysis based on ArcGIS and Artificial Neural Network for a large catchment in Three Gorges region, China. Environ. Earth Sci. 2014, 72, 1925–1938. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Polykretis, C.; Ferentinou, M.; Chalkias, C. A comparative study of landslide susceptibility mapping using landslide susceptibility index and artificial neural networks in the Krios River and Krathis River catchments (northern Peloponnesus, Greece). Bull. Eng. Geol. Environ. 2015, 74, 27–45. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Sdao, F.; Lioi, D.S.; Pascale, S.; Caniani, D.; Mancini, I.M. Landslide susceptibility assessment by using a neuro-fuzzy model: A case study in the Rupestrian heritage rich area of Matera. Nat. Hazards Earth Syst. Sci. 2013, 13, 395–407. [Google Scholar] [CrossRef]
- Park, I.; Lee, S. Spatial prediction of landslide susceptibility using a decision tree approach: A case study of the Pyeongchang area, Korea. Int. J. Remote Sens. 2014, 35, 6089–6112. [Google Scholar] [CrossRef]
- He, Y.; Beighley, R.E. GIS-based regional landslide susceptibility mapping: A case study in southern California. Earth Surf. Process. Landf. 2008, 33, 380–393. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Mohammadi, M.; Moradi, H.R. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at Haraz watershed. Iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Epifânio, B.; Zêzere, J.L.; Neves, M. Susceptibility assessment to different types of landslides in the coastal cliffs of Lourinhã (Central Portugal). J. Sea Res. 2014, 93, 150–159. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Kumaravel, P.; Rajamanickam, G.V. Assessing landslide susceptibility using Bayesian probability-based weight of evidence model. Bull. Eng. Geol. Environ. 2014, 73, 147–161. [Google Scholar] [CrossRef]
- Youssef, A.M.; Al-Kathery, M.; Pradhan, B. Landslide susceptibility mapping at Al-Hasher Area, Jizan (Saudi Arabia) using GIS-based frequency ratio and index of entropy models. Geosci. J. 2015, 19, 113–134. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Kalivas, D.P.; Skilodimou, H.D. GIS-based landslide susceptibility mapping models applied to natural and urban planning in Trikala, Central Greece. Estud. Geol. 2009, 65, 49–65. [Google Scholar] [CrossRef]
- Bai, S.B.; Wang, J.; Thiebes, B.; Cheng, C.; Chang, Z.Y. Susceptibility assessments of the Wenchuan earthquake-triggered landslides in Longnan using logistic regression. Environ. Earth Sci. 2014, 71, 731–743. [Google Scholar] [CrossRef]
- Reichenbach, P.; Busca, C.; Mondini, A.C.; Rossi, M. The influence of land use change on landslide susceptibility zonation: The Briga catchment test site (Messina, Italy). Environ. Manag. 2014, 54, 1372–1384. [Google Scholar] [CrossRef] [PubMed]
- Bourenane, H.; Bouhadad, Y.; Guettouche, M.S.; Braham, M. GIS-based landslide susceptibility zonation using bivariate statistical and expert approaches in the city of Constantine (Northeast Algeria). Bull. Eng. Geol. Environ. 2015, 74, 337–355. [Google Scholar] [CrossRef]
- Chalkias, C.; Ferentinou, M.; Polykretis, C. GIS-based landslide susceptibility mapping on the Peloponnese Peninsula, Greece. Geosciences 2014, 4, 176–190. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Rajamanickam, V. Landslide susceptibility mapping of Tevankarai Ar sub-watershed, Kodaikkanal taluk, India, using weighted similar choice fuzzy model. Nat. Hazards 2011, 59, 401–425. [Google Scholar] [CrossRef]
- Zhu, A.X.; Wang, R.; Qiao, J.; Qin, C.Z.; Chen, Y.; Liu, J.; Du, F.; Lin, Y.; Zhu, T. An expert knowledge-based approach to landslide susceptibility mapping using GIS and fuzzy logic. Geomorphology 2014, 214, 128–138. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and Analytical Hierarchy Process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Kayastha, P.; Bijukchhen, S.M.; Dhital, M.R.; De Smedt, F. GIS based landslide susceptibility mapping using a fuzzy logic approach: A case study from Ghurmi-Dhad Khola area, eastern Nepal. J. Geol. Soc. India 2013, 82, 249–261. [Google Scholar] [CrossRef]
- Wang, W.D.; Xie, C.M.; Du, X.G. Landslides susceptibility mapping based on geographical information system, GuiZhou, south-west China. Environ. Geol. 2009, 58, 33–43. [Google Scholar] [CrossRef]
- Wang, W.D.; Guo, J.; Fang, L.G.; Chang, X.S. A subjective and objective integrated weighting method for landslides susceptibility mapping based on GIS. Environ. Earth Sci. 2012, 65, 1705–1714. [Google Scholar] [CrossRef]
- Rozos, D.; Bathrellos, G.D.; Skillodimou, H.D. Comparison of the implementation of rock engineering system and analytic hierarchy process methods, upon landslide susceptibility mapping, using GIS: A case study from the Eastern Achaia County of Peloponnesus, Greece. Environ. Earth Sci. 2011, 63, 49–63. [Google Scholar] [CrossRef]
- Kritikos, T.; Davies, T.R.H. GIS-based multi-criteria decision analysis for landslide susceptibility mapping at northern Evia, Greece. Z. Deutsch. Ges. Geowiss. 2011, 162, 421–434. [Google Scholar]
- Kouli, M.; Loupasakis, C.; Soupios, P.; Rozos, D.; Vallianatos, F. Landslide susceptibility mapping by comparing the WLC and WofE multi-criteria methods in the West Crete Island, Greece. Environ. Earth Sci. 2014, 72, 5197–5219. [Google Scholar] [CrossRef]
- Papathanassiou, G.; Valkaniotis, S.; Ganas, A.; Pavlides, S. GIS-based statistical analysis of the spatial distribution of earthquake-induced landslides in the island of Lefkada, Ionian Islands, Greece. Landslides 2013, 10, 771–783. [Google Scholar] [CrossRef]
- Chalkias, C.; Kalogirou, S.; Ferentinou, M. Landslide susceptibility, Peloponnese Peninsula in South Greece. J. Maps 2014, 10, 211–222. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Benardos, A. Estimating landslide susceptibility through an artificial neural network classifier. Nat. Hazards 2014, 74, 1489–1516. [Google Scholar] [CrossRef]
- Gemitzi, A.; Falakakis, G.; Eskioglou, P.; Petalas, C. Evaluating landslide susceptibility using environmental factors, fuzzy membership functions and GIS. Glob. NEST J. 2011, 13, 28–40. [Google Scholar]
- Ferentinou, M.; Chalkias, C. Mapping mass movement susceptibility across Greece with GIS, ANN and statistical methods. Landslide Sci. Pract. 2013, 321–327. [Google Scholar]
- Sabatakakis, N.; Koukis, G.; Vassiliades, E.; Lainas, S. Landslide susceptibility zonation in Greece. Nat. Hazards 2013, 65, 523–543. [Google Scholar] [CrossRef]
- Gournellos, T.; Chalkias, C.; Tsagas, D. Landslide susceptibility zonation of Greece using fuzzy logic and GIS. Geographies 2006, 12, 114–126. [Google Scholar]
- Hellenic Statistical Authority (ELSTAT). Population and Housing Census: Resident Population; ELSTAT: Piraeus, Greece, 2011. [Google Scholar]
- Pnevmatikos, J.D.; Katsoulis, B.D. The changing rainfall regime in Greece and its impact on climatological means. Meteorol. Appl. 2006, 13, 331–345. [Google Scholar] [CrossRef]
- Koukis, G.; Tsiambaos, G.; Sabatakakis, N. Landslides movements in Greece: Engineering geologicalcharacteristics and environmental consequences. In Proceedings of the 7th International Symposium of Engineering Geology and Environment, Athens, Greece, 23–27 June 1997; Volume 1, pp. 789–792.
- Hellenic Military Geographical Service (HMGS). Aerial Photography of Various Areas of Greece, Scale 1:40,000; HMGS: Athens, Greece, 1969. [Google Scholar]
- Che, V.B.; Kervyn, M.; Suh, C.E.; Fontijn, K.; Ernst, G.G.J.; del Marmol, M.A.; Trefois, P.; Jacobs, P. Landslide susceptibility assessment in Limbe (SW Cameroon): A field calibrated seed cell and information value method. Catena 2012, 92, 83–98. [Google Scholar] [CrossRef]
- De Guidi, G.; Scudero, S. Landslide susceptibility assessment in the Peloritani Mts. (Sicily, Italy) and clues for tectonic control of relief processes. Nat. Hazards Earth Syst. Sci. 2013, 13, 949–963. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pradhan, B.; Pourghasemi, H.R.; Abdullahi, S. Landslide susceptibility assessment at Wadi Jawrah Basin, Jizan region, Saudi Arabia using two bivariate models in GIS. Geosci. J. 2015, 19, 449–469. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides: Investigation and Mitigation, Special Report; Turner, A.K., Schuster, R.L., Eds.; National Academy Press: Washington, DC, USA, 1996. [Google Scholar]
- Fell, R. Landslide risk assessment and acceptable risk. Can. Geotech. J. 1994, 31, 261–272. [Google Scholar] [CrossRef]
- Magliulo, P.; Lisio, A.; Russo, F.; Zelano, A. Geomorphology and landslide susceptibility assessment using GIS and bivariate statistics: A case study in southern Italy. Nat. Hazards 2008, 47, 411–435. [Google Scholar] [CrossRef]
- Das, O.; Sonmez, H.; Gokceoglu, C.; Nefeslioglu, H. A study on the effect of the ground acceleration on landslide susceptibility maps. Geophys. Res. Abstr. 2010, 12, EGU2010-5885-1. [Google Scholar]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Hasekioǧullari, G.D.; Ercanoglu, M. A new approach to use AHP in landslide susceptibility mapping: A case study at Yenice (Karabuk, NW Turkey). Nat. Hazards 2012, 63, 1157–1179. [Google Scholar] [CrossRef]
- Heymann, Y.; Steenmans, C.; Croisille, G.; Bossard, M. CORINE Land Cover: Technical Guide; Office for Official Publications of the European Communities: Luxembourg City, Luxembourg, 1994. [Google Scholar]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS techniques and statistical models in evaluating landslide hazard. Earth Surf. Process. Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Institute of Geology and Mineral Exploration (IGME). Geological Map of Greece, Scale 1:500,000, 2nd ed.; IGME: Athens, Greece, 1983. [Google Scholar]
- Underhill, J.R. Late Cenozoic deformation of the Hellenide foreland, western Greece. Geol. Soc. Am. Bull. 1989, 101, 613–634. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Rahmani, M.; Hosieni, S.A.; Molla Aghajanzadeh, A.; Mashayekhan, A.; Mahalleh, S.M.M. Landslide hazard zonation using the MCE method (Case study: Agh Mashhad, Mazandaran Province, Iran). Int. J. AgriSci. 2013, 3, 240–244. [Google Scholar]
- Ahmed, M.F.; Rogers, J.D.; Ismail, E.H. A regional level preliminary landslide susceptibility study of the upper Indus river basin. Eur. J. Remote Sens. 2014, 47, 343–373. [Google Scholar] [CrossRef]
- Sato, H.P.; Hasegawa, H.; Fujiwara, S.; Tobita, M.; Koarai, M.; Une, H.; Iwahashi, J. Interpretation of landslide distribution triggered by the 2005 Northern Pakistan earthquake using SPOT 5 imagery. Landslides 2007, 4, 113–122. [Google Scholar] [CrossRef]
- Owen, L.A.; Kamp, U.; Khattak, G.A.; Harp, E.L.; Keefer, D.K.; Bauer, M.A. Landslides triggered by the 8 October 2005 Kashmir earthquake. Geomorphology 2008, 94, 1–9. [Google Scholar] [CrossRef]
- Huade, G.; Wilson, J.L.; Makhnin, O. Geostatistical mapping of mountain precipitation incorporating autosearched effects of terrain and climatic characteristics. J. Hydrometeorol. 2005, 6, 1018–1031. [Google Scholar]
- Arjun, C.R.; Kumar, A. Artificial neural network-based estimation of peak ground acceleration. ISET J. Earthq. Technol. 2009, 46, 19–28. [Google Scholar]
- Stournaras, G.; Tsimpidis, G.; Tsoumanis, P.; Yannatos, G.; Guillande, R. Instability Phenomena in the Neogenne Deposits of Northern Peloponnese. Bull. Eng. Geol. Environ. 1998, 57, 65–68. [Google Scholar] [CrossRef]
- Papathanassiou, G. Estimating slope failure potential in an earthquake prone area: A case study at Skolis Mountain, NW Peloponnesus, Greece. Bull. Eng. Geol. Environ. 2012, 71, 187–194. [Google Scholar] [CrossRef]
- Dounias, G.; Fikiris, I.F.; Kollios, A.; Kabbadas, M.; Marinos, P. The Nemea Landslide. Trigger Mechanism–Remedial Measures. In Proceedings of the 5th Panellenic Conference of Geotechnics and Geoenvironmental Engineering, Xanthi, Greece, 31 May–2 June 2006.
- Papadopoulos, G.A.; Plessa, A. Magnitude-distance relations for earthquake-induced landslides in Greece. Eng. Geol. 2000, 58, 377–386. [Google Scholar] [CrossRef]
- Chousianitis, K.; Del Gaudio, V.; Sabatakakis, N.; Kavoura, K.; Drakatos, G.; Bathrellos, G.D.; Skilodimou, H.D. Assessment of earthquake-induced landslide hazard in Greece: From Arias Intensity to spatial distribution of slope resistance demand. Bull. Seismol. Soc. Am. 2016. [Google Scholar] [CrossRef]
- Van Westen, C.J. Statistical landslide hazard analysis. In ILWIS 2.1 for Windows Application Guide; ITC Publication: Utrecht, The Netherlands, 1997; pp. 73–84. [Google Scholar]
- Jenks, G.F. The data model concept in statistical mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Lee, E.M.; Jones, D.K.C. Landslide Risk Assessment; Thomas Telford: London, UK, 2004; p. 161. [Google Scholar]
- Malczewski, J. GIS and Multicriteria Decision Analysis; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Remondo, J.; González-Díez, A.; Díaz de Terán, J.R.; Cendrero, A. Landslide susceptibility models utilizing spatial data analysis techniques. A case study from the Lower Deba Valley, Guipúzcoa (Spain). Nat. Hazards 2003, 30, 267–279. [Google Scholar] [CrossRef]
- Nandi, A.; Shakoor, A. Preparation of a landslide susceptibility map of summit county, Ohio, USA, using numerical models. In Proceedings of the 10th IAEG Congress, Nottingham, UK, 6–10 September 2006.
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Dragićević, S.; Lai, T.; Balram, S. GIS-based multicriteria evaluation with multiscale analysis to characterize urban landslide susceptibility in data-scarce environments. Habitat Int. 2015, 45, 114–125. [Google Scholar] [CrossRef]
- Faraji Sabokbar, H.; Shadman Roodposhti, M.; Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Yang, Z.H.; Lan, H.X.; Gao, X.; Li, L.P.; Meng, Y.S.; Wu, Y.M. Urgent landslide susceptibility assessment in the 2013 Lushan earthquake-impacted area, Sichuan Province, China. Nat. Hazards 2015, 75, 2467–2487. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Rengers, N.; Terlien, M.T.J.; Soeters, R. Prediction of the occurrence of slope instability phenomena through GIS-based hazard zonation. Geol. Rundsch. 1997, 86, 404–414. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H.; Maruib, H.; Takami, K. Landslides in Sado Island of Japan: Part II. GIS-based susceptibility mapping with comparisons of results from two methods and verifications. Eng. Geol. 2005, 81, 432–445. [Google Scholar] [CrossRef]
- Tien Bui, D.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the Hoa Binh province of Vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413–1444. [Google Scholar]
- Van Westen, C.J.; Rengers, N.; Soeters, R. Use of geomorphological information in indirect landslide susceptibility assessment. Nat. Hazards 2003, 30, 399–419. [Google Scholar] [CrossRef]
- Saboya, F., Jr.; da Glória Alves, M.; Dias Pinto, W. Assessment of failure susceptibility of soil slopes using fuzzy logic. Eng. Geol. 2006, 86, 211–224. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Gaki-Papanastassiou, K.; Skilodimou, H.D.; Papanastassiou, D.; Chousianitis, K.G. Potential suitability for urban planning and industry development by using natural hazard maps and geological—Geomorphological parameters. Environ. Earth Sci. 2012, 66, 537–548. [Google Scholar] [CrossRef]
- Rozos, D.; Skilodimou, H.D.; Loupasakis, C.; Bathrellos, G.D. Application of the revised universal soil loss equation model on landslide prevention. An example from N. Euboea (Evia) Island, Greece. Environ. Earth Sci. 2013, 70, 3255–3266. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).