Snow Depth Retrieval with UAS Using Photogrammetric Techniques
Abstract
:1. Introduction
1.1. The Need for Accurate Depth Estimates of Snow Depths and Existing Methods
1.2. Use of Micro Unmanned Aerial Systems (UAS)
1.3. Prior Photogrammetric Efforts for Snow Depth Retrieval
2. Study Area and Data
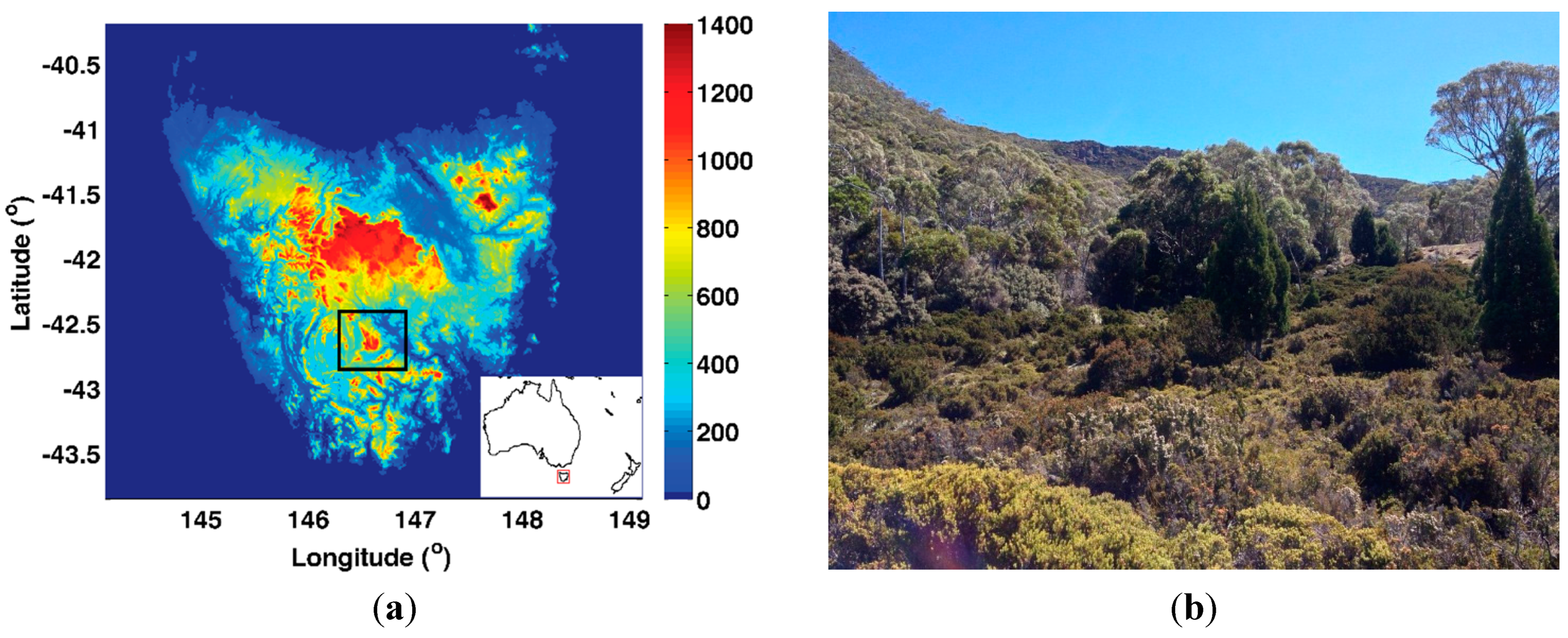

| Platform/Sensor | Indirect Bundle Adjustment | Price (USD) |
|---|---|---|
| Manufacturer/Model | ||
| UAS | Droidworx SkyJiB | |
| Camera | Canon 550D DSLR | |
| Total Cost | $10,900 | |
| UAS | Droidworx SkyJiB | |
| Camera | Canon 550D DSLR | |
| IMU | Microstrain 3DM-GX3 35 | |
| Computer | Gumstix Verdex Pro | |
| GNSS Antenna | Maxtenna L1/L2 helical | |
| GNSS Receiver | Novatel OEMV1-df | |
| Total Cost | $17,900 |
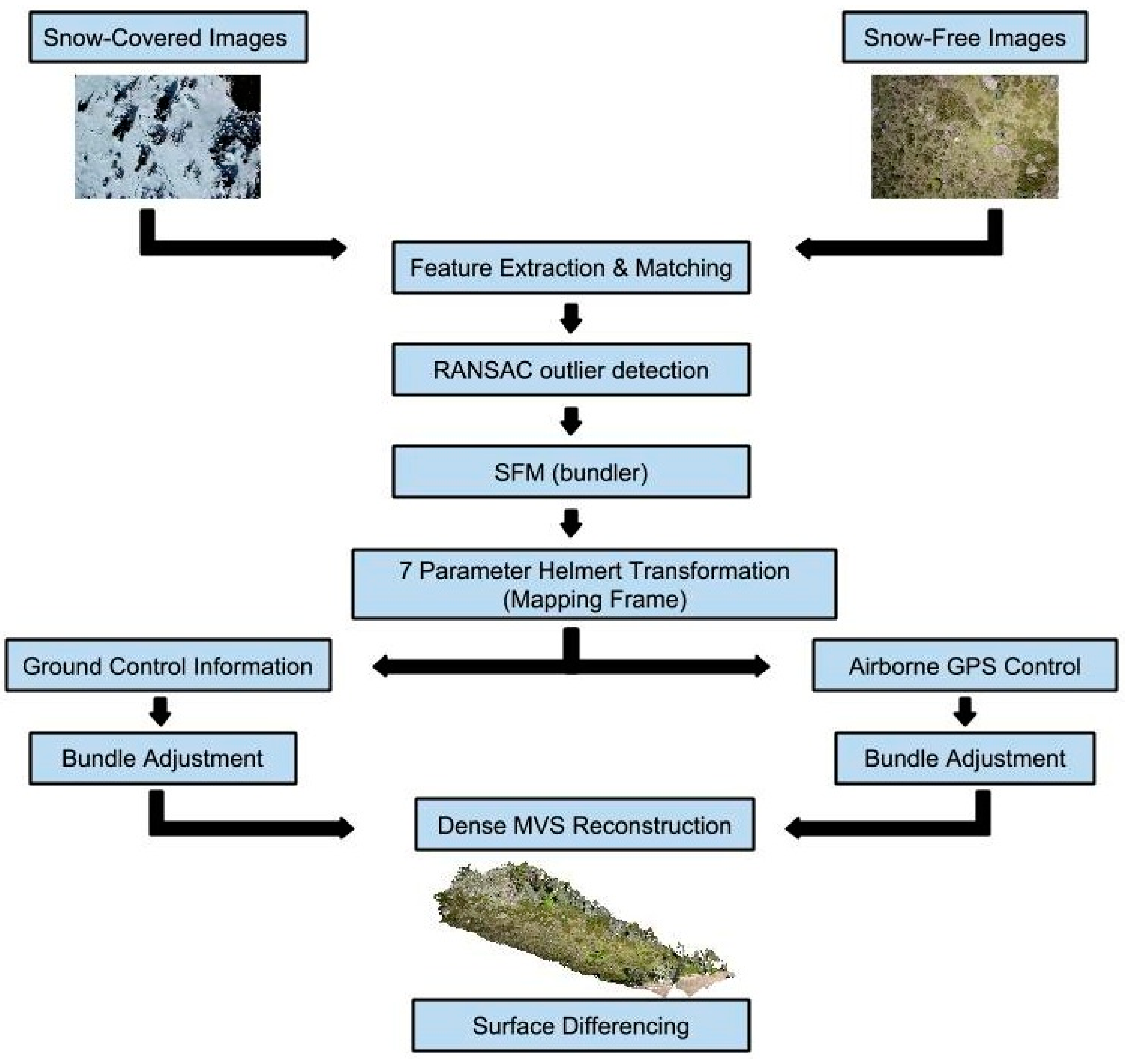
3. Methods
3.1. Photogrammetric Reconstruction
- xim, yim—measured image coordinates
- f—focal length
- Xo, Yo , Zo—Cartesian coordinates of camera perspective center
- XA, YA, ZA—Cartesian coordinates of object point A
- rij—elements of rotation matrix R of angles (ɷ, ɸ, к)
| Observation | Indirect (1σ) | Direct (1σ) |
|---|---|---|
| Xo, Yo, Zo (UAS GNSS) | 1 m | 0.03 m |
| X, Y, Z (GCP) | 0.02 m | none |
| ɷ, ɸ, к | 2° | 2° |
| xo, yo | 3 pixels | 3 pixels |
| f | 3 pixels | 2 pixels |
| k1, k2 | 0.1 pixels | 0.1 pixels |
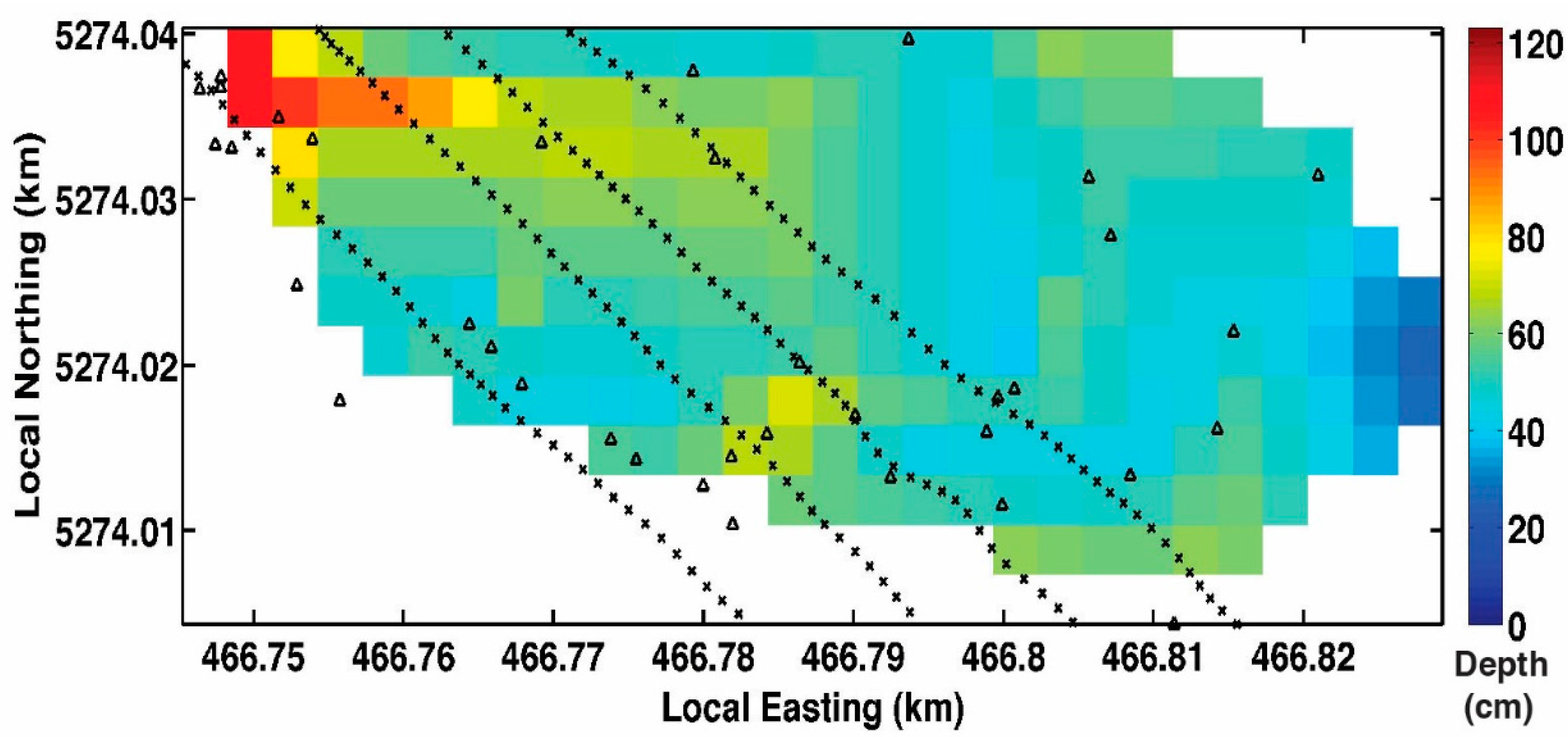
3.2. Error Sources: Snow and Vegetation
4. Results
4.1. Predicted Snow Depth Accuracy

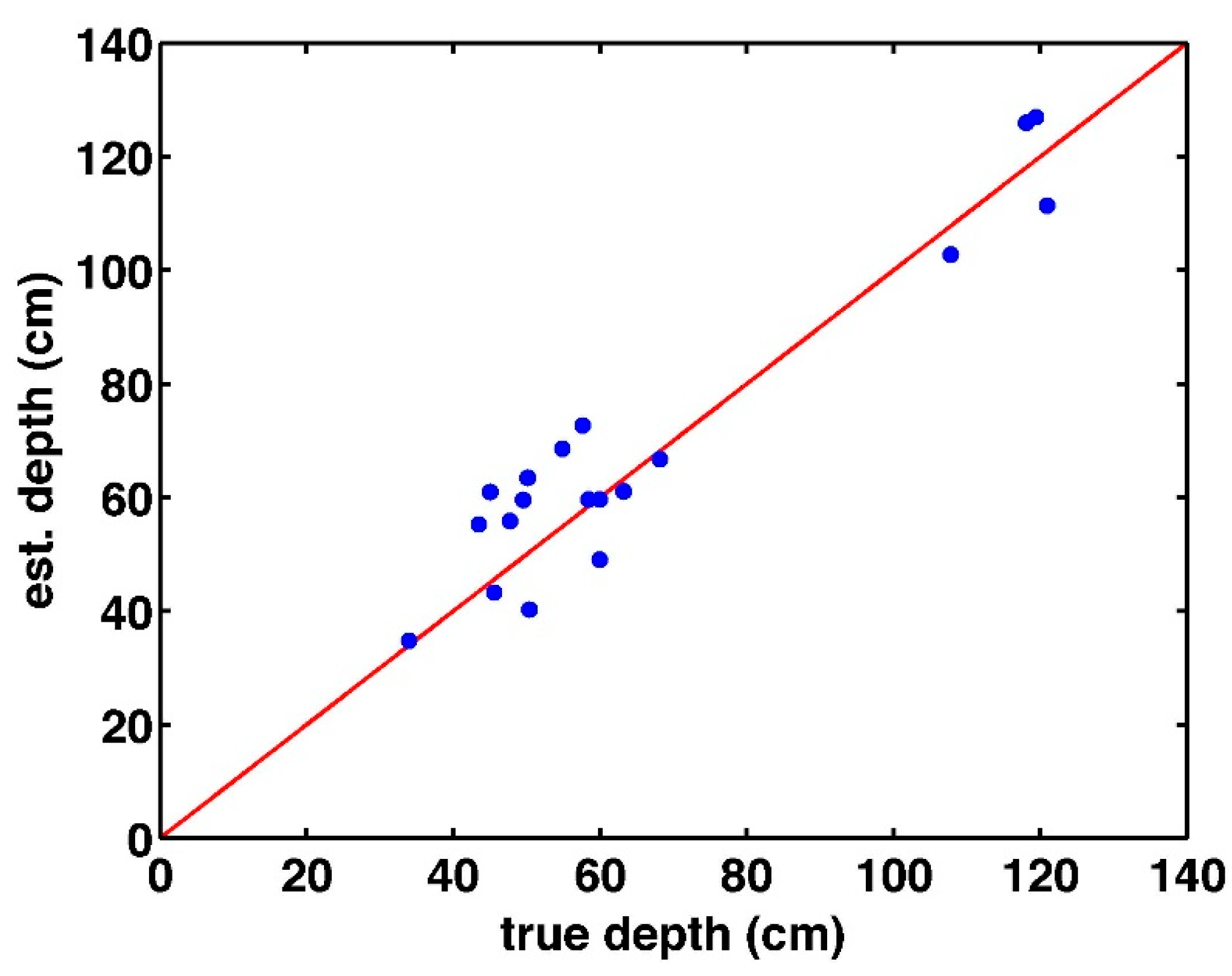
4.2. Snow Depth via Conventional BA with GCPs
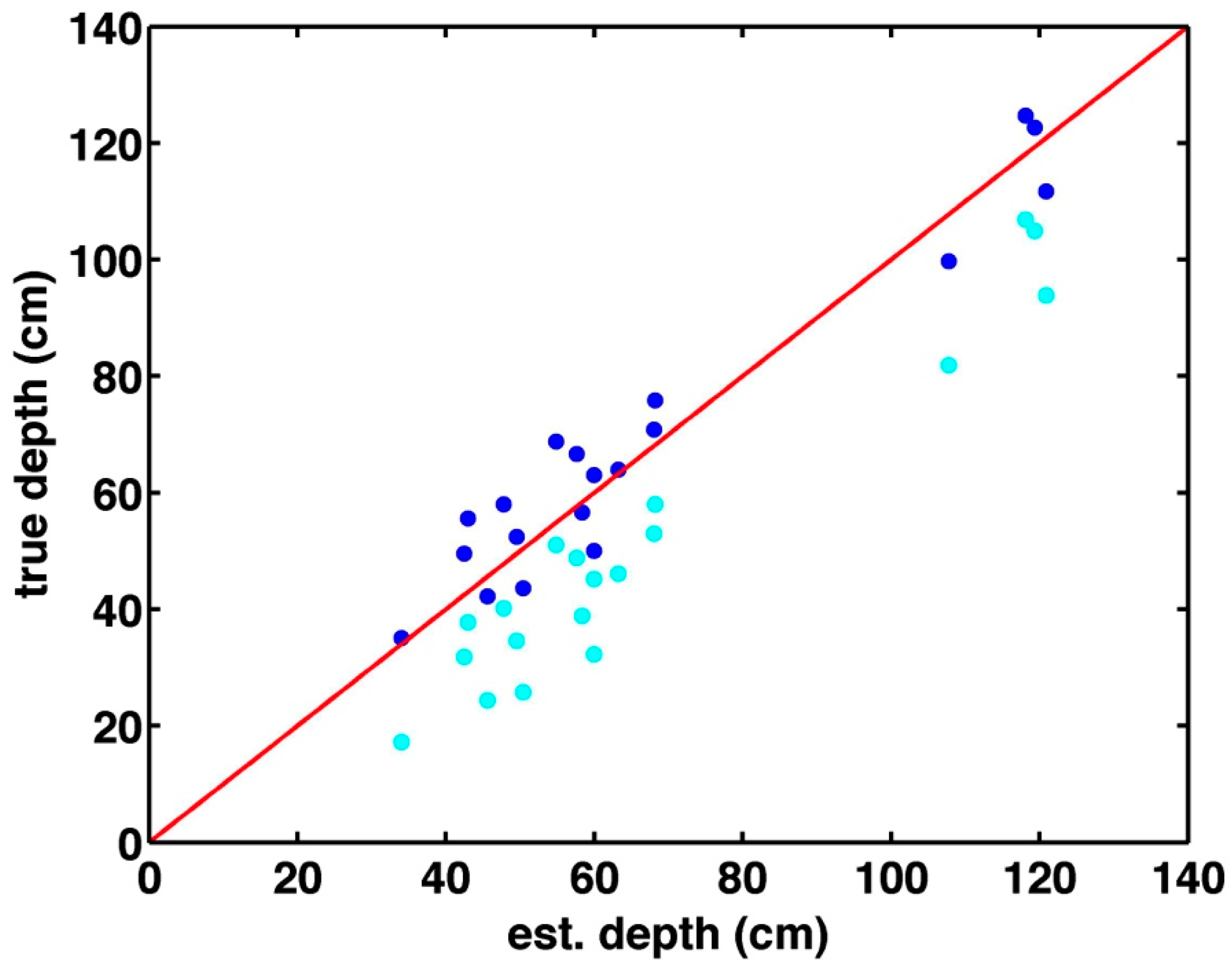
4.3. Snow Depth via Direct BA Using Airborne GPS
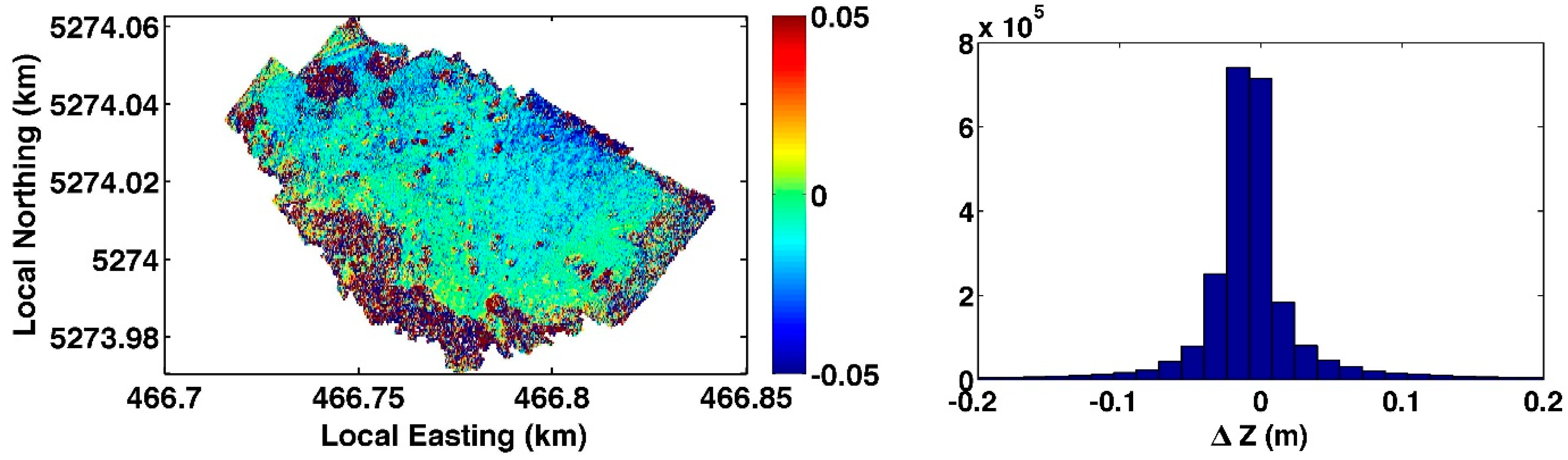
4.4. Co-Registration Using Affine Transformation

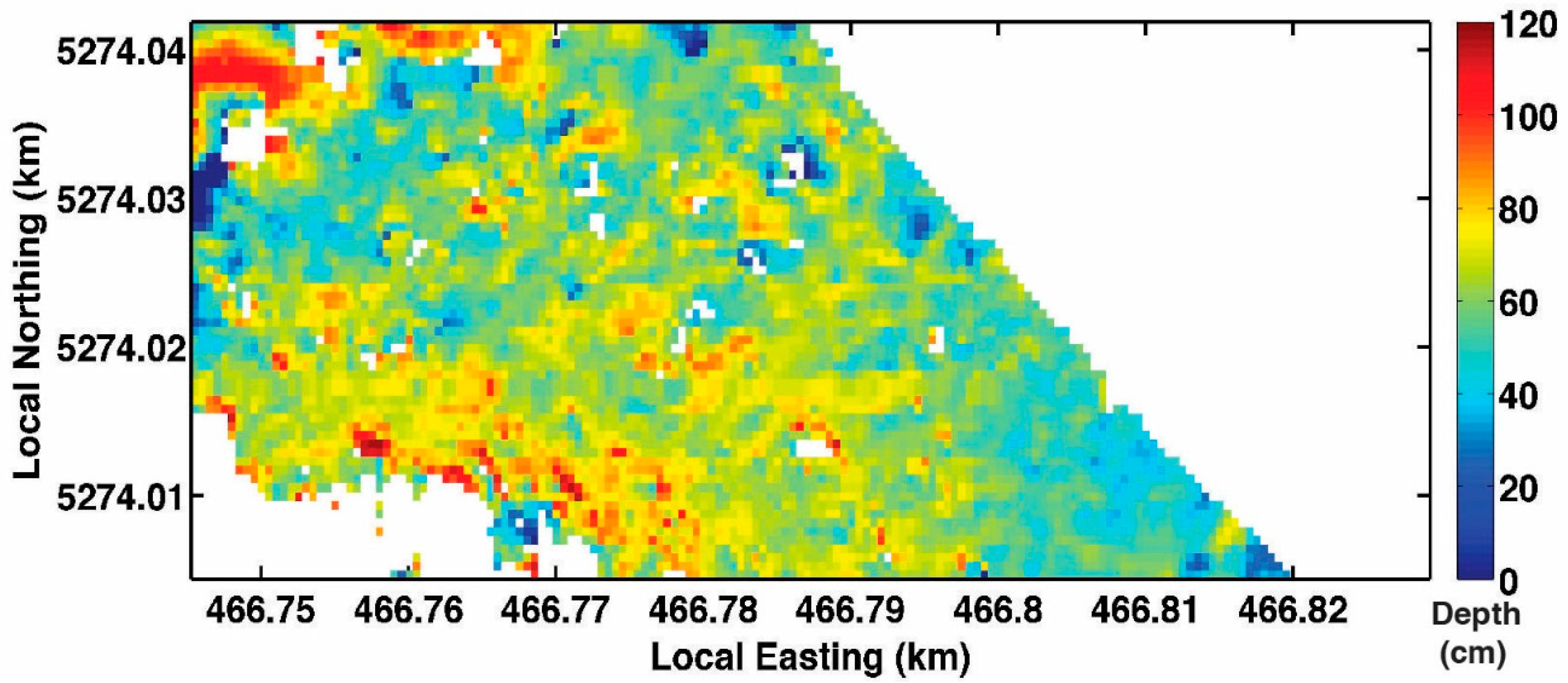
4.5. High-Resolution Snow Depth Estimates
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.I.A.; Moore, D.J.; Burns, S.P.; Monson, R.K. Longer growing seasons lead to less carbon sequestration by a subalpine forest. Glob. Chang. Biol. 2010, 16, 771–783. [Google Scholar] [CrossRef]
- Peck, E.L. Snow measurement predicament. Water Resour. Res. 1972, 8, 244–248. [Google Scholar] [CrossRef]
- Hall, D.K.; Sturm, M.; Benson, C.S.; Chang, A.T.C.; Foster, J.L.; Garbeil, H.; Chacho, E. Passive microwave remote and in situ measurements of artic and subarctic snow covers in Alaska. Remote Sens. Environ. 1991, 38, 161–172. [Google Scholar] [CrossRef]
- Erxleben, J.; Elder, K.; Davis, R. Comparison of spatial interpolation methods for estimating snow distribution in the Colorado Rocky Mountains. Hydrol. Process. 2002, 16, 3627–3649. [Google Scholar] [CrossRef]
- Chang, A.T.C.; Foster, J.L.; Hall, D.K. Nimbus-7 SMMR derived global snow cover parameters. Ann. Glaciol. 1987, 9, 39–44. [Google Scholar]
- Foster, J.L.; Hall, D.K.; Chang, A.T.C.; Rango, A. An overview of passive microwave snow research and results. Rev. Geophys. 1984, 22, 195–208. [Google Scholar] [CrossRef]
- Foster, J.L.; Chang, A.T.C.; Hall, D.K. Comparison of snow mass estimates from a prototype passive microwave snow algorithm, a revised algorithm and a snow depth climatology. Remote Sens. Environ. 1997, 62, 132–142. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Vander Jagt, B.J.; Durand, M.T.; Margulis, S.A.; Kim, E.J.; Molotch, N.P. The effect of spatial variability on the sensitivity of passive microwave measurements to snow water equivalent. Remote Sens. Environ. 2013, 136, 163–179. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Eisenbeiss, H.; Zhang, L. Comparison of DSMs generated from mini UAS imagery and terrestrial laser scanner in a cultural heritage application. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 90–96. [Google Scholar]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Lucieer, A.; de Jong, S.; Turner, D. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAS photography. Progress Phys. Geogr. 2013. [Google Scholar] [CrossRef]
- Ryan, J.C.; Hubbard, A.L.; Todd, J.; Carr, J.R.; Box, J.E.; Christoffersen, P.; Snooke, N. Repeat UAV photogrammetry to assess calving front dynamics at a large outlet glacier draining the Greenland Ice Sheet. Cryosphere Discuss. 2014, 8, 2243–2275. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAS-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAS) imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- Tao, W.; Lei, Y.; Mooney, P. Dense point cloud extraction from UAV captured images in forest area. In Proceedings of the 2011 IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM), Fuzhou, China, 29 June–1 July 2011; pp. 389–392.
- Cooper, C.F. Snow cover measurement. Photogramm. Eng. 1965, 31, 611–619. [Google Scholar]
- Smith, F.M.; Cooper, C.F.; Chapman, E.G. Measuring Snow Depths by Aerial Photography. In Proceedings of the 35th Annual Western Snow Conference, Boise, ID, USA, 18–20 April 1967; pp. 66–72.
- Nolan, M.; Larsen, C.F.; Sturm, M. Mapping snow-depth from manned-aircraft on landscape scales at centimeter resolution using Structure-from-Motion photogrammetry. Cryosphere Discuss. 2015, 9, 333–381. [Google Scholar] [CrossRef]
- Ledwith, M.; Lundén, B. Digital photogrammetry for air-photo-based construction of a digital elevation model over snow-covered areas-Blamannsisen, Norway. Nor. J. Geogr. 2001, 55, 267–273. [Google Scholar] [CrossRef]
- Ebadi, H. A Comprehensive Study on GPS-Assisted Aerial Triangulation. Ph.D. Dissertation, University of Calgary, Calgary, AB, Canada, 1997. [Google Scholar]
- Cramer, M.; Stallmann, D.; Haala, N. Direct georeferencing using GPS/inertial exterior orientations for photogrammetric applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2000, 33, 198–205. [Google Scholar]
- Mostafa, M.M.; Schwarz, K.P. Digital image georeferencing from a multiple camera system by GPS/INS. ISPRS J. Photogramm. Remote Sens. 2001, 56, 1–12. [Google Scholar] [CrossRef]
- Lee, C.Y.; Jones, S.D.; Bellman, C.J.; Buxton, L. DEM creation of a snow covered surface using digital aerial photography. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 18–27. [Google Scholar]
- Lemmon, T.R.; Gerdan, G.P. The Influence of the Number of Satellites on the Accuracy of RTK GPS Positions. Aust. Surv. 1990, 44, 64–70. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct georeferencing of ultrahigh-resolution UAV imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Wan, E.A. Sigma-point Kalman filters for integrated navigation. In Proceedings of the 60th Annual Meeting of the Institute of Navigation, Dayton, OH, USA, 7–9 June 2004; pp. 641–654.
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley & Sons Inc.: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Brown, D. Close-range camera calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Triggs, B.; McLauchlan, P.F.; Hartley, R.I.; Fitzgibbon, A.W. Bundle adjustment—A modern synthesis. In Vision Algorithms: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2000; pp. 298–372. [Google Scholar]
- Zhang, L.; Gruen, A. Multi-image matching for DSM generation from IKONOS imagery. ISPRS J. Photogramm. Remote Sens. 2006, 60, 195–211. [Google Scholar] [CrossRef]
- Scambos, T.A.; Dutkiewicz, M.J.; Wilson, J.C.; Bindschadler, R.A. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157.
- Snavely, N.; Seitz, S.M.; Szeliski, R. Photo tourism: Exploring photo collections in 3D. ACM Trans. Graph. 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Nistér, D. Preemptive RANSAC for live structure and motion estimation. Mach. Vis. Appl. 2005, 16, 321–329. [Google Scholar] [CrossRef]
- Brown, D.C. The bundle adjustment—Progress and prospects. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 1976, 21, 1. [Google Scholar]
- Huang, T.S.; Netravali, A.N. Motion and structure from feature correspondences: A review. Proc. IEEE 2004, 82, 252–268. [Google Scholar] [CrossRef]
- Agarwal, S.; Snavely, N.; Seitz, S.M.; Szeliski, R. Bundle adjustment in the large. In Computer Vision–ECCV 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 29–42. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Rio de Janeiro, Brazil, 17–22 June 2006; Volume 1, pp. 519–528.
- Furukawa, Y.; Ponce, J. Accurate, dense, and robust multiview stereopsis. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1362–1376. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.S.; Hudak, A.T. A multiscale curvature algorithm for classifying discrete return Lidar in forested environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Efron, B.; Gong, G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. 1983, 37, 36–48. [Google Scholar]
- Howat, I.M.; Smith, B.E.; Joughin, I.; Scambos, T.A. Rates of southeast Greenland ice volume loss from combined ICESat and ASTER observations. Geophys. Res. Lett. 2008, 35, L17505. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A. Radiance assimilation shows promise for snowpack characterization. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating snow water equivalent using snow depth data and climate classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vander Jagt, B.; Lucieer, A.; Wallace, L.; Turner, D.; Durand, M. Snow Depth Retrieval with UAS Using Photogrammetric Techniques. Geosciences 2015, 5, 264-285. https://doi.org/10.3390/geosciences5030264
Vander Jagt B, Lucieer A, Wallace L, Turner D, Durand M. Snow Depth Retrieval with UAS Using Photogrammetric Techniques. Geosciences. 2015; 5(3):264-285. https://doi.org/10.3390/geosciences5030264
Chicago/Turabian StyleVander Jagt, Benjamin, Arko Lucieer, Luke Wallace, Darren Turner, and Michael Durand. 2015. "Snow Depth Retrieval with UAS Using Photogrammetric Techniques" Geosciences 5, no. 3: 264-285. https://doi.org/10.3390/geosciences5030264
APA StyleVander Jagt, B., Lucieer, A., Wallace, L., Turner, D., & Durand, M. (2015). Snow Depth Retrieval with UAS Using Photogrammetric Techniques. Geosciences, 5(3), 264-285. https://doi.org/10.3390/geosciences5030264








