Dynamic Process of Dry Snow Slab Avalanche Formation: Theory, Experiment and Numerical Simulation
Abstract
1. Introduction
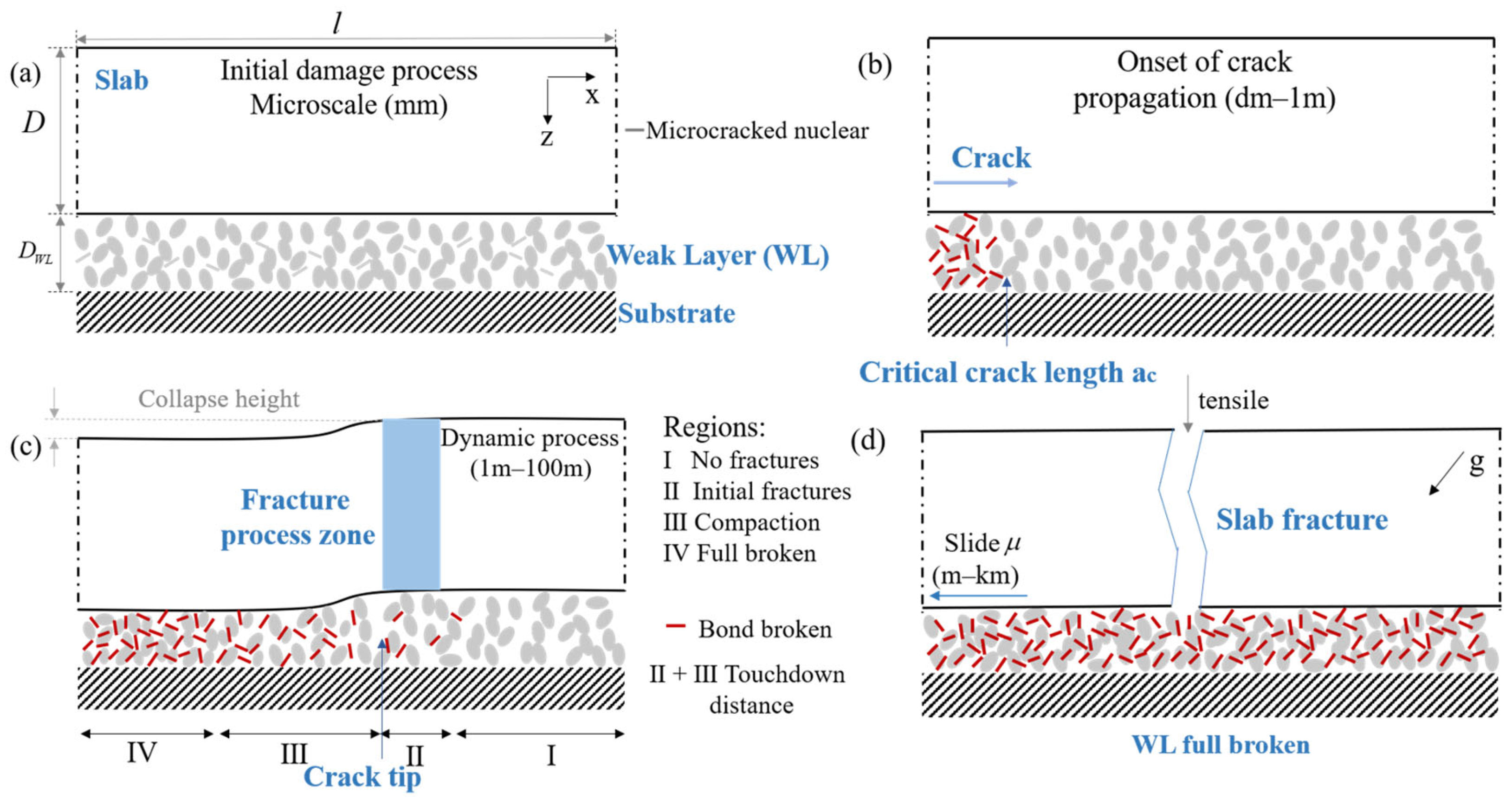
2. Dynamic Processes of Avalanche Formation
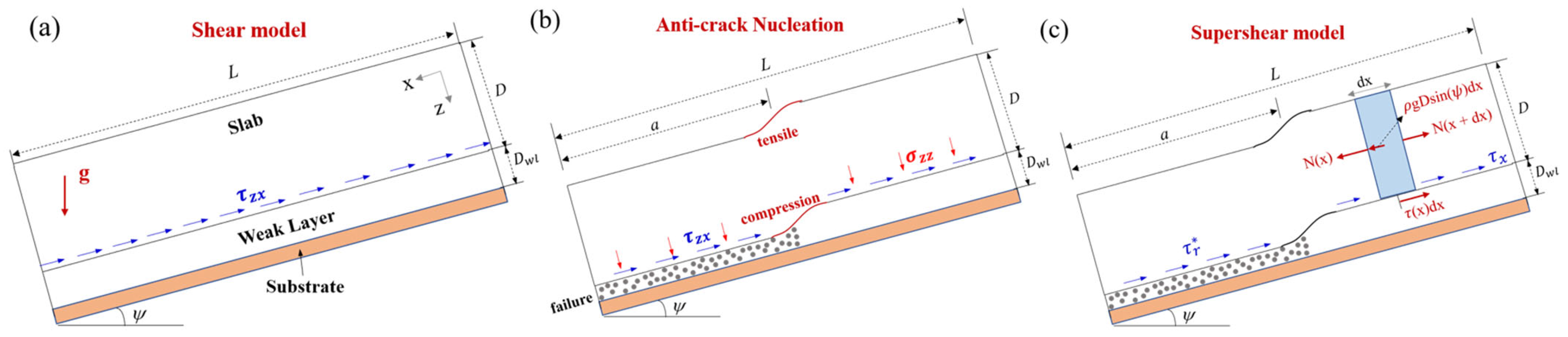
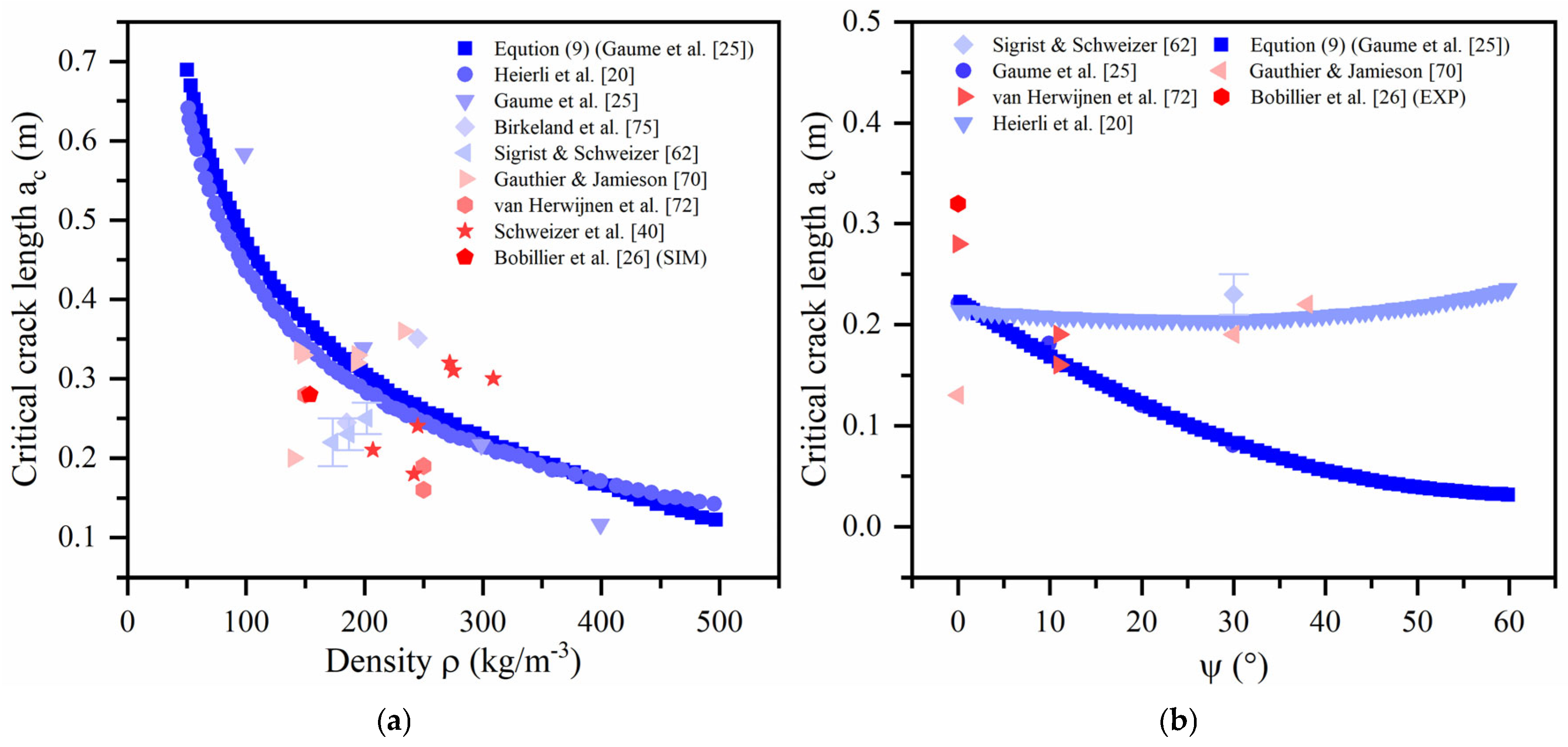
2.1. Critical Crack Length
2.2. Crack Propagation Speed
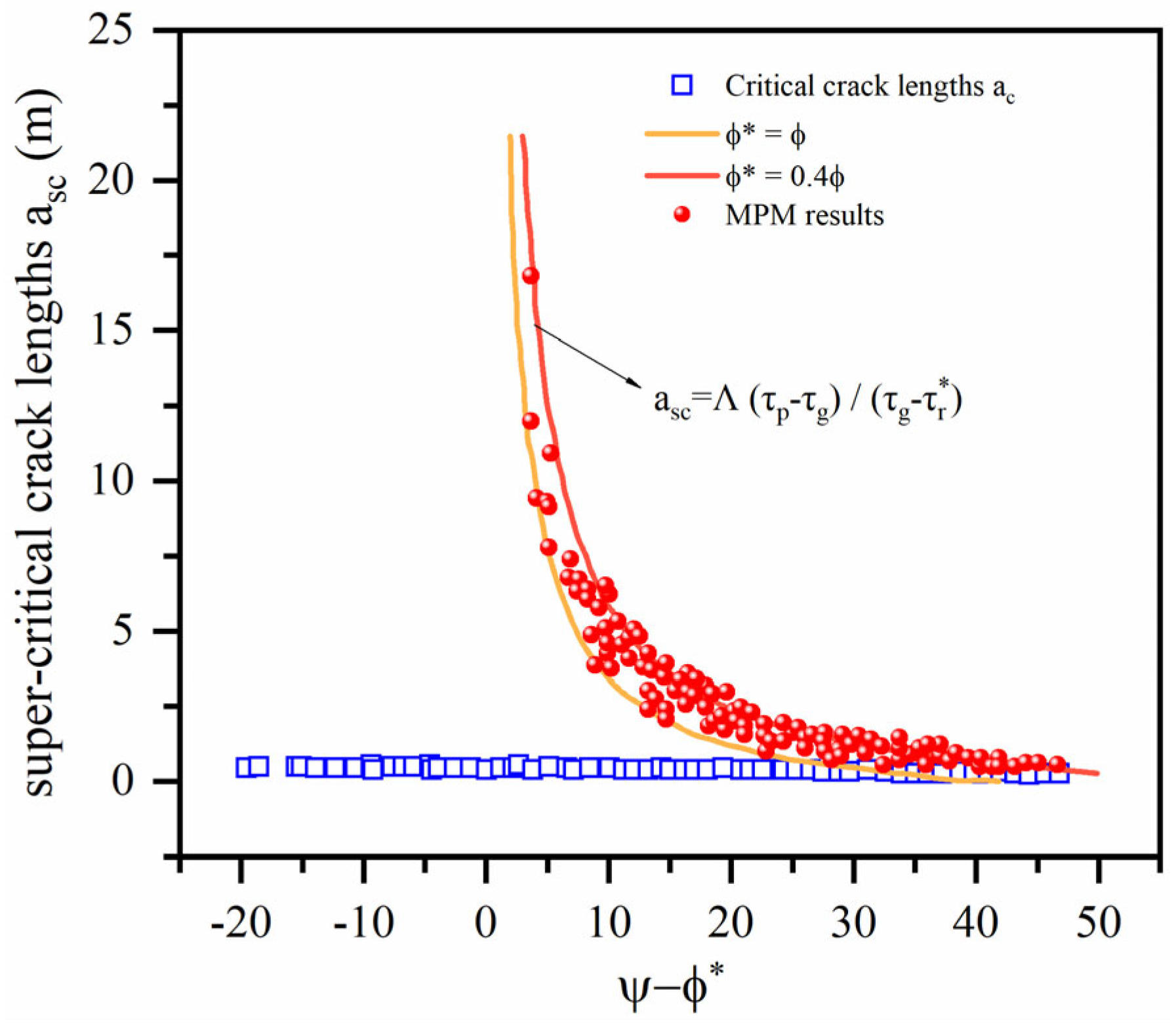
2.3. Crack Arrest and Propagation Distance
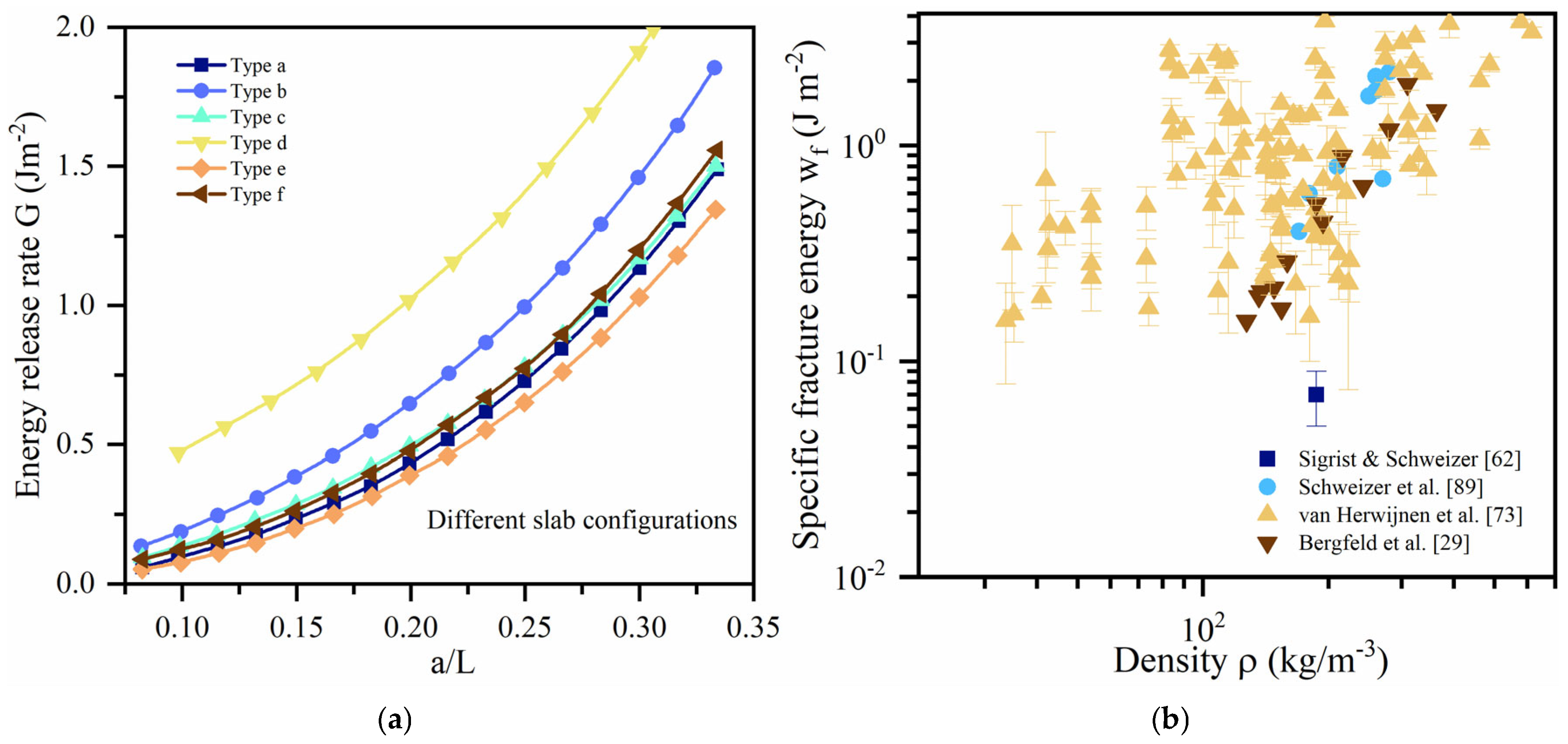
2.4. Energy Release Rate and Specific Fracture Energy
3. Numerical Modelling
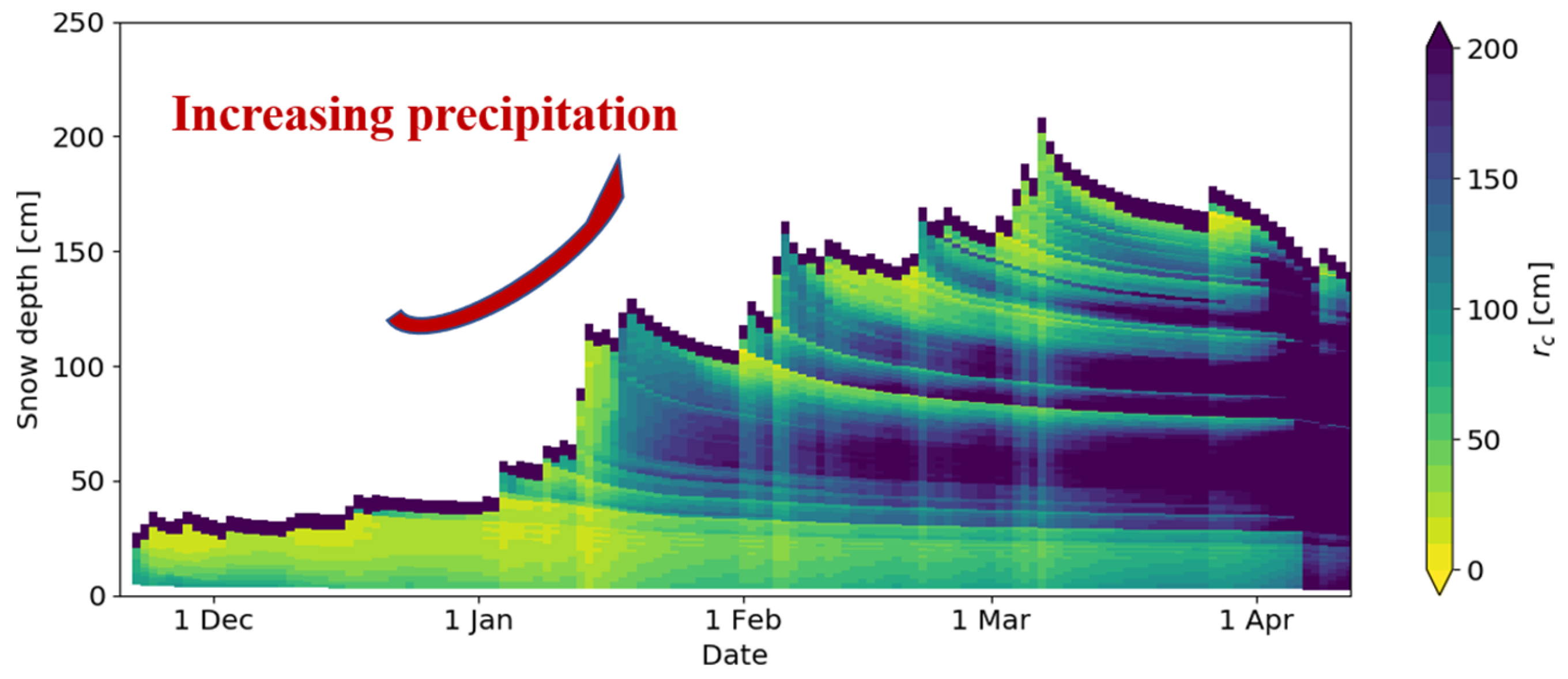
3.1. FEM and SNOWPACK
3.2. DEM and MPM
4. Discussion
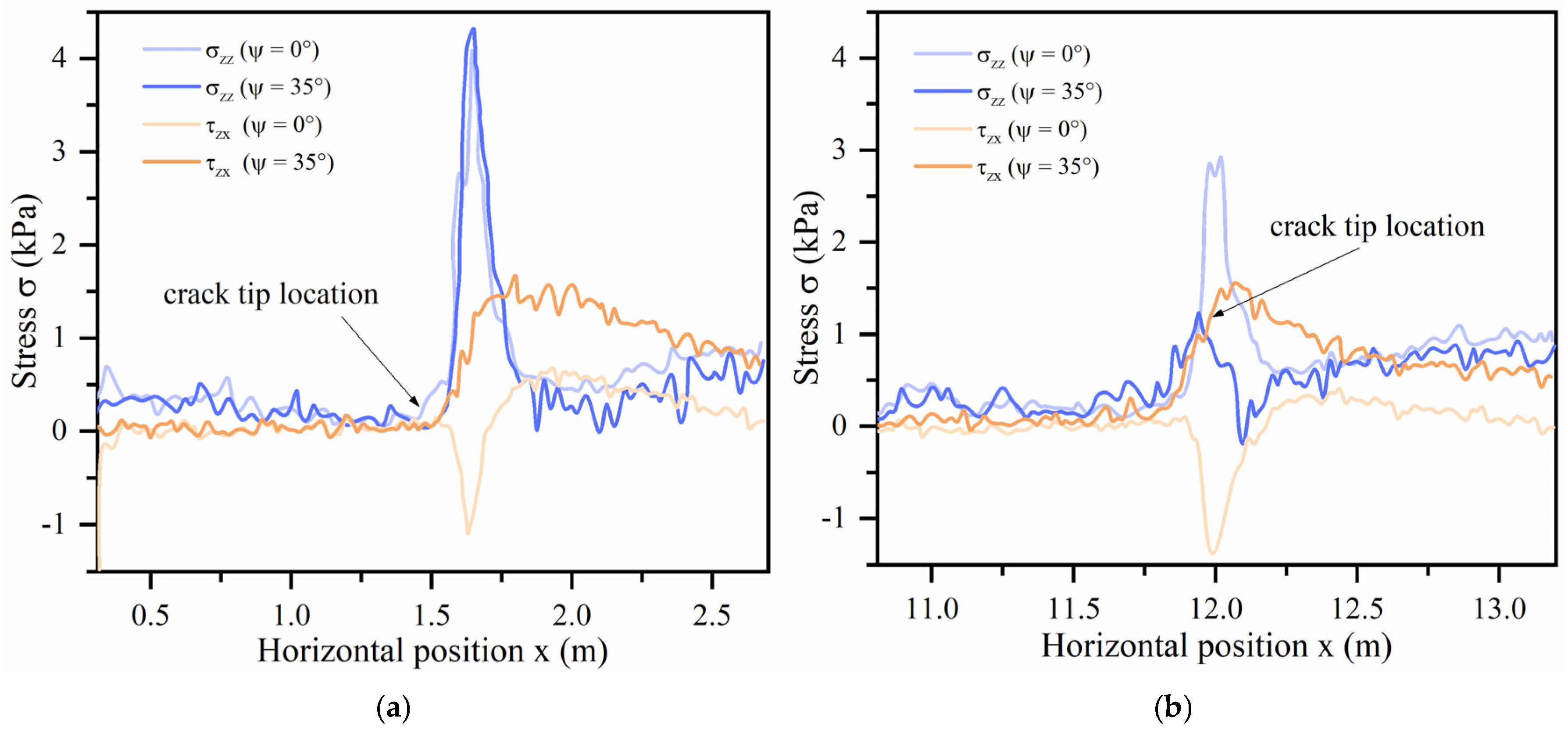
4.1. The Stress Pattern of Avalanche Formation
4.2. The Response of Critical Crack Length to Slope Angle
4.3. Towards a Unified Model of Avalanche Formation and Avalanche Flow
5. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Huang, N. Numerical simulation of the falling snow deposition over complex terrain. J. Geophys. Res. 2017, 122, 980–1000. [Google Scholar] [CrossRef]
- Hao, X.; Luo, S.; Che, T.; Wang, J.; Li, H.; Dai, L.; Feng, Q. Accuracy assessment of four cloud-free snow cover products over the Qinghai-Tibetan Plateau. Int. J. Digit. Earth 2019, 12, 375–393. [Google Scholar] [CrossRef]
- Huang, N.; Shao, Y.; Zhou, X.; Fan, F. Snow and ice disaster: Formation mechanism and control engineering. Front. Earth Sci. 2023, 10, 1019745. [Google Scholar] [CrossRef]
- Hao, J.; Cui, P.; Zhang, X.; Li, L. The triggering mechanisms for different types of snow avalanches in the continental snow climate of the central Tianshan Mountains. Sci. China Earth Sci. 2022, 65, 2308–2321. [Google Scholar] [CrossRef]
- Hao, J.; Zhang, X.; Cui, P.; Li, L.; Wang, Y.; Zhang, G.; Li, C. Impacts of climate change on snow avalanche activity along a transportation corridor in the Tianshan Mountains. Int. J. Disaster Risk Sci. 2023, 14, 510–522. [Google Scholar] [CrossRef]
- Schweizer, J.; Bruce Jamieson, J.; Schneebeli, M. Snow avalanche formation. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Schweizer, J. The influence of the layered character of snow cover on the triggering of slab avalanches. Ann. Glaciol. 1993, 18, 193–198. [Google Scholar] [CrossRef]
- Mede, T.; Chambon, G.; Hagenmuller, P.; Nicot, F. Snow failure modes under mixed loading. Geophys. Res. Lett. 2018, 45, 13–351. [Google Scholar] [CrossRef]
- Bobillier, G.; Bergfeld, B.; Capelli, A.; Dual, J.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Micromechanical modeling of snow failure. Cryosphere 2020, 14, 39–49. [Google Scholar] [CrossRef]
- Gaume, J.; Chambon, G.; Eckert, N.; Naaim, M.; Schweizer, J. Influence of weak layer heterogeneity and slab properties on slab tensile failure propensity and avalanche release area. Cryosphere 2015, 9, 795–804. [Google Scholar] [CrossRef]
- Yu, H.; Li, G.; Walter, B.; Lehning, M.; Zhang, J.; Huang, N. Wind conditions for snow cornice formation in a wind tunnel. Cryosphere 2023, 17, 639–651. [Google Scholar] [CrossRef]
- Reuter, B.; Schweizer, J. Describing snow instability by failure initiation, crack propagation, and slab tensile support. Geophys. Res. Lett. 2018, 45, 7019–7027. [Google Scholar] [CrossRef]
- Schweizer, J.; Bartelt, P.; van Herwijnen, A. Snow avalanches. In Snow and Ice-Related Hazards, Risks, and Disasters; Elsevier: Amsterdam, The Netherlands, 2021; pp. 377–416. [Google Scholar]
- Viallon-Galinier, L.; Hagenmuller, P.; Reuter, B.; Eckert, N. Modelling snowpack stability from simulated snow stratigraphy: Summary and implementation examples. Cold Reg. Sci. Technol. 2022, 201, 103596. [Google Scholar] [CrossRef]
- Li, L.; Nahayo, L.; Habiyaremye, G.; Christophe, M. Applicability and performance of statistical index, certain factor and frequency ratio models in mapping landslides susceptibility in Rwanda. Geocarto Int. 2022, 37, 638–656. [Google Scholar] [CrossRef]
- Hao, J.S.; Wang, Y.; Li, L.H. Snowpack variations and their hazardous effects under climate warming in the central Tianshan Mountains. Adv. Clim. Change Res. 2024, 15, 442–451. [Google Scholar] [CrossRef]
- Nishimura, K.; Barpi, F.; Issler, D. Perspectives on Snow Avalanche Dynamics Research. Geosciences 2021, 11, 57. [Google Scholar] [CrossRef]
- Durlević, U.; Valjarević, A.; Novković, I.; Vujović, F.; Josifov, N.; Krušić, J.; Komac, B.; Djekić, T.; Singh, S.K.; Jović, G.; et al. Universal Snow Avalanche Modeling Index Based on SAFI–Flow-R Approach in Poorly-Gauged Regions. ISPRS Int. J. Geo-Inf. 2024, 13, 315. [Google Scholar] [CrossRef]
- McClung, D.M. Shear fracture precipitated by strain softening as a mechanism of dry slab avalanche release. J. Geophys. Res. 1979, 84, 3519–3526. [Google Scholar] [CrossRef]
- Heierli, J.; Gumbsch, P.; Zaiser, M. Anticrack nucleation as triggering mechanism for snow slab avalanches. Science 2008, 321, 240–243. [Google Scholar] [CrossRef]
- Gaume, J.; van Herwijnen, A.; Chambon, G.; Birkeland, K.W.; Schweizer, J. Modeling of crack propagation in weak snowpack layers using the discrete element method. Cryosphere 2015, 9, 1915–1932. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Russi, T.; Stöckli, U.; Zimmerli, M. SNOWPACK model calculations for avalanche warning based upon a new network of weather and snow stations. Cold Reg. Sci. Technol. 1999, 30, 145–157. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Fierz, C.; Satyawali, P. A physical SNOWPACK model for the Swiss avalanche warning: Part II. Snow microstructure. Cold Reg. Sci. Technol. 2002, 35, 147–167. [Google Scholar] [CrossRef]
- Mahajan, P.; Senthil, S. Cohesive element modeling of crack growth in a layered snowpack. Cold Reg. Sci. Technol. 2004, 40, 111–122. [Google Scholar] [CrossRef]
- Gaume, J.; van Herwijnen, A.; Chambon, G.; Wever, N.; Schweizer, J. Snow fracture in relation to slab avalanche release: Critical state for the onset of crack propagation. Cryosphere 2017, 11, 217–228. [Google Scholar] [CrossRef]
- Bobillier, G.; Bergfeld, B.; Dual, J.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Micro-mechanical insights into the dynamics of crack propagation in snow fracture experiments. Sci. Rep. 2021, 11, 11711. [Google Scholar] [CrossRef]
- Reiweger, I.; Schweizer, J. Failure of a layer of buried surface hoar. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Reiweger, I.; Schweizer, J. Weak layer fracture: Facets and depth hoar. Cryosphere 2013, 7, 1447–1453. [Google Scholar] [CrossRef]
- Bergfeld, B.; van Herwijnen, A.; Bobillier, G.; Rosendahl, P.L.; Weißgraeber, P.; Adam, V.; Dual, J.; Schweizer, J. Temporal evolution of crack propagation characteristics in a weak snowpack layer: Conditions of crack arrest and sustained propagation. Nat. Hazards Earth Syst. Sci. 2023, 23, 293–315. [Google Scholar] [CrossRef]
- McClung, D.M. Effects of temperature on fracture in dry slab avalanche release. J. Geophys. Res. 1996, 101, 21907–21920. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Jamieson, B. Fracture character in compression tests. Cold Reg. Sci. Technol. 2007, 47, 60–68. [Google Scholar] [CrossRef]
- Rosendahl, P.L.; Weißgraeber, P. Modeling snow slab avalanches caused by weak-layer failure—Part 1: Slabs on compliant and collapsible weak layers. Cryosphere 2020, 14, 115–130. [Google Scholar] [CrossRef]
- Rosendahl, P.L.; Weißgraeber, P. Modeling snow slab avalanches caused by weak-layer failure—Part 2: Coupled mixed-mode criterion for skier-triggered anticracks. Cryosphere 2020, 14, 131–145. [Google Scholar] [CrossRef]
- Siron, M.; Trottet, B.; Gaume, J. A theoretical framework for dynamic anticrack and supershear propagation in snow slab avalanches. J. Mech. Phys. Solids 2023, 181, 105428. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Heierli, J. Measurement of crack-face friction in collapsed weak snow layers. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Gaume, J.; Gast, T.; Teran, J.; van Herwijnen, A.; Jiang, C. Dynamic anticrack propagation in snow. Nat. Commun. 2018, 9, 3047. [Google Scholar] [CrossRef]
- Trottet, B.; Simenhois, R.; Bobillier, G.; Bergfeld, B.; van Herwijnen, A.; Jiang, C.; Gaume, J. Transition from sub-Rayleigh anticrack to supershear crack propagation in snow avalanches. Nat. Phys. 2022, 18, 1094–1098. [Google Scholar] [CrossRef]
- Camponovo, C.; Schweizer, J. Rheological measurements of the viscoelastic properties of snow. Ann. Glaciol. 2001, 32, 44–50. [Google Scholar] [CrossRef][Green Version]
- Schweizer, J.; Jamieson, J.B. Snowpack tests for assessing snow-slope instability. Ann. Glaciol. 2010, 51, 187–194. [Google Scholar] [CrossRef]
- Schweizer, J.; Reuter, B.; van Herwijnen, A.; Richter, B.; Gaume, J. Temporal evolution of crack propagation propensity in snow in relation to slab and weak layer properties. Cryosphere 2016, 10, 2637–2653. [Google Scholar] [CrossRef]
- McClung, D.M.; Schweizer, J. Skier triggering, snow temperatures and the stability index for dry-slab avalanche initiation. J. Glaciol. 1999, 45, 190–200. [Google Scholar] [CrossRef]
- Adam, V.; Bergfeld, B.; Weißgraeber, P.; van Herwijnen, A.; Rosendahl, P.L. Fracture toughness of mixed-mode anticracks in highly porous materials. Nat. Commun. 2024, 15, 7379. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.C.; Jamieson, J.B.; Stewart, R.R. Seismic measurement of fracture speed in a weak snowpack layer. Cold Reg. Sci. Technol. 2004, 40, 41–45. [Google Scholar] [CrossRef]
- Bergfeld, B.; van Herwijnen, A.; Reuter, B.; Bobillier, G.; Dual, J.; Schweizer, J. Dynamic crack propagation in weak snowpack layers: Insights from high-resolution, high-speed photography. Cryosphere 2021, 15, 3539–3553. [Google Scholar] [CrossRef]
- Bergfeld, B.; van Herwijnen, A.; Bobillier, G.; Larose, E.; Moreau, L.; Trottet, B.; Schweizer, J. Crack propagation speeds in weak snowpack layers. J. Glaciol. 2022, 68, 557–570. [Google Scholar] [CrossRef]
- Bobillier, G.; Bergfeld, B.; Dual, J.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Numerical investigation of crack propagation regimes in snow fracture experiments. Granul. Matter 2024, 26, 58. [Google Scholar] [CrossRef]
- Bobillier, G.; Trottet, B.; Bergfeld, B.; Simenhois, R.; van Herwijnen, A.; Schweizer, J.; Gaume, J. Supershear crack propagation in snow slab avalanche release: New insights from numerical simulations and field measurements. Nat. Hazards Earth Syst. Sci. Discuss, 2024; in review. [Google Scholar] [CrossRef]
- Hamre, D.; Simenhois, R.; Birkeland, K. Fracture speeds of triggered avalanches. In Proceedings of the ISSW 2014, Banff, AB, Canada, 3 September 2014; Volume 585, pp. 174–178. [Google Scholar]
- Jamieson, J.B.; Johnston, C.D. A fracture-arrest model for unconfined dry slab avalanches. Can. Geotech. J. 1992, 29, 61–66. [Google Scholar] [CrossRef]
- Bair, E.H.; Simenhois, R.; Birkeland, K.; Dozier, J. A field study on failure of storm snow slab avalanches. Cold Reg. Sci. Technol. 2012, 79, 20–28. [Google Scholar] [CrossRef]
- Sovilla, B.; McElwaine, J.N.; Louge, M.Y. The structure of powder snow avalanches. Comptes Rendus. Phys. 2015, 16, 97–104. [Google Scholar] [CrossRef]
- Li, X.; Sovilla, B.; Gray, J.M.N.T.; Gaume, J. Transient wave activity in snow avalanches is controlled by entrainment and topography. Commun. Earth Environ. 2024, 5, 77. [Google Scholar] [CrossRef]
- Sigrist, C. Measurement of Fracture Mechanical Properties of Snow and Application to Dry Snow Slab Avalanche Release. Doctoral Thesis, ETH Zürich, Zurich, Switzerland, 2006. [Google Scholar]
- Heierli, J.; Birkeland, K.W.; Simenhois, R.; Gumbsch, P. Anticrack model for skier triggering of slab avalanches. Cold Reg. Sci. Technol. 2011, 65, 372–381. [Google Scholar] [CrossRef]
- Gaume, J.; Chambon, G.; Herwijnen, A.V.; Schweizer, J. Stress concentrations in weak snowpack layers and conditions for slab avalanche release. Geophys. Res. Lett. 2018, 45, 8363–8369. [Google Scholar] [CrossRef]
- Föhn, P.M. The stability index and various triggering mechanisms. IAHS Publ. 1987, 162, 195–214. [Google Scholar]
- Schneebeli, M.; Johnson, J.B. A constant-speed penetrometer for high-resolution snow stratigraphy. Ann. Glaciol. 1998, 26, 107–111. [Google Scholar] [CrossRef]
- Jamieson, J.B. The compression test-after 25 years. Avalanche Rev. 1999, 18, 10–12. [Google Scholar]
- Simenhois, R.; Birkeland, K. The extended column test: A field test for fracture initiation and propagation. In Proceedings of the the 2006 International Snow Science Workshop, Telluride, CO, USA, 1–6 October 2006; Volume 10, pp. 79–85. [Google Scholar]
- Simenhois, R.; Birkeland, K. The extended column test: Test effectiveness, spatial variability, and comparison with the propagation saw test. Cold Reg. Sci. Technol. 2009, 59, 210–216. [Google Scholar] [CrossRef]
- Gauthier, D.; Jamieson, B. Towards a field test for fracture propagation propensity in weak snowpack layers. J. Glaciol. 2006, 52, 164–168. [Google Scholar] [CrossRef]
- Sigrist, C.; Schweizer, J. Critical energy release rates of weak snowpack layers determined in field experiments. Geophys. Res. Lett. 2007, 34, L03502. [Google Scholar] [CrossRef]
- Reuter, B.; van Herwijnen, A.; Veitinger, J.; Schweizer, J. Relating simple drivers to snow instability. Cold Reg. Sci. Technol. 2015, 120, 168–178. [Google Scholar] [CrossRef]
- Anderson, T. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005; p. 640. [Google Scholar]
- McClung, D.M. Fracture mechanical models of dry slab avalanche release. J. Geophys. Res. 1981, 86, 10783–10790. [Google Scholar] [CrossRef]
- McClung, D.M. The critical size of macroscopic imperfections in dry snow slab avalanche initiation. J. Geophys. Res. 2011, 116, F03003:1–F03003:8. [Google Scholar] [CrossRef]
- Chiaia, B.M.; Cornetti, P.; Frigo, B. Triggering of dry snow slab avalanches: Stress versus fracture mechanical approach. Cold Reg. Sci. Technol. 2008, 53, 170–178. [Google Scholar] [CrossRef]
- Heierli, J.; Zaiser, M. An analytical model for fracture nucleation in collapsible stratifications. Geophys. Res. Lett. 2006, 33, L06501. [Google Scholar] [CrossRef]
- Schweizer, J. On recent advances in avalanche research. Cold Reg. Sci. Technol. 2017, 144, 1–5. [Google Scholar] [CrossRef]
- Gauthier, D.; Jamieson, B. Evaluation of a prototype field test for fracture and failure propagation propensity in weak snowpack layers. Cold Reg. Sci. Technol. 2008, 51, 87–97. [Google Scholar] [CrossRef]
- Gauthier, D.; Jamieson, B. The Propagation Saw Test (PST): A review of its development, applications, and recent research. In Proceedings of the 2012 International Snow Science Workshop, Anchorage, AK, USA, 16–21 September 2012; pp. 1047–1053. [Google Scholar]
- van Herwijnen, A.; Schweizer, J.; Heierli, J. Measurement of the deformation field associated with fracture propagation in weak snowpack layers. J. Geophys. Res. 2010, 115, F03042. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Gaume, J.; Bair, E.H.; Reuter, B.; Birkeland, K.W.; Schweizer, J. Estimating the effective elastic modulus and specific fracture energy of snowpack layers from field experiments. J. Glaciol. 2016, 62, 997–1007. [Google Scholar] [CrossRef]
- Ross, C.K.; Jamieson, B. The propagation saw test: Slope scale validation and alternative test methods. J. Glaciol. 2012, 58, 407–416. [Google Scholar] [CrossRef]
- Birkeland, K.W.; van Herwijnen, A.; Reuter, B.; Bergfeld, B. Temporal changes in the mechanical properties of snow related to crack propagation after loading. Cold Reg. Sci. Technol. 2019, 159, 142–152. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Schweizer, J. Monitoring avalanche activity using a seismic sensor. Cold Reg. Sci. Technol. 2011, 69, 165–176. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Jamieson, B. High-speed photography of fractures in weak snowpack layers. Cold Reg. Sci. Technol. 2005, 43, 71–82. [Google Scholar] [CrossRef]
- van Herwijnen, A.; Birkeland, K.W. Measurements of snow slab displacement in Extended Column Tests and comparison with Propagation Saw Tests. Cold Reg. Sci. Technol. 2014, 97, 97–103. [Google Scholar] [CrossRef]
- Bair, E.H.; Simenhois, R.; van Herwijnen, A.; Birkeland, K. The influence of edge effects on crack propagation in snow stability tests. Cryosphere 2014, 8, 1407–1418. [Google Scholar] [CrossRef][Green Version]
- Simenhois, R.; Birkeland, K.W.; Gaume, J.; van Herwijnen, A.; Bergfeld, B.; Trottet, B.; Greene, E. Using video detection of snow surface movements to estimate weak layer crack propagation speeds. Ann. Glaciol. 2023, 65, e2. [Google Scholar] [CrossRef]
- Yue, P.; Huang, N. The formation and release mechanism of dry snow slab avalanche. In Proceedings of the XXVIII General Assembly of the International Union of Geodesy and Geophysics (IUGG), Berlin, Germany, 11–20 July 2023. [Google Scholar]
- Scapozza, C. Entwicklung Eines Dichte- und Temperaturabhängigen Stoffgesetzes zur Beschreibung des Visko-Elastischen Verhaltens von Schnee. Ph.D. Thesis, ETH Zürich, Zurich, Switzerland, 2004; p. 250. [Google Scholar]
- Rosakis, A.J.; Samudrala, O.; Coker, D. Cracks faster than the shear wave speed. Science 1999, 284, 1337–1340. [Google Scholar] [CrossRef]
- Gaume, J.; van Herwijnen, A.; Gast, T.; Teran, J.; Jiang, C. Investigating the release and flow of snow avalanches at the slope-scale using a unified model based on the material point method. Cold Reg. Sci. Technol. 2019, 168, 102847. [Google Scholar] [CrossRef]
- Birkeland, K.W.; Bair, E.; Chabot, D. The effect of changing slope angle on compression test results. In Proceedings of the International Snow Science Workshop 2014, Banff, AB, Canada, 29 September–3 October 2014; pp. 746–751. [Google Scholar]
- Benedetti, L.; Gaume, J.; Fischer, J.T. A mechanically-based model of snow slab and weak layer fracture in the Propagation Saw Test. Int. J. Solids Struct. 2019, 158, 1–20. [Google Scholar] [CrossRef]
- Gauthier, D.; Jamieson, B. Fracture propagation propensity in relation to snow slab avalanche release: Validating the Propagation Saw Test. Geophys. Res. Lett. 2008, 35, L13501. [Google Scholar] [CrossRef]
- Meloche, F.; Bobillier, G.; Guillet, L.; Gauthier, F.; Langlois, A.; Gaume, J. Modeling crack arrest in snow slab avalanches-towards estimating avalanche release sizes. arXiv 2024, arXiv:2406.01360. [Google Scholar]
- Schweizer, J.; van Herwijnen, A.; Reuter, B. Measurements of weak layer fracture energy. Cold Reg. Sci. Technol. 2011, 69, 139–144. [Google Scholar] [CrossRef]
- Schweizer, J.; Camponovo, C.; Fierz, C.; Föhn, P. Skier triggered slab avalanche release. Some practical implications. In Les Apports de la Recherche Scientifique à la Sécurité Neige Glace et Avalanche; Irstea: Antony, France, 1995; pp. 309–315. [Google Scholar]
- Hagenmuller, P.; Theile, T.C.; Schneebeli, M. Numerical simulation of microstructural damage and tensile strength of snow. Geophys. Res. Lett. 2014, 41, 86–89. [Google Scholar] [CrossRef]
- Podolskiy, E.A.; Chambon, G.; Naaim, M.; Gaume, J. Evaluating snow weak-layer failure parameters through inverse finite element modelling of shaking-platform experiments. Nat. Hazards Earth Syst. Sci. 2015, 15, 119–134. [Google Scholar] [CrossRef]
- Richter, B.; Schweizer, J.; Rotach, M.W.; van Herwijnen, A. Validating modeled critical crack length for crack propagation in the snow cover model SNOWPACK. Cryosphere 2019, 13, 3353–3366. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Fierz, C. A physical SNOWPACK model for the Swiss avalanche warning: Part III: Meteorological forcing, thin layer formation and evaluation. Cold Reg. Sci. Technol. 2002, 35, 169–184. [Google Scholar] [CrossRef]
- Bartelt, P.; Lehning, M. A physical SNOWPACK model for the Swiss avalanche warning: Part I: Numerical model. Cold Reg. Sci. Technol. 2002, 35, 123–145. [Google Scholar] [CrossRef]
- Lehning, M.; Fierz, C.; Brown, B.; Jamieson, B. Modeling snow instability with the snow-cover model SNOWPACK. Ann. Glaciol. 2004, 38, 331–338. [Google Scholar] [CrossRef]
- Monti, F.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Snow instability evaluation: Calculating the skier-induced stress in a multi-layered snowpack. Nat. Hazards Earth Syst. Sci. 2016, 16, 775–788. [Google Scholar] [CrossRef]
- Mede, T.; Chambon, G.; Nicot, F.; Hagenmuller, P. Micromechanical investigation of snow failure under mixed-mode loading. Int. J. Solids Struct. 2020, 199, 95–108. [Google Scholar] [CrossRef]
- Mulak, D.; Gaume, J. Numerical investigation of the mixed-mode failure of snow. Comput. Part. Mech. 2019, 6, 439–447. [Google Scholar] [CrossRef]
- Guillet, L.; Blatny, L.; Trottet, B.; Steffen, D.; Gaume, J. A depth-averaged material point method for shallow landslides: Applications to snow slab avalanche release. J. Geophys. Res. 2023, 128. [Google Scholar] [CrossRef]
- Conway, H.; Abrahamson, J. Snow-Slope Stability—A Probabilistic Approach. J. Glaciol. 1988, 34, 170–177. [Google Scholar] [CrossRef]
- Gubler, H.; Bader, H.P. A model of initial failure in slab-avalanche release. Ann. Glaciol. 1989, 13, 90–95. [Google Scholar] [CrossRef]
- Jamieson, J.B.; Johnston, C.D. Evaluation of the shear frame test for weak snowpack layers. Ann. Glaciol. 2001, 32, 59–69. [Google Scholar] [CrossRef]
- McClung, D.M. Application of dynamic fracture mechanics to dry snow slab avalanche release. Int. J. Fract. 2021, 227, 95–110. [Google Scholar] [CrossRef]
- Heierli, J.; Gumbsch, P.; Sherman, D. Anticrack-type fracture in brittle foam under compressive stress. Scr. Mater. 2012, 67, 96–99. [Google Scholar] [CrossRef]
- Ritter, J.; Löwe, H.; Gaume, J. Microstructural controls of anticrack nucleation in highly porous brittle solids. Sci. Rep. 2020, 10, 12383. [Google Scholar] [CrossRef]
- Eglit, M.; Yakubenko, A.; Zayko, J. A review of Russian snow avalanche models—From analytical solutions to novel 3D models. Geosciences 2020, 10, 77. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Gu, M.; Sun, L. A new simulation method on sliding snow load on sloped roofs. Nat. Hazards 2015, 77, 39–65. [Google Scholar] [CrossRef]
- Huang, N.; Yu, Y.; Shao, Y.; Zhang, J. Numerical Simulation of Falling-Snow Deposition Pattern Over 3D-Hill. J. Geophys. Res. 2024, 129, e2023JD039898. [Google Scholar] [CrossRef]
- Li, X.; Sovilla, B.; Ligneau, C.; Jiang, C.; Gaume, J. Different erosion and entrainment mechanisms in snow avalanches. Mech. Res. Commun. 2022, 124, 103914. [Google Scholar] [CrossRef]
- Camponovo, C.; Schweizer, J. Measurements on skier triggering. In Proceedings of the International Snow Science Workshop, Banff, AB, Canada, 6–10 October 1996. [Google Scholar]
- van Herwijnen, A.; Jamieson, B. Snowpack properties associated with fracture initiation and propagation resulting in skier-triggered dry snow slab avalanches. Cold Reg. Sci. Technol. 2007, 50, 13–22. [Google Scholar] [CrossRef]
- Habermann, M.; Schweizer, J.; Jamieson, J.B. Influence of snowpack layering on human-triggered snow slab avalanche release. Cold Reg. Sci. Technol. 2008, 54, 176–182. [Google Scholar] [CrossRef]
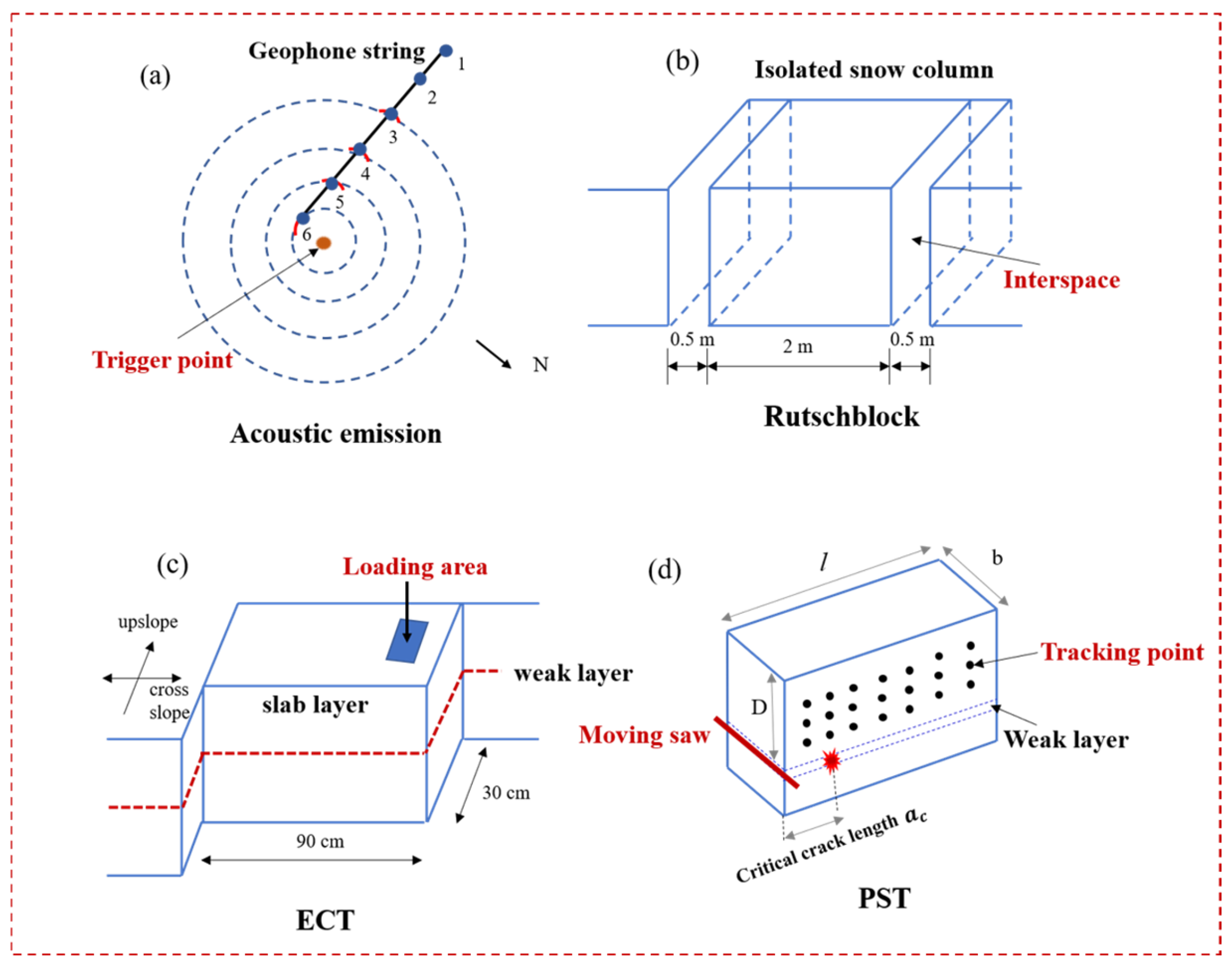
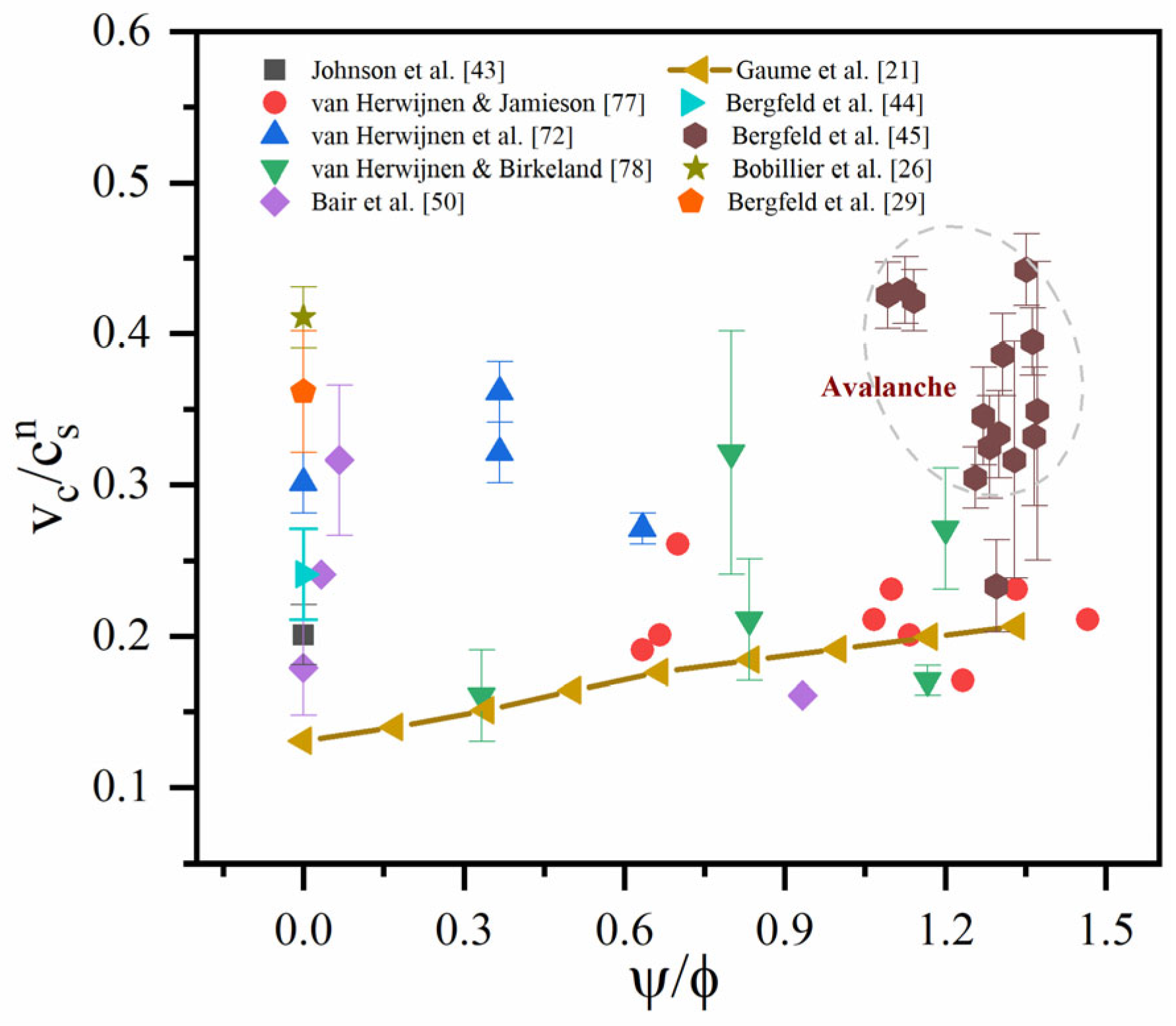
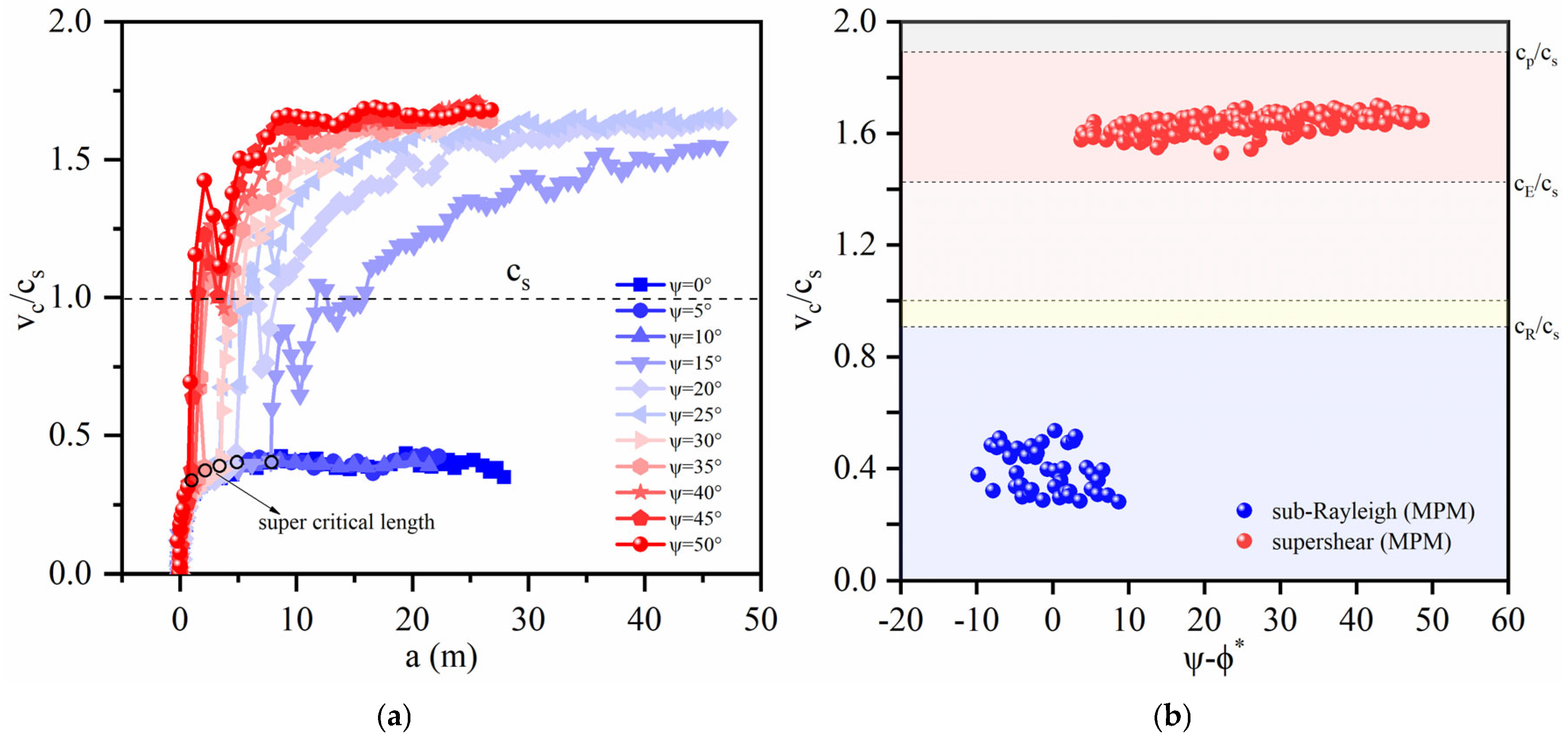
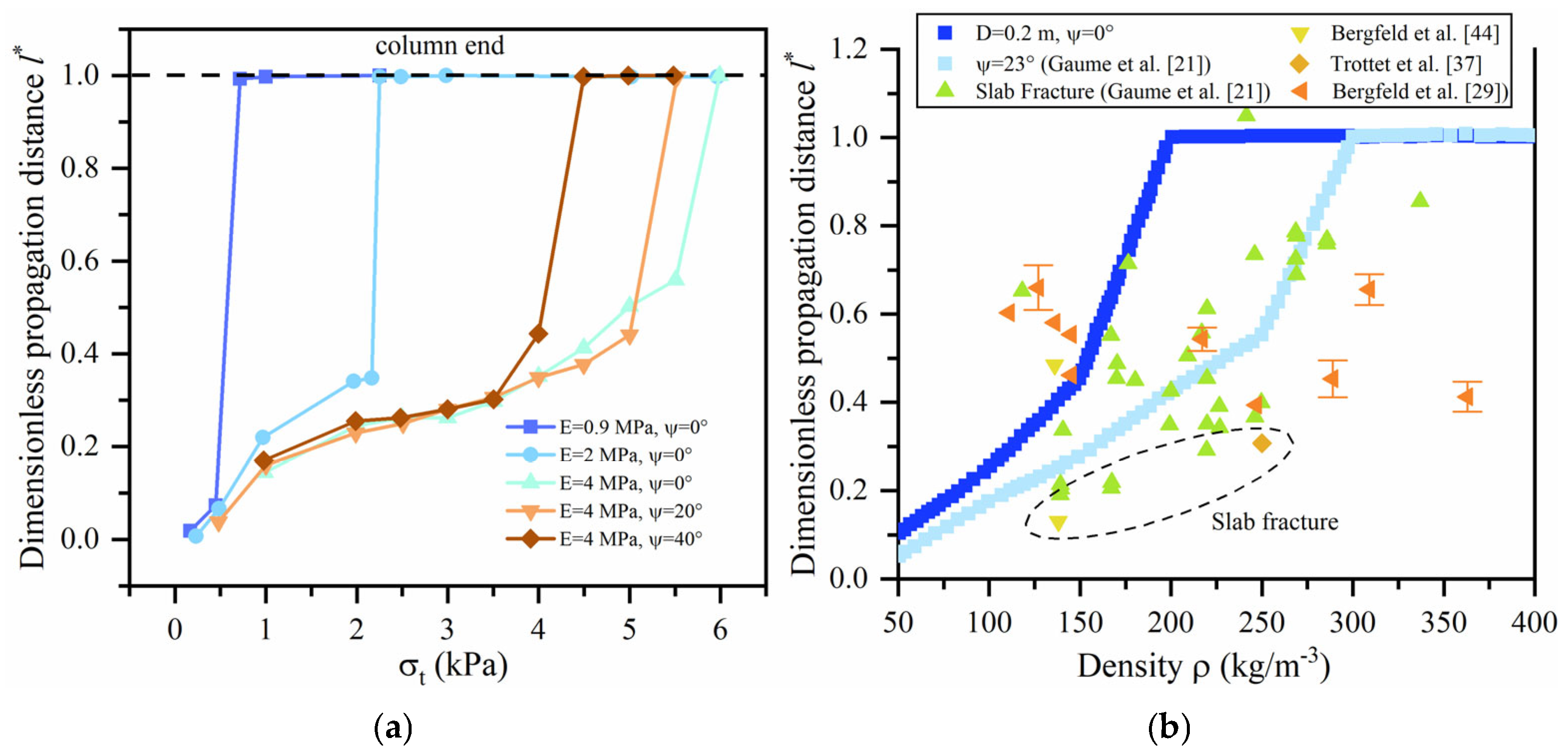
| Literature | Methods | Slab Density (kg/m3) | Slab Elasticity Modulus (MPa) | Slab Thickness (cm) | Weak Layer Thickness (cm) | Slope Angle () | Critical Crack Length (cm) | Specific Fracture Energy (J/m2) |
|---|---|---|---|---|---|---|---|---|
| Sigrist and Schweizer [62] | PST (EXP) | 187 | 7.5 ± 2.5 | 26 | 0.2 | 30 | 23 ± 2 | 0.07 ± 0.2 |
| Gauthier and Jamieson [70] | PST (EXP) | 134 | 1.5 ± 0.8 | 14 | 2–4 | 0 | 13 | 0.03 |
| 30 | 29 | - | ||||||
| 38 | 22 | - | ||||||
| Chiaia et al. [67] | Theory | 200 | 0.5–10 | 0.5 | 1 | 30–45 | 60–70 | 0.1–0.3 (mode II) |
| Heierli et al. [20] | Notch experiments | 187 | 7.5 ± 2.5 | 26 | Rigid WL | 30 | 29 ± 5 | 0.1 |
| van Herwijnen et al. [72] | PST | 150–250 | - | 38–66 | 1–9 | 0–19 | 16–44 | - |
| Reuter et al. [63] | SMP | 50–400 | 16 | 10–200 | - | 30 | 10–60 | 0.07–2.9 |
| van Herwijnen et al. [73] | PST | 73–316 | 0.08–34 | 10–150 | Surface hoar (39.6%) | 0–50 | 2–89 | 0.08–2.7 |
| Schweizer et al. [40] | PST | 207–309 | 2.5–10 | 56–148 | 5–8 | Field topography | 20–50 | 0.5–1.4 (SMP) |
| Gaume et al. [25] | DEM | 50–500 | 0.1–50 | 20–100 | 3–6 | 0 | 22 | - (material strength) |
| 10 | 18 | |||||||
| 20 | 12 | |||||||
| 30 | 8 | |||||||
| Gaume et al. [55] | MPM | 180 | 2 | 20 | 2 | 0–50 | 0–60 | - |
| Birkeland et al. [75] | Load-PST (EXP) | 157–246 253–340 (loading) | 0.14–2.5 | 12–40 40–60 (loading) | 4 | 20–27 | 4.5–25.8 | 0.07–0.9 |
| Bobillier et al. [26] | DEM | 154 | 5.2 | 110 | 2 | 0 | 28 | - |
| Trottet et al. [37] | MPM | 250 | 5–30 | 50 | 12.5 | 0–50 | (300–500) super crack | - |
| Type | Column Length (m) | Slab Thickness (WL) (cm) | Average Slab Density (kg/m−3) | Crack Propagation Speed (m/s) | WL Crystal Structure | Literature |
|---|---|---|---|---|---|---|
| whumpfs | 12.7 | 40 (1) | 190 | 20 ± 2 | SH | Johnson et al. [43] |
| compression tests, Rutschblock and cantilever beam | 0.3–2 | 42–94 (0.7–2.1) | 171.25 | 17–26 | SH, FC and DH | van Herwijnen and Jamieson [77] |
| ECT | 0.9 | 32–67 | 143–316 | 20–30 | SH, FC and DH | van Herwijnen and Birkeland [78] |
| 3–7 | 45–58 (6) | 216–249 | 14–35 | FC | Bair et al. [50] | |
| PST | 3–4 | 38–66 (1–9) | 150–250 | 20–60 | SH and FC | van Herwijnen et al. [72] |
| 2.3–3.3 | 0.23–0.74 | 138–149 | 20–30 | SH | Bergfeld et al. [44] | |
| 1–400 | 0.88–1.09 (1.5–21) | 157–181 | 30–54 | SH, PP and RG | Bergfeld et al. [45] | |
| 9 | 23–109 (1–1.5) | 110–360 | 32–40 | SH, | Bergfeld et al. [29] | |
| DEM | 2 | 20–100 (1–6) | 250 | 10–50 | triangle structure | Gaume et al. [21] |
| 4.35 | 110 (2) | 154 | 42 | cohesive ballistic (SH) | Bobillier et al. [26] | |
| 5–20 | 40 (2) | 250 | 0.6–1.6cs | cohesive ballistic (SH) | Bobillier et al. [46] | |
| MPM | 25–140 | 50 (12.5) | 250 | 0.4–1.6cs | SH | Trottet et al. [37] |
| Avalanche experiment | 12–590 | - | - | 18–428 | - | Hamre et al. [48] |
| 400 | 88 (21) | 157 | 36 | RG | Bergfeld et al. [45] | |
| 6–54 | - | - | 11–250 | - | Simenhois et al. [80] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, P.; Pei, B.; Zhang, J.; Huang, N. Dynamic Process of Dry Snow Slab Avalanche Formation: Theory, Experiment and Numerical Simulation. Geosciences 2025, 15, 201. https://doi.org/10.3390/geosciences15060201
Yue P, Pei B, Zhang J, Huang N. Dynamic Process of Dry Snow Slab Avalanche Formation: Theory, Experiment and Numerical Simulation. Geosciences. 2025; 15(6):201. https://doi.org/10.3390/geosciences15060201
Chicago/Turabian StyleYue, Peng, Binbin Pei, Jie Zhang, and Ning Huang. 2025. "Dynamic Process of Dry Snow Slab Avalanche Formation: Theory, Experiment and Numerical Simulation" Geosciences 15, no. 6: 201. https://doi.org/10.3390/geosciences15060201
APA StyleYue, P., Pei, B., Zhang, J., & Huang, N. (2025). Dynamic Process of Dry Snow Slab Avalanche Formation: Theory, Experiment and Numerical Simulation. Geosciences, 15(6), 201. https://doi.org/10.3390/geosciences15060201








