A Digital Analysis of the ‘Phoenix Trackway’ at the Hanxi Cretaceous Dinosaur Tracksite, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Digital Landmarking and Analysis
2.2. Trackway Parameter Calculations
2.3. Trackmaker Biometrics
2.4. Trackmaker Biometric Calculation
2.5. Digital Trackmaker Animation
3. Results
3.1. Trackway Parameters
3.2. Trackmaker Biometrics 1
3.3. Trackmaker Biometrics 2
3.4. Trackmaker Biometrics—Traditional Estimate
3.5. Digital Trackmaker Animation
4. Discussion
4.1. Digital Re-Analysis of Trackway Parameters and Biomechanics
4.2. Documenting Long Theropod Trackways—Limitations and Comparisons
4.3. Future Directions in Trackway Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HX-T3 | Hanxi Village Theropod trackway number 3 |
References
- Gatesy, S.M. Skin impressions of Triassic theropods as records of foot movement. Bull. Mus. Comp. Zool. 2001, 156, 137–149. [Google Scholar]
- Gatesy, S.M. Direct and indirect track features: What sediment did a dinosaur touch? Ichnos 2003, 10, 91–98. [Google Scholar] [CrossRef]
- Lockley, M.G. Dinosaur tracks. Ichnos 1992, 2, 79–83. [Google Scholar] [CrossRef]
- Thulborn, R.A.; Wade, M.J. Dinosaur trackways in the Winton Formation (mid-Cretaceous) of Queensland. Mem. Queensl. Mus. 1984, 21, 413–517. [Google Scholar]
- Moratalla, J.J.; Sanz, J.L.; Jimenez, S. Dinosaur tracks from the Lower Cretaceous of Regumiel de la Sierra (Province of Burgos, Spain): Inferences on a new quadrupedal ornithopod trackway. Ichnos 1994, 3, 89–97. [Google Scholar] [CrossRef]
- Gatesy, S.M.; Middleton, K.M.; Jenkins, F.A., Jr.; Shubin, N.H. Three-dimensional preservation of foot movements in Triassic theropod dinosaurs. Nature 1999, 399, 141–144. [Google Scholar] [CrossRef]
- Mazzetta, G.V.; Blanco, E.R. Speeds of dinosaurs from the Albian-Cenomonian of Patagonia and sauropod stance and gait. Acta Palaeontol. Pol. 2001, 46, 235–246. [Google Scholar]
- Day, J.J.; Norman, D.B.; Upchurch, P.; Powell, H.P. Dinosaur locomotion from a new trackway. Nature 2002, 415, 494–495. [Google Scholar] [CrossRef]
- Dalman, S. Footprint morphology and biomechanics of small ornithischian dinosaur ichnogenus Anomoepus from the Lower Jurassic of western Massachusetts. J. Verterbrate Paleontol. 2006, 26, 54A. [Google Scholar]
- Thulborn, T. Dinosaur Tracks; Chapman and Hill: London, UK, 1990; p. xvii + 410 pp. [Google Scholar]
- Navarro-Lorbes, P.; Ruiz, J.; Diaz-Martinez, I.; Isasmendi, E.; Saez-Benito, P.; Viera, L.; Pereda-Suberbiola, X.; Torices, A. Fast-running theropods tracks from the Early Cretaceous of La Rioja, Spain. Sci. Rep. 2021, 11, 23095. [Google Scholar] [CrossRef]
- Marty, D.; Meyer, C.A.; Billon-Bruyat, J.-P. Sauropod trackway patterns expression of special behaviour related to substrate consistency? An example from the Late Jurassic of northwestern Switzerland. Hantkeniana 2006, 5, 38–41. [Google Scholar]
- Sciscio, L.; Bordy, E.M.; Reid, M.; Abrahams, M. Sedimentology and ichnology of the Mafube dinosaur track site (Lower Jurassic, eastern Free State, South Africa) a report on footprint preservation and palaeoenvironment. PeerJ 2016, 2285, e2285. [Google Scholar] [CrossRef] [PubMed]
- Salisbury, S.W.; Romilio, A.; Herne, M.C.; Tucker, R.T.; Nair, J.P. The Dinosaurian Ichnofauna of the Lower Cretaceous (Valanginian–Barremian) Broome Sandstone of the Walmadany Area (James Price Point), Dampier Peninsula, Western Australia. J. Vertebr. Paleontol. 2016, 36, 1–152. [Google Scholar] [CrossRef]
- Dãaz-Martãnez, I.; Gonzãlez, S.; De Valais, S. Dinosaur footprints in the Early Jurassic of Patagonia (Marifil Volcanic Complex, Argentina): Biochronological and palaeobiogeographical inferences. Geol. Mag. 2017, 154, 914–922. [Google Scholar] [CrossRef]
- Lockley, M.G.; Matsukawa, M. Some observations on trackway evidence for gregarious behavior among small bipedal dinosaurs. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1999, 150, 25–31. [Google Scholar] [CrossRef]
- Schumacher, B.A. An Addition to the Dinosaur Freeway Megatracksite, Dakota Group (Upper Cretaceous), Bent County, Colorado. Ichnos 2003, 10, 255–262. [Google Scholar] [CrossRef]
- Barco, J.L.; Ignacio, C.J.; Ruiz-Omeñaca, J.I. New Data on Therangospodus oncalensis from the Berriasian Fuentesalvo Tracksite (Villar del Río, Soria, Spain): An Example of Gregarious Behaviour in Theropod Dinosaurs. Ichnos 2006, 13, 237–248. [Google Scholar] [CrossRef]
- Lockley, M.G.; Min, H.; Se-Geon, G.; Geun, H.K.; Paik, I.S. Multiple Tracksites with Parallel Trackways from the Cretaceous of the Yeosu City Area Korea: Implications for Gregarious Behavior in Ornithopod and Sauropod Dinosaurs. Ichnos 2012, 19, 105–114. [Google Scholar] [CrossRef]
- Piñuela, L.; García-Ramos, J.C.; Mike, R.; Ruiz-Omeñaca, J.I. First Record of Gregarious Behavior in Robust Medium-Sized Jurassic Ornithopods: Evidence from the Kimmeridgian Trackways of Asturias (N. Spain) and Some General Considerations on Other Medium-Large Ornithopod Tracks in the Mesozoic Record. Ichnos 2016, 23, 298–311. [Google Scholar] [CrossRef]
- Romero-Molina, M.; William, S.; Felix, P.-L.; Antonio, L.; Requeta, E. Orientation and Characteristics of Theropod Trackways from the Las Losas Palaeoichnological Site (La Rioja, Spain). Ichnos 2003, 10, 241–254. [Google Scholar] [CrossRef]
- Marty, D.; Wolfgang, H.; Andreas, I.; Lionel, C.; Christian, M.; Lockley, M. Preliminary Report on the Courtedoux Dinosaur Tracksite from the Kimmeridgian of Switzerland. Ichnos 2003, 10, 209–219. [Google Scholar] [CrossRef]
- Matsukawa, M.; Kenichiro, S.; Reiji, K.; Kazuto, K.; Lockley, M.G. Review of Japanese Dinosaur Track Localities: Implications for Ichnotaxonomy, Paleogeography and Stratigraphic Correlation. Ichnos 2005, 12, 201–222. [Google Scholar] [CrossRef]
- Vila, B.; Oms, O.; Marmi, J.; Galobart Lorente, À. Tracking Fumanya footprints (Maastrichtian, Pyrenees): Historical and ichnological overview. Oryctos 2008, 8, 115–130. [Google Scholar]
- McCrea, R.T.; Buckley, L.G.; Farlow, J.O.; Lockley, M.G.; Currie, P.J.; Matthews, N.A.; Pemberton, S.G. A ‘Terror of Tyrannosaurs’: The First Trackways of Tyrannosaurids and Evidence of Gregariousness and Pathology in Tyrannosauridae. PLoS ONE 2014, 9, e103613. [Google Scholar] [CrossRef]
- Goodell, Z.; Lockley, M.G.; Lucas, S.G.; Schumacher, B.A.; Smith, J.A.; Trujillo, R.; Xing, L. A High-Altitude Sauropod Trackway Site in the Jurassic of Colorado: The Longest Known Consecutive Footprint Sequence Reveals Evidence of Sharp Turning Behavior. N. M. Mus. Nat. Hist. Sci. Bull. 2021, 82, 101–112. [Google Scholar]
- Meyer, C.A.; Marty, D.; Thüring, B.; Thüring, S.; Belvedere, M. The Late Cretaceous dinosaur track record of Bolivia—Review and perspective. J. S. Am. Earth Sci. 2021, 106, 102992. [Google Scholar] [CrossRef]
- McLarty, J.A.; Esperante, R. Stops and turns: Uncommonly preserved theropod locomotive behavior patterns in an Upper Cretaceous tracksite from Torotoro National Park, Bolivia. J. S. Am. Earth Sci. 2024, 143, 105011. [Google Scholar] [CrossRef]
- Lockley, M.G.; Meyer, C.A.; Schultz-Pittman, R.; Forney, G. Late Jurassic dinosaur tracksites from Central Asia: A preliminary report on the world’s longest trackways. Mus. North. Ariz. Bull. 1996, 60, 137–140. [Google Scholar]
- Li, D.; Azuma, Y.; Fujita, M.; Lee, Y.-N.; Yohei, A. A preliminary report on two new vertebrate tracks sites including dinosaurs from the Early Cretaceous Hekou Group, Gansu Province, China. J. Paleontol. Soc. Korea 2006, 22, 29–49. [Google Scholar]
- Fanti, F.; Contessi, M.; Nigarov, A.; Esenov, P. New Data on Two Large Dinosaur Tracksites from the Upper Jurassic of Eastern Turkmenistan (Central Asia). Ichnos 2013, 20, 54–71. [Google Scholar] [CrossRef]
- Kim, K.S.; Lim, J.D.; Lockley, M.G.; Xing, L.; Kim, D.H.; Piñuela, L.; Romilio, A.; Yoo, J.S.; Kim, J.H.; Ahn, J. Smallest known raptor tracks suggest microraptorine activity in lakeshore setting. Sci. Rep. 2018, 8, 16908. [Google Scholar] [CrossRef] [PubMed]
- Lockley, M.; Kim, K.S.; Lim, J.D.; Romilio, A. Bird tracks from the Green River Formation (Eocene) of Utah: Ichnotaxonomy, diversity, community structure and convergence. Hist. Biol. 2021, 33, 2085–2102. [Google Scholar] [CrossRef]
- Xing, L.; Lockley, M.G.; Jia, C.; Klein, H.; Niu, K.; Zhang, L.; Qi, L.; Chou, C.; Romilio, A.; Wang, D.; et al. Lower cretaceous avian-dominated, theropod, thyreophoran, pterosaur and turtle track assemblages from the Tugulu Group, Xinjiang, China: Ichnotaxonomy and palaeoecology. PeerJ 2021, 9, e11476. [Google Scholar] [CrossRef]
- Lockley, M.G.; Hadden, G.; Romilio, A. A Late Triassic theropod track assemblages from the basal Wingate Sandstone, western Colorado: Implications for regional correlation and the megatracksite concept. Hist. Biol. 2023, 35, 589–596. [Google Scholar] [CrossRef]
- Xing, L.; Klein, H.; Lockley, M.G.; Li, H.; Tong, B.; Ye, Y.; Dai, H.; Chunyong, C.; Wang, D.; Romilio, A.; et al. New records of dinosaur tracks in eastern Tibet and a review of Middle Jurassic dinosaur faunas from the eastern Tethys, southwest China. Hist. Biol. 2024, 36, 1244–1258. [Google Scholar] [CrossRef]
- Kim, K.S.; Lockley, M.G.; Lim, J.D.; Bae, S.M.; Romilio, A. Trackway evidence for large bipedal crocodylomorphs from the Cretaceous of Korea. Sci. Rep. 2020, 10, 8680. [Google Scholar] [CrossRef]
- Xing, L.; Lockley, M.G.; Zhang, J.; Klein, H.; Marty, D.; Peng, G.; Ye, Y.; McCrea, R.T.; Persons, W.S.; Xu, T. The longest theropod trackway from East Asia, and a diverse sauropod-, theropod-, and ornithopod-track assemblage from the Lower Cretaceous Jiaguan Formation, southwest China. Cretac. Res. 2015, 56, 345–362. [Google Scholar] [CrossRef]
- Romilio, A.; Shao, C. Analysing trackway-based speed calculations to infer dinosaur locomotive capabilities and behaviours. Hist. Biol. 2024, 36, 2244–2253. [Google Scholar] [CrossRef]
- Romilio, A. Blender as a tool for palaeoichnological research: Case study from Lark Quarry. Geobios 2025, 88–89, 219–226. [Google Scholar] [CrossRef]
- Lockley, M.G.; Xing, L.; Kim, K.S.; Meyer, C.A. Tortuous trackways: Evidence and implications of deviations, turns and changes in direction by dinosaurian trackmakers. Hist. Biol. 2021, 33, 3326–3339. [Google Scholar] [CrossRef]
- Alexander, R.M. Estimates of speeds of dinosaurs. Nature 1976, 261, 129–130. [Google Scholar] [CrossRef]
- Henderson, D.M. Footprints, trackways, and hip heights of bipedal dinosaurs—Testing hip height predictions with computer models. Ichnos 2003, 10, 99–114. [Google Scholar] [CrossRef]
- Xu, X.; Wang, K.; Zhang, K.; Ma, Q.; Xing, L.; Sullivan, C.; Hu, D.; Cheng, S.; Wang, S. A gigantic feathered dinosaur from the Lower Cretaceous of China. Nature 2012, 484, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Romilio, A.; Salisbury, S.W. Large dinosaurian tracks from the Upper Cretaceous (Cenomanian–Turonian) portion of the Winton Formation, Lark Quarry, central-western Queensland, Australia: 3D photogrammetric analysis renders the ‘stampede trigger’ scenario unlikely. Cretac. Res. 2014, 51, 186–207. [Google Scholar] [CrossRef]
- Hou, L.; Pei, J.; Cai, Y.; Zhou, Z.; Tong, Y.; Zhao, Y. Upper Cretaceous-Paleocene magnetostratigraphy of the Longmenshan foreland basin and its implications for the tectonic deformation of the Longmenshan fault zone. Tectonics 2023, 42, e2022TC007660. [Google Scholar] [CrossRef]
- Ruiz, J.; Torices, A. Humans Running at Stadiums and Beaches and the Accuracy of Speed Estimations from Fossil Trackways. Ichnos 2013, 20, 31–35. [Google Scholar] [CrossRef]
- Weems, R.E. Locomotor speeds and patterns of running behavior in non-maniraptoriform theropod dinosaurs. N. M. Mus. Nat. Hist. Sci. Bull. 2006, 37, 379–389. [Google Scholar]
- Larramendi, A.; Paul, G.S.; Hsu, S.Y. A review and reappraisal of the specific gravities of present and past multicellular organisms, with an emphasis on tetrapods. Anat. Rec. 2021, 304, 1833–1888. [Google Scholar] [CrossRef]
- Hirt, M.R.; Jetz, W.; Rall, B.C.; Brose, U. A general scaling law reveals why the largest animals are not the fastest. Nat. Ecol. Evol. 2017, 1, 1116–1122. [Google Scholar] [CrossRef]
- Gatesy, S.M.; Baker, M.; Hutchinson, J.R. Constraint-based exclusion of limb poses for reconstructing theropod dinosaur locomotion. J. Vertebr. Paleontol. 2009, 29, 535–544. [Google Scholar] [CrossRef]
- Gatesy, S.M.; Manafzadeh, A.R.; Bishop, P.J.; Turner, M.L.; Kambic, R.E.; Cuff, A.R.; Hutchinson, J.R. A proposed standard for quantifying 3-D hindlimb joint poses in living and extinct archosaurs. J. Anat. 2022, 241, 101–118. [Google Scholar] [CrossRef]
- Meyer, C.A.; Thuring, B.; Graf, K.; Heim, G. A Marriage between Geotechnique and Palaeontology Three dimensional vizualization of a geological monument for scientific exploration and geotechnical conservation (Cal Orcko, Sucre Bolivia). In Proceedings of the 4th Swiss Geoscience Meeting, Bern, Switzerland, 24–25 November 2006; p. 2. [Google Scholar]
- Meyer, C.A.; Lockley, M.G. Jurassic and Cretaceous dinosaur tracksites from Central Asia (Usbekistan and Turkmenistan). J. Paleontol. Soc. Korea 1997, 2, 77–92. [Google Scholar]
- Mossman, D.J.; Bruning, R.; Powell, H.P. Anatomy of a Jurassic theropod trackway from Ardley, Oxfordshire, U.K. Ichnos 2003, 10, 195–207. [Google Scholar] [CrossRef]
- Day, J.J.; Norman, D.B.; Gale, A.S.; Upchurch, P.; Powell, H.P. A Middle Jurassic dinosaur trackway site from Oxfordshire, UK. Palaeontology 2004, 47, 319–348. [Google Scholar] [CrossRef]
- Lockley, M.G. The dinosaur footprint renaissance. Mod. Geol. 1991, 16, 139–160. [Google Scholar]
- Falkingham, P.L.; Bates, K.T.; Avanzini, M.; Bennett, M.; Bordy, E.; Breithaupt, B.H.; Castanera, D.; Citton, P.; Díaz-Martínez, I.; Farlow, J.O.; et al. A standard protocol for documenting modern and fossil ichnological data. Paleontology 2018, 61, 469–480. [Google Scholar] [CrossRef]
- Romilio, A.; Hacker, J.M.; Zlot, R.; Poropat, G.; Bosse, M.; Salisbury, S.W. A multidisciplinary approach to digital mapping of dinosaurian tracksites in the Lower Cretaceous (Valanginian-Barremian) Broome Sandstone of the Dampier Peninsula, Western Australia. PeerJ 2017, 5, e3013. [Google Scholar] [CrossRef]
- Abrahams, M.; Bordy, E.M.; Knoll, F.; Farlow, J.O. Theropod Tridactyl Tracks Across the Triassic–Jurassic Boundary in Southern Africa: Implications for Pedal Morphology Evolution. Front. Ecol. Evol. 2022, 10, 925313. [Google Scholar] [CrossRef]
- Farina, M.E.; Verónica, K.; Marsicano, C.A. A new avian footprint taxon (Gragliavipes gavenskii, Ignotornidae) from the Cenozoic of South America and a reappraisal of avian ichnofamilies from the Cretaceous and Cenozoic. Hist. Biol. 2025, 1–13. [Google Scholar] [CrossRef]
- De La Fuente, J.M.; Vera, R.B.; Farina, M.E.; Krapovickas, V. Small mammal trackways from the Neogene Vinchina Basin, Argentina: Insights into Xenarthra (Dasypodidae), Notoungulata (Typotheria), and Rodentia (Caviomorpha). J. S. Am. Earth Sci. 2025, 152, 105297. [Google Scholar] [CrossRef]
- Deiques, D.; Barcelos-Silveira, A.; Dentzien-Dias, P.; Francischini, H. Dinosaur tracks from the Guará Formation (Brazil) shed light on the biodiversity of a South American Late Jurassic humid desert. J. S. Am. Earth Sci. 2025, 153, 105364. [Google Scholar] [CrossRef]
- Lallensack, J.N.; Romilio, A.; Falkingham, P.L. A machine learning approach for the discrimination of theropod and ornithischian dinosaur tracks. J. R. Soc. Interface 2022, 19, 20220588. [Google Scholar] [CrossRef]
- Murphey, P.C.; Romilio, A.; Matthews, N.A.; Lockley, M.G.; Breithaupt, B.H.; Houck, K.J.; Chin, K.; Milner, A.; Diaz Martinez, I.; Xing, L.; et al. Track Recognition via Artificial Cognition (TRAC): Preliminary Report on the Application of Machine Learning to Identify Dinosaur Tracks. N. M. Mus. Nat. Hist. Sci. Bull. 2024, 95, 349–356. [Google Scholar]
- Romilio, A.; Dick, R.; Skinner, H.; Millar, J. Uncovering hidden footprints: Revision of the Lower Jurassic (Sinemurian) Razorback Beds—Home to Australia’s earliest reported dinosaur trackway. Hist. Biol. 2025, 37, 596–603. [Google Scholar] [CrossRef]
- Stovall, J.W.; Langston, W. Acrocanthosaurus atokensis, a new genus and species of Lower Cretaceous Theropoda from Oklahoma. Am. Midl. Nat. 1950, 43, 696–728. [Google Scholar] [CrossRef]
- Farlow, J.O.; Pittman, J.G.; Hawthorne, J.M. Brontopodus birdi, Lower Cretaceous sauropod footprints from the U.S. Gulf Coastal Plain. In Dinosaur Tracks and Traces; Gillette, D.D., Lockley, M.G., Eds.; Cambridge University Press: Cambridge, UK, 1989; pp. 371–394. [Google Scholar]
- Farlow, J.; Deschner, E.; Solis, R.; Ward, W. An unusual trackway of a medium-sized dinosaur from the Glen Rose Formation (Lower Cretaceous, Comal County, Texas). J. Verterbrate Paleontol. 2007, 27, 73A. [Google Scholar]
- Farlow, J.O.; O’Brien, M.; Kuban, G.J.; Bates, K.; Falkingham, P.; Pinuela, L.; Rose, A.; Freels, A.; Kumagai, C.; Libben, C.A.; et al. Dinosaur tracksites of the Paluxy River (Glen Rose Formation, Lower Cretaceous), Dinosaur Valley State Park, Somervell County, Texas. Abstr. Programs—Geol. Soc. Am. 2012, 42, 94. [Google Scholar]
- Farlow, J.; Bates, K.; Bonem, R.; Dattilo, B.; Falkingham, P.; Gildner, R.; Jacene, J.; Kuban, G.; Martin, A.; O’Brien, M.; et al. Dinosaur Footprints from The Glen Rose Formation (Paluxy River, Dinosaur Valley State Park, Somervell County, Texas). In Proceedings of the SVP 2015 Meeting Field Trip Guidebook, 75th Annual Meeting of the Society of Vertebrate Palaeontology, Dallas, TX, USA, 13–17 October 2015; pp. 14–37. [Google Scholar]
- Falkingham, P.L.; Gatesy, S.M. The birth of a dinosaur footprint: Subsurface 3D motion reconstruction and discrete element simulation reveal track ontogeny. Proc. Natl. Acad. Sci. USA 2014, 111, 18279–18284. [Google Scholar] [CrossRef]
- Bates, K.T.; Manning, P.L.; Hodgetts, D.; Sellers, W.I. Estimating mass properties of dinosaurs using laser imaging and 3D computer modelling. PLoS ONE 2009, 4, e4532. [Google Scholar] [CrossRef]
- Christiansen, P.; Fariña, R.A. Mass Prediction in Theropod Dinosaurs. Hist. Biol. 2004, 16, 85–92. [Google Scholar] [CrossRef]
- Atkins-Weltman, K.; Snively, E.; Connor, P. Constraining the body mass range of Anzu wyliei using volumetric and extant-scaling methods. Vertebr. Anat. Morphol. Palaeontol. 2021, 9, 95–104. [Google Scholar] [CrossRef]
- Romano, M.; Manucci, F.; Rubidge, B.; Van den Brandt, M.J. Volumetric Body Mass Estimate and in vivo Reconstruction of the Russian Pareiasaur Scutosaurus karpinskii. Front. Ecol. Evol. 2021, 9, 692035. [Google Scholar] [CrossRef]
- Romano, M.; Manucci, F. Resizing Lisowicia bojani: Volumetric body mass estimate and 3D reconstruction of the giant Late Triassic dicynodont. Hist. Biol. 2021, 33, 474–479. [Google Scholar] [CrossRef]
- Romano, M.; Rubidge, B. First 3D reconstruction and volumetric body mass estimate of the tapinocephalid dinocephalian Tapinocaninus pamelae (Synapsida: Therapsida). Hist. Biol. 2021, 33, 498–505. [Google Scholar] [CrossRef]
- Romano, M.; Fabio, M.; Bellucci, L. Body mass estimate and in-vivo reconstruction of Hippopotamus antiquus from Figline, Upper Valdarno (Tuscany). Hist. Biol. 2024, 1–12. [Google Scholar] [CrossRef]
- Moreno, K.; Silva-Salinas, K.; Finsterbusch, O.; Vidal-Murillo, L.; Iglesias, A.; Astorga, G.A.; Arriagada, J.I. Tetradactyl footprints and plant material from the Jurassic-Cretaceous boundary, Tarapaca Region, Northern Chile. J. S. Am. Earth Sci. 2024, 142, 104962. [Google Scholar] [CrossRef]
- Falkingham, P.L. Reconstructing dinosaur locomotion. Biol. Lett. 2025, 21, 20240441. [Google Scholar] [CrossRef]
- Currie, P.J.; Carpenter, K. A new specimen of Acrocanthosaurus atokensis (Theropoda, Dinosauria) from the Lower Cretaceous Antlers Formation (Lower Cretaceous, Aptian) of Oklahoma, USA. Geodiversitas. 2000, 22, 207–246. [Google Scholar]
- D’Emic, M.D.; Melstrom, K.M.; Eddy, D.R. Paleobiology and geographic range of the large-bodied Cretaceous theropod dinosaur Acrocanthosaurus atokensis. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2012, 333–334, 13–23. [Google Scholar] [CrossRef]
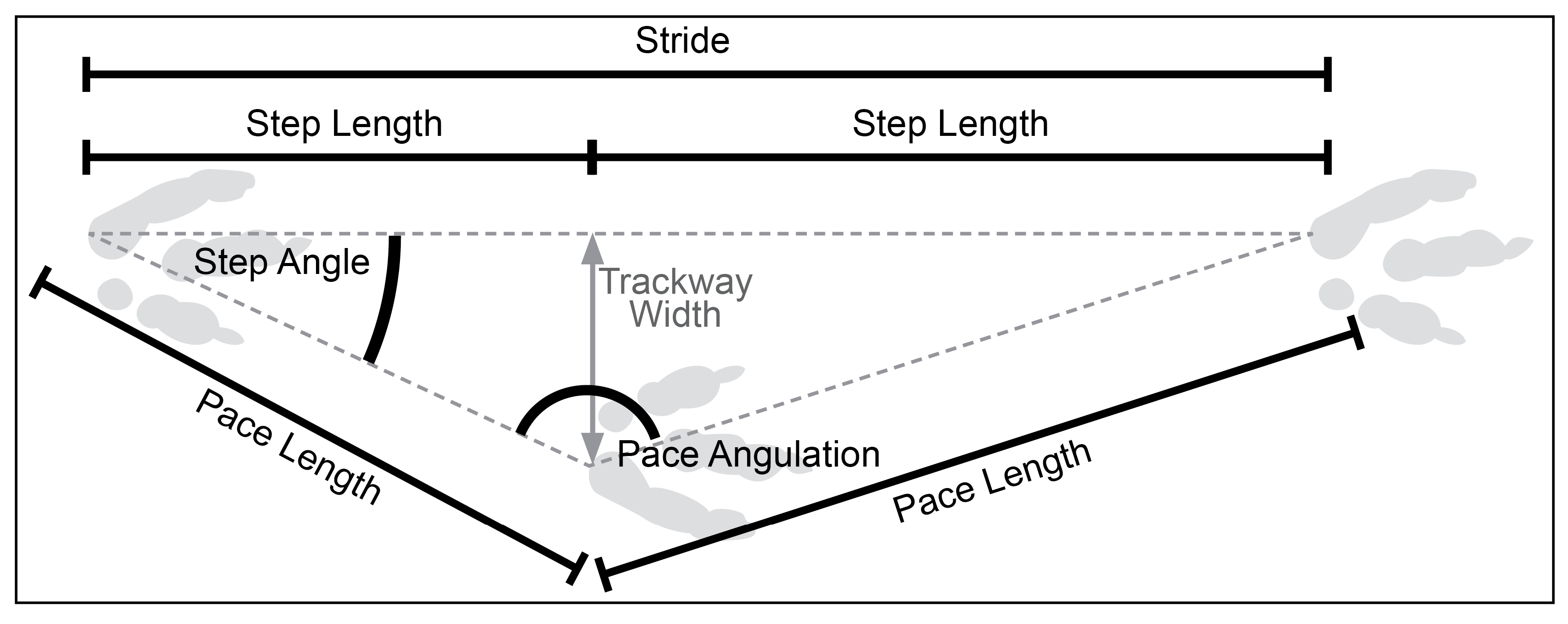
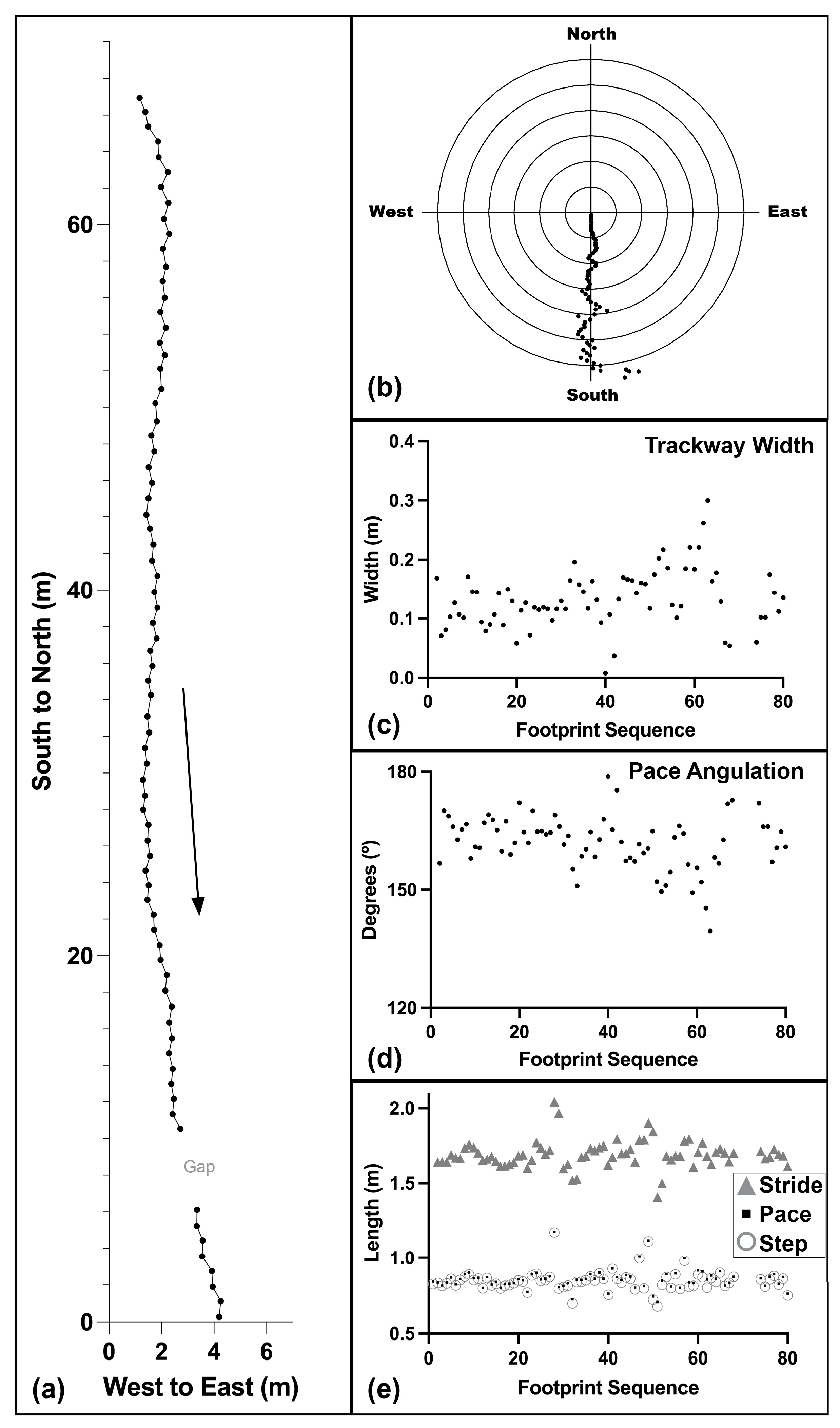

| Trackway Width (=WAP) (m) | Pace (m) | Step (m) | Stride (m) | Pace Ang (°) | Step Angle (°) | Orientation (Cardinal) | Orientation (°) |
|---|---|---|---|---|---|---|---|
| Average: 0.138 | 0.858 | 0.846 | 1.692 | 161 | 9 | S | 178 |
| Median: 0.131 | 0.854 | 0.840 | 1.685 | 162 | 9 | S | 179 |
| (SD 0.049) | (SD 0.071) | (SD 0.071) | (SD 0.093) | (SD 7) | (SD 3) | (SD 6) | |
| Min–Max: 0.008–0.300 | 0.707–1.176 | 0.678–1.171 | 1.408–2.043 | 140–179 | 1–21 | S–SSE | 163–187 |
| Relative Stride (<2 = Walk) | Velocity-Stride (m/s) | Velocity-Stride (km/h) | Relative Step (<1 = Walk) | Velocity-Step (m/s) | Velocity-Step (km/h) | Cadence (Steps/ min) | Step Duration (s) |
|---|---|---|---|---|---|---|---|
| Average: 1.25 | 1.20 | 4.3 | 0.63 | 1.20 | 4.3 | 85 | 0.51 |
| Median: 1.49 (SD 0.07) | 1.19 (SD 0.11) | 4.3 (SD 0.4) | 0.63 (SD 0.05) | 1.18 (SD 0.18) | 4.3 (SD 0.6) | 85 (SD 5) | 0.57 (SD 0.04) |
| Min–Max: 1.04–1.51 | 0.88–1.64 | 3.2–5.9 | 0.50–0.87 | 0.83–2.06 | 3.0–7.4 | 73–106 | 0.57–0.82 |
| Relative Stride (<2 = Walk) | Velocity-Stride (m/s) | Velocity-Stride (km/h) | Relative Step (<1 = Walk) | Velocity-Step (m/s) | Velocity-Step (km/h) | Cadence (Steps/ min) | Step Duration (s) |
|---|---|---|---|---|---|---|---|
| Average: 1.50 | 1.48 | 5.32 | 0.75 | 1.48 | 5.33 | 104 | 0.58 |
| Median: 1.49 (SD 0.08) | 1.47 (SD 0.14) | 5.30 (SD 0.50) | 0.74 (SD 0.06) | 1.46 (SD 0.22) | 5.20 (SD 0.78) | 104 (SD 6) | 0.58 (SD 0.03) |
| Min–Max: 1.25–1.81 | 1.09–2.02 | 3.91–7.27 | 0.60–1.03 | 1.02–2.54 | 3.70–9.10 | 90–130 | 0.46–0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romilio, A.; Xing, L. A Digital Analysis of the ‘Phoenix Trackway’ at the Hanxi Cretaceous Dinosaur Tracksite, China. Geosciences 2025, 15, 165. https://doi.org/10.3390/geosciences15050165
Romilio A, Xing L. A Digital Analysis of the ‘Phoenix Trackway’ at the Hanxi Cretaceous Dinosaur Tracksite, China. Geosciences. 2025; 15(5):165. https://doi.org/10.3390/geosciences15050165
Chicago/Turabian StyleRomilio, Anthony, and Lida Xing. 2025. "A Digital Analysis of the ‘Phoenix Trackway’ at the Hanxi Cretaceous Dinosaur Tracksite, China" Geosciences 15, no. 5: 165. https://doi.org/10.3390/geosciences15050165
APA StyleRomilio, A., & Xing, L. (2025). A Digital Analysis of the ‘Phoenix Trackway’ at the Hanxi Cretaceous Dinosaur Tracksite, China. Geosciences, 15(5), 165. https://doi.org/10.3390/geosciences15050165






