Analysis of Vertical Heterogeneity Measures Based on Routine Core Data of Sandstone Reservoirs
Abstract
1. Introduction
2. Data and Methods
- 1-
- For the probability density function of the log-normal distribution (PDF):
- 2-
- For the probability density function of the cumulative distribution function (CDF):
- 3-
- For the probability density function of the normal distribution:where x is a random variable—in this study, it is the permeability—σ is the standard deviation, μ is the arithmetic mean, and erf is the error function of (x). Each of these functions has its specific equations to determine the standard deviation and expectation.
3. Results
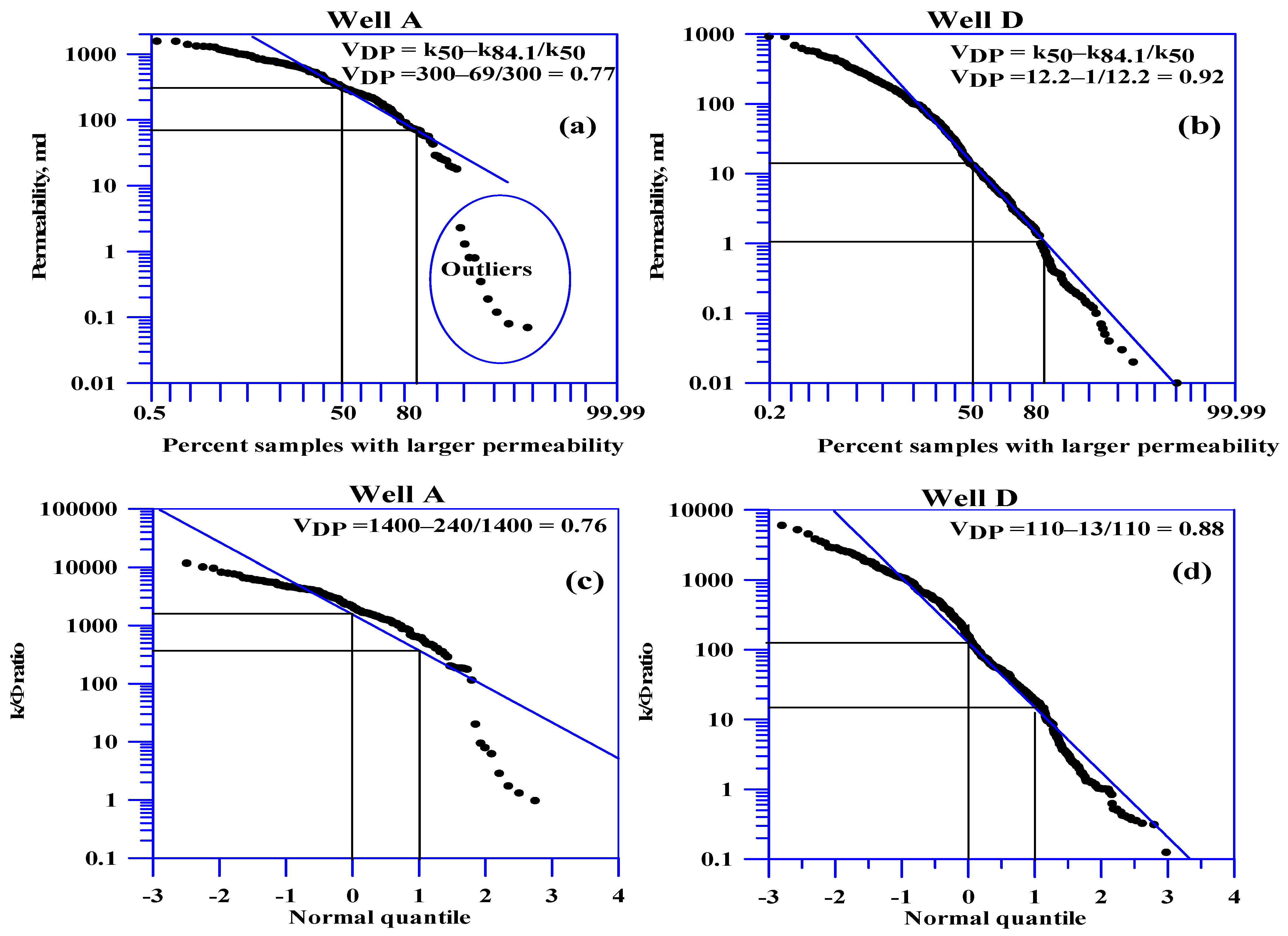
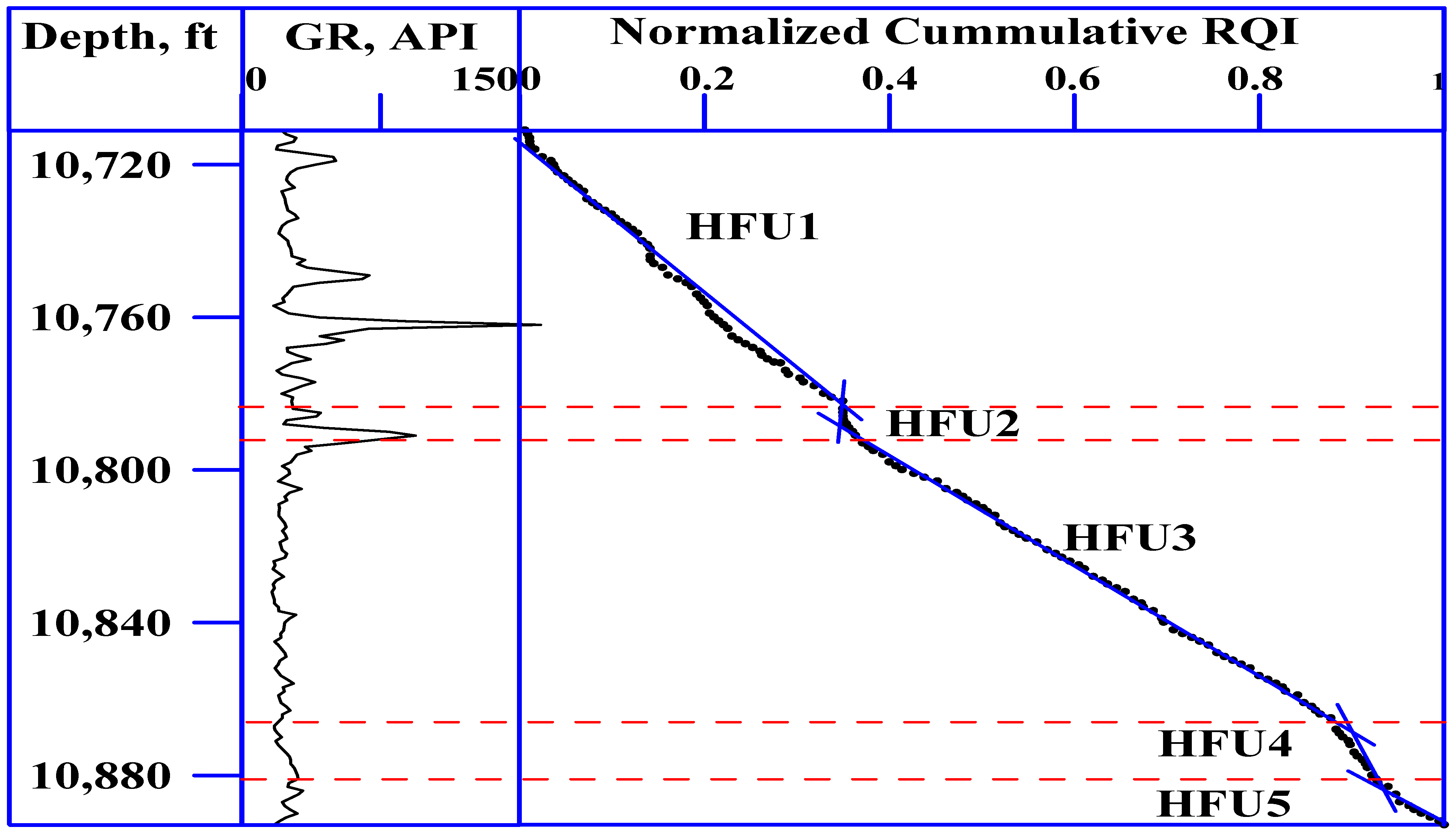
3.1. Data Examination
3.2. Heterogeneity Measures
4. Discussion
4.1. Coefficient of Variation (CV)
4.2. Dykstra–Parsons (VDP)
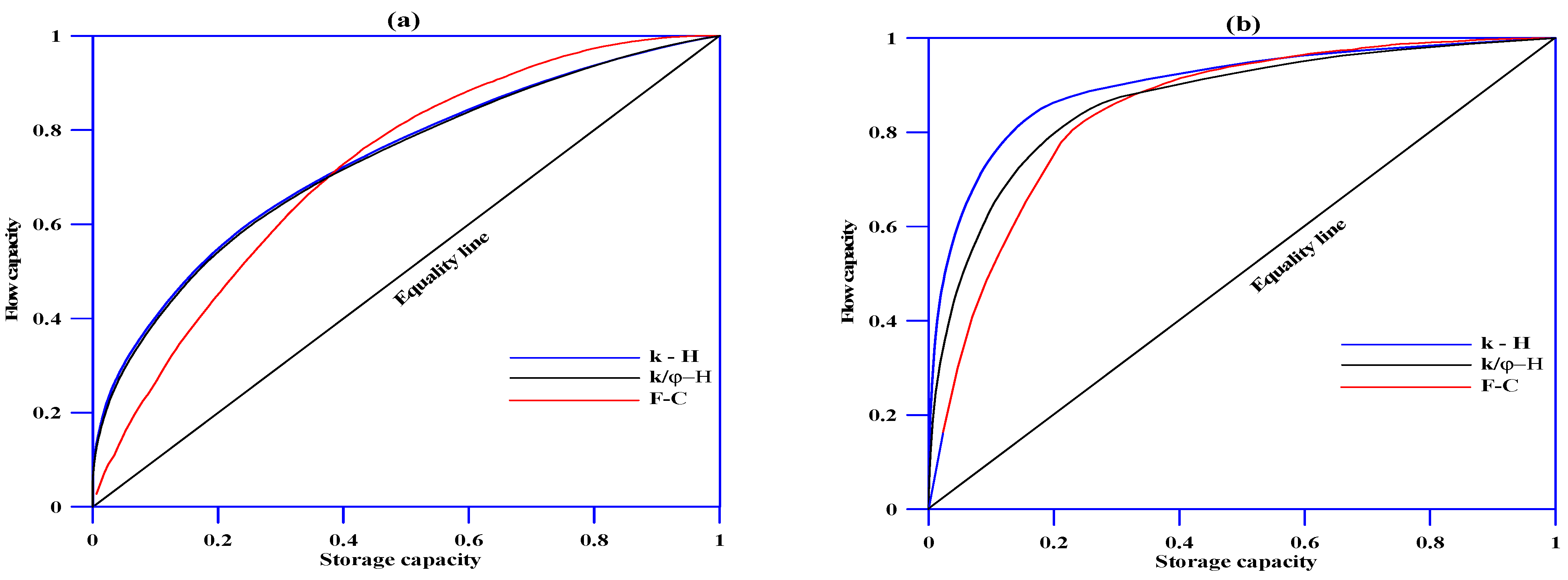
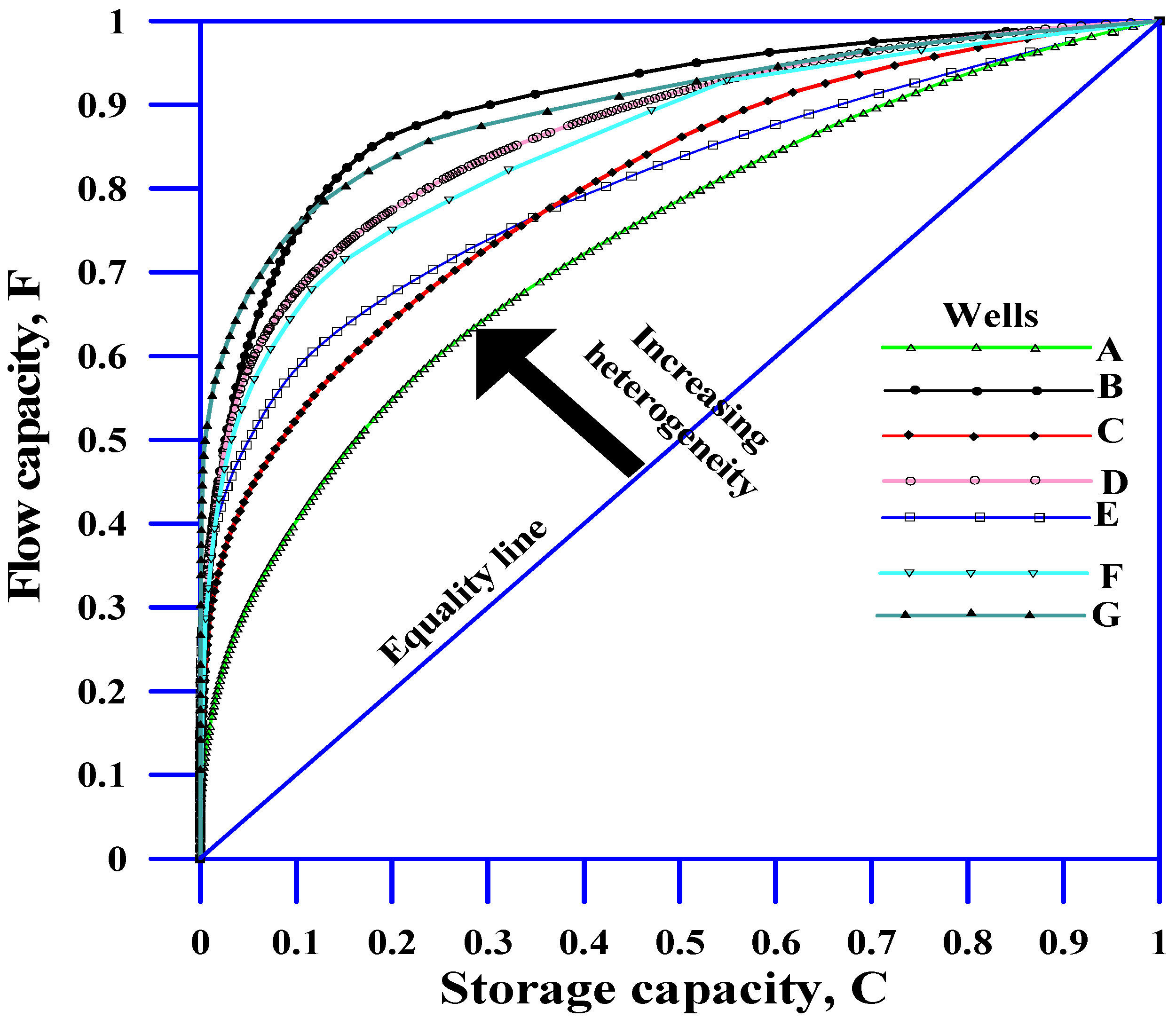
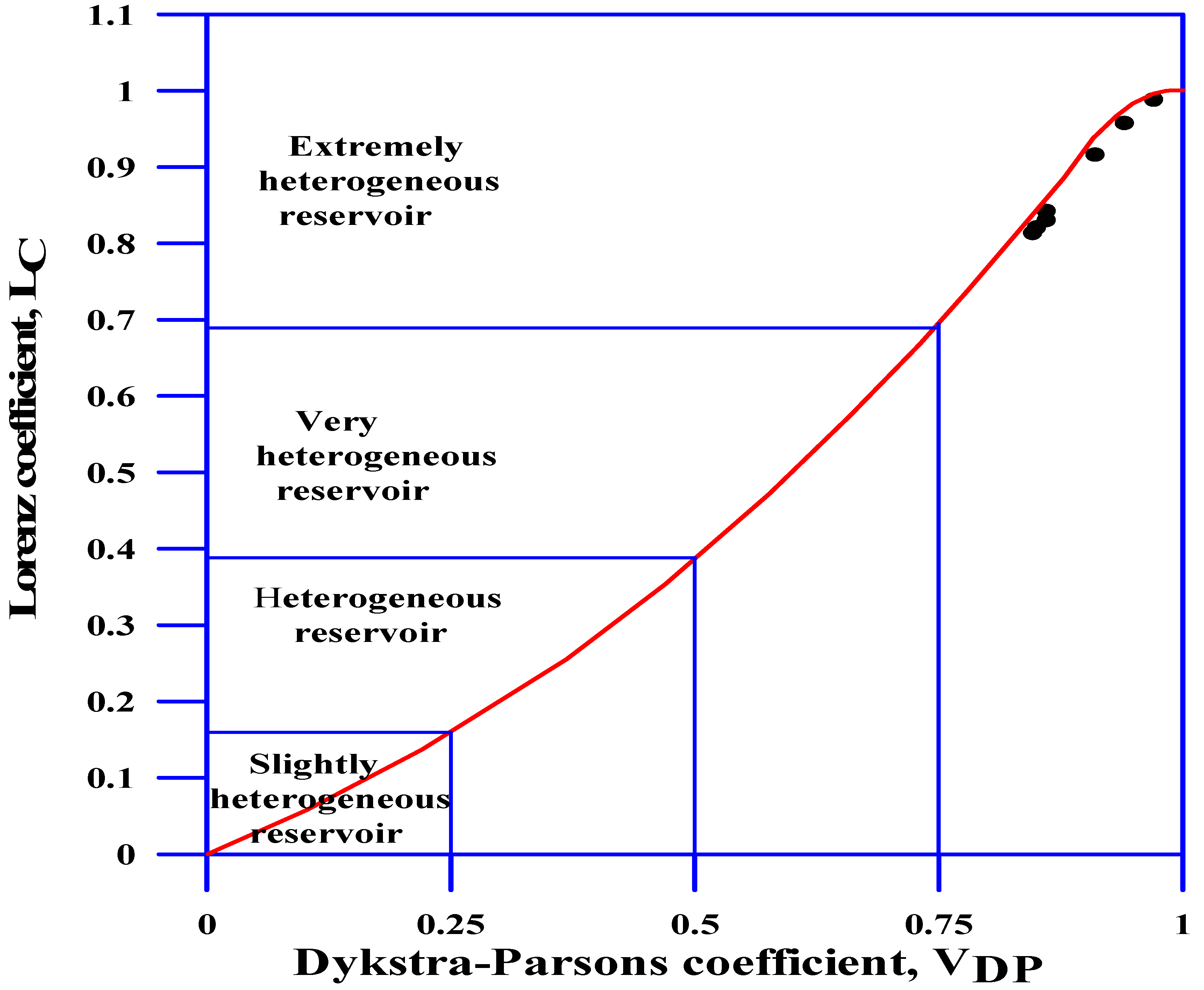
4.3. Lorenz Coefficient, LC
4.4. Relationships Between the Heterogeneity Measures
4.5. Relationship Between Heterogeneity and Reservoir Quality
5. Conclusions
- It is important to define the probability distribution function of permeability in order to determine the proper equations for calculating different heterogeneity measures.
- The coefficient of variation is strongly affected by the outliers. For log-normal distribution and extremely heterogeneous reservoirs, the coefficient of variation gives high values of three digits
- In the instance of log-normal distribution data and the absence of straight lines on the Dykstra–Parsons log-probability plot, it is imperative to disregard the VDP values derived from the data and plot, as well as the LC values derived from Lorenz curves. Instead, it is imperative to utilize the VDP and LC calculated based on the standard deviation.
- For log-normal distribution data with the presence of a straight line on the Dykstra–Parsons log-probability plot, the VDP and LC can be calculated satisfactorily using any method.
- Modified forms of the Dykstra–Parsons method showed inapplicability in the studied data.
- The accurate determination of VDP is critical, as decreasing it by 0.08 could result in doubling of cumulative oil production.
- The inclusion of porosity in the calculation of LC resulted in a decrease in LC values. The percentage of decrease varies depending on the degree of heterogeneity and the average porosity. The effect of porosity decreases in homogeneous to very heterogeneous reservoirs. A tangible effect of porosity was observed in extremely heterogeneous reservoirs with low average porosities.
- The study introduced a heterogeneity classification for various heterogeneity measures.
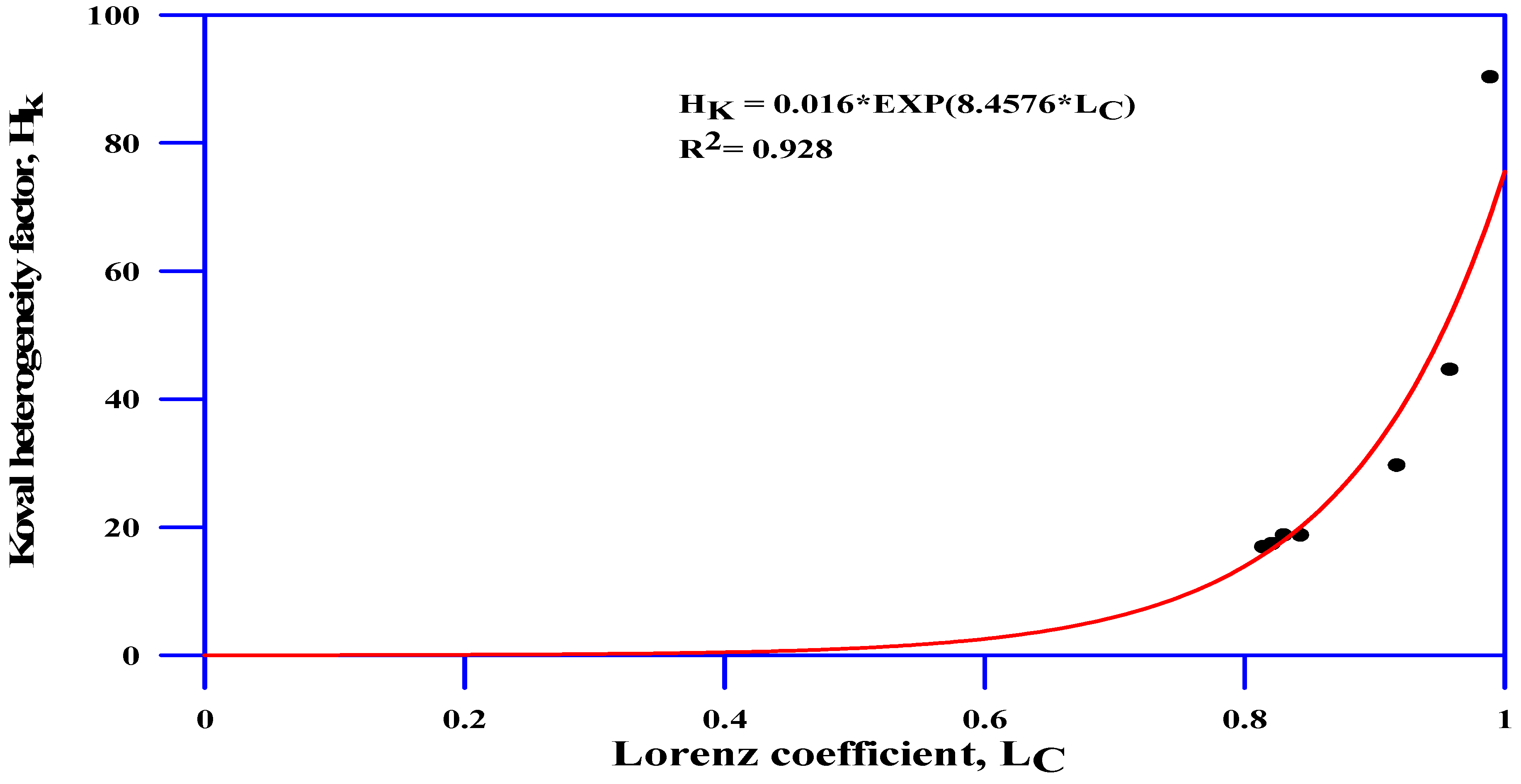
- There is a good correlation between the Lorenz coefficient and the Koval heterogeneity factor.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fitch, P.J.; Lovell, M.A.; Davies, S.J.; Pritchard, T.; Harvey, P.K. An integrated and quantitative approach to petrophysical heterogeneity. Mar. Pet. Geol. 2015, 63, 82–96. [Google Scholar] [CrossRef]
- Tavakoli, V. Carbonate Reservoir Heterogeneity: Overcoming the Challenges; Springer: Berlin/Heidelberg, Germany, 2020; p. 108. [Google Scholar]
- Lake, L.W.; Jensen, J.L. A review of heterogeneity measures used in reservoir characterization. In Situ 1991, 15, 409–439. [Google Scholar]
- Jensen, J.J.; Lake, L.W.; Corbett, P.W.M.; Goggin, D.J. Statistics for Petroleum Engineers and Geoscientists; Prentice Hall Inc.: New York, NY, USA, 1997; p. 390. [Google Scholar]
- Nurmi, R.; Charara, M.; Waterhouse, M.; Park, R. Heterogeneities in carbonate reservoirs: Detection and analysis using borehole electrical imagery. In Geological Applications of Wireline Logs; Hurst, A., Lovell, M.A., Morton, A.C., Eds.; Geological Society Special Publications: London, UK, 1990; Volume 48, pp. 95–111. [Google Scholar]
- Frazer, G.W.; Wulder, M.A.; Niemann, K.O. Simulation and quantification of the fine-scale spatial pattern and heterogeneity of forest canopy structure: A lacunarity-based method designed for analysis of Continuous Canopy Heights. For. Ecol. Manag. 2005, 214, 65–90. [Google Scholar] [CrossRef]
- Weber, K.J. How heterogeneity affects oil recovery. In Reservoir Characterization; Lake, L.W., Carroll, H.B., Eds.; Academic Press: New York, NY, USA, 1986; pp. 487–544. [Google Scholar]
- Willhite, G.P. Waterflooding, 3rd ed.; Society of Petroleum Engineers: Houston, TX, USA, 1986; p. 326. [Google Scholar]
- Tiab, D.; Donaldson, E. Petrophysics: Theory and Practice of Measuring Reservoir Rock and Fluid Properties, 3rd ed.; Gulf Publishing Company: Houston, TX, USA, 2012; p. 950. [Google Scholar]
- Slatt, R.M.; Galloway, W.E. Geological heterogeneities. In Development Geology Manual Reference; Morton-Thompson, D., Woods, A.M., Eds.; AAPG: Tulsa, OK, USA, 1992; pp. 278–281. [Google Scholar]
- Winland, H.D. Oil accumulation in response to pore size changes, Weyburn field, Saskatchewan. In Amoco Production Research Report; Scientific Research Publishing Inc.: Wuhan, China, 1972; p. F72-G-25. [Google Scholar]
- Amaefule, J.O.; Altunbay, M.; Tiab, D.; Kersey, D.G.; Keelan, D.K. Enhanced reservoir description: Using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells. In Proceedings of the 68th Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993; p. 16. [Google Scholar]
- Gunter, G.; Finneran, J.; Hartmann, D.; Miller, J. Early determination of reservoir flow units using an integrated petrophysical method. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 5–8 October 1997; p. 8. [Google Scholar]
- Lucia, F.J. Rock fabric/petrophysical classification of carbonate pore space for reservoir characterization. AAPG Bull. 1995, 79, 1275–1300. [Google Scholar]
- Smith, J.T.; Cobb, W.M. Waterflooding; Midwest Office of the Petroleum Technology Transfer Council: Oak Hill, VA, USA, 1997. [Google Scholar]
- Miller, M.G.; Lents, M.R. Performance of Bodcaw Reservoir, Cotton Valley Field Cycling Project: New Methods of Predicting Gas-Condensate Reservoir Performance Under Cycling Operations Compared to Field Data; American Petroleum Institute: Washington, DC, USA, 1946; API-46-128. [Google Scholar]
- Jensen, J.L. A Statistical Study of Reservoir Permeability Distributions. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1986; p. 234. [Google Scholar]
- Jensen, J.L.; Currie, I.D. New method for estimating the Dykstra-Parsons coefficient to characterize reservoir heterogeneity. SPE Reserv. Eng. 1990, 5, 369–374. [Google Scholar] [CrossRef]
- Nyvoll, A. Correlating Recovery Factors with Measures of Reservoir Heterogeneity. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2008; p. 118. [Google Scholar]
- Jing, W.; Huiqing, L.; Zenglin, W. Quantitative models of development laws for heterogeneous sandstone reservoirs by water flooding. Open Pet. Eng. J. 2012, 5, 26–35. [Google Scholar] [CrossRef][Green Version]
- Canchola, A.; A Canchola, S.T.J.; Hemyari, E.P.P.; Marins, E. Correct Use of Percent Coefficient of Variation (%CV) Formula for Log-Transformed Data. MOJ Proteom. Bioinform. 2017, 6, 316–317. [Google Scholar] [CrossRef]
- Salazar, J.J. Heterogeneity Study of the Little Creek Field from Petrophysical Data. Master’s Thesis, The University of Texas at Austin, Austin, TX, USA, 2018; p. 134. [Google Scholar]
- Salazar, J.J.; Lake, L.W. The physical meaning of the Koval factor. Math. Geosci. 2020, 52, 1017–1033. [Google Scholar] [CrossRef]
- Ren, B.; Jensen, J.; Lake, L.; Duncan, I.; Male, F. Analysis of vertical permeability and its influence on CO2 enhanced oil recovery and storage in a carbonate reservoir. In Proceedings of the Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 21–23 September 2021. [Google Scholar]
- Patton, T.L.; Moustafa, A.R.; Nelson, R.A.; Abdine, A.S. Tectonic evolution and structural setting of the Suez rift. In Interior Rift Basins; Landon, S.M., Ed.; AAPG: Tulsa, OK, USA, 1994; pp. 9–55. [Google Scholar]
- Dykstra, H.; Parsons, R.L. The prediction of oil recovery by waterflood. In Secondary Recovery of Oil in the United States: Principles and Practice; American Petroleum Institute: Washington, DC, USA, 1950; pp. 160–174. [Google Scholar]
- Schmalz, J.P.; Rahme, H.D. The variation of waterflood performance with variation in permeability profile. Prod. Mon. 1950, 15, 9–12. [Google Scholar]
- Stiles, W.E. Use of permeability distribution in water flood calculations. Trans. AIME 1949, 186, 9–13. [Google Scholar] [CrossRef]
- Kendall, M.; Stuart, A. The Advanced Theory of Statistics, Vol. 1: Distribution Theory, 4th ed.; MacMillian Publishing Co.: New York, NY, USA, 1977; p. 472. [Google Scholar]
- Lake, J.W. Enhanced Oil Recovery; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1989; p. 550. [Google Scholar]
- Mirzaei-Paiaman, A.; Asadolahpour, S.R.; Saboorian-Jooybari, H.; Chen, Z.; Ostadhassan, M. A new framework for selection of representative samples for special core analysis. Pet. Res. 2020, 5, 210–226. [Google Scholar] [CrossRef]
- Von Sperling, M.; Verbyla, M.E.; Oliveira, M.A.C. Assessment of Treatment Plant Performance and Water Quality Data: A Guide for Students, Researchers and Practitioners; IWA Publishing: London, UK, 2020; p. 644. [Google Scholar]
- Kvalseth, T.O. Coefficient of variation: The second-order alternative. J. Appl. Stat. 2016, 44, 402–415. [Google Scholar] [CrossRef]
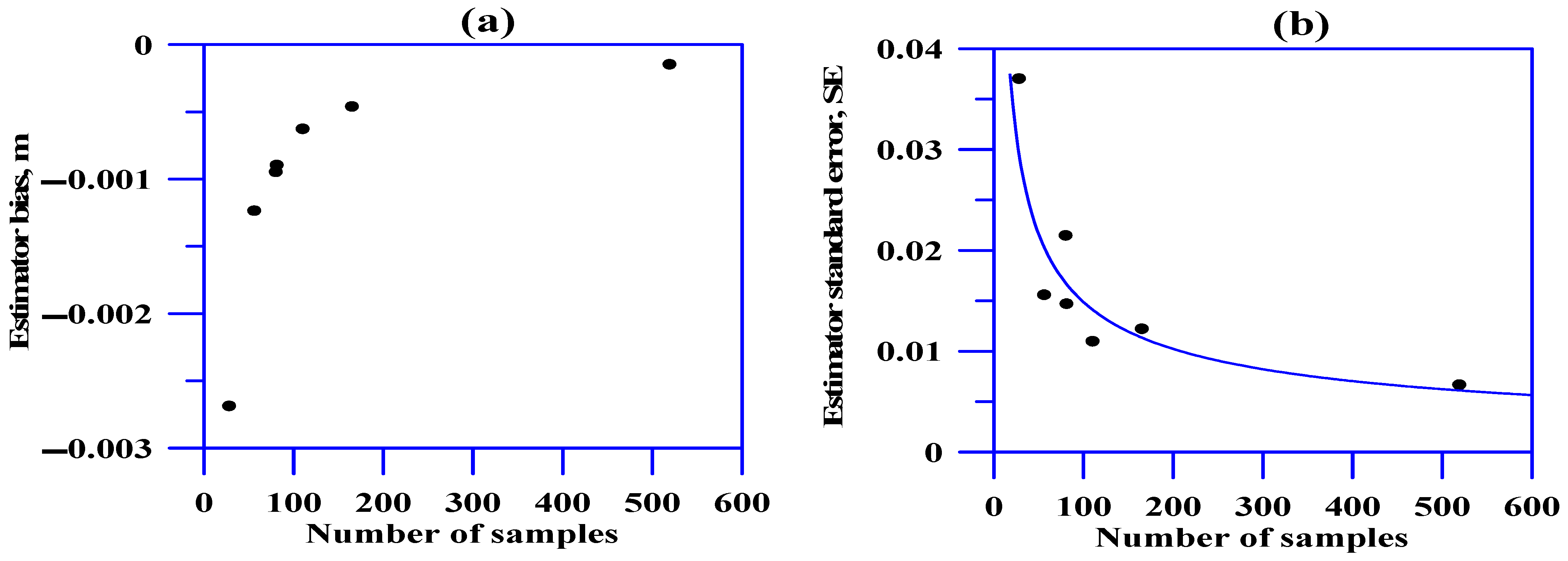
- Corbett, P.; Jensen, J. Estimating the mean permeability: How many measurements do you need? First Break 1992, 10, 89–94. [Google Scholar] [CrossRef]
- El Sharawy, M.S.; Gaafar, G.R. Reservoir zonation based on statistical analyses: A case study of the Nubian sandstone, Gulf of Suez, Egypt. J. Afr. Earth Sci. 2016, 124, 199–210. [Google Scholar] [CrossRef]
- Pintos, S.; Bohorquez, C.; Queipo, N.V. Asymptotic Dykstra–Parsons distribution, estimates and confidence intervals. Math. Geosci. 2011, 43, 329–343. [Google Scholar] [CrossRef]
- Tarhuni, M.N.; Sulaiman, W.R.; Jaafar, M.Z.; Sabil, K.M. A novel energy lifting approach using J-function and flow zone indicator for oil fields. Energy Eng. 2022, 119, 253–273. [Google Scholar] [CrossRef]
- Emerson, J.D.; Stoto, M.A. Exploratory methods for choosing power transformations. J. Am. Stat. Assoc. 1982, 77, 103–108. [Google Scholar] [CrossRef]
- Jensen, J.L.; Hinkley, D.V.; Lake, L.W. A Statistical Study of Reservoir Permeability: Distributions, Correlations and Averages. SPE Form. Eval. 1987, 2, 461–468. [Google Scholar] [CrossRef]
- Ahmed, T. Reservoir Engineering Handbook, 4th ed.; Gulf Professional Publishing: Houston, TX, USA, 2010; p. 1454. [Google Scholar]
- Craig, F.F. The Reservoir Engineering Aspects of Waterflooding, 2nd ed.; Society of Petroleum Engineers: Dallas, TX, USA, 1971; p. 134. [Google Scholar]
- Koval, E.J. A method for predicting the performance of unstable miscible misplacement in heterogeneous media. Soceity Pet. Eng. J. 1963, 3, 145–154. [Google Scholar] [CrossRef]
- Paul, G.W.; Lake, L.W.; Pope, G.A.; Young, G.B. A simplified predictive model for micellar-polymer flooding. In Proceeding of the SPE California Regional Meeting, San Francisco, CA, USA, 24–26 March 1982. [Google Scholar] [CrossRef]
- Siddiqui, S.; Okasha, M.T.M.; Funk, J.J.; Al-Harbi, A.M. New representative sample selection criteria for special core analysis. In Proceedings of the International Symposium of the Society of Core Analysts, Pau, France, 21–24 September 2003; p. 11. [Google Scholar]
- Gameel; Darwish, M. Reservoir behavior of the Pre-Turonian sandstones in south Gulf of Suez province (Sidki field—Case history). In Proceedings of the 12th EGPC Exploration and Production Conference, Cairo, Eegypt, 12–15 November 1994; Volume 2, pp. 449–471. [Google Scholar]

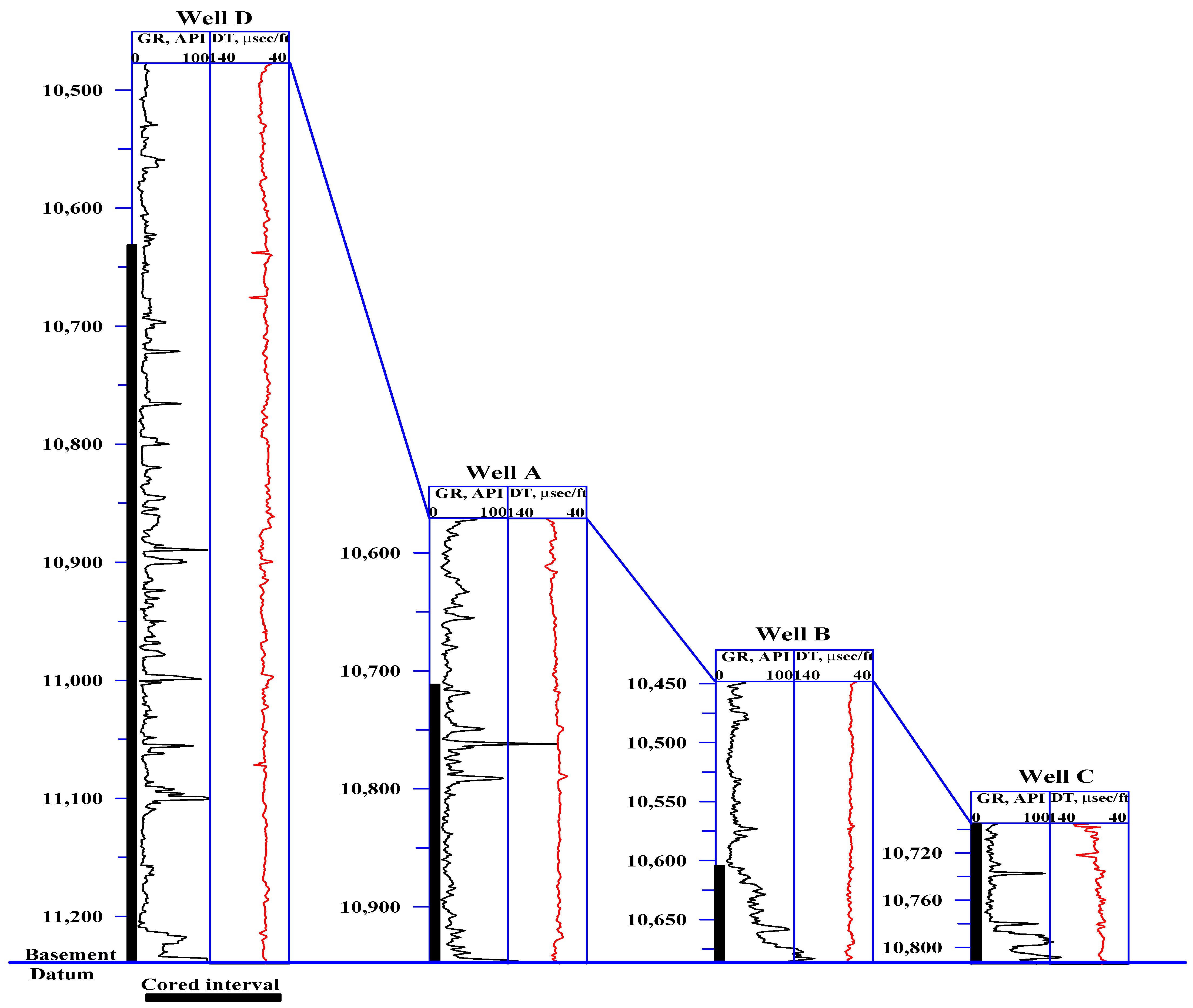
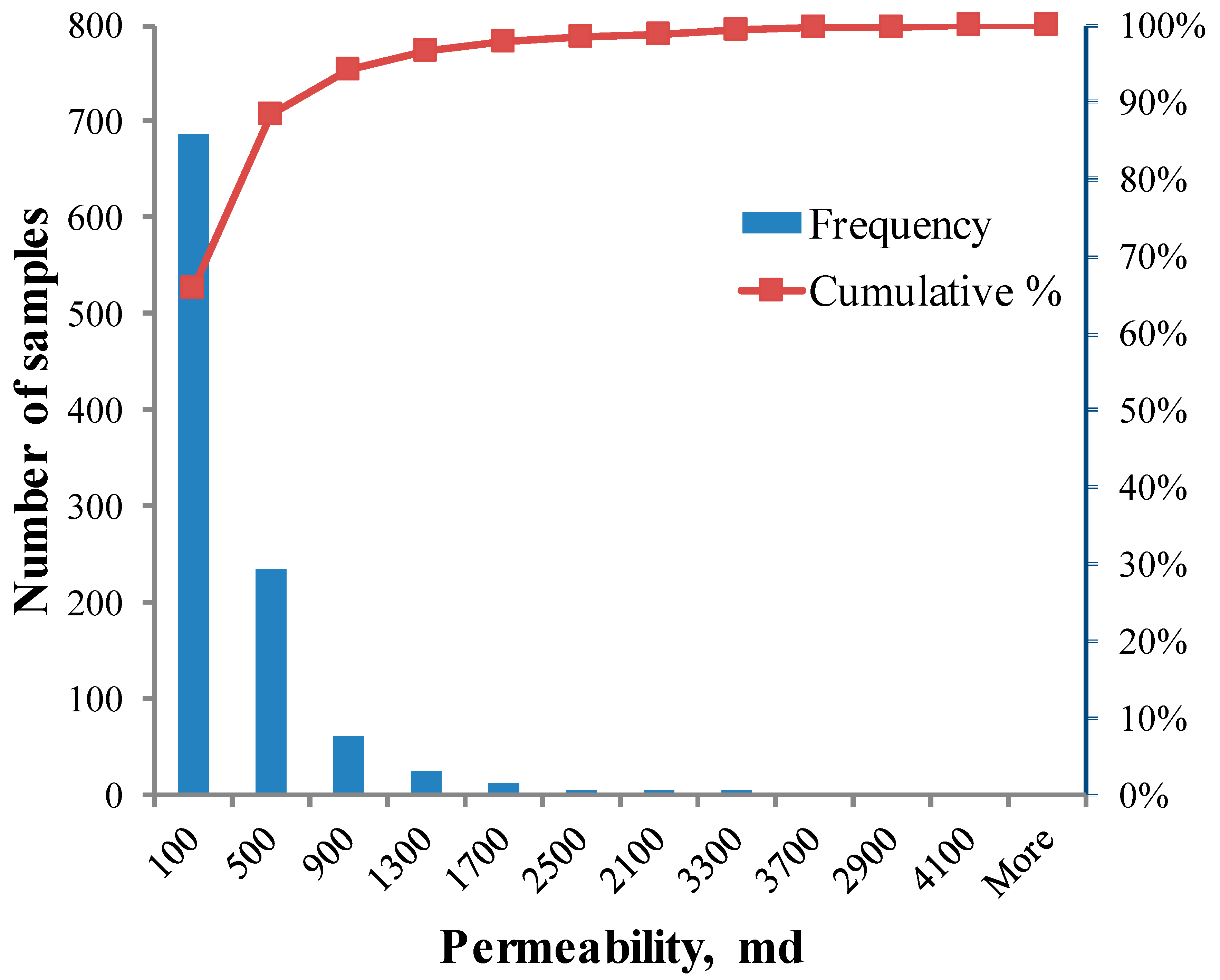
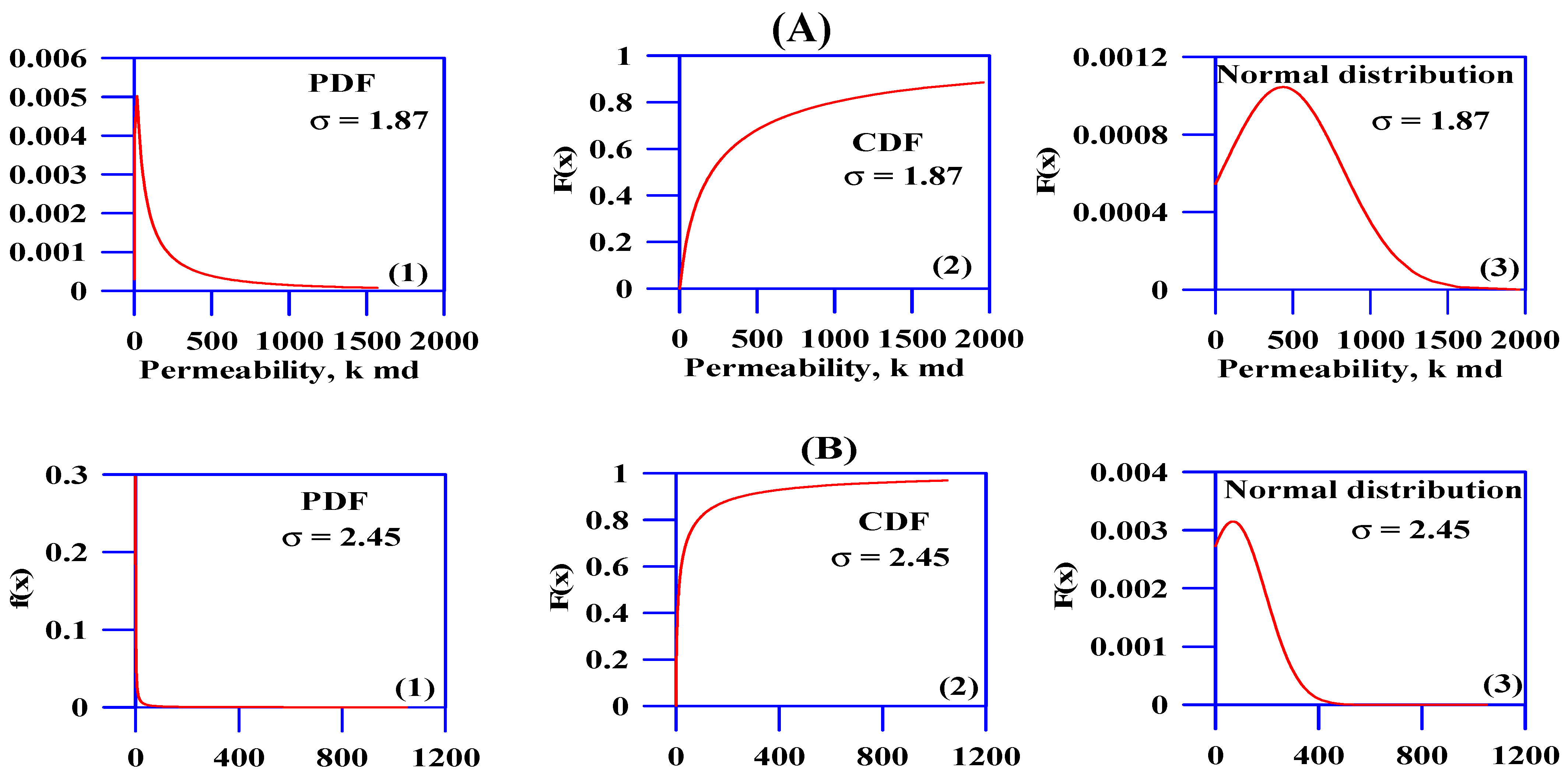
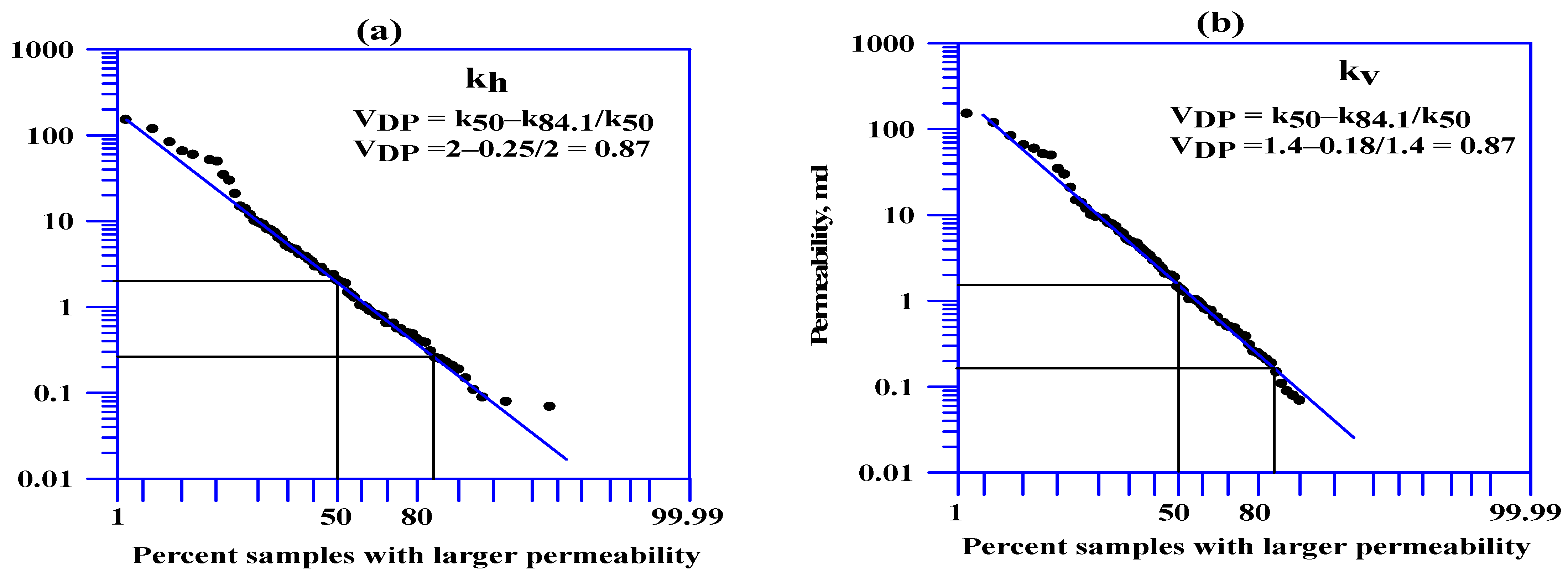

| Well | No. of Sample | Permeability, md | ||||||
|---|---|---|---|---|---|---|---|---|
| St.dev | Min. | Max. | kA | kH | kG | kA/kH | ||
| A | 164 | 381.9 | 0.07 | 1960 | 435.6 | 3.44 | 206.8 | 126.6 |
| B | 80 | 31.96 | 0.07 | 177 | 13.77 | 0.542 | 2.22 | 25.4 |
| C | 94 | 259.47 | 0.462 | 1610 | 198 | 9.17 | 64.78 | 21.59 |
| D | 519 | 126.65 | 0.01 | 1050 | 68.08 | 0.413 | 10.93 | 164.8 |
| E | 81 | 1176 | 0.08 | 4020 | 1035.77 | 1.996 | 177.88 | 517.9 |
| F | 28 | 14.22 | 0.07 | 60 | 8.63 | 0.399 | 1.93 | 21.6 |
| G | 56 | 211 | 0.01 | 1072 | 106.39 | 0.07 | 4.49 | 1519.9 |
| Total | 1022 | |||||||
| Well | St.dev. (σ) of ln k | Mean (μ) of ln k |
|---|---|---|
| A | 1.87 | 5.33 |
| B | 1.94 | 0.8 |
| C | 1.9 | 4.17 |
| D | 2.45 | 2.39 |
| E | 2.87 | 5.18 |
| F | 2 | 0.66 |
| G | 3.58 | 1.5 |
| Well | PHI Avg. | Coefficient of Variation (CV) | |||||
|---|---|---|---|---|---|---|---|
| Equation (4) | Salazar | Equation (7) | Equation (8) | Equation (17) | Equation (30) | ||
| A | 0.161 | 0.88 | 0.86 | 5.65 | 11.27 | 3.46 | 5.67 |
| B | 0.091 | 2.32 | 1.98 | 6.54 | 4.94 | 4.01 | 6.84 |
| C | 0.163 | 1.31 | 1.31 | 5.99 | 4.54 | 3.82 | 5.96 |
| D | 0.133 | 1.86 | 1.7 | 19.9 | 12.8 | 12.09 | 18.13 |
| E | 0.168 | 1.14 | 1.1 | 62.16 | 22.76 | 37.7 | 52.32 |
| F | 0.099 | 1.65 | 1.35 | 7.31 | 4.54 | 4.47 | 6.84 |
| G | 0.120 | 1.98 | 1.93 | 597.6 | 38.88 | 362.45 | 467.77 |
| Well | Dykstra–Parsons Coefficient (VDP) | HK | ||||||
|---|---|---|---|---|---|---|---|---|
| VDP Plot | VDP Data | Equation (20) | Equation (21) | Quantile | Equation (31) | HK Plot | Equation (36) | |
| A | 0.77 | 0.77 | 0.846 | 0.89 | 0.76 | 0.56 | 3.2 | 17 |
| B | 0.86 | 0.86 | 0.86 | 0.83 | 0.85 | 0.82 | 8.7 | 18.8 |
| C | 0.95 | 0.95 | 0.85 | 0.93 | 0.81 | 0.71 | 5 | 17.5 |
| D | 0.92 | 0.93 | 0.91 | 0.9 | 0.88 | 0.77 | 7.8 | 29.7 |
| E | 0.99 | 0.99 | 0.94 | 0.92 | 0.86 | 0.67 | 4.1 | 44.7 |
| F | 0.93 | 0.92 | 0.86 | 0.83 | 0.8 | 0.74 | 5.3 | 18.8 |
| G | 0.99 | 0.99 | 0.97 | 0.93 | 0.945 | 0.81 | 5.1 | 90.3 |
| Well | PHI Avg. | Lorenz Coefficient (LC) | ||||||
|---|---|---|---|---|---|---|---|---|
| k-H | k/phi-H | F-C | Equation (32) | Equation (33) | Equation (34) | Equation (35) | ||
| A | 0.161 | 0.47 | 0.46 | 0.44 | 0.83 | 0.81 | 0.81 | 0.81 |
| B | 0.091 | 0.80 | 0.74 | 0.70 | 0.85 | 0.83 | 0.84 | 0.83 |
| C | 0.163 | 0.6 | 0.59 | 0.54 | 0.83 | 0.82 | 0.82 | 0.82 |
| D | 0.133 | 0.74 | 0.71 | 0.68 | 0.91 | 0.92 | 0.91 | 0.92 |
| E | 0.168 | 0.61 | 0.59 | 0.52 | 0.95 | 0.96 | 0.95 | 0.96 |
| F | 0.099 | 0.71 | 0.65 | 0.60 | 0.85 | 0.84 | 0.84 | 0.84 |
| G | 0.120 | 0.79 | 0.77 | 0.66 | 0.99 | 0.99 | 0.99 | 0.99 |
| Heterogeneity Measures | Homogeneous | Slightly Heterogeneity | Heterogeneity | Very Heterogeneity | Extremely Heterogeneity | ||||
|---|---|---|---|---|---|---|---|---|---|
| More Than | Less Than | More Than | Less Than | More Than | Less Than | More Than | Less Than | ||
| CV | 0 | 0. | 0.29 | 0.29 | 0.79 | 0.79 | 2.4 | >2.4 | |
| VDP | 0 | 0 | 0.25 | 0.25 | 0.5 | 0.5 | 0.75 | 0.75 | 1 |
| LC | 0 | 0 | 0.16 | 0.16 | 0.38 | 0.38 | 0.67 | 0.67 | 1 |
| HK | 1 | 1 | 1.84 | 1.84 | 3.75 | 3.75 | 9.75 | >9.75 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Sharawy, M.S. Analysis of Vertical Heterogeneity Measures Based on Routine Core Data of Sandstone Reservoirs. Geosciences 2025, 15, 98. https://doi.org/10.3390/geosciences15030098
El Sharawy MS. Analysis of Vertical Heterogeneity Measures Based on Routine Core Data of Sandstone Reservoirs. Geosciences. 2025; 15(3):98. https://doi.org/10.3390/geosciences15030098
Chicago/Turabian StyleEl Sharawy, Mohamed S. 2025. "Analysis of Vertical Heterogeneity Measures Based on Routine Core Data of Sandstone Reservoirs" Geosciences 15, no. 3: 98. https://doi.org/10.3390/geosciences15030098
APA StyleEl Sharawy, M. S. (2025). Analysis of Vertical Heterogeneity Measures Based on Routine Core Data of Sandstone Reservoirs. Geosciences, 15(3), 98. https://doi.org/10.3390/geosciences15030098






