Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils
Abstract
Featured Application
Abstract
1. Introduction
2. Study Area and Methods for Spatial Variability Quantification
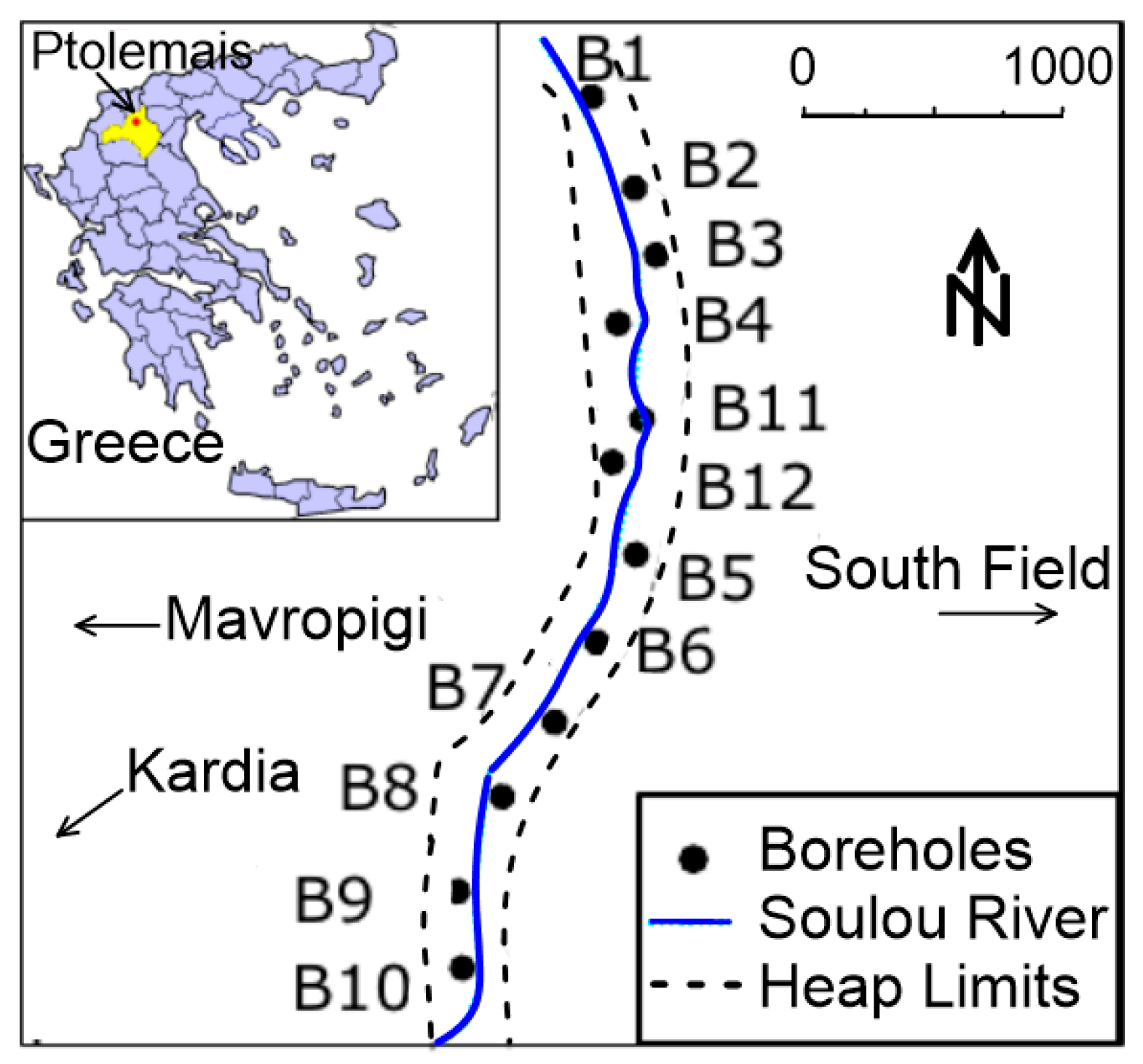
2.1. Study Area
2.2. Quantification of Spoils’ Spatial Variability
3. Spoil Spatial Variability
3.1. Overview
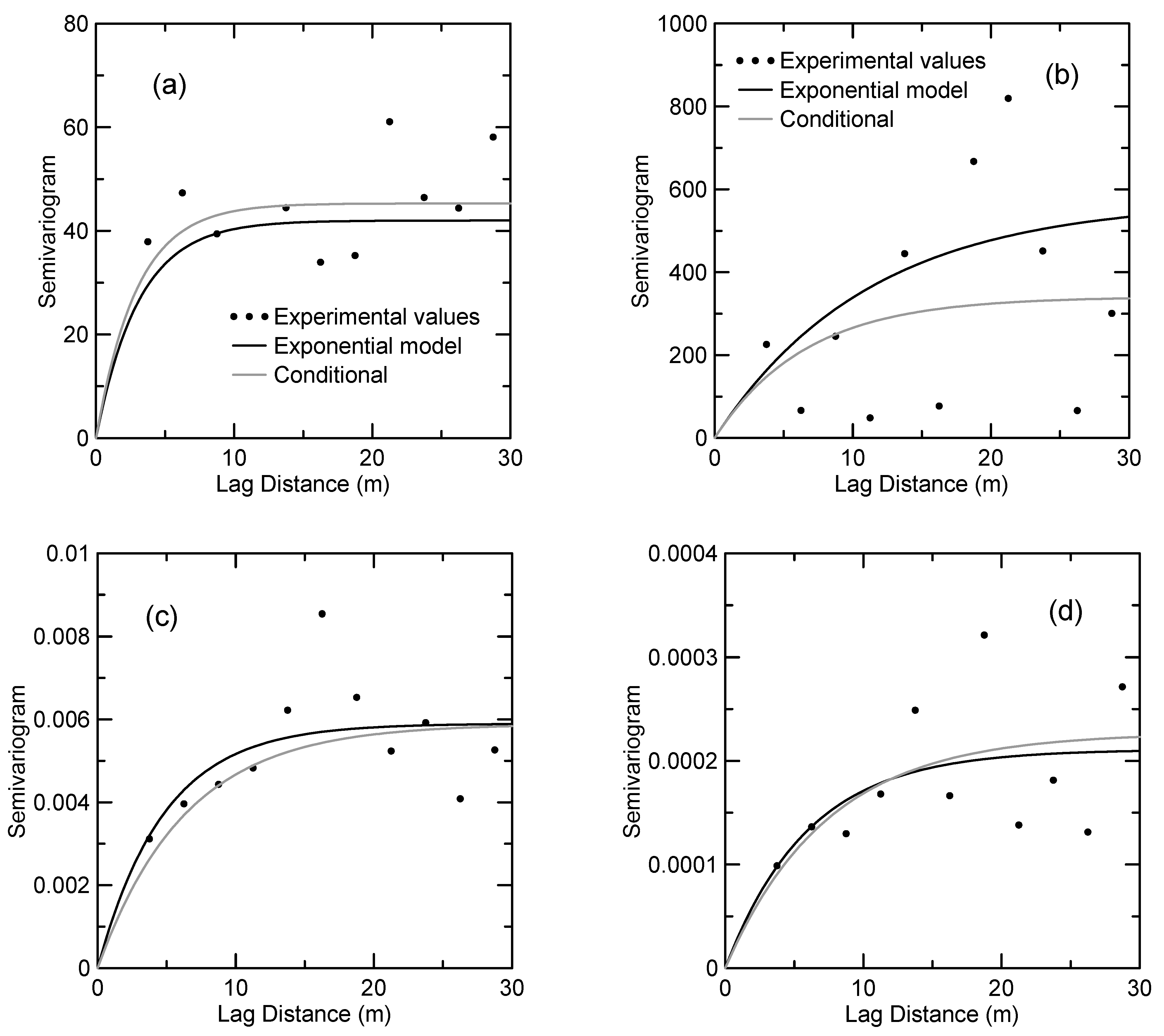
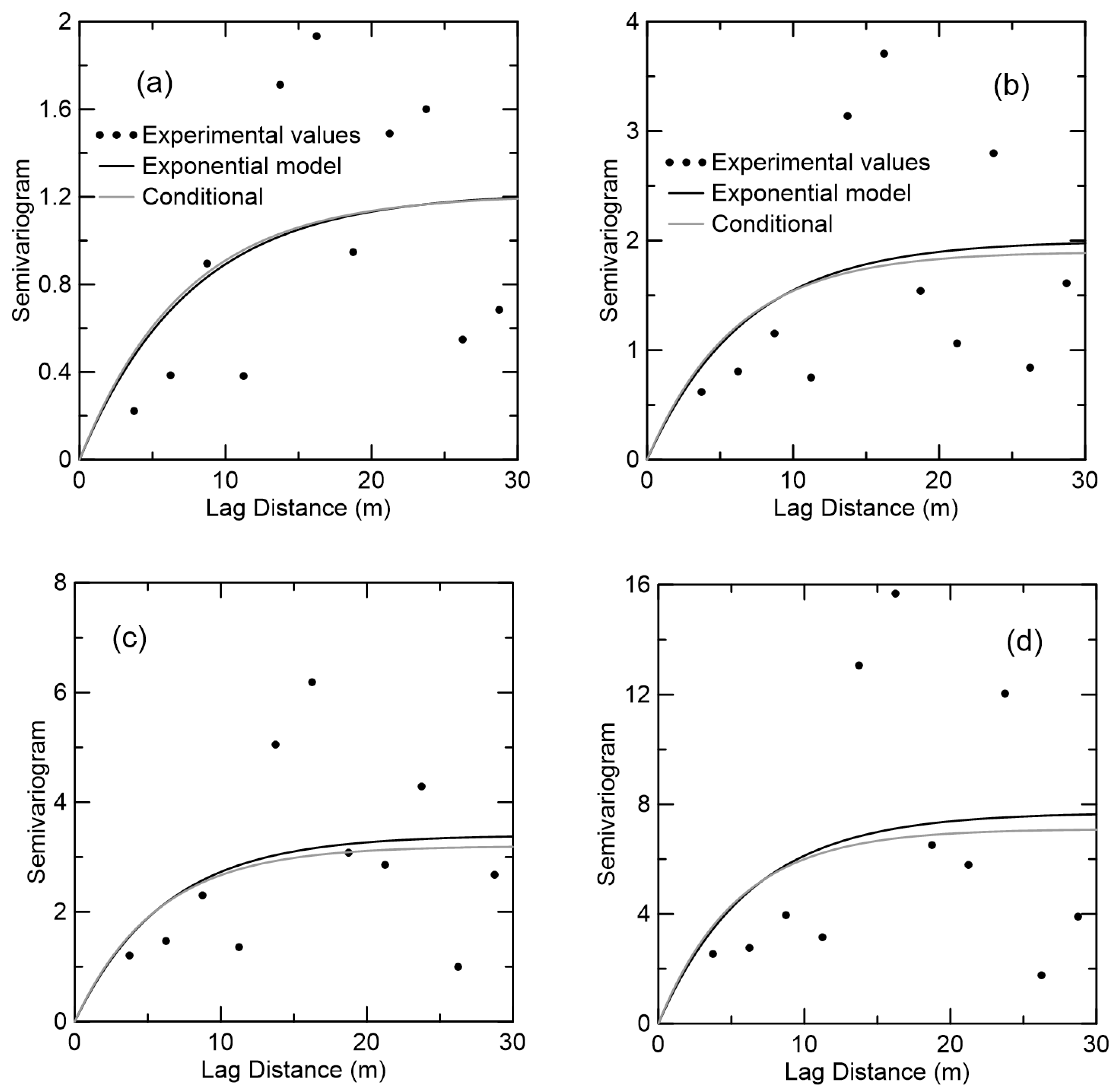
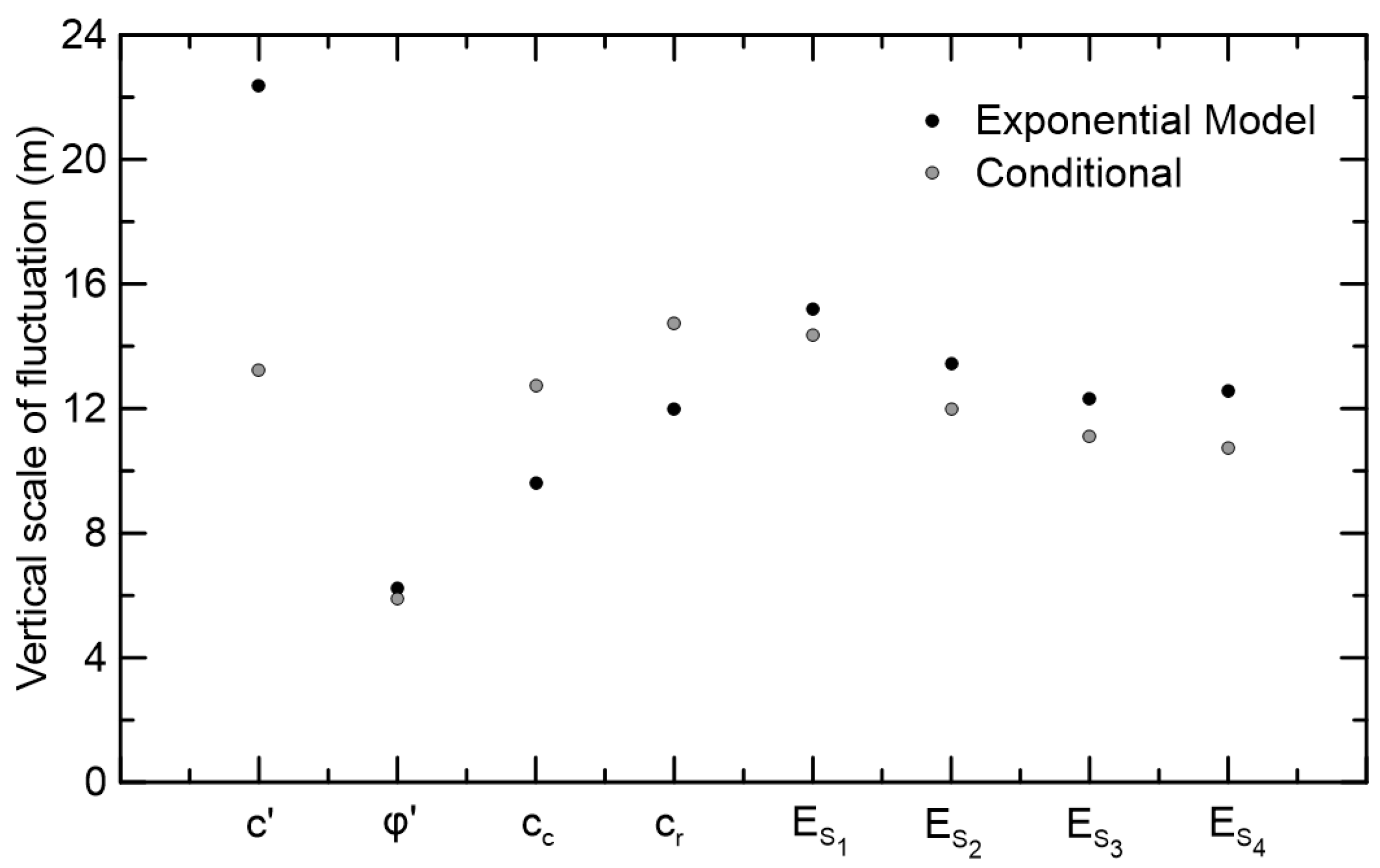
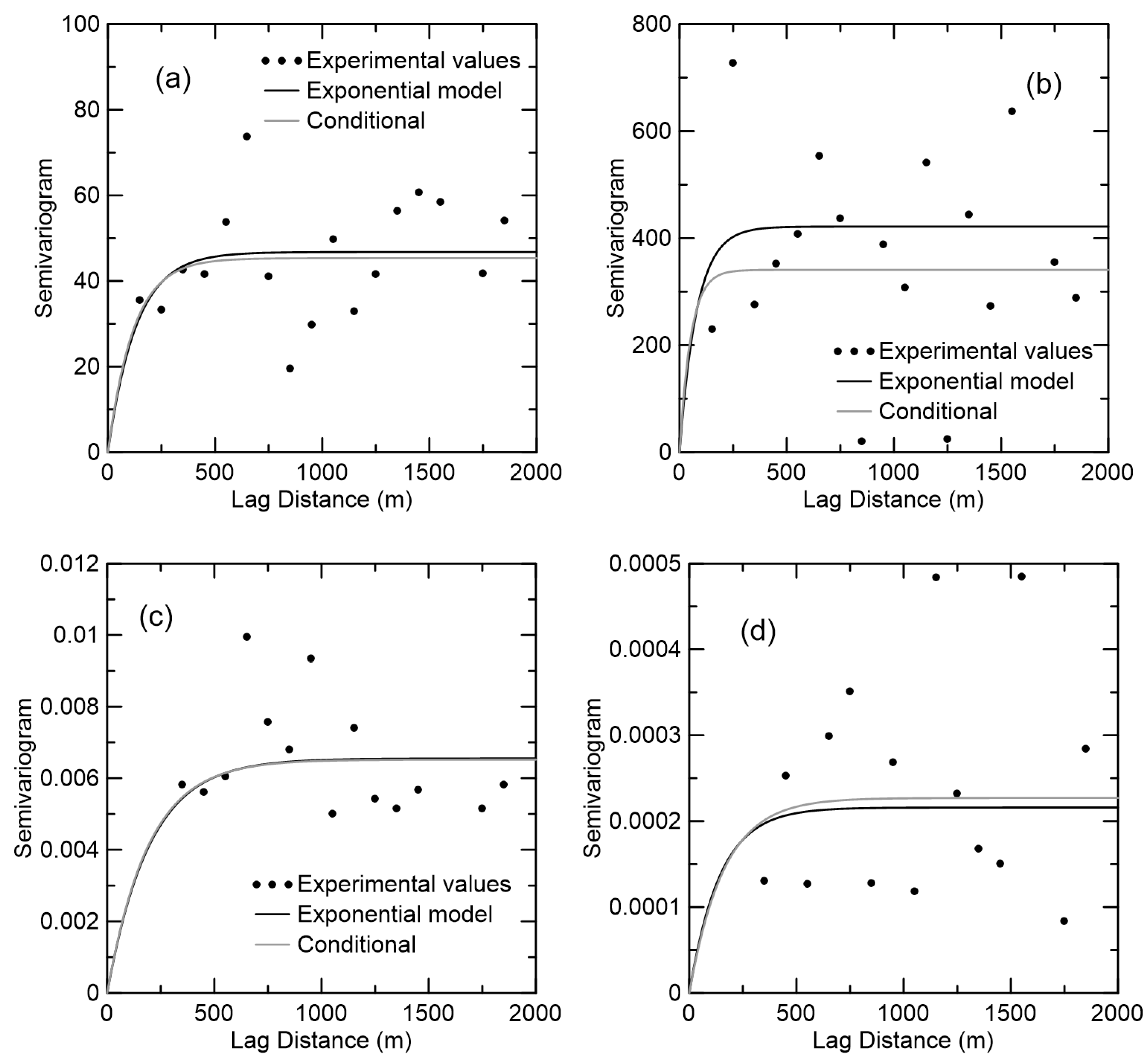
3.2. Vertical Scale of Fluctuation
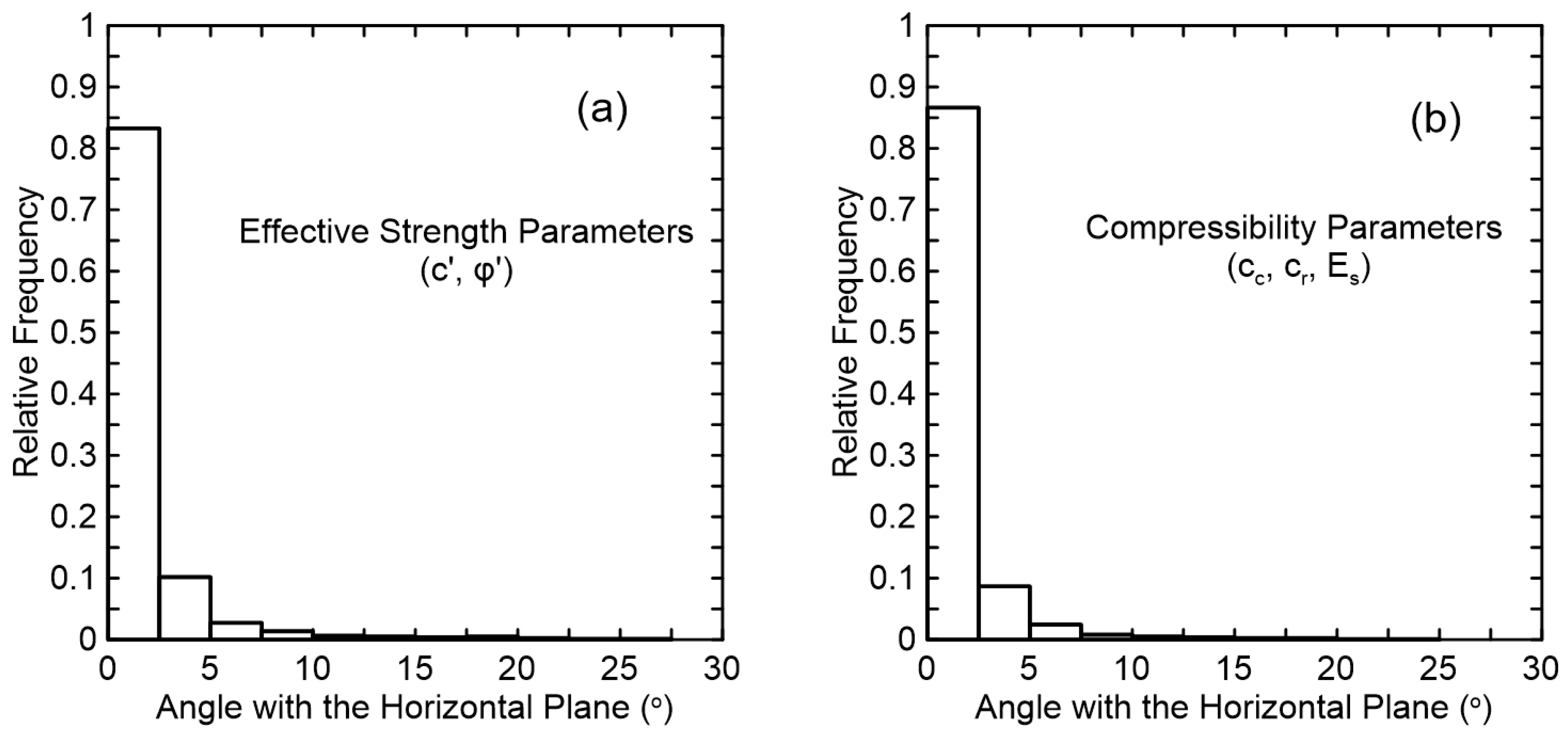
3.3. Horizontal Scale of Fluctuation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Coal 2023—Analysis and Forecast to 2026. 2023. Available online: www.iea.org (accessed on 24 February 2025).
- Masoudian, M.S.; Zevgolis, I.E.; Deliveris, A.V.; Marshall, A.M.; Heron, C.M.; Koukouzas, N.C. Stability and characterisation of spoil heaps in European surface lignite mines: A state-of-the-art review in light of new data. Environ. Earth Sci. 2019, 78, 505. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Theocharis, A.I.; Deliveris, A.V.; Koukouzas, N.C.; Roumpos, C.; Marshall, A.M. Geotechnical Characterization of Fine-Grained Spoil Material from Surface Coal Mines. J. Geotech. Geoenviron. Eng. 2021, 147, 04021050. [Google Scholar] [CrossRef]
- Kasmer, O.; Ulusay, R.; Gokceoglu, C. Spoil pile instabilities with reference to a strip coal mine in Turkey: Mechanisms and assessment of deformations. Environ. Geol. 2006, 49, 570–585. [Google Scholar] [CrossRef]
- Vaníček, I.; Záleský, J.; Lamboj, L.; Kurka, J. Two examples of clay slope stability in areas affected by previous man-made activity—Open pit mines, landfills. In Proceedings of the 16th International Conference on Soil Mechanics and Geotechnical Engineering: Geotechnology in Harmony with the Global Environment, Osaka, Japan, 12–16 September 2005; pp. 2603–2606. [Google Scholar]
- Zevgolis, I.E. Geotechnical characterization of mining rock waste dumps in central Evia, Greece. Environ. Earth Sci. 2018, 77, 566. [Google Scholar] [CrossRef]
- Cadierno, J.F.; Romero, M.I.G.; Valdés, A.J.; del Pozo, J.M.M.; González, J.G.; Robles, D.R.; Espinosa, J.V. Characterization of Colliery Spoils in León: Potential Uses in Rural Infrastructures. Geotech. Geol. Eng. 2014, 32, 439–452. [Google Scholar] [CrossRef]
- Ulusay, R.; Arikan, F.; Yoleri, M.; Çaǧlan, D. Engineering geological characterization of coal mine waste material and an evaluation in the context of back-analysis of spoil pile instabilities in a strip mine, SW Turkey. Eng. Geol. 1995, 40, 77–101. [Google Scholar] [CrossRef]
- Wu, T.H.; Kraft, L.M. The Probability of Foundation Safety. J. Soil Mech. Found. Div. 1967, 93, 213–231. [Google Scholar] [CrossRef]
- Ching, J.; Lee, S.-W.; Phoon, K.-K. Undrained strength for a 3D spatially variable clay column subjected to compression or shear. Probabilistic Eng. Mech. 2016, 45, 127–139. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T.; Cao, Z. Site-specific probability distribution of geotechnical properties. Comput. Geotech. 2015, 70, 159–168. [Google Scholar] [CrossRef]
- Baecher, G.B.; Marr, W.A.; Lin, J.S.; Consla, J.A. Critical Parameters for Tailings Embankments; U.S. Department of the Interior: Denver, CO, USA, 1983.
- Fenton, G.A.; Griffiths, D.V.; Zhang, X. Load and resistance factor design of shallow foundations against bearing failure. Can. Geotech. J. 2008, 45, 1556–1571. [Google Scholar] [CrossRef]
- Griffiths, D.; Huang, J.; Fenton, G.A. Probabilistic infinite slope analysis. Comput. Geotech. 2011, 38, 577–584. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V.; Williams, M.B. Reliability of traditional retaining wall design. Geotechnique 2005, 55, 55–62. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Three-Dimensional Seepage through Spatially Random Soil. J. Geotech. Geoenviron. Eng. 1997, 123, 153–160. [Google Scholar] [CrossRef]
- Ching, J.; Hu, Y.-G.; Phoon, K.-K. Effective Young’s modulus of a spatially variable soil mass under a footing. Struct. Saf. 2018, 73, 99–113. [Google Scholar] [CrossRef]
- Firouzianbandpey, S.; Griffiths, D.; Ibsen, L.; Andersen, L. Spatial correlation length of normalized cone data in sand: Case study in the north of Denmark. Can. Geotech. J. 2014, 51, 844–857. [Google Scholar] [CrossRef]
- Lloret-Cabot, M.; Fenton, G.; Hicks, M. On the estimation of scale of fluctuation in geostatistics. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2014, 8, 129–140. [Google Scholar] [CrossRef]
- Bagińska, I.; Kawa, M.; Janecki, W. Estimation of spatial variability of lignite mine dumping ground soil properties using CPTu results. Stud. Geotech. Mech. 2016, 38, 3–13. [Google Scholar] [CrossRef]
- Bagińska, I.; Kawa, M.; Janecki, W. Estimation of spatial variability properties of mine waste dump using CPTu results—Case study. In Cone Penetration Testing 2018; Hicks, M.A., Pisanò, F., Peuchen, J., Eds.; CRC Press: Delft, The Netherlands, 2018; pp. 109–115. [Google Scholar]
- Olesiak, S. Influence of the heterogeneity of a dump soil on the assessment of its selected properties. Stud. Geotech. Mech. 2020, 42, 263–275. [Google Scholar] [CrossRef]
- Thiruchittampalam, S.; Banerjee, B.P.; Glenn, N.F.; Raval, S. An Evaluation of Calibrated and Uncalibrated High-Resolution RGB Data in Time Series Analysis for Coal Spoil Characterisation: A Comparative Study. arXiv 2024, arXiv:2402.00170. Available online: https://arxiv.org/abs/2402.00170v1 (accessed on 5 March 2025).
- Kumar, A.; Das, S.K.; Nainegali, L.; Reddy, K.R. Phytostabilization of coalmine overburden waste rock dump slopes: Current status, challenges, and perspectives. Bull. Eng. Geol. Environ. 2023, 82, 1–31. [Google Scholar] [CrossRef]
- Theocharis, A.I.; Zevgolis, I.E.; Roumpos, C.; Koukouzas, N.C. Probability distributions of geotechnical properties for heterogeneous lignite mine spoils. Int. J. Geotech. Eng. 2024, 18, 528–536. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Random Fields, Analysis and Synthesis; MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Vanmarcke, E.H. Probabilistic Modeling of Soil Profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Bong, T.; Stuedlein, A.W. Spatial Variability of CPT Parameters and Silty Fines in Liquefiable Beach Sands. J. Geotech. Geoenviron. Eng. 2017, 143, 04017093. [Google Scholar] [CrossRef]
- Stuedlein, A.W.; Kramer, S.L.; Arduino, P.; Holtz, R.D. Geotechnical Characterization and Random Field Modeling of Desiccated Clay. J. Geotech. Geoenviron. Eng. 2012, 138, 1301–1313. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; John Wiley & Sons: West Sussex, UK, 2003. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Kriging with a Small Number of Data Points Supported by Jack-Knifing, a Case Study in the Sava Depression (Northern Croatia). Geosciences 2019, 9, 36. [Google Scholar] [CrossRef]
- Caballero, S.R.; Bheemasetti, T.V.; Puppala, A.J.; Chakraborty, S. Geotechnical Visualization and Three-Dimensional Geostatistics Modeling of Highly Variable Soils of a Hydraulic Fill Dam. J. Geotech. Geoenviron. Eng. 2022, 148, 05022006. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Samui, P. Geostatistical modelling of spatial and depth variability of SPT data for Bangalore. Géoméch. Geoeng. 2007, 2, 307–316. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data Revised Edition; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Journel, A.G.; Huijbregts, C.J. Mining Geo-Statistics; Academic Press: London, UK, 1978. [Google Scholar]
- Technical Committee of Engineering Practice of Risk Assessment & Management (TC304 ISSMGE). State-of-the-Art Review of Inherent Variability and Uncertainty in Geotechnical Properties and Models; ISSMGE. 2021. Available online: https://issmge.org/files/reports/TC304-State-of-the-art-review-of-inherent-variability-and-uncertainty-in-geotechnical-properties-and-models.pdf (accessed on 5 March 2025). [CrossRef]
- Cami, B.; Javankhoshdel, S.; Phoon, K.-K.; Ching, J. Scale of Fluctuation for Spatially Varying Soils: Estimation Methods and Values. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 03120002. [Google Scholar] [CrossRef]
- Onyejekwe, S.; Ge, L. Scale of Fluctuation of Geotechnical Parameters Estimated from CPTu and Laboratory Test Data. In Foundation Engineering in the Face of Uncertainty; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 434–443. [Google Scholar] [CrossRef]
- Garala, T.K.; Cui, G.; Kantesaria, N.; Heron, C.M.; Marshall, A.M.; Žižka, L. Characterisation of spoil materials to develop an equivalent spoil material for physical model tests. Górnictwo Odkrywkowe (Surf. Min.) 2022, 4, 23–29. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zevgolis, I.E.; Theocharis, A.I.; Koukouzas, N.C. Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils. Geosciences 2025, 15, 97. https://doi.org/10.3390/geosciences15030097
Zevgolis IE, Theocharis AI, Koukouzas NC. Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils. Geosciences. 2025; 15(3):97. https://doi.org/10.3390/geosciences15030097
Chicago/Turabian StyleZevgolis, Ioannis E., Alexandros I. Theocharis, and Nikolaos C. Koukouzas. 2025. "Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils" Geosciences 15, no. 3: 97. https://doi.org/10.3390/geosciences15030097
APA StyleZevgolis, I. E., Theocharis, A. I., & Koukouzas, N. C. (2025). Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils. Geosciences, 15(3), 97. https://doi.org/10.3390/geosciences15030097







