Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019
Abstract
1. Introduction
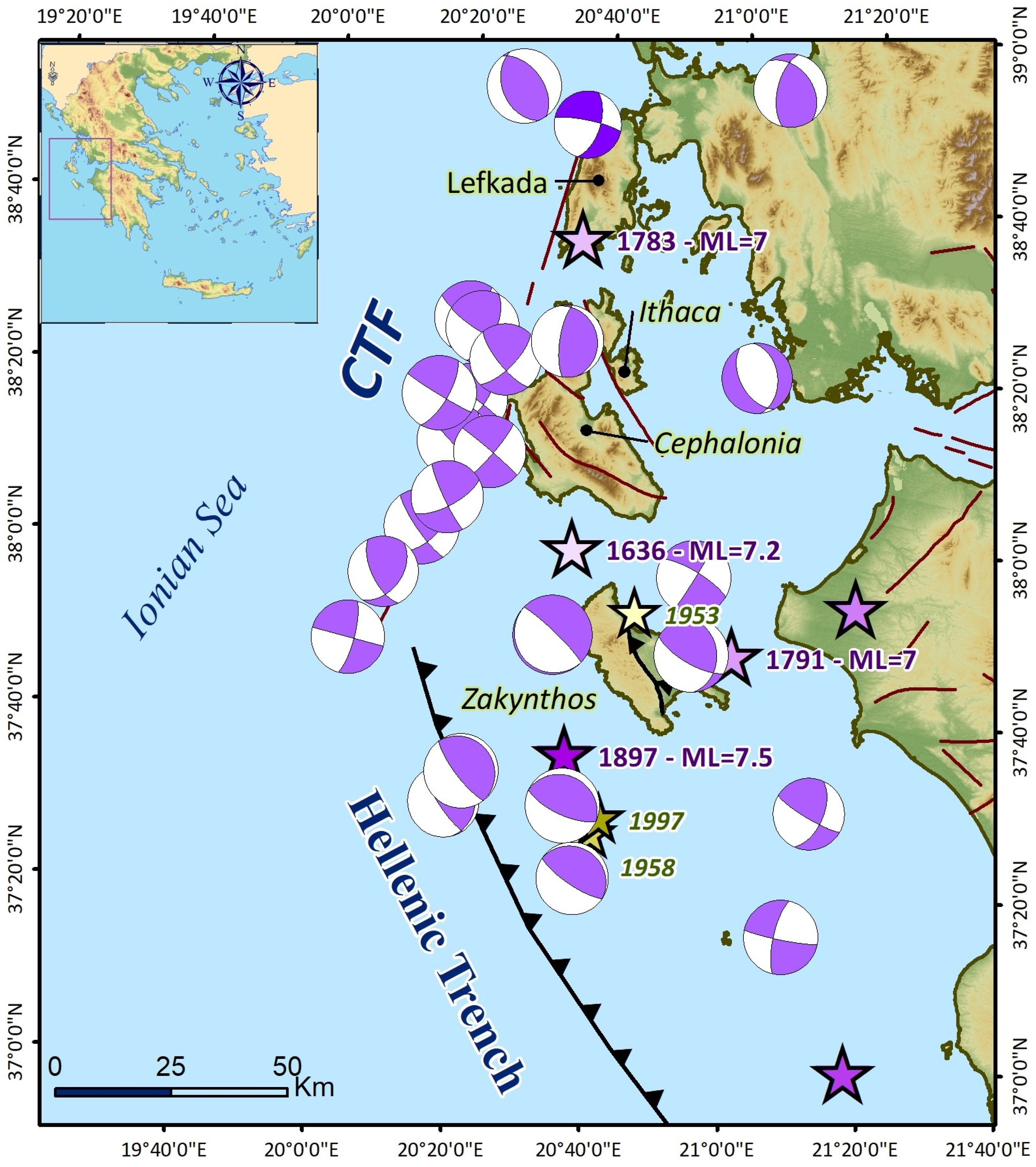
2. Seismotectonic Regime of Cephalonia, Lefkada and Zakynthos Islands
3. Seismological Data
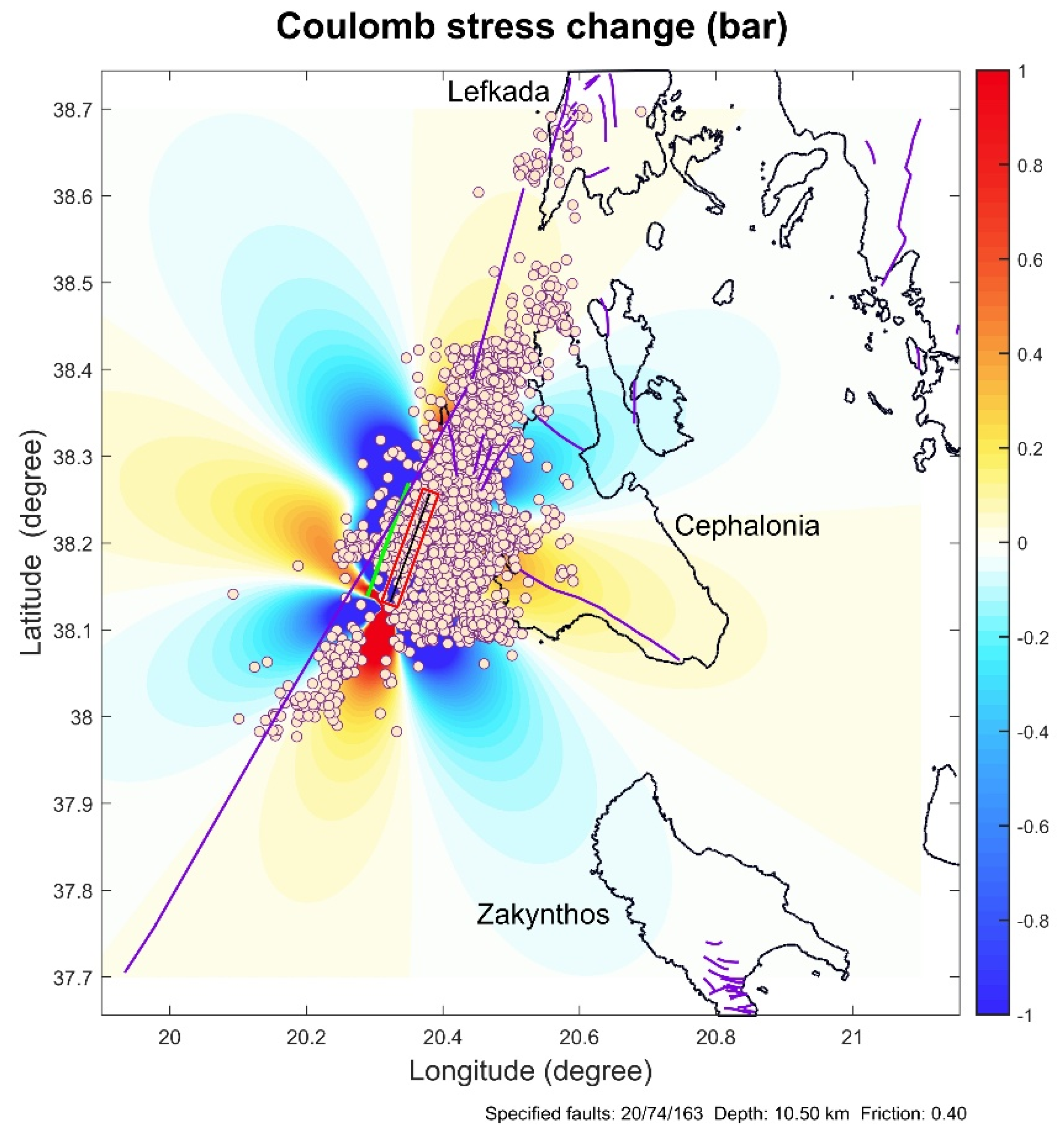
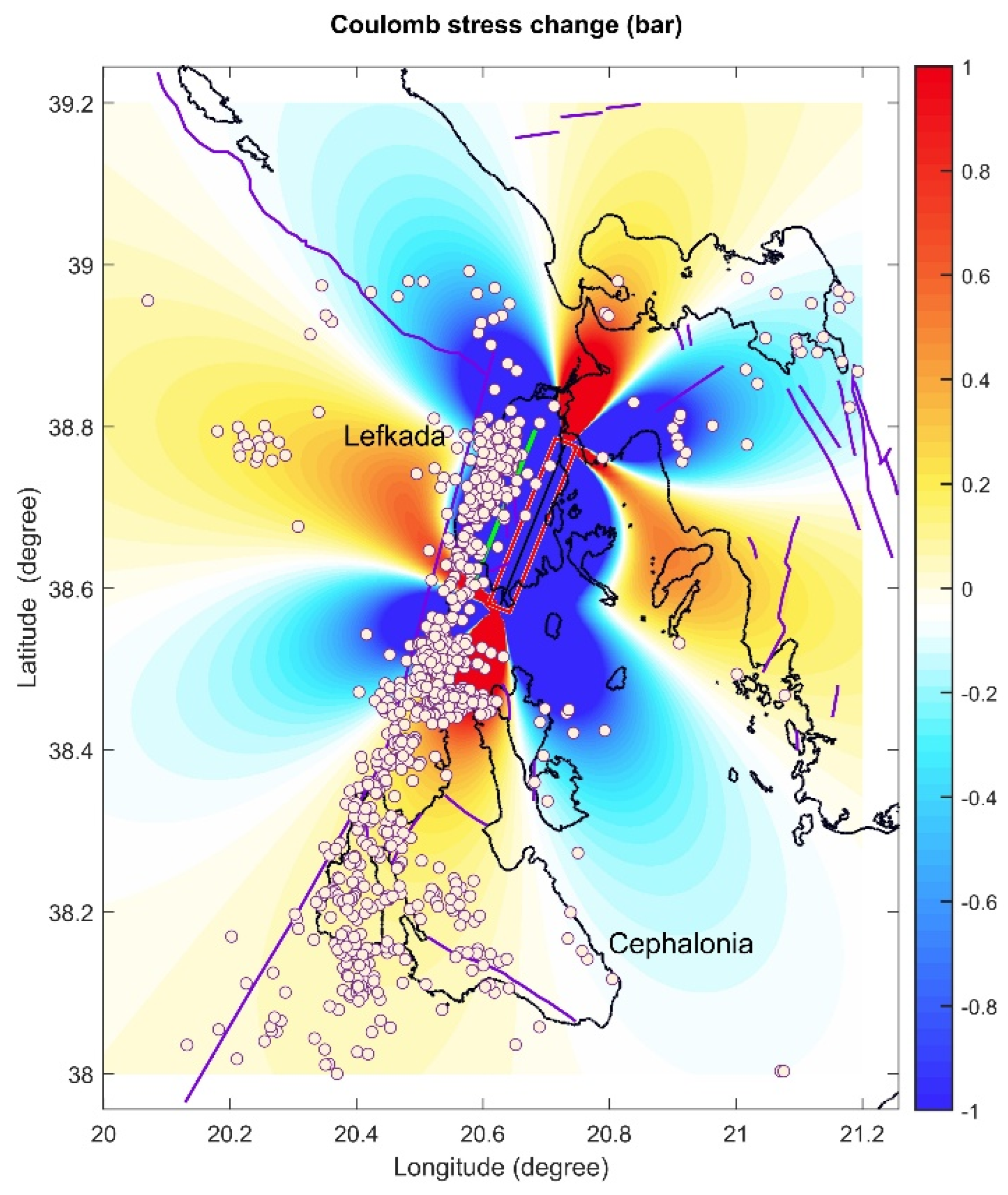
4. Coulomb Stress Changes of the Three Major Ionian Islands Events
5. Scaling Properties in Aftershock Sequences: Methods Used
5.1. The Frequency–Magnitude Distribution
5.2. Temporal Scaling Properties
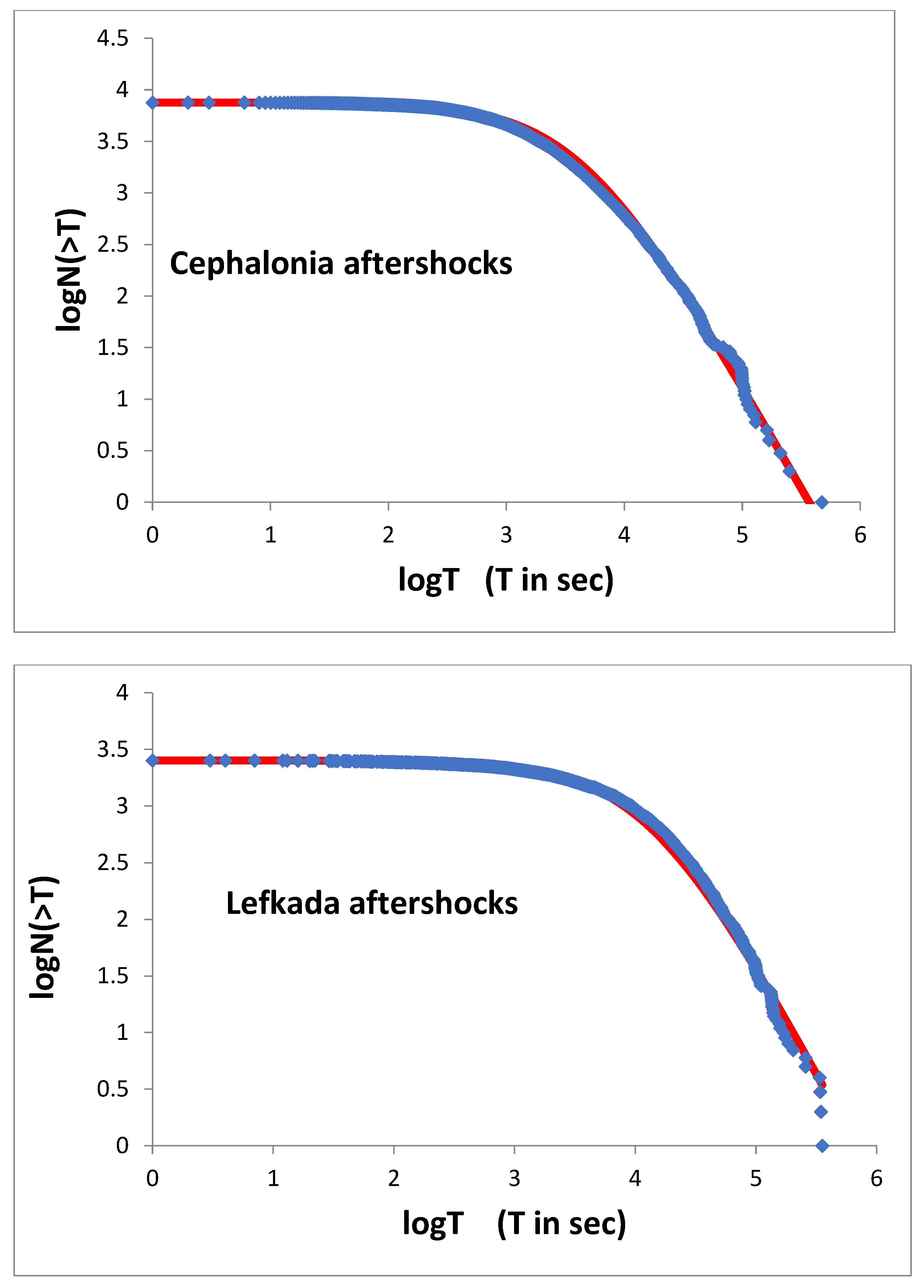
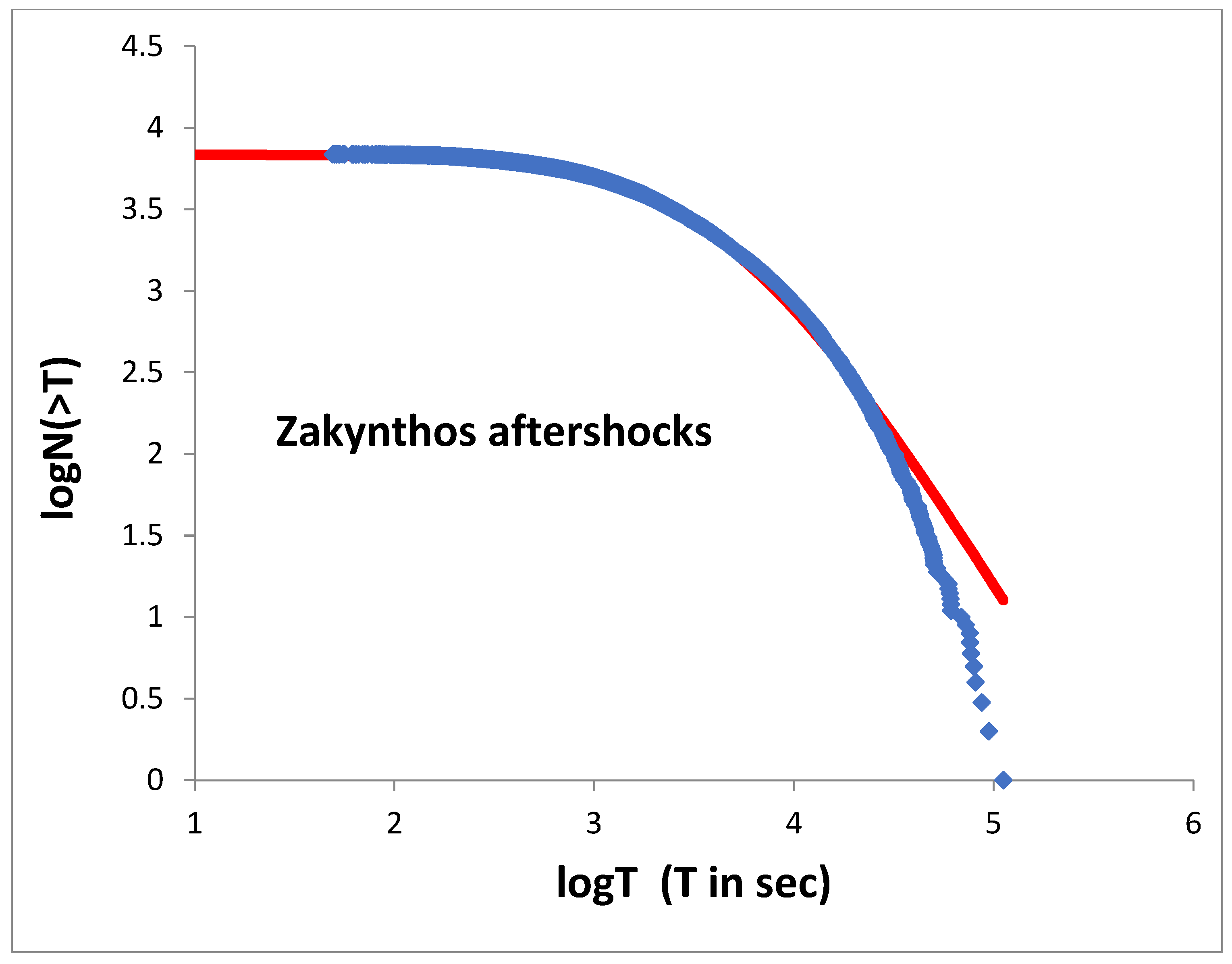
5.3. Earthquake Scaling Properties in Terms of Non-Extensive Statistical Physics
6. Scaling Properties of the Recent Ionian Island Aftershock Sequences: Results
6.1. The Frequency–Magnitude Distribution of the Recent Ionian Island Aftershock Sequences
6.2. Temporal Scaling Properties of the Recent Ionian Island Aftershock Sequences
6.3. Scaling Properties of the Recent Ionian Island Aftershock Sequences in Terms of Non-Extensive Statistical Physics
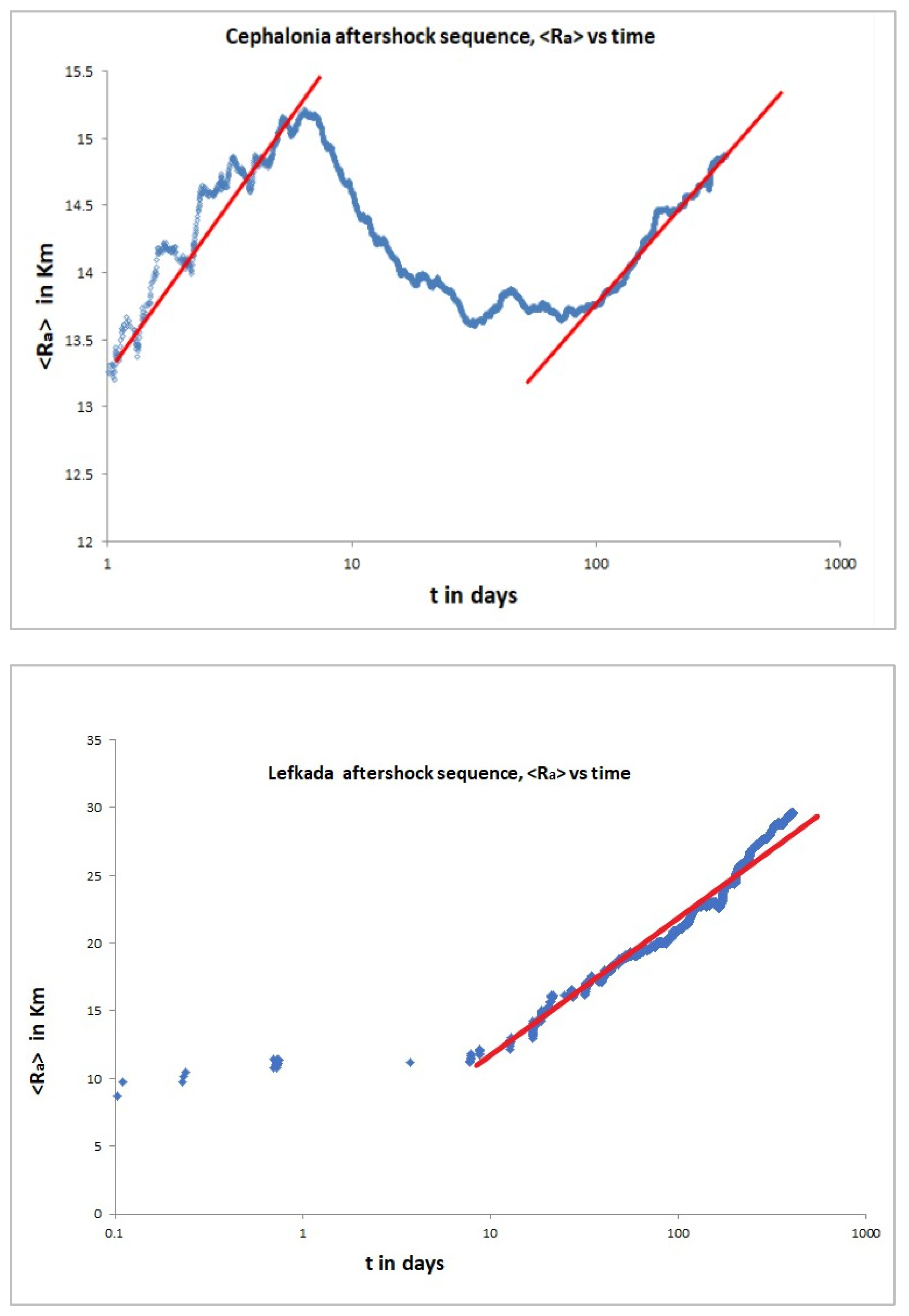
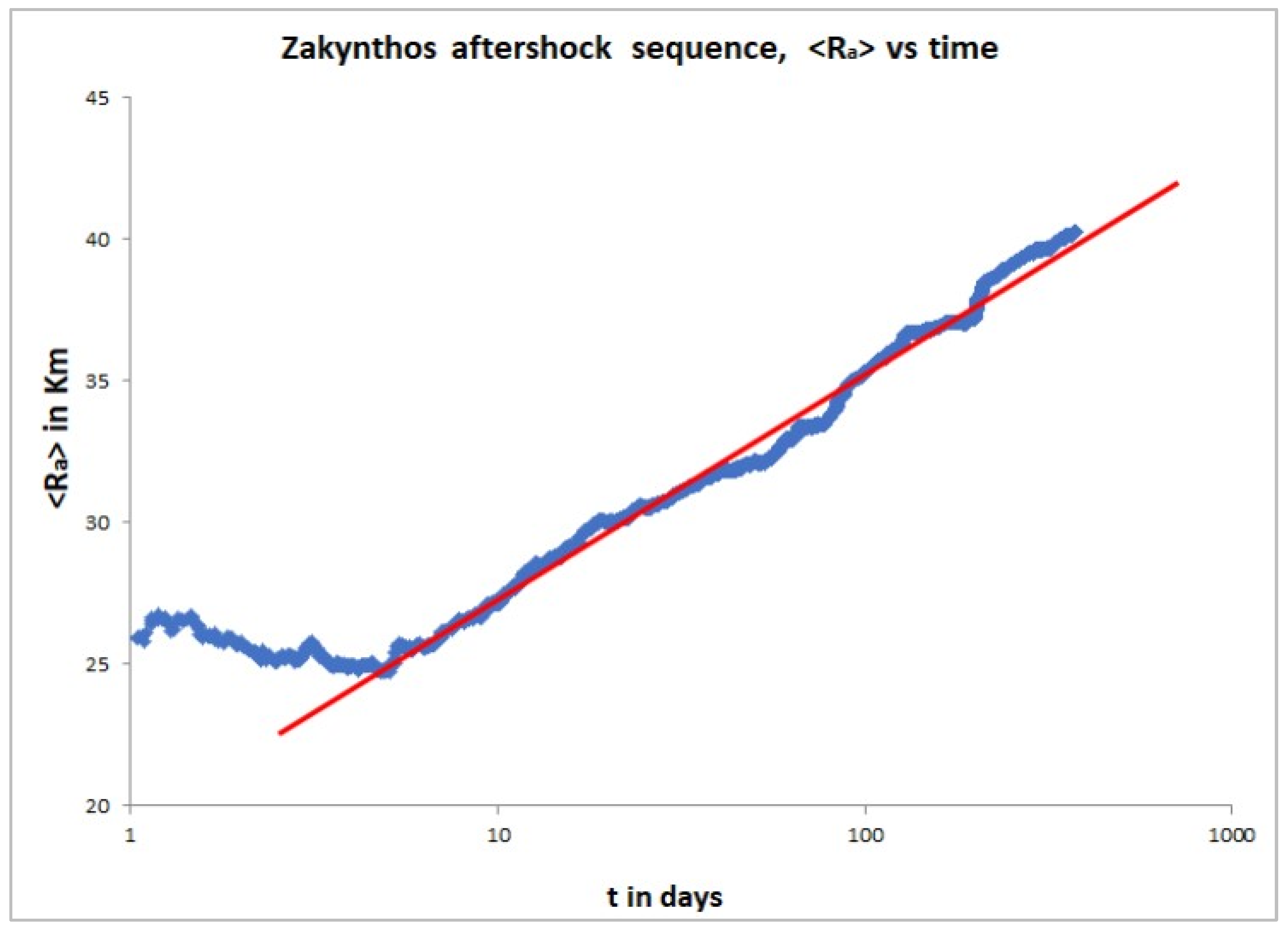
7. Scaling of Aftershock Zone with Time
8. Discussion
9. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ganas, A.; Cannavò, F.; González, P.J.; Drakatos, G. The Geodetic Signature of the January 26, 2014 Earthquake Onshore Kefalonia, Greece. Unpublished Report 2014. Available online: https://www.gein.noa.gr/Documents/pdf/VLSM_co-seismic_26-1-2014_13_55_UTC.pdf (accessed on 20 September 2024).
- Valkaniotis, S.; Ganas, A.; Papathanassiou, G.; Papanikolaou, M. Field observations of geological effects triggered by the January–February 2014 Kefalonia (Ionian Sea, Greece) earthquakes. Tectonophysics 2014, 630, 150–157. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Karakostas, V.; Mesimeri, M.; Chouliaras, G.; Kourouklas, C. The M6.7 17 November 2015 Lefkada (Greece) earthquake: Structural interpretation by means of aftershock analysis. Pure Appl. Geophys. 2017, 174, 3869–3888. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Kapetanidis, V.; Karakonstantis, A.; Spingos, I.; Pavlou, K.; Kaviris, G.; Kassaras, I.; Sakkas, V.; Voulgaris, N. The 25 October 2018 Zakynthos (Greece) earthquake: Seismic activity at the transition between a transform fault and a subduction zone. Geophys. J. Int. 2021, 225, 15–36. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papazachou, C.B. The Earthquakes of Greece; Ziti Publications: Thessaloniki, Greece, 2003; p. 304. [Google Scholar]
- Kiratzi, A.; Langston, C. Moment tensor inversion of the January 17, 1983 Kefallinia event of Ionian Islands. Geophys. J. Int. 1991, 105, 529–535. [Google Scholar] [CrossRef]
- Tzanis, A.; Vallianatos, F.; Makropoulos, K. Seismic and electrical precursors to the 17-1-1983, M7 Kefallinia earthquake, Greece: Signatures of a SOC system. Phys. Chem. Earth Part A Solid Earth Geod. 2000, 25, 281–287. [Google Scholar] [CrossRef]
- Papadimitriou, E. Mode of strong earthquake recurrence in the central Ionian Islands (Greece): Possible triggering due to Coulomb stress changes generated by the occurrence of previous strong shocks. Bull. Seismol. Soc. Am. 2002, 92, 3293–3308. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E.; Mesimeri, M.; Gkarlaouni, C.; Paradisopoulou, P. The 2014 Kefalonia doublet (Mw6.1 and Mw6.0), Central Ionian Islands, Greece: Seismotectonic implications along the Kefalonia transform fault zone. ActaGeophysica 2014, 63, 1–16. [Google Scholar] [CrossRef]
- Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. 1961, 30, 521–605. [Google Scholar]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C. Earthquakes as a self-organized critical phenomenon. J. Geophys. Res. Solid Earth 1989, 94, 15635–15637. [Google Scholar] [CrossRef]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 1019. [Google Scholar] [CrossRef]
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A 2016, 472, 20160497. [Google Scholar] [CrossRef]
- Vallianatos, F.; Chatzopoulos, G. A Complexity View into the Physics of the Accelerating Seismic Release Hypothesis: Theoretical Principles. Entropy 2018, 20, 754. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L.; Lapenna, V.; Vallianatos, F. Monofractal and multifractal approaches in investigating scaling properties in temporal patterns of the 1983–2000 seismicity in the western Corinth graben, Greece. Phys. Earth Planet. Int. 2002, 131, 63–79. [Google Scholar] [CrossRef]
- Telesca, L.; Macchiato, M. Time-scaling properties of the Umbria-Marche 1997–1998 seismic crisis, investigated by the detrended fluctuation analysis of interevent time series Chaos. Solitons Fractals 2004, 19, 377–385. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. A description of seismicity based on non-extensive statistical physics: A review. In Earthquakes and Their Impact on Society; D’Amico, S., Ed.; Springer Natural Hazards: Heidelberg, Germany, 2016; pp. 1–42. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Evidence of Nonextensive Statistical Physics behavior of the Hellenic Subduction Zone seismicity. Tectonophysics 2013, 608, 1037–1048. [Google Scholar] [CrossRef]
- Davidsen, J.; Goltz, C. Are seismic waiting time distributions universal? Geophys. Res. Lett. 2004, 31, L21612. [Google Scholar] [CrossRef]
- Corral, Á.; Christensen, K. Comment on “earthquakes descaled: On waiting time distributions and scaling laws”. Phys. Rev. Lett. 2006, 96, 109801. [Google Scholar] [CrossRef] [PubMed]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and long-range correlations in the earthquake activity at the West Corinth rift (Greece). Nonlin. Processes Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-0-387-85358-1. [Google Scholar] [CrossRef]
- Kokinou, E.; Papadimitriou, E.; Karakostas, V.; Kamberis, V.; Vallianatos, F. The Kefalonia Transform Zone (offshore Western Greece) with special emphasis to its prolongation towards the Ionian Abyssal Plain. Mar. Geophys. Res. 2006, 27, 241–252. [Google Scholar] [CrossRef]
- Scordilis, E.; Karakaisis, G.; Karakostas, V.; Panagiotopoulos, D.; Comninakis, P.; Papazachos, B.C. Evidence for transform faulting in the Ionian Sea: The Kefalonia Island earthquake sequence of 1983. Pure Appl. Geophys. 1985, 123, 388–397. [Google Scholar] [CrossRef]
- Sachpazi, M.; Hirn, A.; Clement, C.; Haslinger, F.; Laigle, M.; Kissling, E.; Charvis, P.; Hello, Y.; Lepine, J.C.; Sapin, M.; et al. Western Hellenic subduction and Kefalonia Transform: Local earthquakes and plate transport and strain. Tectonophysics 2000, 319, 301–319. [Google Scholar] [CrossRef]
- Le Pichon, X.; Lallemant, S.J.; Chamot-Rooke, N.; Lemeur, D.; Pascal, G. The Mediterranean Ridge backstop and the Hellenic nappes. Mar. Geol. 2002, 186, 111–125. [Google Scholar] [CrossRef]
- Hollenstein, C.; Müller, M.D.; Geiger, A.; Kahle, H.G. Crustal motion and deformation in Greece from a decade of GPS measurements, 1993–2003. Tectonophysics 2008, 449, 17–40. [Google Scholar] [CrossRef]
- Papazachos, C.B.; Kiratzi, A. A detailed study of the active crustal deformation in the Aegean and surrounding area. Tectonophysics 1996, 253, 129–153. [Google Scholar] [CrossRef]
- Louvari, E.; Kiratzi, A.; Papazachos, B.C. The Cephalonia Transform Fault and its extension to western Lefkada island (Greece). Tectonophysics 1999, 308, 223–236. [Google Scholar] [CrossRef]
- Makropoulos, K.; Kaviris, G.; Kouskouna, V. An extended earthquake catalogue for Greece and adjacent areas since 1900, enriched with the Mw addition. Nat. Hazards Earth Syst. Sci. 2012, 12, 1425–1430. [Google Scholar] [CrossRef]
- Bonatis, P.; Karakostas, V.G.; Papadimitriou, E.E.; Kaviris, G. Investigation of the Factors Controlling the Duration and Productivity of Aftershocks Following Strong Earthquakes in Greece. Geosciences 2022, 12, 328. [Google Scholar] [CrossRef]
- Evangelidis, C.P.; Triantafyllis, N.; Samios, M.; Boukouras, K.; Kontakos, K.; Ktenidou, O.J.; Fountoulakis, I.; Kalogeras, I.; Melis, N.S.; Galanis, O.; et al. Seismic Waveform Data from Greece and Cyprus: Integration, Archival, and Open Access. Seismol. Res. Lett. 2021, 92, 1672–1684. [Google Scholar] [CrossRef]
- Klein, F.W. Users guide to HYPOINVERSE-2000: A Fortran Program to Solve for Earthquake Locations and Magnitudes. U.S. Geol. Surv. Open-File Rept. 02-171, Version 1.0. 2002. Available online: https://pubs.usgs.gov/of/2002/0171/pdf/of02-171.pdf (accessed on 20 September 2024).
- Papadimitriou, P.; Chousianitis, K.; Agalos, A.; Moshou, A.; Lagios, E.; Makropoylos, K. The spatially extended 2006 April Zakynthos (Ionian Islands, Greece) seismic sequence and evidence for stress transfer. Geophys. J. Int. 2012, 191, 1025–1040. [Google Scholar] [CrossRef]
- Xiong, X.; Shan, B.; Zhou, Y.M.; Wei, S.J.; Li, Y.D.; Wang, R.; Zheng, Y. Coulomb stress transfer and accumulation on the Sagaing Fault, Myanmar, over the past 110 years and its implications for seismic hazard. Geophys.Res. Lett. 2017, 44, 4781–4789. [Google Scholar] [CrossRef]
- Wu, J.; Hu, Q.; Li, W.; Lei, D. Study on Coulomb Stress Triggering of the April 2015 M7.8 Nepal Earthquake Sequence. Int. J. Geophys. 2016, 2016, 7378920. [Google Scholar] [CrossRef]
- Mayorga, E.F.; Sánchez, J.J. Modelling of Coulomb stress changes during the great (Mw=8.8) 1906 Colombia-Ecuador earthquake. J. South Am. Earth Sci. 2016, 70, 268–278. [Google Scholar] [CrossRef]
- Kilb, D.; Gomberg, J.; Bodin, P. Aftershock triggering by complete Coulomb stress changes. JGR Solid Earth 2002, 107, ESE 2-1–ESE 2-14. [Google Scholar] [CrossRef]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- King, G.C.; Stein, R.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. 2005, 110, 1–17. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-Rich Deformation and Stress-Change Software for Earthquake, Tectonic, and Volcano Research and Teaching-User Guide. U.S. Geological Survey Open-File Report 2011-1060. 2011; p. 63. Available online: http://pubs.usgs.gov/of/2011/1060/ (accessed on 20 September 2024).
- Kilb, D.; Gomberg, J.; Bodin, P. Triggering of earthquake aftershocks by dynamic stresses. Nature 2002, 408, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Cattania, C.; Hainzl, S.; Wang, L.; Roth, F.; Enescu, B. Propagation of Coulomb stress uncertainties in physics-based aftershock models. J. Geophys. Res. 2014, 119, 7846–7864. [Google Scholar] [CrossRef]
- Sokos, E.; Kiratzi, A.; Gallovič, F.; Zahradník, J.; Serpetsidaki, A.; Plicka, V. Rupture process of the 2014 Cephalonia, Greece, earthquake doublet (Mw6) as inferred from regional and local seismic data. Tectonophysics 2015, 656, 131–141. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Karakonstantis, A.; Bozionelos, G.; Kapetanidis, V.; Kaviris, G.; Spingos, I.; Millas, C. Preliminary Report on the Lefkada 17 November 2015 Mw=6.4 Earthquake, Report Released to EMSC-CSEM. 2016. Available online: https://www.emsc-csem.org/Doc/Additional_Earthquake_Report/470390/20151117_lefkada_report_nkua.pdf (accessed on 20 September 2024).
- Harris, R.A. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. 1998, 103, 347–358. [Google Scholar] [CrossRef]
- Beeler, N.; Simpson, R.; Hickman, S.; Lockner, D. Pore fluid pressure, apparent friction, and Coulomb failure. J. Geophys. Res. 2000, 105, 25533–25542. [Google Scholar] [CrossRef]
- Rice, J.; Cleary, M. Some basic stress diffusion solutions for fluid saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Bonatis, P.; Karakostas, V.; Papadimitriou, E.; Kouroukla, C. The 2022 Mw5.5 earthquake off-shore Kefalonia Island—Relocated aftershocks, statistical analysis and seismotectonic implications. J. Seismol. 2024, 1–17. [Google Scholar] [CrossRef]
- Kourouklas, C.; Papadimitriou, E.; Karakostas, V. Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation. Geosciences 2023, 13, 295. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Magnitude and energy of earthquakes. Ann. Geofis 1954, 9, 1–15. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Teleseismic b values; Or, much ado about 1.0. J. Geophys. Res. Solid Earth 1993, 98, 631–644. [Google Scholar] [CrossRef]
- Scholz, C. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Kisslinger, C. Aftershocks and fault-zone properties. Adv. Geophys. 1996, 38, 1–36. [Google Scholar] [CrossRef]
- Utsu, T. A statistical significance test of the difference in b-value between two earthquakes groups. J. Phys. Earth 1966, 14, 37–40. [Google Scholar] [CrossRef]
- Shi, Y.; Bolt, B.A. The standard error of the magnitude-frequency b-value. Bull. Seismol. Soc. Am. 1982, 87, 1074–1077. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of complete reporting in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Ogata, Y. Estimation of the parameters in the modified Omori formula for aftershock frequencies by the maximum likelihood procedure. J. Phys. Earth. 1983, 31, 115–124. [Google Scholar] [CrossRef]
- Michas, G.; Pavlou, K.; Avgerinou, S.E.; Anyfadi, E.A.; Vallianatos, F. Aftershock patterns of the 2021 Mw 6.3 Northern Thessaly (Greece) earthquake. J. Seismol. 2022, 26, 201–225. [Google Scholar] [CrossRef]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics—An overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Silva, R.; Franca, G.S.; Vilar, C.S.; Alcaniz, J.S. Nonextensive models for earthquakes. Phys. Rev. E 2006, 73, 026102. [Google Scholar] [CrossRef]
- Telesca, L. Investigating the temporal variations of the time-clustering behavior of the Koyna–Warna (India) reservoir-triggered seismicity, Chaos. Solitons Fractals 2011, 44, 108–113. [Google Scholar] [CrossRef]
- Telesca, L. Maximum likelihood estimation of the nonextensive parameters of the earthquake cumulative magnitude distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A 2005, 350, 588–596. [Google Scholar] [CrossRef]
- Avgerinou, S.E.; Anyfadi, E.A.; Michas, G.; Vallianatos, F.A. Non-Extensive Statistical Physics View of the Temporal Properties of the Recent Aftershock Sequences of Strong Earthquakes in Greece. Appl. Sci. 2023, 13, 1995. [Google Scholar] [CrossRef]
- Anyfadi, E.A.; Avgerinou, S.E.; Michas, G.; Vallianatos, F. Universal Non-Extensive Statistical Physics Temporal Pattern of Major Subduction Zone Aftershock Sequences. Entropy 2022, 24, 1850. [Google Scholar] [CrossRef]
- Vallianatos, F.; Karakonstantis, A.; Michas, G.; Pavlou, K.; Kouli, M.; Sakkas, V. On the Patterns and Scaling Properties of the 2021–2022 Arkalochori Earthquake Sequence (Central Crete, Greece) Based on Seismological, Geophysical and Satellite Observations. Appl. Sci. 2022, 12, 7716. [Google Scholar] [CrossRef]
- Lippiello, E.; Giacco, F.; Marzocchi, W.; Godano, C.; de Arcangelis, L. Mechanical origin of aftershocks. Sci. Rep. 2015, 5, 15560. [Google Scholar] [CrossRef]
- Helmstetter, A.; Sornette, D. Diffusion of epicenters of earthquake aftershocks, Omori’s law, and generalized continuous-time random walk models. Phys. Rev. E 2002, 66, 061104. [Google Scholar] [CrossRef] [PubMed]
- Felzer, K.R.; Brodsky, E.E. Decay of aftershock density with distance indicates triggering by dynamic stress. Nature 2006, 441, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Lippiello, E.; de Arcangelis, L.; Godano, C. Role of Static Stress Diffusion in the Spatiotemporal Organization of Aftershocks. Phys. Rev. Lett. 2009, 103, 038501. [Google Scholar] [CrossRef] [PubMed]
- Kato, A.; Obara, K. Step-like migration of early aftershocks following the 2007 Mw 6.7 Noto-Hanto earthquake, Japan. Geophys. Res. Lett. 2014, 41, 3864–3869. [Google Scholar] [CrossRef]
- Obana, K.; Takahashi, T.; No, T.; Kaiho, Y.; Kodaira, S.; Yamashita, M.; Sato, T.; Nakamura, T. Distribution and migration of aftershocks of the 2010 Mw 7.4 Ogasawara Islands intraplate normal-faulting earthquake related to a fracture zone in the Pacific plate. Geochem. Geophys. Geosyst. 2014, 15, 1363–1373. [Google Scholar] [CrossRef]
- Tang, C.C.; Lin, C.H.; Peng, Z. Spatial-temporal evolution of early aftershocks following the 2010 ML6.4 Jiashian earthquake in southern Taiwan. Geophys. J. Int. 2014, 199, 1772–1783. [Google Scholar] [CrossRef]
- Meng, X.; Peng, Z. Increasing lengths of aftershock zones with depths of moderate-size earthquakes on the San Jacinto Fault suggests triggering of deep creep in the middle crust. Geophys. J. Int. 2016, 204, 250–261. [Google Scholar] [CrossRef]
- Frank, W.B.; Poli, P.; Perfettini, H. Mapping the rheology of the Central Chile subduction zone with aftershocks. Geophys. Res. Lett. 2017, 44, 5374–5382. [Google Scholar] [CrossRef]
- Perfettini, H.; Frank, W.B.; Marsan, D.; Bouchon, M.A. Model of Aftershock Migration Driven by Afterslip. Geophys. Res. Lett. 2018, 45, 2283–2293. [Google Scholar] [CrossRef]
- Vallianatos, F.; Pavlou, K. Scaling properties of the Mw7.0 Samos (Greece), 2020 aftershock sequence. Acta Geophy. 2021, 69, 1067–1084. [Google Scholar] [CrossRef]
- Ariyoshi, K.; Matsuzawa, T.; Hasegawa, A. The key frictional parameters controlling spatial variations in the speed of postseismic-slip propagation on a subduction plate boundary. Earth Planet. Sci. Lett. 2007, 256, 136–146. [Google Scholar] [CrossRef]
- Kato, N. Expansion of aftershock areas caused by propagating post-seismic sliding. Geophys. J. Int. 2007, 168, 797–808. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. Solid Earth 2004, 109, 1–25. [Google Scholar] [CrossRef]
- Kanamori, H.; Anderson, D.L. Theoretical basis of some empirical relations in seismology. Bull. Seismol. Soc. Am. 1975, 65, 1073–1095. [Google Scholar] [CrossRef]
- Dologlou, E. Critical dynamic processes prior to destructive earthquakes. Int. J. Remote Sens. 2014, 35, 8208–8216. [Google Scholar] [CrossRef]
- Margaris, B.; Hatzidimitriou, P. Source spectral scaling and stress release estimates using strong-motion records in Greece. Bull. Seismol. Soc. Am. 2002, 92, 1040–1059. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P.; Tavera, H.; Kositsky, A.; Nocquet, J.M.; Bondoux, F.; Chlieh, M.; Sladen, A.; Audin, L.; Farber, L.; et al. Seismic and aseismic slip on the Central Peru megathrust. Nature 2010, 465, 78–81. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P. Modeling afterslip and aftershocks following the 1992 Landers earthquake. J. Geophys. Res. 2007, 112, B07409. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A Stat. Mech. Its Appl. 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Beck, C. Recent developments in superstatistics. Braz. J. Physics 2009, 39, 357–363. [Google Scholar] [CrossRef]
- Vallianatos, F. A non-extensive statistical physics approach to the polarity reversals of the geomagnetic field. Phys. A 2011, 390, 1773–1778. [Google Scholar] [CrossRef]
- Vallianatos, F.; Karakostas, V.; Papadimitriou, E. A Non-Extensive Statistical Physics View in the Spatiotemporal Properties of the 2003 (Mw6.2) Lefkada, Ionian Island Greece, Aftershock Sequence. Pure Appl. Geophys. 2014, 171, 1343–1534. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
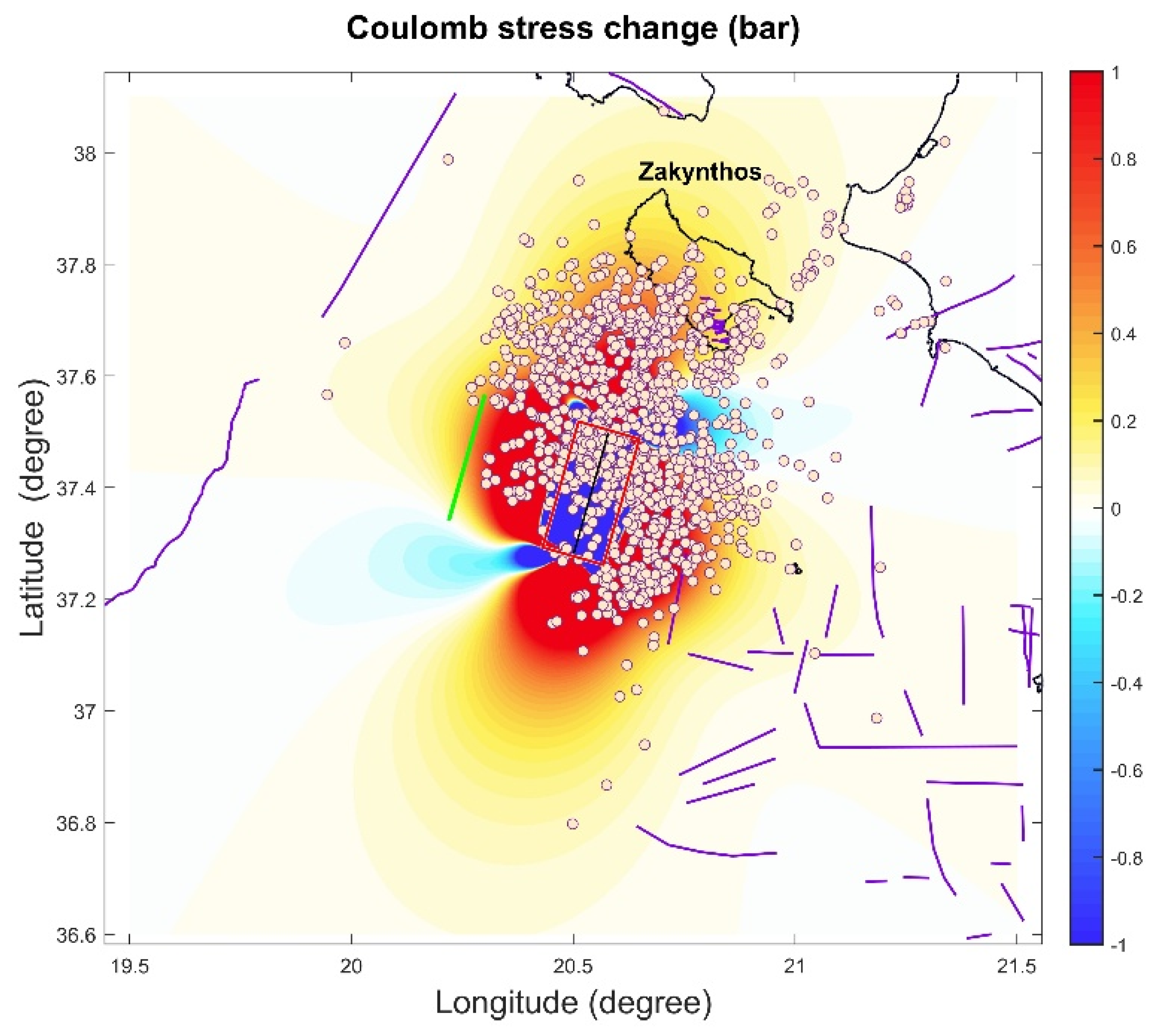
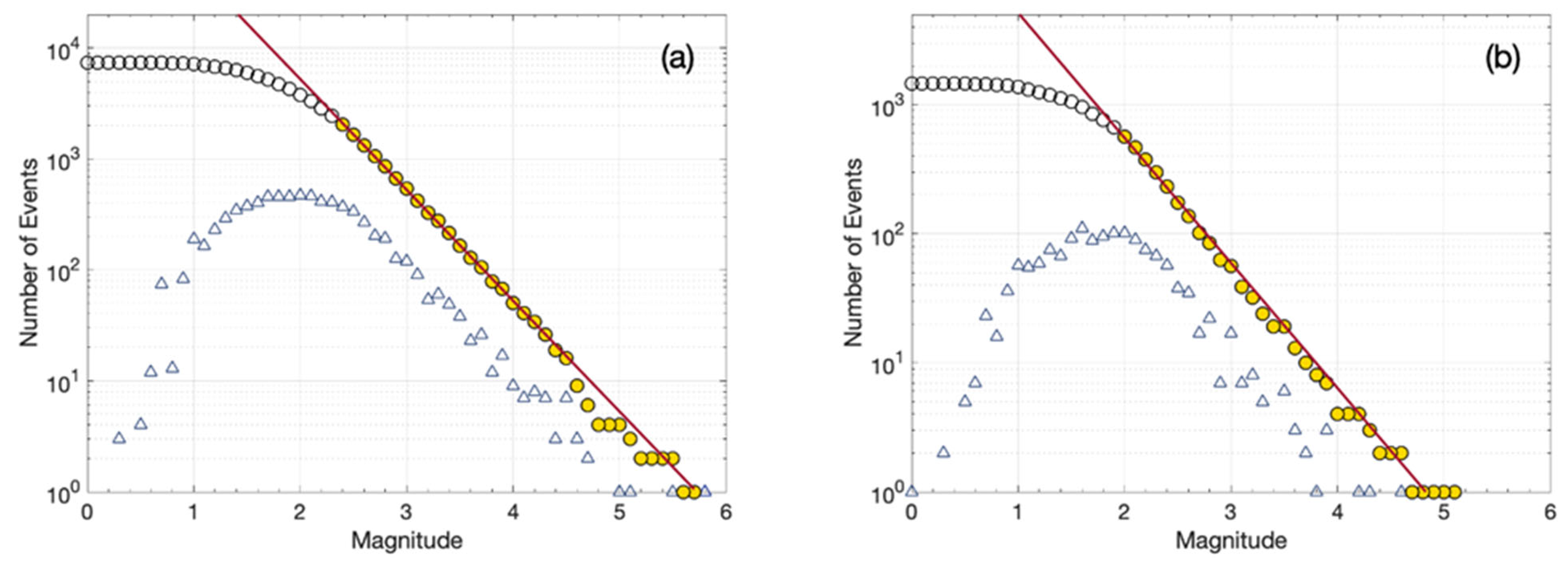

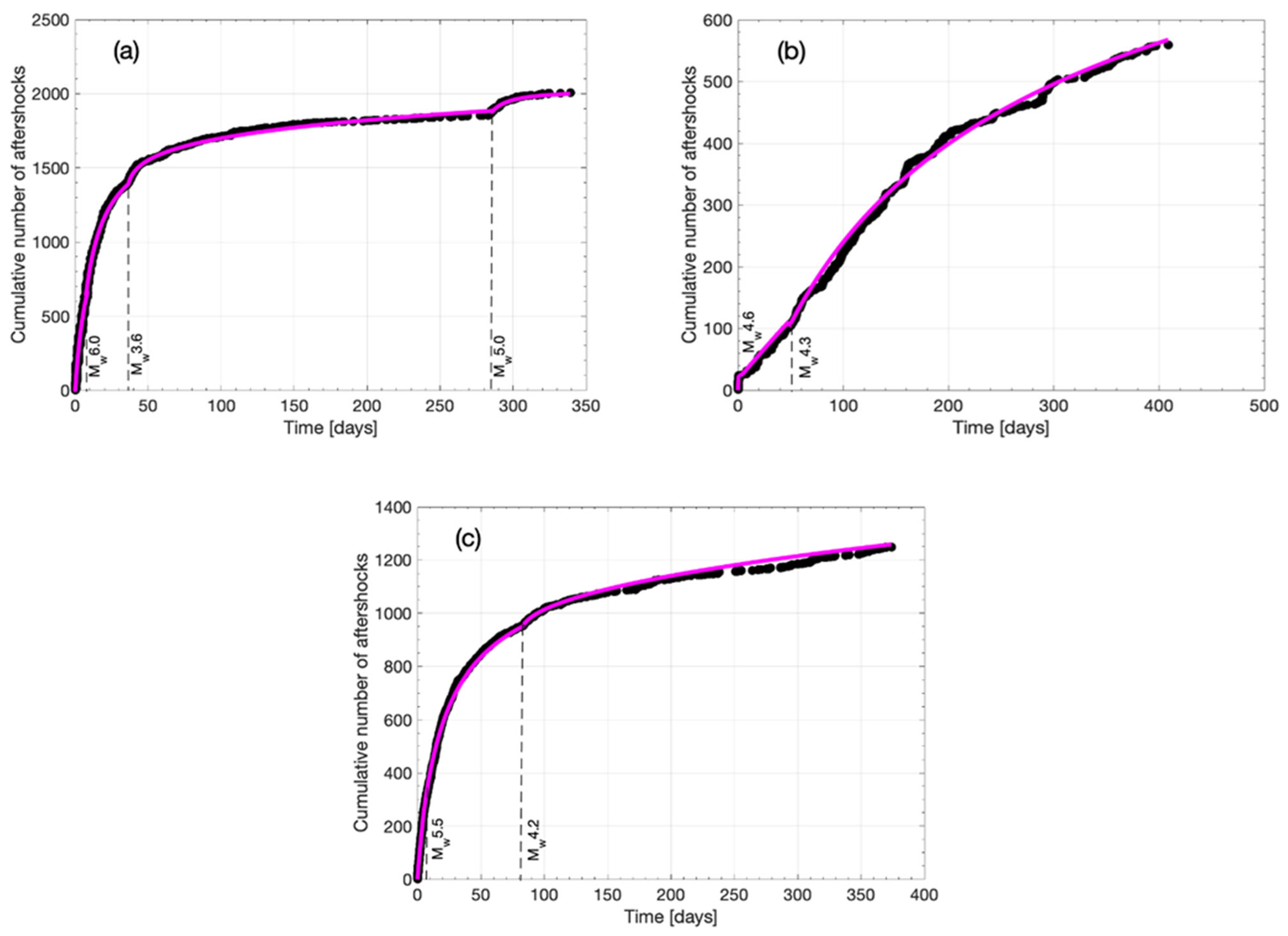
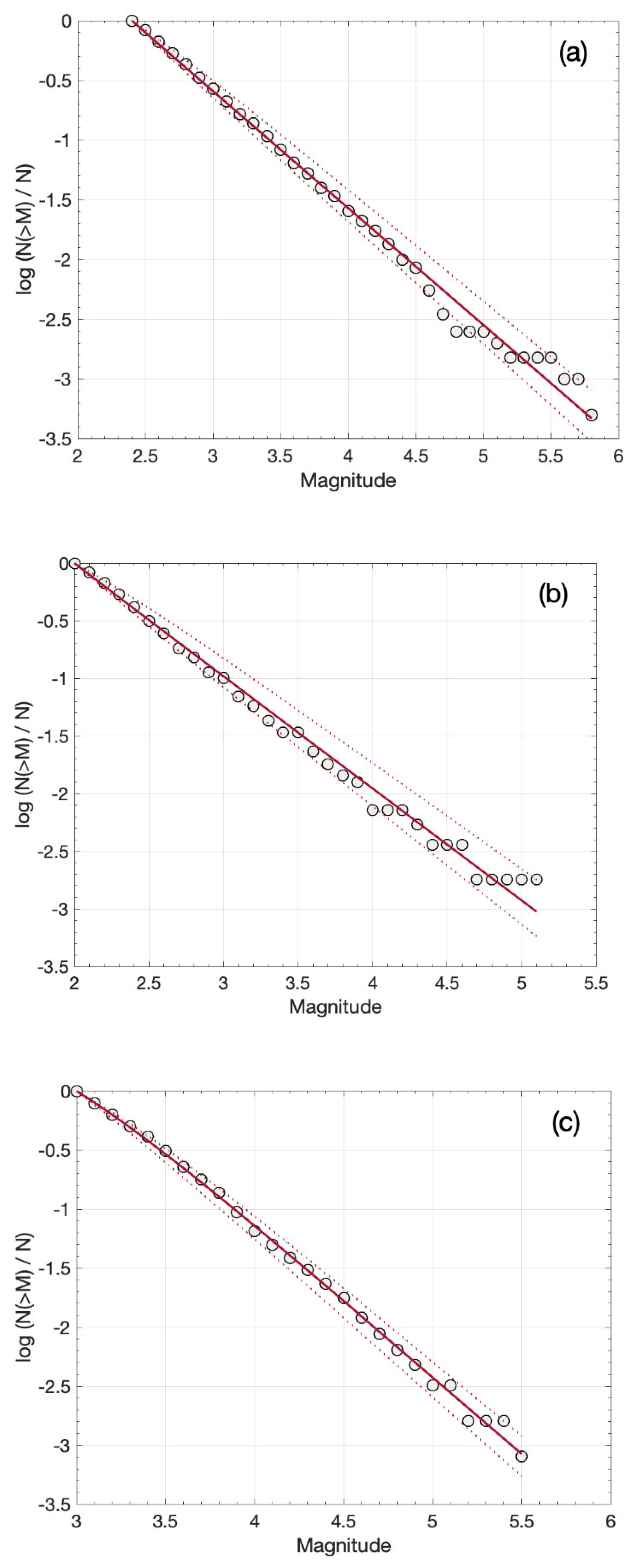
| Date Time | Lat | Lon | Depth (km) | Mw | Strike | Dip | Rake | Seismic Moment (in Nm) |
|---|---|---|---|---|---|---|---|---|
| 26 January 2014 13:55 [47] | 38.1944 | 20.3519 | 10.5 | 6.1 | 20 | 74 | 163 | 1.40 × 1018 |
| 17 November 2015 07:10 [48] | 38.6785 | 20.5889 | 14 | 6.4 | 22 | 72 | 161 | 4.30 × 1018 |
| 25 October 2018 22:54 [4] | 37.3939 | 20.5400 | 12 | 6.7 | 16 | 25 | 166 | 9.05 × 1018 |
| Island | N | Mc | a | b | RMSEG-R | A | qM | RMSEF-A |
|---|---|---|---|---|---|---|---|---|
| Cephalonia | 7358 | 2.4 | 5.72 ± 0.16 | 1.00 ± 0.04 | 0.101 | −16.09 ± 81.31 | 1.51 ± 0.01 | 0.090 |
| Lefkada | 1458 | 2.0 | 4.68 ± 0.12 | 0.97 ± 0.04 | 0.090 | −14.71 ± 93.14 | 1.51 ± 0.01 | 0.086 |
| Zakynthos | 5931 | 3.0 | 6.50 ± 0.17 | 1.13 ± 0.04 | 0.140 | 4755.5 ± 3135.9 | 1.43 ± 0.01 | 0.046 |
| Mainshock | Duration | N | K | c | p | AIC |
|---|---|---|---|---|---|---|
| (days) | (days) | |||||
| Mw6.1 | 340 days | 2006 | 2668.6 ± 193.4 | 6.96 ± 0.37 | 1.46 ± 0.22 | –8091 |
| Mw6.1 26 January 2014 | 7.55 days | 654 | 4999.3 ± 588.6 | 7.54 ± 2.13 | 1.73 ± 0.42 | –8254 |
| Mw6.0 1 February 2014 | 29.35 days | 753 | 4999.7 ± 220.8 | 11.14 ± 1.99 | 1.72 ± 0.35 | |
| Mw3.6 4 March 2014 | 249.48 days | 479 | 47.1 ± 13.8 | 1.79 ± 0.86 | 0.78 ± 0.06 | |
| Mw5.0 8 November 2014 | 52.83 days | 120 | 4999.2 ± 420.4 | 16.28 ± 1.68 | 2.22 ± 0.14 |
| Mainshock | Duration | N | K | c | p | AIC |
|---|---|---|---|---|---|---|
| (days) | (days) | |||||
| Mw6.0 | 409 days | 559 | 4998.6 ± 474.6 | 195.82 ± 2.47 | 1.40 ± 0.32 | 650.9 |
| Mw6.0 17 November 2015 | 3.73 days | 25 | 10.0 ± 6.2 | 0.41 ± 0.69 | 2.69 ± 0.84 | 541.6 |
| Mw4.6 21 November 2015 | 44.72 days | 77 | 15.5 ± 2.9 | 186.08 ± 3.67 | 0.39 ± 0.03 | |
| Mw4.3 4 January 2016 | 360.41 days | 457 | 4998.4 ± 586.6 | 150.76 ± 1.95 | 1.46 ± 0.35 |
| Mainshock | Duration | N | K | c | p | AIC |
|---|---|---|---|---|---|---|
| (days) | (days) | |||||
| Mw6.6 | 374 days | 1249 | 1340.4 ± 46.8 | 8.99 ± 2.35 | 1.36 ± 0.12 | –3033 |
| Mw6.6 25 October 2018 | 4.68 days | 240 | 64.7 ± 41.96 | 1.22 ± 0.29 | 0.20 ± 0.11 | –3057 |
| Mw5.5 30 October 2018 | 79.27 days | 717 | 4999.9 ± 316.3 | 19.16 ± 2.28 | 1.66 ± 0.06 | |
| Mw4.2 17 January 2019 | 290.13 days | 292 | 10.0 ± 4.9 | 1.87 ± 1.31 | 0.51 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlou, K.; Michas, G.; Vallianatos, F. Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019. Geosciences 2025, 15, 84. https://doi.org/10.3390/geosciences15030084
Pavlou K, Michas G, Vallianatos F. Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019. Geosciences. 2025; 15(3):84. https://doi.org/10.3390/geosciences15030084
Chicago/Turabian StylePavlou, Kyriaki, Georgios Michas, and Filippos Vallianatos. 2025. "Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019" Geosciences 15, no. 3: 84. https://doi.org/10.3390/geosciences15030084
APA StylePavlou, K., Michas, G., & Vallianatos, F. (2025). Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019. Geosciences, 15(3), 84. https://doi.org/10.3390/geosciences15030084








