Quantifiable Elements of Seismic Image Fidelity: A Tutorial Review
Abstract
1. Introduction
2. Three Quantifiable Elements of Seismic Image Fidelity
2.1. Image Resolution and Influencing Factors
- Data frequency content;
- Seismic illumination of the acquisition setup;
- Methodology of data processing and imaging.
2.1.1. Resolution of Seismic Images
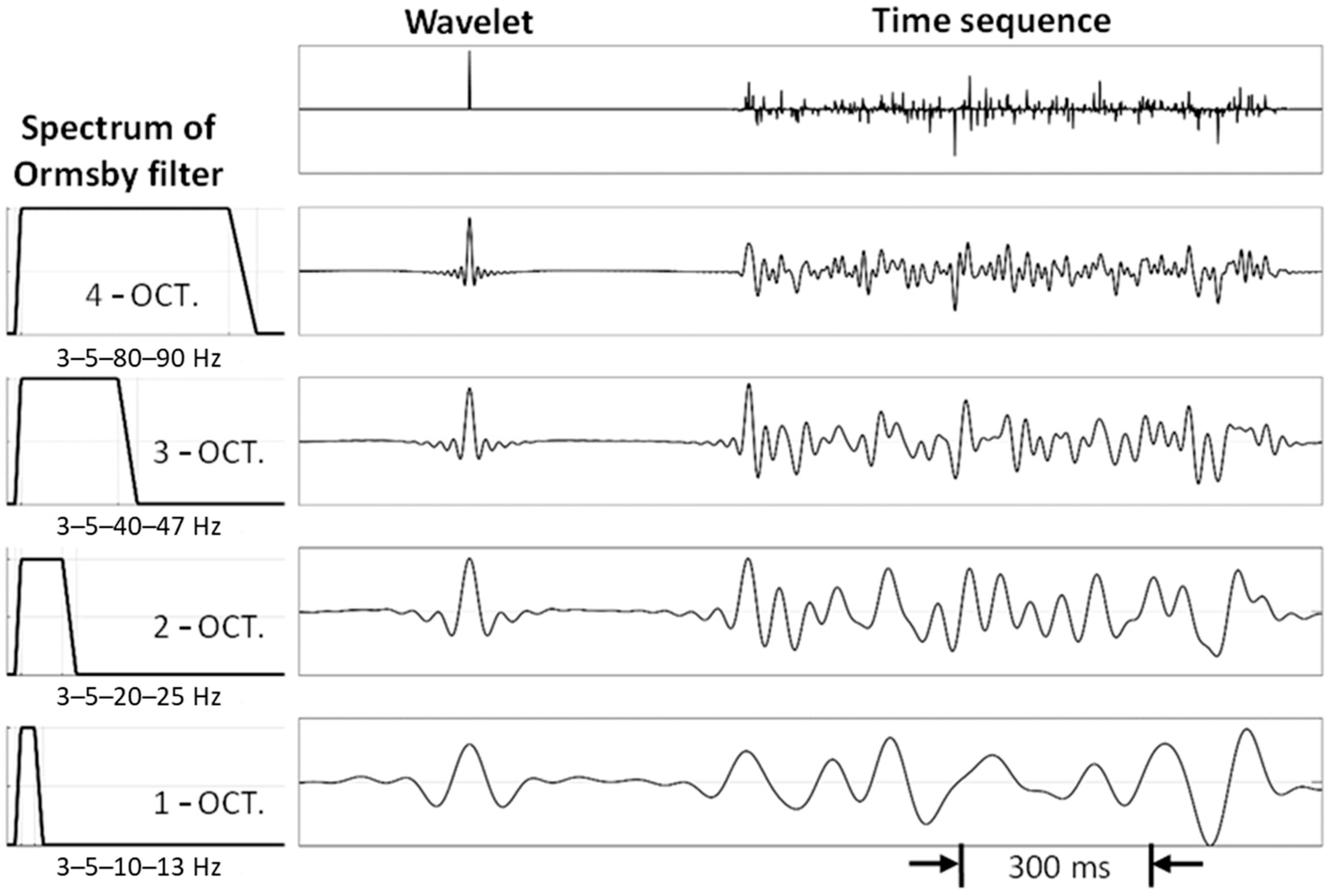
2.1.2. The Influence on Image Resolution by Data Frequency Content
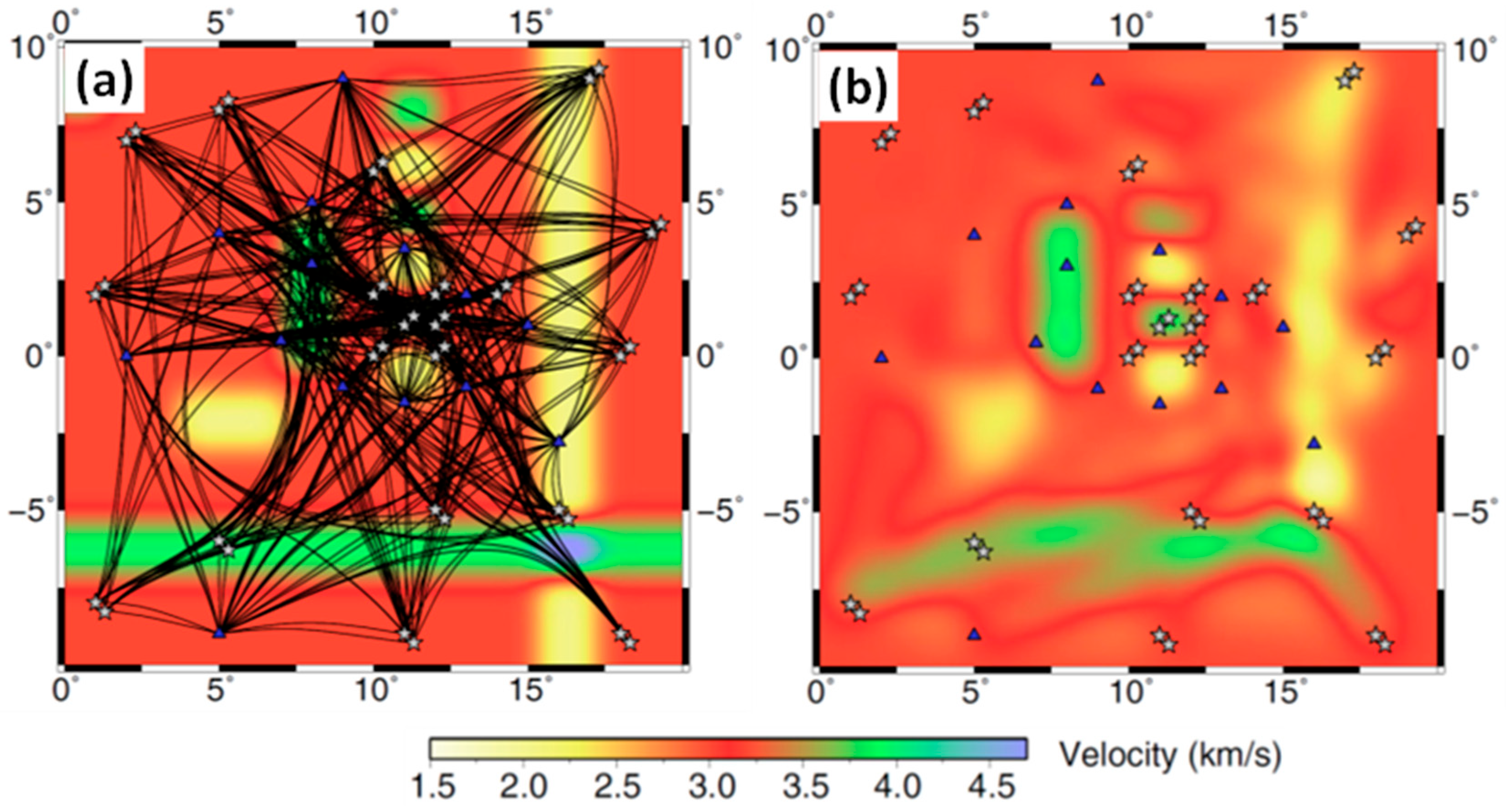
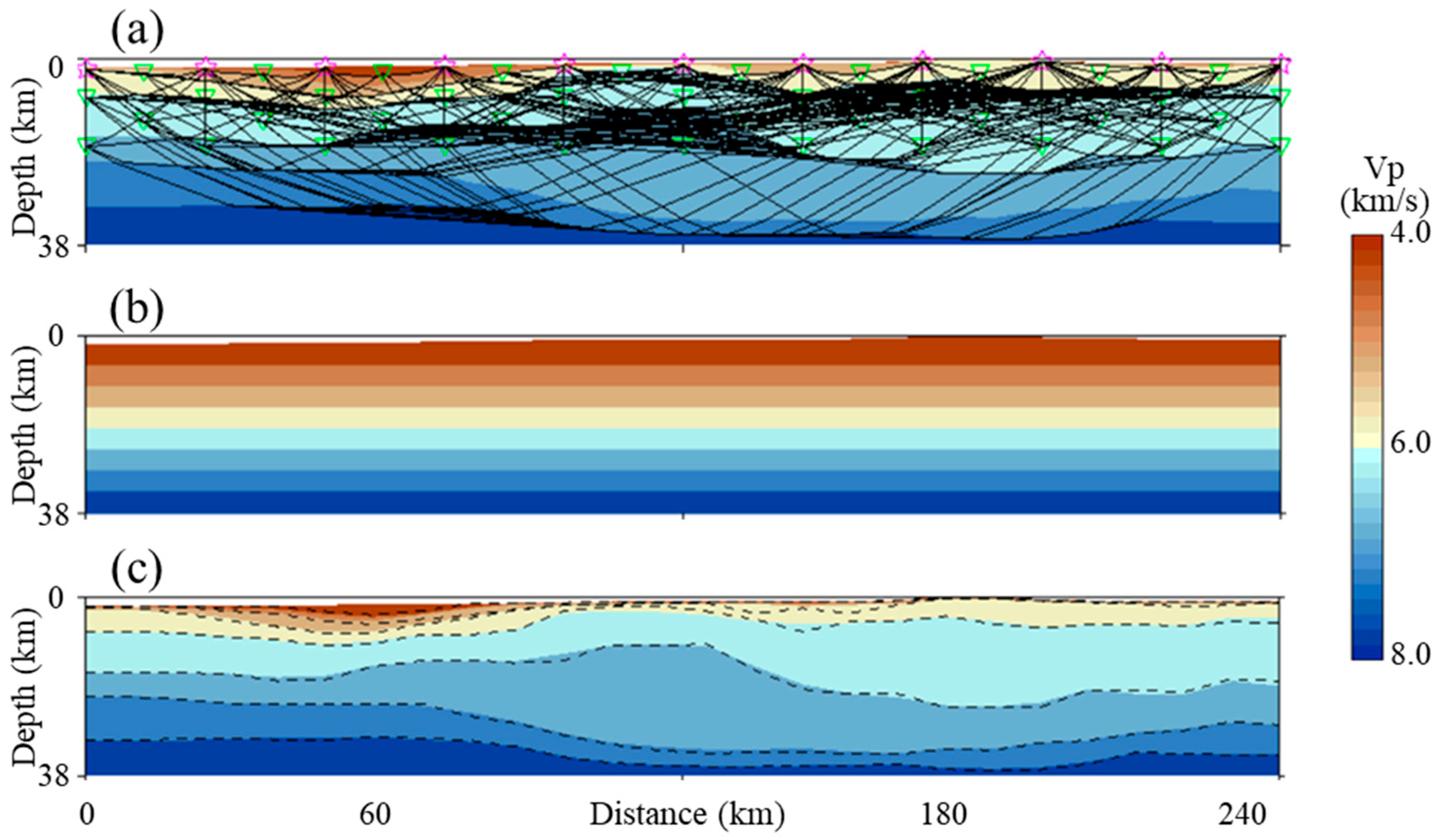
2.1.3. The Influence on Image Resolution by Seismic Illumination
2.1.4. The Influence on Image Resolution by Processing and Imaging Methods
2.1.5. Quantification of Seismic Image Resolution
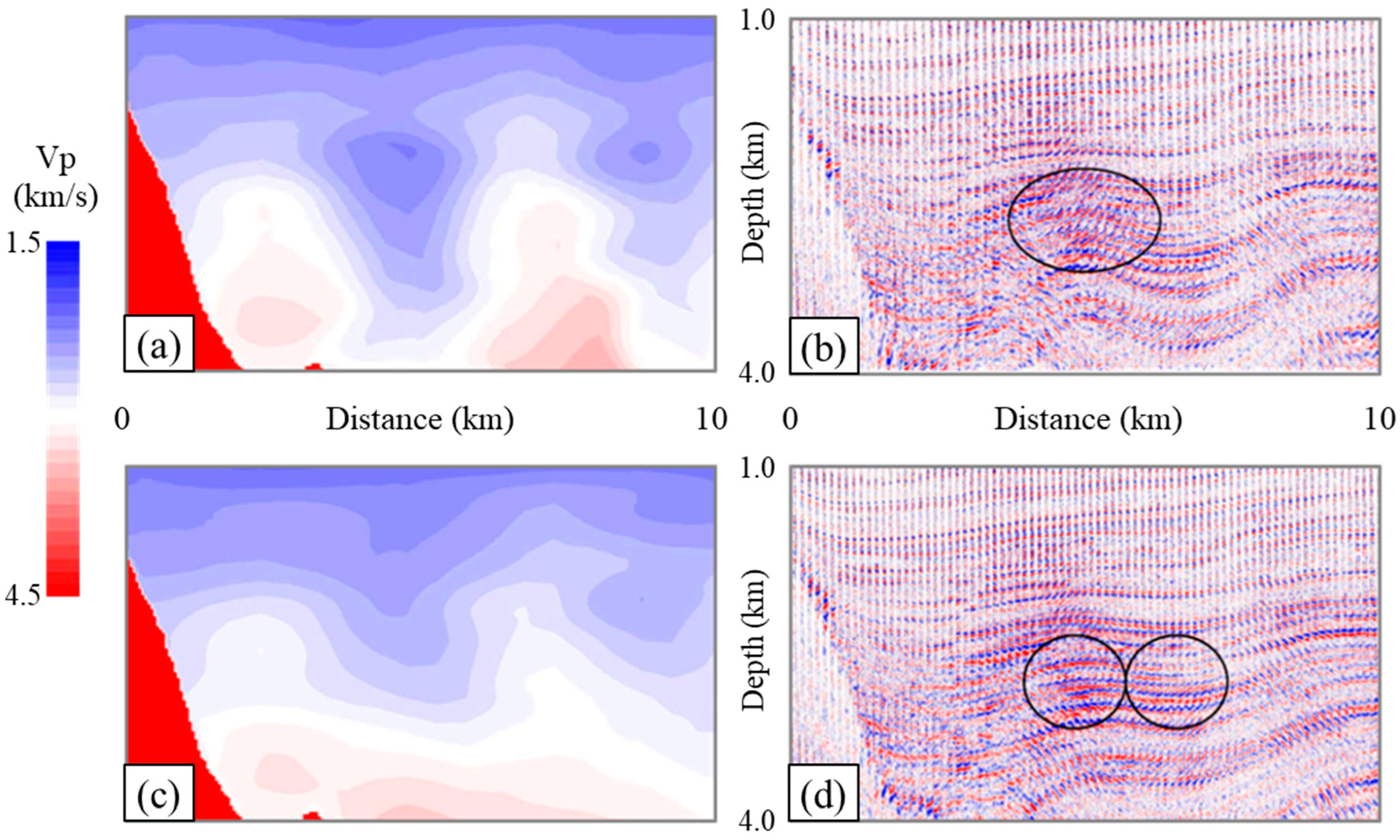
2.2. Artifacts in Seismic Images
- Poor and uneven seismic illumination;
- Using improper signals in seismic imaging;
- Limitations in data processing and interpretation;
- Erroneous velocity models.
2.2.1. Image Artifacts from Insufficient Seismic Illumination
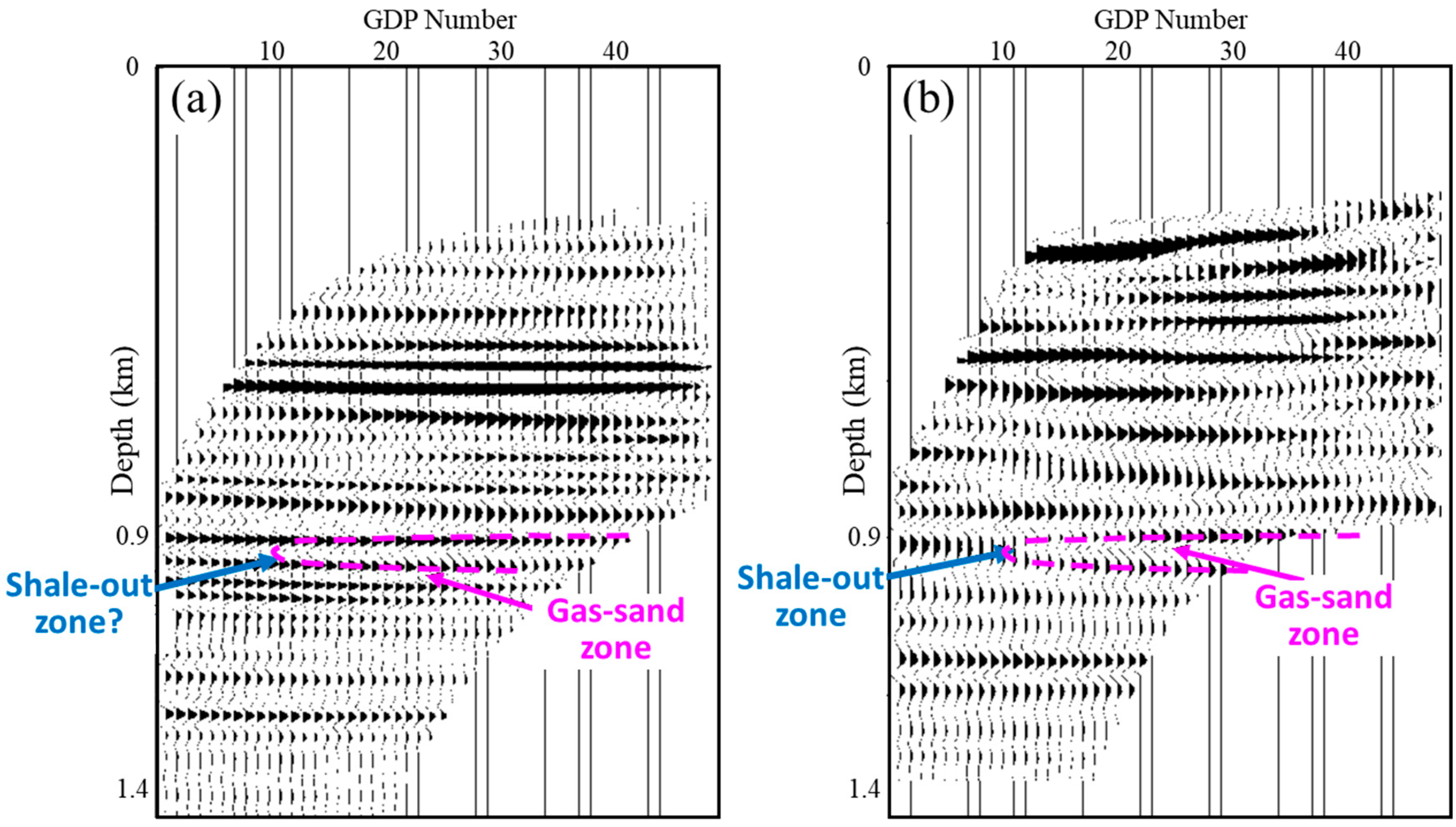
2.2.2. Image Artifacts from Using Improper Signals
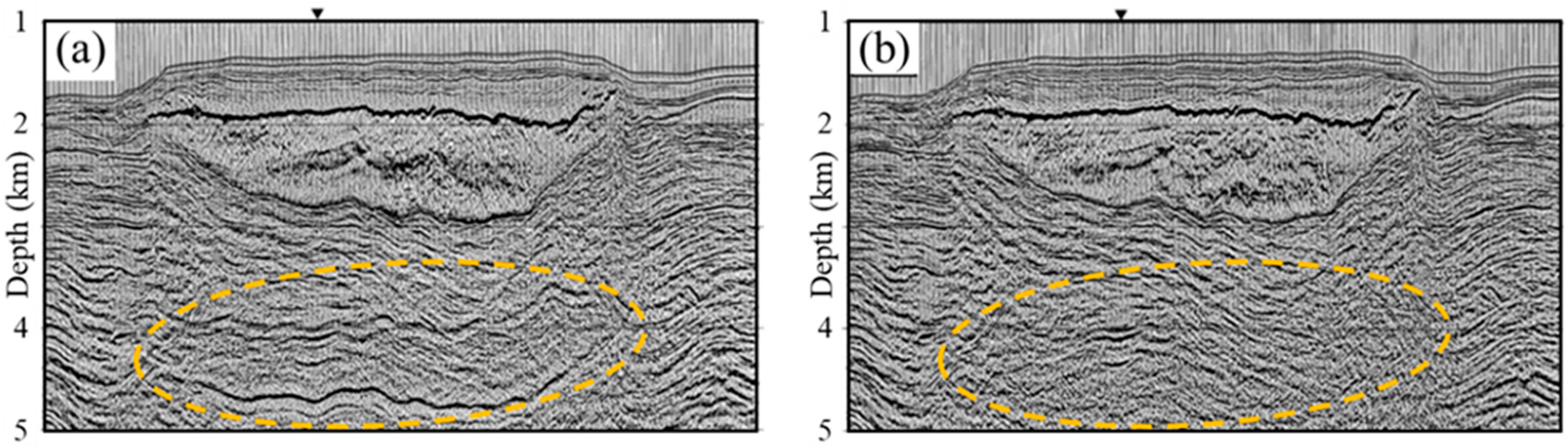
2.2.3. Image Artifacts from Limitations in Data Processing and Interpretation
2.2.4. Image Artifacts from Using an Erroneous Velocity Model
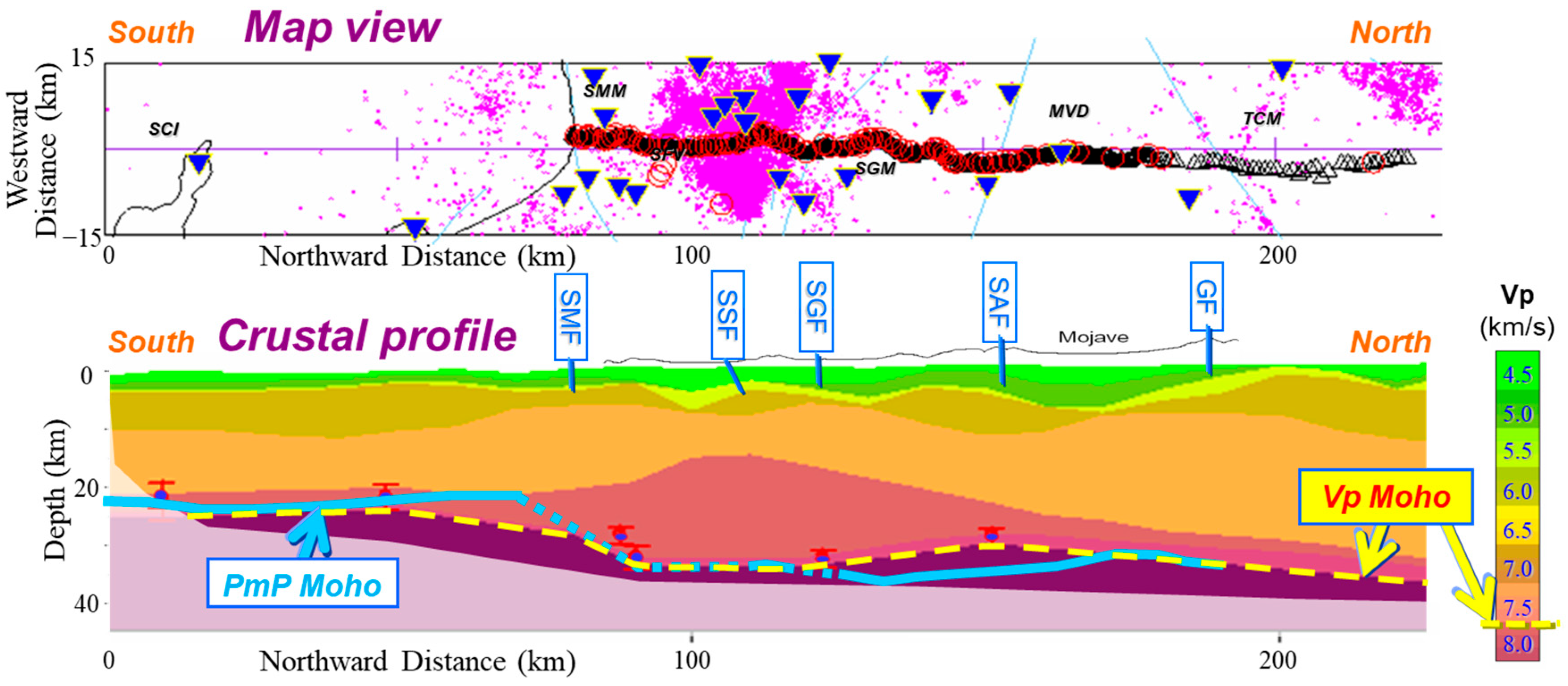
2.3. Position Accuracy of Seismic Images
2.3.1. The Reliance of Image Position on Imaging Velocity Model
2.3.2. Quantifying the Absolute Accuracy in Seismic Image Position
2.3.3. Quantifying the Relative Accuracy in Seismic Image Position
2.3.4. Quantifying the Uncertainties in Imaging Velocity Models
3. Challenges to Quantify Seismic Image Fidelity Beyond Drilling Limit
3.1. Data Quality Factors Impacting Seismic Image Fidelity
- Low data SNR at far mapping distance. The SNR of seismic data depends on the following: (1) quality of the sources in terms of their strength and the radiation patterns; (2) attenuation property and complexity of the media above the imaging targets; and (3) quality of the receivers and data processing process. Low SNR is a major reason for generating the deceiving artifacts due to mistaking improper data as the signal in seismic imaging. A rule of thumb in Section 2.1.2 is that the SNR of seismic data becomes insufficient after one to two hundred wavelengths of wave propagation in sediments.
- Insufficient data frequency content. Depending on the following: (1) source frequency content and radiation pattern; (2) property of the media above the imaging targets; and (3) ability of receivers in recording low-frequency signals and sample rate. Insufficient signal bandwidth will result in losing the ability to distinguish each reflector from other reflectors. Another rule of thumb in Section 2.1.2 is that we need at least 2 octaves in signal bandwidth in exploration seismology.
- Poor seismic illumination. The fidelity of seismic images requires sufficient seismic illumination for the imaging targets and their overburden, the media overlying the targets to the survey sources and receivers. Poor and uneven seismic illumination not only leads to the generation of various image artifacts but also hinders the VMB effort to reduce image position errors.
3.2. Challenges to Improving and Quantifying Seismic Image Fidelity
4. Strategies for Quantifying Seismic Image Fidelity
4.1. Establishing Practical Rules for Assessing Image Fidelity
4.1.1. Promoting Best Practice Rules in Creating and Using Seismic Images
- Scientific principles for the study;
- Practical ways to QC main technical parameters;
- Practical limitations and the underlying reasons;
- Pitfalls in practice and examples of success and failure cases.
4.1.2. Ensuring QC Tests on Image Fidelity
4.1.3. Establishing Standards for Verifying Image Fidelity
- Direct proof;
- Verifiable independently;
- Consistency with all measurable data.
4.2. Finding the Resolvable Targets and Suitable Signals for Study Goals
4.3. Improving Seismic Illumination and Signal Bandwidth
4.4. Mitigating the Non-Uniqueness in Seismic Imaging
4.5. Quantifying Seismic Image Fidelity via Machine Learning
5. Discussion
6. Conclusions
Funding
Conflicts of Interest
Abbreviations
| CIG | Common image gather |
| CMB | Core-mantle boundary |
| FSIM | Feature similarity indexing measure |
| FWI | Full waveform inversion |
| MSE | Mean squared error |
| mbsf | Meters below seafloor |
| msbsf | Milliseconds below seafloor |
| QC | Quality control |
| RTM | Reverse time migration |
| SNR | Signal-to-noise ratio |
| SSIM | Structural similarity index measure |
| SDSS | Structural similarity model |
| SYN | Synthetic seismogram |
| TWT | Two-way traveltime |
| VMB | Velocity model building |
| VSP | Vertical seismic profile |
| VTI | Vertical transverse isotropy |
References
- Zhou, H. Practical Seismic Data Analysis; Cambridge University Press: Cambridge, UK, 2014; p. 482. [Google Scholar]
- Ricker, N. Wavelet contraction, wavelet expansion, and the control of seismic resolution. Geophysics 1953, 18, 769–792. [Google Scholar] [CrossRef]
- Widess, M.B. Quantifying resolving power of seismic systems. Geophysics 1982, 47, 1160–1173. [Google Scholar] [CrossRef]
- Zhou, H. How well can we resolve the deep seismic slab with seismic tomography. Geophys. Res. Lett. 1988, 15, 1425–1428. [Google Scholar] [CrossRef]
- Li, Q. The Way Toward Accurate Seismic Prospecting; Petroleum Industry Press: Beijing, China, 1993; p. 196. [Google Scholar]
- Li, Q. High Resolution Seismic Exploration; Society of Exploration Geophysicists: Tulsa, OK, USA, 2017; p. 318. [Google Scholar]
- Sheriff, R.E.; Geldart, L.P. Exploration Seismology; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Zelt, C.A. Lateral velocity resolution from three-dimensional seismic refraction data. Geophys. J. Int. 1998, 135, 1101–1112. [Google Scholar] [CrossRef]
- Zelt, C.A.; Haines, S.; Powers, M.H.; Sheehan, J.; Rohdewald, S.; Link, C.; Hayashi, K.; Zhao, D.; Zhou, H.; Burton, B.L.; et al. Blind test of methods for obtaining 2-D near-surface seismic velocity models from first-arrival traveltimes. J. Environ. Eng. Geophys. 2013, 18, 183–194. [Google Scholar] [CrossRef]
- Anderson, D.L. Theory of the Earth; Blackwell Scientific Publications: Oxford, UK, 1989. [Google Scholar]
- Zhou, H. A high-resolution P wave model for the top 1200 km of the mantle. J. Geophys. Res. Solid Earth 1996, 101, 27791–27810. [Google Scholar] [CrossRef]
- Song, X.D. Anisotropy of the earth’s inner core. Rev. Geophys. 1997, 35, 297–313. [Google Scholar] [CrossRef]
- Song, X.D.; Helmberger, D.V. Seismic evidence for an inner core transition zone. Science 1998, 282, 924–927. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Sausalito, CA, USA, 2002. [Google Scholar]
- Zheng, Y.C.; Lay, T.; Flanagan, M.P.; Williams, Q. Pervasive seismic wave reflectivity and metasomatism of the Tonga mantle wedge. Science 2007, 316, 855–859. [Google Scholar] [CrossRef]
- Nolet, G. A Breviary of Seismic Tomography; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Devaney, A.J. Geophysical diffraction tomography. IEEE Trans. Geosci. Remote Sens. 1984, 22, 3–13. [Google Scholar] [CrossRef]
- Wu, R.S.; Toksöz, M.N. Diffraction tomography and multisource holography applied to seismic imaging. Geophysics 1987, 52, 11–25. [Google Scholar] [CrossRef]
- Zhou, H.; Clayton, R.W. P and S-wave travel time inversions for subducting slab under the island arcs of the Northwest Pacific. J. Geophys. Res. Solid Earth 1990, 95, 6829–6851. [Google Scholar] [CrossRef]
- Nolet, G. Partitioned wave-form inversion and 2-dimensional structure under the network of autonomously recording seismographs. J. Geophys. Res. Solid Earth 1990, 95, 8499–8512. [Google Scholar] [CrossRef]
- Billien, M.; Leveque, J.J.; Trampert, J. Global maps of Rayleigh wave attenuation for periods between 40 and 150 seconds. Geophys. Res. Lett. 2000, 27, 3619–3622. [Google Scholar] [CrossRef]
- Zheng, S.H.; Sun, X.L.; Song, X.D.; Yang, Y.J.; Ritzwoller, M.H. Surface wave tomography of China from ambient seismic noise correlation. Geochem. Geophys. Geosyst. 2008, 9, Q02018. [Google Scholar] [CrossRef]
- Berkhout, A.J. Seismic Migration, Imaging of Acoustic Energy by Wavefield Extrapolation, Theoretical Aspects; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Gardner, G.H. Migration of Seismic Data; Society of Exploration Geophysicists: Tulsa, OK, USA, 1985. [Google Scholar]
- Steer, D.N.; Knapp, J.H.; Brown, L.D. Super-deep reflection profiling: Exploring the continental mantle lid. Tectonophysics 1998, 286, 111–121. [Google Scholar] [CrossRef]
- Etgen, J.; Gray, S.H.; Zhang, Y. An overview of depth imaging in exploration geophysics. Geophysics 2009, 74, WCA5–WCA17. [Google Scholar] [CrossRef]
- Langston, C.A. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. J. Geophys. Res. 1979, 84, 4749–4762. [Google Scholar] [CrossRef]
- Zhu, L.; Kanamori, H. Moho depth variation in southern California from teleseismic receiver functions. J. Geophys. Res. Solid Earth 2000, 105, 2969–2980. [Google Scholar] [CrossRef]
- Savage, M.K.; Park, J.; Todd, H. Velocity and anisotropy structure at the Hikurangi subduction margin, New Zealand from receiver functions. Geophys. J. Int. 2007, 168, 1034–1050. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics, 2nd ed.; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Biondi, B.L. 3D Seismic Imaging; SEG: Tulsa, OK, USA, 2006. [Google Scholar]
- Ikelle, L.T.; Amundsen, L. Introduction to Petroleum Seismology, 2nd ed.; SEG: Tulsa, OK, USA, 2018. [Google Scholar]
- Dziewonski, A.M.; Romanowicz, B.A. Deep Earth seismology. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 1, pp. 11–50. [Google Scholar]
- Stern, T.A.; Henrys, S.A.; Okaya, D.; Louie, J.N.; Savage, M.K.; Lamb, S.; Sato, H.; Sutherland, R.; Iwasaki, T. A seismic reflection image for the base of a tectonic plate. Nature 2015, 518, 85–88. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H. On the layering artifacts in seismic imageries. J. Earth Sci. 2011, 22, 182–194. [Google Scholar] [CrossRef]
- Zhou, H.; Zou, Z.; Li, Z. Detecting artifacts in seismic profiles. Rev. Geophys. Planet. Phys. 2021, 52, 45–53. [Google Scholar] [CrossRef]
- Barbosa, N.D.; Prado, R.; Costa, J.C.; Siqueira, S.R. Workflow for seismic imaging with quantified uncertainty. Geophysics 2020, 85, 104615. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Huang, L.; Zhang, H. Uncertainty quantification in full-waveform inversion using BFGS-based Hessian approximations. Geophysics 2022, 87, R425–R440. [Google Scholar]
- Yilmaz, O. Seismic Data Processing; Investigations in Geophysics, No. 2; Society of Exploration Geophysicists: Tulsa, OK, USA, 1987. [Google Scholar]
- Sheriff, R.E. Encyclopedic Dictionary of Exploration Geophysics, 3rd ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1991. [Google Scholar]
- Pratt, R.G. A Short Course on Waveform Tomography; Queen’s University: Kingston, ON, Canada, 2005. [Google Scholar]
- Wielandt, E. On the validity of the ray approximation for interpreting delay times. In Seismic Tomography; Nolet, G., Ed.; Springer: Dordrecht, The Netherlands, 1987; pp. 85–98. [Google Scholar]
- Kallweit, R.S.; Wood, L.C. The limits of resolution of zero-phase wavelets. Geophysics 1982, 47, 1035–1046. [Google Scholar] [CrossRef]
- Knopoff, L. Q. Rev. Geophys. 1964, 2, 625–660. [Google Scholar]
- Xie, X.B.; Jin, S.W.; Wu, R.S. Wave-equation-based seismic illumination analysis. Geophysics 2006, 71, S169–S177. [Google Scholar] [CrossRef]
- Rawlinson, N.; Spakman, W. On the use of sensitivity tests in seismic tomography. Geophys. J. Int. 2016, 205, 1221–1243. [Google Scholar] [CrossRef]
- Rawlinson, N.; Fichtner, A.; Sambridge, M.; Young, M.K. Seismic tomography and the assessment of uncertainty. In Advances in Geophysics; Dmowska, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; Volume 55, pp. 1–76. [Google Scholar]
- Zhou, H.; Li, L.; Bjorklund, T.; Thornton, M. A comparative analysis of deformable layer tomography and cell tomography along the LARSE lines in southern California. Geophys. J. Int. 2010, 180, 1200–1222. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Yang, N.; Duan, Y. Human vision system-based structural similarity model for evaluating seismic image quality. Geophysics 2018, 83, F49–F54. [Google Scholar] [CrossRef]
- Chacon-Buitrago, N.; Pyrcz, M.J. Machine learning-based soft data checking for subsurface modeling. Geosciences 2025, 15, 288. [Google Scholar] [CrossRef]
- Louie, J.N.; Chavez-Perez, S.; Henrys, S.; Bannister, S. Multimode migration of scattered and converted waves for the structure of the Hikurangi slab interface, New Zealand. Tectonophysics 2002, 355, 227–246. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, H.; Zou, Z.; Wo, Y.; Youn, O. Reverse time migration: A prospect of seismic imaging methodology. Earth-Sci. Rev. 2018, 179, 207–227. [Google Scholar] [CrossRef]
- Rumpfhuber, E.M.; Keller, G.R.; Sandvol, E.; Velasco, A.A.; Wilson, D.C. Rocky Mountain evolution: Tying Continental Dynamics of the Rocky Mountains and Deep Probe seismic experiments with receiver functions. J. Geophys. Res. Solid Earth 2009, 114, B08312. [Google Scholar] [CrossRef]
- Youn, O.K.; Zhou, H. Depth imaging with multiples. Geophysics 2001, 66, 246–255. [Google Scholar] [CrossRef]
- Zhou, H.; Mendoza, J.A.; Link, C.A.; Jech, J.; McDonald, J.A. Crosswell imaging in a shallow unconsolidated reservoir. Lead. Edge 1993, 12, 32–36. [Google Scholar] [CrossRef]
- Zelt, C.A. Modelling strategies and model assessment for wide-angle seismic traveltime data. Geophys. J. Int. 1999, 139, 183–204. [Google Scholar] [CrossRef]
- Shearer, P.M. Introduction to Seismology, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Zhang, Y.; Sun, J.C.; Gray, S.H. Aliasing in wavefield extrapolation prestack migration. Geophysics 2003, 68, 629–633. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Y.; Chang, X.; Xie, S. Migration of free-surface-related multiples: Removing artifacts using a water-layer model. J. Appl. Geophys. 2015, 112, 147–156. [Google Scholar] [CrossRef]
- Dragoset, W.H.; Jericevic, Z. Some remarks on surface multiple attenuation. Geophysics 1998, 63, 772–789. [Google Scholar] [CrossRef]
- Gantela, C.; Bian, A.; Zhou, H.; Bjorklund, H. De-masking multiple artifact in crustal seismic images from marine reflection data in southern California borderland. J. Earth Sci. 2015, 26, 592–597. [Google Scholar] [CrossRef]
- Guitton, A.; Kaelin, B.; Biondi, B. Least-squares attenuation of reverse-time-migration artifacts. Geophysics 2007, 72, S19–S23. [Google Scholar] [CrossRef]
- Zhao, D. Seismic structure and origin of hotspots and mantle plumes. Earth Planet. Sci. Lett. 2001, 192, 251–265. [Google Scholar] [CrossRef]
- Lazarevic, I. Impact of Kirchhoff and Wave Equation Prestack Depth Migrations in Improving Lateral Resolution in a Land Data Environment. Master’s Thesis, University of Houston, Houston, TX, USA, 2004. [Google Scholar]
- Alyahya, K. Velocity analysis by iterative profile migration. Geophysics 1989, 54, 718–729. [Google Scholar] [CrossRef]
- Mackay, S.; Abma, R. Imaging and velocity estimation with depth-focusing analysis. Geophysics 1992, 57, 1608–1622. [Google Scholar] [CrossRef]
- Kosloff, D.; Sherwood, J.; Koren, Z.; Machet, E.; Falkovitz, Y. Velocity and interface depth determination by tomography of depth migrated gathers. Geophysics 1996, 61, 1511–1523. [Google Scholar] [CrossRef]
- Sarkar, D.; Tsvankin, I. Anisotropic migration velocity analysis: Application to a data set from West Africa. Geophys. Prospect. 2006, 54, 575–587. [Google Scholar] [CrossRef]
- Abrams, L.J. Correlation between core, logging, and seismic data at Site 1149 in the Nadezhda Basin. In Proceedings of the Ocean Drilling Program, Scientific Results; Ludden, J.N., Plank, T., Escutia, C., Eds.; Texas A&M University: College Station, TX, USA, 2002; Volume 185, pp. 1–14. [Google Scholar]
- O’Brien, J.; Harris, R. Multicomponent VSP imaging of tight-gas sands. Geophysics 2006, 71, E83–E90. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of seismic-reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005; p. 354. [Google Scholar]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Tromp, J. Seismic wavefield imaging of Earth’s interior across scales. Nat. Rev. Earth Environ. 2019, 1, 40–53. [Google Scholar] [CrossRef]
- Cao, H.M.; Xie, J.; Kim, Y.; Zhou, H. Multiscale migration tomography to constrain depth-imaging artifacts. Geophysics 2008, 73, VE217–VE222. [Google Scholar] [CrossRef]
- Zhou, H. Multiscale traveltime tomography. Geophysics 2003, 68, 1639–1649. [Google Scholar] [CrossRef]
- Mosser, L.; Kimman, W.; Dramsch, J.; Purves, S.; De la Fuente, A.; Ganssle, G. Rapid seismic domain transfer: Seismic velocity inversion and modeling using deep generative neural networks. In Proceedings of the 80th EAGE Conference and Exhibition 2018, Copenhagen, Denmark, 11–14 June 2018; pp. 1–5. [Google Scholar]
- Wu, Y.; Lin, Y.Z.; Zhou, Z. InversionNet: Accurate and efficient seismic waveform inversion with convolutional neural networks. SEG Expand. Abstr. 2018, 2096–2100. [Google Scholar] [CrossRef]
- Yang, F.; Ma, J. Deep-learning inversion: A next-generation seismic velocity model building method. Geophysics 2019, 84, R583–R599. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Lin, Y.Z. Data-driven seismic waveform inversion: A study on the robustness and generalization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6900–6913. [Google Scholar] [CrossRef]
- Wang, W.L.; Ma, J.W. Velocity model building in a crosswell acquisition geometry with image-trained artificial neural networks. Geophysics 2019, 85, U31–U46. [Google Scholar] [CrossRef]
- Yuan, C.; Zhang, X.; Jia, X.F.; Zhang, J. Time-lapse velocity imaging via deep learning. Geophys. J. Int. 2020, 220, 1228–1241. [Google Scholar] [CrossRef]
- Araya-Polo, M.; Jennings, J.; Adler, A.; Dahlke, T. Deep-learning tomography. Lead. Edge 2018, 37, 58–66. [Google Scholar] [CrossRef]
- Han, M.L.; Zou, Z.H.; Ma, R. Deep learning-driven velocity modeling based on seismic reflection data and multi-scale training sets. Oil Geophys. Prospect. 2021, 56, 935–946. (In Chinese) [Google Scholar]
- Geng, Z.C.; Zhao, Z.Y.; Shi, Y.Z.; Wu, X.M.; Fomel, S.; Sen, M. Deep learning for velocity model building with common-image gather volumes. Geophys. J. Int. 2022, 228, 1054–1070. [Google Scholar] [CrossRef]
- Li, S.C.; Liu, B.; Ren, Y.X.; Chen, Y.; Yang, S.; Wang, Y.; Jiang, P. Deep-learning inversion of seismic data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2135–2149. [Google Scholar] [CrossRef]
- Liu, B.; Yang, S.L.; Ren, Y.X.; Xu, X.J.; Jiang, P.; Chen, Y.K. Deep-learning seismic full-waveform inversion for realistic structural models. Geophysics 2021, 86, R31–R44. [Google Scholar] [CrossRef]
- Guo, R.; Li, M.K.; Xu, S.H.; Abubakar, A. First-arrival traveltime tomography using supervised descent learning technique. Inverse Probl. 2019, 35, 105008. [Google Scholar] [CrossRef]
- Zhou, H. Direct inversion of velocity interfaces. Geophys. Res. Lett. 2004, 31, 447–450. [Google Scholar] [CrossRef]
- Zhu, L. Deformation in the lower crust and downward extent of the San Andreas Fault as revealed by teleseismic waveforms. Earth Planets Space 2002, 54, 1005–1010. [Google Scholar] [CrossRef]
- Fuis, G.S.; Kohler, M.D.; Scherwath, M.; Ten Brink, U.; Van Avendonk, H.J.; Murphy, J.M. A comparison between the transpressional plate boundaries of South Island, New Zealand, and southern California, USA: The Alpine and San Andreas fault systems. Tectonophysics 2007, 429, 307–327. [Google Scholar]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R. Traveltimes for global earthquake location and phase identification. Geophys. J. Int. 1991, 105, 429–465. [Google Scholar] [CrossRef]
- Rabbel, W.; Kaban, M.; Tesauro, M. Contrasts of seismic velocity, density and strength across the Moho. Tectonophysics 2013, 609, 437–455. [Google Scholar] [CrossRef]
- Wang, B.; Dirks, V.; Guillaume, P.; Audebert, F.; Epili, D. A 3D subsalt tomography based on wave-equation migration-perturbation scans. Geophysics 2006, 71, E1–E6. [Google Scholar] [CrossRef]
- Liu, J.; Quan, H.; Li, X.; Marcinkovich, C. Velocity tomography using property scans. SEG Expand. Abstr. 2018, 5157–5162. [Google Scholar] [CrossRef]
- Li, Z.; Qu, Y. Research progress on seismic imaging technology. Pet. Sci. 2022, 19, 128–146. [Google Scholar] [CrossRef]
- Li, J.; Qu, Y.; Li, Y.; Huang, C.; Li, Z. Ocean bottom dual-sensor Q-compensated elastic least-squares reverse time migration based on acoustic and separated-viscoelastic coupling. Geophysics 2024, 89, S155–S173. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Qu, Y.; Li, M.; Li, J. Velocity-adaptive irregular point spread function deconvolution imaging using X-shaped denoising diffusion filtering. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–8. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, J.; Chen, Z.; Huang, C.; Wang, Y.; Liu, C. Q-compensated least-squares reverse time migration with velocity-anisotropy correction based on the first-order velocity-pressure equations. Geophysics 2022, 87, S335–S350. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
- Cano, E.V.; Akram, J.; Peter, D.B. Automatic seismic phase picking based on unsupervised machine-learning classification and content information analysis. Geophysics 2021, 86, V299–V315. [Google Scholar] [CrossRef]
- Zhu, W.; Tai, K.S.; Mousavi, S.M.; Bailis, P.; Beroza, G.C. An end-to-end earthquake detection method for joint phase picking and association using deep learning. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023283. [Google Scholar] [CrossRef]
- Wang, Z.; Di, H.; Shafiq, M.A.; Alaudah, Y.; AlRegib, G. Successful leveraging of image processing and machine learning in seismic structural interpretation: A review. Lead. Edge 2018, 37, 451–461. [Google Scholar] [CrossRef]
- Xiong, W.; Ji, X.; Ma, Y.; Wang, Y.; AlBinHassan, N.M.; Ali, M.N.; Luo, Y. Seismic fault detection with convolutional neural network. Geophysics 2018, 83, O97–O103. [Google Scholar] [CrossRef]
- Wu, X.; Liang, L.; Shi, Y.; Fomel, S. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation. Geophysics 2019, 84, IM35–IM45. [Google Scholar] [CrossRef]
- Anjom, F.K.; Vaccarino, F.; Socco, L.V. Machine learning for seismic exploration: Where are we and how far are we from the holy grail? Geophysics 2024, 89, WA157–WA178. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, P.; Li, G.; Li, H. Seismic noise attenuation by signal reconstruction: An unsupervised machine learning approach. Geophys. Prospect. 2021, 69, 984–1002. [Google Scholar] [CrossRef]
- Yang, L.; Chen, W.; Wang, H.; Chen, Y. Deep-learning seismic random-noise attenuation via improved residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7968–7981. [Google Scholar] [CrossRef]
- Yoo, J.; Zwartjes, P. Attenuation of seismic migration smile artifacts with deep learning. Artif. Intell. Geosci. 2022, 3, 123–131. [Google Scholar] [CrossRef]
- Kaur, H.; Pham, N.; Fomel, S. Improving the resolution of migrated images by approximating the inverse Hessian using deep learning. Geophysics 2020, 85, WA173–WA183. [Google Scholar] [CrossRef]
- Yang, H.; Li, P.; Ma, F.; Zhang, J. Building near-surface velocity models by integrating the first-arrival traveltime tomography and supervised deep learning. Geophys. J. Int. 2023, 235, 326–341. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Zhu, W.; Xu, K.; Darve, E.; Biondi, B.; Beroza, G.C. Integrating deep neural networks with full-waveform inversion: Reparameterization, regularization, and uncertainty quantification. Geophysics 2022, 87, R93–R109. [Google Scholar] [CrossRef]
- Lu, K.; Wang, Y. Seismic full-waveform inversion regularized with a migration image. Geophysics 2025, 90, R143–R157. [Google Scholar] [CrossRef]
- Marquering, H.; Dahlen, F.A.; Nolet, G. Three-dimensional sensitivity kernels for finite-frequency traveltimes: The banana-doughnut paradox. Geophys. J. Int. 1999, 137, 805–815. [Google Scholar] [CrossRef]
- Tape, C.; Liu, Q.; Tromp, J. Finite-frequency tomography using adjoint methods: Methodology and examples using membrane surface waves. Geophys. J. Int. 2007, 168, 1105–1129. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Campillo, M. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise. Geophys. Res. Lett. 2004, 31, L07614. [Google Scholar] [CrossRef]
- Shapiro, N.M.; Campillo, M.; Stehly, L.; Ritzwoller, M.H. High-resolution surface-wave tomography from ambient seismic noise. Science 2005, 307, 1615–1618. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.Y. The nature of noise wavefield and its applications for site effects studies—A literature review. Earth-Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Shuey, R.T. A simplification of the Zoeppritz equations. Geophysics 1985, 50, 609–614. [Google Scholar] [CrossRef]
- Hilterman, F.J. Is AVO the seismic signature of rock properties? SEG Expand. Abstr. 1989, 559. [Google Scholar] [CrossRef]
- Rutherford, S.R.; Williams, R.H. Amplitude-versus-offset variations in gas sands. Geophysics 1989, 54, 680–688. [Google Scholar] [CrossRef]
- Persh, S.E.; Vidale, J.E. Reflection properties of the core-mantle boundary from global stacks of PcP and ScP. J. Geophys. Res. Solid Earth 2004, 109, B04309. [Google Scholar] [CrossRef]
- Shapiro, N.; Ritzwoller, M. Monte Carlo inversion for a global shear-velocity model of the crust and upper mantle. Geophys. J. Int. 2002, 151, 88–105. [Google Scholar] [CrossRef]
- Yao, H.; Van der Hilst, R.D. Analysis of ambient-noise energy distribution and phase-velocity bias in ambient-noise tomography, with application to SE Tibet. Geophys. J. Int. 2009, 179, 1113–1132. [Google Scholar] [CrossRef]
- Zhang, X.; Curtis, A.; Galetti, E.; de Ridder, S. 3-D Monte Carlo surface-wave tomography. Geophys. J. Int. 2018, 215, 1644–1658. [Google Scholar] [CrossRef]
- Dreiling, J.; Tilmann, F. BayHunter—McMC Transdimensional Bayesian Inversion of Receiver Functions and Surface Wave Dispersion; Version 1.0; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar]
- Dreiling, J.; Tilmann, F.; Yuan, X.; Haberland, C.; Seneviratne, C.W.M. Crustal structure of Sri Lanka derived from joint inversion of surface-wave dispersion and receiver functions using a Bayesian approach. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018688. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Y.; Curtis, A. Surface-wave dispersion inversion using an energy likelihood function. Geophys. J. Int. 2023, 232, 523–536. [Google Scholar] [CrossRef]


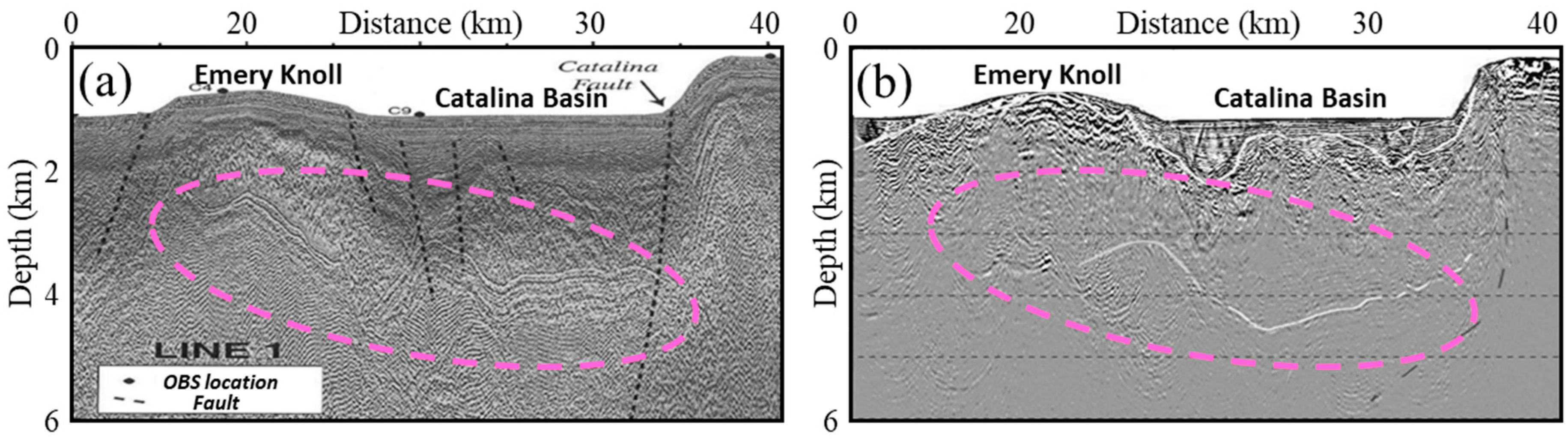
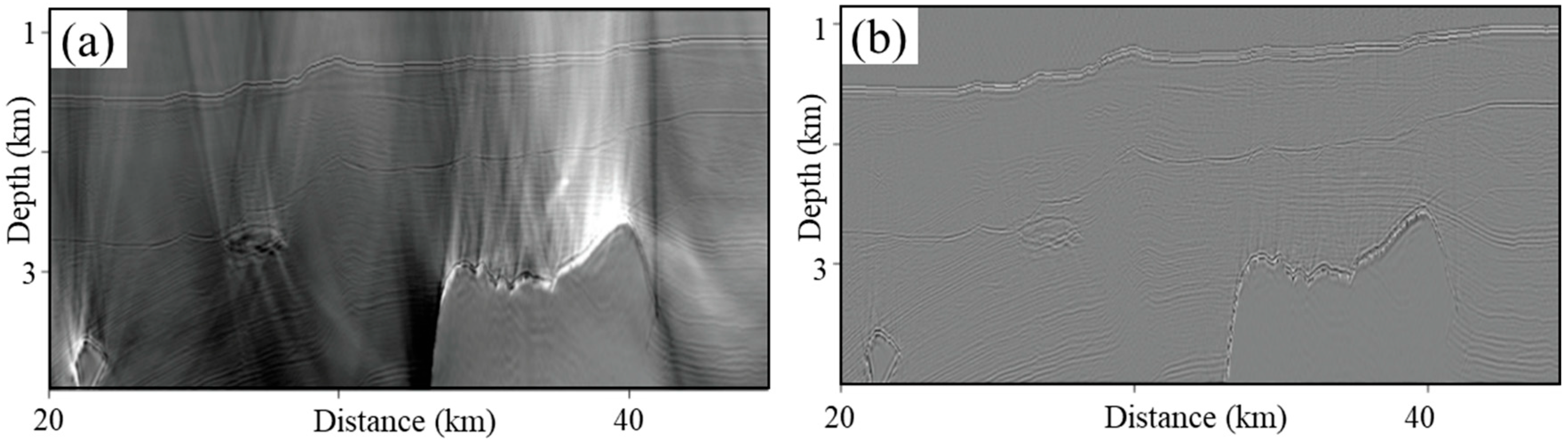
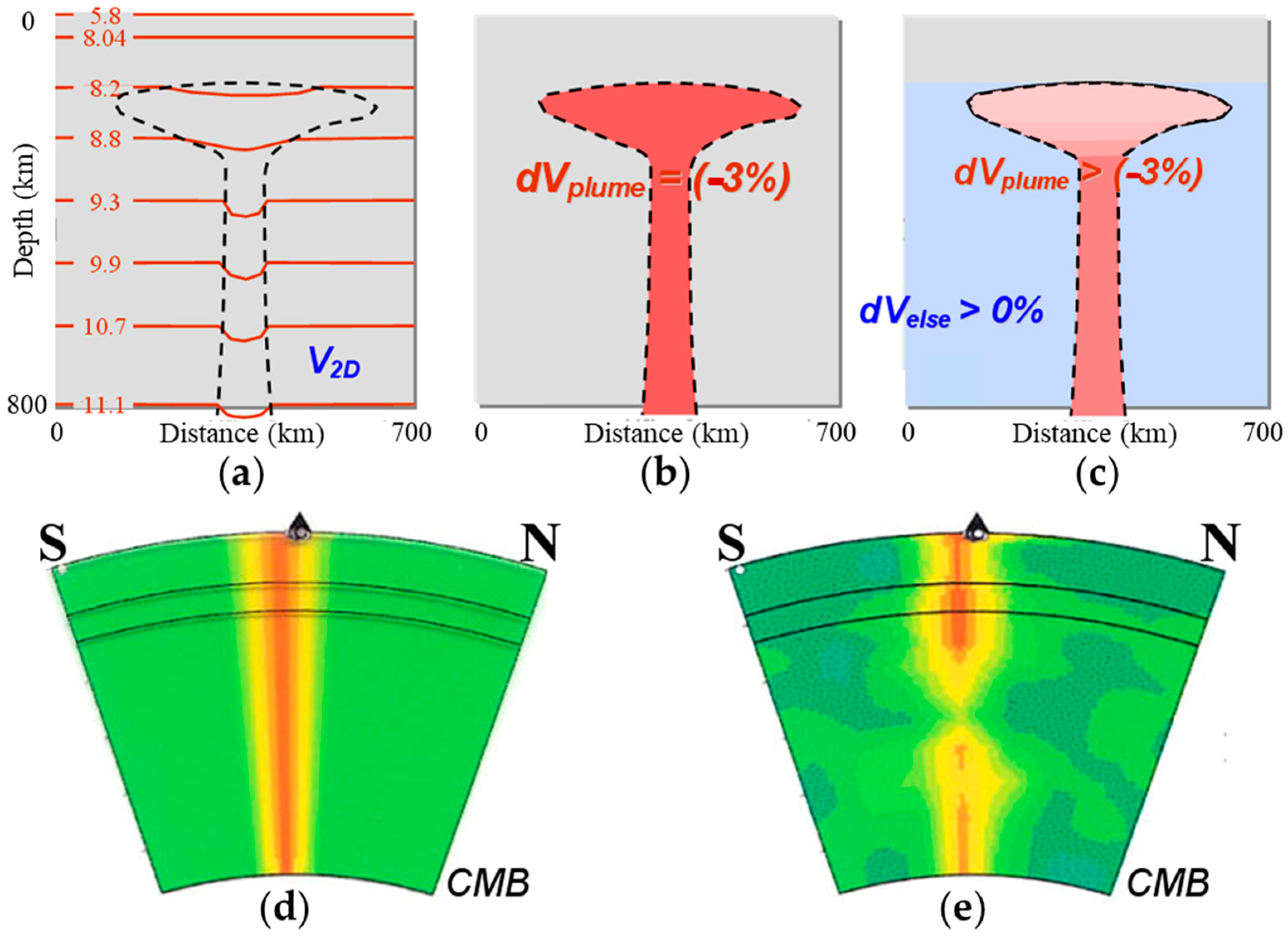

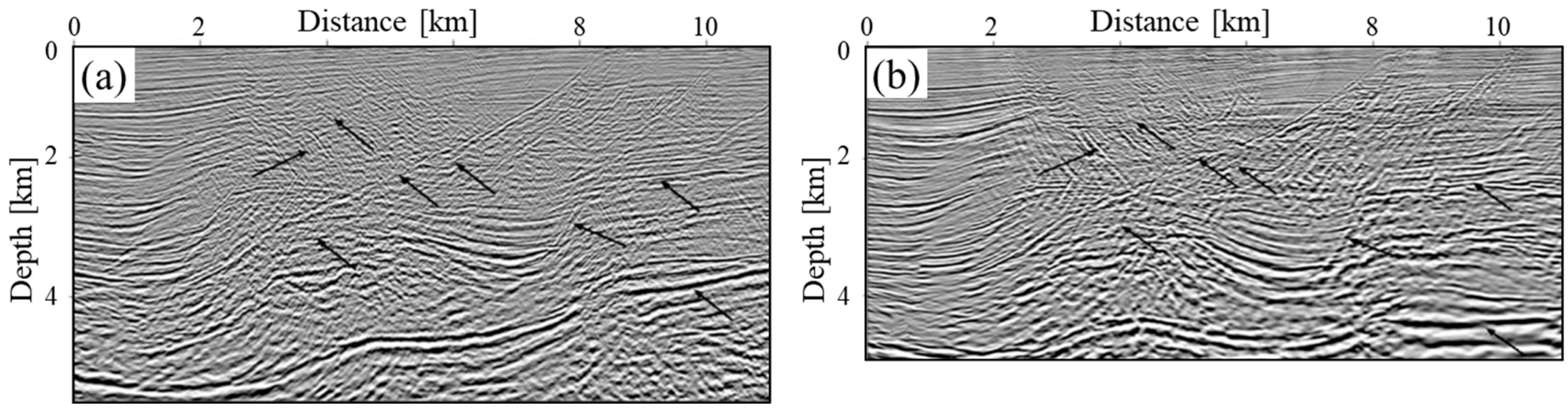


| Data Quality Factor | Impacts on Seismic Image Fidelity |
|---|---|
| Setting practical limits on data size and image fidelity |
| Defining the quality of signals, requiring sufficiently high-quality sources and receivers and sufficiently good control on site effects |
| High time resolution requires broad signal bandwidth (especially low frequencies) and high central frequency |
| Sufficiently fine and even spatial coverage of targets require sufficiently wide-angle and dense survey layout; Key for spatial resolution to suppress artifacts, and for VMB to reduce position errors |
| Sufficiently fine to avoid temporal aliasing in each data trace and spatial aliasing in multi-dimensional images |
| Increasing information content that can be especially beneficial at hard-to-access locations (e.g., borehole and ocean bottom) |
| Challenges | Common Symptoms | Likely Causes |
|---|---|---|
| 1. Limited seismic illumination | Weak/missing reflectors; poor continuity | Acquisition gaps; complex overburden |
| 2. Acquisition footprint | Stripping; azimuthal bias | Sparse/irregular sampling; footprint artifacts |
| 3. Random noise | Loss of coherence; low SNR | Environmental/cultural noise; weak sources |
| 4. Limited resolution | Blurred thin beds; merged reflectors | Bandwidth/aperture limits; overlapping wavelet sidelobes |
| 5. Internal multiples and coherent noise | False reflectors; spurious events | Unable to recognize interbed multiples; reverberations |
| 6. Limited low-frequency signal | Poor large-scale recovery; cycle skipping | Source and receiver limits; absorption/attenuation |
| 7. Velocity model uncertainty | Mispositioned reflectors; image distortion | Inaccurate picking; unaccounted velocity anisotropy |
| 8. Anisotropy effects | Curved reflections on gathers; depth errors | Neglecting VTI/TTI; poor azimuth/offset coverage |
| 9. Lack of uncertainty quantification | No error bounds; misleading images | Deterministic workflows; few probabilistic methods |
| 10. Imaging artifacts | Smearing; smiles and frown; fake features | Limited illumination; improper signal and processing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Zhou, H.-W.; Zou, Z.; Hu, H.; Wo, Y.; Ding, Y. Quantifiable Elements of Seismic Image Fidelity: A Tutorial Review. Geosciences 2025, 15, 445. https://doi.org/10.3390/geosciences15120445
Sun L, Zhou H-W, Zou Z, Hu H, Wo Y, Ding Y. Quantifiable Elements of Seismic Image Fidelity: A Tutorial Review. Geosciences. 2025; 15(12):445. https://doi.org/10.3390/geosciences15120445
Chicago/Turabian StyleSun, Lelin, Hua-Wei Zhou, Zhihui Zou, Hao Hu, Yukai Wo, and Yinshuai Ding. 2025. "Quantifiable Elements of Seismic Image Fidelity: A Tutorial Review" Geosciences 15, no. 12: 445. https://doi.org/10.3390/geosciences15120445
APA StyleSun, L., Zhou, H.-W., Zou, Z., Hu, H., Wo, Y., & Ding, Y. (2025). Quantifiable Elements of Seismic Image Fidelity: A Tutorial Review. Geosciences, 15(12), 445. https://doi.org/10.3390/geosciences15120445





