Effective Elastic Moduli at Reservoir Scale: A Case Study of the Soultz-sous-Forêts Fractured Reservoir
Abstract
1. Introduction
2. Materials and Methods
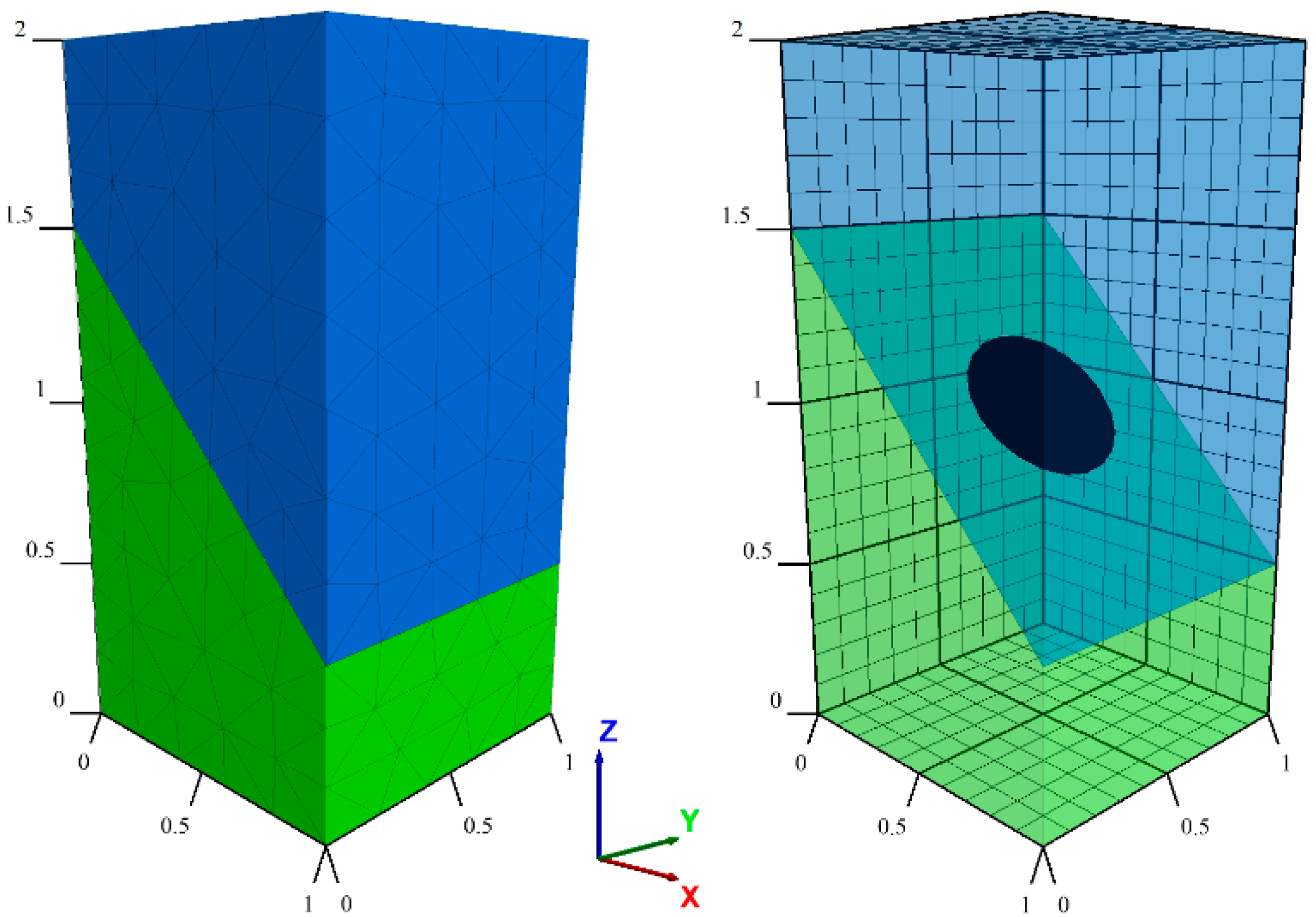
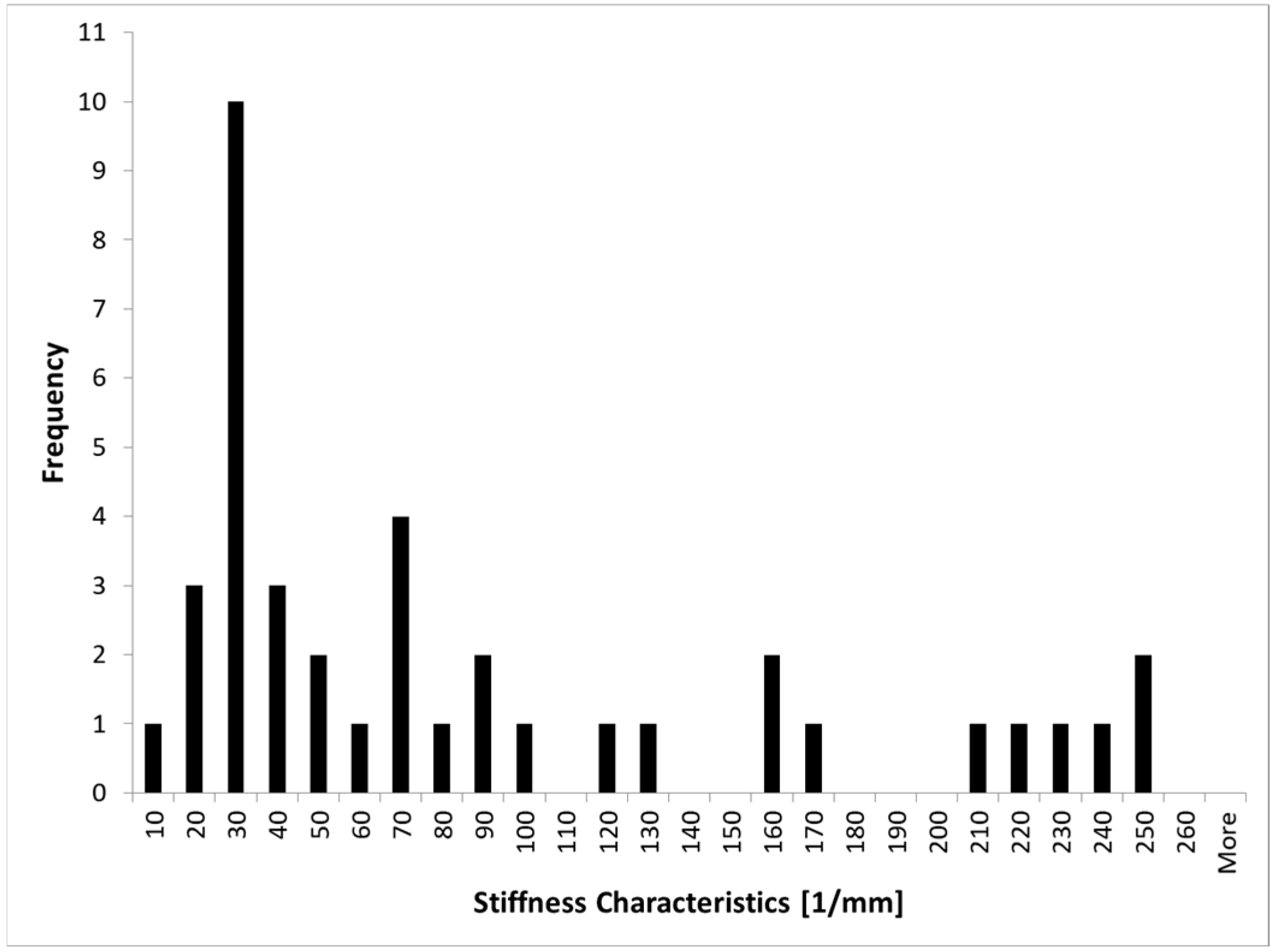
2.1. Discrete Fracture Network (DFN)
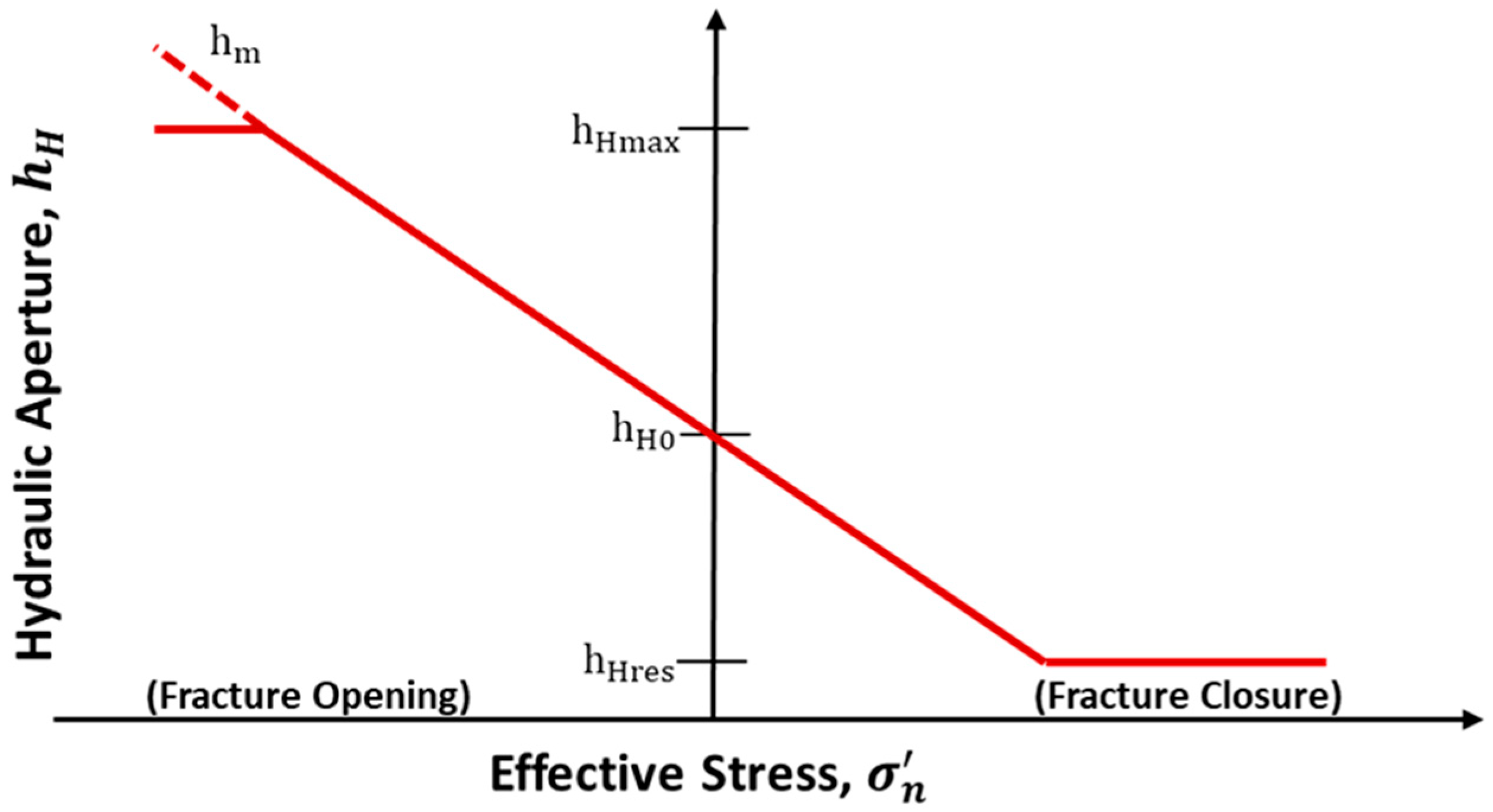
2.2. Fracture Deformation
2.3. Numerical Scheme
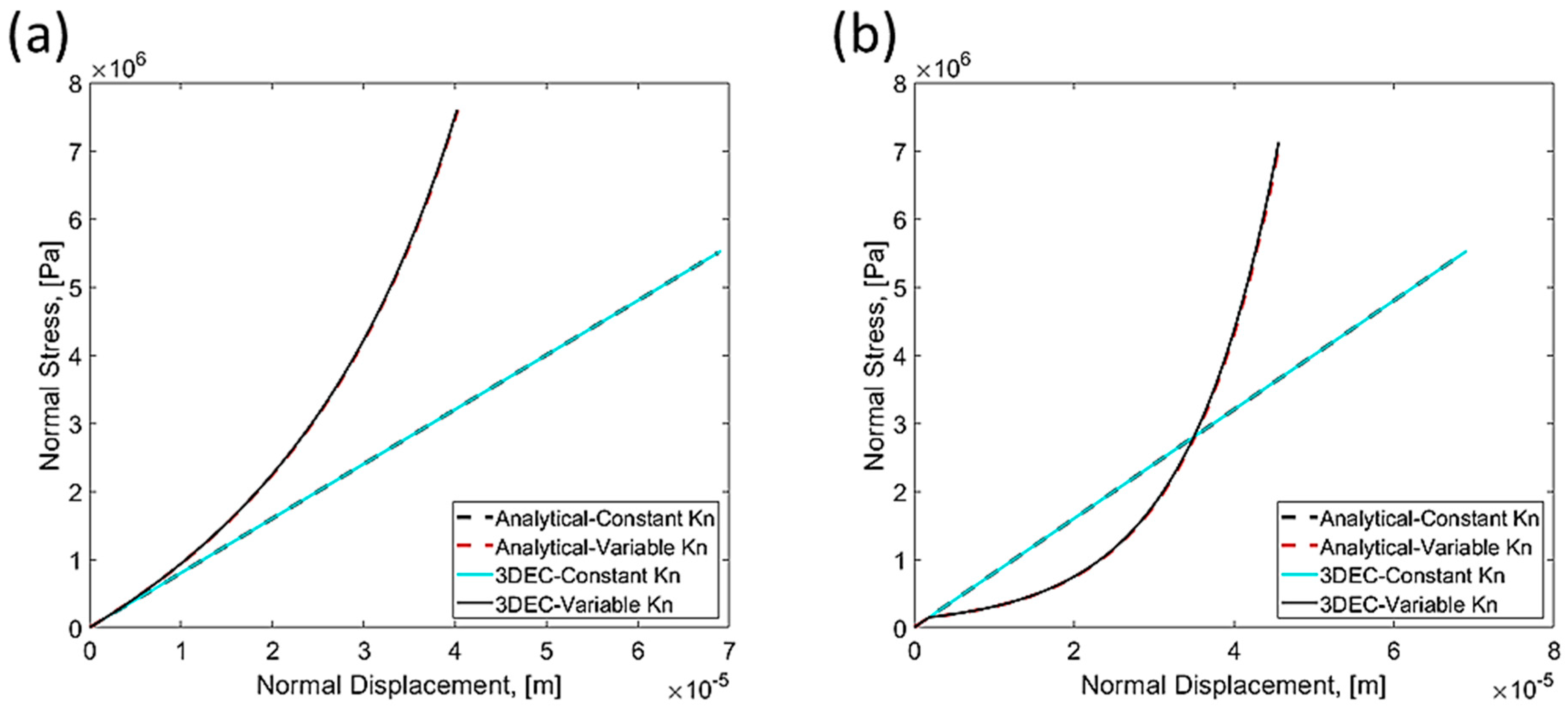
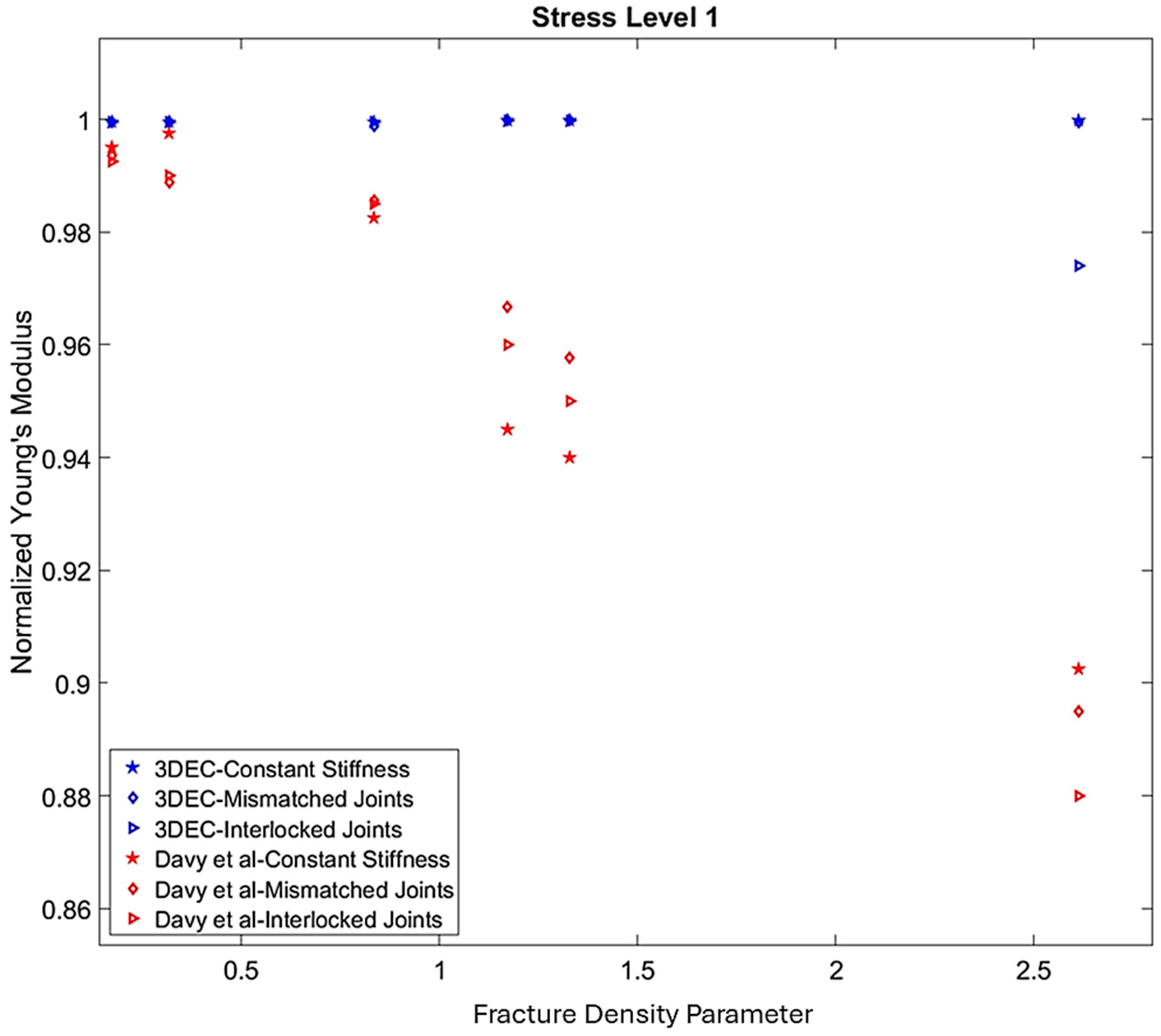
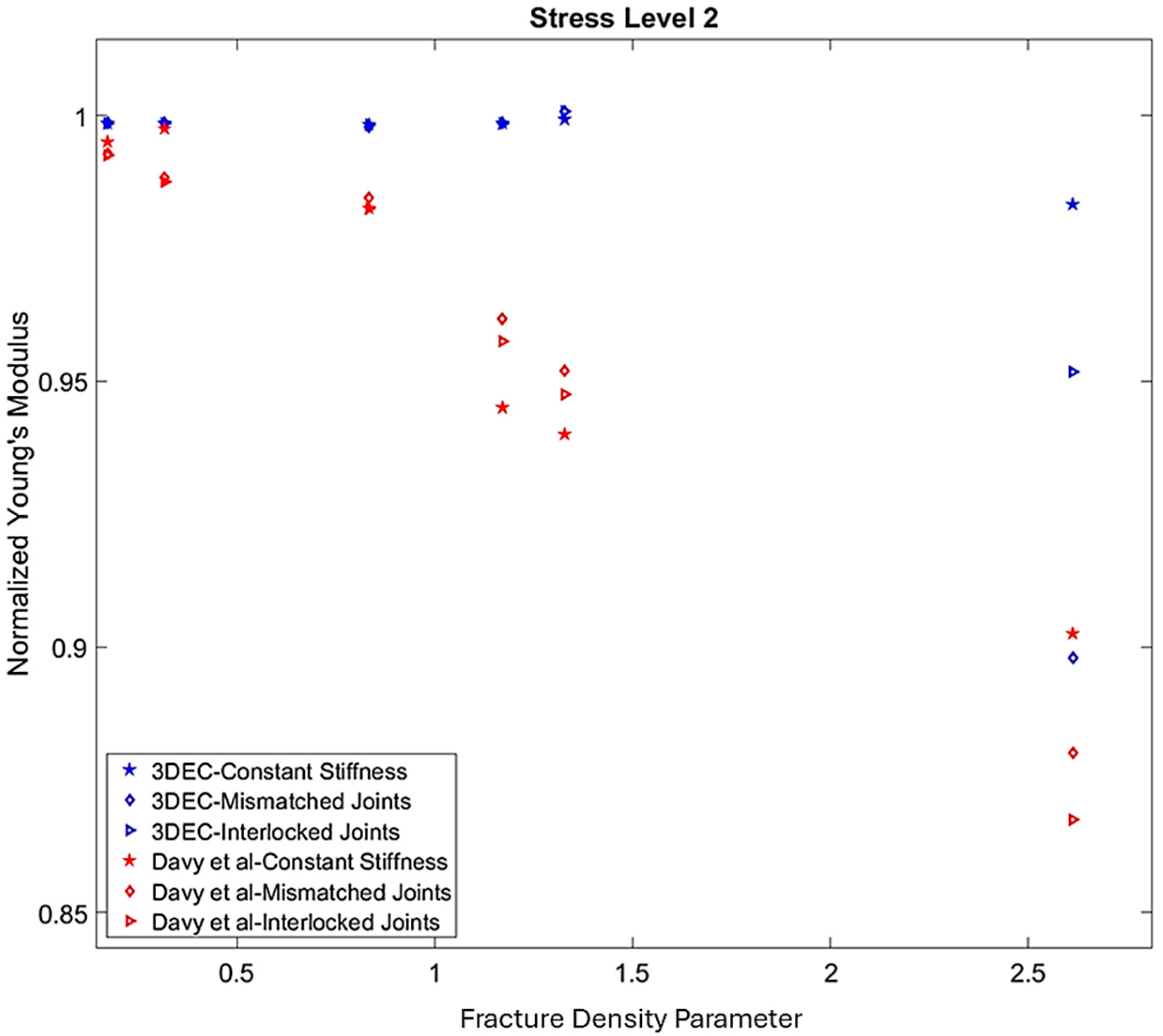
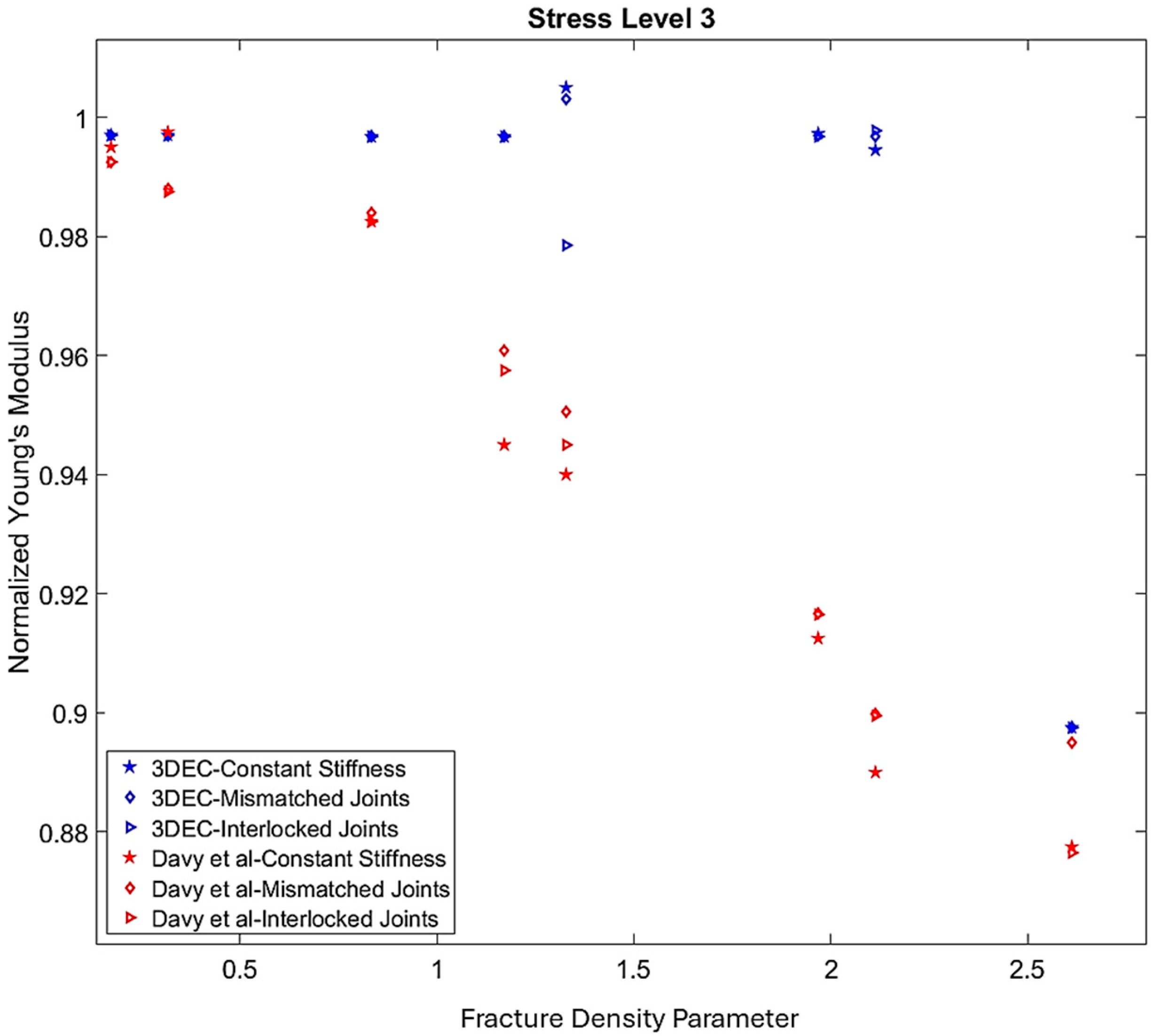
3. Verification Models
4. Results and Discussion
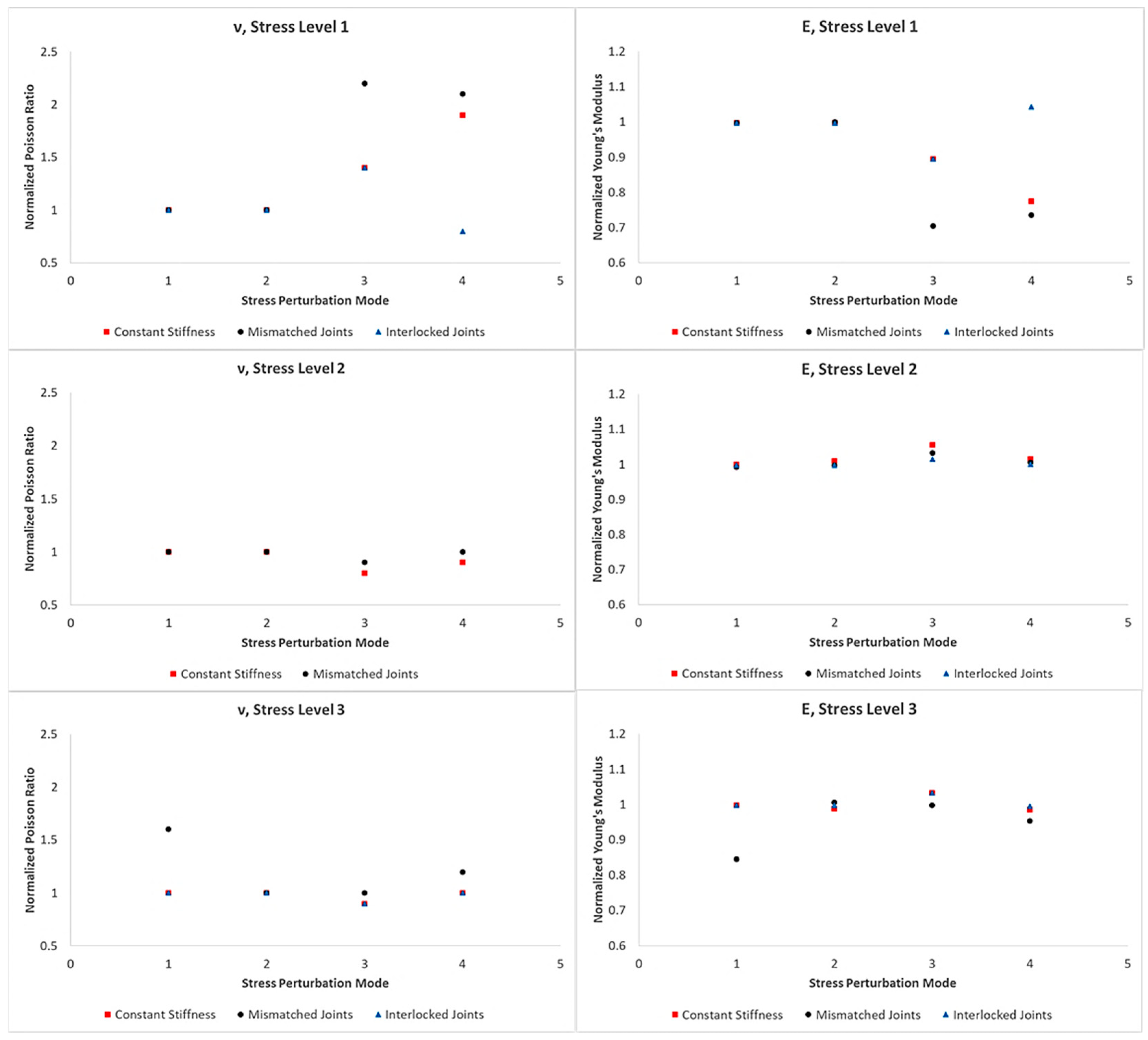
4.1. Elastic Moduli
- 500 m;
- 2.3 km;
- 4.7 km.
- 10% of principal stress values;
- 1% of principal stress values;
- 1 MPa of isotropic stress.
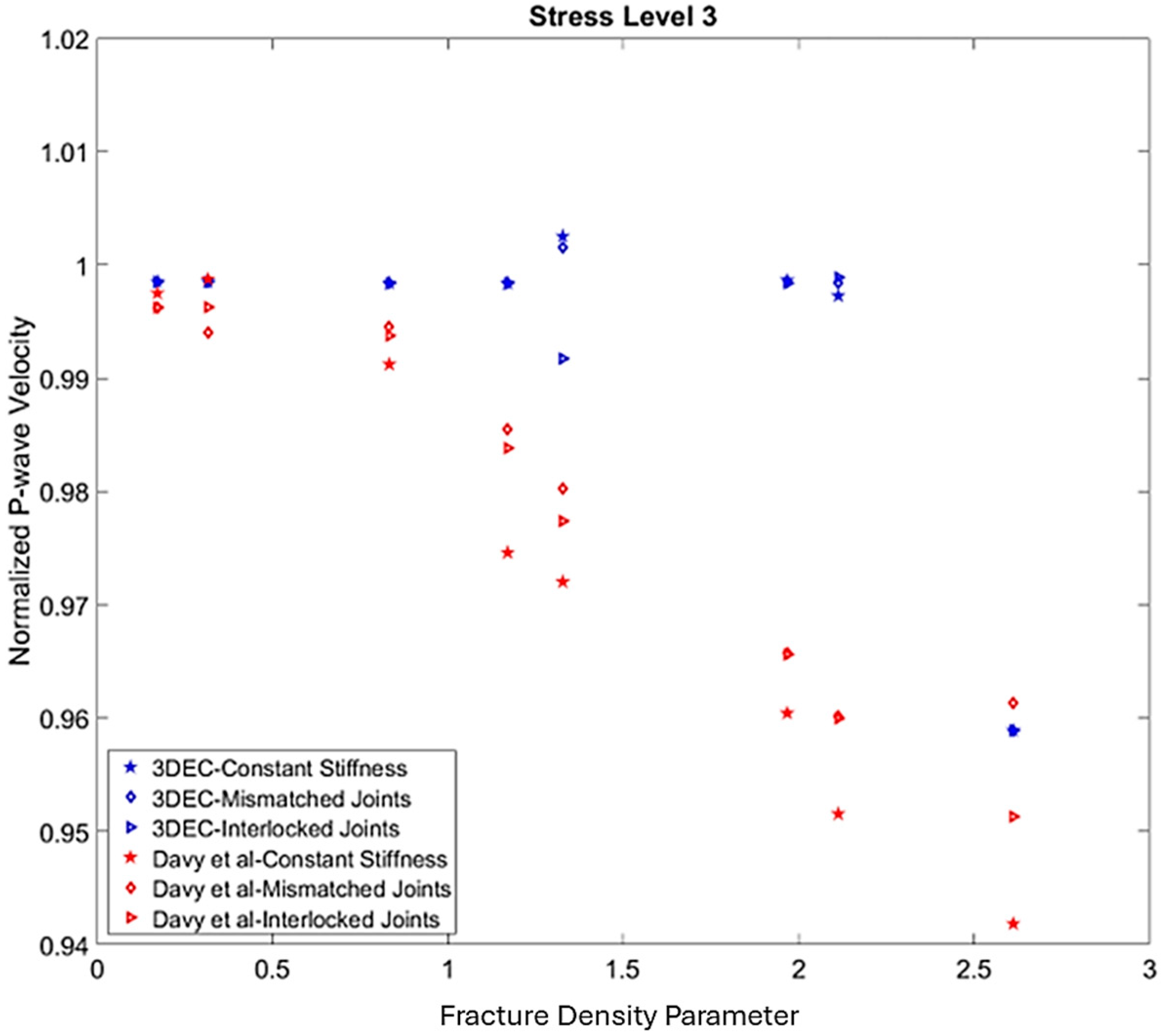
4.2. P-Wave Velocity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFN | Discrete Fracture Network |
| DEM | Distinct Element Method |
| HM | Hydro-Mechanical |
References
- Cornet, F.H. Elements of Crustal Geomechanics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef][Green Version]
- Simmons, G.; Brace, W. Comparison of static and dynamic measurements of compressibility of rocks. J. Geophys. Res. 1965, 70, 5649–5656. [Google Scholar] [CrossRef]
- Walsh, J.B. The effect of cracks on the compressibility of rock. J. Geophys. Res. 1965, 70, 5249–5257. [Google Scholar] [CrossRef]
- Singh, B. Continuum characterization of jointed rock masses: Part I—The constitutive equations. Int. J. Rock Mech. Min. Sci. 1973, 10, 311–335. [Google Scholar] [CrossRef]
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 335–344. [Google Scholar]
- Bieniawski, Z. Determining rock mass deformability: Experience from case histories. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 237–247. [Google Scholar] [CrossRef]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Amadei, B.; Goodman, R. A 3-D constitutive relation for fractured rock masses. In Proceedings of the International Symposium on Mechanical Behavior of Rock Structured Media—Part B, Ottawa, ON, Canada, 18–21 May 1981; pp. 249–268. [Google Scholar]
- Hoek, E. Strength of rock and rock masses. ISRM News J. 1994, 2, 4–16. [Google Scholar]
- Hoek, E.; Kaiser, P.K.; Bawden, W.F. Support of Underground Excavations in Hard Rock; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Cai, M.; Horii, H. A Constitutive Model and FEM Analysis of Jointed Rock Masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 351–359. [Google Scholar] [CrossRef]
- Sneddon, I.N.; Lowengrub, M. Crack Problems in the Classical Theory of Elasticity; Wiley and Sons: New York, NY, USA, 1969. [Google Scholar]
- Atkinson, B.K. Fracture Mechanics of Rock, Geology; Academic Press: London, UK, 1987. [Google Scholar] [CrossRef]
- Fabrikant, V.I. Complete solutions to some mixed boundary value problems in elasticity. Eng. Frac. Mech. 1988, 27, 153–223. [Google Scholar] [CrossRef]
- Zimmerman, R.W. The effect of microcracks on the elastic moduli of brittle materials. J. Mater. Sci. Let. 1985, 4, 1457–1460. [Google Scholar] [CrossRef]
- Budianski, R.; O’Connell, R.J. Elastic Moduli of cracked solid. Int. J. Solids Struct. 1976, 12, 81–97. [Google Scholar] [CrossRef]
- Kachanov, M. Elastic solids with many cracks and related problems. Adv. Appl. Mech. 1993, 30, 259–445. [Google Scholar] [CrossRef]
- Sayers, C.M.; Kachanov, M. A simple technique for finding effective elastic constants of cracked solids for arbitrary crack orientation statistics. Int. J. Soli. Struc. 1991, 27, 671–680. [Google Scholar] [CrossRef]
- Sayers, C.M.; Kachanov, M. Microcrack-induced elastic wave anisotropy of brittle rocks. J. Geophys. Res. 1995, 100, 4149–4156. [Google Scholar] [CrossRef]
- Schoenberg, M.; Sayers, C.M. Seismic anisotropy of fractured rock. Geophysics 1995, 60, 204–211. [Google Scholar] [CrossRef]
- Grechka, V.; Kachanov, M. Effective elasticity of fractured rocks: A snapshot of the work in progress. Geophysics 2006, 71, W45–W58. [Google Scholar] [CrossRef]
- Guéguen, Y.; Kachanov, M. Effective elastic properties of cracked rocks—An overview. In Mechanics of Crustal Rocks; Leroy, Y., Lehner, F., Eds.; Springer: Vienna, Austria, 2011; pp. 73–125. [Google Scholar] [CrossRef]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of Rock Joint Deformation. Int. J. Rock Mech. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rocks. J. Soil Mech. Found. Div. 1968, 94, 637–660. [Google Scholar] [CrossRef]
- Yoshioka, N.; Scholz, C.H. Elastic properties of contacting surfaces under normal and shear loads: 1. Theory. J. Geophys. Res. 1989, 94, 17681–17690. [Google Scholar] [CrossRef]
- Yoshioka, N.; Scholz, C.H. Elastic properties of contacting surfaces under normal and shear loads: 2. Comparison of theory with experiment. J. Geophys. Res. 1989, 94, 17691–17700. [Google Scholar] [CrossRef]
- Byerlee, J.D.; Brace, W.F. Stick slip, stable sliding, and earthquakes—Effect of rock type, pressure, strain rate, and stiffness. J. Geophys. Res. 1968, 73, 6031–6037. [Google Scholar] [CrossRef]
- Min, K.; Jing, L.; Stephanson, O. Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach: Method and application to the field data from Sellafield, UK. Hydrogeol. J. 2004, 12, 497–510. [Google Scholar] [CrossRef]
- Darcel, C.; Le Goc, R.; Doolaeghe, D.; Ghazal, R.; Davy, P. Rock Mass Effective Properties from a DFN Approach Phase 1—Elastic Properties; No. R-20-05; SKB: Solna, Sweden, 2021. [Google Scholar]
- Kulatilake, P.H.S.W. Effects of finite-size joints on the deformability of jointed rock in three dimensions. Int. J. Rock Mech. Min. Sci. Geomech. Abst. 1993, 30, 479–501. [Google Scholar] [CrossRef]
- Pouya, A.; Ghoreychi, M. Determination of rock mass strength properties by homogenization. Int. J. Num. Ana. Meth. Geomech. 2001, 25, 1285–1303. [Google Scholar] [CrossRef]
- Min, K.; Jing, L. Numerical determination of the equivalent elastic compliance tensor for fractured rock masses using the distinct element method. Int. J. Rock Mech. Min. Sci. 2003, 40, 796–816. [Google Scholar] [CrossRef]
- Esmaieli, K.; Hadjigeorgiou, J.; Grenon, M. Estimating geometrical and mechanical REV based on synthetic rock mass models at Brunswick mine. Int. J. Rock Mech. Min. Sci. 2010, 47, 915–926. [Google Scholar] [CrossRef]
- Wu, Q.; Kulatilake, P.H.S.W. REV and its properties on fracture system and mechanical properties, and an orthotropic constitutive model for a jointed rock mass in a dam site in China. Comput. Geotech. 2012, 43, 124–142. [Google Scholar] [CrossRef]
- Khani, A.; Baghbanan, A.; Norouzi, S.; Hashemolhosseini, H. Effects of fracture geometry and stress on the strength of a fractured rock mass. Int. J. Rock Mech. Min. Sci. 2013, 60, 345–352. [Google Scholar] [CrossRef]
- Davy, P.; Darcel, C.; Le Goc, R.; Mas Ivras, D. Elastic Properties of Fractured Rock Masses with Frictional Properties and Power Law Fracture Size Distributions. J. Geophys. Res. Solid Earth 2018, 123, 6521–6539. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture system in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of discontinuity spacing and trace length using scanline survey. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 183–197. [Google Scholar] [CrossRef]
- Rouleau, A.; Gale, J.E. Statistical characterization of the fracture system in the Stripa granite, Sweden. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 353–367. [Google Scholar] [CrossRef]
- Cruden, D.M. Describing the size of discontinuitie. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1977, 14, 133–137. [Google Scholar] [CrossRef]
- Hudson, J.A.; Priest, S.D. Discontinuities and rock mass geometry. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 339–362. [Google Scholar] [CrossRef]
- Hudson, J.A.; Priest, S.D. Discontinuity frequency in rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 73–89. [Google Scholar] [CrossRef]
- Nur, A. The origin of tensile fracture lineament. J. Struct. Geol. 1982, 4, 31–40. [Google Scholar] [CrossRef]
- Carbotte, S.M.; Mc Donald, K.C. Comparison of seafloor tectonic fabric at intermediate, fast, and super-fast spreading ridges’ Influence of spreading rate, plate motions, and ridge segmentation on fault patterns. J. Geophys. Res. 1994, 99, 13609–13631. [Google Scholar] [CrossRef]
- Cowie, P.A.; Vanneste, C.; Sornette, A. Statistical physics model for the spatiotemporal evolution of faults. J. Geophys. Res. 1993, 98, 21809–21822. [Google Scholar] [CrossRef]
- Davy, P. On the frequency-length distribution of the San Andreas fault system. J. Geophys. Res. 1993, 98, 12141–12151. [Google Scholar] [CrossRef]
- Kagan, Y.Y. Seismic moment-frequency relation for shallow earthquakes: Regional comparison. J. Geophys. Res. 1997, 102, 2835–2852. [Google Scholar] [CrossRef]
- Sornette, D.; Sornette, A. General theory of the modified Gutenberg-Richter law for large seismic moments. Bull. Seismol. Soc. Am. 1999, 89, 1121–1130. [Google Scholar] [CrossRef]
- Davy, P.; Sornette, A.; Sornette, D. Some consequences of a proposed fractal nature of continental faulting. Nature 1990, 348, 56–58. [Google Scholar] [CrossRef]
- Bour, O.; Davy, P.; Darcel, C.; Odling, N.E. A statistical scaling model for fracture network geometry, with validation on a multiscale mapping of a joint network (Hornelen Basin, Norway). J. Geophys. Res. 2002, 107, ETG-4-1–ETG-4-12. [Google Scholar] [CrossRef]
- Barton, N.R.; Bandis, S.C. Characterization and modelling of the shear strength, stiffness and hydraulic behavior of rock joints for engineering purposes. In Rock Mechanics and Engineering; CRC Press: Boca Raton, FL, USA, 2017; p. 38. [Google Scholar]
- Lei, Q.; Barton, N.R. On the selection of joint constitutive models for geomechanics simulation of fractured rocks. Comp. Geothech. 2022, 145, 104707. [Google Scholar] [CrossRef]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Experimental Studies of Scale Effects on the Shear Behaviour of Rock Joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 1–21. [Google Scholar] [CrossRef]
- Deng, Q.; Schmittbuhl, J.; Cacace, M.; Blöcher, G. Mechanical stiffness and permeability of a reservoir-scale rough fracture during closure. J. Geophys. Res. Solid Earth 2024, 129, e2024JB029001. [Google Scholar] [CrossRef]
- Evans, K.F.; Kohl, T.; Rybach, L.; Hopkirk, R.J. The effects of fracture normal compliance on the long-term circulation behaviour of a hot dry rock reservoir: A parameter study using the new fully coupled code fracture. GRC Trans. 1992, 16, 449–456. [Google Scholar]
- Zangerl, C.; Evans, K.F.; Eberhardt, E.; Loew, S. Normal stiffness of fractures in granitic rock: A compilation of laboratory and in-situ experiments. Int. J. Rock Mech. Min. Sci. 2008, 45, 1500–1507. [Google Scholar] [CrossRef]
- Kulhaway, F.H. Stress-deformation properties of rock and rock discontinuities. Eng. Geol. 1975, 8, 327–350. [Google Scholar] [CrossRef]
- 3DEC Software User Manual; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2016.
- Hart, R.D. An introduction to Distinct Element Modeling for Rock Engineering; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Alshkane, Y.M.; Marshall, M.A.; Stace, L.R. Prediction of strength and deformability of an interlocked blocky rock mass using UDEC. J. Rock. Mech. Geothec. Eng. 2017, 9, 531–542. [Google Scholar] [CrossRef]
- Pan, P.Z.; Feng, X.T.; Hudson, J.A. Numerical simulations of Class I and Class II uniaxial compression curves using an elasto-plastic cellular automaton and a linear combination of stress and strain as the control method. Int. J. Rock Mech. Min. Sci. 2006, 43, 1109–1117. [Google Scholar] [CrossRef]
- Shimizu, H.; Koyama, T.; Ishida, T.; Chijimatsu, M.; Fujita, T.; Nakama, S. Distinct element analysis for Class II behavior of rocks under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2010, 47, 323–333. [Google Scholar] [CrossRef]
- Villeneuve, M.C.; Heap, M.J.; Kushnir, A.R.; Qin, T.; Baud, P.; Zhou, G.; Xu, T. Estimating in situ rock mass strength and elastic modulus of granite from the Soultz-sous-Forêts geothermal reservoir (France). Geotherm. Energy 2018, 6, 11. [Google Scholar] [CrossRef]
- Gentier, S.; Rachez, X.; Dezayes, C.; Blaisonneau, A.; Genter, A. How to Understand the Effect of the Hydraulic Stimulation in Terms of Hydro-Mechanical Behavior at Soultz-sous-Forêts (France). GRC Trans. 2005, 29, 159–166. [Google Scholar]
- Cornet, F.H.; Bérard, T.; Bourouis, S. How close to failure is a granite rock mass at a 5km depth? Int. J. Rock Mech. Min. Sci. 2007, 44, 47–66. [Google Scholar] [CrossRef]
- Valley, B.; Evans, K.F. Stress state at Soultz-sous-Forêts to 5 km depth from wellbore failure and hydraulic observations. In Proceedings of the Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 January 2007; Stanford University: Stanford, CA, USA, 2007. [Google Scholar]
- Valley, B. The Relation Between Natural Fracturing and Stress Heterogeneities in Deep-Seated Crystalline Rocks at Soultz-sousForêts (France); ETH Zurich: Zurich, Switzerland, 2007. [Google Scholar]
- Massart, B.; Paillet, M.; Henrion, V.; Sausse, J.; Dezayes, C.; Genter, A.; Bisset, A. Fracture Characterization and Stochastic Modeling of the Granitic Basement in the HDR Soultz Project (France). In Proceedings of the World Geothermal Congress, International Geothermal Association, Bali, Indonesia, 25–30 April 2010. [Google Scholar]
- Afshari Moein, M.J.; Valley, B.; Evans, K.F. Scaling of Fracture Patterns in Three Deep Boreholes and Implications for Constraining Fractal Discrete Fracture Network Models. Rock Mech. Rock Eng. 2019, 52, 1723–1743. [Google Scholar] [CrossRef]
- Afshari Moein, M.J.; Bar, K.; Valley, B.; Genter, A.; Sass, I. Depth-Dependent Scaling of Fracture Patterns Inferred from Borehole Images in GPK3 and GPK4 Wells at Soultz-sous-Forêts Geothermal Site. In Proceedings of the World Geothermal Congress 2020+1, Reykjavik, Iceland, 24–27 October 2021. [Google Scholar]
- Javani, D. Modélisation des Variations de Vitesse des Ondes P Liées au Glissement Asismique dans un Réservoir Fracturé. Ph.D. Thesis, ITES/EOST, University of Strasbourg, Strasbourg, France, 2023. Available online: https://theses.hal.science/tel-04573885v1 (accessed on 5 September 2025).
- Anderson, E.W. The dynamics of faulting. Trans. Edinb. Geol. Soc. 1905, 8, 387–402. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R.W. Fundamentals of Rock Mechanics, 4th ed.; Blackwell: Oxford, UK, 2007. [Google Scholar]
- Stacey, F.D.; Davis, P.M. Physics of the Earth, 4th ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Dershowitz, W.S.; Herda, H.H. Interpretation of fracture spacing and intensity. In Proceedings of the 33rd U.S. Symposium on Rock Mechanics (USRMS), ARMA-92-0757. Santa Fe, NM, USA, 8–10 June 1992. [Google Scholar]
- Place, J.; Diraison, M.; Naville, C.; Geraud, Y.; Schaming, M.; Dezayes, C. Decoupling of deformation in the Upper Rhine Graben sediments. Seismic reflection and diffraction on 3-component Vertical Seismic Profiling (Soultz-sous-Forêts area). Comptes Rendus Geosci. 2010, 342, 575–586. [Google Scholar] [CrossRef]
- Calò, M.; Dorbath, C.; Cornet, F.H.; Cuenot, N. Large-scale aseismic motion identified through 4-D P-wave tomography. Geophys. J. Int. 2011, 186, 1295–1314. [Google Scholar] [CrossRef]
- Cornet, F.H. The relationship between seismic and aseismic motions induced by forced fluid injections. Hydrogeo. J. 2012, 20, 1463–1466. [Google Scholar] [CrossRef]
- Calò, M.; Dorbath, C. Different behaviours of the seismic velocity field at Soultz-sous-Forêts revealed by 4-D seismic tomography: Case study of GPK3 and GPK2 injection tests. Geophys. J. Int. 2013, 194, 1119–1137. [Google Scholar] [CrossRef]
- Cauchie, L.; Lengline, O.; Schmittbuhl, J. Seismic asperity size evolution during fluid injection: Case study of the 1993 Soultz-sous-Forêts injection. Geophys. J. Int. 2020, 221, 968–980. [Google Scholar] [CrossRef]
- Fjaer, E. Relations between Static and Dynamic Moduli of Sedimentary Rocks. Geophys. Prospect. 2019, 67, 128–139. [Google Scholar] [CrossRef]




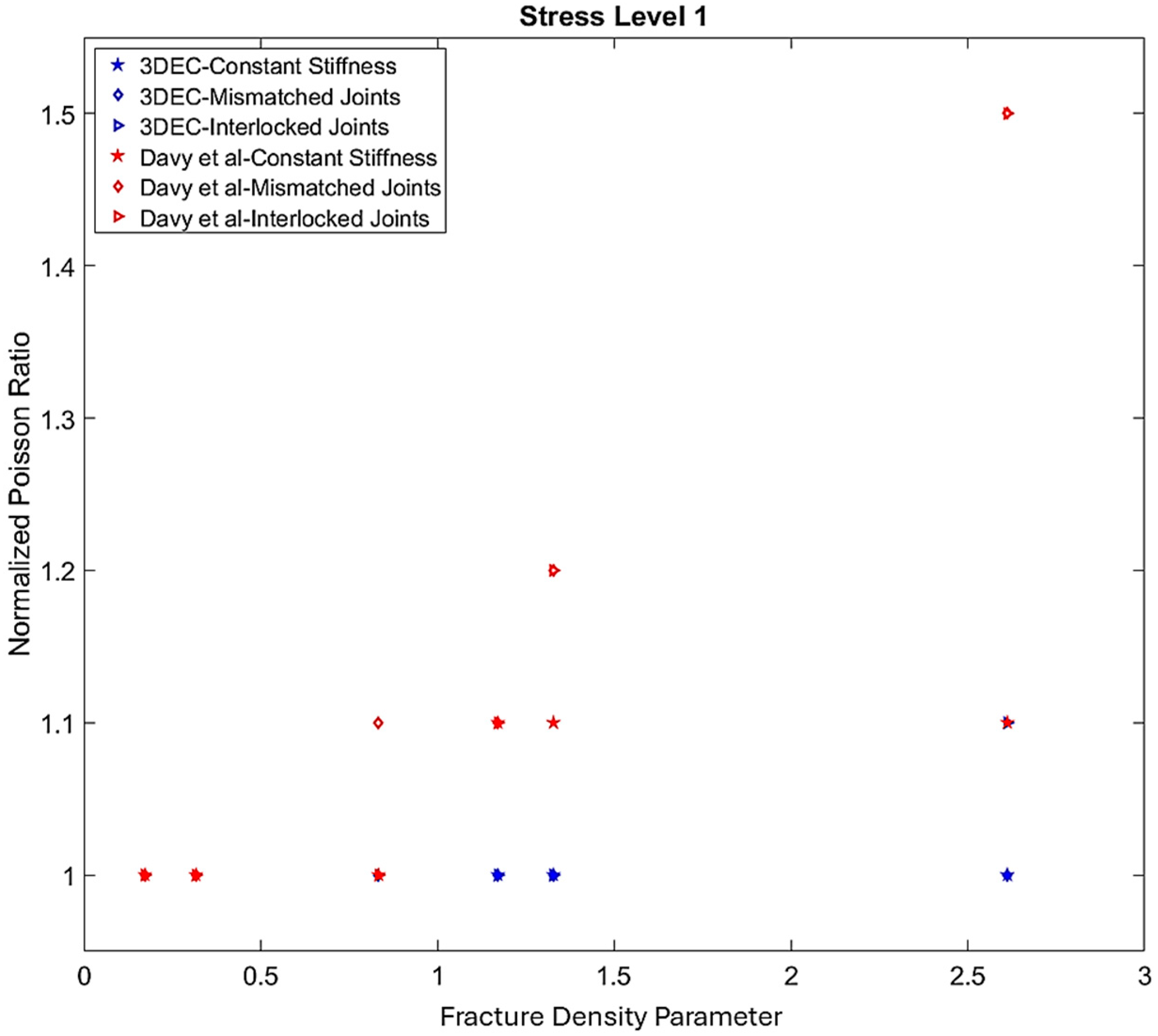
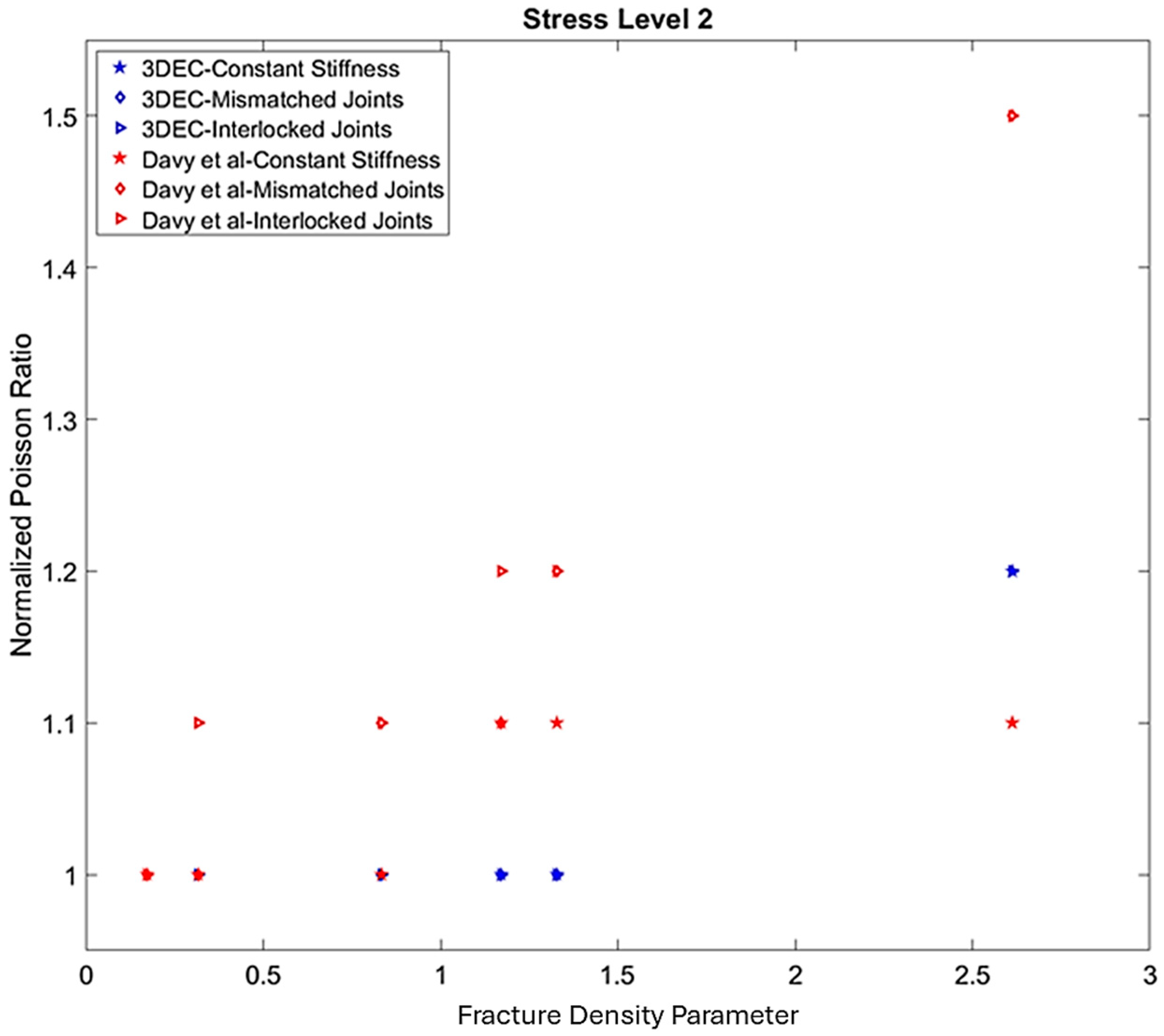

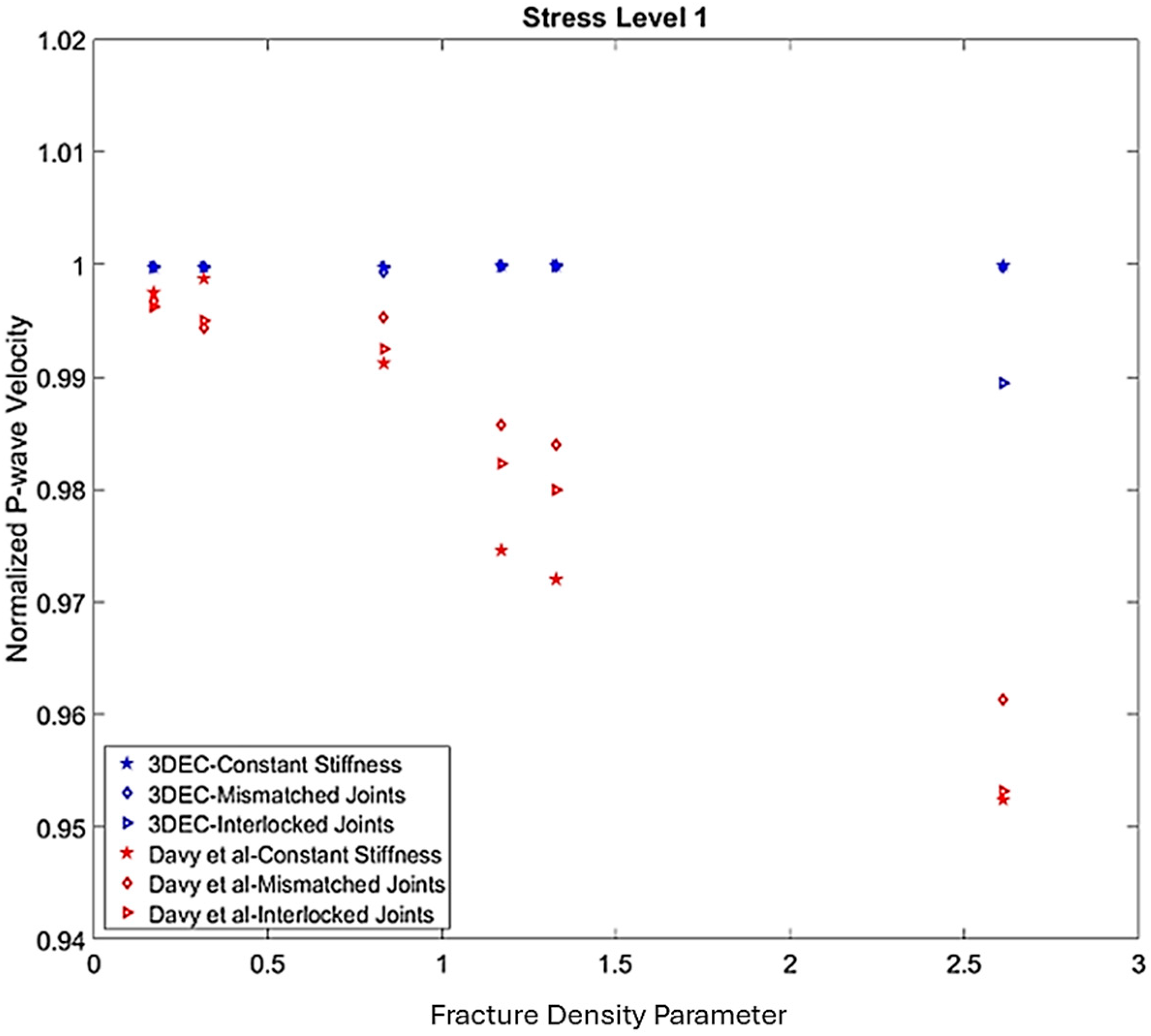
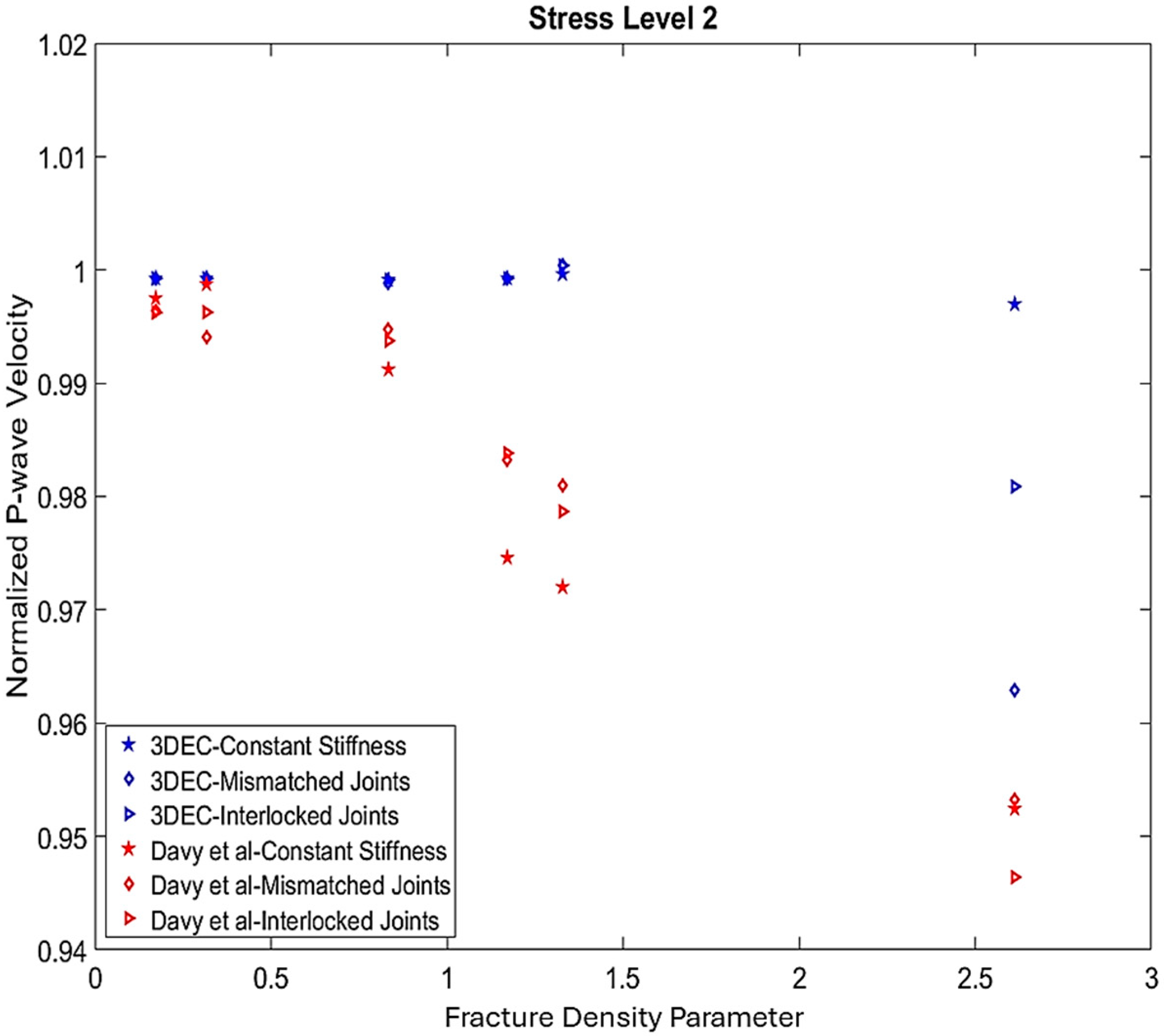
| Element | Property | Symbol | Value | Unit | Reference |
|---|---|---|---|---|---|
| Rock Matrix | Young’s Modulus | Ei | 40 | GPa | [64] |
| Poisson’s Ratio | υi | 0.1 | - | [64] | |
| Bulk Density | ρi | 2680 | kg/m3 | [65] | |
| Height | H | 2 | m | - | |
| Length | L | 1 | m | - | |
| Width | W | 1 | m | - | |
| Fracture | Initial Shear Stiffness | ksi | 20 | GPa/m | [65] |
| Initial Normal Stiffness | kni | 80 | GPa/m | [65] | |
| Friction Angle | φ | 39 | ° | [66] | |
| Cohesion | S0 | 6.5 | MPa | [67] | |
| Radius | R | 0.25 | m | - | |
| Dip | D | 45 | ° | - | |
| Dip Direction | DD | 90 | ° | - | |
| Initial Aperture | h0 | 14 · 10−5 | m | [65] | |
| Residual Aperture | hres | 7 · 10−5 | m | [65] | |
| Maximum Aperture | hmax | 12 · 10−3 | m | [65] |
| Stress Level | Fracture Stiffness | Initial Loading | Secondary Loading |
|---|---|---|---|
| 10% of in situ stress field at 4.7 km 50% of in situ stress field at 4.7 km 100% of in situ stress field at 4.7 km | Constant stiffness Stress-Dependent Stiffness (Interlocked Joints) Stress-Dependent Stiffness (Mismatched Joints) | In situ stress field | 10% of in situ stress field |
| In situ stress field | 1% of in situ stress field | ||
| In situ stress field | 1 MPa of isotropic triaxial stress | ||
| Isotropic triaxial S1 | 1 MPa of isotropic triaxial stress |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javani, D.; Schmittbuhl, J.; Cornet, F.H. Effective Elastic Moduli at Reservoir Scale: A Case Study of the Soultz-sous-Forêts Fractured Reservoir. Geosciences 2025, 15, 371. https://doi.org/10.3390/geosciences15100371
Javani D, Schmittbuhl J, Cornet FH. Effective Elastic Moduli at Reservoir Scale: A Case Study of the Soultz-sous-Forêts Fractured Reservoir. Geosciences. 2025; 15(10):371. https://doi.org/10.3390/geosciences15100371
Chicago/Turabian StyleJavani, Dariush, Jean Schmittbuhl, and François H. Cornet. 2025. "Effective Elastic Moduli at Reservoir Scale: A Case Study of the Soultz-sous-Forêts Fractured Reservoir" Geosciences 15, no. 10: 371. https://doi.org/10.3390/geosciences15100371
APA StyleJavani, D., Schmittbuhl, J., & Cornet, F. H. (2025). Effective Elastic Moduli at Reservoir Scale: A Case Study of the Soultz-sous-Forêts Fractured Reservoir. Geosciences, 15(10), 371. https://doi.org/10.3390/geosciences15100371







