Abstract
The present study is devoted to the analysis of extreme sea level oscillations of the Laptev Sea using the ADCIRC model. The numerical modeling is performed on a high-resolution grid and verified for sea level observations from three tide gauges. We have revealed regional characteristics of extreme sea level oscillations for different parts of the Laptev Sea coast. The maximum total sea level range was 544 cm in Ebelyakh Bay, while the minimum was 267 cm in Khatanga Bay, where maximum tidal ranges were obtained. Some areas in Khatanga Bay and Anabar Bay had maximum tidal ranges exceeding 200 cm. The study provided an estimation of the possible magnitude of coastal flooding by calculating the extreme total and residual sea levels for different return periods: 1, 2, 5, 10, 20, 50, and 100 years. The amplitude of extreme surges calculated for the 100-year return period can exceed 300 cm for several sections of the Laptev Sea coast, with the maximum sea level range being about 680 cm for Anabar and Ebelyakh Bays.
Keywords:
sea level oscillations; numerical modeling; ADCIRC; arctic; tides; storm surges; marine geohazards; tsunami 1. Introduction
The Laptev Sea is a shallow epicontinental sea located in the Russian Arctic and has a complex coastline shape of about 1300 km long. It is characterized by a broad continental shelf with shallow depths (<50 m of 53% water area), while in the northern Laptev Sea, the seabed descends to depths of over 1000 m, with a maximum of 3385 m. In winter, almost half of the Laptev Sea is covered by landfast ice, and recurring polynyas often form [1]. During the ice-free period in summer, the Lena River contributes the largest volume of freshwater discharge into the Laptev Sea [2]. The freshwater plume from the Lena River increases stratification in the Laptev Sea, which can be strong enough to persist throughout the year [3].
The extreme sea level oscillations in the Laptev Sea depend on location; bottom topography; the coastline geometry and steep continental slope; stratification, especially driven by the Lena River; and sea ice cover with recurrent polynyas. It is also formed under the influence of extensive cyclonic activity, which impacts whole areas of the sea [4]. In this study, extreme sea levels are described, characterized by extremes in terms of the combined effects of high tide and storm surge [5]. The Laptev Sea tide features an irregular, semidiurnal tidal wave that approaches the shore from the north and decreases in intensity as it approaches the coast, with a range of about 50 cm. Tides are of great importance for the south-western part of the sea encompassing the Khatanga and the Anabar Bay. However, the tidal magnitudes in the Anabar and Khatanga bays are significantly stronger, and can exceed 80–100 cm compared to other parts of the Laptev Sea, especially in the outer part of the Khatanga Bay [2,6]. Storm surges cause the greatest alterations in sea level in the Laptev Sea and depend on the season. They are most significant for the eastern part of the Olenek, Yana, and Buor-Khaya bays. In this region, they often exceed the danger level and, under certain conditions, they may be catastrophic [7].
The investigation of extreme sea level oscillations in the Russian Arctic coastal zones, particularly in the Laptev Sea, plays a crucial role in forecasting and ensuring operational and navigational safety, development of the Northern Sea Route, and marine engineering [8]. The prediction is also of great importance for tsunami hazard areas, as the highest seismic activity occurs on the southwestern coast of the Laptev Sea, particularly in the Olenek Bay region, and is fragmentary in the sublongitudinal strike of the complex deformation zone in the Lena River Delta [9,10]. The Laptev Sea is the most seismically active region in the Arctic Ocean because of its proximity to the mid-oceanic ridge known as the Gakkel Ridge, as well as the tension that dominates the shelf [11,12,13,14]. There is a particular interest in studying the Laptev Sea to evaluate geological and hydrometeorological hazards. Thus, a series of expeditions have been conducted to establish a network of ocean-bottom seismographs and tide gauges on the Laptev Sea shelf [15,16].
Kowalik and Proshutinsky [17] developed a two-dimensional numerical model of the major tidal constituents for the Arctic Ocean. Ashik [18] applied a 2-D model of storm surges and ice conditions to the Laptev and East Siberian Seas. However, the 8-constituent dynamics-based tidal model for the Arctic Ocean (AOTIM) outperformed the previous benchmark Arctic tidal model of Padman and Erofeeva (2004) [19]. The Finite Volume Coastal Ocean Model (FVCOM) was first developed to study tidal elevations and currents in the Arctic Ocean by Chen et al. [20] and was successful performed to simulate the tidal dynamics in the Lena Delta region of the Laptev Sea in an ice-free barotropic case [21]. Main modern tidal models were also presented and classified by Stammer et al. [22]. Kowalik [23] simulated three storm surge events in the Beaufort and Chukchi Seas using interpolated surface winds from 6 h interval calculations based on the geostrophic wind computation with and without an ice cover. A two-dimensional hydrodynamic model developed in TELEMAC-2D was used by Kim et al. [24] to simulate storm surges incorporating the effects of sea ice in the Beaufort Sea.
In the Arctic, the ADCIRC model has been used to study the influence of sea ice on resulting storm surges in the Bering Sea along the coast of western Alaska [25], ice-induced tidal variability in the Canadian Arctic [26], and storm surges in the White and Barents seas [27]. Numerical simulations of tsunamis and estimation of an inundation hazard zone for the northern Pacific Ocean have been also performed using the ADCIRC model [28]. Thus, there are many modeling studies on the dynamics of the Arctic Ocean, but there is a lack of research focused on the whole coastal area of the Laptev Sea. In one study, the ADCIRC model was applied for the Laptev Sea because the unstructured computational grids used in the model provide good results for high-resolution modeling in coastal areas with shallow water [29].
The study aimed to examine the features of extreme oscillations of total, tidal, and residual levels along the Laptev Sea coastline using the circulation ADCIRC model and data from the NCEP/CFSR reanalysis.
2. Materials and Methods
2.1. Setup of the ADCIRC Circulation Model Setup
The ADvanced three-dimensional CIRCulation model (ADCIRC) is a finite element model developed by Luettich et al. [30]. The model is specifically designed to simulate long periods of hydrodynamic circulation along shelves and coasts and within estuaries.
A two-dimensional depth-integrated model (2DDI) was used to estimate the features of extreme water level oscillations on the Laptev Sea coast. The input data, such as atmospheric pressure, surface wind, and ice concentration data, for the model were taken from the NCEP (National Centers for Environmental Prediction) CFSR (Climate Forecast System Reanalysis) (NCEP/CFSR) reanalysis [31]. This reanalysis was used due to its high quality and consistency with in situ data on storm surge modeling, including in other Arctic seas [27,32,33]. The spatial resolution of the atmospheric fields was about 0.3125° × 0.312° and the data covered the period from 1980 to 2000 (21 years), with a time interval of 1 h. The computational grid confined the investigative region to the north with the conventional border of perennial ice distribution (at 81° N) and to the south with the continent’s coastline. The computational area used for modeling in the water area of the Laptev Sea corresponded to the bathymetric boundaries of the Laptev Sea shown in Figure 1. The elevation model used was the IBCAO digital elevation model version 3.0, with 30 s increments (1/120 degree) to input bottom topography. The modeling was performed on unstructured grids with a spatial resolution ranging from 0.2 km along most of the coast of the Laptev Sea bays up to 20 km at the outer boundary of the computational domain. The ADCIRC model was run using a grid of 6684 nodes and 12,131 triangular elements which was created in the Aquaveo Surface-water Modeling System (SMS 12.2.12) application. The model simulation was conducted at the Department of Oceanology at Lomonosov Moscow State University. The nonlinear hybrid (depth-dependent) friction formulation is used for computing the bottom friction in ADCIRC [30]. The computational time increment was 2 s and computation time for 1 year was about 5 h.
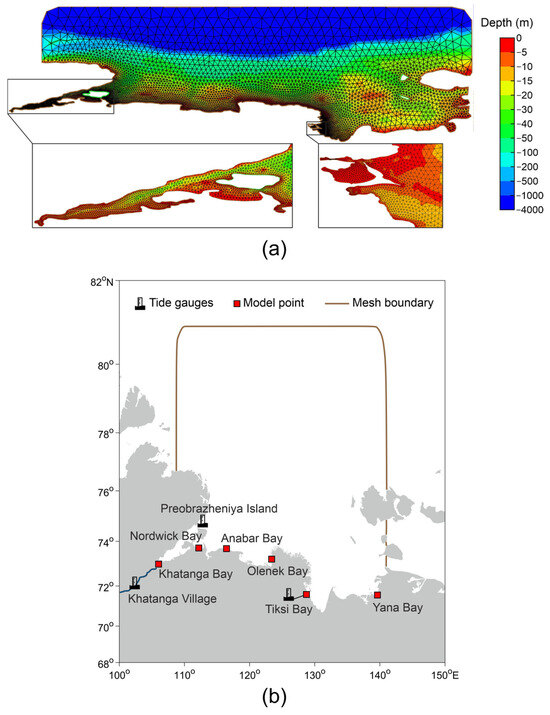
Figure 1.
The computational unstructured grid (a) for the ADCIRC model and (b) the map of the Laptev Sea depth.
The eight most significant tidal harmonic constituents (K1, O1, P1, Q1, N2, M2, S2, K2) were collected using the FES2004 database [34]. We divided tidal measurement periods into annual time series and estimated vector-averaged amplitudes for each series. The obtained amplitudes from different years were then averaged to calculate the mean long-term values of the amplitudes of the tidal harmonics [35]. The tidal harmonic constants were set at the open boundary of the computational domain in the model. The total sea level was simulated after integrating the reanalysis input data and tidal constituents for the Laptev Sea coastline, which consisted of 1195 points. Then, based on the modeled total sea level, the characteristics of total tidal and residual levels were investigated. The eight tidal harmonic constituents were determined using harmonic analysis and a least squares approach with the Matlab toolbox T_Tide, version 1.4 [36]. The residual sea level is the result of the subtraction of the tidal component from the total sea level.
The coast of the Laptev Sea was divided into 39 sections, each section being about 100 km long. The maximum and minimum values of total sea level, variance values of tidal and residual sea level oscillations, and the tidal non-harmonic components were determined and averaged for each section. Thus, the total sea level ranges and the total and residual extreme sea levels for different return periods were calculated within each section for the modeling period.
2.2. Verification of Model and In Situ Data
To evaluate the quality of the ADCIRC model, the results of the long-term mean values of the amplitudes of the four tidal harmonics (M2, S2, O1, K1,) obtained over the course of use of this model were compared with the tide gauge observations at the stations Tiksi Bay from 1981 to 2000 and Preobrazheniya Island from 1986 to 1988. The tidal amplitude measurements at these tide gauges were obtained from the ESIMO portal (Unified State System of Information on the Environment in the World Ocean).
The ADCIRC tidal values computed by the model at six points along the Laptev Sea coastline were also compared with data from the AOTIM5 tide model at the corresponding points. The Arctic Ocean Tidal Inverse Model (AOTIM5) is based on a data assimilation scheme [37] and represents an inverse solution that assimilates almost all available tide gauge data in the Arctic Ocean [19]. The AOTIM5 tide model provides an advantage by estimating tidal oscillations along the Laptev Sea coastline where in situ observations are not available.
We also analyzed the difference between the residual sea level of the model data and the hourly in situ observations at the two tide gauges mentioned above—Preobrazheniya Island, Tiksi Bay, and an additional station at Khatanga Village. The time series that were selected represented two distinct periods: one with ice cover (February–April) and the other which was ice-free (July–September). For Tiksi Bay, high-quality data were available for the entire year. At the Khatanga Village station, in situ data were available only from July to October 1983. The model point was situated at the entrance of Khatanga Bay at the mouth of the river and was different from the station at Khatanga Village (Figure 1), resulting in an 18 h time shift in the calculations.
We applied the Butterworth low-pass filter to completely remove the tidal component with a cutoff frequency of 0.04 cph, corresponding to a period of approximately 25 h [38]. The long-period component of the sea level oscillations was also removed from the residual series. Each time series was filtered with a 10-day Hamming window [39]. We measured and analyzed the correlation coefficient (R) and root-mean-square error (RMSE) to compare data between the model results and observations. The Figure 2 shows a fragment of the residual sea level time series, including 3 months (April–June 1986) of filtered model and in situ data at the Tiksi Bay.
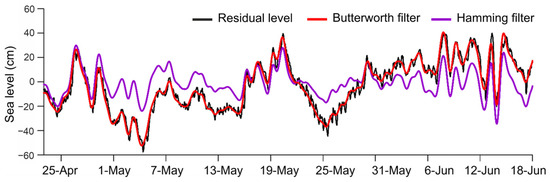
Figure 2.
Fragment of the residual sea-level time series (in 1986) at the Tiksi Bay.
2.3. Calculation of Nonharmonic Tidal Components
Two tidal non-harmonic characteristics were calculated: the mean spring range (Rspr) and the maximum range (Rabs) [40].
The mean spring range, which reflects its diurnal extent in high spring (maximum range of tides observed twice a month at “full” and “new” moon between low and high water), was calculated as the mean of the doubled sum of the amplitudes of the two main semidiurnal components:
The maximum range was determined as the maximum difference between high and low water during a lunar day over a tidal time series predicted for 18.6 years based on the results of harmonic analysis. The Rabs values significantly exceeded the Rspr because all major diurnal, semidiurnal, and shallow tidal harmonics were included in the calculation of Rabs.
2.4. Total and Residual Extreme Sea Level Calculation
In this study, the extreme values of total and residual sea levels were calculated to assess the risk of coastal flooding for different return periods (1, 2, 5, 10, 20, 50, and 100 years) using the Gumbel distribution [41], which can be expressed as:
where P(h) is the probability that sea level exceeds height h and y is a reduced variable with linear dependence on h and y:
The return period (T) of an extreme event of a certain magnitude is the average time interval during which the event occurs or is exceeded only once:
where F(x) is the probability density function of the Gumbel distribution. Therefore, if an event has a probability of occurring within a year equal to p, then it is necessary to have a series of observations with an average duration of 1/p years for the event to occur once.
In order to calculate the return period of an extreme event (in this case, reaching or exceeding a certain value h), it is first necessary to sort all the recorded events in ascending order, numbering them by index j from the smallest h1 to the largest hN, where N is the number of events. For a given value of j, the number of events with h ≥ hj is N − j + 1 and, accordingly, the repeatability can be estimated as:
where Δt is the sampling discreteness (in this case one day). The probability distribution F(x) of the sea level hj can be expressed as:
After ranking the daily maximum and minimum values of the total and residual sea level records, we extrapolated for periods of 20, 50, and 100 years based on 20 extreme values.
We also calculated that one of the metrics for storm surge research is skew surge—the difference between the observed and predicted high sea level within a tidal cycle [42]. To obtain the skew surge record, we determined the values of this parameter within each semidiurnal tidal cycle (~12.5 h) of the sea level records.
3. Results
In comparison with the tidal model AOTIM5, the presented ADCIRC model performed significantly better for the major diurnal (O1, K1) and semidiurnal (M2, S2) tidal waves constituent at Preobrazheniya Island, but the opposite was observed at most other stations (model points in Figure 1), where these components were underestimated (Table 1). Differences in the amplitudes of four major tidal harmonics were also found by comparing the obtained ADCIRC amplitude with tide gauge data at the two stations. The amplitudes calculated with ADCIRC were overestimated compared to observations by 0.5–1.6 cm for the main diurnal harmonics O1 and K1, by 0.5–1.2 cm for the S2 constituent, and by 6.6–11.8 cm for the major semidiurnal constituent M2, respectively.

Table 1.
Validation of the ADCIRC model of long-term mean amplitudes and the tide model AOTIM5 in comparison with in situ tide gauge observations (obs, in bold) in cm.
The correlation coefficient (R) between the observed data and simulated residual sea levels varied from 0.67 to 0.83 (with an all-year average of 0.75) at Tiksi Bay for annual records (1981–2000), while the root-mean-square error (RMSE) ranged from 10.3 to 14.9 cm (with an average of 13.2 cm) (Table 2). The R value for Khatanga Village for the period of continuous observations from July 16 to October 7 was 0.70, whereas the RMSE value was 9.3. Seasonal variations in the coefficient of correlation were observed at Preobrazheniya Island. The correlation coefficients were moderate during the ice-covered period (February–April), ranging from 0.50 to 0.71. However, during the ice-free months (July–September), the coefficients were lower, ranging from 0.29 to 0.56. The RMSE values for all continuous periods for Preobrazheniya Island ranged from 9.5 to 16.7 cm. However, the R and RMSE values were significantly higher for individual 2-week sea level records during storm surges at three stations (Figure 3). For Tiksi Bay, the values were R = 0.98 and RMSE = 9.9 cm from September 16 to 30, 1986; for Preobrazheniya Island, R = 0.84 and RMSE = 6 cm from April 16 to 30, 1988; and for Khatanga Bay and Village, R = 0.81 and RMSE = 8.4 cm from July 16 to 30, 1983.

Table 2.
Correlation coefficient (R) and mean value of root-mean-square error (RMSE) in the ADCIRC model and in situ data for the residual levels at 3 stations.
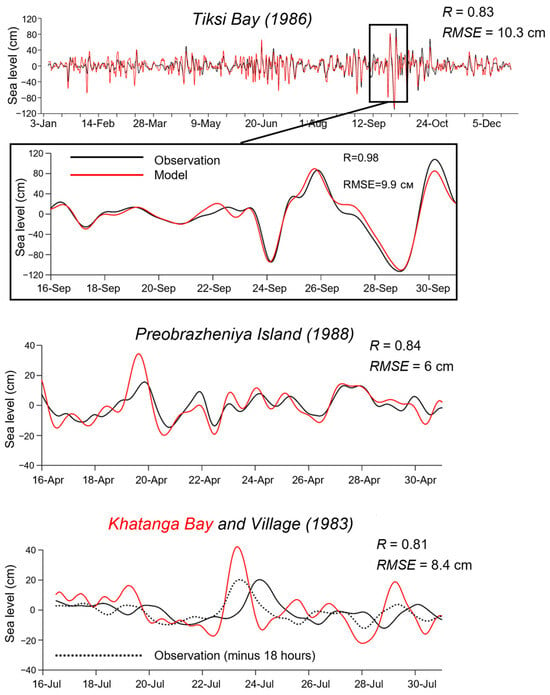
Figure 3.
Comparison of modeled (red line) and observed (black line) residual sea level at three stations in the Laptev Sea.
The maximum and minimum values of the total sea level, averaged for each of the 39 sections, were obtained for the Laptev Sea coast during the modeling period of 1980–2000 (Figure 4). The maximum for the total sea level was obtained for Ebelyakh Bay 264 cm, and 273 cm was obtained for the residual water level (Figure 4a). High values of total sea level were also calculated at four sections of Anabar Bay, the eastern parts of Olenek and Yana bays, and Kotelny Island, ranging from 245 to 252 cm (for the residual level, it was 242–261 cm, respectively) (Figure 4c). The maximum values of the total sea level also did not exceed 200 cm for the Khatanga Bay and the eastern part of the Lena River delta. The minimum values of the total sea level were obtained in Anabar Bay and were −190 cm (Figure 4b). The lower values varied in the range from −157 to −170 cm in the southeastern part of the Laptev Sea (Tiksi Bay, Ebelyakh Bay and Bolshoy Lyakhovsky Island) (Figure 4d). In the Lena River delta and on Kotelny and Belkovsky Islands, the sea level did not drop below 100 cm. In the Khatanga Bay, there were differences in different parts of the water area. The total sea level values decreased to −148 cm at the top of Khatanga Bay, while they reached −90 cm in the southeastern part of the bay.
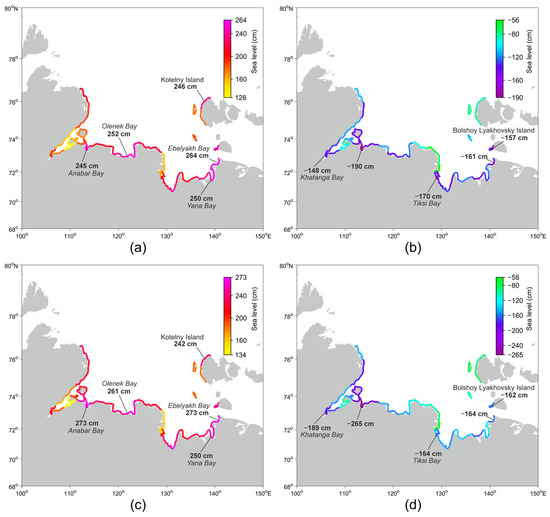
Figure 4.
Sea levels of the Laptev Sea coast: (a,c) maximum and (b,d) minimum, (a,b) total and (c,d) residual.
The range of the total sea level varied from 267 cm in the southern part of the Khatanga Bay (on the coast of the Khara-Tumus peninsula) to 544 cm in the Ebelyakh Bay (Figure 5a). In the upper part of the Khatanga Bay, as well as in the Anabar, Olenek, and Yana bays and on the Bolshoy Lyakhovsky Island, the total sea level range exceeded 450 cm. The mean value of the range of water levels for the entire coast (including islands) of the Laptev Sea was 389 ± 63.4 cm. The maximum residual sea level range found in Anabar, Nordvik, Khatanga and Ebelyakh bays showed values of 625, 552–554, and 544 cm, respectively (Figure 5b). The minimum of the residual sea level range was only 282 cm on the coast of the Khara-Tumus peninsula in the southern part of the Khatanga Bay.
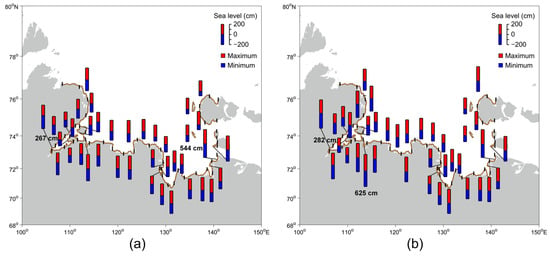
Figure 5.
Range of the (a) total and (b) residual sea levels of the Laptev Sea coast.
In the western part of the Laptev Sea, which includes the northeastern part of the Taimyr Peninsula and Khatanga and Anabar Bays, the mean spring range (Rspr) and maximum range (Rabs) reached high values of 35–176 cm and 64–264 cm, respectively (Figure 6). Maximum values were observed in Anabar Bay (Rspr = 176 cm, Rabs = 264 cm). The northern coast of the Lena River delta and Buor-Khaya Bay, as well as Tiksi Bay, comprise the central part of the Laptev Sea coast. This region was characterized by Rspr and Rabs values ranging from 41–69 cm and 69–103 cm. The eastern and western parts of the Lena River delta and the eastern part of the Laptev Sea exhibited the lowest values of tidal nonharmonic characteristics. In these regions, Rspr values ranged from 7 to 41 cm and Rabs varied from 24 to 71 cm. The coast of the New Siberian Islands showed a significant excess of Rabs over Rspr, likely due to the considerable contribution of diurnal and shallow tidal harmonics in that part of the Laptev Sea.
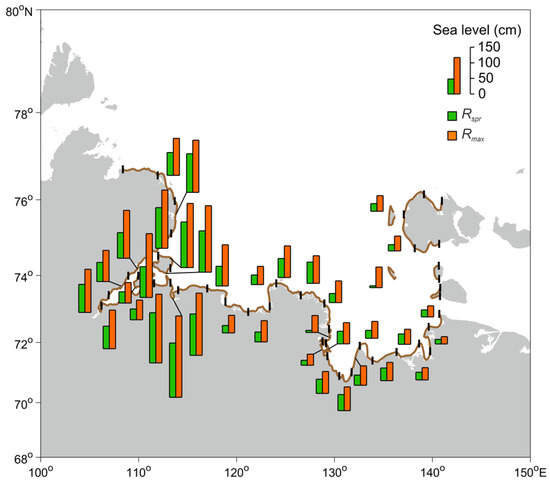
Figure 6.
The magnitude of the mean spring range (Rspr) and maximum range (Rabs) of the Laptev Sea coast.
In the Laptev Sea, tidal oscillations accounted for 30% of the total sea level variance (Figure 7). However, in areas such as Khatanga Bay, tidal contribution could reach up to 90%, whereas in Olenek, Buor-Khaya (in Tiksi Bay), and Yana Bay, the contribution is no more than 5–10%. Residual sea level oscillations had the greatest impact in Yana Bay (94%) and the least impact in Nordvik Bay of Khatanga Bay (14%). On average, the Laptev Sea had a residual sea level contribution to the total variance that was more than twice as high as the share of tides.
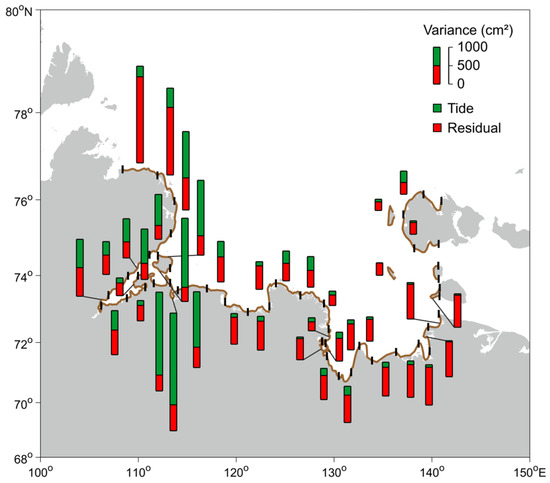
Figure 7.
Variance ratios of tidal and residual sea level oscillations on the Laptev Sea coast.
An extrapolation of daily maximum and minimum values of the residual level for periods from 1 year to 100 years is given for the six major bays of the Laptev Sea (Table 3). For the 100-year return period, the extreme values of total and residual sea levels (Figure 8) have an amplitude of more than 300 cm in some sections of the Laptev Sea coastline. The maximum magnitude of storm surges was obtained for a part of Olenek (393 cm), Ebelyakh (353 cm), Anabar (335 cm), and Yana (334 cm) bays (Figure 8c). The minimum values of the negative surges (set-down events) were calculated for Anabar (−344 cm), Khatanga (−337 cm), and Ebelyakh (−325 cm) bays (Figure 8d). In Anabar and Ebelyakh bays, the range of extreme values of the residual water level was almost 6.8 m (678–679 cm).

Table 3.
Maximum amplitudes of positive storm surges (SS) and negative surges (NS) for different return periods: 1, 2, 5, 10, 20, 50 and 100 years.
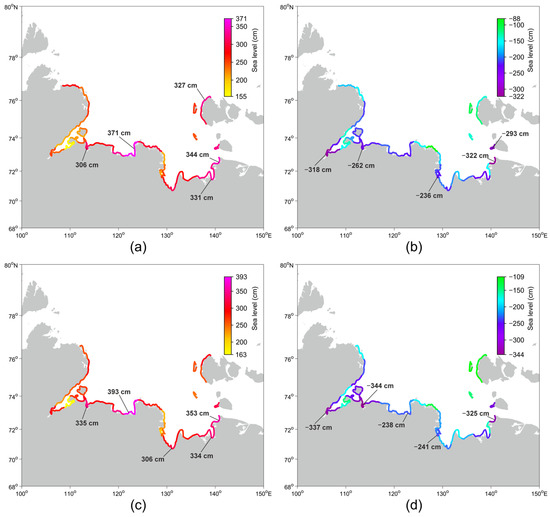
Figure 8.
Sea levels for a 100-year return period at the Laptev Sea coast: (a,c) maximum and (b,d) minimum; (a,b) total and (c,d) residual.
In places with strong tides (Khatanga and Anabar bays), the skew surge did not exceed 2.1 m, while in places with weak tidal variance, it reached up to 2.5–2.7 m (Olenek, Yana and Ebelyakh bays) (Figure 9). In Tiksi Bay, the maximum value of this parameter was 1.8 m. The time offset between the maximums of the total sea level and the next high tide ranged from −4 h (the maximum of the total sea level was observed 4 h after high tide) to 5 h (the corresponding maximum was observed 2 h before high tide) (Table 4). The maximum skew surge values were obtained for the fall season, from early September to early November.
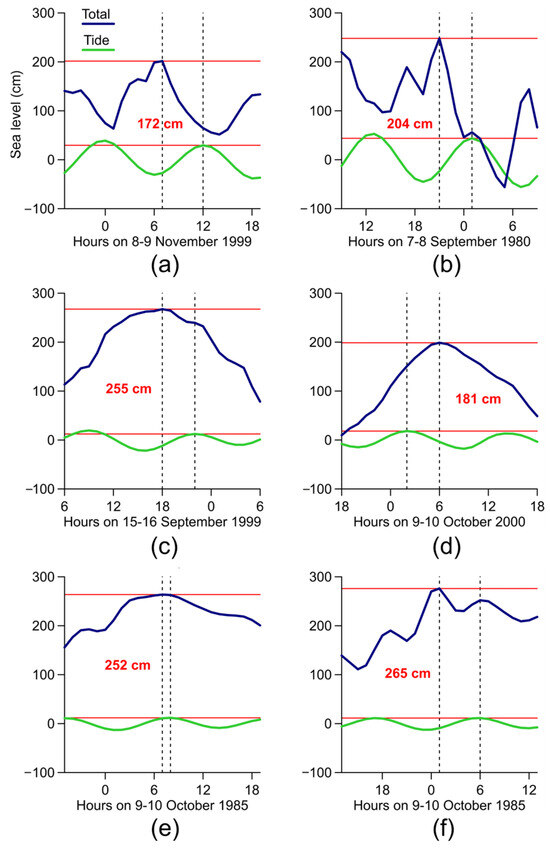
Figure 9.
Maximum skew surge values for (a) Khatanga, (b) Anabar, (c) Olenek, (d) Tiksi, (e) Yana, and (f) Ebelyakh bays. The displacement between the onset of high tide (green line) and the maximum of the total sea level (blue line) is shown by the dashed line.

Table 4.
Sea level characteristics for the skew surge parameter.
4. Discussion
In the Laptev Sea, as in the marginal seas in general, water level oscillations have a complex character caused by a combination of different factors. The peculiarities of the formation of extreme sea levels in different water areas of the sea are related to the coastal morphometry, heterogeneity of the bottom relief, seasonal phenomena (ice cover, river discharge), dynamic processes in the atmosphere, and periodic sea level oscillations. The highest storm surges are mainly generated under the influence of deep cyclones, which cover the entire water area of the Laptev Sea.
In this study, a detailed grid adapted specifically for the Laptev Sea coastline and major islands was used, covering a multi-year period, which allowed for the calculation of possible sea levels for a 100-year return period. According to the obtained model data, the maximum sea level range is possible both in places with strong storm surges with weak tides (Ebelyakh Bay) and in places where the maximum sea level range is influenced by a superposition of storm surge plus tide (Anabara Bay). According to our estimates of the 100-year return period, a region with a maximum storm surge amplitude of about 4 m was identified in the western part of the Lena River delta adjacent to Olenek Bay. Also, for the first time, we estimated the skew surge for the Laptev Sea, which was 2–2.7 m relative to the high tidal waters. Thus, for a large part of the coast of the Laptev Sea, the maximum values of the residual sea level exceed the total sea level due to the coincidence with the low tide.
In general, the largest tidal ranges in the Arctic are in the White and Barents Seas, exceeding 3 m, with a maximum of 9 m in Mezen Bay. Specifically, the highest tidal ranges were found in Khatanga and Anabara bays (1–2 m) on the western coast of the Laptev Sea, among the entire Siberian continental shelf seas (Kara, East Siberian, and Chukchi Seas). Previously, Ashik [18] applied the two-dimensional model of storm surges for the Laptev Sea and the East Siberian Sea for the navigation period of 1993. Almost for the whole navigation period, the amplitude of the storm surge deviated by 1 m from the mean sea level in the coast of the Laptev Sea. Kowalik and Proshutinsky [43] carried out a tidal model for the whole Arctic, including the Laptev Sea, and simulated the semidiurnal (M2, S2) and diurnal (K1, O1) tidal waves. Stammer et al. [22] stated that the FES model is a highly effective tidal model for shelf areas. Its application on the ADCIRC grid accurately reproduced tidal values on the coast of the Laptev Sea, which were in good agreement with in situ observations of tidal harmonic constituents [44].
We have identified residual series extremes, and storm surges along the Laptev Sea coast are very high, up to 2.5 m. In other areas of the Arctic, for example, in the White and Barents Seas, the values of storm surges can reach up to 1–2 m. In the Kara Sea, they usually do not exceed 1 m, and in the Chukchi Sea, 1.5 m [45]. In the East Siberian Sea, however, the values of storm surges reach 2 m and are close to those of the Laptev Sea because the physical and geographical conditions (shallow waters, large shelf) are conducive to the formation of storm surges. In the western Arctic region of Canada, storm surges of up to 1.90 m have been recorded in the tide gauge [24].
Tides, winds, and waves can be superimposed on a storm surge, resulting in a higher measured extreme sea level [40]. The sea level changes resulting from a combination of air pressure and winds, called storm surges or residual sea levels, can cause catastrophic flooding, coastal destruction, and shoreline changes. The sea level oscillations in the Laptev Sea, especially in the southern part, have a significant influence on the hydrological conditions of the adjacent water area, on its ecological conditions as the spreading of sea water over long distances into the Lena delta river, and on the economic activities in the Arctic sea port Tiksi.
Forecasts and calculations of possible extreme sea levels provide a basis for navigation and cargo operations on the Northern Sea Route, as well as for planning and construction on the coast and shelf of the Laptev Sea. The maximum catastrophic magnitude of storm surges was observed in the southeastern part of the Laptev Sea. At the station Svyatoy Nos, the value of storm surges during the flood of September 15–16, 1958 exceeded the mean monthly sea level for September 1958 by 5.2 m. [46]. A maximum sea level of 3.3 m and a minimum sea level of −2.7 m were determined for the Ust-Olenyok station, Tiksi Bay, and Svyatoy Nos Mountain from the observational data from the second half of the XX century [45].
In addition to tides and storm surges, other factors such as tsunamis, wind waves, and water level rises associated with flooding in the area of large river discharges can also be accounted for. For these events, it is necessary to calculate the joint recurrence [47], but the reliability of predicting extreme levels is reduced due to the different timescales of events of different geneses.
This Laptev Sea region is situated in a special plate tectonic setting. The North American and Eurasian plates are separated in the Eurasian Basin by an active mid-oceanic ridge, the Gakkel Ridge, and then by the continental shelf of the Laptev Sea, forming the huge rift system [48]. It is believed that the strongest coastal earthquakes and the largest probability of tsunami formation could occur in the Baffin, Greenland, and Beaufort Seas, as well as in the Laptev Sea [49]. According to Kulikov et al. [50], the modeled maximum estimated tsunami wave amplitudes for the Laptev Sea coast are 10–15 cm for a 500-year return period and do not exceed 100–150 cm for a 10,000-year return period. In the present study, for the 100-year return period, the maximum amplitude of extreme total and residual sea levels in Olenek Bay was 393 cm. Thus, the contribution of tsunamis to extreme sea level oscillations along the Laptev Sea coasts would theoretically be significant only for long return periods. However, if a tsunami coincides with a storm surge or maximum tidal range, the damage to coastal areas and structures would increase considerably.
5. Conclusions
The study analyzed the total, tidal, and residual sea level characteristics of the Laptev Sea coast using the ADCIRC model for the period of 1980–2000. The highest total sea levels were observed in Ebelyakh Bay, measuring 264 cm, the lowest were recorded in Anabar Bay (−190 cm). The modeling results show that the maximum range of the total sea level varies from 267 cm (Khatanga Bay) to 544 cm (Ebelyakh Bay). Residual sea level oscillations made a significant contribution to variance along the Laptev Sea coast. However, in the Khatanga Bay area, tides are prevalent, with their maximum range reaching 264 cm. The eastern part of the sea experiences weak tides, with a mean spring range not exceeding 20–30 cm. For the 100-year recurrence period, Anabar and Ebelyakh bays had the highest non-tidal sea level extent at 678–679 cm. Olenek, Yana, and Ebelyakh bays also had maximum skew surge values of 252–265 cm relative to the high tidal water. For 100-year and longer return periods, extreme total and residual sea levels can reach more than 300 cm along the Laptev Sea coastline. This area may also be subject to tsunamis with infrequent recurrence, which could result in significant damage from the coincidence of extreme tidal and storm surges with the tsunami wave.
Author Contributions
Conceptualization, M.E.K. and I.P.M.; methodology, V.S.A. and I.P.M.; software, V.S.A.; validation, M.E.K.; formal analysis, M.E.K.; investigation, M.E.K.; resources, V.S.A. and I.P.M.; data curation, M.E.K.; writing—original draft preparation, M.E.K.; writing—review and editing, I.P.M., A.A.K., V.S.A. and S.A.K.; visualization, M.E.K.; supervision, I.P.M. and A.A.K.; project administration, A.A.K.; funding acquisition, A.A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially funded by the Russian Science Foundation (RSF) under the research project No. 23–17–00125 (assessment of maximum and minimum sea levels for different return periods and their contribution with respect to tsunami hazard) and within the framework of the Shirshov Institute of Oceanology Russian Academy of Science state assignment No. FMWE–2024–0018 (numerical model setup and verification).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We are sincerely grateful to Stanislav Myslenkov for preparing the NCEP/CFSR reanalysis data. We thank Alexander Rabinovich for discussions and helpful advice.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Janout, M.A.; Lenn, Y.D. Semidiurnal tides on the Laptev Sea shelf with implications for shear and vertical mixing. J. Phys. Oceanogr. 2014, 44, 202–219. [Google Scholar] [CrossRef]
- Osadchiev, A.; Medvedev, I.; Shchuka, S.; Kulikov, M.; Spivak, E.; Pisareva, M.; Semiletov, I. Influence of estuarine tidal mixing on structure and spatial scales of large river plumes. Ocean Sci. 2020, 16, 781–798. [Google Scholar] [CrossRef]
- Janout, M.A.; Hölemann, J.; Laukert, G.; Smirnov, A.; Krumpen, T.; Bauch, D.; Timokhov, L. On the variability of stratification in the freshwater-influenced Laptev Sea Region. Front. Mar. Sci. 2020, 7, 543489. [Google Scholar] [CrossRef]
- Ashik, I.; Dvorkin, Y.; Vanda, Y. Extreme oscillations of the sea level in the Laptev Sea. In Land-Ocean Systems in the Siberian Arctic; Kassens, H., Bauch, H.A., Dmitrenko, I.A., Eicken, H., Hubberten, H.W., Melles, M., Thiede, J., Timokhov, L.A., Eds.; Springer: Berlin, Germany, 1999; pp. 37–41. [Google Scholar]
- Shevchenko, G.; Ivelskaya, T. Estimation of extreme sea levels for the Russian coasts of the Kuril Islands and the Sea of Okhotsk. Pure Appl. Geophys. 2015, 172, 3537–3555. [Google Scholar] [CrossRef]
- Korovkin, I.P.; Antonov, V.S. Tides in the Khatanga River and the Khatanga Bay. Proc. All-Union Sci. Res. Inst. 1938, 105, 125–141. (In Russian) [Google Scholar]
- Ashik, I.M.; Vanda, Y.A. Catastrophic storm surges in the southern part of the Laptev Sea. Berichte. Zur. Polarforsch. 1995, 176, 43–46. [Google Scholar]
- Squire, V.A.; Kovalev, D.P.; Kovalev, P.D.; Medvedev, I.P.; Kulikov, M.E. A cornucopia of oscillations on the Laptev Sea shelf. Cont. Shelf. Res. 2021, 227, 104514. [Google Scholar] [CrossRef]
- Seredkina, A.I.; Melnikova, V.I. New data on earthquake focal mechanisms in the Laptev Sea region of the Arctic-Asian seismic belt. J. Seism. 2018, 22, 1211–1224. [Google Scholar] [CrossRef]
- Imaeva, L.P.; Gusev, G.S.; Imaev, V.S. Dynamics of the Relief and Seismotectonic Activity of the Modern Structures in the Delta of the River Lena. Geotectonics 2019, 5, 62–77. [Google Scholar] [CrossRef]
- Drachev, S.S. Laptev Sea Rifted Continental Margin: Modern Knowledge and Unsolved Questions. Polarforschung 2000, 68, 41–50. [Google Scholar] [CrossRef]
- Avetisov, G.P. Once again on the earthquakes in the Laptev Sea. Geological-geophysical characteristics of Arctic region lithosphere. VNIIOkeangeologiya St. Petersburg 2000, 3, 104–114. (In Russian) [Google Scholar]
- Imaeva, L.P.; Kolodeznikov, I.I. Seismotectonics of the Northeastern Sector of Russian Arctic; Publishing House of the Siberian Branch of the Russian Academy of Sciences: Novosibirsk, Russia, 2017. (In Russian) [Google Scholar]
- Krylov, A.A.; Lobkovskii, L.I.; Kovachev, S.A.; Baranov, B.V.; Rukavishnikova, D.D.; Tsukanov, N.V.; Dozorova, K.A.; Semiletov, I.P. Geodynamic Regimes in the Laptev Sea Region According to the Latest Seismological Data. Dokl. Earth Sci. 2023, 513, 1338–1343. [Google Scholar] [CrossRef]
- Krylov, A.A.; Kulikov, M.E.; Kovachev, S.A.; Medvedev, I.P.; Lobkovsky, L.I.; Semiletov, I.P. Peculiarities of the HVSR Method Application to Seismic Records Obtained by Ocean-Bottom Seismographs in the Arctic. Appl. Sci. 2022, 12, 9576. [Google Scholar] [CrossRef]
- Krylov, A.A.; Novikov, M.A.; Kovachev, S.A.; Roginskiy, K.A.; Ilinsky, D.A.; Ganzha, O.Y.; Ivanov, V.N.; Timashkevich, G.K.; Samylina, O.S.; Lobkovsky, L.I.; et al. Features of Seismological Observations in the Arctic Seas. J. Mar. Sci. Eng. 2023, 11, 2221. [Google Scholar] [CrossRef]
- Kowalik, Z.; Proshutinsky, A.Y. Diurnal tides in the Arctic Ocean. J. Geophys. Res. Oceans 1993, 98, 16449–16468. [Google Scholar] [CrossRef]
- Ashik, I.M. Numerical prediction of sea surges and ice conditions in the Laptev and East-Siberian seas. In Russian-German Cooperation: Laptev Sea System; Russian-German Cooperation: Moscow, Russia, 1995; pp. 47–54. [Google Scholar]
- Padman, L.; Erofeeva, S. A barotropic inverse tidal model for the Arctic Ocean. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.C.; Cowles, G. An unstructured grid, finite-volume coastal ocean model (FVCOM) system. Oceanography 2006, 19, 78–89. [Google Scholar] [CrossRef]
- Fofonova, V.; Androsov, A.; Danilov, S.; Janout, M.; Sofina, E.; Wiltshire, K. Semidiurnal tides in the Laptev Sea Shelf zone in the summer season. Cont. Shelf Res. 2014, 73, 119–132. [Google Scholar] [CrossRef][Green Version]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Kowalik, Z. Storm surges in the Beaufort and Chukchi seas. J. Geophys. Res. Oceans 1984, 89, 10570–10578. [Google Scholar] [CrossRef]
- Kim, J.; Murphy, E.; Nistor, I.; Ferguson, S.; Provan, M. Numerical analysis of storm surges on Canada’s western Arctic coastline. J. Mar. Sci. Eng. 2021, 9, 326. [Google Scholar] [CrossRef]
- Joyce, B.R.; Pringle, W.J.; Wirasaet, D.; Westerink, J.J.; Van der Westhuysen, A.J.; Grumbine, R.; Feyen, J. High resolution modeling of western Alaskan tides and storm surge under varying sea ice conditions. Ocean Model. 2019, 141, 101421. [Google Scholar] [CrossRef]
- Kleptsova, O.; Pietrzak, J.D. High resolution tidal model of Canadian Arctic Archipelago, Baffin and Hudson Bay. Ocean Model. 2018, 128, 15–47. [Google Scholar] [CrossRef]
- Korablina, A.D.; Kondrin, A.T.; Arkhipkin, V.S. Numerical simulations and statistics of surges in the White and Barents seas. Russ. J. Earth Sci. 2017, 17, ES4004. [Google Scholar] [CrossRef]
- Myers, E.P.; Baptista, A.M. Analysis of factors influencing simulations of the 1993 Hokkaido Nansei-Oki and 1964 Alaska tsunamis. Nat. Hazards. 2001, 23, 1–28. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Tanaka, S.; Westerink, J.J.; Dawson, C.N.; Luettich, R.A., Jr.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the unstructured-mesh, SWAN+ADCIRC model in computing hurricane waves and surge. J. Sci. Comput. 2012, 52, 468–497. [Google Scholar] [CrossRef]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries; Report 1, Theory and Methodology of ADCIRC-2DD1 and ADCIRC-3DL.; Technical Report DRP-92-6; US Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, November 1992. [Google Scholar]
- Saha, S.; Moorthi, S.; Pan, H.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meterol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Lindsay, R.; Wensnahan, M.; Schweiger, A.; Zhang, J. Evaluation of seven different atmospheric reanalysis products in the Arctic. J. Clim. 2014, 27, 2588–2606. [Google Scholar] [CrossRef]
- Myslenkov, S.A.; Arkhipkin, V.S.; Koltermann, K.P. Estimation of the height of swell in the White and Barents seas. Vestnik Moskov. Univ. Ser. Geogr. 2015, 5, 59–66. (In Russian) [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Medvedev, I.P.; Rabinovich, A.B.; Kulikov, E.A. Tidal oscillations in the Baltic Sea. Oceanology 2013, 53, 526–538. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. Oceans 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Raymond, W.H. High-order low-pass implicit tangent filters for use in finite area calculations. Mon. Weather Rev. 1988, 116, 2132–2141. [Google Scholar] [CrossRef]
- Kaiser, J.; Hamming, R. Sharpening the response of a symmetric nonrecursive filter by multiple use of the same filter. In Proceedings of the ICASSP ’77, IEEE International Conference on Acoustics, Speech, and Signal Processing, Hartford, CT, USA, 9–11 May 1977; Volume 2, pp. 82–85. [Google Scholar] [CrossRef]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar] [CrossRef]
- Williams, J.; Horsburgh, K.J.; Williams, J.A.; Proctor, R.N. Tide and skew surge independence: New insights for flood risk. Geophys. Res. Lett. 2016, 43, 6410–6417. [Google Scholar] [CrossRef]
- Kowalik, Z.; Proshutinsky, A.Y. The Arctic ocean tides. Geophysical monograph series. Geophys. Monogr. Ser. 1994, 85, 137–158. [Google Scholar] [CrossRef]
- Kulikov, M.E.; Medvedev, I.P.; Kondrin, A.T. Seasonal variability of tides in the Arctic Sea. Russ. J. Earth Sci. 2018, 18, ES5003. [Google Scholar] [CrossRef]
- Ashik, I.M.; Ryzhov, I.V. Extreme sea level oscillations in the Arctic seas and their long-term changes. Probl. Arktiki I Antarkt. 2012, 4, 74–89. (In Russian) [Google Scholar]
- Mustafin, N.V. On catastrophic storm surges in the south-eastern part of the Laptev Sea. Probl. Arktiki I Antarkt. 1961, 7, 33–36. (In Russian) [Google Scholar]
- Tawn, J.A. Estimating probabilities of extreme sea-levels. J. R. Stat. Soc. C Appl. Stat. 1992, 41, 77–93. [Google Scholar] [CrossRef]
- Franke, D.; Hinz, K.; Oncken, O. The Laptev sea rift. Mar. Petrol. Geol. 2001, 18, 1083–1127. [Google Scholar] [CrossRef]
- Mazova, R.K.; Kurkin, A.A.; Vinokurov, M.S. Possible tsunamis in the Arctic. Sci. Tsunami Hazards 2022, 41, 245–263. [Google Scholar]
- Kulikov, E.A.; Ivashchenko, A.I.; Medvedev, I.P.; Yakovenko, O.I.; Fine, I.V. Tsunami hazards for the Arctic coast of Russia. Part 2. Numerical tsunami modelling. Georisk World 2019, 13, 6–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).