Abstract
This study investigates the geomechanical behavior of five terrace orders in the Crotone Basin. The purpose is to understand the physical–mechanical parameters of these terraces to determine whether rock or soil mechanics principles should be applied for stability analysis. Samples were collected from each terrace following an extensive field survey. Laboratory analyses were conducted to measure pulse velocities, uniaxial unconfined compressive strength, and compressive strength with truncated conical platens. The findings revealed key physical–mechanical parameters of the rocks, which are crucial for stability assessments. The Crotone Basin, known for its mineral resources such as hydrocarbons and rock salts, has been studied geologically since before the 1950s, but there is a lack of geomechanical data in existing literature. Therefore, the results presented here are novel and provide a basis for future studies on the instability of rocky slopes composed of similar soft rock types. These results will aid in accurate geological–geotechnical model reconstructions. While the findings can be applied to similar cases, it is important to note that each analysis site, despite showing similar phenomena, is unique and requires individual investigation.
1. Introduction
Uniaxial compressive strength (UCS) is a mechanical property of rock which is fundamental to determining the quality and strength of rock masses. In fact, the results of the main geomechanical classifications depend on the compressive strength (e.g., [1,2] etc.).
In the context of geomechanical studies, this compressive strength value can be determined by laboratory tests such as the uniaxial unconfined compression test and the point load test or in situ test through the Schmidt hammer. For this work, the first two tests (laboratory analysis) were taken into account.
The uniaxial free lateral expansion (unconfined) test allows us to determine the compressive strength value of the rock directly through the ratio of the force exerted by the instrumentation and the area of the intact rock core specimen. The compressive strength value is also obtained through the point load test, but this must subsequently be modified with corrective factors. The latter test (PLT), in the professional field, is preferred to the first due to its ease of use, speed in carrying out the test, and its low cost.
The widespread use of the PLT makes it necessary to analyze the reliability of the results obtained from the tests on rocks compared to those obtained with the uniaxial compression test.
To conduct this analysis, several samples from the Crotone Basin area were considered. This basin was chosen due to its extensive study of tectono–stratigraphic features associated with its mineral and reservoir wealth, as well as its distinctive coastal geology and geomorphology for morphodynamic evolution. Located in southern Italy, it is renowned for its complex geological history, stratigraphy, and sedimentary sequences. Numerous methods and scientific studies have been employed in this region to elucidate its geological history, sedimentology, and geodynamic evolution (e.g., [3,4,5,6,7]). However, there is a relative paucity of geotechnical and geomechanical data at the scale of the slope (e.g., [8,9]).
In particular, 112 sandstone and limestone samples were collected from various terrace orders within the Basin.
On 53 samples the uniaxial unconfined test was carried out, while 59 samples were subjected to the PLT. Compressive strength data are very important for the sizing of any engineering work/project, and therefore it would be favorable to use cheaper tests whose effectiveness is validated. The possibility of using irregular specimens, avoiding the grinding operation, makes the PLT extremely simple to perform and, above all, aimed at a greater number of rocks. Therefore, it is extremely important to calibrate and compare the two tests described above.
Considering the limitations of each test, the analyses demonstrated that the PLT provides reliable estimates of rock compressive strength for some samples.
The large number of samples tested yielded valuable insights, both for assessing the reliability of the PLT and for enhancing the understanding of the mechanical behavior of the arenaceous complex widely outcropping in the Crotone basin.
2. Geological Setting
The studied area is part of the geological unit known in scientific literature as the Crotone Basin, which represents the exposed part of a Neogene-to-present sedimentary basin developed along the Ionian Sea (e.g., [3,4,5,10]; (Figure 1). Its development is related to the southeastern migration of the Calabrian Arc, as a consequent subduction of the Ionian crust and the opening of the Tyrrhenian Basin, starting from the Serravallian–Tortonian [11,12]. Considering the geological context in which it is configured and which accompanied the accumulation of sediments, the Plio–Pleistocene portion is exceptionally well preserved and consists of a suite of sediments ranging from continental to deep sea organized in tectonic–sedimentary cycles [5,11,13,14,15]. The depositional history of the Crotone Basin was mainly accompanied by wrenching tectonics alternating between transtensional and transpressional local deformation [6,16,17], connected to the extension that characterizes the foreland area. This extensional regime was however interrupted episodically by deformation events, with a compressive component during the Messinian and strike slip phases during the late Pliocene–early Pleistocene. These deformational phases led to generalized uplift and the formation of discordances [18,19]. Starting from the Middle Pleistocene, the Calabrian Arc experienced uplift leading to the emergence of flanks and various basins including the Crotone Basin. This uplift is testified to by some orders of marine terraces [18,19,20,21]. The number of terraces, their age, and their distribution are debated in the literature (e.g., [19,20,21,22]). The most accredited and realistic study is that of [19], which identified five orders of terraces (Table 1). The uplift rates calculated by the various authors range from 0.4 to 1.8 m/ka [18,23].
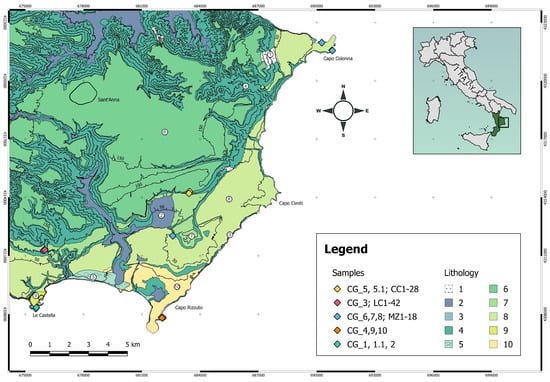
Figure 1.
Geological sketch map of the study area and location of the samples taken from different terrace orders. Lithology symbol legend: 1. Slope deposits (Holocene); 2. Alluvial deposits (Holocene); 3. Beach deposits, conglomerates, and sands (Holocene); 4. Marly clays (Plio–Lower Pleistocene); 5. Dune sands (Holocene); 6. Sandstones, conglomerates, biocalcarenites (Terrace I, Middle Pleistocene); 7. Clastic deposits (Terrace II, Upper Pleistocene); 8. Bioturbed sandstones, biocalcarenites (Terrace III, Upper Pleistocene); 9. Calcarenites (Terrace IV, Upper Pleistocene); 10. Laminated and bioturbated sandstones (Terrace V, Upper Pleistocene).

Table 1.
Comparison of the nomenclature of terrace orders according to the recent scientific literature and relative age.
From a lithological point of view, throughout the study area, the marly clay of the Cutro Formation is present at the bottom of the various terraces. This unit forms the substrate of a series of synthems [19], which form terraced surfaces linked to various cycles of marine transgression–regression referable to the Middle and Upper Pleistocene. In some cases, at the scale of the outcrop, the deposits of the synthems that make up the marine terraces show minor cycles delimited by unconformity surfaces. Since these minor cycles do not show an areal continuity, it is not possible to make a further subdivision into subunits.
For this work, a series of samples were taken from different orders of terraces. Therefore, for a better understanding of the area, of the geology, and above all the lithotechnical aspect, which will be discussed in depth in the following chapters, it was necessary to describe each terrace from which the samples were taken.
The first terrace order in the study area is the synthem of the Lago di Sant’Anna [5,19], whose name derives from the artificial lake in the locality of Sant’Anna. This older terrace is known in the literature as “Cutro terrace” [21,25]. It is the largest marine terrace and starts from the north of the map in Figure 1, occupying the central portion up to the south (Figure 1).
In the study area, the unit reaches a maximum thickness of 10 m and a maximum height of approximately 200 m and rests on the deposits of the underlying Cutro Clay through a net and erosive contact. As far as dating is concerned, the synthem was correlated with the isotopic stage 7, corresponding to 200 Ka B.P. [19,22].
This terrace is the result of the superposition of several sedimentation cycles and shows a certain variability of sedimentary facies. The outcrop from which some samples were taken for this study belongs to the clastic lithofacies and records the regressive phase of the first cycle, corresponding to the erosion of bioconstructed lithofacies (cycle I) and of an age attributable to the Middle Pleistocene.
The Soverito synthem represents the second-order terrace, and its outcrops are arranged to form a narrow arch-shaped band. Within the study area, the terraced surface reaches heights of 95 m a.s.l., and its age is about 125 ka B.P., according to the correlation with the isotopic stage 5e [19,22]. The synthem consists of two lithofacies: one clastic and the other bioconstructed. From the first, some samples were taken which could be partly the result of the erosion of cliff limestones during a regressive phase.
The synthem of Capo Cimiti represents the third-order terrace and, like the previous terrace, it also extends with an arch shape reaching 70 m in the southern portion, north of Le Castella, and develops northwards along 50 m in the central portion to the west of Capo Cimiti and in the northern portion to the west of Capo Colonna. This terrace, according to the correlation with the isotope stage 5c [19], has an age of about 100 Ka B.P. The deposits recognized in this terrace have two lithofacies: clastic and bioconstructed.
The fourth terrace corresponds to the synthem of Capo Rizzuto, reaches a maximum altitude of 35 m a.s.l., and is about 80 Ka B.P., corresponding to the isotopic stage 5a [19]. The deposits are mainly made up of carbonate facies.
The fifth terrace corresponds to the synthem of Le Castella, reaches a maximum altitude of 15 m a.s.l., and has an age of about 50 Ka B.P., corresponding to the isotopic stage 3 [19,25]. The deposits are made up of limestone and sandstone.
3. Sampling
The sampling took place in different areas pertaining to the Crotone Basin (Figure 1) and, specifically, from north to south, they are: Capo Colonna, loc. Fratte, Casa Cardinale, Isola di Capo Rizzuto, Le Castella, and loc. Campolongo. In particular, 112 lithoid samples were taken of sandstone and limestone (signed CG, CC, MZ, LC).
Considering the subdivision into terraced orders, we started to carry out field surveys and take samples starting from the oldest order up to the youngest.
From the first terrace order, Cutro terrace, 22 samples were taken (CG_5, 5.1; CC1-20; Figure 1 and Figure 2). These are located north of the Casa Cardinale and southeast of the Isola di Capo Rizzuto. The outcrop is made up of coarse reddish arenaceous deposits (very coarse) and yellowish calcarenites (grain-size from granules to pebbles) with cross-layering and without macrofauna. As can be seen on the scale of the hand sample, the samples show a different rate of cementation and porosity, influencing their resistance to erosion. The permeability is high.

Figure 2.
(A) Panoramic photo along the stretch of the ridge of Semaforo located in Via Olimpia, Crotone in which the flat areas of the terraces of the Sintema del Lago S.Anna are clearly visible (first-order terrace) and the badlands of the Cutro Clay formation. (B) Samples taken from the outcropping wall of the first-order terrace. (C) Detail of the limestone sample GC_5. (D) Detail of the arenaceous specimen CG_5.1. (E) Some cubic sandstone samples subjected to laboratory tests.
From the second terrace order, Campolongo–La Mazzotta terrace, 43 samples were taken (CG_3; LC1-42; Figure 1 and Figure 3). These are located southeast of Località Campolongo. The outcrop is made up of limestone and sandstone with the presence of local carbonate nodules (Figure 3A). At the scale of the hand sample, the samples show a different rate of cementation, porosity, and particle size (passing from very fine-grained at the bottom to coarse-grained towards the top), affecting their resistance to erosion.

Figure 3.
(A) Limestone outcrop belonging to the second-order terrace. (B) Sample CG_3 detail where there is an arenaceous and a calcarenite portion. (C) Detail of the calcarenite portion of the cubic-shaped CG_3 sample. (D) Cubic sandstone and limestone samples subjected to laboratory tests.
From the third terrace order, Le Castella–Capo Cimiti terrace, 29 samples were taken (MZ1-26; CG_6,7,8; Figure 1 and Figure 4). Eighteen samples were taken east of Località Mazzotta in loc. Fratte; the rest in Capo Colonna. The first samples consisted of reef and coarse calcarenites containing macrofossils. The lateral contacts between the two lithotypes are clear, and the grain size varies from granules–pebbles to granules–very coarse-grained.

Figure 4.
(A) Overview of the third-order terraces NW of Capo Colonna. (B–F) Calcarenite samples taken near Capo Colonna; (C,E,G) are the respective cubic-shaped specimens CG_6, 7, and 8. (H) Cubic-shaped specimens derived from samples of loc. Fratte.
From the fourth terrace order, Capo Rizzuto terrace, eight samples were taken (CG_4; CG_9; CG_10; CG_11; GC_4a,b,c,d; Figure 1 and Figure 5). These are located near the Torre Vecchia of Isola Capo Rizzuto. The outcrop is made up of limestone and fossiliferous limestones. On the scale of the hand sample, the samples show a different rate of cementation and porosity, influencing their resistance to erosion. In fact, in some places they lose their competent behavior and become sand under the action of weathering.

Figure 5.
Area south of Isola Capo Rizzuto. (A) Fourth-order terrace southwest of the “Torre Vecchia” of Isola Capo Rizzuto. (B) Outcrop of the “Torre Vecchia” of Capo Rizzuto, showing evident slopes of landslides and materials deposited into the sea; note also the presence of clay tongues at the base (Cutro Clay). In areas with stable slopes, the measured calcarenite thicknesses reach approximately 10 m. (C) Altered calcarenite sample CG_4 with fossils. (D) CG_4 sample not exactly cubic in shape due to the low cementation rate and high porosity.
From the fifth terrace order, Le Castella terrace, 10 samples were taken (CG_1; CG_1.1; CG_2; CG_2.1; GC_2a,b,c,d,e,f; Figure 1 and Figure 6). These are located southeast of the Aragonese Castle of Le Castella. The outcrop is made up of limestone and sandstone with shells and traces of bioturbation (Figure 3A). Samples show medium to coarse-grained particle size.

Figure 6.
Area south of Le Castella. (A) Stratified limestone with evidence of traces of bioturbations belonging to the fifth-order terrace. (B) Detail of the arenaceous specimen CG_1 with fossil elements; (C) Detail of the stratified arenaceous specimen CG_1.1; (D) Detail of the sample of calcarenite CG_2; (E–G) Cubic specimens of the respective samples (B–D).
4. Materials and Methods
For the geomechanical characterization, the lithoid rocks (calcarenites/limestones and sandstones) were subjected to the following tests:
- (a)
- Determination of ultrasonic wave velocities
- (b)
- Determination of the unconfined compressive strength;
- (c)
- Determination of the point load strength index.
Before carrying out the tests, the samples were cut and rectified using a mechanical saw in order to obtain cubic specimens of 5 cm × 5 cm × 5 cm (Figure 2C–E, Figure 3C,D, Figure 4C,E,G,H, Figure 5D, Figure 6E–G and Figure 7A); subsequently, they were placed in the oven (Figure 7B) for 24 h cycles at a temperature of 40 °C to eliminate the water content, weighed from time to time until a constant value of their mass was reached. Finally, for each specimen, the dimensions were measured using a precision digital caliper (Borletti CDJB15–50 mm; Figure 7C).

Figure 7.
(A) Cubic specimens. (B) Oven at 40 °C. (C) Digital caliper BORLETTI CDJB15 150 mm. Equipment: (D) Matest ultrasonic pulse velocity tester; (E) Matest C070 for uniaxial compression test; (F) point load test.
4.1. The Ultrasonic Velocity Method
The propagation speed of the ultrasonic waves was determined by measuring the time (μs) required for the transmission of an ultrasonic pulse emitted by a transmitter and received by a receiver on two opposite parallel surfaces of a cubic specimen; then, the travel distance of the pulse through the cubic rock sample was measured and propagation velocity determined.
The test was performed following the ASTM standard [26] using the Matest ultrasonic velocity meter (Figure 7D). The instrument is equipped with a pair of electroacoustic transducers with a frequency of 55 kHz, a longitudinal wave generator, a signal amplifier, and a wave transit time meter. This test method is valid for wave velocity measurements for both anisotropic and isotropic rocks, although the velocities obtained in roughly anisotropic rocks can be affected by factors such as direction, distance traveled, and transducer diameter.
After identifying the propagation speeds in the three directions, we assigned the highest speed to the z-axis, the middle speed to the y-axis, and the lowest speed to the x-axis (see also Section 5.1).
4.2. The Uniaxial Compression Test
Once the three spatial directions were identified, for each specimen it was possible to perform the uniaxial compression test using the Matest C070 press (Figure 7E). The test method applied for the measurement of uniaxial compressive strength is that proposed by [27] and ISRM recommendations [28,29]. This procedure considers an intact cubic-shaped rock sample whose ends are machined flat and uniform to be placed in a loading frame.
One of the three axes was chosen at random for the uniaxial compression test (see Section 5.2). The specimens were positioned and centered between the press plates to ensure a continuous and uniform application of load, increasing steadily by (1 ± 0.5) MPa until reaching peak load and specimen failure. Finally, the compressive strength was measured (see Section 5.2).
4.3. The Point Load Test
The point load test (PLT) allows us to determine the index of resistance to punching of the rocks (point load test strength index of rock), useful for the mechanical classification of stone materials, and correlated to the uniaxial compressive strength [30]. The index for each sample was obtained by subjecting the rock specimens to an increasingly concentrated point load, applied by a pair of conical tips (Figure 7F), until failure occurred.
Since the standard test refers to cylindrical samples with a diameter equal to 50 mm, it is necessary, for samples of different sizes, to introduce a correction factor F which allows us to obtain, starting from Is, the new corrected value, Is(50):
where De represents the “equivalent” diameter of the specimen, calculated as:
where A = minimum specimen area.
For the determination of the uniaxial compressive strength UCS according to the ISRM, reference can be made to the following expression:
where the correlation coefficient K can be obtained from the literature as a function of the type of rock or, generically, as a function of size (ASTM). Taking into account not the type of rock but only the size, in this work, this K index is set equal to 23 as indicated by [31] (see also Section 5.3).
5. Results
5.1. Ultrasonic Velocity Measurements
Once the speed of propagation in the three directions of space was identified, the condition Vz > Vy > Vx was considered, so the z-axis has been assigned the maximum value of the wave propagation velocity, the y direction the intermediate value and, finally, the x direction has been assigned the minimum speed value (Table 2; Figure 8).

Table 2.
Velocity propagation values along the three spatial directions (x, y, z); Vm = velocity average. Samples from different terrace orders are color-coded for clarity. Five colors are used, from dark green for the oldest terrace order to yellow for the youngest. These colors will be consistently used in subsequent graphs to easily identify information for each terrace order.
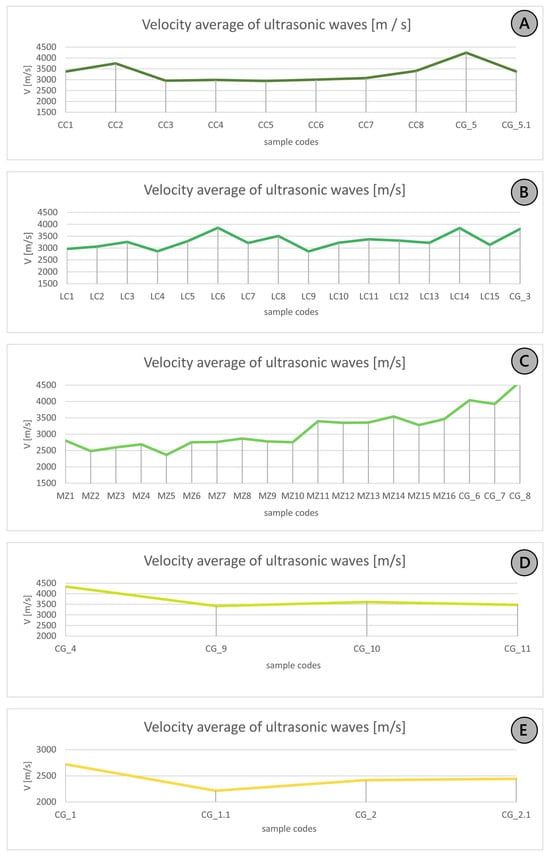
Figure 8.
Graphs depicting the projected mean velocity values of ultrasonic waves (from Table 2) for each sample from the different terrace orders. Specifically, Graph (A) corresponds to the first terrace order, Graph (B) to the second order, Graph (C) to the third order, Graph (D) to the fourth order, and Graph (E) to the fifth order. The colors in the graphs match those in the previous table to immediately identify and distinguish the different terrace orders. Specifically, there are five colors representing the five terrace orders, ranging from dark green (for the oldest terrace) to yellow (for the youngest terrace).
Considering the average values of the propagation velocity of ultrasonic waves, according to the semi-quantitative classification proposed by [32], it is possible to attribute to the velocities the term “low” (Vp = 2500–3500 m/s) and “medium” (Vp = 3500–4000 m/s).
The averages considered for the five-sample series (Figure 9) are:
- 3311.89 m/s for the samples of the first terrace order;
- 3301.76 m/s for the samples of the second terrace order;
- 3066.60 m/s, 3710.74 m/s, and 3270.25 m/s for the respective terraces of order III, IV, and V.
From the analysis of the histograms in Figure 9, it is possible to infer that the velocities of the lithotypes LC, MZ, and CC are similar to each other, unlike those of the fourth order which differ slightly from the others. This is attributable to the samples that are mainly calcarenitic rocks, and therefore more consistent and cemented and less porous than the other lithologies, which are predominantly arenaceous, little cemented, and very porous.
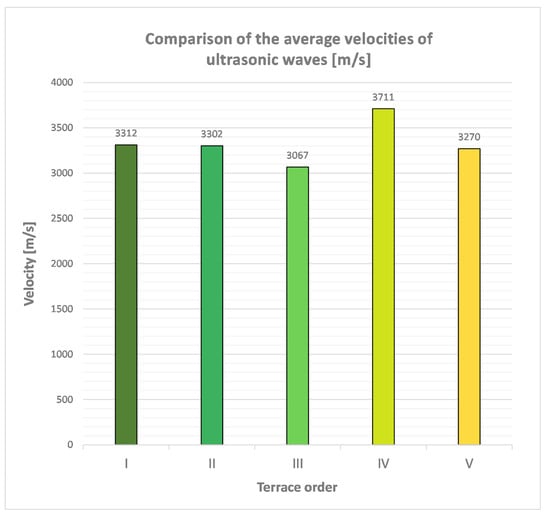
Figure 9.
Average velocities for the four series of analyzed samples. The colors in the graphs match those in the previous table to immediately identify and distinguish the different terrace orders. Specifically, there are five colors representing the five terrace orders, ranging from dark green (for the oldest terrace) to yellow (for the youngest terrace).
Taking into account the fields of propagation velocity of the elastic compression waves typical for some lithotypes (es. [33]), the average values fall precisely in the fields of arenaceous (1400 < Vp < 4200) and limestone (2500 < Vp < 6000) lithotypes.
5.2. Determination of the Unconfined Uniaxial Compressive Strength
As shown in Table 3, one of the three axes (highlighted in gray cells) was chosen arbitrarily along which to carry out the unconfined uniaxial compression. A uniaxial compressive strength (σ) expressed in MPa was obtained for each specimen. The values obtained for each specimen are shown in Table 3.

Table 3.
Values of velocities and compressive strength. Symbols and abbreviations: I, II, and III refer to the distances between two parallel plane surfaces of a specimen; x, y, and z denote the axes along which travel time and velocities were measured; F represents the maximum load [N]; A is the cross-sectional area [mm2]; and σ denotes compressive strength [MPa]. The gray cells indicate the axis along which failure occurred. Samples from different terrace orders are color-coded for clarity. Five colors are used, from dark green for the oldest terrace order to yellow for the youngest. These colors will be consistently used in subsequent graphs to easily identify information for each terrace order.
Considering the averages of the strength along the three axes for each series of specimens (Table 4), in accordance with the classification of [34], all samples are characterized by a “very low” strength (σ < 25 MPa). Considering, however, the classification proposed by the ISRM [29,30], the rock samples fall into class R1 and R2, corresponding to “very soft” rocks (crushed by hitting with the tip of the hammer) and “soft” (hitting with the tip of the hammer produces small incisions). As also reported by [35], a rock is defined as “soft” when the uniaxial compressive strength value does not exceed 25 MPa.

Table 4.
Comparison of uniaxial compressive strength values (on the left) and ultrasonic velocity propagation values (on the right) along x, y, and z axes. nd = not detected.
By plotting the average values of the uniaxial compressive strength along the three axes (x, y, z; Figure 10), it can be seen that all the samples show approximately the same trend. Furthermore, by comparing the average velocity values (along the three axes x, y, and z) with the average strength values (always along the three axes) for the five groups of samples, it is observed that higher propagation velocity values correspond to relatively higher strength values (Table 4).
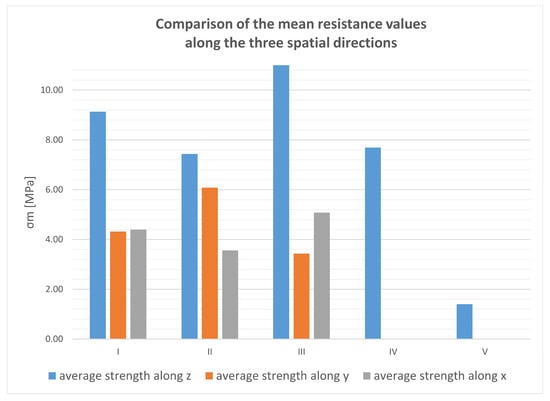
Figure 10.
Comparison between the mean strength values across the three axial directions for the five sample groups. The mean strength values along y and x for samples from the fourth and fifth terrace orders were not determined due to an insufficient number of samples.
5.3. Determination of the Point Load Strength Index
The PLT was performed for 12, 27, 10, 4, and 6 samples belonging to the terrace orders I, II, III, IV, and V, respectively; the results are reported in Table 5.

Table 5.
Values obtained from the PLT for the different samples. D = sample diameter, L = maximum size, P = failure load, De = equivalent diameter, Is = strength index, F = size correction factor, Is(50) = corrected strength index.
Several studies on detailed calculations of the UCS value (e.g., [1,33,36,37,38,39] and others) have considered various types of rocks (shale, siltstone, sandstone, limestone, quartzite, etc.) from different regions (UK, South Africa, USA, Turkey, Arabia, etc.). On this basis, we chose to consider the correlation equations with their conversion factors (K) obtained from samples attributable to sedimentary rocks, sandstones, and limestones, proposed by various authors to make a better comparison with the arenaceous/calcarenitic studied samples (Table 6).

Table 6.
Correlating equations given by previous researchers. [1,33,38,39,40,41] consider sandstone rock types; the other authors consider general sedimentary rocks.
Figure 11 shows the comparison between the results obtained from the uniaxial compression test and from the PLT, considering the equations proposed by the various authors.
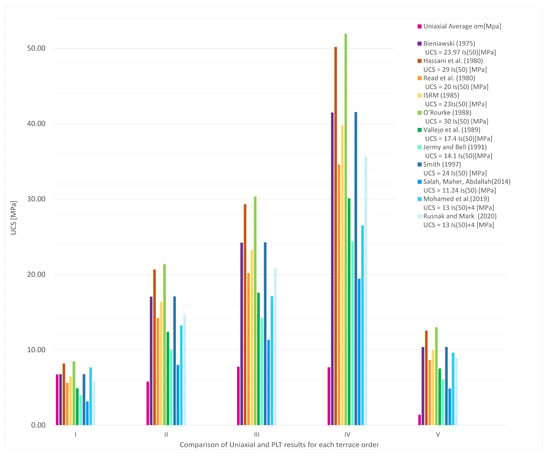
Figure 11.
Comparison between the results obtained from the uniaxial compressive strength test and the point load test [33,36,37,38,39,40,41,42,43,45,46].
It can be observed that only for the samples belonging to the first terrace order were obtained values comparable with the uniaxial compression test results (Figure 11 and Table 7). In particular, a strong correlation is noted with the equations proposed by [1,30,33,39,40]. The remaining ones show no correlation; therefore, the correlation K-factor has been maintained as the one suggested by the ASTM standard [31] and ISRM [29], which mainly take into account the size of the sample rather than the type of rock. Therefore, the K value considered is equal to 23 for all the samples of each type of terrace.

Table 7.
Summary of results of the UCS test and PLT for rock samples of each terrace order.
It is noted, however, that overall, the resistance values do not exceed 25 MPa and, therefore, these results can be considered congruent with the hypothesis that they are “soft” rocks. Only the samples of the fourth terrace order show values between 25 and 50 MPa and are therefore classifiable as “moderately hard”. The difference between the obtained values can be ascribable to the different ways in which the specimens are broken; in fact, for the PLTs, there are high strength values because the contact area between the conical tips and the specimen is extremely small, while for the uniaxial compression test, theoretically, the stress is distributed over the entire surface of the specimen. Furthermore, the PLT is strongly conditioned by the presence of microfractures or weak levels within the samples and their orientation with respect to the conical tips.
For the evaluation of the correlation rate between the PLT results (with K = 23) and the uniaxial test, a graph was created (Figure 12) in which each observed value (compressive strength value obtained by PLT) corresponds to a predicted value (compressive strength value obtained by uniaxial test). Within the graph, there is also a line (y = mx) which identifies two fields: the area below the line identifies underestimated uniaxial compressive strength values, while the field above the line identifies overestimated values.
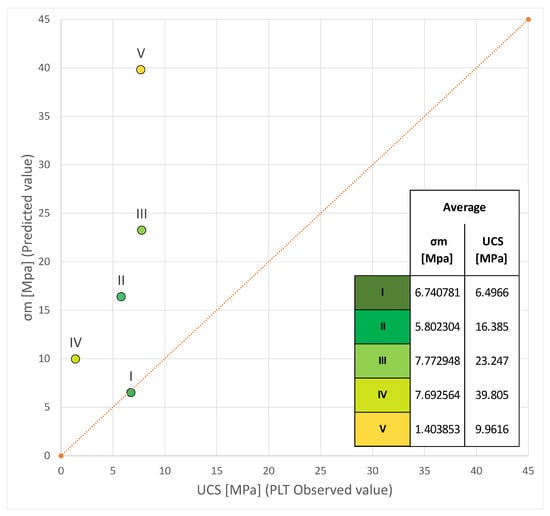
Figure 12.
Correlation of uniaxial unconfined compressive strength and PLT results. The area under the orange dotted line represents the underestimation field of the UCS value by indirect methods, while the area above the line is the overestimation field.
From Figure 12, it is observed that all the points deviate from the straight line, marking a poor correlation between the two strengths. The only strong correlation is showed by the average of the samples belonging to the first terrace order, while the remaining samples show an overestimation of the UCS value; these values were probably obtained because the samples are strongly fractured and altered and/or the number of samples considered is not sufficient to carry out a similar evaluation.
5.4. Correlation by Statistical Coefficients
Finally, two statistical coefficients were also calculated to evaluate the correlation rate, variance accounted for (VAF) and root mean square error (RMSE). These are typically used to check the reliability of a predictive model. The best model is obtained when VAF (%) is close to 100 and RMSE tends to zero [47]. In this study, the values obtained by the uniaxial compression test were considered as “exact” or “predicted”, while those obtained by the PLT, based on ASTM standards [31], were considered as “to evaluate” or “observed”.
The performance of the model was assessed by considering the averages of the 112 samples of the five terrace orders. The results for RMSE and VAF were 17.10 and 79.27%, respectively. Given the low correlation rate with the equations proposed by various authors, these values are entirely acceptable.
6. Discussion
In this study, we compared the strength values obtained through uniaxial compression tests and PLTs to verify the reliability of the data obtained from the latter. These tests were conducted on 112 samples of calcarenite and sandstone from five different terrace orders in the Crotone Basin area.
The resistance values for both types of tests show a gradual increase from the oldest terrace order to the youngest. This suggests that rocks from older terrace orders, having been subjected to alteration processes for a longer period compared to the younger terraces, have experienced a deterioration in their mechanical properties· Future studies should explore new K-factor proposals for these types of rocks.
The comparison was conducted both graphically and numerically by calculating the VAF and RMSE correlation indices. For the UCS values, we used an equation with a coefficient K set to 23 for all samples from each terrace. This value was chosen because, despite considering several factors proposed by different authors based on rock type, none provided a good correlation with the predicted data from the uniaxial test. Hence, a classic value proposed by ASTM [31] and ISRM [29,44] was selected, considering sample size rather than rock type.
The analysis revealed that the uniaxial compressive strength values estimated through PLTs align with those obtained from the uniaxial compressive strength test only for samples from the oldest terrace order. This highlights the importance of carefully selecting the appropriate test based on lithology, taking into account the limitations of each method.
The Crotone Basin area suffers from significant instability issues, particularly in the coastal region (corresponding to the youngest terrace orders: III, IV, and V). These issues manifest as landslides, including rock falls, topples, spreads, and sliding along calcarenite slopes, as well as rotational sliding involving the underlying clays of the Cutro Clay Formation.
Contributing factors to gravitational deformations include (i) the infiltration of rainwater into fractures in the rock masses, leading to enlargement due to both chemical alteration processes and washout, resulting in overturning and slips; (ii) progressive decay of geotechnical characteristics of soil beneath calcarenite blocks caused by water veins interposed between calcarenites and underlying clays, promoting differential block movements and lateral spreading phenomena; and (iii) degradation and progressive disintegration of outcropping calcarenites caused by atmospheric agents. As noted in the sampling section, the arenites have high permeability, mainly due to porosity and fractures which create a dense network of discontinuities within the mass. This implies that the lithotypes are highly sensitive to atmospheric agents due to the ease with which rainwater can percolate.
These conditions contribute to the vulnerability of the calcarenite slopes of the studied terraces. Additionally, in coastal areas, wave action further exacerbates instability by eroding the base of the slopes. These slopes undergo retrogressive erosion, starting from the outer cliff and gradually moving inward, altering the mechanical properties of the rocks and shifting the terraces from a state of equilibrium to instability.
7. Conclusions
The study highlights the gradual increase in rock resistance from the oldest to the youngest terrace orders, indicating a deterioration in mechanical properties due to prolonged alteration processes.
The analysis shows that the uniaxial compressive strength values estimated through PLTs are consistent with those obtained from uniaxial compressive tests only for the oldest terrace order. This emphasizes the importance of selecting the appropriate test method based on lithology and considering the limitations of each method.
The findings also underscore the significant instability issues in the Crotone Basin area, particularly in coastal regions. Effective monitoring and management strategies are essential to mitigate the impact of these instability phenomena on the mechanical properties of the rocks and the overall stability of the area.
Author Contributions
Conceptualization, G.C.; methodology, G.C.; software, F.C.; validation, M.P.; formal analysis, G.C.; investigation, G.C. and D.M.; resources, S.C.; data curation, G.C. and M.P.; writing—original draft preparation, G.C.; writing—review and editing, all authors.; supervision, M.P., F.M. and S.C.; project administration, F.M. and S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Acknowledgments
The activity of Gloria Campilongo was funded by the program POR Calabria FSE/FESR 2014/2020 related to her PhD school (SIACE) at the University of Calabria.
Conflicts of Interest
The author Filippo Catanzariti was employed by the Geostru SC Engsoft S.r.l. company. All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- Romana, M. New Adjustment Ratings for Application of Bieniawski Classification to Slopes. In Proceedings of the International Symposium on Role of Rock Mechanics, Zacatecas, Mexico, 2–5 September 1985; pp. 49–53. [Google Scholar]
- Critelli, S.; Martín-Martín, M. History of Western Tethys Ocean and the Birth of the Circum-Mediterranean Orogeny as Reflected by Source-to-Sink Relations. Int. Geol. Rev. 2024, 66, 505–515. [Google Scholar] [CrossRef]
- Falsetta, E.; Bullejos, M.; Critelli, S.; Martín-Martín, M. 3D Modeling of the Stratigraphic and Structural Architecture of the Crotone Basin (Southern Italy) Using Machine Learning with Python. Mar. Pet. Geol. 2024, 164, 106825. [Google Scholar] [CrossRef]
- Zecchin, M.; Civile, D.; Caffau, M.; Critelli, S.; Muto, F.; Mangano, G.; Ceramicola, S. Sedimentary Evolution of the Neogene-Quaternary Crotone Basin (Southern Italy) and Relationships with Large-Scale Tectonics: A Sequence Stratigraphic Approach. Mar. Pet. Geol. 2020, 117, 104381. [Google Scholar] [CrossRef]
- Muto, F.; Spina, V.; Tripodi, V.; Critelli, S.; Roda, C. Neogene Tectonostratigraphic Evolution of Allochthonous Terranes in the Eastern Calabrian Foreland (Southern Italy). Ital. J. Geosci. 2014, 133, 455–473. [Google Scholar] [CrossRef]
- Zecchin, M.; Praeg, D.; Ceramicola, S.; Muto, F. Onshore to Offshore Correlation of Regional Unconformities in the Plio-Pleistocene Sedimentary Successions of the Calabrian Arc (Central Mediterranean). Earth-Sci. Rev. 2015, 142, 60–78. [Google Scholar] [CrossRef]
- Campilongo, G.; Ponte, M.; Muto, F.; Critelli, S.; Catanzariti, F.; Perri, F. Geotechnical and Minero-Chemical Data of the Cutro Clay Formation (Calabria, Southern Italy). J. Mediterr. Earth Sci. 2022, 14, 11–26. [Google Scholar] [CrossRef]
- Caselli, G.; Cocco, E.; Gisotti, G.; Spadea, R. Evoluzione Geomorfologica Di Capo Colonna (Crotone) Nel Periodo Storico Ei Suoi Rapporti Col Tempio Greco Di Hera Lacinia. Boll. Serv. Geol. d’Italia 2003, 117, 3–16. [Google Scholar]
- Critelli, S.; Muto, F.; Perri, F.; Tripodi, V. Interpreting Provenance Relations from Sandstone Detrital Modes, Southern Italy Foreland Region: Stratigraphic Record of the Miocene Tectonic Evolution. Mar. Pet. Geol. 2017, 87, 47–59. [Google Scholar] [CrossRef]
- Campilongo, G.; Campilongo, E.; Catanzariti, F.; Muto, F.; Ponte, M.; Critelli, S. Subsidence Analysis by Mean of DeGloT Software: Application to the Key-Case of the Miocene-Quaternary Crotone Basin (Calabria, S. Italy). Mar. Pet. Geol. 2022, 146, 105964. [Google Scholar] [CrossRef]
- Zecchin, M.; Massari, F.; Mellere, D.; Prosser, G. Anatomy and Evolution of a Mediterranean-Type Fault Bounded Basin: The Lower Pliocene of the Northern Crotone Basin (Southern Italy). Basin Res. 2004, 16, 117–143. [Google Scholar] [CrossRef]
- Mattei, M.; Cifelli, F.; D’Agostino, N. The Evolution of the Calabrian Arc: Evidence from Paleomagnetic and GPS Observations. Earth Planet. Sci. Lett. 2007, 263, 259–274. [Google Scholar] [CrossRef]
- Roda, C. Distribuzione e Facies Dei Sedimenti Neogenici Nel Bacino Crotonese. Geol. Rom. 1964, 3, 319–366. [Google Scholar]
- VanDijk, J.P. Sequence Stratigraphy, Kinematics and Dynamic Geohistory of the Crotone Basin (Calbrian Arc, Central Mediterranean): An Integrated Approach. Mem. Soc. Geol. It. 1990, 44, 259–285. [Google Scholar]
- Barone, M.; Dominici, R.; Muto, F.; Critelli, S. Detrital Modes in a Late Miocene Wedge-Top Basin, Northeastern Calabria, Italy: Compositional Record of Wedge-Top Partitioning. J. Sediment. Res. 2008, 78, 693–711. [Google Scholar] [CrossRef]
- Massari, F.; Prosser, G.; Capraro, L.; Fornaciari, E.; Consolaro, C. A Revision of the Stratigraphy and Geology of the South-Western Part of the Crotone Basin (South Italy). Ital. J. Geosci. 2010, 129, 353–384. [Google Scholar] [CrossRef]
- Cosentino, D.; Gliozzi, E.; Salvini, F. Brittle Deformations in the Upper Pleistocene Deposits of the Crotone Peninsula, Calabria, Southern Italy. Tectonophysics 1989, 163, 205–217. [Google Scholar] [CrossRef]
- Zecchin, M.; Nalin, R.; Roda, C. Raised Pleistocene Marine Terraces of the Crotone Peninsula (Calabria, Southern Italy): Facies Analysis and Organization of Their Deposits. Sediment. Geol. 2004, 1–2, 165–185. [Google Scholar] [CrossRef]
- Gignoux, M. Sur La Classification Du Pliocène et Du Quaternarie Dans l’I-Talie Du Sud. Comptes Rendus L’academie Sci. 1910, 150, 841–844. [Google Scholar]
- Nalin, R.; Massari, F.; Zecchin, M. Superimposed Cycles of Composite Marine Terraces: The Example of Cutro Terrace (Calabria, Southern Italy). J. Sediment. Res. 2007, 77, 340–354. [Google Scholar] [CrossRef]
- Gliozzi, E. I Terrazzi Marini Del Pleistocene Superiore Della Penisola Di Crotone, Geol. Roma. Ph.D. Thesis, Università degli Studi di Napoli, Naples, Italy, 1988; pp. 1–153. [Google Scholar]
- Palmentola, G.; Carobene, L.; Mastronuzzi, G.; Sanso, P. I Terrazzi Marini Pleistocenici Della Penisola Di Crotone (Calabria). Geogr. Fis. Din. Quat. 1990, 13, 75–80. [Google Scholar]
- Zecchin, M.; Ceramicola, S.; Civile, D.; Sturiale, G.; Ramella, R.; Roda, C. Note illustrative della carta geologica d’Italia alla scala 1:50.000 Foglio 571 Crotone. Ispra, Servizio Geologico d’Italia Organo Carografico dello Stato, Progetto CARG 2014, 1–96. Available online: https://ricerca.ogs.it/handle/20.500.14083/6394?mode=simple (accessed on 1 August 2024).
- Zecchin, M.; Civile, D.; Caffau, M.; Sturiale, G.; Roda, C. Sequence Stratigraphy in the Context of Rapid Regional Uplift and High-Amplitude Glacio-Eustatic Changes: The Pleistocene Cutro Terrace (Calabria, Southern Italy). Sedimentology 2011, 58, 442–477. [Google Scholar] [CrossRef]
- ASTM, D. 2845-00; Standard Test Method for Laboratory Determination of Pulse Velocities and Ultrasonic Elastic Constants of Rock. ASTM International: West Conshohocken, PA, USA, 2000.
- ASTM, D. 2938; Standard Test Method for Unconfined Compressive Strength of Intact Rock Core Specimens. ASTM International: West Conshohocken, PA, USA, 1995.
- Bieniawski, Z.T.; Hawkes, I. Suggested Methods for Determining Tensile Strength of Rock Materials. Int. J. Rock Mech. Min. Sci. 1978, 15, 99–103. [Google Scholar]
- Hatheway, A.W. The complete ISRM suggested methods for rock characterization, testing and monitoring. Environ. Eng. Geosci. 2009, 15, 47–48. [Google Scholar] [CrossRef]
- Broch, E.; Franklin, J.A. The point-load strength test. Int. J. Rock Mech. Min. Sci. Geomech. Abstracts 1972, 9, 669–676. [Google Scholar] [CrossRef]
- ASTM, D. 5731; Standard Test Method for Determination of the Point Load Strength Index of Rock and Application to Rock Strength Classifications. American Society for Testing and Materials: West Conshohocken, PA, USA, 2008.
- Anon, O.H. Classification of Rocks and Soils for Engineering Geological Mapping. Part 1: Rock and Soil Materials. Bull. Int. Assoc. Eng. Geol. 1979, 19, 364–437. [Google Scholar]
- Vallejo, L.E.; Welsh, R.A.; Robinson, M.K. Correlation between Unconfined Compressive and Point Load Strengths for Appalachian Rocks. In Proceedings of the 30th U.S. Symposium on Rock Mechanics, USRMS, Morgantown, WV, USA, 19–22 June 1989. [Google Scholar]
- Deere, D.V.; Miller, R.P. Engineering Classification and Index Properties for Intact Rock; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1966. [Google Scholar]
- Sciotti, A.; Calabresi, G. Deep-Seated Movements in Stiff Jointed Clays: The Role of Structural Discontinuities. In Proceedings of the Advances in Geotechnical Engineering: The Skempton Conference—Proceedings of a Three Day Conference on Advances in Geotechnical Engineering, London, UK, 29–31 March 2004; Institution of Civil Engineers: London, UK, 2004. [Google Scholar]
- Hassani, F.P.; Scoble, M.J.; Whittaker, B.N. Application of the Point Load Index Test to Strength Determination of Rock and Proposals for a New Size-Correction Chart. In Proceedings of the 21st U.S. Symposium on Rock Mechanics, USRMS, Rolla, MO, USA, 27–30 May 1980. [Google Scholar]
- Read, J.R.L.; Thornton, P.N.; Regan, W.M. Rational approach to the point load test. In Proceedings of the Australia-New Zealand Conference on Geomechanics, Wellington, New Zealand, 12–16 May 1980; Institution of Professional Engineers New Zealand: Wellington, New Zealand, 1980; Volume 2. [Google Scholar]
- Mohamed, M.S.E.; Saeed, M.; Radwan, A.A. Prediction of unconfined compressive strength of rocks by point load strength index. J. Al-Azhar Univ. Eng. Sect. 2019, 14, 453–459. [Google Scholar] [CrossRef][Green Version]
- Rusnak, J.; Mark, C. Using the Point Load to Determine the Uniaxial Compressive Strength of Coal Measure Rock. In Proceedings of the 19th International Conference on Ground Control in Mining, Morgantown, WV, USA, 8–10 August 2000. [Google Scholar]
- Smith, H.J. The Point Load Test for Weak Rock in Dredging Applications. Int. J. Rock Mech. Min. Sci. 1997, 34, 295.e1–295.e13. [Google Scholar] [CrossRef]
- Salah, H.; Omar, M.; Shanableh, A. Estimating Unconfined Compressive Strength of Sedimentary Rocks in United Arab Emirates from Point Load Strength Index. J. Appl. Math. Phys. 2014, 2, 296. [Google Scholar] [CrossRef]
- Bieniawski, Z.T. The point-load test in geotechnical practice. Eng. Geol. 1975, 9, 1–11. [Google Scholar] [CrossRef]
- ISRM, P.L.T. Suggested Method for Determining Point Load Strength. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1985, 22, 51–60. [Google Scholar]
- Brown, E.T. Rock Characterization, Testing & Monitoring, ISRM Suggested Methods. Pergamon 1981, 171–183. [Google Scholar]
- O’Rourke, J.E. Rock Index Properties for Geoengineering Design in Underground Development. SME Repr. 1988, 48–88. [Google Scholar]
- Jermy, C.A.; Bell, F.G. Coal Bearing Strata and the Stability of Coal Mines in South Africa. In Proceedings of the 7th International Congress on Rock Mech, Aachen, Germany, 16–20 September 1991; pp. 1125–1131. [Google Scholar]
- Sayadi, A.; Monjezi, M.; Talebi, N.; Khandelwal, M. A Comparative Study on the Application of Various Artificial Neural Networks to Simultaneous Prediction of Rock Fragmentation and Backbreak. J. Rock Mech. Geotech. Eng. 2013, 5, 318–324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).