1. Introduction
Inverse Distance Weighting (
IDW) is an interpolation method that is widely used in geosciences. The method is applied to small and large input data sets. Various authors have applied
IDW during different mappings of variables: mapping the distribution of a nickel deposit [
1], geomorphology [
2], estimated copper, molybdenum, gold and silver with respect to lithogeochemical data in the Kahang porphyry deposit in Central Iran [
3], modeling of ionospheric time delay [
4], spatial distribution maps of groundwater [
5], spatial distribution of groundwater pollution maps [
6], mapping of gold deposits based on drilled shallow wells [
7], soil salinity mapping in the Mirzaabad District, Syrdarya Province [
8], and the estimation of tin resources [
9].
It is obvious that
IDW is a widely used interpolation method in different geosciences for spatial 2D visualization, and it is often compared with other interpolations like the Kriging techniques, Nearest Neighborhood or Moving Average. Its popularity arises from the simple algorithm, where the weighting of measured values comes from their distances, but users also can vary such weights with a power exponent. So, some control is retained but calculation is simple and fast for very large data sets (hundreds of points). The decades-long use of
IDW and comparison with other methods is not the goal of this paper; however, some examples from Croatia are useful to mention to lead readers to knowledge of the “main” interpolation “competitors” of
IDW, their advantages and disadvantages. So, ref. [
10] showed the spatial variability of soil organic matter content in Eastern Croatia assessed using different interpolation methods, namely,
IDW, Ordinary Kriging and Bayesian Kriging. Only the Kriging techniques are main competitors of
IDW, assuming that spatial variability could be better described with such an algorithm, which is not always true (especially for data sets with less than 20 points, or for more numerous but highly clustered data sets).
The hydrocarbon reservoirs in the Northern Croatia Miocene subsurface sandstones are just such borderline examples, where the numbers of the data are at the limits for creating a detailed spatial model using a variogram and continuing with the Kriging techniques, as opposed to choosing a simpler mathematical method like
IDW and decreasing the error of faulty complex modeling. Sometimes, for the larger fields, the Kriging techniques can be successfully applied for smaller data sets, e.g., the depth data for 18 wells on the Upper Pannonian/Lower Pontian border (i.e., E-log marker Z’) in the Šandrovac Field [
11] interpolated with the Universal Kriging. However, this is mostly an exception, not the standard rule.
Obviously, reliable subsurface mapping is crucial for all hydrocarbon reservoirs in the Sava Depression, and northern Croatia in general, especial in the current late production stage, when the maximum predicted recovery has been almost reached in all fields. As the porosity is one of the major reservoir variables, such mapping must be (re)made as reliable as possible, especially when not all wells have reliable log measurements and core analysis. So, the available data sets are often much smaller than the total number of wells drilled in the field’s structure. Also, porosity mapping in the Croatian hydrocarbon reservoirs was done using other algorithms and interpretation methods, mostly successfully reaching the possible visualization of reservoir models. Further, ref. [
12] compared the sweetness seismic attribute and (also) porosity and porosity-thickness maps (obtained by Ordinary Kriging) in the Sava Depression. Also, ref. [
13] used stochastic simulation for mapping reservoir geological variables (porosity, thickness, depth) in the Sava Depression (18–23 wells available for the mapped structure). The authors recommended that sequential Gaussian simulation can be used for structural variations, and Indicator Kriging and sequential indicator simulation for the mapping of depositional environment morphology.
Application of the
IDW algorithm is dependent on its simple equations. The estimated value of the
IDW variable is calculated using the following formula: [
14,
15,
16]:
where:
| ZIDW | estimated value; |
| d1 … dn | distance between estimated value and known value 1 … n; |
| p | power distance exponent; |
| z1 … zn | known values at locations 1 … n. |
The mapping results are greatly influenced by the power distance exponent (p); this is clear because it represents the exponent of a value that is inversely reciprocal to the known “hard” data, as can be seen from Formula (1). This is why it is important to choose p correctly so that the obtained interpolated maps are usable and mathematically based. Both the size (small or large) and the nature of the input data set should be considered when choosing p. The wrong selection of p can lead to asymmetry in the resulting interpolation maps, which should be avoided. In this paper, the selection of p will be analyzed considering the quantitative (sample size, cross-validation) and qualitative (visual inspection and interpretation) aspects of the obtained interpolation maps.
2. Materials and Methods
For the analysis of the value of p, it is necessary to take into account the material and applied methods. The material data were contained in the values of the porosity of the reservoirs K and L. In addition to the previously described IDW, the coefficient of interquartile deviation, root mean square error, mean absolute error and median absolute deviation calculations were applied for the analysis.
2.1. Coefficient of Interquartile Deviation
Coefficient of interquartile deviation (
VQ) is a measure of the incomplete dispersion of a data set, and is defined as [
17,
18]:
where:
| VQ | coefficient of interquartile deviation; |
| Q1 | the value of the lower (first) quartile of the sample; |
| Q3 | the value of the upper (third) quartile of the sample. |
The value of the coefficient is between 0 and 1, and the condition for its application is that all input data are positive values (>0). The dispersion of the data is smaller the closer VQ is to 0, and relatively larger the closer VQ is to 1.
2.2. Root Mean Square Error (RMSE)
Cross-validation is a numerical value obtained as the difference of the square of the measured and estimated data values. Mean square error is calculated according to [
19,
20]:
where:
| MSE | mean square error value; |
| n | number of known values; |
| SV | measured value of point “i”; |
| P | estimated value of point “i”; |
| i | ith point. |
It quantitatively expresses the quality of the interpolation map; the lower the
RMSE value is, the higher the acceptability of the interpolated map. During the interpolation process, while changing various parameters,
RMSE is a corrective for interpolation maps because it reduces the space for gross errors. The root mean square error value is calculated according to [
21,
22]:
where:
| RMSE | root mean square error value; |
| MSE | mean square error value. |
The fact that the RMSE is based on the root function of the error itself means that larger errors will contribute less in absolute terms. This is very important when analyzing a large input data set.
2.3. Mean Absolute Error (MAE)
Mean absolute error is a measure of error calculated as the difference between the measured and estimated sample values. The formula for calculating
MAE is [
23,
24]:
where:
| MAE | mean absolute error; |
| n | number of known values; |
| SV | measured value of point “i”; |
| P | estimated value of point “i”; |
| i | ith point. |
As can be seen from Expression (5), the MAE represents a comparison between the “firm” data and the estimated data. The MAE method is sensitive to extreme values within the input data set.
2.4. Median Absolute Deviation (MAD)
Median absolute deviation is the median value of the difference between the estimated value and the value of the “solid” data.
MAD is calculated according to the following equation [
25,
26]:
where:
| MAD | median absolute deviation; |
| SV | measured value of point “i”; |
| P | estimated value of point “i”; |
| i | ith point. |
3. Geographic Location, Geological Settings and Raw Data of Analyzed Reservoirs
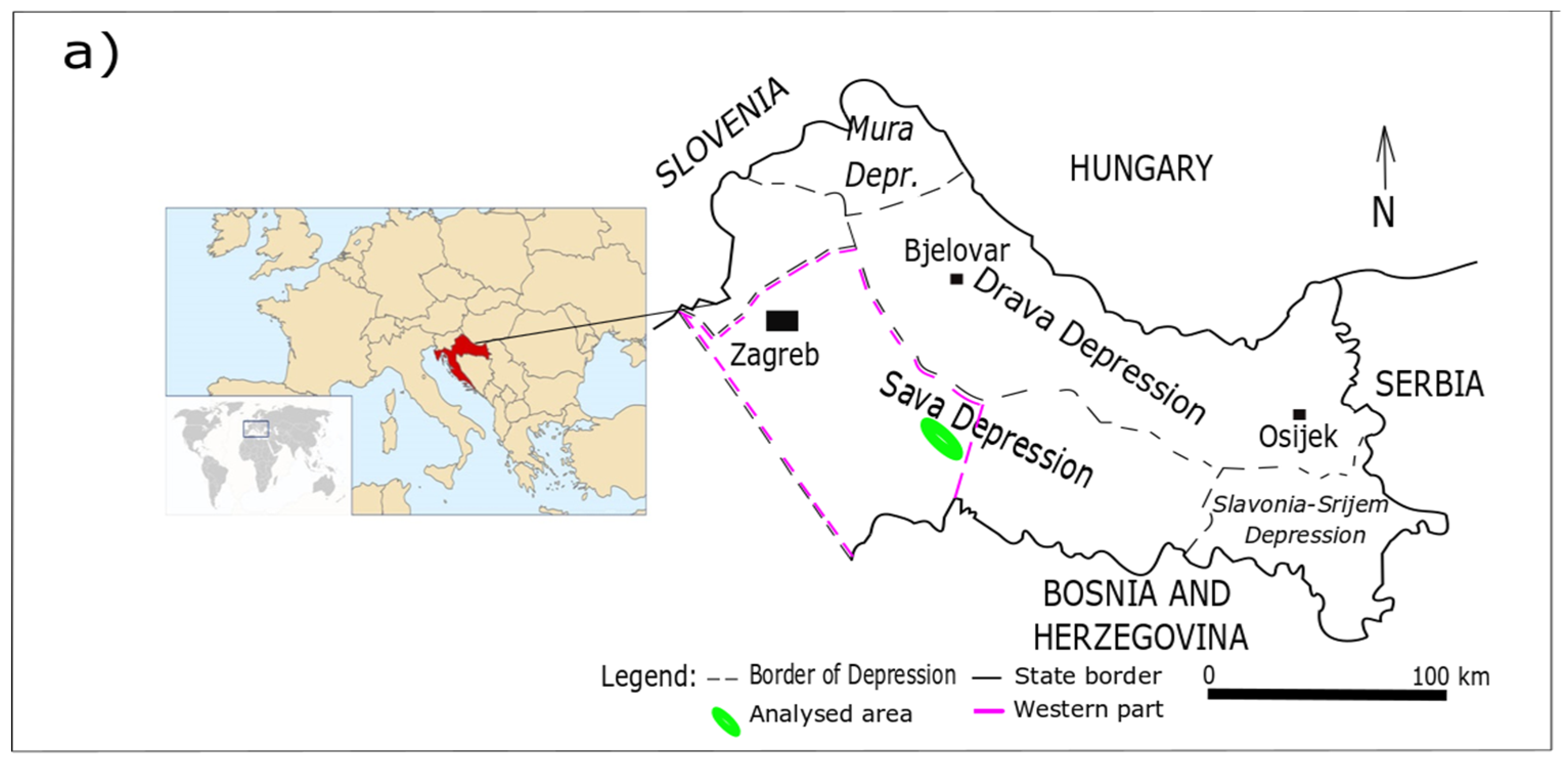
Research fields “A” and “B” were located within the Sava Depression, in the Croatian part of the Pannonian Basin System (CPBS) (see
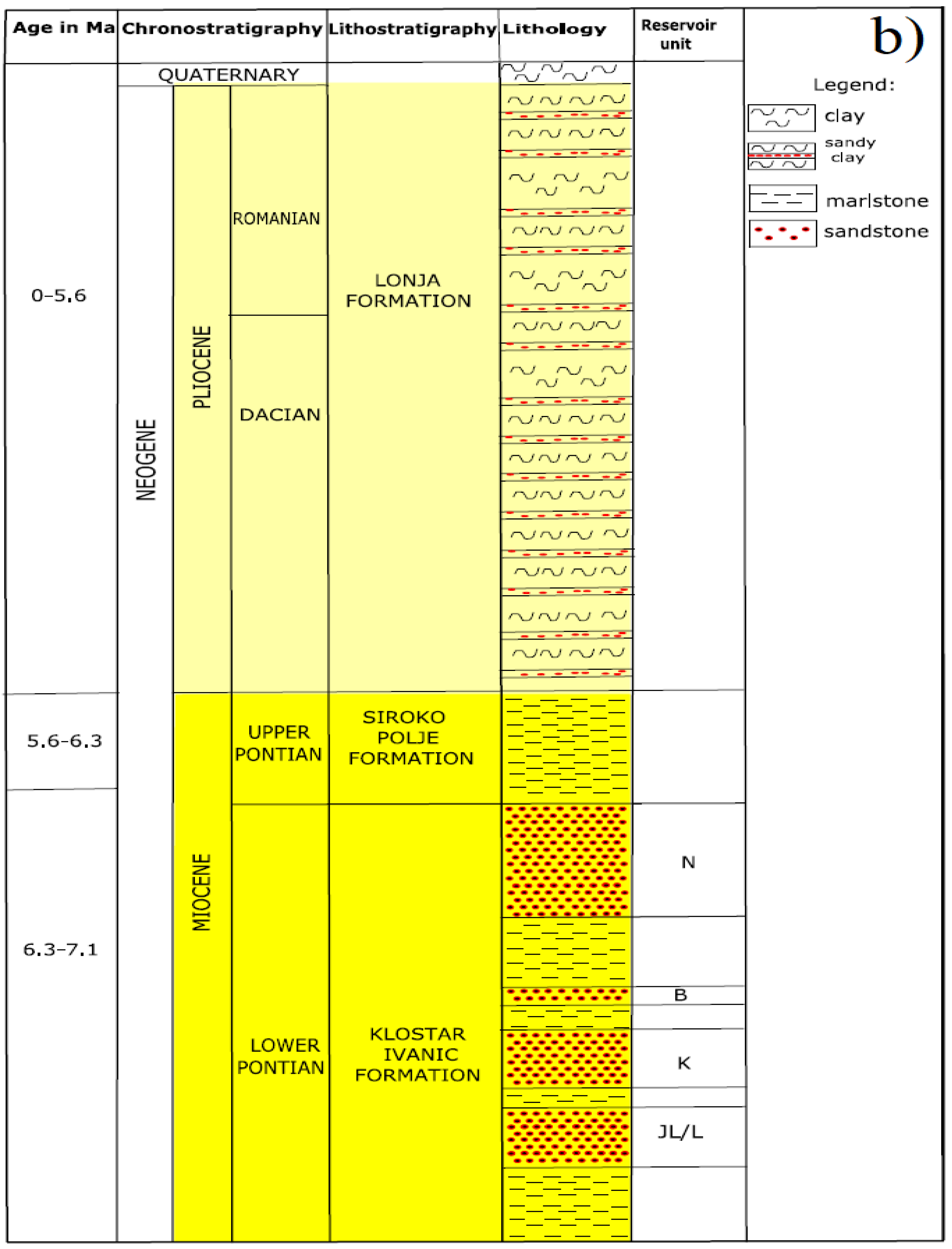
Figure 1a). Sediments filling the Sava Depression started already in the Early Neogene (Otnangian), and in this study, Lower Pontian reservoir rocks (reservoirs K and L) belonging to the Kloštar-Ivanić Formation were analyzed (see geological column in
Figure 1b).
These are mainly well-sorted arenitic sandstones, becoming fine-grained and loose toward the top of the Široko Polje Formation, and intercalated with marl intervals. Reservoir rocks are well-lithified sandstones, with an average thickness of 20–150 m. Isolator rocks are gray to gray-brown marls, moderately lithified, appearing in 30–150 m thick intervals between sandstones.
The Lower Pontian sediments (also known informally by their older name, the Abichi deposits, after the characteristic fossil shell Paradacna abichi) extended across the entire Sava Depression, but in the westernmost part can be referred to as the Kloštar-Ivanić Marls (as a lateral equivalent of the Kloštar-Ivanić Formation), or locally as the Brezine or Graberje Marl. The analyzed sandstones (as part of the Poljana Sandstones) are the result of periodically activated turbidites and are deposited in the deepest part of the depression. The rest had been filled with marls, occasionally silty ones.
The most important petrophysical parameter during reservoir analysis is porosity. Data on the porosity of the deposits K and L were obtained by analyzing cores from a well or by interpreting logging diagrams. Particularly, the porosity data were calculated by interpretation of resistivity, density and neutron logs. For the K reservoir, data from 3 wells (25, 120 and 168), and for the L reservoir 10 wells (2, 5, 57, 60, 62, 68, 73, 85, 87 and 145), were also available from lab analysis, but were not used for this mapping [
29]. The reason lay in the values from the lab analyses, which were somewhat higher than those from the logs, so a conservative approach to reservoir quality favored using the lower, i.e., log-interpreted/calculated, values. The permeability (not used here) was solely derived from laboratory analysis of cores.
The porosity value for the K reservoir was obtained from 19 wells (average depth 975 m), while for the L reservoir it was obtained from 25 wells (average depth 1370 m), and these were considered “solid” data, i.e., the original data during various analyses. Basic statistical data on the porosity of the reservoirs K and L are shown in
Table 1. It is obvious that the quality and resolution of the measuring devices and the transformation of indirect signals into values had significant limitations, especially in reservoir K, where numerous wells have the same average porosity value as for sandstone. However, this is a common limitation that must be overcome using the most appropriate interpolation algorithm, and handled using the same values as for the same kinds of “clusters”, even if they are not located in the same neighborhood.
4. Results and Discussion
The choice of reservoirs was made considering the sizes of the input data sets. The sizes of the input data sets were taken from the authors of [
31], according to which reservoir K belongs to a small data set, while reservoir L belongs to a large data set. The values of the coefficient of interquartile deviation for the K and L reservoirs are presented in
Table 2.
According to
Table 2, the
VQ value for the K reservoir is 0.013, while for the L reservoir it is 0.054. According to these values, the porosity of these reservoirs is significantly dispersed. This was to be expected due to the nature of the input data and the method used to obtain them. Due to the high economic cost of obtaining data, the input data set is in most cases very dispersed. Precisely because of the high dispersion of the data, the
IDW method was applied for mapping reservoirs K and L.
4.1. Qualitative Analysis of Maps
A qualitative analysis of interpolated maps implies a visual inspection of the map and the existence of the following visual mapping results: bull’s-eye (circular), butterfly (ellipsoidal) and mosaic [
32]. During the visual analysis of the maps, maps with a value of
p = 0 were not analyzed, because according to Equation (1), in that case the solution of the equation would be the same. The results of the mapping of reservoirs K and L using the
IDW method for
p values of 1, 2, 3 and 4 are shown in
Figure 2 and
Figure 3.
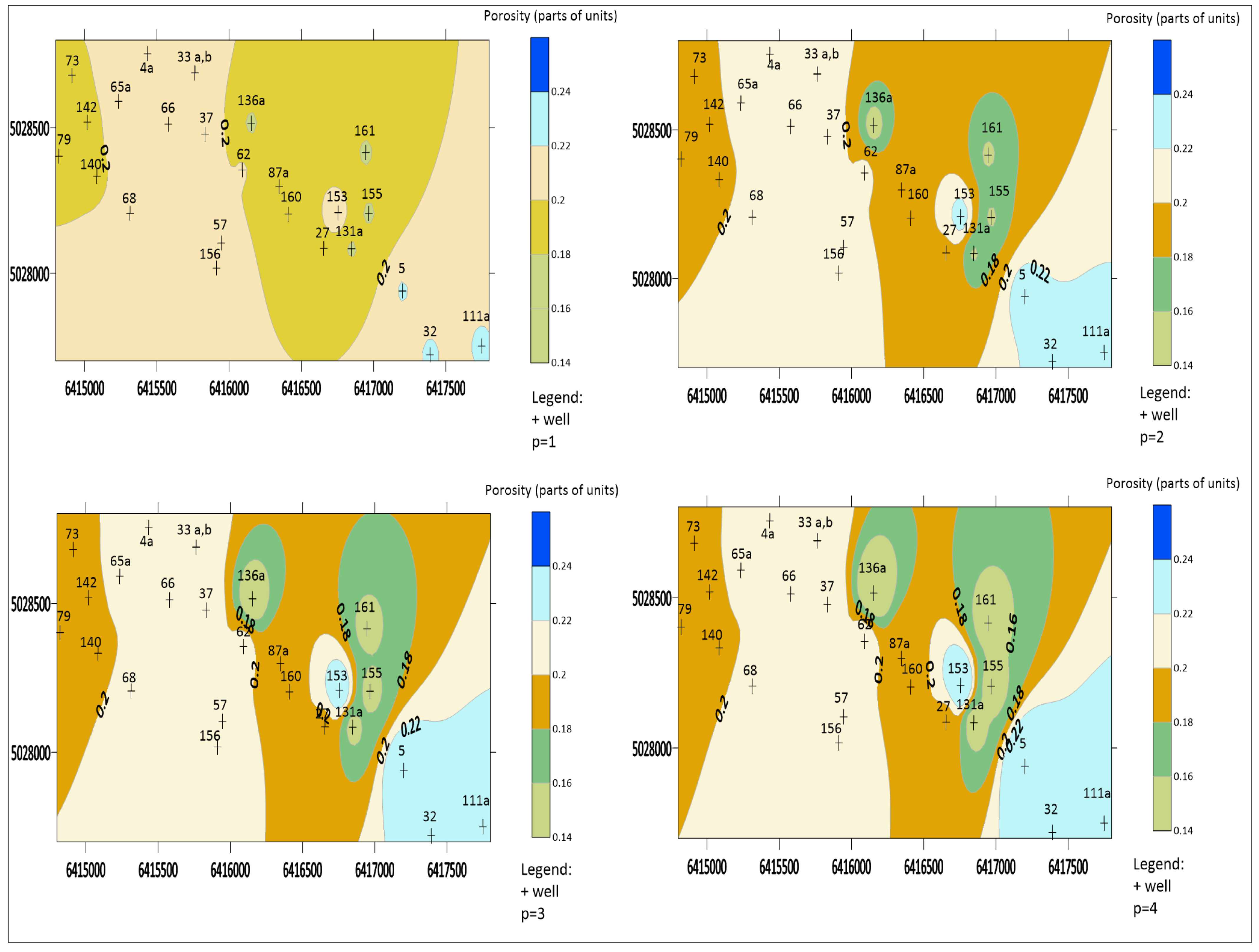
In the case of reservoir K (see
Figure 2), with an increasing value of
p, a pronounced bulls-eye effect (
p = 1,
p = 2) and butterfly effect (
p = 3,
p = 4) appears. At higher values, as seen with J-25, J-168, etc., regardless of the change in the value of
p, the effect was not removed, but the changes were detected as a pronounced bulls-eye effect changing into a butterfly effect. With an increase in the value of
p, there was no mosaic effect, which is positive. The transition zones were different in all cases of a change in p; the clearest transition zone was seen in the case of
p = 2, and it did not have such a pronounced asymmetric value change as in the other cases. Also, a
p value of 2 can reduce the number of bull’s-eyes to show only extreme values in the input data. In cases where bull’s-eye and butterfly effects are expressed on the maps, from a visual point of view, interpolated maps with a bulls-eye effect are preferred. With the bull’s-eye effect, the value is evenly distributed around the point data, while with the butterfly effect, there is an ellipsoidal surface around the point data, which due to its appearance can encompass more space, which is not realistic. Therefore, for the example of the interpolated map obtained in
Figure 2, i.e., in the case of a small data set, the value of
p is 1 and 2 when using the
IDW method.
The porosity map of reservoir L (see
Figure 3) has a pronounced butterfly effect for all cases of
p values. As the value of
p increases in this case, the bull’s-eye and mosaic effect are not present, which is evident from the obtained interpolation map. The reason for this is that it is a large data set, and the input data set is sufficient to perform a satisfactory interpolation in the given area. The transition area between different input data values is clearer when interpolating with
p values of 3 and 4. For
p values of 3 and 4, it is very clear that reservoir L is tectonically very clearly divided and the stability of transition zones is conditioned by the relative values of individual data with neighboring ones, which can be seen in the eastern parts of the interpolated maps as a rather asymmetric area of porosity values. Considering the transition zones and the inclusion of input data in the interpolated maps, for a large data set, the recommendation from the visual inspection of the maps is to use
p values of 3 and 4 when applying the
IDW method.
4.2. Quantitative Analysis of Maps
The quantitative analysis was expressed by the numerical values of
RMSE,
MAE and
MAD, the results of which are shown in
Table 3 for the K and L reservoirs.
The values of
RMSE and
MAE for reservoir K increased as the value of the coefficient
p increased, while the value of
MAD varied. The
RMSE values were 0.00104–0.00155, and the values of
MAE were 0.01700–0.02319, which shows continuous but almost linear growth. The
MAD values were not linear and had values of 0.00360–0.00734. According to the
RMSE,
MAE and
MAD values, the smallest values on the interpolated porosity map of reservoir K were with
p values of 1 and 2. Unlike reservoir K, the
RMSE,
MAE and
MAD values for reservoir L were not in a linear relationship.
RMSE values were 0.0263–0.02470,
MAE values were 0.01924–0.01490 and
MAD values were 0.00869–0.00343. As can be seen from
Table 3, it was for a value of
p of 1 that reservoir L had the highest values on the interpolated porosity map, while for values of
p of 3 and 4, it had the lowest values. According to the quantitative methods and the
RMSE,
MAE and
MAD values, for a small sample, the optimal value of
p is 1 or 2, while for a large sample, the optimal value of
p is 3 or 4.
4.3. Qualitative–Quantitative Approach in Selection of p-Value
Most of the authors who have analyzed
p values for the
IDW method have used a large data set. Moreover,
IDW is one of the most applied interpolation methods overall in many sciences that deal with spatial data, e.g., in mining [
33] or soil mapping for military applications [
34]. However, the selection of a
p-value to be the standard for any scientific field is a very hard, if not impossible, task, and it often depends not only on the discipline, but also on the geographical location of data. Such a geographically specific analysis is presented here as an example of subsurface geological mapping in the northern Croatia Neogene sandstones, and the geological background defined what were considered as “small” and “large” data sets (in some other disciplines and locations, such definitions could be totally different).
4.4. Discussion
All the applied data and methods in this research included some uncertainties. For this reason, both data sets were considered for the comprehensive p-value analysis, including both qualitative and quantitative analyses, that was used for the hydrocarbon reservoirs K and L of Lower Pontian age.
Looking only at the numerical values of the
RMSE,
MAE and
MAD could lead to the conclusion that only the lowest values are criteria for the “best”
p-value. Obviously, this could be a wrong and misleading approach. It is valid especially because the Neogene northern Croatian sandstones are often of very heterogeneous porosity, including primary and secondary ones, as a result of compaction and dissolutions, as shown in
Figure 4 for Middle Miocene sandstones.
The Upper Miocene calcarenite (see
Figure 4) developed from the Middle Miocene ones, giving the same complexity of inter- and intragranular space as well as detritus composition. For example, the L reservoir sandstones are typical Lower Pontian deposits in the Sava Depression, with a high proportion of silt (silty sandstones) decreasing their “homogeneity” and “isotropy”, i.e., reservoir quality. Calcite detritus in matrix is abundant, which makes it the dominant material for dissolution and subsequent calcite cementation. This is similarly valid for the K reservoir sandstone. Consequently, although the log porosity often surpasses 20%, their values are hardly precisely determined from logs (often the values are very similar in different wells). Moreover, silty components influenced reservoir porosity variations in intervals of a few percent, but also made it very unpredictable because the differences in detritus sources are hard to interpret in such small structures. Eventually, the result is a reservoir lithologically fragmented in zones of lower petrophysical values, which makes production challenging over years, requiring the permanent fitting of a producing regime and injection well network.
Due to the inherited and numerically indescribable uncertainties belonging to a reservoir space, it is obligatory to also use a quantitative approach. This implies visually inspecting the porosity maps and eliminating ones where some impossible subsurface shapes exist (like butterfly or too strong bull’s-eye effects), or known faults with distorted isoporosity lines of continuity. Using both criteria, quantitative and qualitative, it is clear that for a small data set (like the K reservoir), the optimal p is 2, while for a large data set (like the L reservoir), the optimal value is 3 or 4. This is a recommendation for the application of the IDW method in the porosity mapping of northern Croatia’s Lower Pontian sandstones, at least in the subsurface of the Sava Depression, while it is also definitely recommended for other sciences for analyzing input data sets and performing a quantitative–qualitative analysis.