Induced Partial Saturation: From Mechanical Principles to Engineering Design of an Innovative and Eco-Friendly Countermeasure against Earthquake-Induced Soil Liquefaction
Abstract
1. Introduction
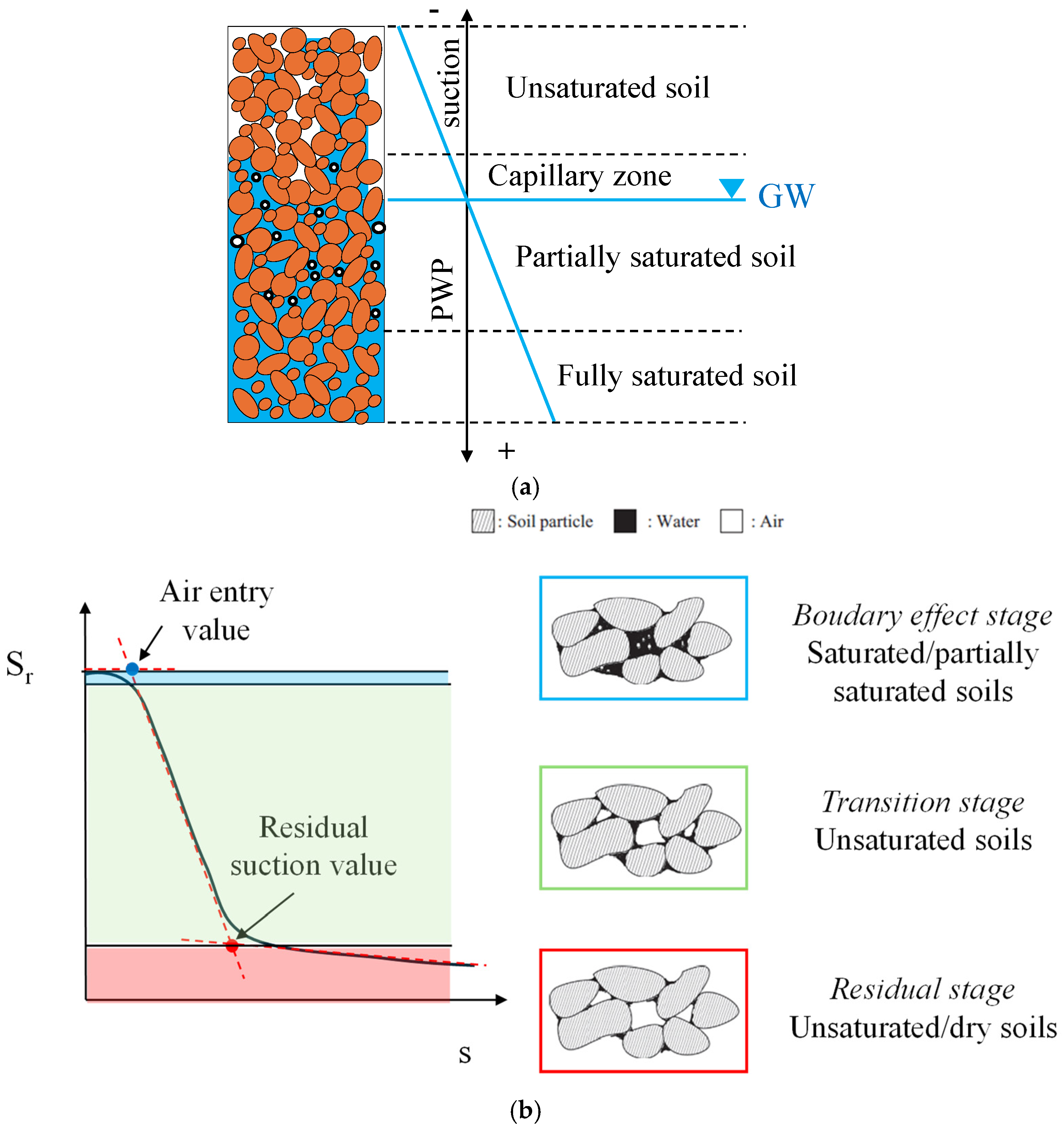
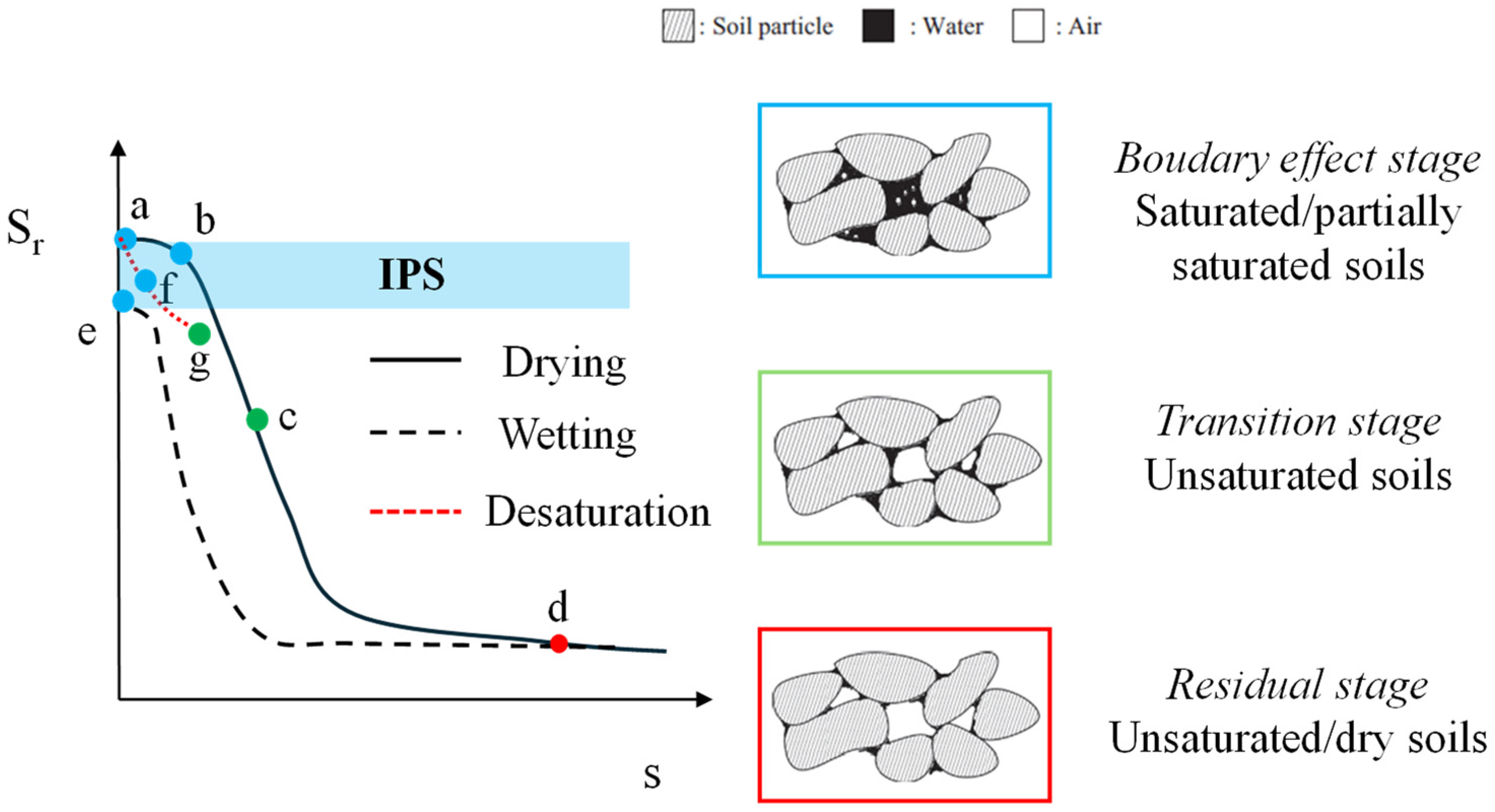
2. Degree of Saturation in Sandy Soil Deposits
- –
- In the boundary effect stage, pore air only exits as air bubbles surrounded by water (partially saturated soils). Suction is lower than the air entry value, recognized as the suction state where the entrance of air into the largest soil pore is first permitted during the desaturation of saturated soil [14]. This stage is also known as the insular air saturation condition.
- –
- In the residual stage, menisci formed around grain contact points are relevant. This stage is also known as the pendular saturation condition.
- –
- In the transition stage, there is an intermediate condition between the above stages. This stage is also known as the fuzzy saturation condition.
3. Equivalent Compressibility and Effects of Air/Gas Bubbles on Cyclic Behaviour of Sands
4. Laboratory Tests on Partially Saturated Sandy Soils
4.1. Preparation of Partially Saturated Specimens
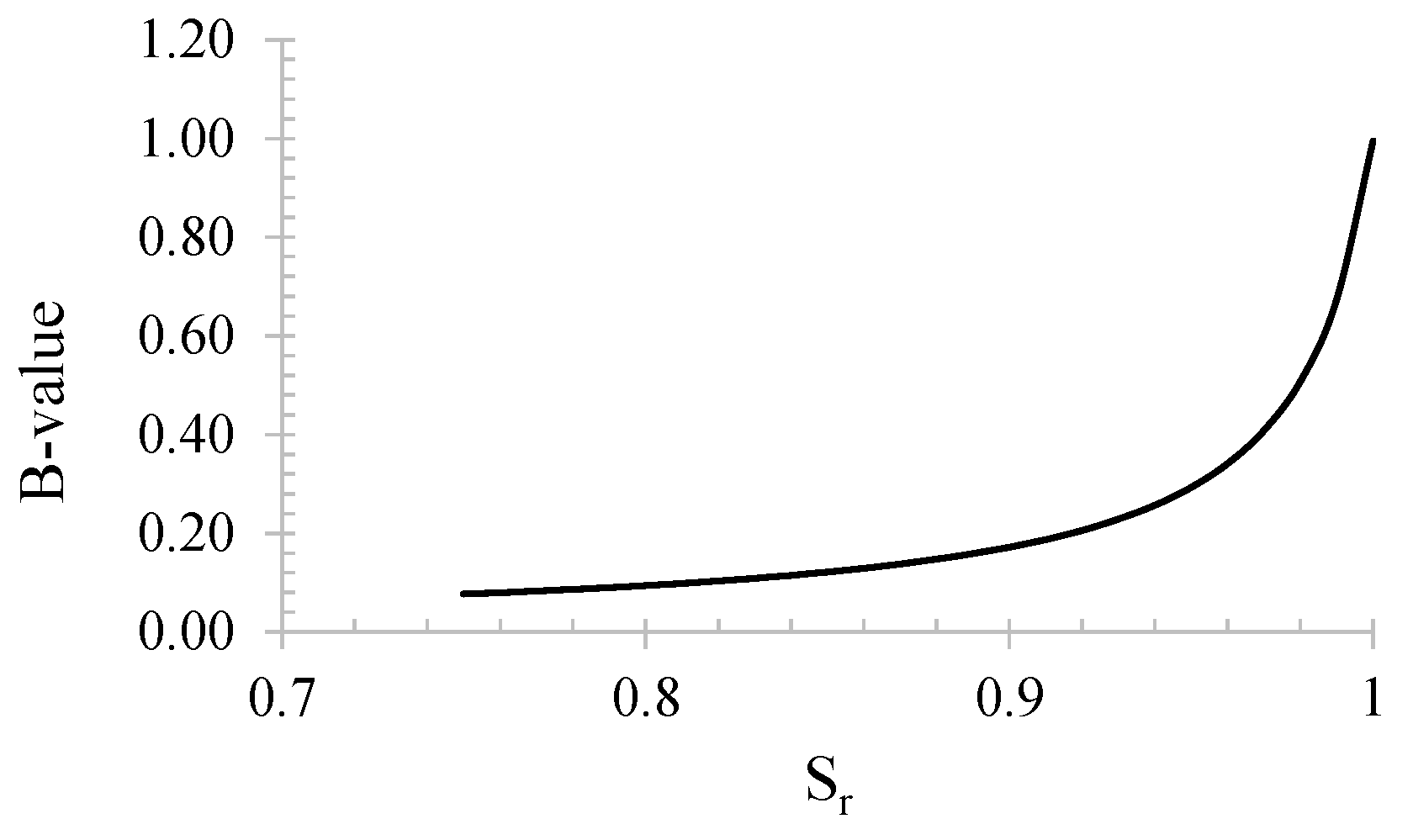
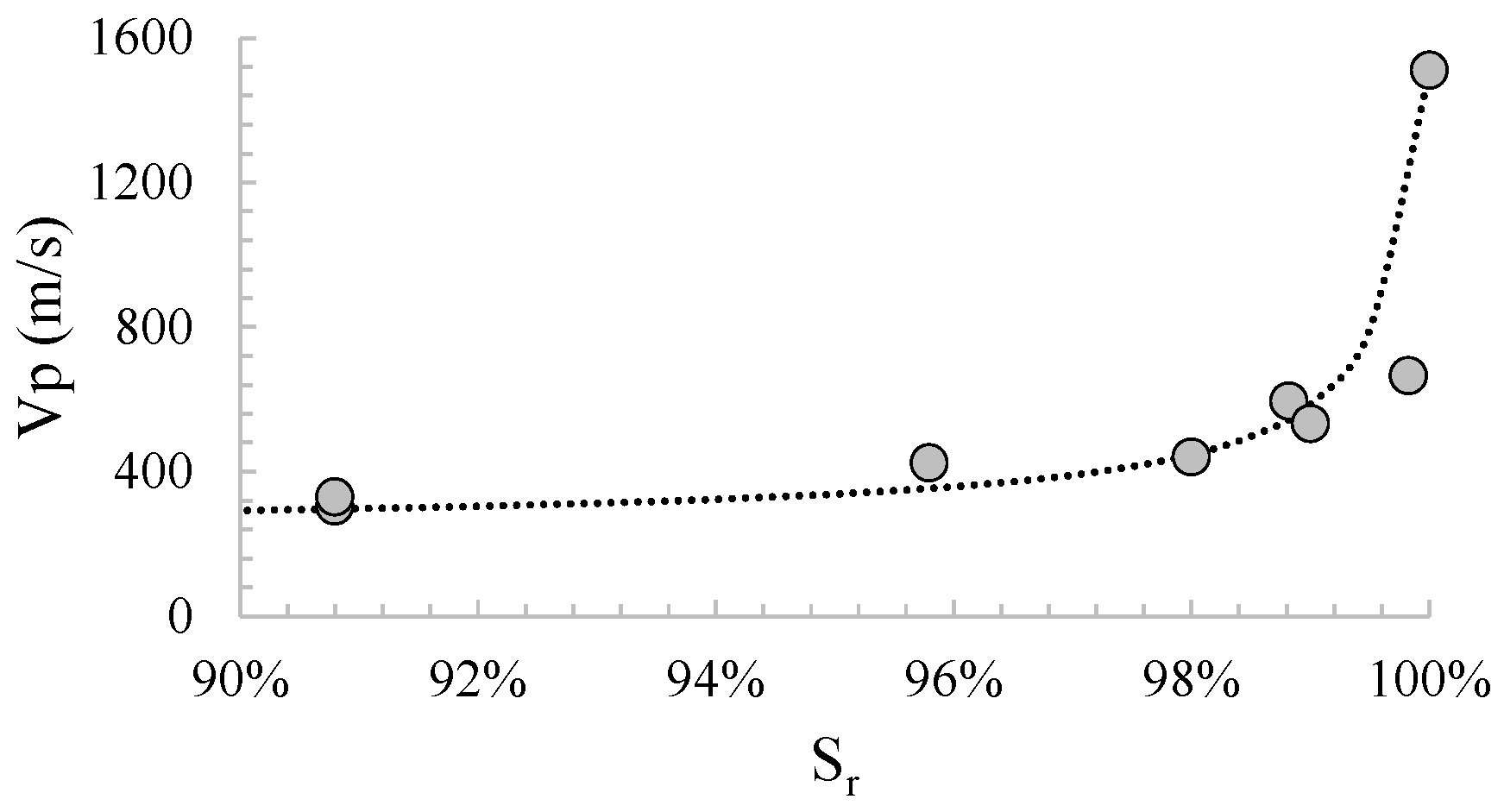
4.2. Estimation of the Degree of Saturation
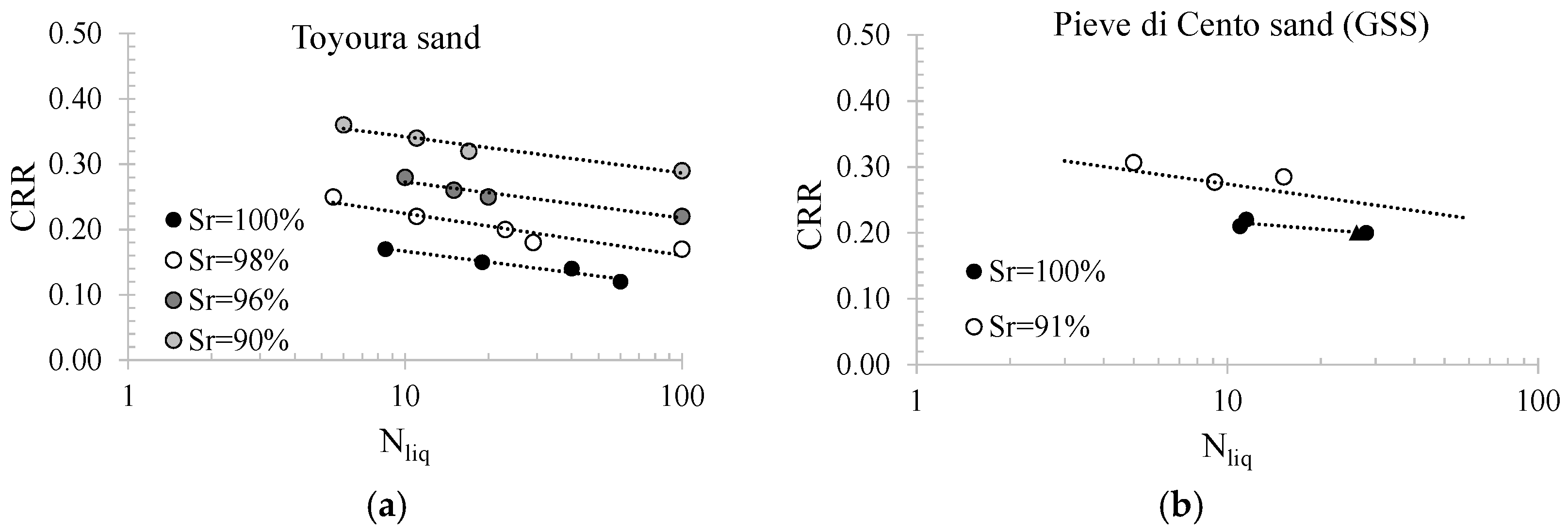
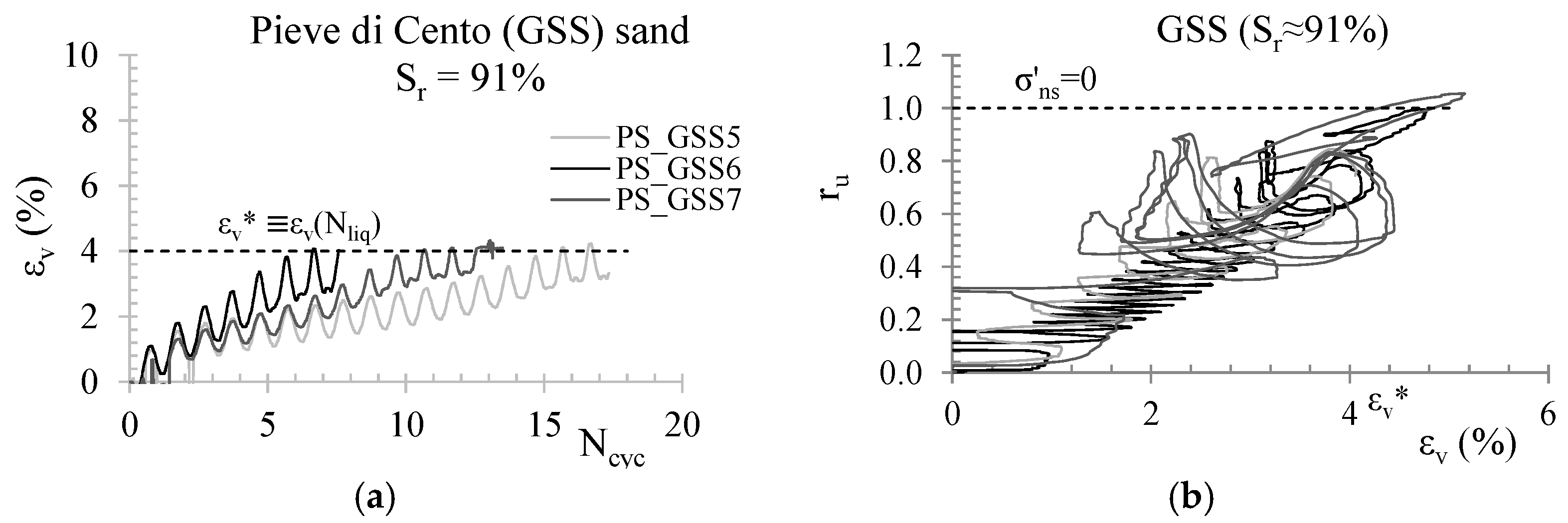
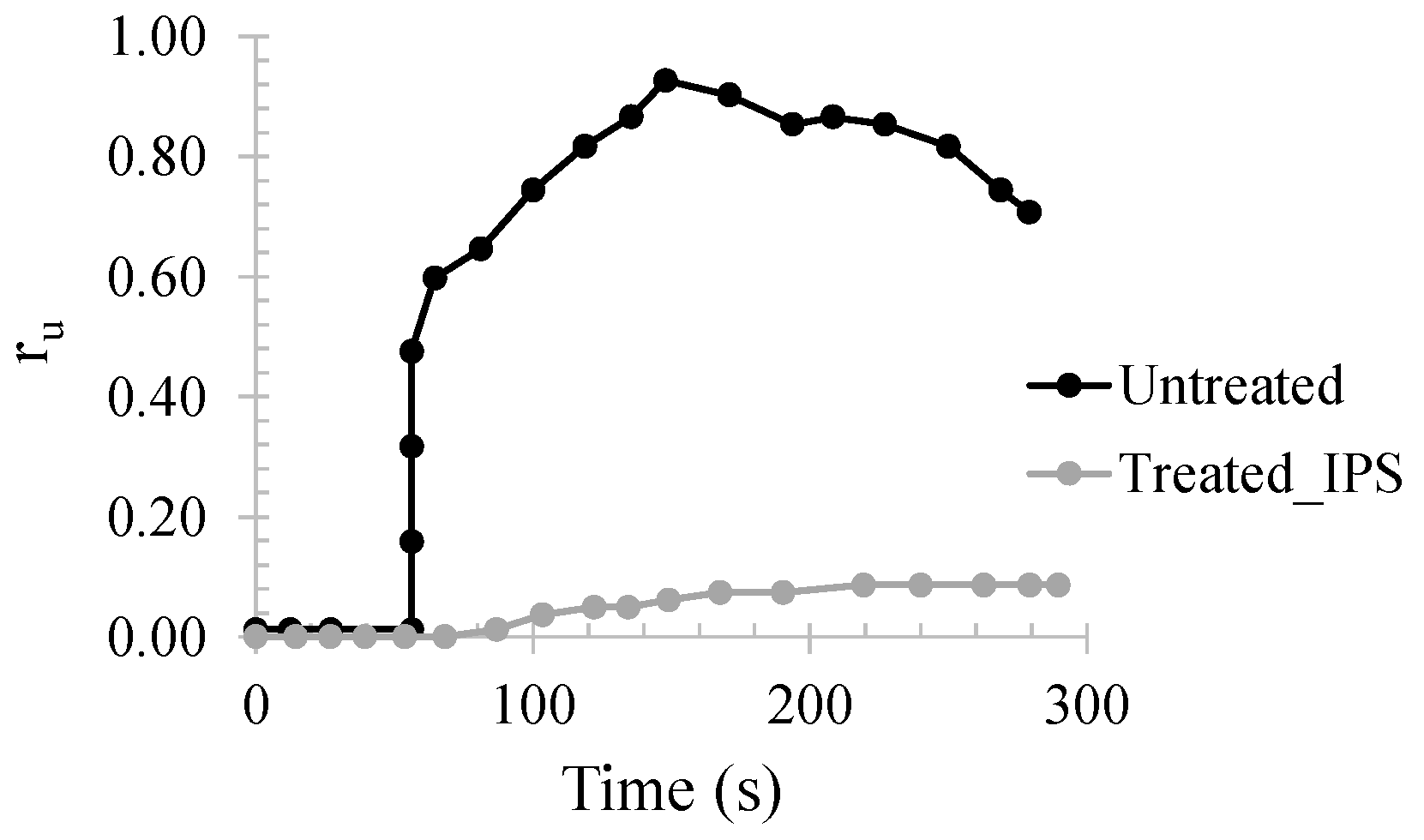
4.3. Liquefaction Resistance of Partially Saturated Sands
4.4. Limitations of Cyclic Tests on the Liquefaction Behaviour of Partially Saturated Sands
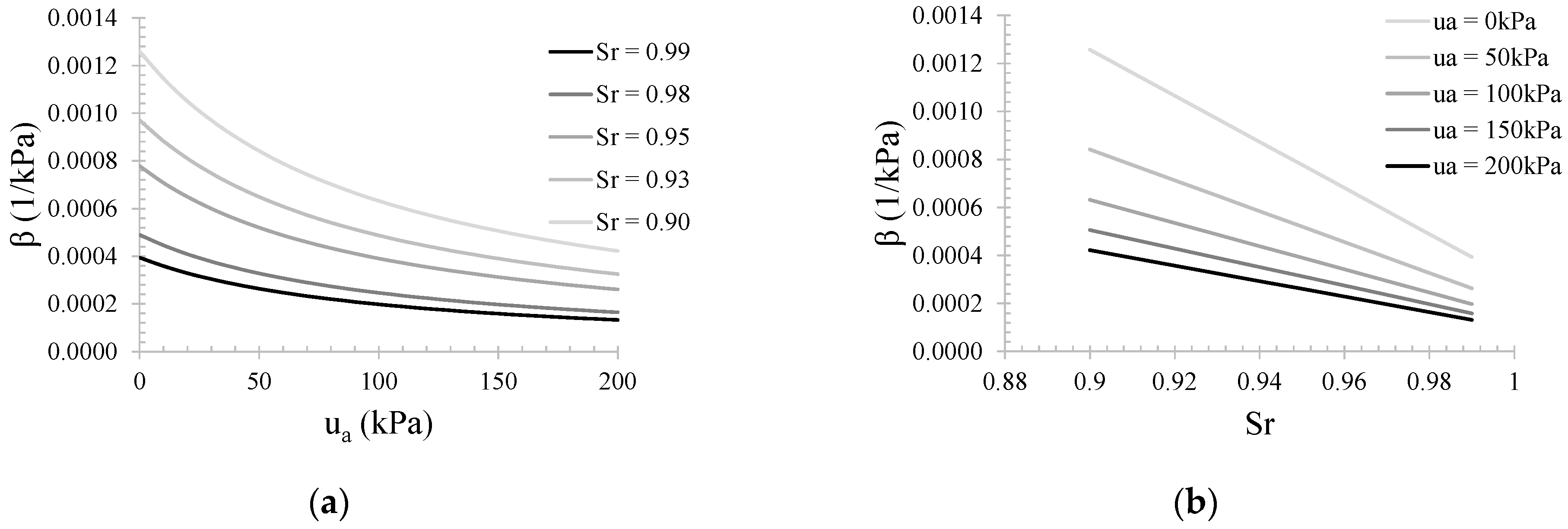
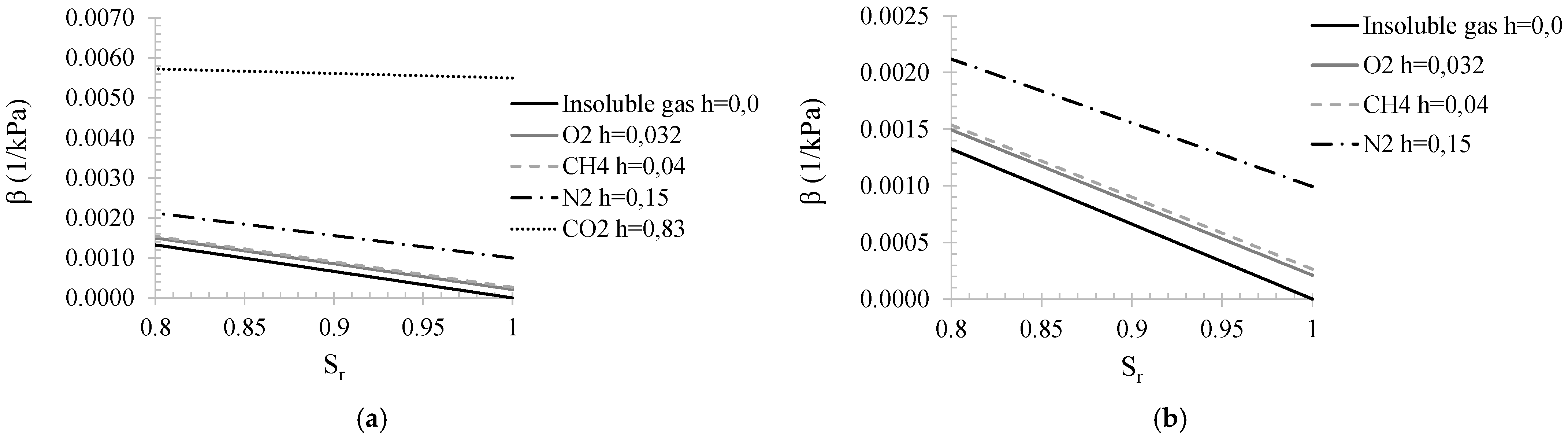
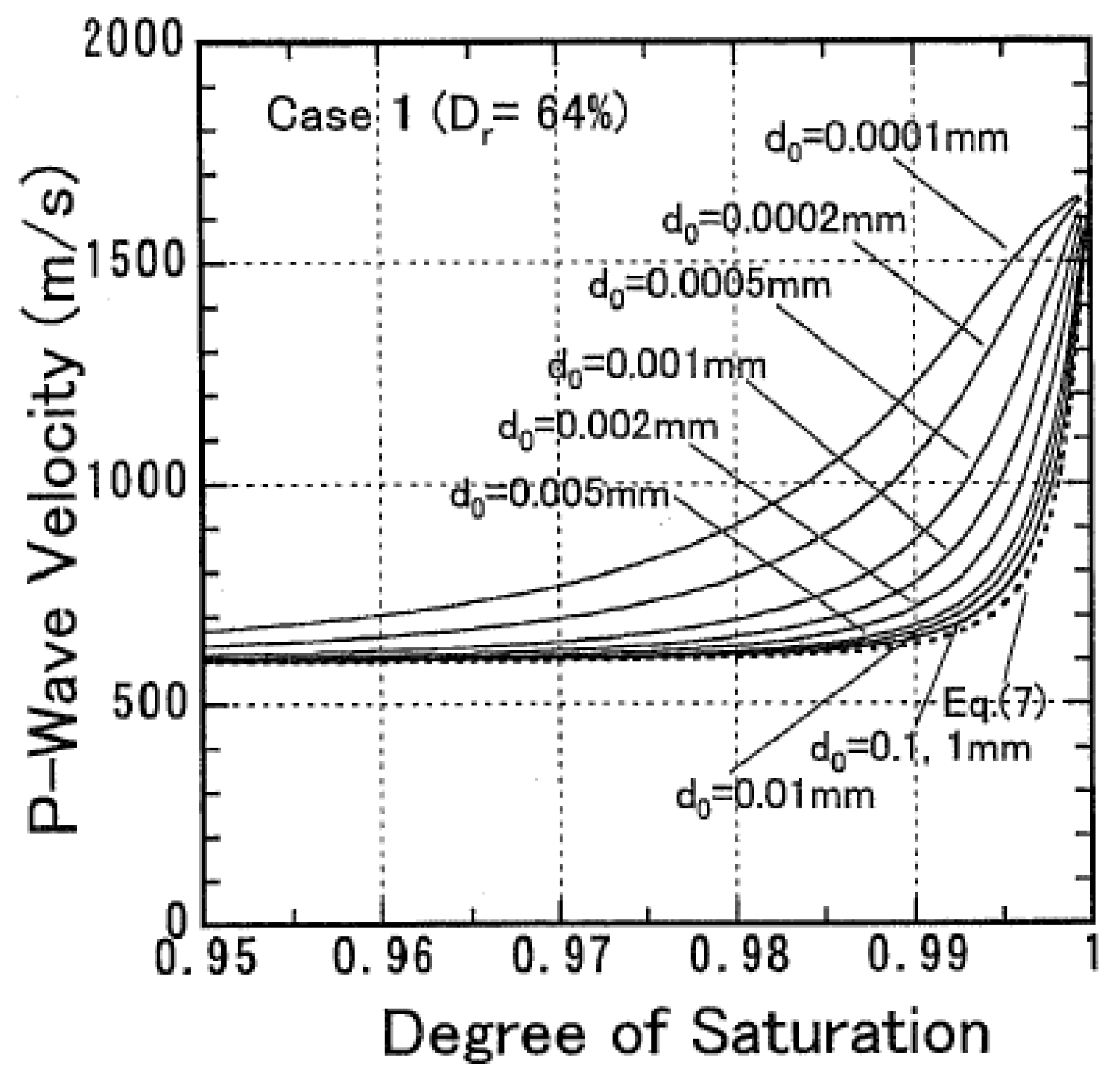
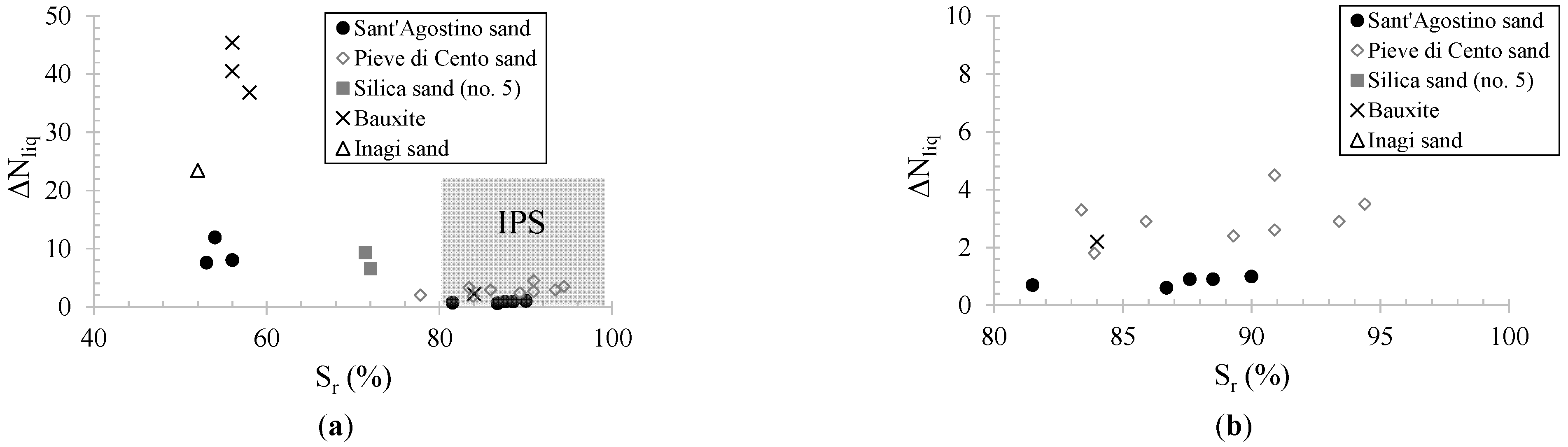
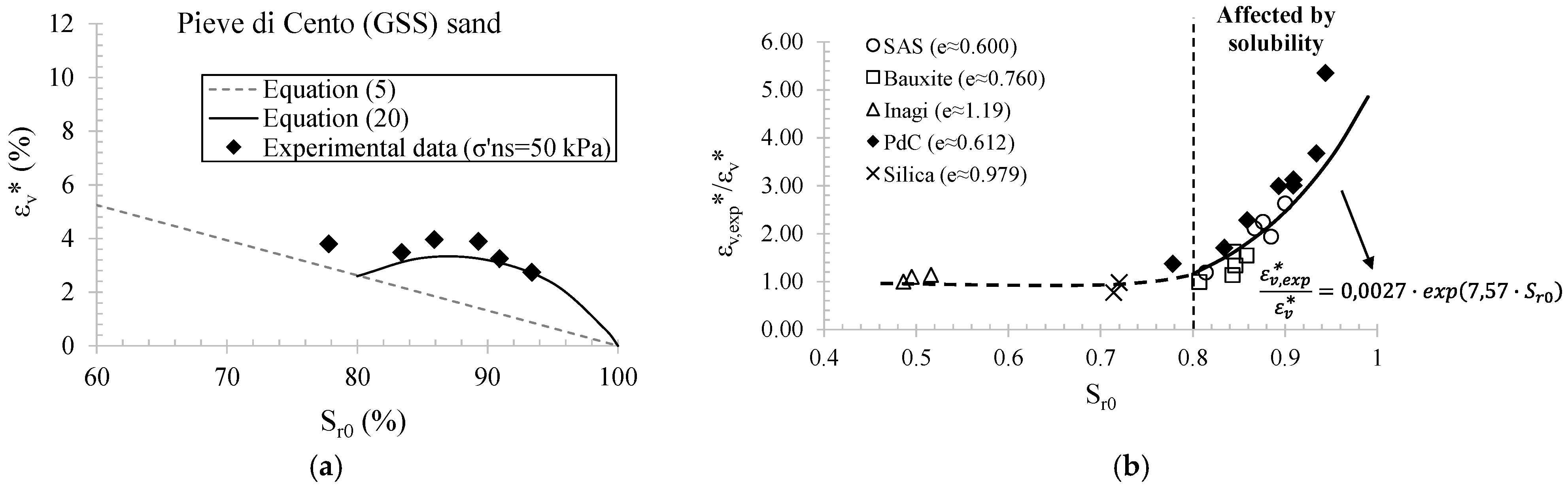
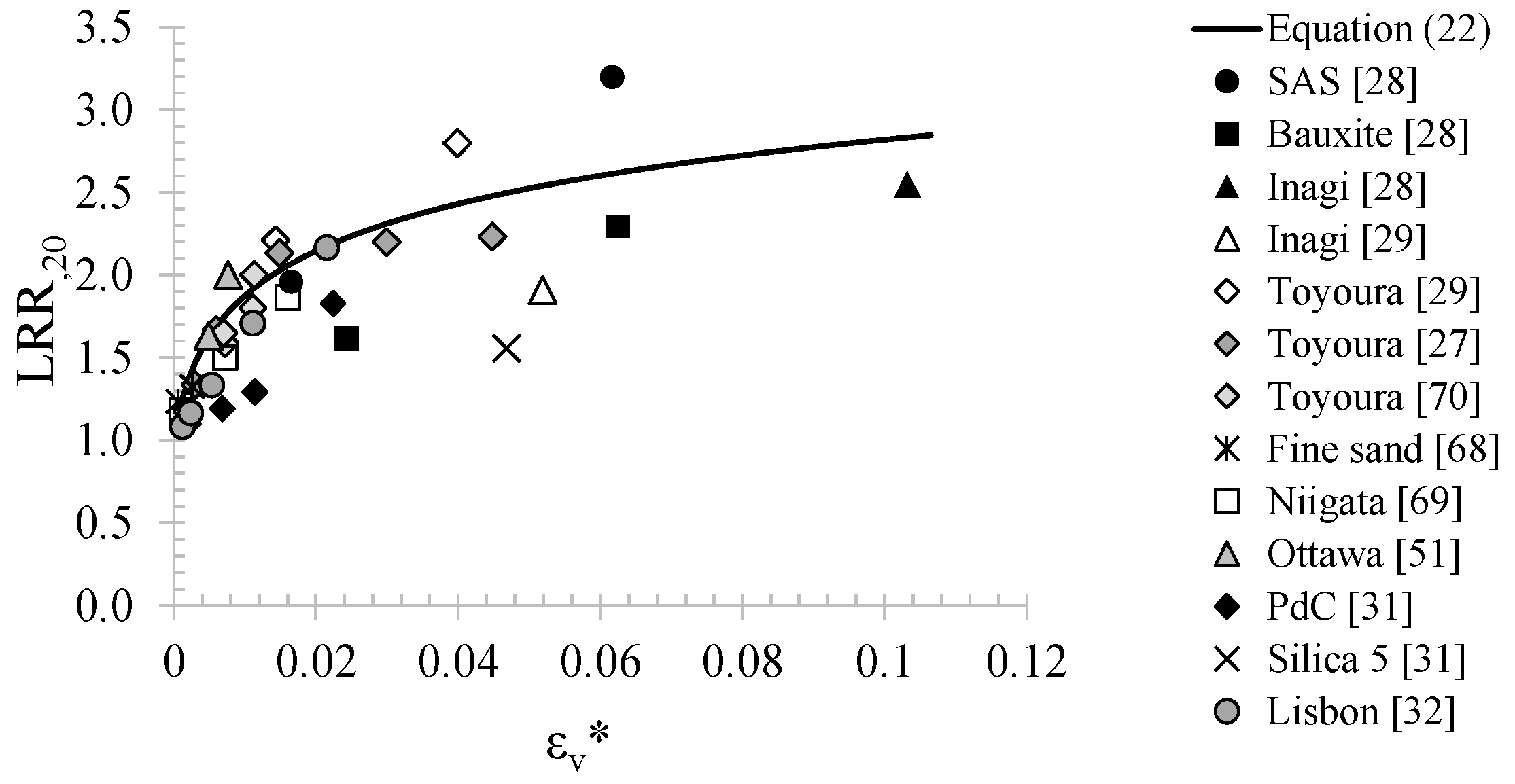
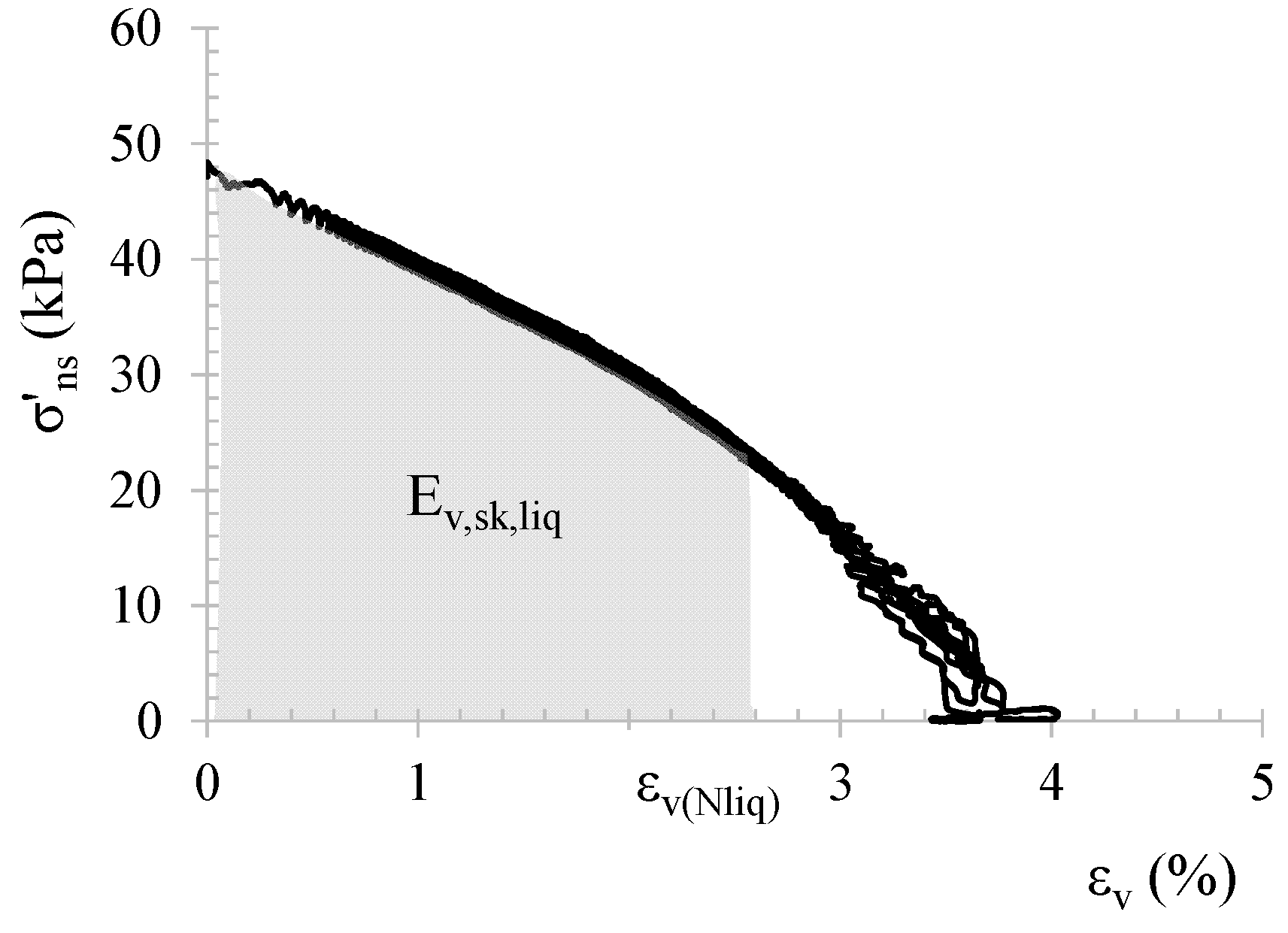
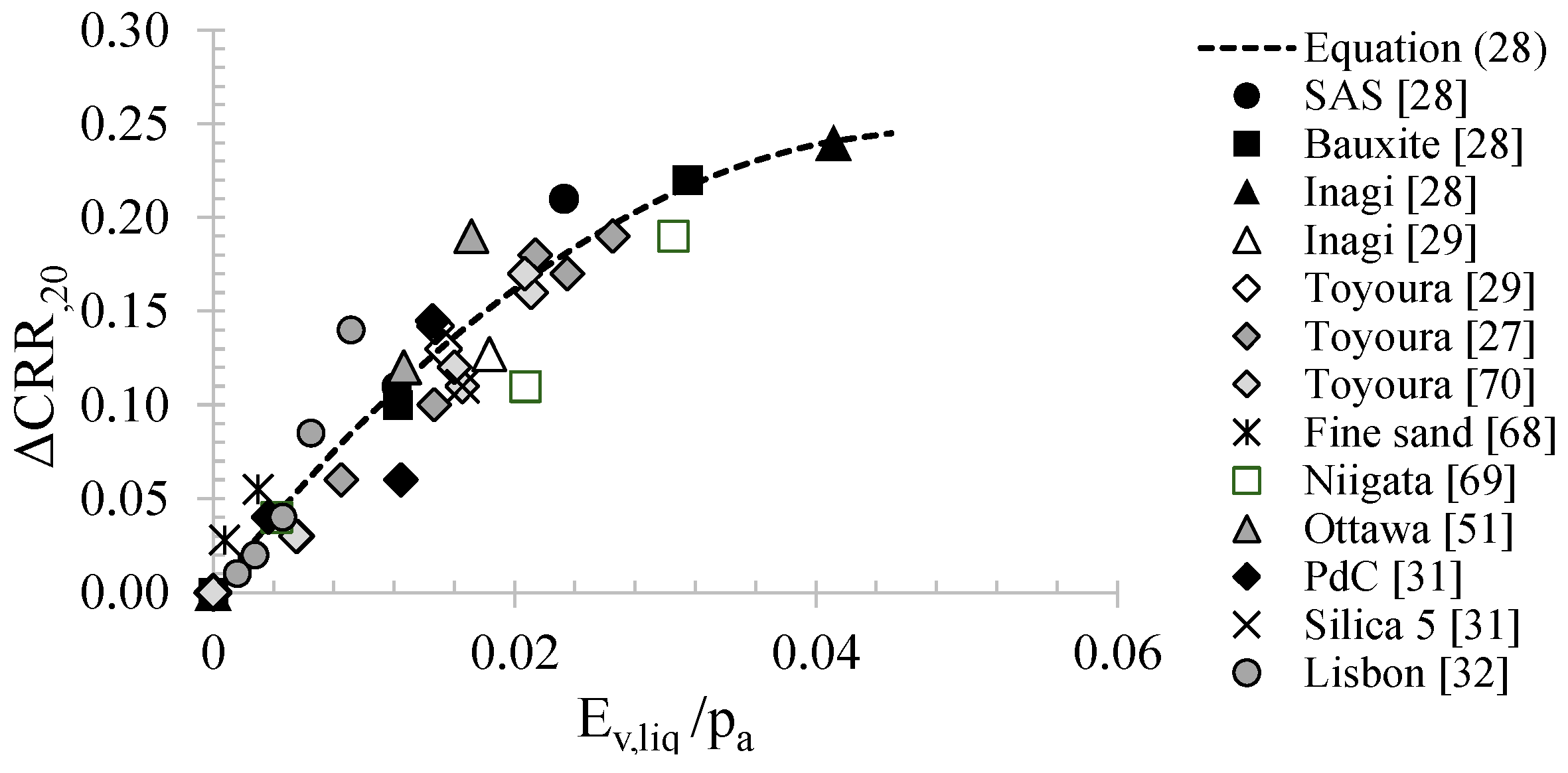
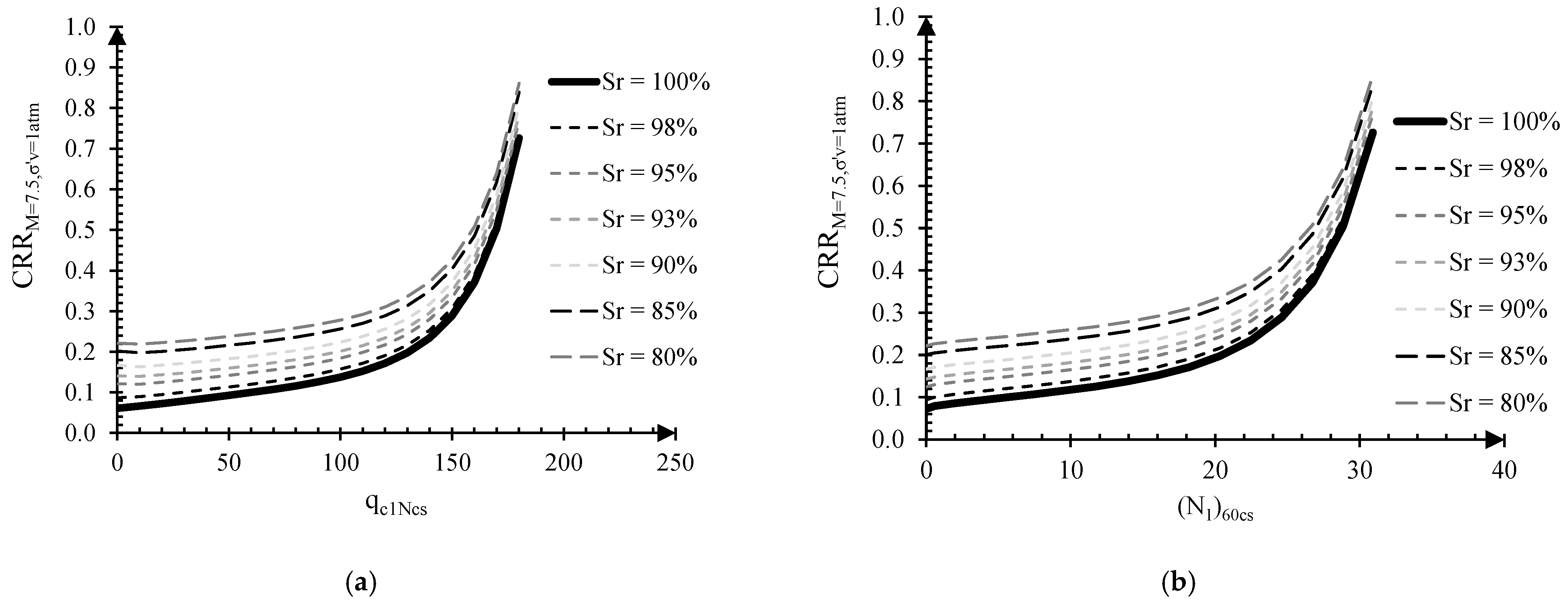
5. Parameters Ruling the Liquefaction Resistance of Partially Saturated Soils
6. IPS: From Small to Large Scale
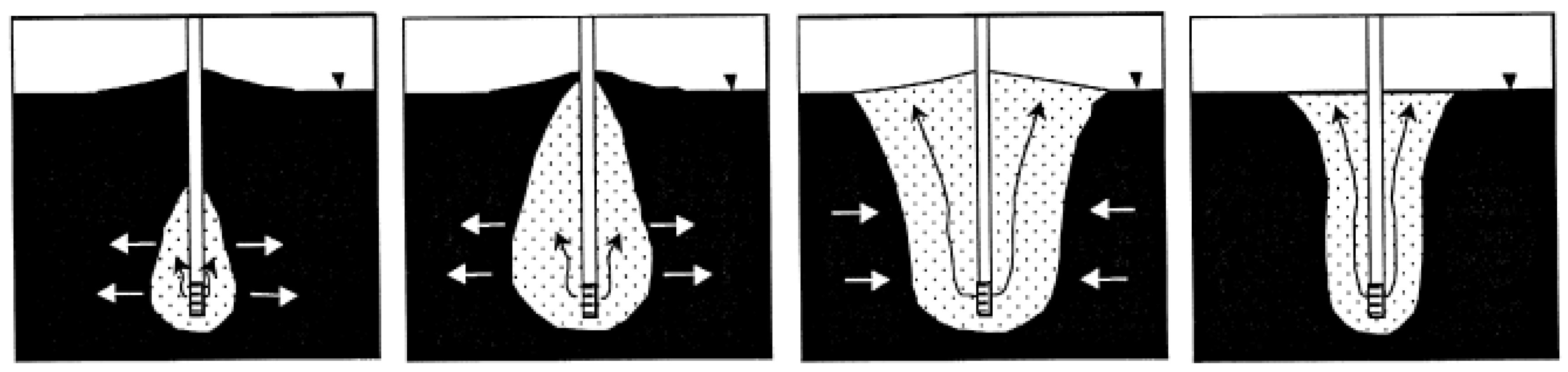
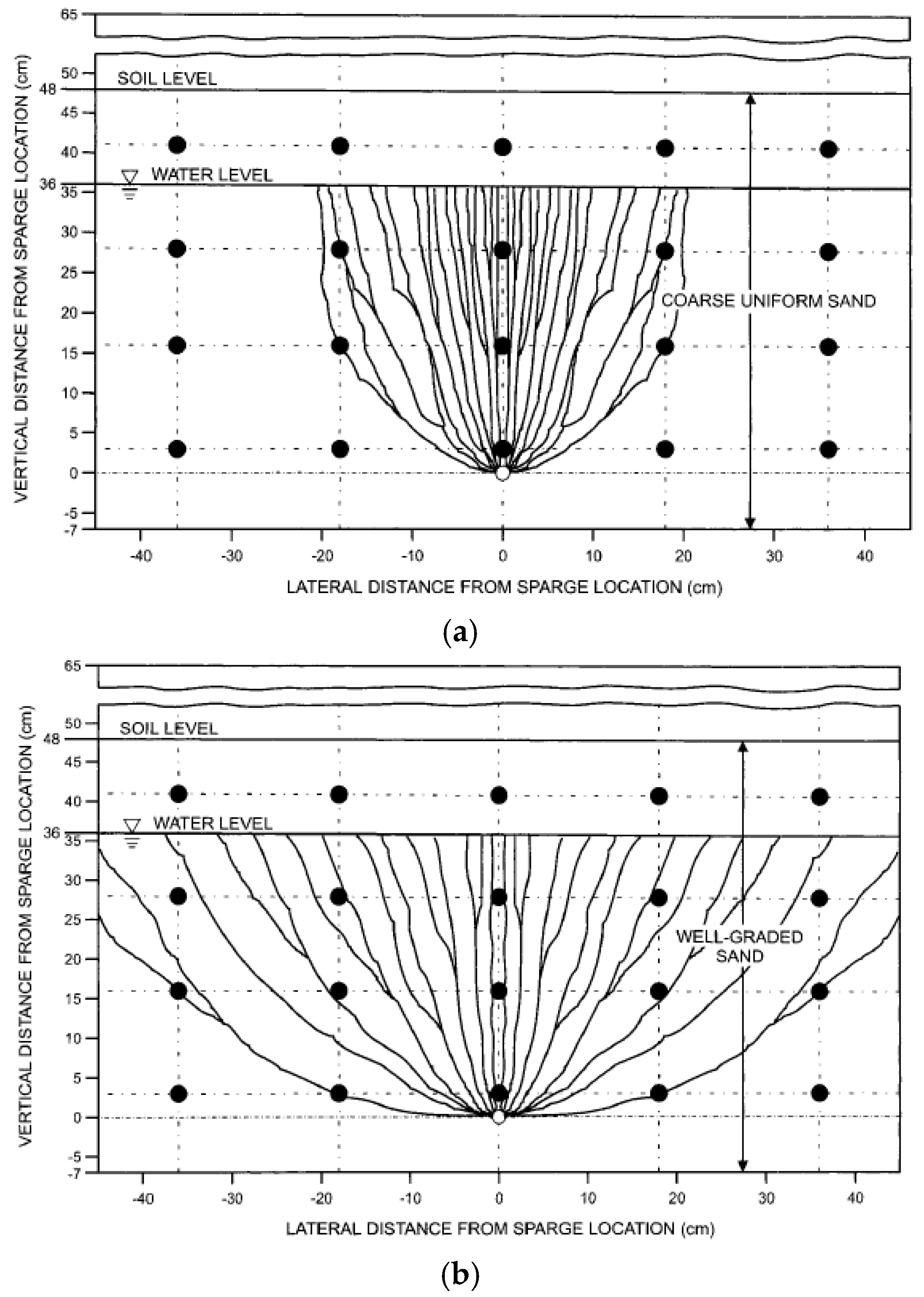
6.1. Desaturation of Soil in Real Scale: Methodologies, Durability and Sr-Monitoring
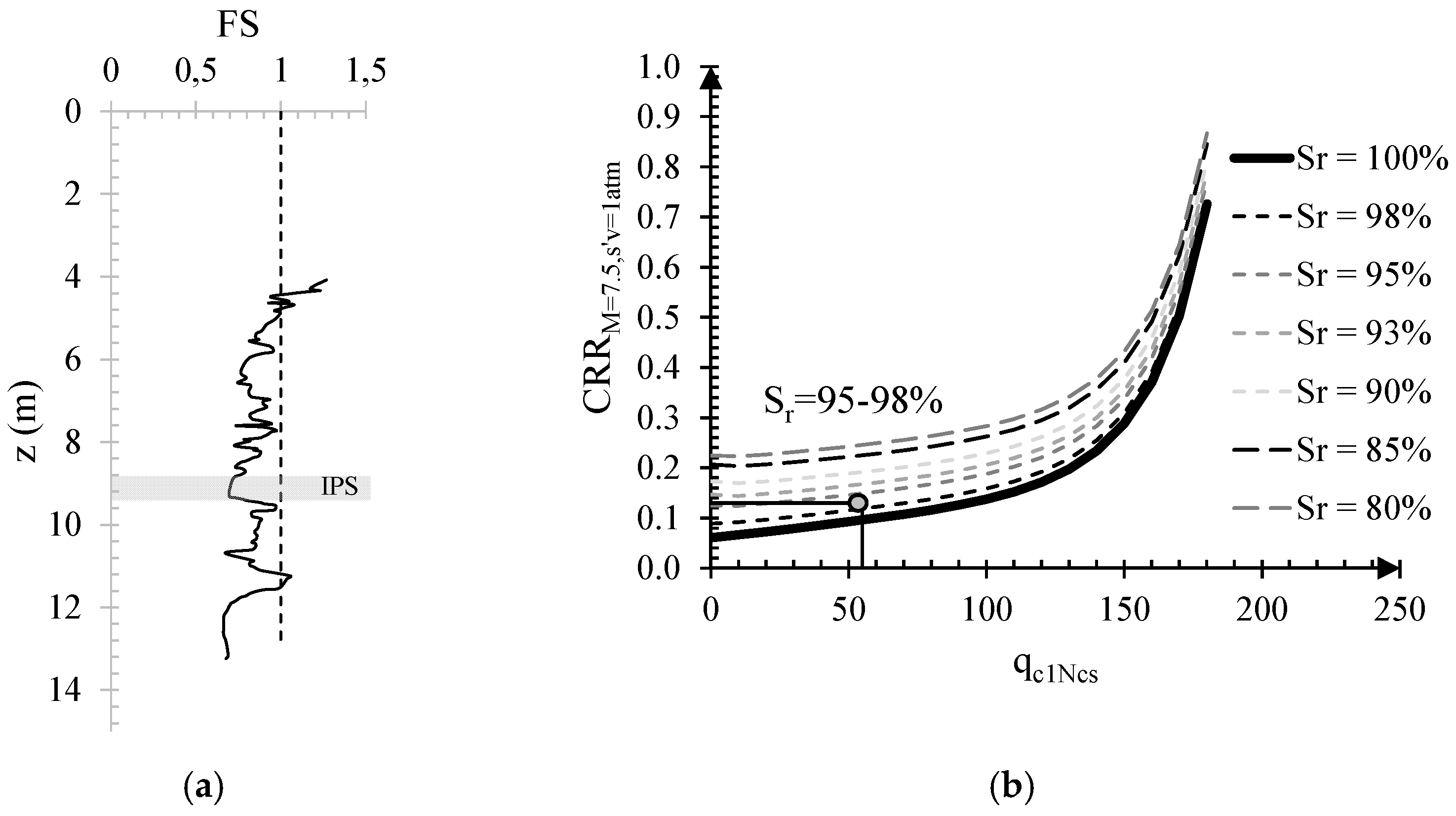
6.2. Effectiveness of IPS and Design Charts
Use of the Proposed Design Charts for IPS Technique
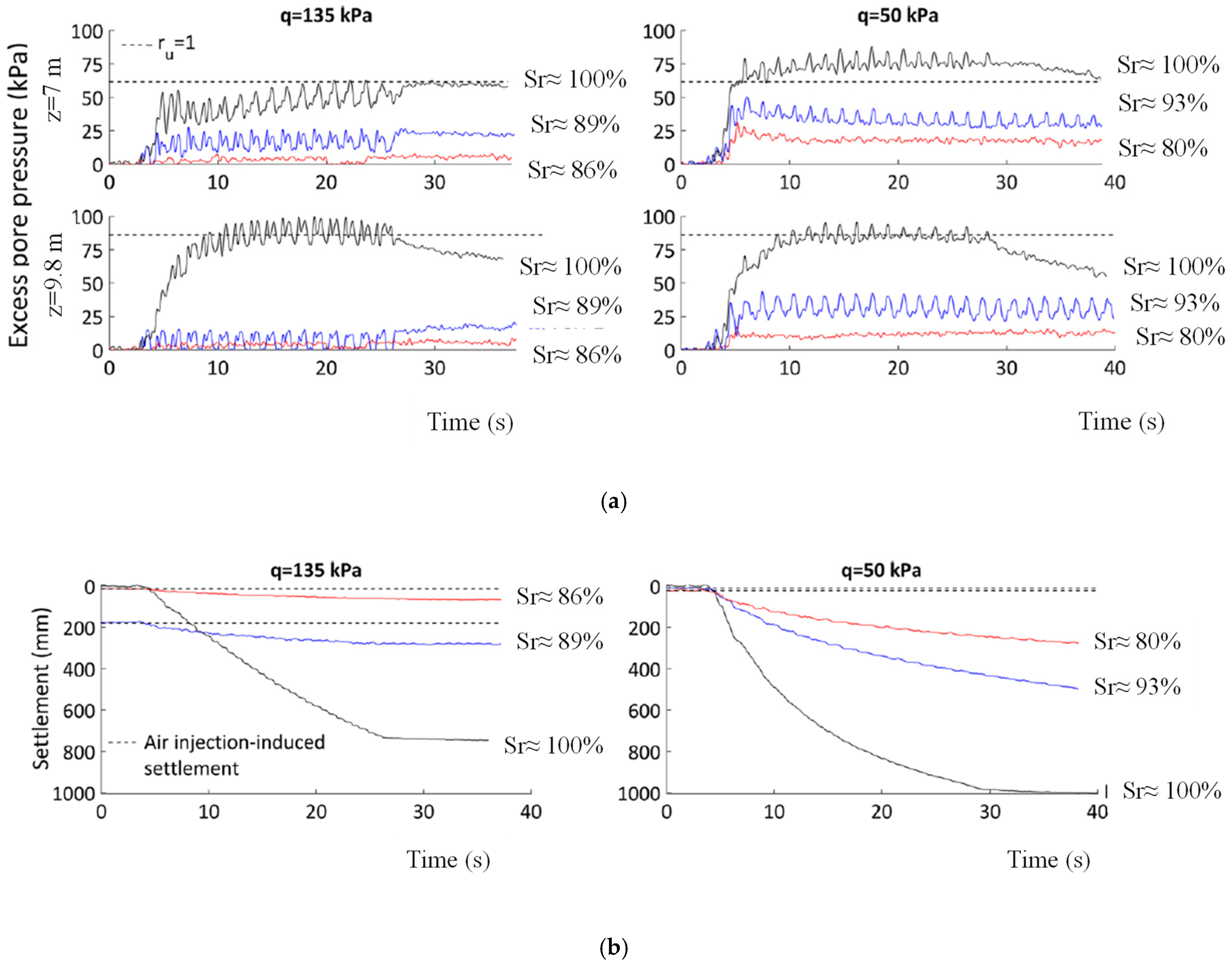
7. Effect of IPS under Shallow Foundations
8. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lirer, S.; Mele, L. On the apparent viscosity of granular soils during liquefaction tests. Bull. Earthq. Eng. 2019, 17, 5809–5824. [Google Scholar] [CrossRef]
- Mele, L. An experimental study on the apparent viscosity of sandy soils: From liquefaction triggering to pseudo-plastic behaviour of liquefied sands. Acta Geotech. 2022, 17, 463–481. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, W.; Yi, R.; Gao, H.; Wang, Z.; Liu, L. A unified thixotropic fluid model considering stage characteristics for soil liquefaction. Acta Geotech. 2023, 18, 5755–5771. [Google Scholar]
- Sharma, M.; Satyam, N.; Reddy, K.R. State of the art review of emerging and biogeotechnical methods for liquefaction mitigation in sands. J. Hazard. Toxic Radioact. Waste 2021, 25, 03120002. [Google Scholar] [CrossRef]
- Karol Reuben, H. Chemical Grouting and Soil Stabilization; American Society of Civil Engineers: Reston, VA, USA, 2003; Volume 536. [Google Scholar]
- Zeybek, A.; Madabhushi, S.P.G. Closure to “Simplified procedure for prediction of earthquake-induced settlements in partially saturated soils” by Abdülhakim Zeybek and Santana Phani Gopal Madabhushi. J. Geotech. Geoenviron. Eng. 2021, 147, 07020027. [Google Scholar] [CrossRef]
- Pham, T.A.; Sutman, M.; Medero, G.M. Validation, Reliability, and Performance of Shear Strength Models for Unsaturated Soils. Geotech. Geol. Eng. 2023, 41, 4271–4309. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some aspects of effective stress in saturated and partly saturated soils. Geotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Santamarina, J.C. Biological considerations in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2005, 131, 1222–1233. [Google Scholar] [CrossRef]
- Houlsby, G.T. The work input to an unsaturated granular material. Géotechnique 1997, 47, 193–196. [Google Scholar] [CrossRef]
- Finno, R.J.; Zhang, Y.; Buscarnera, G. Experimental validation of Terzaghi’s effective stress principle for gassy sand. J. Geotech. Geoenviron. Eng. 2017, 143, 04017092. [Google Scholar] [CrossRef]
- Kohgo, Y.; Asano, I.; Hayashida, Y. An elastoplastic model for unsaturated rockfills and its simulations of laboratory tests. Soils Found. 2007, 47, 919–929. [Google Scholar] [CrossRef]
- Fredlund, D.G. Unsaturated soil mechanics in engineering practice. J. Geotech. Geoenviron. Eng. 2006, 132, 286–321. [Google Scholar] [CrossRef]
- Soltani, A.; Azimi, M.; Boroomandnia, A.; O’Kelly, B.C. An objective framework for determination of the air-entry value from the soil–water characteristic curve. Results Eng. 2021, 12, 100298. [Google Scholar] [CrossRef]
- Bear, J. Hydraulic of Groundwater; McGraw-Hill Series in Water Resource and Environmental Eng; McGraw-Hill: New York, NY, USA, 1979; 567p. [Google Scholar]
- Mousavi, S. Dynamic Performance of Partially Saturated and Unsaturated Soils. Ph.D. Thesis, University of New Hampshire, Durham, NH, USA, 2020. [Google Scholar]
- Grozic, J.L.H.; Nadim, F.; Kvalstad, T.J. On the undrained shear strength of gassy clays. Comput. Geotech. 2005, 32, 483–490. [Google Scholar] [CrossRef]
- Schuurman, I.E. The compressibility of an air/water mixture and a theoretical relation between the air and water pressures. Geotechnique 1966, 16, 269–281. [Google Scholar] [CrossRef]
- Fredlund, D.G. Density and compressibility characteristics of air–water mixtures. Can. Geotech. J. 1976, 13, 386–396. [Google Scholar] [CrossRef]
- Rau, G.; Chaney, R.C. Triaxial testing of marine sediments with high gas contents. In Advanced Triaxial Testing of Soil and Rock; ASTM International: West Conshohocken, PA, USA, 1988; pp. 338–352. [Google Scholar]
- Pietruszczak, S.; Pande, G.N. Constitutive relations for partially saturated soils containing gas inclusions. J. Geotech. Eng. 1996, 122, 50–59. [Google Scholar] [CrossRef]
- Pande, G.N.; Pietruszczak, S. Assessment of risk of liquefaction in granular materials and it’s mitigation. In Proceedings of the International Conference of “International Association for Computer Methods and Advances in Geomechanics (IACMAG)”, Goa, India, 1–6 October 2008. [Google Scholar]
- Jablonská, J. Compressibility of the fluid. In Proceedings of the EPJ Web of Conferences, Paris, France, 7–10 October 2014; EDP Sciences: Les Ulis, France, 2014; Volume 67, p. 02048. [Google Scholar]
- Mihalache, C.; Buscarnera, G. Controllability criteria for soils saturated by a compressible fluid. J. Eng. Mech. 2016, 142, 04016076. [Google Scholar] [CrossRef]
- Seyedi-Viand, S.M.; Eseller-Bayat, E.E. An alternative empirical function to predict air–water mixture bulk modulus for numerical modeling of liquefaction behavior of induced partially saturated sands. Bull. Earthq. Eng. 2021, 19, 1987–2011. [Google Scholar] [CrossRef]
- Mele, L.; Marinelli, F.; Lirer, S.; Flora, A. Model prediction of cyclic liquefaction resistance of gassy soils. Acta Geotechnica 2024, 1–21. [Google Scholar] [CrossRef]
- Okamura, M.; Soga, Y. Effects of pore fluid compressibility on liquefaction resistance of partially saturated sand. Soils Found. 2006, 46, 695–700. [Google Scholar] [CrossRef]
- Mele, L. Experimental and Theoretical Investigation on Cyclic Liquefaction and on the Effects of Some Mitigation Techniques. Ph.D. Thesis, Università degli Studi di Napoli Federico II, Napoli, Italy, 2020. [Google Scholar]
- Wang, H.; Koseki, J.; Sato, T.; Chiaro, G.; Tian, J.T. Effect of saturation on liquefaction resistance of iron ore fines and two sandy soils. Soils Found. 2016, 56, 732–744. [Google Scholar] [CrossRef]
- Eseller-Bayat, E.E.; Gulen, D.B. Undrained dynamic response of partially saturated sands tested in a DSS-C device. J. Geotech. Geoenviron. Eng. 2020, 146, 04020118. [Google Scholar] [CrossRef]
- Mele, L.; Lirer, S.; Flora, A. An energetic interpretation of liquefaction laboratory tests on partially saturated soils. J. Geotech. Geoenviron. Eng. 2022, 148, 04022082. [Google Scholar] [CrossRef]
- Molina-Gómez, F.; da Fonseca, A.V.; Ferreira, C.; Caicedo, B. Improvement of cyclic liquefaction resistance induced by partial saturation: An interpretation using wave-based approaches. Soil Dyn. Earthq. Eng. 2023, 167, 107819. [Google Scholar] [CrossRef]
- Molina-Gómez, F.; da Fonseca, A.V.; Ferreira, C.; Caicedo, B. Experimental Wave-Based Assessment of Liquefaction Resistance for Different Degrees of Saturation. Geotech. Test. J. 2023, 46. [Google Scholar] [CrossRef]
- Baki MA, L.; Cubrinovski, M.; Stringer, M.E.; van Ballegooy, S.; Ntritsos, N. Effects of partial saturation on the liquefaction resistance of sand and silty sand from Christchurch. Soils Found. 2023, 63, 101400. [Google Scholar] [CrossRef]
- Okamura, M.; Teraoka, T. Shaking table tests to investigate soil desaturation as a liquefaction countermeasure. In Proceedings of the Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground, Davis, CA, USA, 16–18 March 2006; pp. 282–293. [Google Scholar]
- He, J.; Chu, J.; Ivanov, V. Mitigation of liquefaction of saturated sand using biogas. In Proceedings of the Bio-and Chemo-Mechanical Processes in Geotechnical Engineering: Géotechnique Symposium in Print 2013, London, UK, 3 June 2013; ICE Publishing: London, UK, 2014; pp. 116–124. [Google Scholar]
- Eseller-Bayat, E.; Yegian, M.K.; Alshawabkeh, A.; Gokyer, S. Liquefaction response of partially saturated sands. I: Experimental results. J. Geotech. Geoenviron. Eng. 2013, 139, 863–871. [Google Scholar] [CrossRef]
- Peng, E.; Hou, Z.; Sheng, Y.; Hu, X.; Zhang, D.; Song, L.; Chou, Y. Anti-liquefaction performance of partially saturated sand induced by biogas under high intensity vibration. J. Clean. Prod. 2021, 319, 128794. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, D.; Ren, H. Evaluation indicators of saturation on partially saturated sand induced by microbial gas. Case Stud. Constr. Mater. 2022, 17, e01641. [Google Scholar] [CrossRef]
- Takemura, J.; Igarashi, R.; Izawa, J.; Okamura, M.; Masuda, M. Centrifuge model tests on soil desaturation as a liquefaction countermeasure. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; IOS Press: Amsterdam, The Netherlands, 2009; Volumes 1–4, pp. 502–505. [Google Scholar]
- Marasini, N.P.; Okamura, M. Air injection to mitigate liquefaction under light structures. Int. J. Phys. Model. Geotech. 2015, 15, 129–140. [Google Scholar]
- Zeybek, A.; Madabhushi, S.P.G. Influence of air injection on the liquefaction-induced deformation mechanisms beneath shallow foundations. Soil Dyn. Earthq. Eng. 2017, 97, 266–276. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, S.P.G. Centrifuge testing to evaluate the liquefaction response of air-injected partially saturated soils beneath shallow foundations. Bull. Earthq. Eng. 2017, 15, 339–356. [Google Scholar] [CrossRef]
- Kumar, R.; Horikoshi, K.; Takahashi, A. Centrifuge testing to investigate effects of partial saturation on the response of shallow foundation in liquefiable ground under strong sequential ground motions. Soil Dyn. Earthq. Eng. 2019, 125, 105728. [Google Scholar] [CrossRef]
- Bao, X.; Jin, Z.; Cui, H.; Chen, X.; Xie, X. Soil liquefaction mitigation in geotechnical engineering: An overview of recently developed methods. Soil Dyn. Earthq. Eng. 2019, 120, 273–291. [Google Scholar] [CrossRef]
- Ogata, H.; Okamura, M. Experimental study on air behaviour in saturated soil under air injection. In Proceedings of the Symposium on Natural Disaster Prevention, JSCE, Tokushima, Japan, 30–31 October 2006; pp. 89–90. [Google Scholar]
- Sills, G.C.; Gonzalez, R. Consolidation of naturally gassy soft soil. Geotechnique 2001, 51, 629–639. [Google Scholar] [CrossRef]
- Rebata-Landa, V.; Santamarina, J.C. Mechanical effects of biogenic nitrogen gas bubbles in soils. J. Geotech. Geoenviron. Eng. 2012, 138, 128–137. [Google Scholar] [CrossRef]
- He, J.; Chu, J.; Wu, S.F.; Peng, J. Mitigation of soil liquefaction using microbially induced desaturation. J. Zhejiang Univ.-Sci. A 2016, 17, 577–588. [Google Scholar] [CrossRef]
- He, J.; Chu, J.; Liu, H. Undrained shear strength of desaturated loose sand under monotonic shearing. Soils Found. 2014, 54, 910–916. [Google Scholar] [CrossRef]
- Wang, K.; Chu, J.; Wu, S.; He, J. Stress–strain behaviour of bio-desaturated sand under undrained monotonic and cyclic loading. Géotechnique 2021, 71, 521–533. [Google Scholar] [CrossRef]
- O’Donnell, S.T.; Rittmann, B.E.; Kavazanjian, E., Jr. MIDP: Liquefaction mitigation via microbial denitrification as a two-stage process. I: Desaturation. J. Geotech. Geoenviron. Eng. 2017, 143, 04017094. [Google Scholar] [CrossRef]
- Mousavi, S.; Ghayoomi, M. Liquefaction mitigation of sands with non-plastic fines via microbial-induced partial saturation. J. Geotech. Geoenviron. Eng. 2021, 147, 04020156. [Google Scholar] [CrossRef]
- Yegian, M.K.; Eseller-Bayat, E.; Alshawabkeh, A.; Ali, S. Induced-Partial Saturation for liquefaction mitigation: Experimental investigation. J. Geotech. Geoenviron. Eng. ASCE 2007, 133, 372–380. [Google Scholar] [CrossRef]
- Zeybek, A. Shaking table tests on seismic performance of shallow foundations resting on partially saturated sands. Arab. J. Geosci. 2022, 15, 774. [Google Scholar] [CrossRef]
- Amini, P.F.; Yang, J. Liquefaction susceptibility of clayey sands under saturated and partially saturated conditions. Géotechnique 2023, 1–39. [Google Scholar] [CrossRef]
- Vega-Posada, C.A.; Finno, R.J.; Zapata-Medina, D.G. Effect of gas on the mechanical behavior of medium-dense sands. J. Geotech. Geoenviron. Eng. 2014, 140, 04014063. [Google Scholar] [CrossRef]
- Skempton, A.W. The pore-pressure coefficients A and B. Geotechnique 1954, 4, 143–147. [Google Scholar] [CrossRef]
- Yang, J. Liquefaction resistance of sand in relation to P-wave velocity. Geotechnique 2002, 52, 295–298. [Google Scholar] [CrossRef]
- Astuto, G.; Molina-Gomez, F.; Bilotta, E.; Viana da Fonseca, A.; Flora, A. Some remarks on the assessment of P-wave velocity in laboratory tests for evaluating the degree of saturation. Acta Geotech. 2023, 18, 777–790. [Google Scholar] [CrossRef]
- Yang, J.; Sato, T. Interpretation of seismic vertical amplification observed at an array site. Bull. Seism. Soc. Am. 2000, 90, 275–285. [Google Scholar] [CrossRef]
- Flora, A.; Chiaradonna, A.; Bilotta, E.; Fasano, G.; Mele, L.; Lirer, S.; Pingue, L.; Fanti, F. Field tests to assess the effectiveness of ground improvement for liquefaction mitigation. In Earthquake Geotechnical Engineering for Protection and Development of Environment and Constructions; CRC Press: Boca Raton, FL, USA, 2019; pp. 740–752. [Google Scholar]
- Guo, Y.; Yang, J. Use of shear wave velocity to evaluate in-situ state of silty sands. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–21 September 2017; Volume TC102, pp. 603–606. [Google Scholar]
- Tamura, S.; Tokimatsu, K.; Abe, A.; Sato, M. Effects of air bubbles on B-value and P-wave velocity of a partly saturated sand. Soils Found. 2002, 42, 121–129. [Google Scholar] [CrossRef]
- Sherif, M.A.; Tsuchiya, C.; Ishibashi, I. Saturation effects on initial soil liquefaction. J. Geotech. Eng. Div. 1977, 103, 914–917. [Google Scholar] [CrossRef]
- Chaney, R. Saturation effects on the cyclic strength of sands. In Proceedings of the ASCE Special Conference on Earthquake Engineering and Soil Dynamics, New York, NY, USA, 19–21 June 1978; pp. 342–358. [Google Scholar]
- Yoshimi, Y.; Tanaka, K.; Tokimatsu, K. Liquefaction resistance of a partially saturated sand. Soils Found. 1989, 29, 157–162. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Hu, T. Effects of saturation and back pressure on sand liquefaction. J. Geotech. Eng. 1991, 117, 1347–1362. [Google Scholar] [CrossRef]
- Ishihara, K.; Tsuchiya, H.; Huang, H.; Kamada, K. Recent studies on liquefaction resistance of sand-effect of saturation. In Proceedings of the 4th International Conference on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics, San Diego, CA, USA, 26–31 March 2001. [Google Scholar]
- Ishihara, K.; Tsukamoto, Y.; Kamada, K. Undrained behavior of near-saturated sand in cyclic and monotonic loading. In Proceedings of the Cyclic Behavior of Soils and Liquefaction Phenomena, Bochum, Germany, 31 March–2 April 2004; pp. 27–39. [Google Scholar]
- Cordeiro, D.; Molina-Gomez, F.; Ferreira, C.; Rios, S.; Viana da Fonseca, A. Cyclic liquefaction resistance of an alluvial natural sand: A comparison between fully and partially saturated conditions. Geotechnics 2002, 2, 1–13. [Google Scholar] [CrossRef]
- Wu, J.; Kammerer, A.M.; Riemer, M.F.; Seed, R.B.; Pestana, J.M. Laboratory study of liquefaction triggering criteria. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper (No. 2580). [Google Scholar]
- Mele, L.; Lirer, S.; Flora, A. Liquefaction triggering of non-saturated sandy soils. Géotechnique Lett. 2023, 13, 35–40. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, E.; Wang, Z.; Wang, B.; Li, X. Experimental study on fluid characteristics of medium dense saturated fine sand in pre- and post-liquefaction. Bull. Earthq. Engng. 2016, 14, 2185–2212. [Google Scholar]
- Unno, T.; Kazama, M.; Uzuoka, R.; Sento, N. Liquefaction of unsaturated sand considering the pore air pressure and volume compressibility of the soil particle skeleton. Soils Found. 2008, 48, 87–99. [Google Scholar] [CrossRef]
- Arab, A.; Shahrour, I.; Lancelot, L. A laboratory study of liquefaction of partially saturated sand. J. Iber. Geol. 2011, 37, 29–36. [Google Scholar]
- Huang, Y.; Tsuchiya, H.; Ishihara, K. Estimation of partial saturation effect on liquefaction resistance of sand using P-wave velocity. In Proceedings of the Symposium on Liquefaction Mechanism Prediction and Design Method; 1999; Volume 113, pp. 431–434. [Google Scholar]
- Tsukamoto, Y.; Ishihara, K.; Nakazawa, H.; Kamada, K.; Huang, Y. Resistance of partly saturated sand to liquefaction with reference to longitudinal and shear wave velocities. Soils Found. 2002, 42, 93–104. [Google Scholar] [CrossRef]
- Yang, J.; Savidis, S.; Roemer, M. Evaluating liquefaction strength of partially saturated sand. J. Geotech. Geoenviron. Eng. 2004, 130, 975–979. [Google Scholar] [CrossRef]
- Mele, L.; Flora, A. On the prediction of liquefaction resistance of unsaturated sands. Soil Dyn. Earthq. Eng. 2019, 125, 105689. [Google Scholar] [CrossRef]
- Moug, D.M.; Sorenson, K.R.; Khosravifar, A.; Preciado, M.; Young, E.S.; van Paassen, L.; Kavazanjian, E.; Zhang, B.; Stokoe, K.H.; Menq, F.M.; et al. Field trials of microbially induced desaturation in low-plasticity silt. J. Geotech. Geoenviron. Eng. 2022, 148, 05022005. [Google Scholar] [CrossRef]
- Sorenson, K.; Preciado, A.M.; Moug, D.; Khosravifar, A.; van Paassen, L.; Kavazanjian, E.; Stokoe, K.; Menq, F. Field monitoring of the persistence of microbially induced desaturation for mitigation of earthquake induced soil liquefaction in silty soil. In Proceedings of the ASCE Lifelines Conference, Reston, VA, USA, 1–3 February 2021; ASCE: Reston, VA, USA, 2021. [Google Scholar]
- Hu, L.; Wu, X.; Liu, Y.; Meegoda, J.N.; Gao, S. Physical modeling of air flow during air sparging remediation. Environ. Sci. Technol. 2010, 44, 3883–3888. [Google Scholar] [CrossRef]
- Thomson, N.R.; Johnson, R.L. Air distribution during in situ air sparging: An overview of mathematical modeling. J. Hazard. Mater. 2000, 72, 265–282. [Google Scholar] [CrossRef]
- Reddy, K.R.; Adams, J.A. Effects of soil heterogeneity on airflow patterns and hydrocarbon removal during in situ air sparging. J. Geotech. Geoenviron. Eng. 2001, 127, 234–247. [Google Scholar] [CrossRef]
- Marulanda, C.; Culligan, P.J.; Germaine, J.T. Centrifuge modeling of air sparging—A study of air flow through saturated porous media. J. Hazard. Mater. 2000, 72, 179–215. [Google Scholar] [CrossRef] [PubMed]
- Okamura, M.; Takebayashi, M.; Nishida, K.; Fujii, N.; Jinguji, M.; Imasato, T.; Yasuhara, H.; Nakagawa, E. In-situ desaturation test by air injection and its evaluation through field monitoring and multiphase flow simulation. J. Geotech. Geoenviron. Eng. 2011, 137, 643–652. [Google Scholar] [CrossRef]
- Flora, A.; Bilotta, E.; Chiaradonna, A.; Lirer, S.; Mele, L.; Pingue, L. A field trial to test the efficiency of induced partial saturation and horizontal drains to mitigate the susceptibility of soils to liquefaction. Bull. Earthq. Eng. 2021, 19, 3835–3864. [Google Scholar] [CrossRef]
- Okamura, M.; Ishihara, M.; Tamura, K. Degree of saturation and liquefaction resistances of sand improved with sand compaction pile. J. Geotech. Geoenviron. Eng. 2006, 132, 258–264. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, G.S.P. Durability of partial saturation to counteract liquefaction. Proc. Inst. Civ. Eng.-Ground Improv. 2017, 170, 102–111. [Google Scholar] [CrossRef]
- Fioravante, V.; Giretti, D.; Abate, G.; Aversa, S.; Boldini, D.; Capilleri, P.P.; Cavallaro, A.; Chamlagain, D.; Crespellani, T.; Dezi, F.; et al. Earthquake geotechnical engineering aspects of the 2012 Emilia-Romagna earthquake (Italy). In Proceedings of the 7th International Conference on Case Histories in Geotechnical Engineering, Chicago, IL, USA, 29 April 29–4 May 2013. [Google Scholar]
- Lai, C.G.; Bozzoni, F.; Mangriotis, M.D.; Martinelli, M. Soil liquefaction during the 20 May 2012 M5. 9 Emilia earthquake, Northern Italy: Field reconnaissance and post-event assessment. Earthq. Spectra 2015, 31, 2351–2373. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I.M. CPT and SPT Liquefaction Triggering Procedures; Report No UCD/GCM-14/01; University of California at Davis: Davis, CA, USA, 2014. [Google Scholar]
- Hanks, T.C.; Brady, A.G. The Loma Prieta earthquake, ground motion, and damage in Oakland, Treasure Island, and San Francisco. Bull. Seism. Soc. Am. 1991, 81, 2019–2047. [Google Scholar] [CrossRef]
- Chiaradonna, A.; d’Onofrio, A.; Bilotta, E. Assessment of post-liquefaction consolidation settlement. Bull. Earthq. Eng. 2019, 17, 5825–5848. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rodríguez-Pérez, Á.M.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. A finite element method integrated with Terzaghi’s principle to estimate settlement of a building due to tunnel construction. Buildings 2023, 13, 1343. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rodríguez Pérez, Á.M.; López, R.; Caparrós Mancera, J.J. Comparative analysis and evaluation of seismic response in structures: Perspectives from non-linear dynamic analysis to pushover analysis. Appl. Sci. 2024, 14, 2504. [Google Scholar] [CrossRef]
- Zeybek, A.; Madabhushi, S.P.G. Simplified procedure for prediction of earthquake-induced settlements in partially saturated soils. J. Geotech. Geoenviron. Eng. 2019, 145, 04019100. [Google Scholar] [CrossRef]
- Ishihara, K.; Yoshimine, M. Evaluation of settlements in sand deposits following liquefaction during earthquakes. Soils Found. 1992, 32, 173–188. [Google Scholar] [CrossRef]






| Type of Deformation | Mechanisms of Deformation | |
|---|---|---|
| During Air Injection | During and after Seismic Event | |
| Volumetric | Positive volumetric strains due to the decrease in effective stress induced by upward flow and due to the increase in the compressibility of soil matrix; | Positive volumetric strains due to the increase in the compressibility of soil matrix; |
| Negative volumetric strains (expansion) due to the coagulation of air bubbles and upward air escape. | Limited volumetric strains due to the re-consolidation during the dissipation of excess pore pressures. | |
| Deviatoric | Localised and partial bearing failure due to strength loss in the foundation soil during upward flow. | Limited bearing capacity failure; |
| Limited cumulative foundation settlements due to shear deformation. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mele, L.; Lirer, S.; Flora, A. Induced Partial Saturation: From Mechanical Principles to Engineering Design of an Innovative and Eco-Friendly Countermeasure against Earthquake-Induced Soil Liquefaction. Geosciences 2024, 14, 140. https://doi.org/10.3390/geosciences14060140
Mele L, Lirer S, Flora A. Induced Partial Saturation: From Mechanical Principles to Engineering Design of an Innovative and Eco-Friendly Countermeasure against Earthquake-Induced Soil Liquefaction. Geosciences. 2024; 14(6):140. https://doi.org/10.3390/geosciences14060140
Chicago/Turabian StyleMele, Lucia, Stefania Lirer, and Alessandro Flora. 2024. "Induced Partial Saturation: From Mechanical Principles to Engineering Design of an Innovative and Eco-Friendly Countermeasure against Earthquake-Induced Soil Liquefaction" Geosciences 14, no. 6: 140. https://doi.org/10.3390/geosciences14060140
APA StyleMele, L., Lirer, S., & Flora, A. (2024). Induced Partial Saturation: From Mechanical Principles to Engineering Design of an Innovative and Eco-Friendly Countermeasure against Earthquake-Induced Soil Liquefaction. Geosciences, 14(6), 140. https://doi.org/10.3390/geosciences14060140







