The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area Description
2.2. Local Factor of Safety
2.3. Coupled Hydro-Mechanical Framework
2.4. Establishment of Conceptual Models
3. Results and Discussions
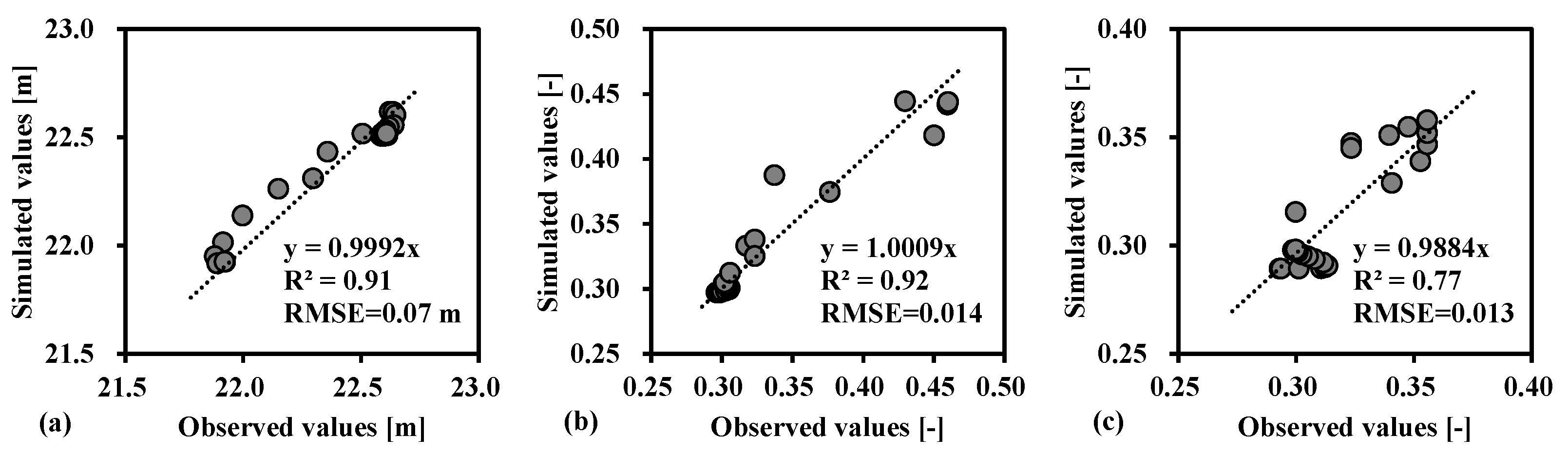
3.1. Model Calibration Analysis
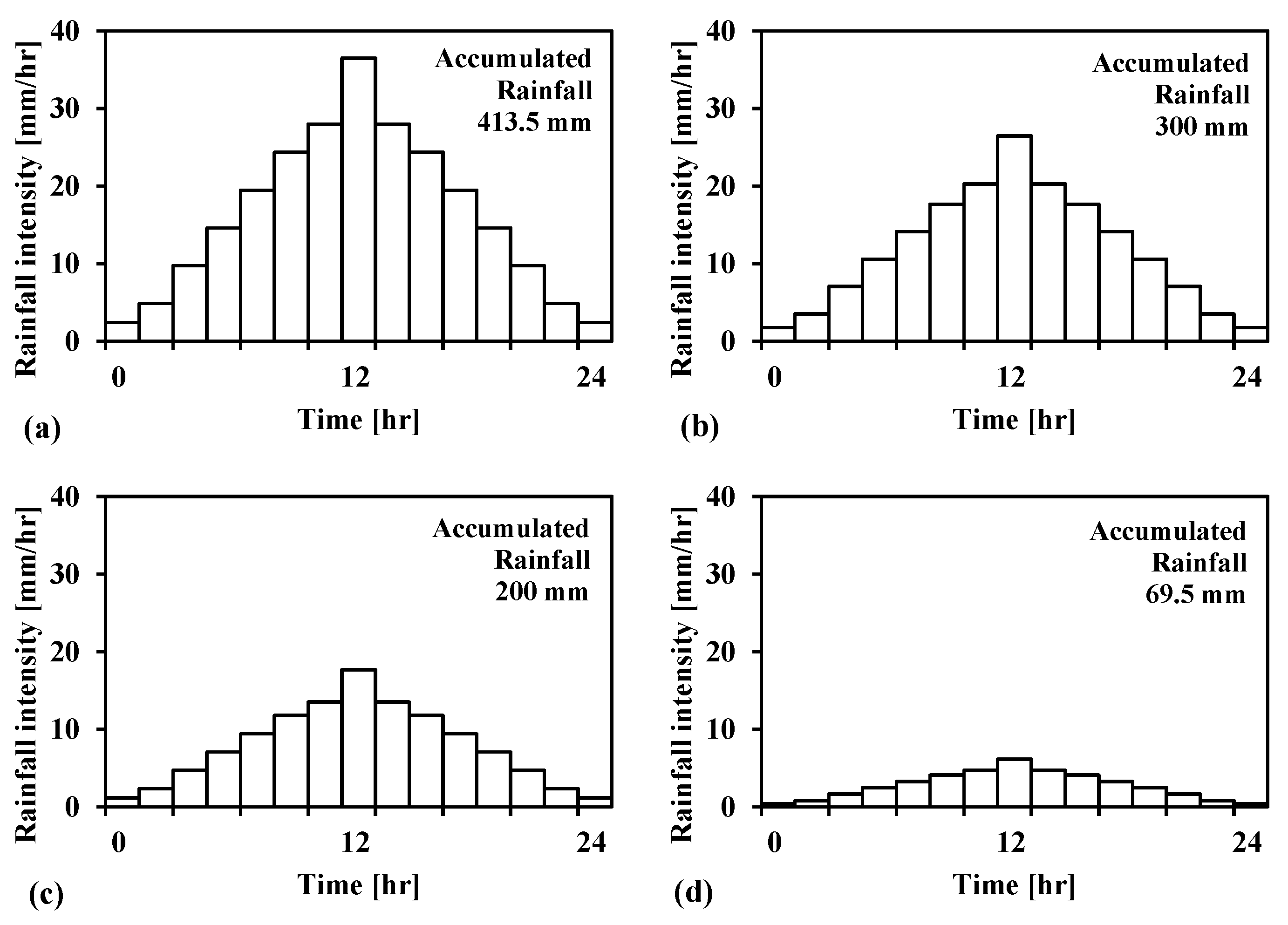
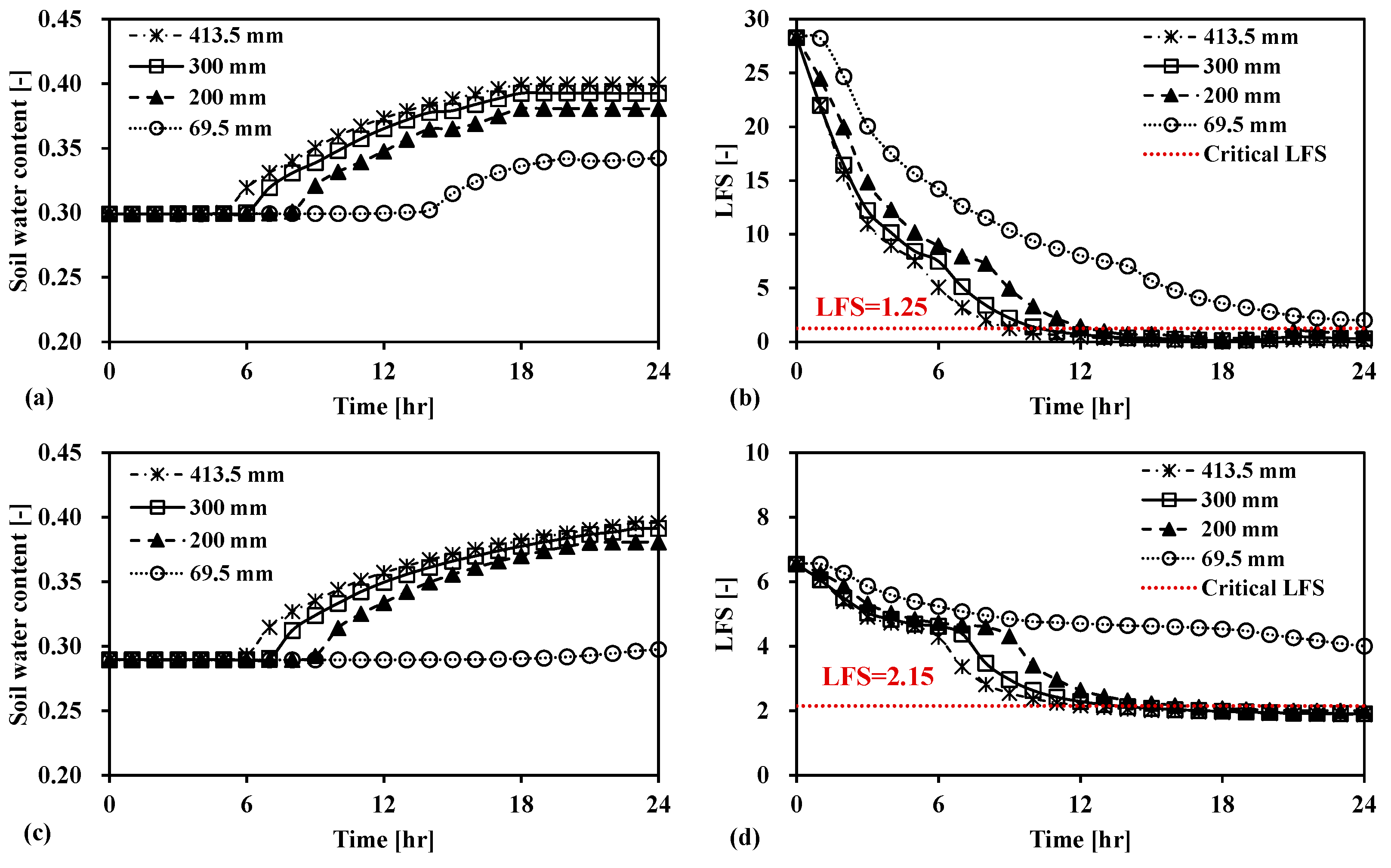
3.2. Stability Analysis and Simulation of Rainfall Scenarios
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- von Ruette, J.; Lehmann, P.; Or, D. Rainfall-triggered shallow landslides at catchment scale: Threshold mechanics-based modeling for abruptness and localization. Water Resour. Res. 2013, 49, 6266–6285. [Google Scholar] [CrossRef]
- Emberson, R.; Kirschbaum, D.B.; Amatya, P.; Tanyas, H.; Marc, O. Insights from the topographic characteristics of a large global catalog of rainfall-induced landslide event inventories. Nat. Hazards Earth Syst. Sci. 2022, 22, 1129–1149. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wiley Interdiscip. Rev. Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Fan, L.; Lehmann, P.; Or, D. Effects of hydromechanical loading history and antecedent soil mechanical damage on shallow landslide triggering. J. Geophys. Res. Earth Surf. 2015, 120, 1990–2015. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44, W11404. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Ivanov, V.; Arosio, D.; Tresoldi, G.; Hojat, A.; Zanzi, L.; Papini, M.; Longoni, L. Investigation on the role of water for the stability of shallow landslides—Insights from experimental tests. Water 2020, 12, 1203. [Google Scholar] [CrossRef]
- Fusco, F.; Bordoni, M.; Tufano, R.; Vivaldi, V.; Meisina, C.; Valentino, R.; Bittelli, M.; De Vita, P. Hydrological regimes in different slope environments and implications on rainfall thresholds triggering shallow landslides. Nat. Hazards 2022, 114, 907–939. [Google Scholar] [CrossRef]
- Cai, J.-S.; Yeh, T.-C.J.; Yan, E.-C.; Tang, R.-X.; Hao, Y.-H.; Huang, S.-Y.; Wen, J.-C. Importance of variability in initial soil moisture and rainfalls on slope stability. J. Hydrol. 2019, 571, 265–278. [Google Scholar] [CrossRef]
- Amarasinghe, M.P.; Kulathilaka, S.A.S.; Robert, D.J.; Zhou, A.; Jayathissa, H.A.G. Risk assessment and management of rainfall-induced landslides in tropical regions: A review. Nat. Hazards 2024, 120, 2179–2231. [Google Scholar] [CrossRef]
- Sultana, N.; Tan, S. Landslide mitigation strategies in southeast Bangladesh: Lessons learned from the institutional responses. Int. J. Disaster Risk Reduct. 2021, 62, 102402. [Google Scholar] [CrossRef]
- Kadamb, R.R.; Savoikar, P.P. Rainfall Induced Landslides—A Review, in Recent Developments in Sustainable Infrastructure (ICRDSI-2020)—GEO-TRA-ENV-WRM: Conference Proceedings from ICRDSI-2020 Vol. 2; Das, B.B., Hettiarachchi, H., Sahu, P.K., Nanda, S., Eds.; Springer: Singapore, 2022; pp. 321–331. [Google Scholar]
- Arantes, L.T.; Carvalho, A.C.P.; Lorandi, R.; Moschini, L.E.; Di Lollo, J.A. Surface runoff associated with climate change and land use and land cover in southeast region of Brazil. Environ. Chall. 2021, 3, 100054. [Google Scholar] [CrossRef]
- Urciuoli, G.; Pirone, M. Subsurface Drainage for Slope Stabilization. In Landslide Science and Practice: Volume 6: Risk Assessment, Management and Mitigation; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 577–585. [Google Scholar]
- Popescu, M.; Commission on Landslide Remediation; International Union of Geological Sciences Working Group on Landslides. A suggested method for reporting landslide remedial measures. Bull. Eng. Geol. Environ. 2001, 60, 69–74. [Google Scholar] [CrossRef]
- Masi, E.B.; Segoni, S.; Tofani, V. Root Reinforcement in Slope Stability Models: A Review. Geosciences 2021, 11, 212. [Google Scholar] [CrossRef]
- Yang, H.-Q.; Zhang, L.; Gao, L.; Phoon, K.-K.; Wei, X. On the importance of landslide management: Insights from a 32-year database of landslide consequences and rainfall in Hong Kong. Eng. Geol. 2022, 299, 106578. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Liu, W.; Huang, J.; Hong, H.; Chen, W. Regional rainfall-induced landslide hazard warning based on landslide susceptibility mapping and a critical rainfall threshold. Geomorphology 2022, 408, 108236. [Google Scholar] [CrossRef]
- Sala, G.; Lanfranconi, C.; Frattini, P.; Rusconi, G.; Crosta, G.B. Cost-sensitive rainfall thresholds for shallow landslides. Landslides 2021, 18, 2979–2992. [Google Scholar] [CrossRef]
- Peruccacci, S.; Gariano, S.L.; Melillo, M.; Solimano, M.; Guzzetti, F.; Brunetti, M.T. The ITAlian rainfall-induced LandslIdes CAtalogue, an extensive and accurate spatio-temporal catalogue of rainfall-induced landslides in Italy. Earth Syst. Sci. Data 2023, 15, 2863–2877. [Google Scholar] [CrossRef]
- Huang, J.; Ju, N.P.; Liao, Y.J.; Liu, D.D. Determination of rainfall thresholds for shallow landslides by a probabilistic and empirical method. Nat. Hazards Earth Syst. Sci. 2015, 15, 2715–2723. [Google Scholar] [CrossRef]
- Giannecchini, R.; Galanti, Y.; D’Amato Avanzi, G. Critical rainfall thresholds for triggering shallow landslides in the Serchio River Valley (Tuscany, Italy). Nat. Hazards Earth Syst. Sci. 2012, 12, 829–842. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. Gariano, A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. 1980, 62, 23–27. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Roccati, A.; Paliaga, G.; Luino, F.; Faccini, F.; Turconi, L. Rainfall Threshold for Shallow Landslides Initiation and Analysis of Long-Term Rainfall Trends in a Mediterranean Area. Atmosphere 2020, 11, 1367. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Valentino, R.; Bittelli, M.; Vivaldi, V.; Meisina, C. Empirical and Physically Based Thresholds for the Occurrence of Shallow Landslides in a Prone Area of Northern Italian Apennines. Water 2019, 11, 2653. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Collins, B.D. Identifying Physics-Based Thresholds for Rainfall-Induced Landsliding. Geophys. Res. Lett. 2018, 45, 9651–9661. [Google Scholar] [CrossRef]
- De Vita, P.; Napolitano, E.; Godt, J.W.; Baum, R.L. Deterministic estimation of hydrological thresholds for shallow landslide initiation and slope stability models: Case study from the Somma-Vesuvius area of southern Italy. Landslides 2013, 10, 713–728. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Sosio, R. Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides. Hydrol. Process. 2009, 23, 1444–1460. [Google Scholar] [CrossRef]
- Marin, R.J. Physically based and distributed rainfall intensity and duration thresholds for shallow landslides. Landslides 2020, 17, 2907–2917. [Google Scholar] [CrossRef]
- Ma, S.; Shao, X.; Xu, C. Physically-based rainfall-induced landslide thresholds for the Tianshui area of Loess Plateau, China by TRIGRS model. CATENA 2023, 233, 107499. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. Factors controlling instability of homogeneous soil slopes under rainfall. J. Geotech. Geoenviron. Eng. 2007, 133, 1532–1543. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of hydraulic properties of soil on rainfall-induced slope failure. Eng. Geol. 2010, 114, 135–143. [Google Scholar] [CrossRef]
- Chang, W.-J.; Chou, S.-H.; Huang, H.-P.; Chao, C.-Y. Development and verification of coupled hydro-mechanical analysis for rainfall-induced shallow landslides. Eng. Geol. 2021, 293, 106337. [Google Scholar] [CrossRef]
- Gu, X.; Wang, L.; Ou, Q.; Zhang, W.; Sun, G.H. Reliability assessment of rainfall-induced slope stability using Chebyshev–Galerkin–KL expansion and Bayesian approach. Can. Geotech. J. 2023, 60, 1909–1922. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Guo, H.; NI, J.; Zhang, Q.; Chen, Z. Effects of soil–plant-biochar interactions on water retention and slope stability under various rainfall patterns. Landslides 2022, 19, 1379–1390. [Google Scholar] [CrossRef]
- Liu, H.; Feng, S.; Ng, C. Analytical analysis of hydraulic effect of vegetation on shallow slope stability with different root architectures. Comput. Geotech. 2016, 80, 115–120. [Google Scholar] [CrossRef]
- Fellenius, W. Calculation of stability of earth dam. In Transactions. 2nd Congress Large Dams; United State Gov. Print. Off.: Washington, DC, USA, 1936. [Google Scholar]
- Janbu, N. Application of composite slip surface for stability analysis. In Proceedings of the European Conference on Stability of Earth Slopes, Stockholm, Sweden, 20–25 September 1954. [Google Scholar]
- Bishop, A.W. The use of slip circle in the stability analysis of slopes. Géotechnique 1955, 5, 7–11. [Google Scholar] [CrossRef]
- Morgentern, N.; Price, V. The analysis of stability of general slip surface. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Jeremić, B. Finite Element Methods for 3D Slope Stability Analysis. In Slope Stability 2000; Griffiths, D.V., Fenton, G.A., Martin, T.R., Eds.; American Society of Civil Engineers: Denver, CO, USA, 2000; pp. 224–238. [Google Scholar]
- Zheng, H.; Liu, D.F.; Li, C.G. Slope stability analysis based on elasto-plastic finite element method. Int. J. Numer. Methods Eng. 2005, 64, 1871–1888. [Google Scholar] [CrossRef]
- Cheng, Y.; Lansivaara, T.; Wei, W. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Comput. Geotech. 2007, 34, 137–150. [Google Scholar] [CrossRef]
- Zheng, H.; Sun, G.; Liu, D. A practical procedure for searching critical slip surfaces of slopes based on the strength reduction technique. Comput. Geotech. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Liu, S.; Shao, L.; Li, H. Slope stability analysis using the limit equilibrium method and two finite element methods. Comput. Geotech. 2015, 63, 291–298. [Google Scholar] [CrossRef]
- Maji, V.B. An insight into slope stability using strength reduction technique. J. Geol. Soc. India 2017, 89, 77–81. [Google Scholar] [CrossRef]
- Liu, S.; Shao, L. Limit equilibrium conditions and stability analysis for soils. In Proceedings of the GeoShanghai International Conference, Shanghai, China, 27–30 May 2018; Springer: Singapore, 2018. [Google Scholar]
- Chen, X.; Zhang, L.; Zhang, L.; Zhou, Y.; Ye, G.; Guo, N. Modelling rainfall-induced landslides from initiation of instability to post-failure. Comput. Geotech. 2021, 129, 103877. [Google Scholar] [CrossRef]
- Li, S.; Qiu, C.; Huang, J.; Guo, X.; Hu, Y.; Mugahed, A.-S.Q.; Tan, J. Stability Analysis of a High-Steep Dump Slope under Different Rainfall Conditions. Sustainability 2022, 14, 11148. [Google Scholar] [CrossRef]
- Marin, R.J.; Velásquez, M.F. Velásquez, Influence of hydraulic properties on physically modelling slope stability and the definition of rainfall thresholds for shallow landslides. Geomorphology 2020, 351, 106976. [Google Scholar] [CrossRef]
- Bordoni, M.; Meisina, C.; Valentino, R.; Lu, N.; Bittelli, M.; Chersich, S. Hydrological factors affecting rainfall-induced shallow landslides: From the field monitoring to a simplified slope stability analysis. Eng. Geol. 2015, 193, 19–37. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 939. [Google Scholar]
- Lu, N.; Kaya, M.; Collins, B.D.; Godt, J.W. Hysteresis of unsaturated hydromechanical properties of a silty soil. J. Geotech. Geoenviron. Eng. 2013, 139, 507–510. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Oh, S.; Lu, N.; Kim, Y.K.; Lee, S.J.; Lee, S.R. Relationship between the soil-water characteristic curve and the suction stress characteristic curve: Experimental evidence from residual soils. J. Geotech. Geoenviron. Eng. 2012, 138, 47–57. [Google Scholar] [CrossRef]
- Lu, N.; Kaya, M.; Godt, J.W. Interrelations among the Soil-Water Retention, Hydraulic Conductivity, and Suction-Stress Characteristic Curves. J. Geotech. Geoenviron. Eng. 2014, 140, 04014007. [Google Scholar] [CrossRef]
- Lu, N.; Şener-Kaya, B.; Wayllace, A.; Godt, J.W. Analysis of rainfall-induced slope instability using a field of local factor of safety. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Agency of Rural Development and Soil and Water Conservation, Nantou Branch, MOA. Development and Analysis of Multi-Scale Monitoring Systems for Treatment Strategy Planning in Babaoliao Large-Scale Landslide; Agency of Rural Development and Soil and Water Conservation, Nantou Branch, MOA: Nantou, Taiwan, 2020; p. 325. (In Chinese)
- Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Wei, L.-W. Assessing shallow slope stability using electrical conductivity data and soil hydraulic characteristics. Eng. Geol. 2024, 331, 107447. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, W05515. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Lu, N.; Wayllace, A.; Godt, J. A hydro-mechanical model for predicting infiltration-induced landslides. In Proceedings of the 3 rd USGS Modeling Conference, Broomfield, Colo, 7–11 June 2010. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D software package for simulating the movement of water, heat, and multiple solutes in variably saturated media, Version 4.0. HYDRUS Softw. Ser. 2008, 3, 315. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993; Volume 2, p. 704. [Google Scholar]
- Malvern, L.E. Introduction to the Mechanics of a Continuous Medium; Prentice-Hall: Upper Saddle River, NJ, USA, 1969; p. 713. [Google Scholar]
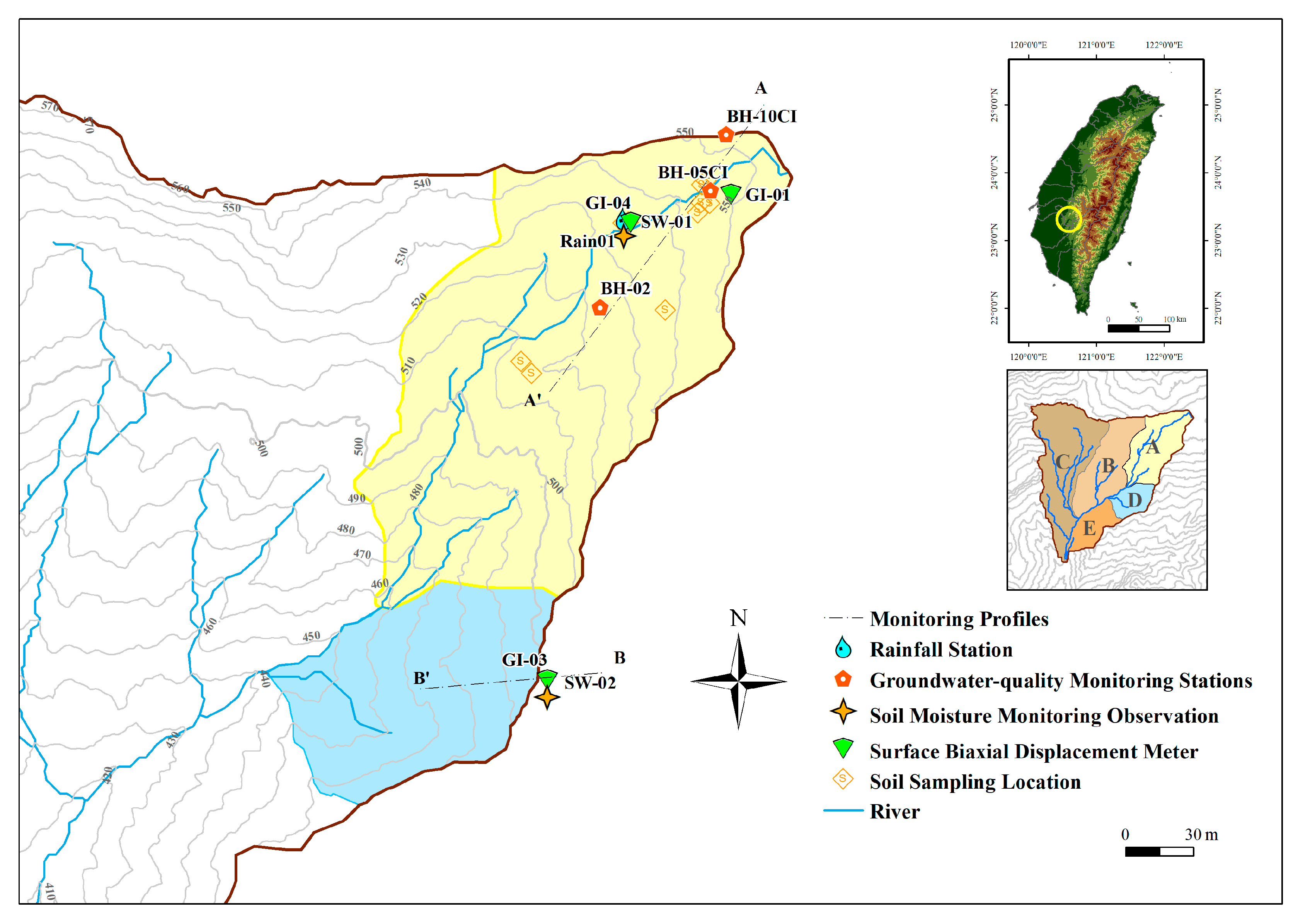
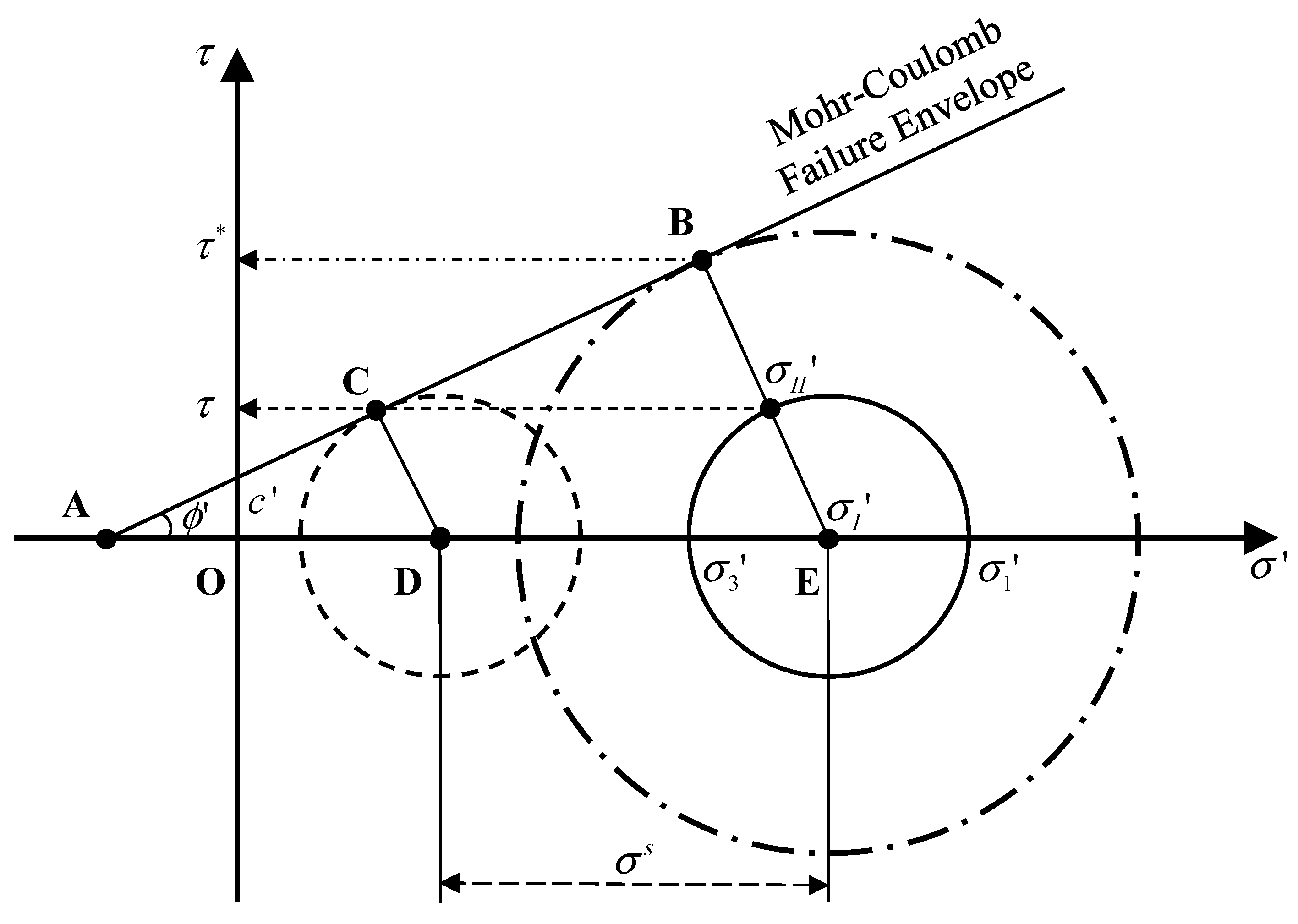

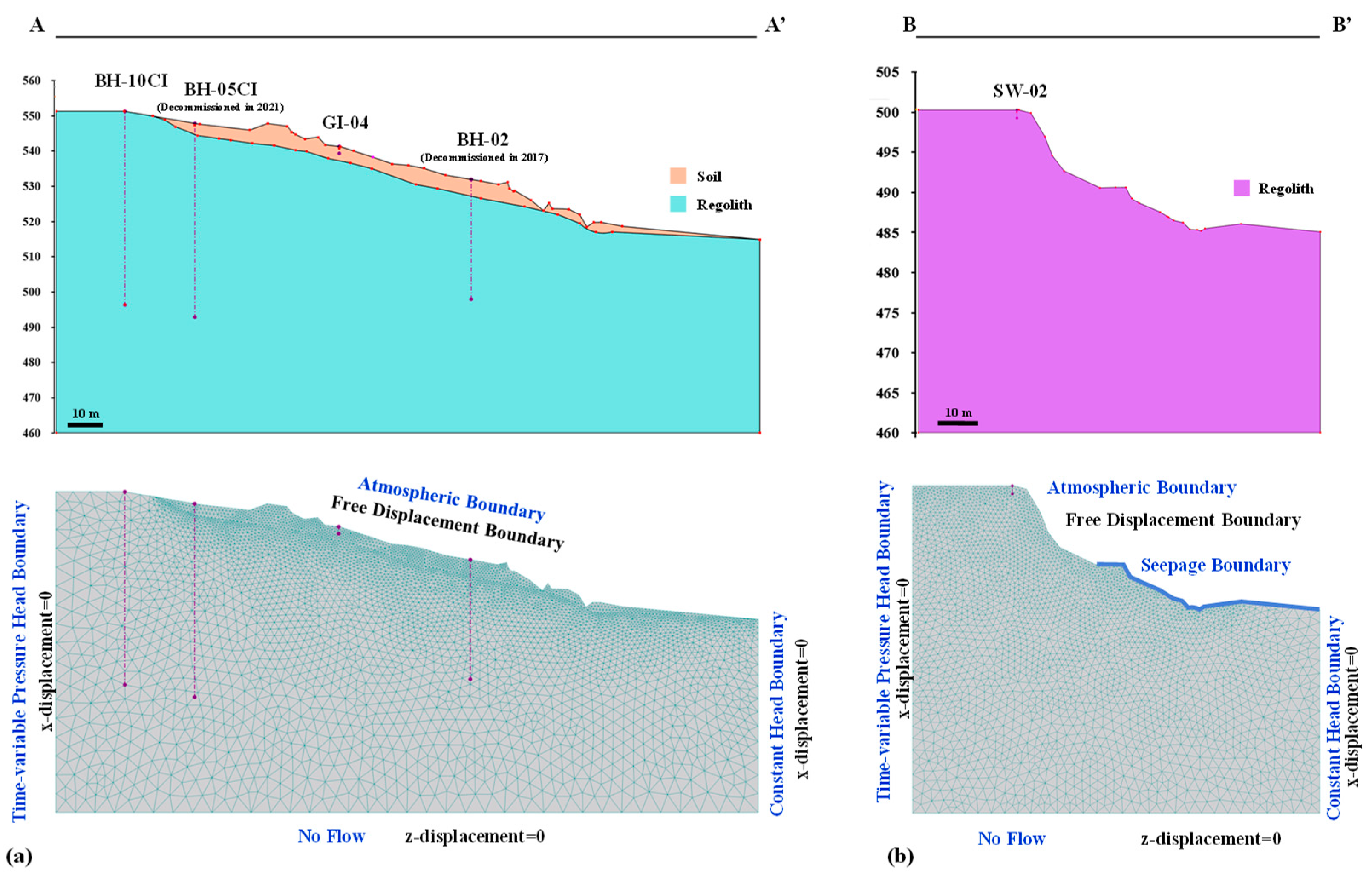
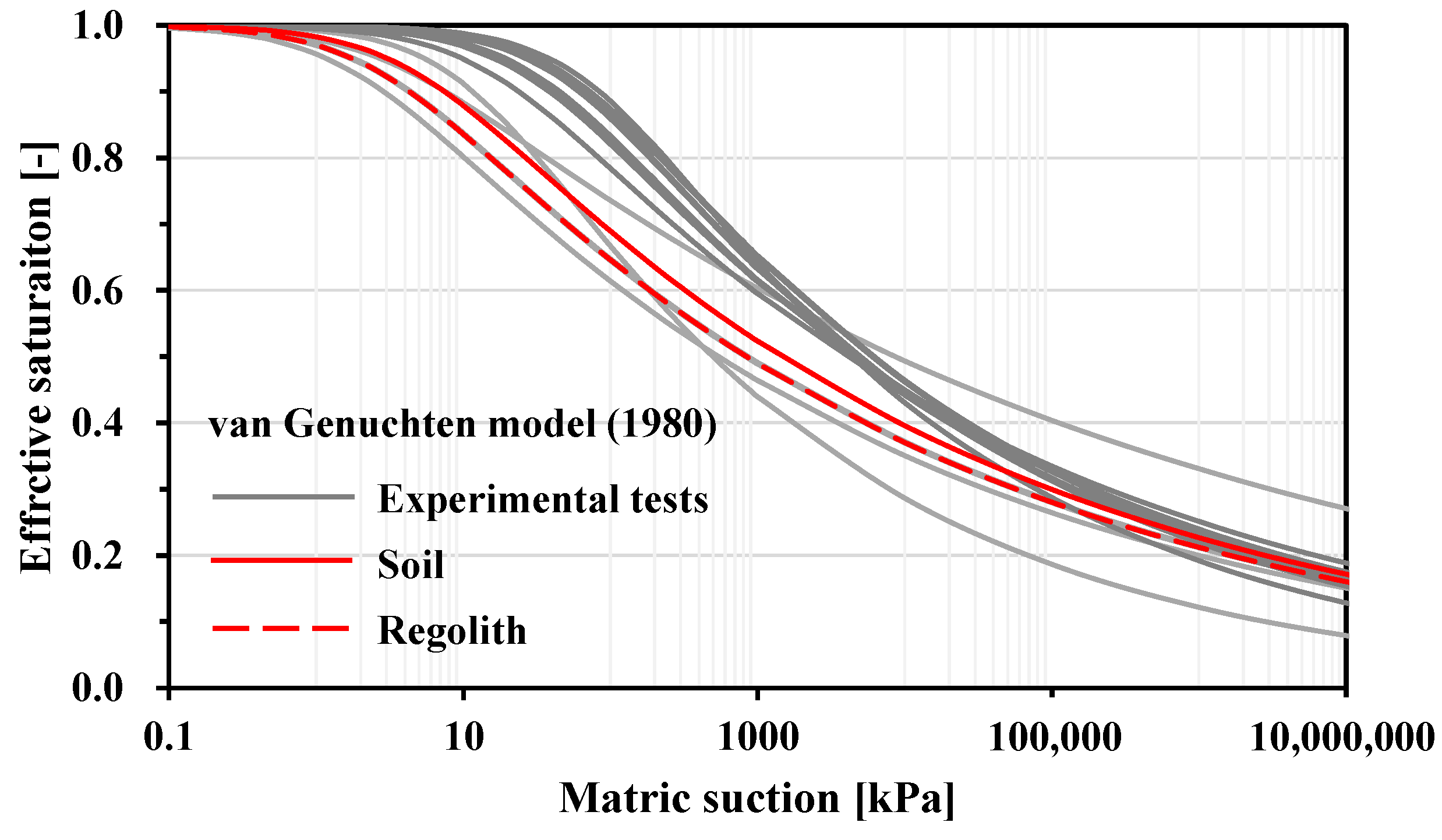
| Zone | No. | Instrument | Model | Parameter | Unit | Depth [cm] | Start Date |
|---|---|---|---|---|---|---|---|
| A | Rain 01 | Rain gauge | TK-1 Rain Gauge | Rainfall | [mm] | 0 | 23 May 2018 |
| SW-01 | Soil Moisture–Temperature–Electrical Conductivity Meter | SWTC-100 | Volumetric water content | [%] | 30, 100 | 4 June 2019 | |
| 50 | 25 March 2021 | ||||||
| Temperature | [°C] | 50 | |||||
| Electrical Conductivity | [μs/cm] | 50 | |||||
| GI-04 | Surface dual-axis inclinometer | Procal | Displacement_X | [degree] | 50 | 17 June 2020 | |
| Displacement_Y | [degree] | 50 | |||||
| D | GI-03 | Surface dual-axis inclinometer | Procal | Displacement_X | [degree] | 50 | 17 June 2020 |
| Displacement_Y | [degree] | 50 | |||||
| SW-02 | Soil Moisture–Temperature–Electrical Conductivity Meter | SWTC-100 | Volumetric water content | [%] | 50 | 25 March 2021 | |
| Temperature | [°C] | 50 | |||||
| Electrical Conductivity | [μs/cm] | 50 |
| Hydraulic Parameters | θr [-] | θs* [-] | α* [m−1] | n* [-] | Ks* [m/s] | |
| A | Soil | 10−5 | 0.49 | 0.66 | 1.17 | 10−5 |
| Regolith | 0.03 | 0.47 | 3.64 | 1.12 | 10−9 | |
| D | Regolith | 0.03 | 0.47 | 3.64 | 1.12 | 10−6 |
| Mechanical parameters | Gs [-] | c [kPa] | [°] | E [kPa] | ν [-] | |
| A | Soil | 2.72 | 17.16 | 32 | 20,000 | 0.33 |
| Regolith | 2.64 | 68.65 | 23 | 40,000 | 0.33 | |
| D | Regolith | 2.64 | 68.65 | 23 | 40,000 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.-S.; Yeh, H.-F.; Ke, C.-C.; Wei, L.-W.; Chen, N.-C. The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory. Geosciences 2024, 14, 274. https://doi.org/10.3390/geosciences14100274
Yang Y-S, Yeh H-F, Ke C-C, Wei L-W, Chen N-C. The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory. Geosciences. 2024; 14(10):274. https://doi.org/10.3390/geosciences14100274
Chicago/Turabian StyleYang, Ya-Sin, Hsin-Fu Yeh, Chien-Chung Ke, Lun-Wei Wei, and Nai-Chin Chen. 2024. "The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory" Geosciences 14, no. 10: 274. https://doi.org/10.3390/geosciences14100274
APA StyleYang, Y.-S., Yeh, H.-F., Ke, C.-C., Wei, L.-W., & Chen, N.-C. (2024). The Evaluation of Rainfall Warning Thresholds for Shallow Slope Stability Based on the Local Safety Factor Theory. Geosciences, 14(10), 274. https://doi.org/10.3390/geosciences14100274










